Infrared Absorption of Laser Patterned Sapphire Al2O3 for Radiative Cooling
Abstract
1. Introduction
2. Materials and Methods
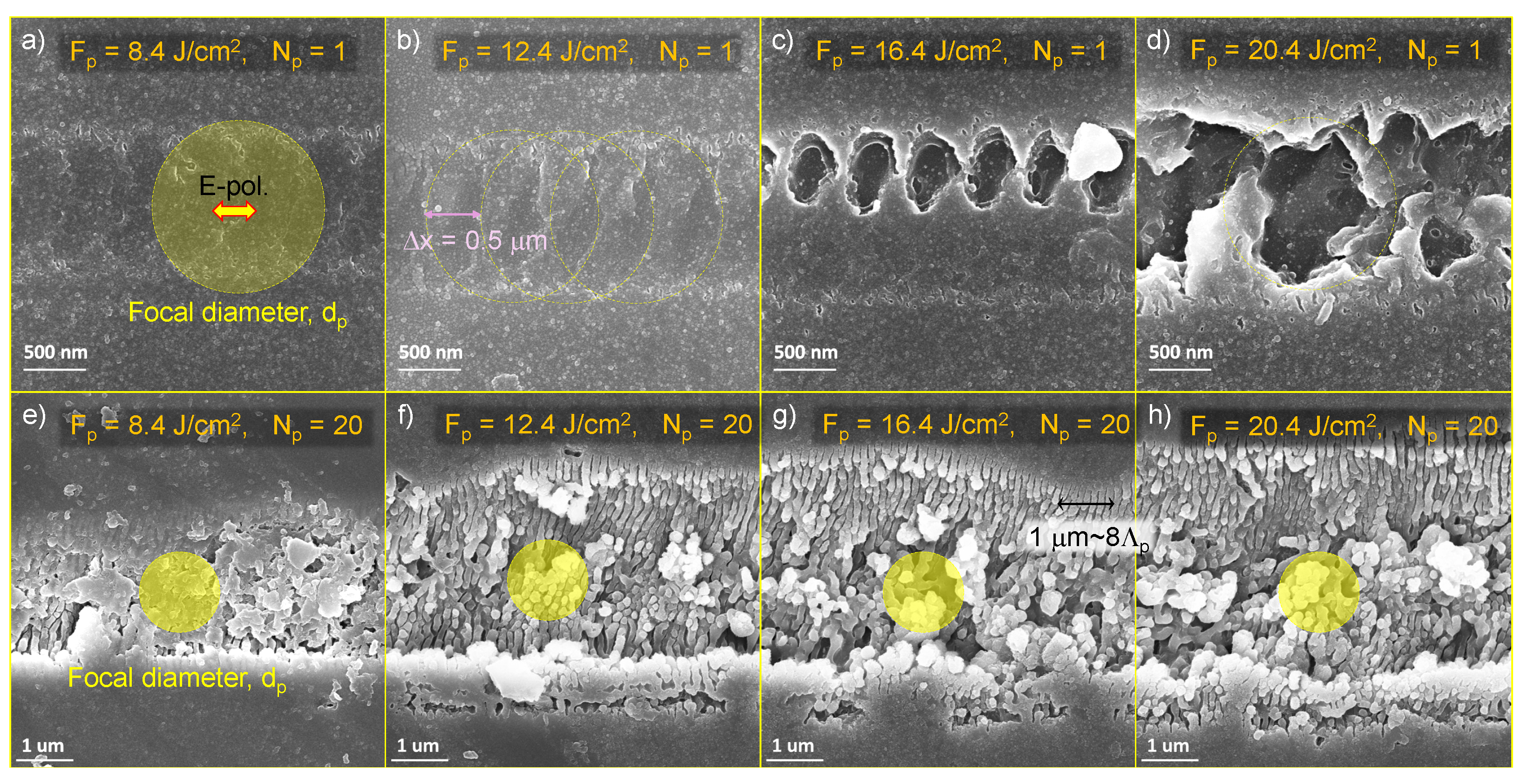
2.1. Ablation of Grooves on Sapphire with a Gaussian Beam
2.2. Structural Characterisation
2.3. Spectral Characterisation
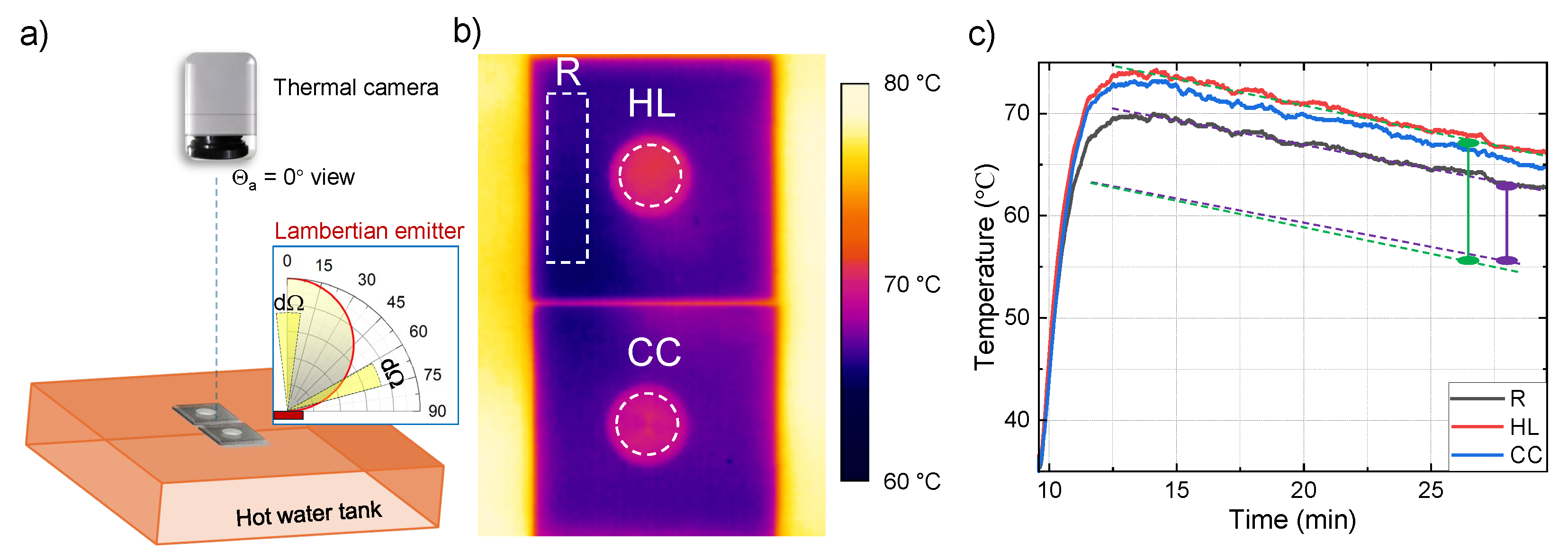
2.4. Thermal Emission
3. Results and Discussion
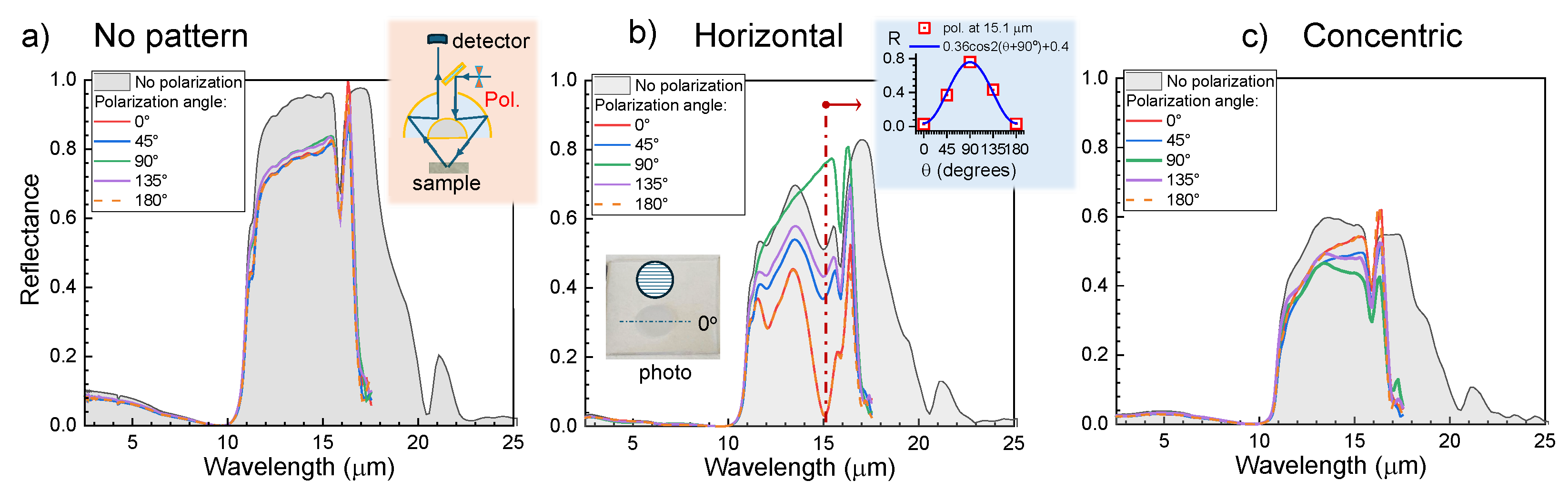
3.1. Effect of Orientation and Depth of Ablated Groves on T and R
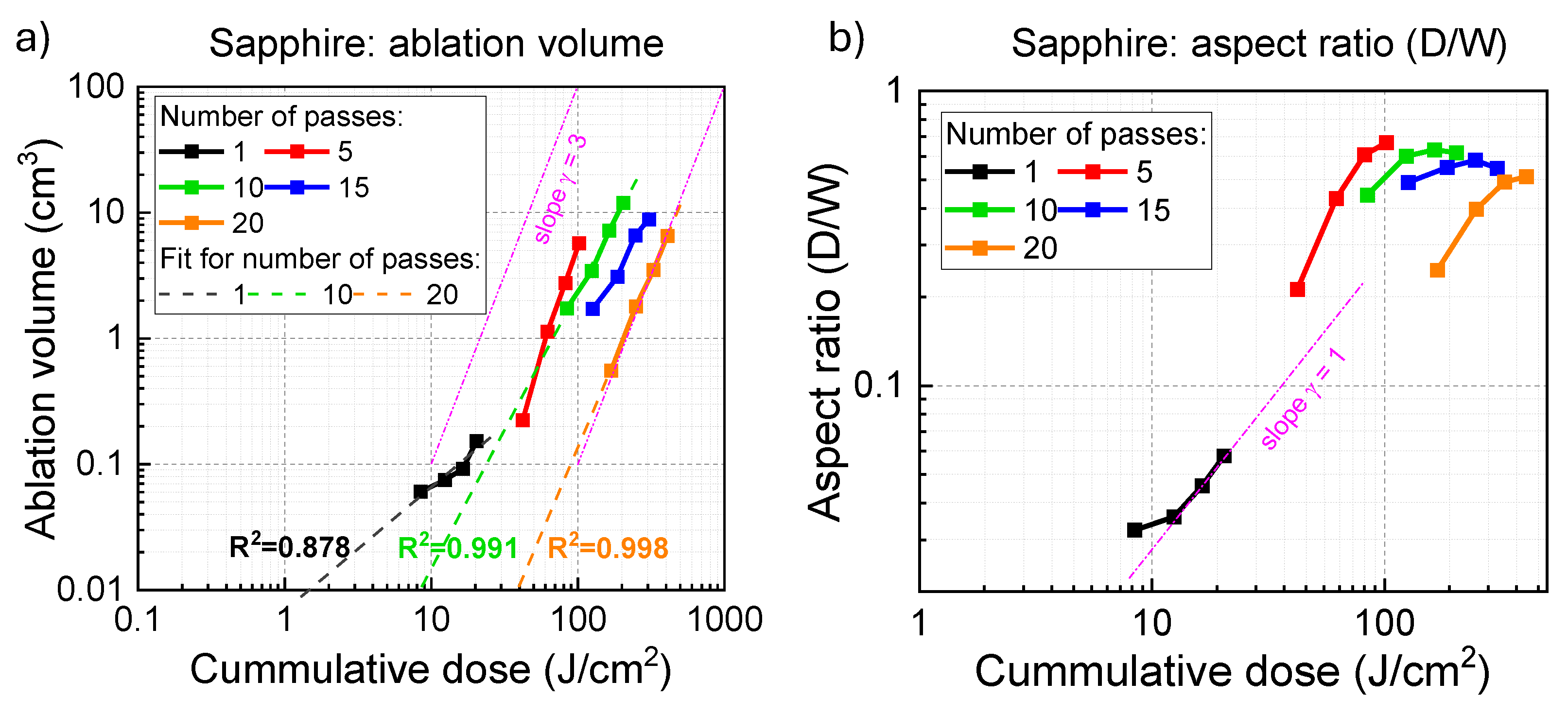
3.2. Characterisation of Back-Side Ablation: Threshold, Structure, R, and T Spectra
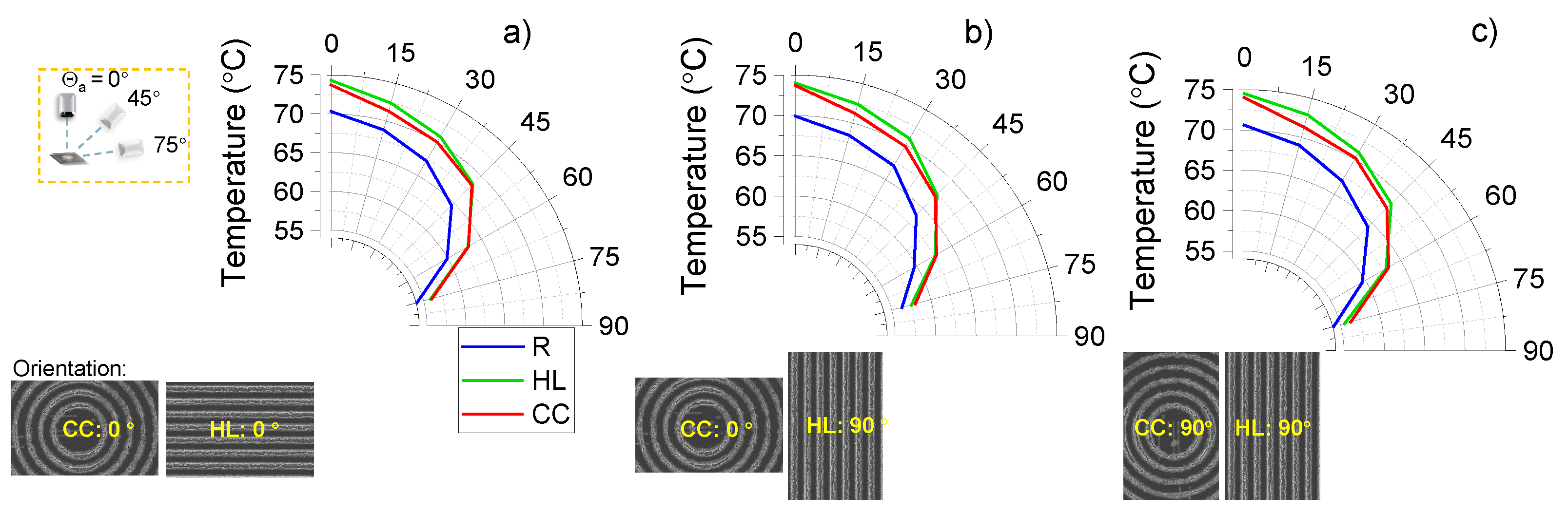
3.3. Thermal Emission and Angular Dependence
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Four Polarisation R(λ) from Linear and Circular Al2O3 Gratings
Appendix B. Keldysh Parameter
References
- Shimotsuma, Y.; Miura, K.; Kazuyuki, H. Nanomodification of Glass Using fs Laser. Int. J. Appl. Glass Sci. 2013, 4, 182–191. [Google Scholar] [CrossRef]
- Hu, J.; Xu, K.; Huang, P.; Wang, M.; Xu, S.; Wei, Q.H. Hierarchical Conical Metasurfaces as Ultra-Broadband Perfect Absorbers from Visible to Far-Infrared Regime. Adv. Funct. Mater. 2024, 34, 2309229. [Google Scholar] [CrossRef]
- Reicks, A.; Tsubaki, A.; Anderson, M.; Wieseler, J.; Khorashad, L.K.; Shield, J.E.; Gogos, G.; Alexander, D.; Argyropoulos, C.; Zuhlke, C. Near-unity broadband omnidirectional emissivity via femtosecond laser surface processing. Commun. Mater. 2021, 2, 36. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J. Femtosecond Laser-Fabricated Photonic Chips for Optical Communications: A Review. Micromachines 2022, 13, 630. [Google Scholar] [CrossRef]
- Choi, J.; Schwarz, C. Advances in femtosecond laser processing of optical material for device applications. Int. J. Appl. Glass Sci. 2020, 11, 480–490. [Google Scholar] [CrossRef]
- Nishijima, Y.; Kimura, S.; Takeshima, Y.; Juodkazis, S. Metasurfaces as Energy Valves for Sustainable Energy Management. Micromachines 2022, 13, 1769. [Google Scholar] [CrossRef]
- Jin, W.; Li, W.; Khandekar, C.; Orenstein, M.; Fan, S. Laser Cooling Assisted Thermal Management of Lightsails. ACS Photonics 2022, 9, 3384–3390. [Google Scholar] [CrossRef]
- Bonse, J.; Kirner, S.V.; Griepentrog, M.; Spaltmann, D.; Krüger, J. Femtosecond Laser Texturing of Surfaces for Tribological Applications. Materials 2018, 11, 801. [Google Scholar] [CrossRef]
- Mao, B.; Siddaiah, A.; Liao, Y.; Menezes, P.L. Laser surface texturing and related techniques for enhancing tribological performance of engineering materials: A review. J. Manuf. Process. 2020, 53, 153–173. [Google Scholar] [CrossRef]
- Bhaduri, D.; Batal, A.; Dimov, S.S.; Zhang, Z.; Dong, H.; Fallqvist, M.; M’Saoubi, R. On Design and Tribological Behaviour of Laser Textured Surfaces. Procedia CIRP 2017, 60, 20–25. [Google Scholar] [CrossRef]
- Murzin, S.P.; Balyakin, V.B.; Liedl, G.; Melnikov, A.A.; Fürbacher, R. Improving Tribological Properties of Stainless Steel Surfaces by Femtosecond Laser Irradiation. Coatings 2020, 10, 606. [Google Scholar] [CrossRef]
- Ijaola, A.O.; Bamidele, E.A.; Akisin, C.J.; Bello, I.T.; Oyatobo, A.T.; Abdulkareem, A.; Farayibi, P.K.; Asmatulu, E. Wettability Transition for Laser Textured Surfaces: A Comprehensive Review. Surf. Interfaces 2020, 21, 100802. [Google Scholar] [CrossRef]
- Yang, C.J.; Mei, X.S.; Tian, Y.L.; Zhang, D.W.; Li, Y.; Liu, X.P. Modification of wettability property of titanium by laser texturing. Int. J. Adv. Manuf. Technol. 2016, 87, 1663–1670. [Google Scholar] [CrossRef]
- Yong, J.; Chen, F.; Yang, Q.; Hou, X. Femtosecond laser controlled wettability of solid surfaces. Soft Matter 2015, 11, 8897–8906. [Google Scholar] [CrossRef]
- Bizi-Bandoki, P.; Benayoun, S.; Valette, S.; Beaugiraud, B.; Audouard, E. Modifications of roughness and wettability properties of metals induced by femtosecond laser treatment. Appl. Surf. Sci. 2011, 257, 5213–5218. [Google Scholar] [CrossRef]
- Jalil, S.A.; Lai, B.; ElKabbash, M.; Zhang, J.; Garcell, E.M.; Singh, S.; Guo, C. Spectral absorption control of femtosecond laser-treated metals and application in solar-thermal devices. Light Sci. Appl. 2016, 9, 14. [Google Scholar] [CrossRef]
- Zheng, N.; Buividas, R.; Huang, H.H.; Stonytė, D.; Palanisamy, S.; Katkus, T.; Kretkowski, M.; Stoddart, P.R.; Juodkazis, S. Laser Machining at High ∼PW/cm2 Intensity and High Throughput. Photonics 2024, 11, 598. [Google Scholar] [CrossRef]
- Juodkazis, S.; Buividas, R.; Huang, H.H.; Stonytė, D.; Palanisamy, S.; Zhu, D.M.; Katkus, T.; Kretkowski, M.; Nishijima, Y.; Grineviciute, L.; et al. Femtosecond Laser Textured Surfaces for Radiative Cooling: Black Metals. Appl. Sci. 2025, 15, 2076. [Google Scholar] [CrossRef]
- Efimov, O.; Juodkazis, S.; Misawa, H. Intrinsic single- and multiple-pulse laser-induced damage in silicate glasses in the femtosecond-to-nanosecond region. Phys. Rev. A 2004, 69, 042903. [Google Scholar] [CrossRef]
- Vanagas, E.; Kudryashov, I.; Tuzhilin, D.; Juodkazis, S.; Matsuo, S.; Misawa, H. Surface nanostructuring of borosilicate glass by femtosecond nJ energy pulses. Appl. Phys. Lett. 2003, 82, 2901–2903. [Google Scholar] [CrossRef]
- Juodkazis, S.; Rode, A.; Gamaly, E.; Matsuo, S.; Misawa, H. Recording and reading of three-dimensional optical memory in glasses. Appl. Phys. B 2003, 77, 361–368. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Q.; Long, M.; Han, R.; Cao, K.; Zhang, S.; Feng, D.; Jia, T.; Sun, Z.; Qiu, J.; et al. Femtosecond laser-induced periodic structures: Mechanisms, techniques, and applications. Opto Electron. Sci. 2022, 1, 220005. [Google Scholar] [CrossRef]
- Dharmavarapu, R.; Izumi, K.i.; Katayama, I.; Ng, S.H.; Vongsvivut, J.; Tobin, M.J.; Kuchmizhak, A.; Nishijima, Y.; Bhattacharya, S.; Juodkazis, S. Dielectric cross-shaped-resonator-based metasurface for vortex beam generation at mid-IR and THz wavelengths. Nanophotonics 2019, 8, 1263–1270. [Google Scholar] [CrossRef]
- Mastellone, M.; Bolli, E.; Valentini, V.; Bellucci, A.; Orlando, S.; Santagata, A.; Polini, R.; Lettino, A.; Sani, E.; Trucchi, D. Two-dimensional periodic surface nanotexturing of 6H-SiC by ultrashort laser pulses. Surf. Interfaces 2024, 46, 104006. [Google Scholar] [CrossRef]
- Santagata, A.; Pace, M.L.; Bellucci, A.; Mastellone, M.; Bolli, E.; Valentini, V.; Orlando, S.; Sani, E.; Failla, S.; Sciti, D.; et al. Enhanced and Selective Absorption of Molybdenum Nanostructured Surfaces for Concentrated Solar Energy Applications. Materials 2022, 15, 8333. [Google Scholar] [CrossRef]
- Cappelli, E.; Orlando, S.; Sciti, D.; Bellucci, A.; Lettino, A.; Trucchi, D.M. Improving solar radiation absorbance of high refractory sintered ceramics by fs Ti:sapphire laser surface treatment. Appl. Surf. Sci. 2014, 302, 177–183. [Google Scholar] [CrossRef]
- Sciti, D.; Trucchi, D.M.; Bellucci, A.; Orlando, S.; Zoli, L.; Sani, E. Effect of surface texturing by femtosecond laser on tantalum carbide ceramics for solar receiver applications. Sol. Energy Mater. Sol. Cells 2017, 161, 1–6. [Google Scholar] [CrossRef]
- Sani, E.; Sciti, D.; Silvestroni, L.; Bellucci, A.; Orlando, S.; Trucchi, D.M. Tailoring optical properties of surfaces in wide spectral ranges by multi-scale femtosecond-laser texturing: A case-study for TaB2 ceramics. Opt. Mater. 2020, 109, 110347. [Google Scholar] [CrossRef]
- Lee, S.; Yang, D.; Nikumb, S. Femtosecond laser micromilling of Si wafers. Appl. Surf. Sci. 2008, 254, 2996–3005. [Google Scholar] [CrossRef]
- Baranov, D.G.; Xiao, Y.; Nechepurenko, I.A.; Krasnok, A.; Alù, A.; Kats, M.A. Nanophotonic engineering of far-field thermal emitters. Nat. Mater. 2019, 18, 920–930. [Google Scholar] [CrossRef]
- Sergeeva, K.A.; Pavlov, D.V.; Seredin, A.A.; Mitsai, E.V.; Sergeev, A.A.; Modin, E.B.; Sokolova, A.V.; Lau, T.C.; Baryshnikova, K.V.; Petrov, M.I.; et al. Laser-Printed Plasmonic Metasurface Supporting Bound States in the Continuum Enhances and Shapes Infrared Spontaneous Emission of Coupled HgTe Quantum Dots. Adv. Funct. Mater. 2023, 33, 2307660. [Google Scholar] [CrossRef]
- Engelbrecht, J.A.A.; van Rooyen, I.J.; Henry, A.; Janzén, E.; Olivier, E.J. The origin of a peak in the reststrahlen region of SiC. Phys. B Condens. Matter 2012, 407, 1525–1528. [Google Scholar] [CrossRef]
- Kumar, A.; Chowdhury, A. Reassessment of different antireflection coatings for crystalline silicon solar cell in view of their passive radiative cooling properties. Sol. Energy 2019, 183, 410–418. [Google Scholar] [CrossRef]
- Tu, Y.; Tan, X.; Yang, X.; Qi, G.; Yan, K.; Kang, Z. Antireflection and radiative cooling difunctional coating design for silicon solar cells. Opt. Express 2023, 31, 22296–22307. [Google Scholar] [CrossRef]
- Lee, K.; Park, J.; Seo, K. Neutral-colored transparent solar cells with radiative cooling and wide-angle anti-reflection. Cell Rep. Phys. Sci. 2023, 4, 101744. [Google Scholar] [CrossRef]
- Long, L.; Yang, Y.; Wang, L. Simultaneously enhanced solar absorption and radiative cooling with thin silica micro-grating coatings for silicon solar cells. Sol. Energy Mater. Sol. Cells 2019, 197, 19–24. [Google Scholar] [CrossRef]
- Schubert, M.; Tiwald, T.E.; Herzinger, C.M. Infrared dielectric anisotropy and phonon modes of sapphire. Phys. Rev. B 2000, 61, 8187–8201. [Google Scholar] [CrossRef]
- Streyer, W.H. Reststrahlen Band Optics for the Advancement of Far-Infrared Optical Architecture. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2016. [Google Scholar]
- Lee, S.C.; Ng, S.S.; Abu Hassan, H.; Hassan, Z.; Dumelow, T. Crystal orientation dependence of polarized infrared reflectance response of hexagonal sapphire crystal. Opt. Mater. 2014, 37, 773–779. [Google Scholar] [CrossRef]
- Greffet, J.J.; Carminati, R.; Joulain, K.; Mulet, J.P.; Mainguy, S.; Chen, Y. Coherent emission of light by thermal sources. Nature 2002, 416, 61–64. [Google Scholar] [CrossRef]
- Wolf, E. Non-cosmological redshifts of spectral lines. Nature 1987, 326, 363–365. [Google Scholar] [CrossRef]
- Wolf, E.; James, D.F.V. Correlation-induced spectral changes. Rep. Prog. Phys. 1996, 59, 771. [Google Scholar] [CrossRef]
- Wang, X.W.; Seniutinas, G.; Balcytis, A.; Kasalynas, I.; Jakstas, V.; Janonis, V.; Venckevicius, R.; Buividas, R.; Appadoo, D.; Valusis, G.; et al. Laser structuring for control of coupling between THz light and phonon modes. arXiv 2016, arXiv:1605.04493. [Google Scholar]
- Takayama, N.; Asaka, S.; Yan, J. Nanosecond pulsed laser irradiation of sapphire for developing microstructures with deep V-shaped grooves. Precis. Eng. 2018, 52, 440–450. [Google Scholar] [CrossRef]
- Chang, C.W.; Chen, C.Y.; Chang, T.L.; Ting, C.J.; Wang, C.P.; Chou, C.P. Sapphire surface patterning using femtosecond laser micromachining. Appl. Phys. A 2018, 109, 441–448. [Google Scholar] [CrossRef]
- Stern, L.; Grajower, M.; Levy, U. Fano resonances and all-optical switching in a resonantly coupled plasmonic–atomic system. Nat. Commun. 2014, 5, 4865. [Google Scholar] [CrossRef]
- Rybin, M.V.; Samusev, K.B.; Sinev, I.S.; Semouchkin, G.; Semouchkina, E.; Kivshar, Y.S.; Limonov, M.F. Mie scattering as a cascade of Fano resonances. Opt. Express 2013, 21, 30107–30113. [Google Scholar] [CrossRef]
- Grineviciute, L.; Lukosiunas, I.; Nikitina, J.; Selskis, A.; Meskelaite, I.; Gailevicius, D.; Staliunas, K. Light Trapping by Non-Hermitian Thin Films. arXiv 2024, arXiv:2410.15101. [Google Scholar]
- Grineviciute, L.; Nikitina, J.; Babayigit, C.; Staliunas, K. Fano-like resonances in nanostructured thin films for spatial filtering. Appl. Phys. Lett. 2021, 118, 131114. [Google Scholar] [CrossRef]
- Hua, J.G.; Ren, H.; Huang, J.; Luan, M.L.; Chen, Q.D.; Juodkazis, S.; Sun, H.B. Laser-Induced Cavitation-Assisted True 3D Nano-Sculpturing of Hard Materials. Small 2023, 19, 2207968. [Google Scholar] [CrossRef]
- Beyer, S.; Tornari, V.; Gornicki, D. Comparison of Laser Induced Front- and Rear-Side Ablation. In Proceedings of the Fourth International Symposium on Laser Precision Microfabrication, Munich, Germany, 21–24 June 2003; SPIE: Bellingham, WA, USA, 2003; Volume 5063, pp. 202–207. [Google Scholar] [CrossRef]
- Liu, X.Q.; Zhang, Y.L.; Li, Q.K.; Zheng, J.X.; Lu, Y.M.; Juodkazis, S.; Chen, Q.D.; Sun, H.B. Biomimetic sapphire windows enabled by inside-out femtosecond laser deep-scribing. PhotoniX 2022, 3, 1. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, F.; Wang, C.; Duan, J. Broadband antireflective subwavelength structures for infrared detection. Opt. Laser Technol. 2022, 149, 107931. [Google Scholar] [CrossRef]
- Raguin, D.H.; Morris, G.M. Antireflection structured surfaces for the infrared spectral region. Appl. Opt. 1993, 32, 1154–1167. [Google Scholar] [CrossRef] [PubMed]
- Honsberg, C.; Bowden, S. Absorption Coefficient. 2019. Available online: https://www.pveducation.org/pvcdrom/design-of-silicon-cells/anti-reflection-coatings (accessed on 15 January 2025).
- Temnov, V.V.; Sokolowski-Tinten, K.; Zhou, P.; El-Khamhawy, A.; von der Linde, D. Multiphoton Ionization in Dielectrics: Comparison of Circular and Linear Polarization. Phys. Rev. Lett. 2006, 97, 237403. [Google Scholar] [CrossRef] [PubMed]
- Gamaly, E.G.; Rode, A.V.; Luther-Davies, B.; Tikhonchuk, V.T. Ablation of solids by femtosecond lasers: Ablation mechanism and ablation thresholds for metals and dielectrics. Phys. Plasmas 2002, 9, 949–957. [Google Scholar] [CrossRef]
- Castelletto, S.; Maksimovic, J.; Katkus, T.; Ohshima, T.; Johnson, B.C.; Juodkazis, S. Color Centers Enabled by Direct Femto-Second Laser Writing in Wide Bandgap Semiconductors. Nanomaterials 2021, 11, 72. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, K.; Zhou, Y.; Wang, H.; Zhang, C.; Zhang, X.C. High-power THz to IR emission by femtosecond laser irradiation of random 2D metallic nanostructures. Sci. Rep. 2015, 5, 12536. [Google Scholar] [CrossRef]
- Palanza, V.; Di Martino, D.; Paleari, A.; Spinolo, G.; Prosperi, L. Micro-Raman spectroscopy applied to the study of inclusions within sapphire. J. Raman Spectrosc. 2008, 39, 1007–1011. [Google Scholar] [CrossRef]
- Planck, M.; Masius, M. The Theory of Heat Radiation; P. Blakiston’s Son & Co.: Philadelphia, PA, USA, 1914; pp. 1–3, 14–16, 40–42. [Google Scholar]
- Dao, T.D.; Ishii, S.; Doan, A.T.; Wada, Y.; Ohi, A.; Nabatame, T.; Nagao, T. An On-Chip Quad-Wavelength Pyroelectric Sensor for Spectroscopic Infrared Sensing. Adv. Sci. 2019, 6, 1900579. [Google Scholar] [CrossRef]
- Linklater, D.; Vailionis, A.; Ryu, M.; Kamegaki, S.; Morikawa, J.; Mu, H.; Smith, D.; Maasoumi, P.; Ford, R.; Katkus, T.; et al. Structure and Optical Anisotropy of Spider Scales and Silk: The Use of Chromaticity and Azimuth Colors to Optically Characterize Complex Biological Structures. Nanomaterials 2023, 13, 1894. [Google Scholar] [CrossRef]
- Li, Z.; Yin, Y. Stimuli-Responsive Optical Nanomaterials. Adv. Mater. 2019, 31, 1807061. [Google Scholar] [CrossRef]
- Zonov, R.; Fateev, A.; Obraztsov, A.; Mikheev, G. Wavelength-Dependent Photocurrent Generation Efficiency in the Carbon Nanowall Films. Phys. Status Solidi B 2023, 260, 2200540. [Google Scholar] [CrossRef]
- Hikima, Y.; Morikawa, J.; Hashimoto, T. FT-IR Image Processing Algorithms for In-Plane Orientation Function and Azimuth Angle of Uniaxially Drawn Polyethylene Composite Film. Macromolecules 2011, 44, 3950–3957. [Google Scholar] [CrossRef]
- Meguya, R.; Hock Ng, S.; Han, M.; Anand, V.; Katkus, T.; Vongsvivut, J.; Appadoo, D.; Nishijima, Y.; Juodkazis, S.; Morikawa, J. Polariscopy with optical near-fields. Nanoscale Horizons 2022, 7, 1047–1053. [Google Scholar] [CrossRef] [PubMed]
- Eliseev, P.G.; Krokhin, O.N.; Zavestovskaya, I.N. Nonlinear absorption mechanism in ablation of transparent materials by high power and ultrashort laser pulses. Appl. Surf. Sci. 2005, 248, 313–315. [Google Scholar] [CrossRef]
- Ng, S.H.; Han, M.; Hyde, L.; Durandet, Y.; Katkus, T.; Zaccaria, R.P.; Juodkazis, S. High Intensity Laser Applications: Space Prospective. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 2670–2677, ISSN 1559-9450. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Juodkazis, S.; Nishimura, K.; Misawa, H.; Luther-Davies, B.; Hallo, L.; Nicolai, P.; Tikhonchuk, V.T. Laser-matter interaction in the bulk of a transparent solid: Confined microexplosion and void formation. Phys. Rev. B Condensed Matter Mater. Phys. 2006, 73, 214101. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, N.; Smith, D.; Ng, S.H.; Huang, H.-H.; Stonytė, D.; Appadoo, D.; Vongsvivut, J.; Katkus, T.; Le, N.H.A.; Mu, H.; et al. Infrared Absorption of Laser Patterned Sapphire Al2O3 for Radiative Cooling. Micromachines 2025, 16, 476. https://doi.org/10.3390/mi16040476
Zheng N, Smith D, Ng SH, Huang H-H, Stonytė D, Appadoo D, Vongsvivut J, Katkus T, Le NHA, Mu H, et al. Infrared Absorption of Laser Patterned Sapphire Al2O3 for Radiative Cooling. Micromachines. 2025; 16(4):476. https://doi.org/10.3390/mi16040476
Chicago/Turabian StyleZheng, Nan, Daniel Smith, Soon Hock Ng, Hsin-Hui Huang, Dominyka Stonytė, Dominique Appadoo, Jitraporn Vongsvivut, Tomas Katkus, Nguyen Hoai An Le, Haoran Mu, and et al. 2025. "Infrared Absorption of Laser Patterned Sapphire Al2O3 for Radiative Cooling" Micromachines 16, no. 4: 476. https://doi.org/10.3390/mi16040476
APA StyleZheng, N., Smith, D., Ng, S. H., Huang, H.-H., Stonytė, D., Appadoo, D., Vongsvivut, J., Katkus, T., Le, N. H. A., Mu, H., Nishijima, Y., Grineviciute, L., & Juodkazis, S. (2025). Infrared Absorption of Laser Patterned Sapphire Al2O3 for Radiative Cooling. Micromachines, 16(4), 476. https://doi.org/10.3390/mi16040476








