A Programmable Hybrid Energy Harvester: Leveraging Buckling and Magnetic Multistability
Abstract
1. Introduction
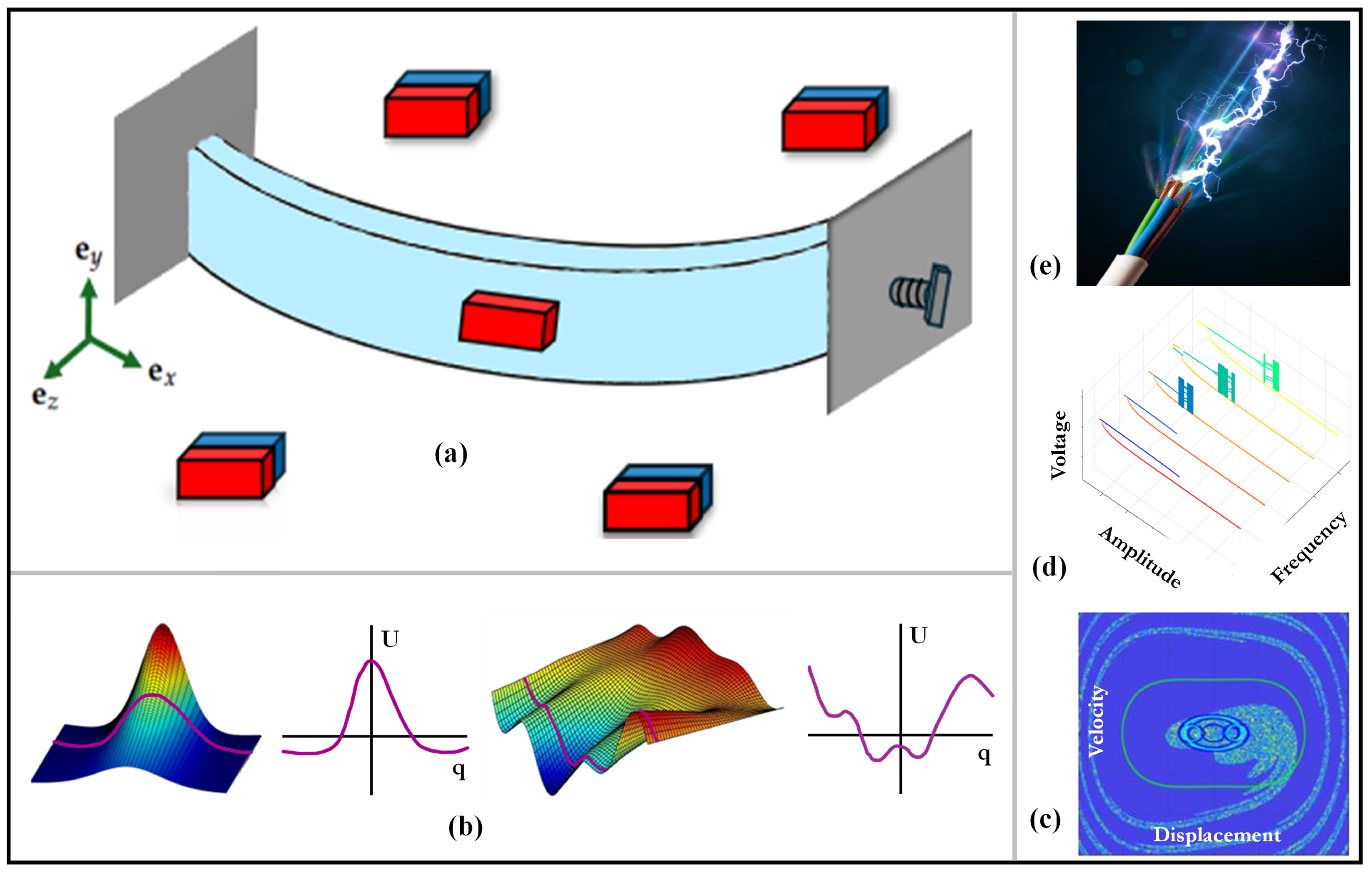
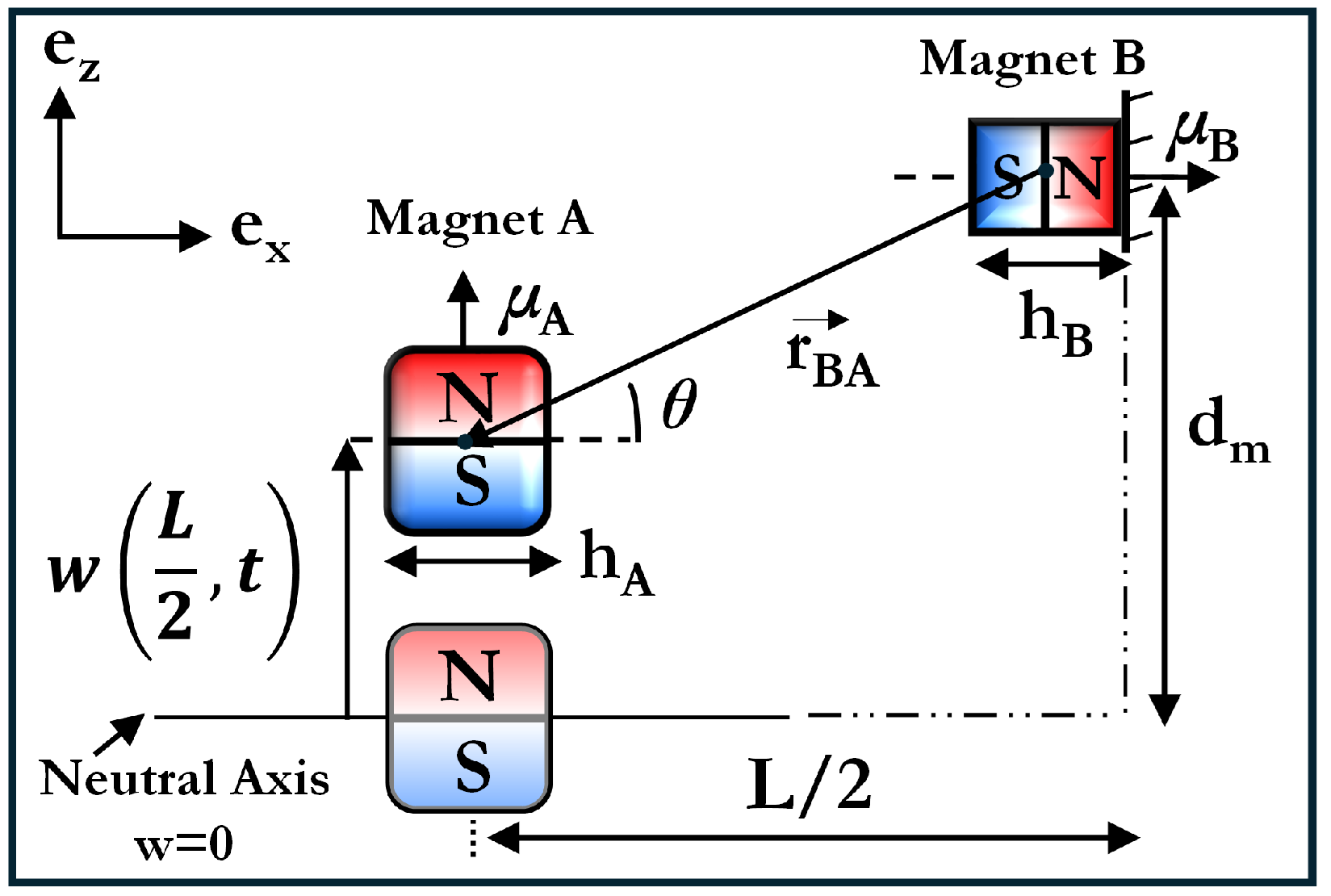
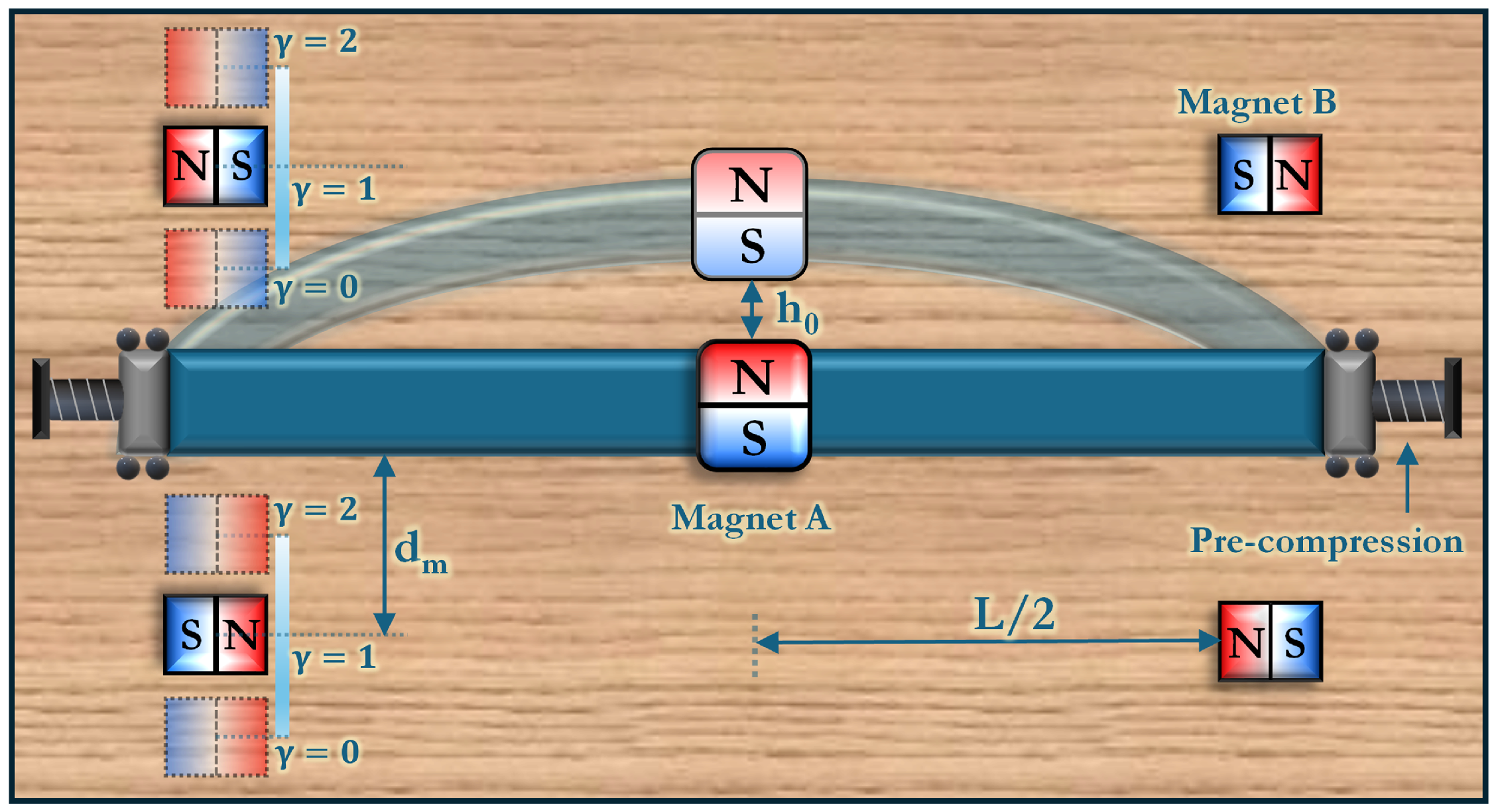
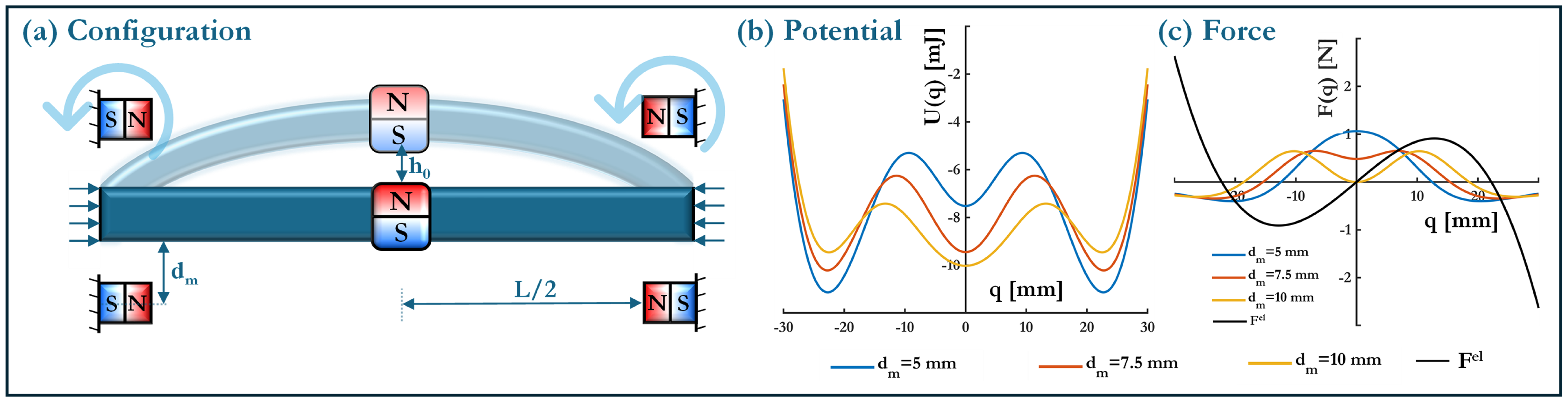
2. Configuration and Key Concepts
3. Mathematical Formulation and Governing Equations
3.1. Elastic Potential Energy and Force
3.2. Magnetic Potential Energy and Force
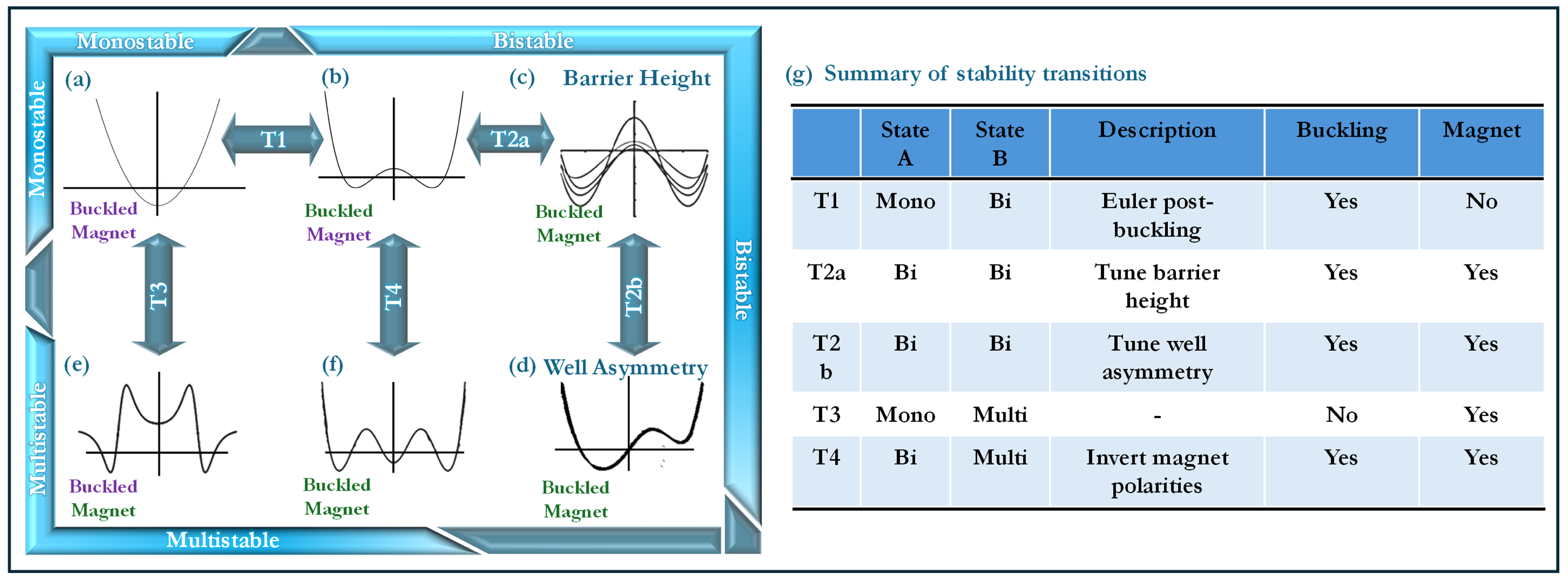
4. Results and Discussion
- Buckling-induced bistability (T1): where an initially monostable system transitions to a bistable configuration.
- Magnetically induced multistability (T3): enabling additional equilibrium states beyond classical buckling effects.
- Magnet-assisted potential well tuning (T2a, T2b, T4): allowing precise control over well depth and barrier height.
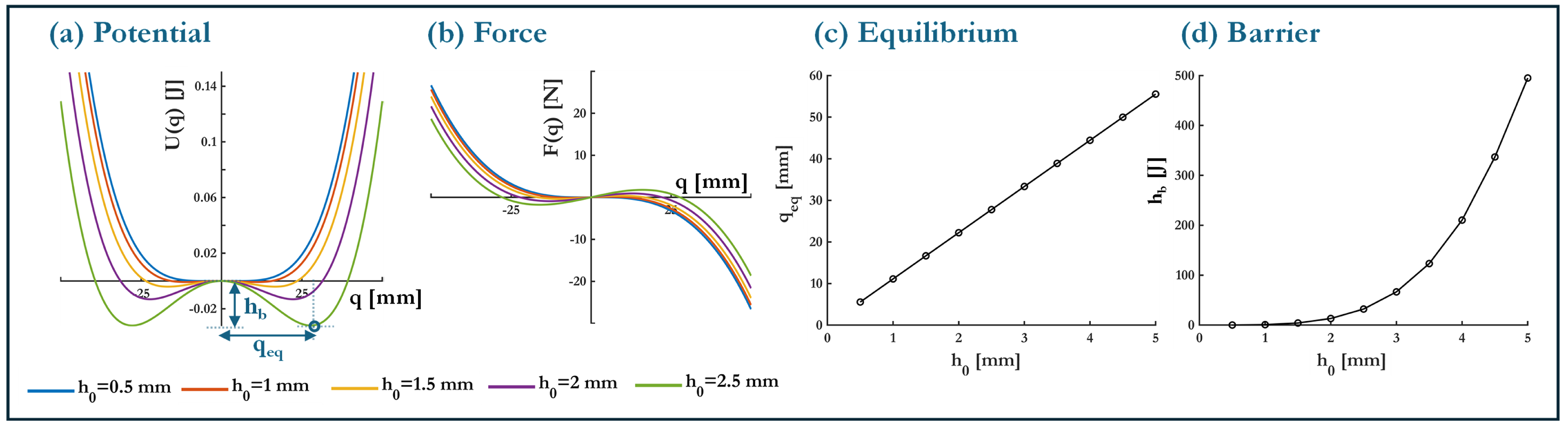
4.1. T1: Monostable to Bistable
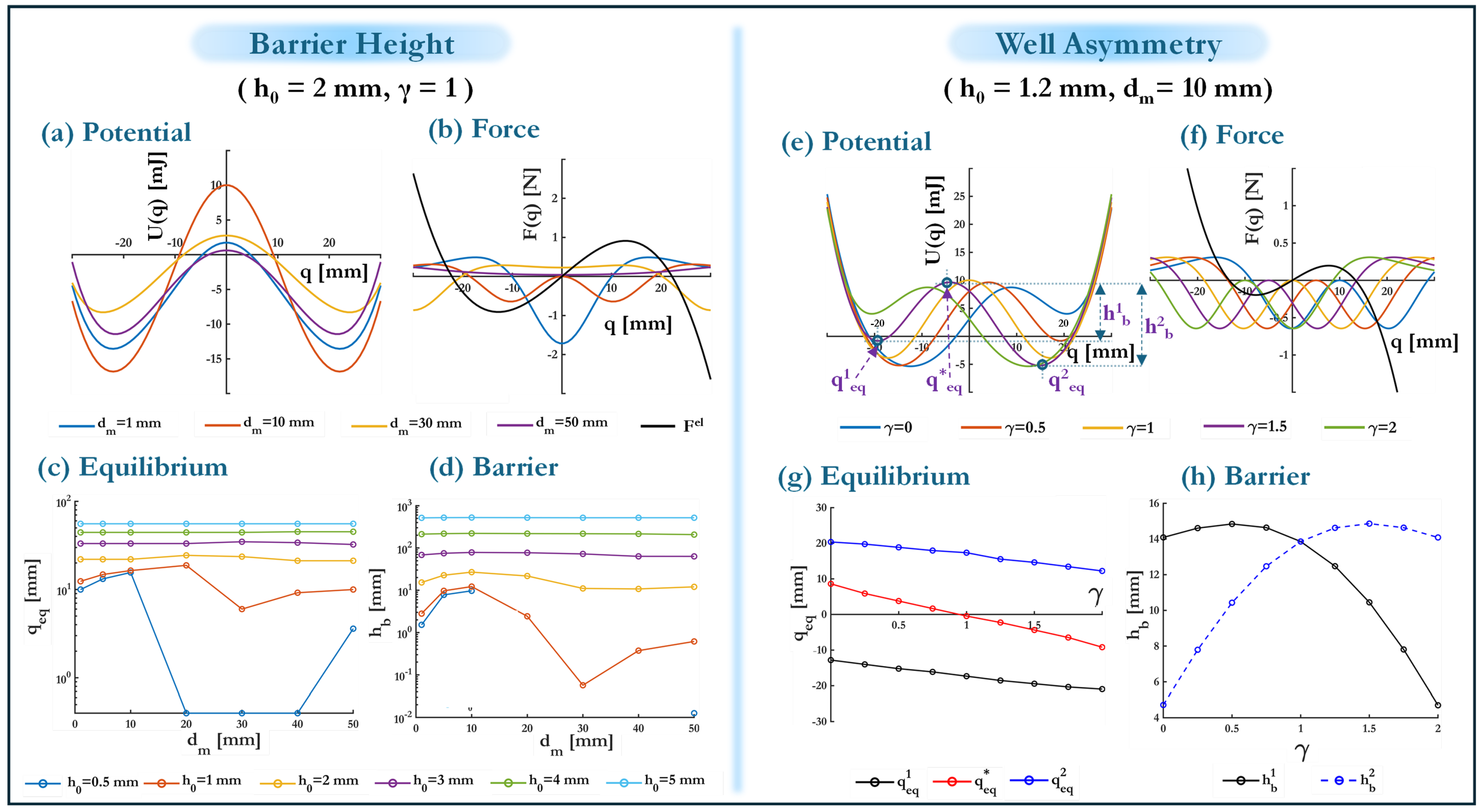
4.2. T2a: Bistable—Tuning the Potential Barrier Height via Magnetic Loading
4.3. T2b: Bistable—Introducing Well Asymmetry for Enhanced Energy Harvesting
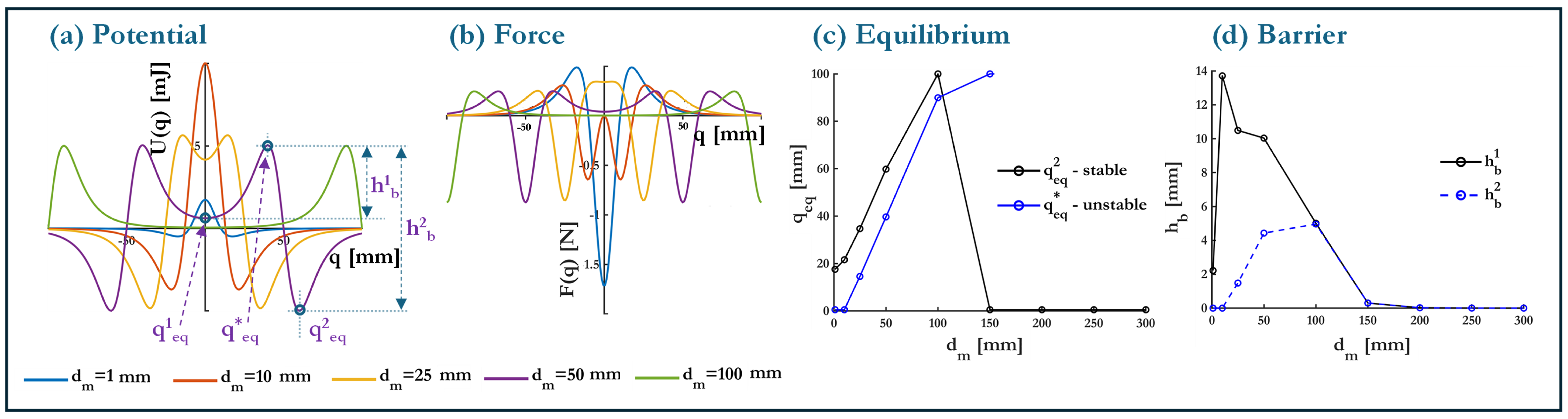
4.4. T3: Monostable to Multistable
4.5. T4: Bistable to Multistable
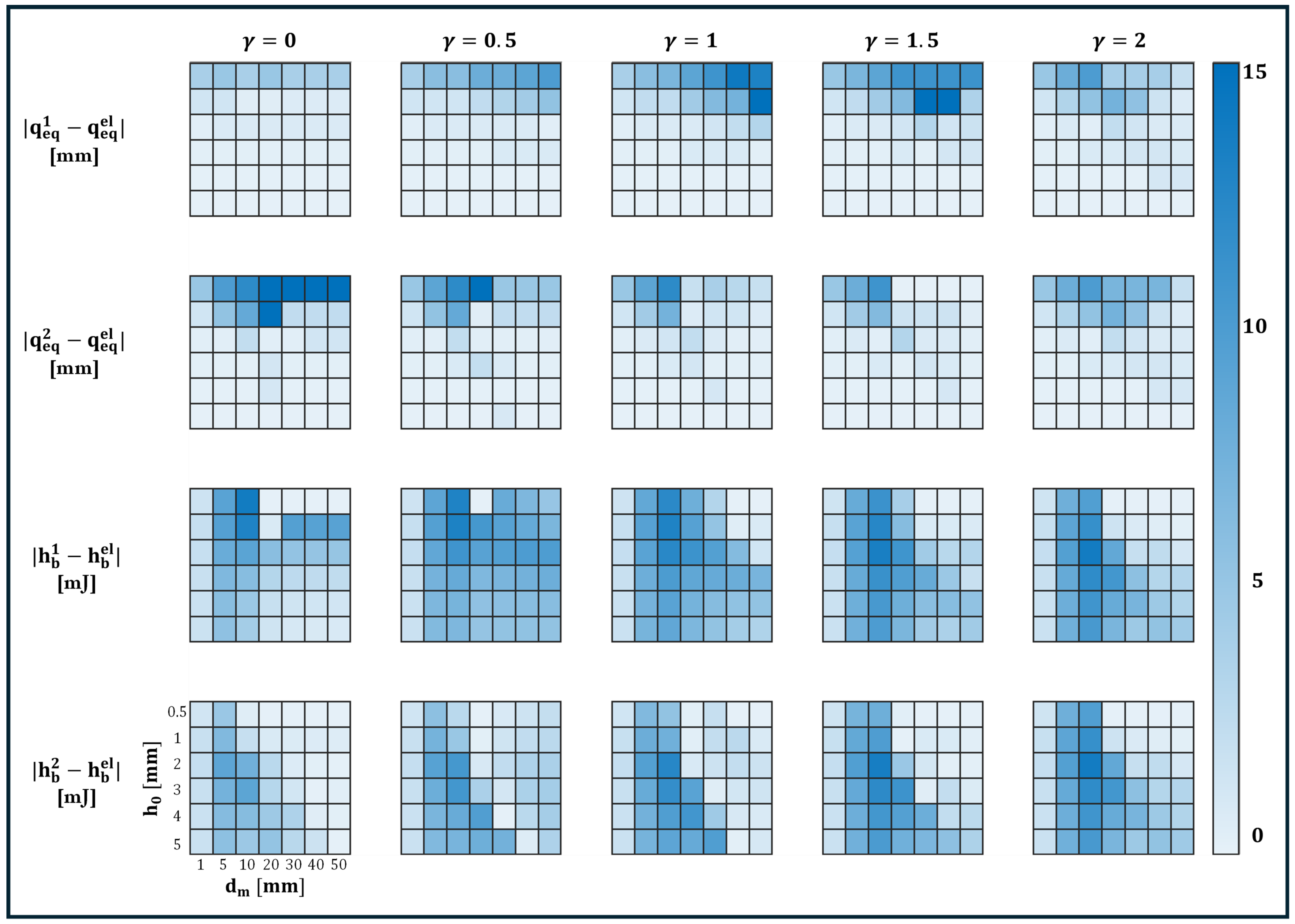
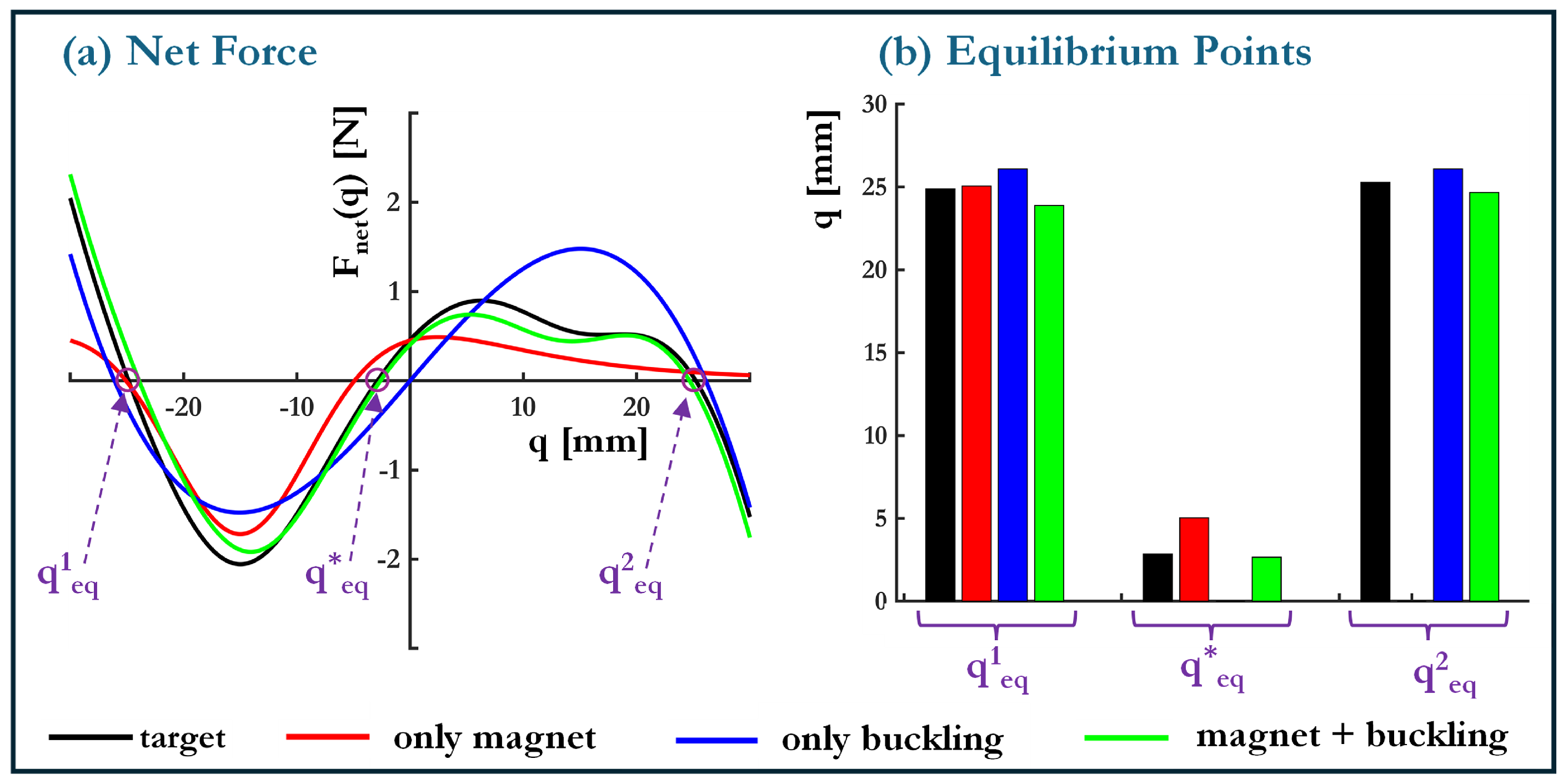
4.6. Inverse Design for Optimizing Force-Displacement Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, D.; Tudor, M.J.; Beeby, S.P. Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas. Sci. Technol. 2012, 21, 022001. [Google Scholar]
- Huguet, T.; Erturk, A. Drastic bandwidth enhancement in nonlinear MEMS electrostatic energy harvesting using bistability and internal resonance. Appl. Phys. Lett. 2018, 113, 203901. [Google Scholar]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Bistable electromagnetic vibration energy harvesters. Smart Mater. Struct. 2014, 23, 025029. [Google Scholar]
- Derakhshani, M.; Hajj, M.R. Analytical and experimental investigation of a bistable piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2021, 32, 3–15. [Google Scholar]
- Pan, C.; Zhang, Y.; Wang, J. Design and optimization of bistable energy harvesters using laser-machined beams. J. Micromech. Microeng. 2025, 35, 015003. [Google Scholar]
- Betts, D.N.; Beeby, S.P.; White, N.M. Static and dynamic analysis of a bistable energy harvester. J. Phys. Conf. Ser. 2012, 476, 012123. [Google Scholar]
- Ando, B.; Baglio, S.; Pistorio, A. Bistable piezoelectric energy harvester for low-frequency vibrations. IEEE Trans. Instrum. Meas. 2014, 63, 1241–1248. [Google Scholar]
- Nan, Z.; Wang, Y.; Li, X. Bistable piezoelectric energy harvester with torsion mechanism for low-frequency vibrations. Mech. Syst. Signal Process. 2021, 150, 107278. [Google Scholar]
- Chen, L.; Liu, J.; Zhang, X. Vibration energy harvesting using double-negative metamaterial structures. Smart Mater. Struct. 2024, 33, 035001. [Google Scholar]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Shahruz, S.M. Increasing the efficiency of vibration energy harvesters by using magnetic forces. J. Sound Vib. 2008, 315, 593–602. [Google Scholar]
- Zhou, S.; Cao, J.; Inman, D.J. Nonlinear energy harvesting from broadband random vibrations using a magnetopiezoelastic system. Appl. Phys. Lett. 2019, 115, 043902. [Google Scholar]
- Cao, J.; Zhou, S.; Inman, D.J. Nonlinear dynamic analysis of a piezomagnetoelastic energy harvester. Nonlinear Dyn. 2015, 79, 1251–1263. [Google Scholar]
- Papež, N.; Pisarenko, T.; Ščasnovič, E.; Sobola, D.; Ţălu, Ş.; Dallaev, R.; Částková, K.; Sedlák, P. A brief introduction and current state of polyvinylidene fluoride as an energy harvester. Coatings 2022, 12, 1429. [Google Scholar] [CrossRef]
- Saxena, P.; Shukla, P. A comprehensive review on fundamental properties and applications of poly (vinylidene fluoride)(PVDF). Adv. Compos. Hybrid Mater. 2021, 4, 8–26. [Google Scholar]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. D Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar]
- Li, H.; Wang, Y.; Zhang, J. Nonlinear energy harvesting from hybrid sources using tunable magnetic forces. J. Intell. Mater. Syst. Struct. 2023, 34, 3–15. [Google Scholar]
- Sun, Q.; Liu, Z.; Wang, X. Design and analysis of a rolling-swing energy harvester with magnetic coupling. Mech. Syst. Signal Process. 2024, 160, 107853. [Google Scholar]
- Yin, X.; Zhang, Y.; Wang, J. AI-driven design of multistable energy harvesters with magnetic interactions. J. Appl. Phys. 2025, 137, 024501. [Google Scholar]
- Wu, J.; Li, H.; Zhang, Y. Analysis of an S-type generator beam for low-frequency energy harvesting. J. Vib. Acoust. 2023, 145, 011001. [Google Scholar]
- Fu, L.; Zhang, X.; Wang, J. Design of hybrid energy harvesters with adjustable energy barriers. J. Intell. Mater. Syst. Struct. 2024, 35, 123–135. [Google Scholar]
- Zhang, J.; Ueno, T.; Kita, S. Improvement of the power generation efficiency of magnetostrictive vibration generators using multiple magnetic circuits. In Proceedings of the Behavior and Mechanics of Multifunctional Materials XVIII, Long Beach, CA, USA, 25–29 March 2024; SPIE: Washington, DC, USA, 2024; Volume 12947, pp. 72–81. [Google Scholar]
- Sreekumar, A.; Triantafyllou, S.P.; Chevillotte, F. Virtual elements for sound propagation in complex poroelastic media. Comput. Mech. 2022, 69, 347–382. [Google Scholar] [CrossRef]
- Norenberg, J.P.; Peterson, J.V.; Lopes, V.G.; Luo, R.; de La Roca, L.; Pereira, M.; Ribeiro, J.G.T.; Cunha, A., Jr. STONEHENGE—Suite for nonlinear analysis of energy harvesting systems. Softw. Impacts 2021, 10, 100161. [Google Scholar] [CrossRef]
- Arefi, A.; Nahvi, H. Stability analysis of an embedded single-walled carbon nanotube with small initial curvature based on nonlocal theory. Mech. Adv. Mater. Struct. 2017, 24, 962–970. [Google Scholar] [CrossRef]
- Arefi, A.; Salimi, M. Investigations on vibration and buckling of carbon nanotubes with small initial curvature by nonlocal elasticity theory. Fuller. Nanotub. Carbon Nanostruct. 2015, 23, 105–112. [Google Scholar]
- Li, J.; Huang, J. Subharmonic resonance of a clamped-clamped buckled beam with 1:1 internal resonance under base harmonic excitations. Appl. Math. Mech. 2020, 41, 1881–1896. [Google Scholar] [CrossRef]
- Yung, K.W.; Landecker, P.B.; Villani, D.D. An analytic solution for the force between two magnetic dipoles. Phys. Sep. Sci. Eng. 1998, 9, 39–52. [Google Scholar]
- Sreekumar, A.; Barman, S.K. Physics-informed model order reduction for laminated composites: A Grassmann manifold approach. Compos. Struct. 2025, 361, 119035. [Google Scholar]
- Arasan, U.; Sreekumar, A.; Chevillotte, F.; Triantafyllou, S.; Chronopoulos, D.; Gourdon, E. Condensed finite element scheme for symmetric multi-layer structures including dilatational motion. J. Sound Vib. 2022, 536, 117105. [Google Scholar] [CrossRef]
- Huguet, T.; Lallart, M.; Badel, A. Orbit jump in bistable energy harvesters through buckling level modification. Mech. Syst. Signal Process. 2019, 128, 202–215. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, W.; Yuan, Y.; Zhang, Z. High-energy orbit attainment of a nonlinear beam generator by adjusting the buckling level. Sen. Actuators A Phys. 2020, 312, 112164. [Google Scholar] [CrossRef]
- Saint-Martin, C.; Morel, A.; Charleux, L.; Roux, E.; Gibus, D.; Benhemou, A.; Badel, A. Optimized and robust orbit jump for nonlinear vibration energy harvesters. Nonlinear Dyn. 2024, 112, 3081–3105. [Google Scholar] [CrossRef]
- Ramamoorthy, V.T.; Özcan, E.; Parkes, A.J.; Sreekumar, A.; Jaouen, L.; Bécot, F.X. Comparison of heuristics and metaheuristics for topology optimisation in acoustic porous materials. J. Acoust. Soc. Am. 2021, 150, 3164–3175. [Google Scholar] [CrossRef] [PubMed]
- Mannel, F.; Aggrawal, H.O.; Modersitzki, J. A structured L-BFGS method and its application to inverse problems. Inverse Probl. 2024, 40, 045022. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Experimental Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 102001. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Simulation of a Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 075022. [Google Scholar] [CrossRef]
- Masuda, A.; Senda, A. A vibration energy harvester using a nonlinear oscillator with self-excitation capability. In Proceedings of the Active and Passive Smart Structures and Integrated Systems 2011, San Diego, CA, USA, 6–10 March 2011; SPIE: Washington, DC, USA, 2011; Volume 7977, pp. 306–314. [Google Scholar]
- Fu, J.; Zeng, X.; Wu, N.; Wu, J.; He, Y.; Xiong, C.; Dai, X.; Jin, P.; Lai, M. Design, modeling and experiments of bistable piezoelectric energy harvester with self-decreasing potential energy barrier effect. Energy 2024, 300, 131572. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Wei, Z.H.; Cao, J. Possible strategies for performance enhancement of asymmetric potential bistable energy harvesters by orbit jumps. Eur. Phys. J. B 2022, 95, 58. [Google Scholar] [CrossRef]
- Giri, A.M.; Ali, S.; Arockiarajan, A. Influence of asymmetric potential on multiple solutions of the bi-stable piezoelectric harvester. Eur. Phys. J. Spec. Top. 2022, 231, 1443–1464. [Google Scholar] [CrossRef]
- Li, Q.; Bu, L.; Lu, S.; Yao, B.; Huang, Q.; Wang, X. Practical asymmetry and its effects on power and bandwidth performance in bi-stable vibration energy harvesters. Mech. Syst. Signal Process. 2024, 206, 110939. [Google Scholar]
- Sreekumar, A.; Kougioumtzoglou, I.A.; Triantafyllou, S.P. Filter approximations for random vibroacoustics of rigid porous media. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2024, 10, 031201. [Google Scholar]
| Operator | Equation Terms | |||
|---|---|---|---|---|
| - | ||||
| 0 | 0 | |||
| 0 | 0 | |||
| 3cBeam Properties | Magnet Properties | ||||
|---|---|---|---|---|---|
| Symbol | Parameter | Value | Symbol | Parameter | Value |
| L | Length | 40 mm | Height of A | 8 mm | |
| h | Thickness | 0.1 mm | Height of B | 10 mm | |
| b | Width | 2 mm | Mass | 5 g | |
| E | Young’s modulus | 0.7 GPa | Residual Flux Density | 1.2 T | |
| Density | 7850 kg/m3 | Permeability of free space | H/m | ||
| Stability Phenomenon | Buckling Involvement () | Magnet Configuration (Polarity, , ) |
|---|---|---|
| Monostable (1 Well) | ||
| Linear elastic | No buckling required () | No magnets required, but can be added for tuning. |
| Bistable (2 Wells) | ||
| Buckling-induced | Requires buckling beyond critical load . Recommended 1–3 mm for practical bistability. | No magnets needed for purely buckling-induced bistability. Can introduce stationary magnets for barrier height tuning. |
| Magnetically-assisted | Can occur with or without buckling, though combining buckling and magnetic tuning gives better tunability. | Stationary magnets placed symmetrically at = 10–30 mm. Magnet polarities aligned for attraction/repulsion depending on tuning objective. |
| Tunable potential barrier (via ) | Buckling can be present or absent; best tuning occurs when mm. | Magnets placed symmetrically at 10–30 mm. Too small (<10 mm) leads to low barriers, while too large (>50 mm) reduces magnet effects. |
| Asymmetric bistable | Typically requires buckling mm for significant asymmetry effects. | Introduced via offset magnets with controlled asymmetry parameter . Best results for , with 10–20 mm. |
| Multistable (3 Wells) | ||
| Magnetically-induced from monostable | No buckling required; multistability arises purely from magnet forces. | Magnets placed symmetrically at = 10–50 mm, with appropriate polarity inversion to generate additional wells. |
| From bistable + magnet tuning | Requires buckling mm for strong bi-stability effects before transitioning to multistability. | Additional magnets introduced above the beam, with reversed polarity to create new equilibrium wells. Optimal range: = 10–30 mm. |
| Extreme case with barrier height modulation | Typically occurs when mm, but excessive buckling reduces magnetic influence. | Requires precise tuning of both and . Best observed for = 10–25 mm with moderate asymmetry . |
| Only Magnet | Only Buckling | Magnet + Buckling | |
|---|---|---|---|
| (mm) | - | 2.35 | 2.18 |
| (mm) | 1 | - | 13.78 |
| 1.5 | - | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arefi, A.; Sreekumar, A.; Chronopoulos, D. A Programmable Hybrid Energy Harvester: Leveraging Buckling and Magnetic Multistability. Micromachines 2025, 16, 359. https://doi.org/10.3390/mi16040359
Arefi A, Sreekumar A, Chronopoulos D. A Programmable Hybrid Energy Harvester: Leveraging Buckling and Magnetic Multistability. Micromachines. 2025; 16(4):359. https://doi.org/10.3390/mi16040359
Chicago/Turabian StyleArefi, Azam, Abhilash Sreekumar, and Dimitrios Chronopoulos. 2025. "A Programmable Hybrid Energy Harvester: Leveraging Buckling and Magnetic Multistability" Micromachines 16, no. 4: 359. https://doi.org/10.3390/mi16040359
APA StyleArefi, A., Sreekumar, A., & Chronopoulos, D. (2025). A Programmable Hybrid Energy Harvester: Leveraging Buckling and Magnetic Multistability. Micromachines, 16(4), 359. https://doi.org/10.3390/mi16040359







