Design, Analysis, and Simulation of a MEMS Tuning Fork Gyroscope with a Mechanical Amplification Structure
Abstract
1. Introduction
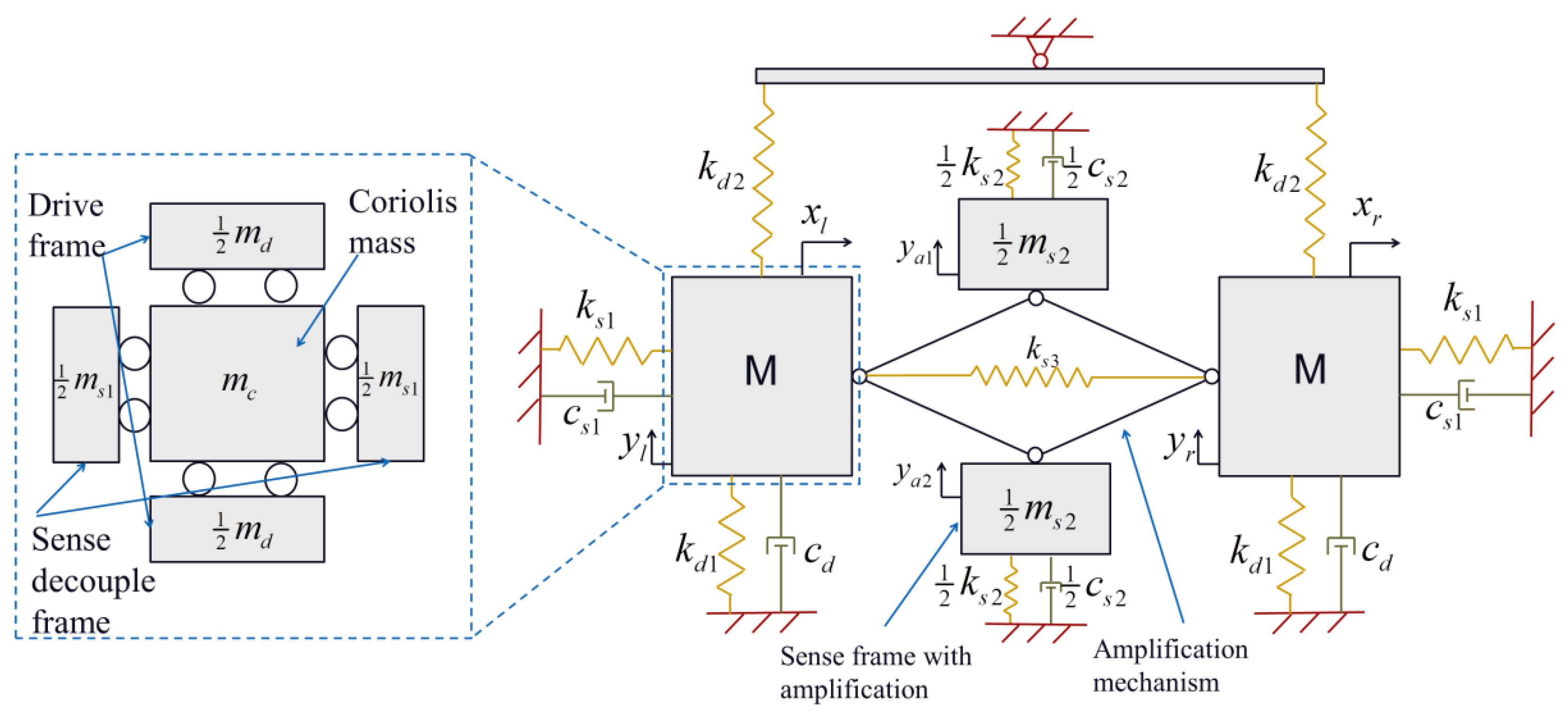
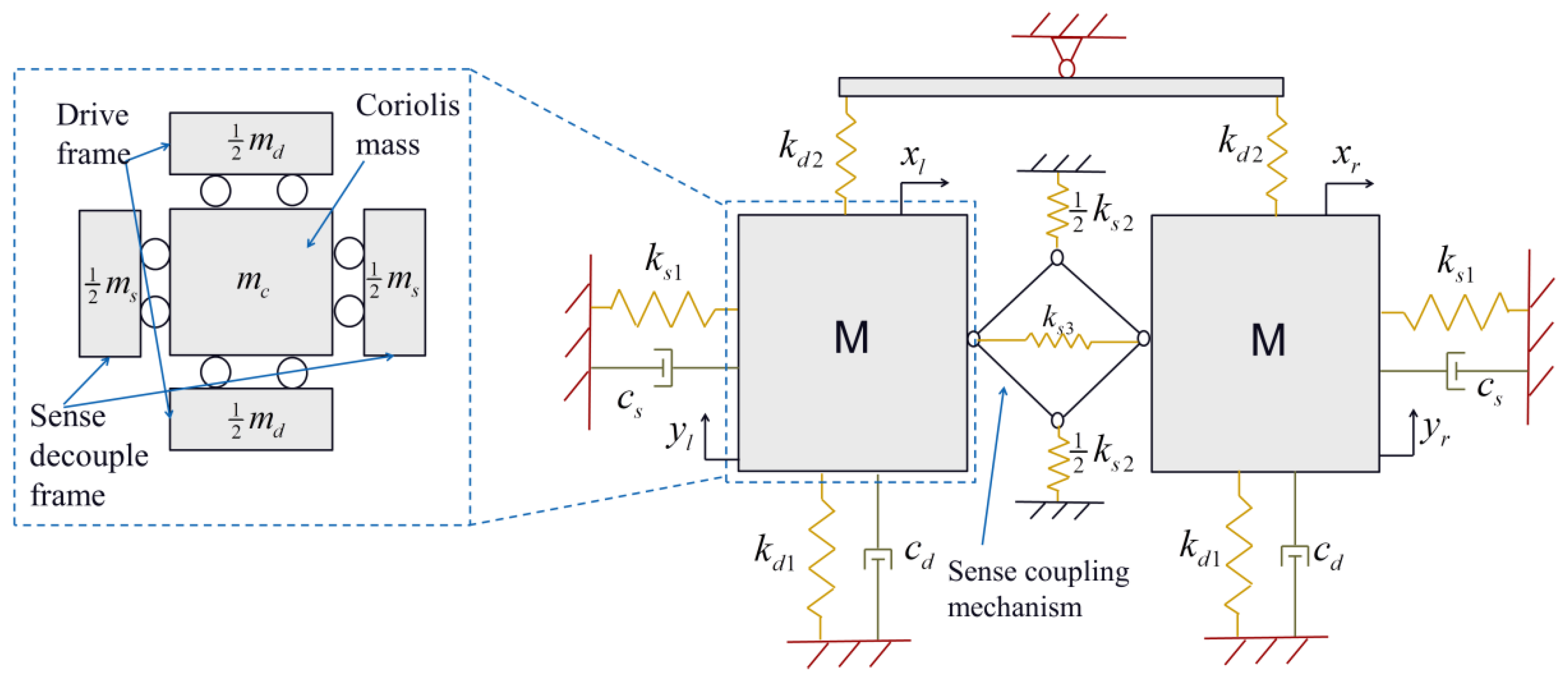
2. Architecture Design and Working Principle
3. Theoretical Analysis of the Proposed TFGs
3.1. Analysis of Scheme I
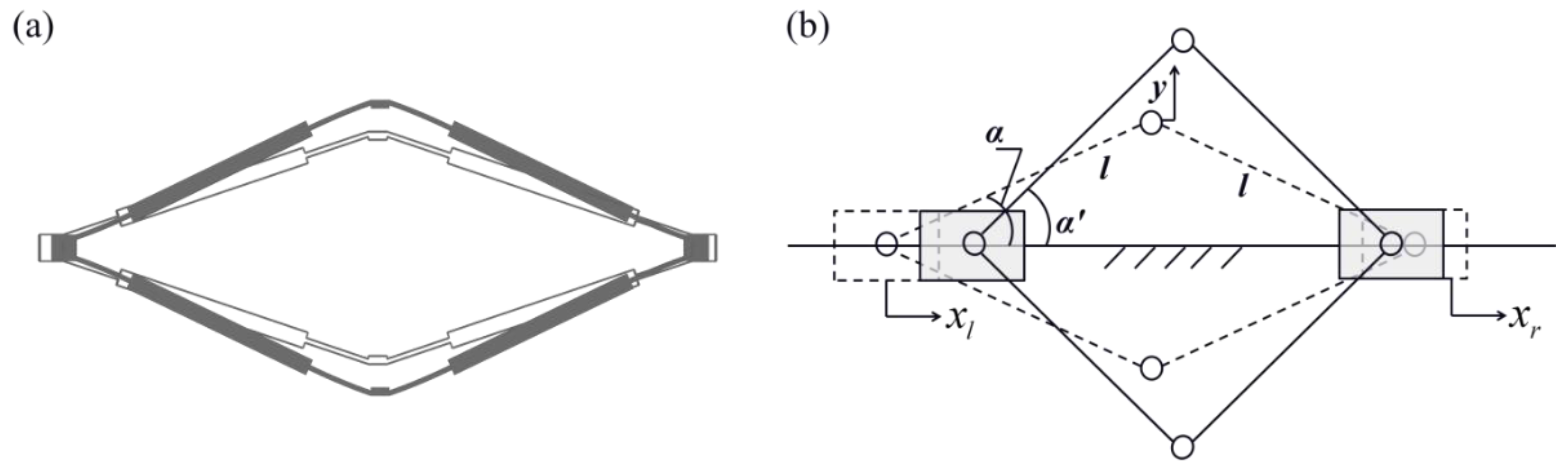
3.1.1. Amplification Mechanism Analysis
3.1.2. Dynamics and Sensitivity Analysis
3.2. Analysis of Scheme II
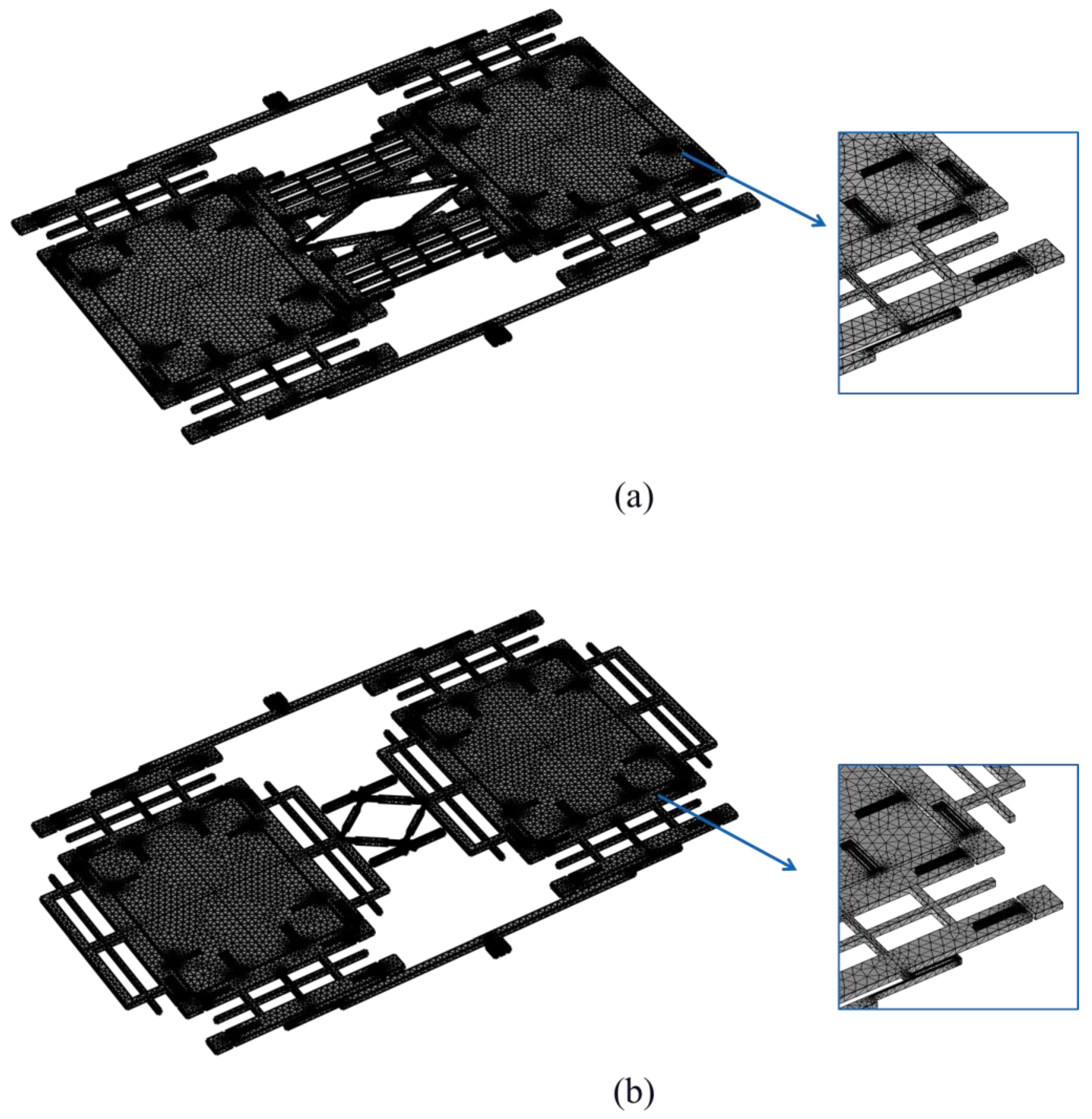
4. Finite Element Analysis of the Proposed Design
5. Results and Discussion
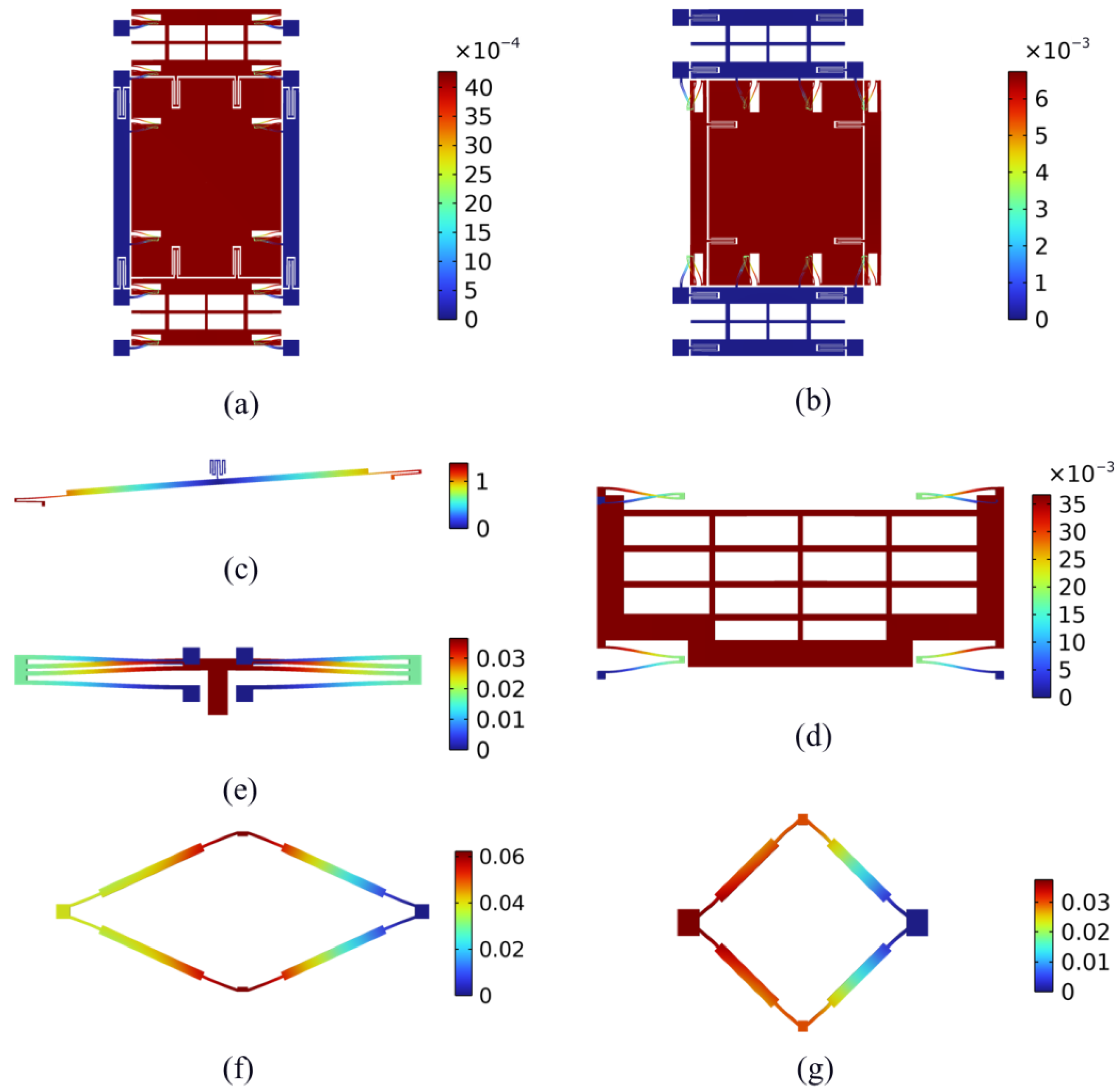
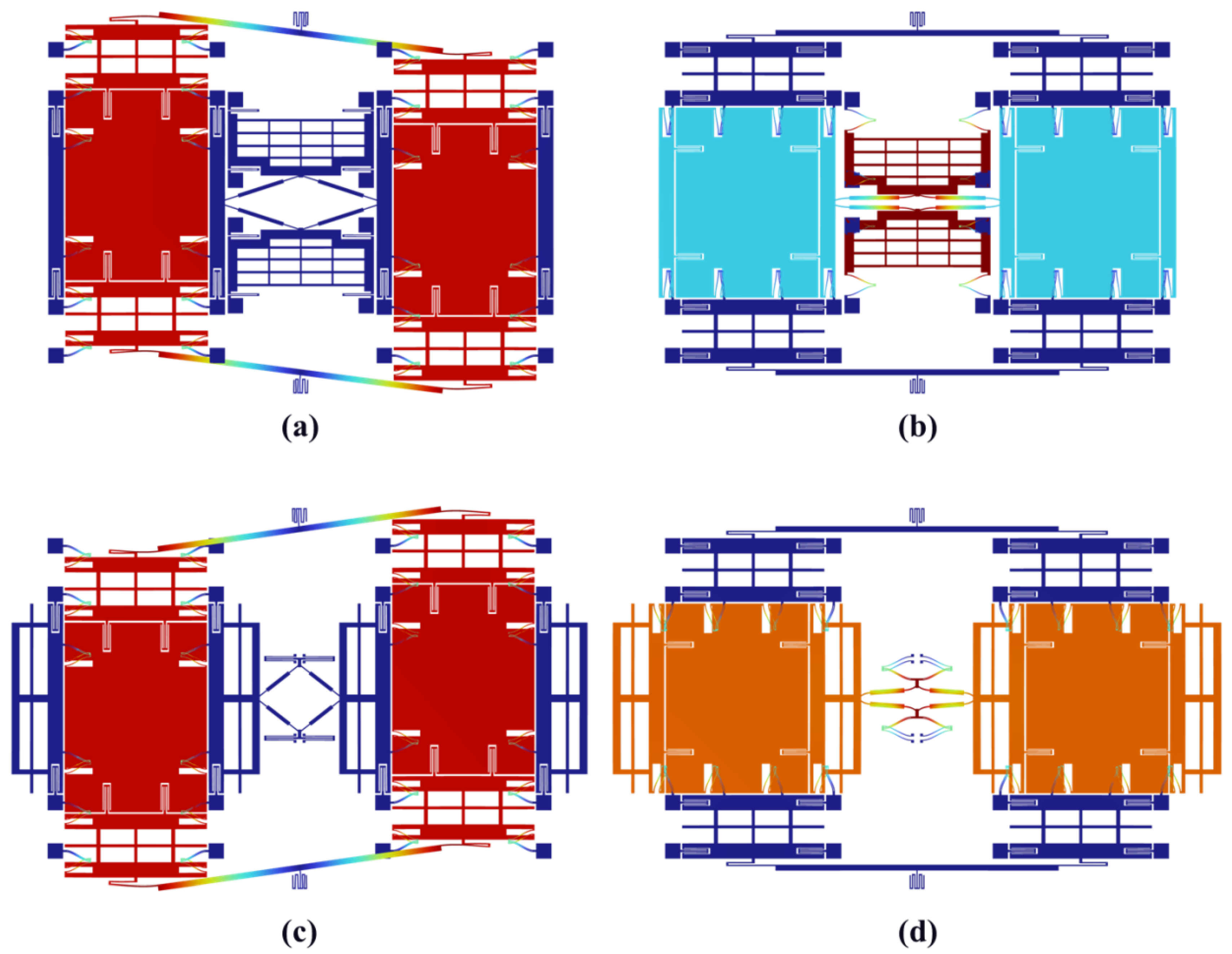
5.1. Static Analysis
5.2. Modal Analysis
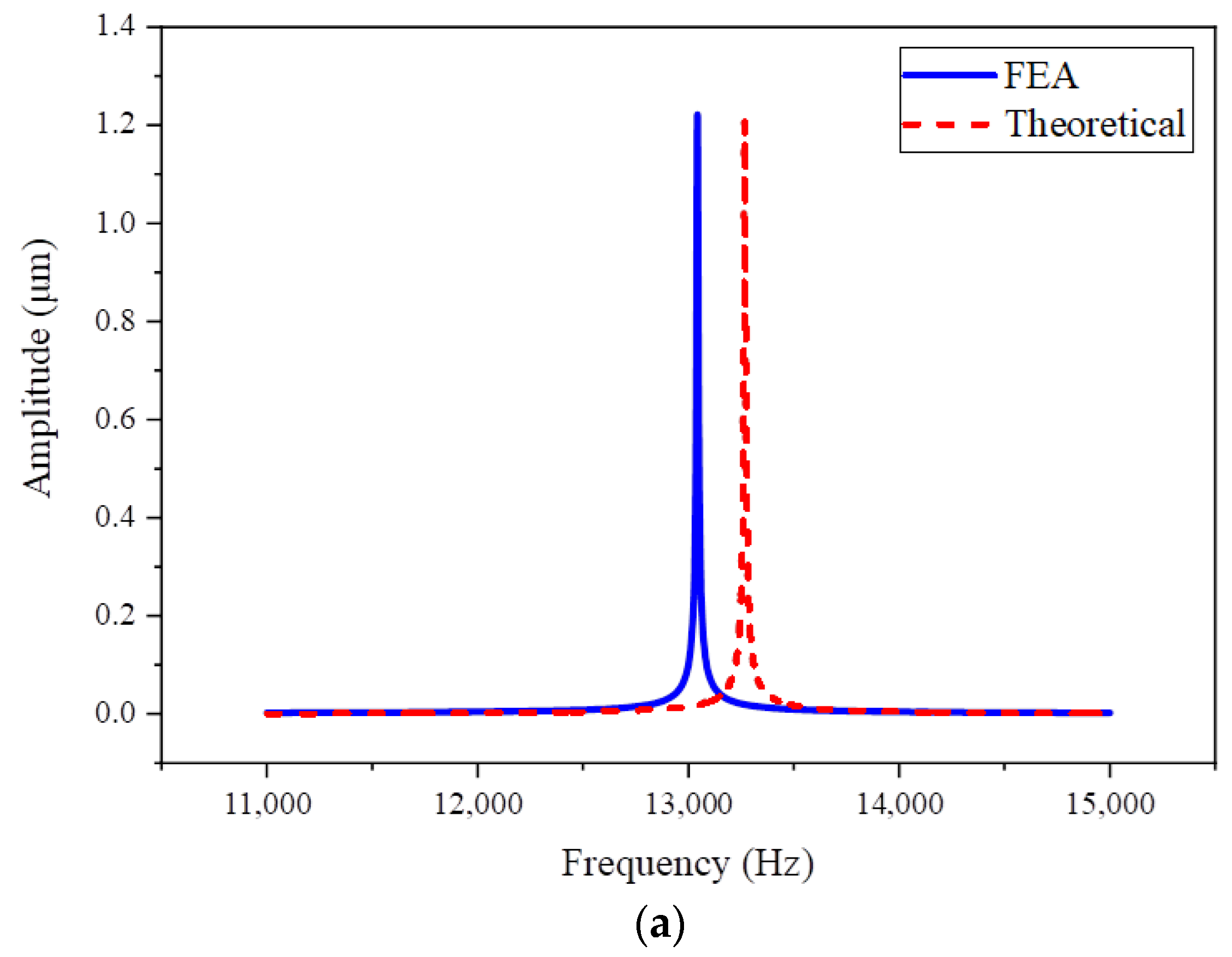
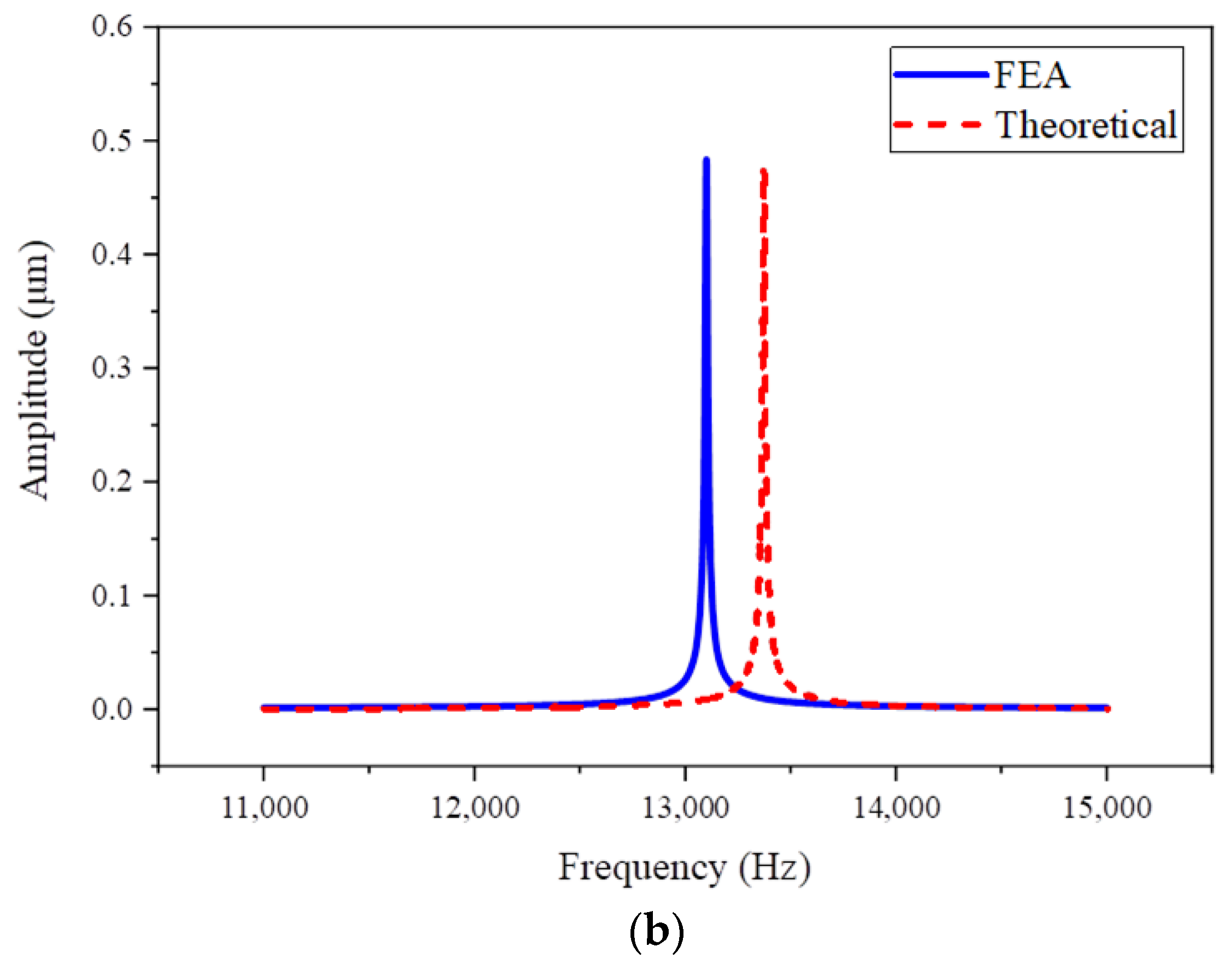
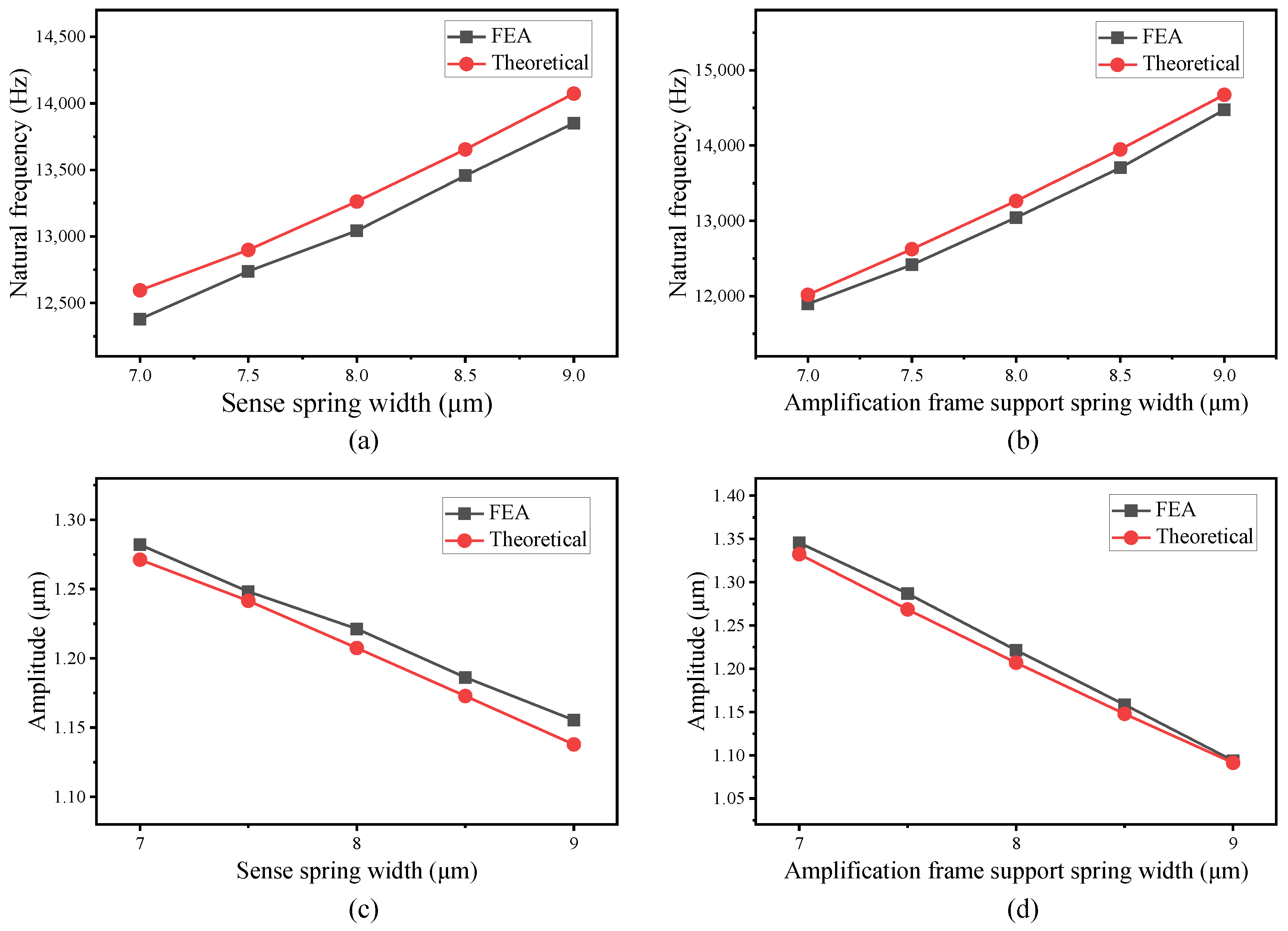
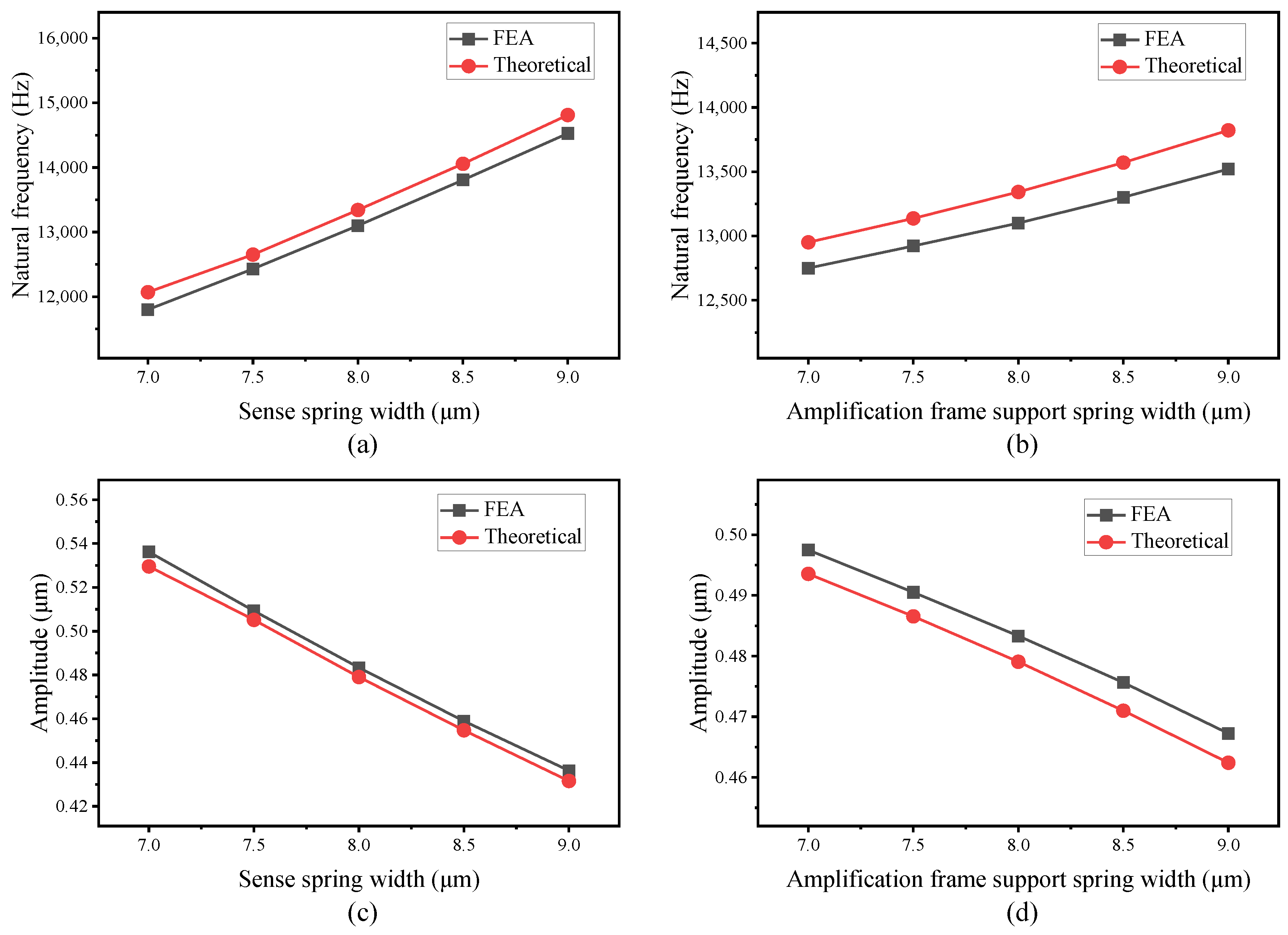
5.3. Frequency Response and Sensitivity Analysis
5.4. Effectiveness and Validity of the Models
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, X.; Sun, C.; Wang, P.; Huang, L. Vision sensor and dual MEMS gyroscope integrated system for attitude determination on moving base. Rev. Sci. Instrum. 2018, 89, 015002. [Google Scholar] [CrossRef]
- Kang, L.; Ye, L.; Song, K.; Zhou, Y. Attitude Heading Reference System Using MEMS Inertial Sensors with Dual-Axis Rotation. Sensors 2014, 14, 18075–18095. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Wang, D.; Xu, L.; Xu, L. MEMS-based rotary strapdown inertial navigation system. Measurement 2013, 46, 2585–2596. [Google Scholar] [CrossRef]
- Suvorkin, V.; Garcia-Fernandez, M.; Gonzalez-Casado, G.; Li, M.; Rovira-Garcia, A. Assessment of Noise of MEMS IMU Sensors of Different Grades for GNSS/IMU Navigation. Sensors 2024, 24, 1953. [Google Scholar] [CrossRef]
- Cai, S.L.; Zhu, R.; Ding, H.G.; Yang, Y.J.; Su, Y. A micromachined integrated gyroscope and accelerometer based on gas thermal expansion. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 50–53. [Google Scholar]
- Feng, R.; Bahari, J.; Jones, J.D.; Leung, A.M. MEMS thermal gyroscope with self-compensation of the linear acceleration effect. Sens. Actuators A Phys. 2013, 203, 413–420. [Google Scholar] [CrossRef]
- Kock, G.; Combette, P.; Tedjini, M.; Schneider, M.; Gauthier-Blum, C.; Giani, A. Experimental and Numerical Study of a Thermal Expansion Gyroscope for Different Gases. Sensors 2019, 19, 360. [Google Scholar] [CrossRef]
- Feng, C.; Jiao, H.; Miao, B.; Gu, Z.; Hu, Y.; Jiang, T.; Li, J.; Li, X.; Li, H.; Li, J. Interferometric Integrated Optical Gyroscope Based on Silicon Nitride Waveguide Ring. IEEE Sens. J. 2024, 24, 23781–23788. [Google Scholar] [CrossRef]
- Zou, W.; Huang, Y.; Lin, H.; Xue, Z. New Application and Research of Ring Laser Gyroscope in the Field of Angle Metrology. IEEE Trans. Instrum. Meas. 2024, 73, 1007212. [Google Scholar] [CrossRef]
- Kumagai, H.; Sugiyama, S.J.S. A single-axis thermal convective gas gyroscope. Sens. Mater. 2005, 17, 453–463. [Google Scholar]
- Cao, H.; Cai, Q.; Zhang, Y.; Shen, C.; Shi, Y.; Liu, J. Design, Fabrication, and Experiment of a Decoupled Multi-Frame Vibration MEMS Gyroscope. IEEE Sens. J. 2021, 21, 19815–19824. [Google Scholar] [CrossRef]
- Guan, Y.; Gao, S.; Liu, H.; Jin, L.; Niu, S. Design and Vibration Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Diamond Coupling Mechanism. Sensors 2016, 16, 468. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.; Han, G.; Wei, Z.; Si, C.; Ning, J.; Yang, F.; Han, W. Design and analysis of MEMS tuning fork gyroscope with dual mode ordering. Microw. Opt. Technol. Lett. 2023, 66, e33754. [Google Scholar] [CrossRef]
- Hassan, J.N.A.; Huang, W.; Wang, M.; Zhang, S.; Wen, G.; Huang, Y. Optomechanical Gyroscope Based on Micro-Hemispherical Shell and Optical Ring Resonators. IEEE Photonics J. 2024, 16, 5800617. [Google Scholar] [CrossRef]
- Laita, G.; Buffoli, A.; Robert, P.; Langfelder, G. Origin and Compensation of Nonlinearity in Near Navigation Grade Piezoresistive MEMS Gyroscope. IEEE Sens. J. 2024, 24, 34162–34169. [Google Scholar] [CrossRef]
- Liang, F.; Liang, D.-D.; Qian, Y.-J. Dynamical analysis of an improved MEMS ring gyroscope encircled by piezoelectric film. Int. J. Mech. Sci. 2020, 187, 105915. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, Q. Bias thermal stability improvement of MEMS gyroscope with quadrature motion correction and temperature self-sensing compensation. Micro Nano Lett. 2020, 15, 234–238. [Google Scholar] [CrossRef]
- Wang, J.; Lou, W.; Wang, D.; Feng, H. Design, analysis, and fabrication of silicon-based MEMS gyroscope for high-g shock platform. Microsyst. Technol. 2019, 25, 4577–4586. [Google Scholar] [CrossRef]
- Guan, Y.; Gao, S.; Liu, H.; Niu, S. Acceleration sensitivity of tuning fork gyroscopes: Theoretical model, simulation and experimental verification. Microsyst. Technol. 2015, 21, 1313–1323. [Google Scholar] [CrossRef]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. Micromachined rate gyroscope architecture with ultra-high quality factor and improved mode ordering. Sens. Actuators A Phys. 2011, 165, 26–34. [Google Scholar] [CrossRef]
- Cao, H.; Xue, R.; Cai, Q.; Gao, J.; Zhao, R.; Shi, Y.; Huang, K.; Shao, X.; Shen, C. Design and Experiment for Dual-Mass MEMS Gyroscope Sensing Closed-Loop System. IEEE Access 2020, 8, 48074–48087. [Google Scholar] [CrossRef]
- Bashir, U.; Bazaz, S.A.; Saleem, M.M.; Shakoor, R.I.; Tariq, M.O.; Kumar, P. Design and analysis of mode-matched decoupled mass MEMS gyroscope with improved thermal stability. Meas. Sci. Technol. 2024, 35, 086319. [Google Scholar] [CrossRef]
- Wu, G.Q.; Chua, G.L.; Gu, Y.D. A dual-mass fully decoupled MEMS gyroscope with wide bandwidth and high linearity. Sens. Actuators A Phys. 2017, 259, 50–56. [Google Scholar] [CrossRef]
- Xu, P.; Si, C.; He, Y.; Wei, Z.; Jia, L.; Han, G.; Ning, J.; Yang, F. A Novel High-Q Dual-Mass MEMS Tuning Fork Gyroscope Based on 3D Wafer-Level Packaging. Sensors 2021, 21, 6428. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, A.Q.; Zhang, Q.X. Tolerance analysis for comb-drive actuator using DRIE fabrication. Sens. Actuators A Phys. 2006, 125, 494–503. [Google Scholar] [CrossRef]
- Walther, A.; Le Blanc, C.; Delorme, N.; Deimerly, Y.; Anciant, R.; Willemin, J. Bias Contributions in a MEMS Tuning Fork Gyroscope. J. Electromech. Syst. 2013, 22, 303–308. [Google Scholar] [CrossRef]
- Zeimpekis, I.; Sari, I.; Kraft, M. Deflection amplification mechanism in a capacitive accelerometer. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 1096–1099. [Google Scholar]
- Davies, E.; George, D.S.; Gower, M.C.; Holmes, A.S. MEMS Fabry–Pérot optical accelerometer employing mechanical amplification via a V-beam structure. Sens. Actuators A Phys. 2014, 215, 22–29. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, S.; Hao, S.; Zhang, Q.; Feng, J. Dynamical Design and Gain Performance Analysis of a 3-DoF Micro-Gyro with an Anchored Leverage Mechanism. Micromachines 2022, 13, 1201. [Google Scholar] [CrossRef]
- Li, Z.; Gao, S.; Jin, L.; Liu, H.; Guan, Y.; Peng, S. Design and Mechanical Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Leverage Mechanism. Sensors 2019, 19, 3455. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, D.; Li, X.; Chen, F. Design of a Micro-Electro Mechanical System Quad Mass Gyroscope with Compliant Mechanical Amplification. Micromachines 2024, 15, 124. [Google Scholar] [CrossRef]
- Patel, C.; McCluskey, P. Modeling and simulation of the MEMS vibratory gyroscope. In Proceedings of the 13th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, San Diego, CA, USA, 30 May–1 June 2012; pp. 928–933. [Google Scholar]
- Chang, H.; Zhang, Y.; Xie, J.; Zhou, Z.; Yuan, W. Integrated Behavior Simulation and Verification for a MEMS Vibratory Gyroscope Using Parametric Model Order Reduction. J. Microelectromech. Syst. 2010, 19, 282–293. [Google Scholar] [CrossRef]


| Parameter | Design Value |
|---|---|
| Coriolis mass volume | 0.1127 mm3 |
| Drive frame volume | 0.0390 mm3 |
| Sense frame volume of Scheme I | 0.0212 mm3 |
| Sense amplification frame volume | 0.0320 mm3 |
| Sense frame volume of Scheme II | 0.0402 mm3 |
| Length of the drive spring | 245 μm |
| Length of the sense spring | 250 μm |
| Length of amplification frame support springs | 280 μm |
| Length of sense coupling support springs | 290 μm |
| Width of springs | 8 μm |
| Horizontal angle of amplification beam of Scheme I | 18° |
| Horizontal angle of sense couple beam of Scheme II | 38° |
| Thickness of the device layer | 40 μm |
| Parameter | Value |
|---|---|
| Density | 2320 kg/m3 |
| Young’s modulus | 170 GPa |
| Poisson’s ratio | 0.22 |
| Parameter | Value |
|---|---|
| Scheme I and II | 2372.2 N/m |
| Scheme I and II | 14.34 N/m |
| Scheme I and II | 1498.1 N/m |
| Scheme I | 544.9 N/m |
| Scheme II | 547.7 N/m |
| Scheme I | 259.9 N/m |
| Scheme II | 266.7 N/m |
| Scheme I | Scheme II | |||
|---|---|---|---|---|
| Drive Mode | Sense Mode | Drive Mode | Sense Mode | |
| Theoretical | 13,105.9 Hz | 13,265.1 Hz | 13,105.9 Hz | 13,342.5 Hz |
| FEA | 12,918.7 Hz | 13,043.1 Hz | 12,924.7 Hz | 13,100.6 Hz |
| Difference | 1.43% | 1.67% | 1.38% | 1.81% |
| Parameter | Description | Value |
|---|---|---|
| Area of proof mass | 2.82 × 106 µm2 | |
| Area of sense electrodes overlap | 1.152 × 105 µm2 | |
| Area of drive electrodes overlap | 3.2 × 105 µm2 | |
| Gap between proof mass and substrate | 2 µm | |
| Gap between the electrodes | 3 µm | |
| Air viscosity | 1.837 × 10−5 Ns/m2 | |
| Mean free path of air | 0.07 µm | |
| Damping coefficient in drive axis | 2.61 × 10−5 Ns/m | |
| Damping coefficient in sense axis of Scheme I | 2.42 × 10−5 Ns/m | |
| Damping coefficient of amplified frame of Scheme I | 1.35 × 10−6 Ns/m | |
| Damping coefficient in sense axis of Scheme II | 2.49 × 10−5 Ns/m |
| Theoretical | FEA | Difference | |
|---|---|---|---|
| Scheme I | 1.2072 µm | 1.2214 µm | −1.193% |
| Scheme II | 0.4790 µm | 0.4833 µm | −0.898% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Calusi, B.; Bagolini, A.; Pantano, M.F. Design, Analysis, and Simulation of a MEMS Tuning Fork Gyroscope with a Mechanical Amplification Structure. Micromachines 2025, 16, 195. https://doi.org/10.3390/mi16020195
Hu H, Calusi B, Bagolini A, Pantano MF. Design, Analysis, and Simulation of a MEMS Tuning Fork Gyroscope with a Mechanical Amplification Structure. Micromachines. 2025; 16(2):195. https://doi.org/10.3390/mi16020195
Chicago/Turabian StyleHu, Haotian, Benedetta Calusi, Alvise Bagolini, and Maria F. Pantano. 2025. "Design, Analysis, and Simulation of a MEMS Tuning Fork Gyroscope with a Mechanical Amplification Structure" Micromachines 16, no. 2: 195. https://doi.org/10.3390/mi16020195
APA StyleHu, H., Calusi, B., Bagolini, A., & Pantano, M. F. (2025). Design, Analysis, and Simulation of a MEMS Tuning Fork Gyroscope with a Mechanical Amplification Structure. Micromachines, 16(2), 195. https://doi.org/10.3390/mi16020195






