Support-Free 3D Printing Based on Model Decomposition
Abstract
1. Introduction
2. Methods
2.1. Problem Modeling
2.2. Optimization Strategy
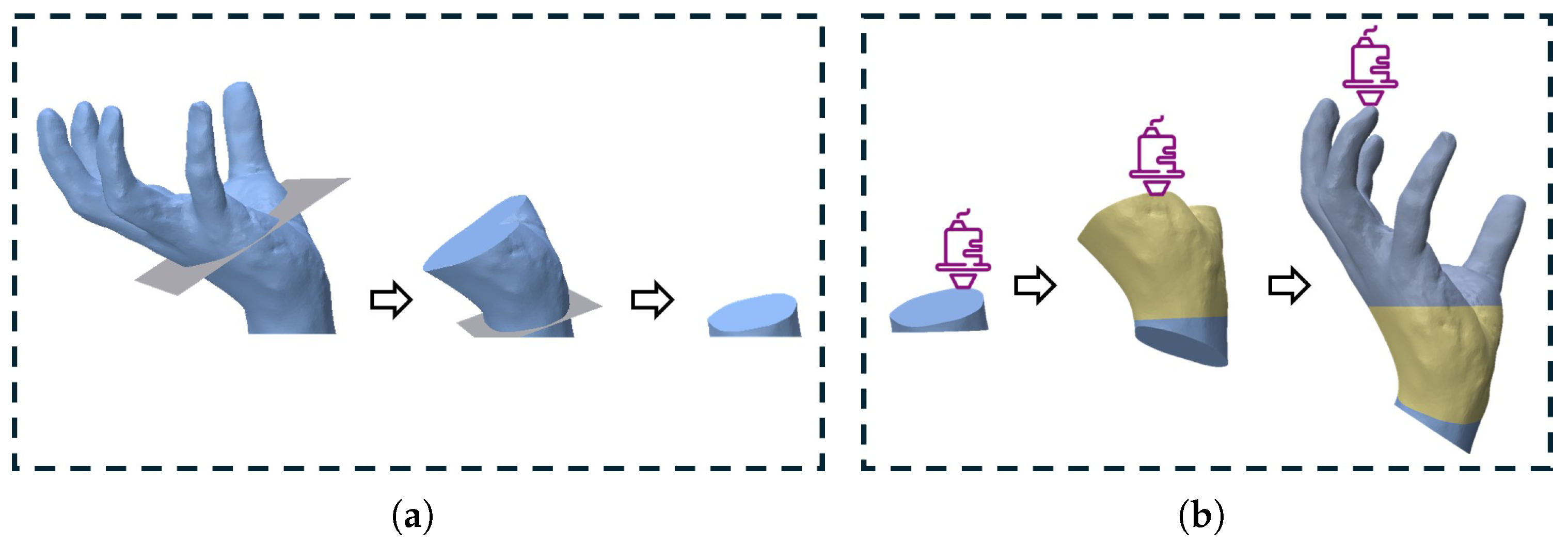
2.2.1. Candidate Plane Generation and Constraints
2.2.2. Evaluation Metrics and Pareto Optimization
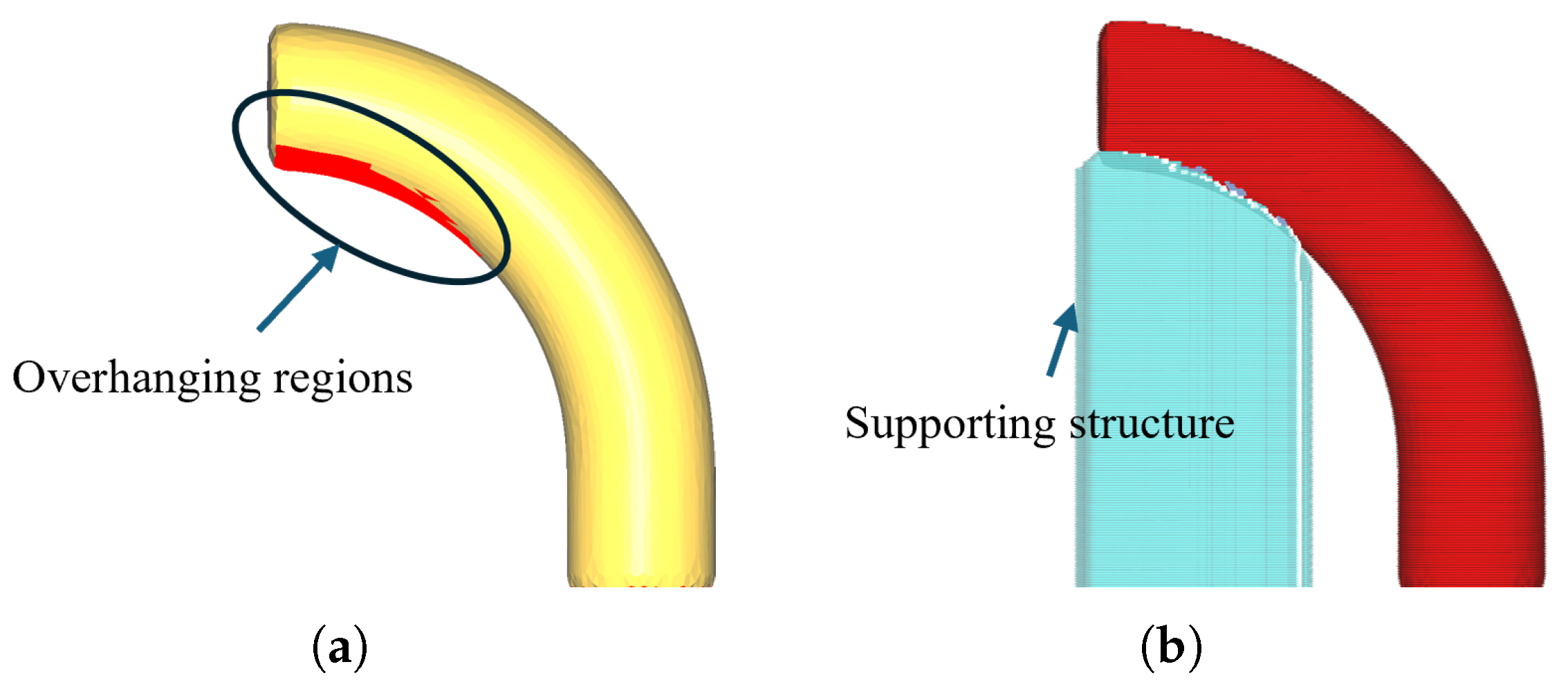
- Support Reduction Rate : For a model, overhanging facets requiring support arise due to angles with the deposition direction exceeding the maximum self-supporting angle. We define the proportion of overhanging facets removed by a plane relative to the total overhanging facets in the current model as the support reduction rate. A higher ratio indicates more overhanging facets removed, reducing the number of subsequent cuts needed.Support Ratio : This is the proportion of facets above plane with angles exceeding the maximum self-supporting angle relative to the total facets. For models where zero support is unachievable, we introduce progressive relaxation, gradually loosening the support ratio constraint to ensure that the decomposition process continues.Facet Coverage Rate : This is the proportion of facets above plane relative to the total facets in the current model. A higher value indicates fewer remaining facets, reducing the need for subsequent cuts.
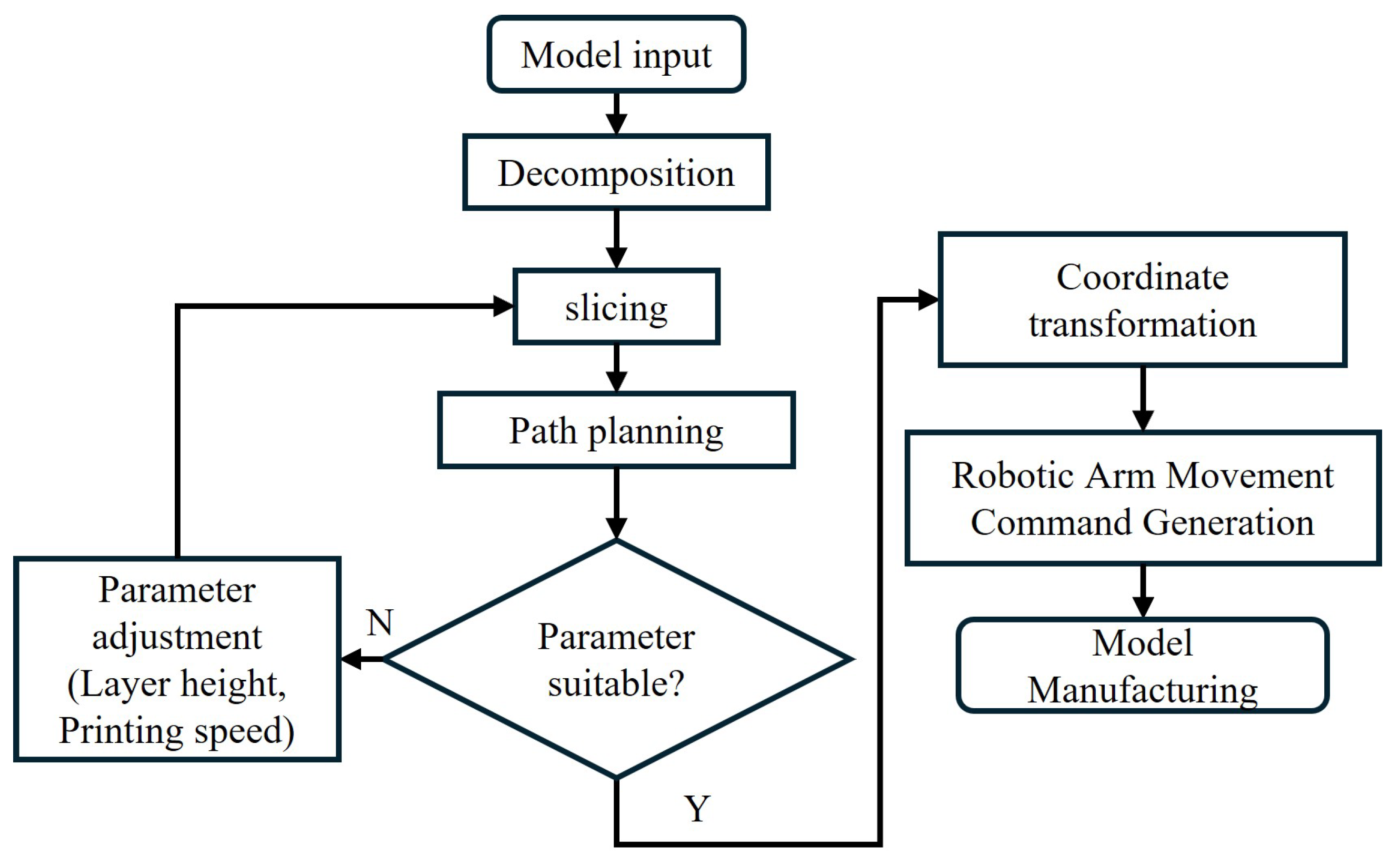
2.2.3. Beam Search and Sequence Generation
| Algorithm 1: Model Decomposition. |
|
3. Multi-Degree-of-Freedom 3D Printing
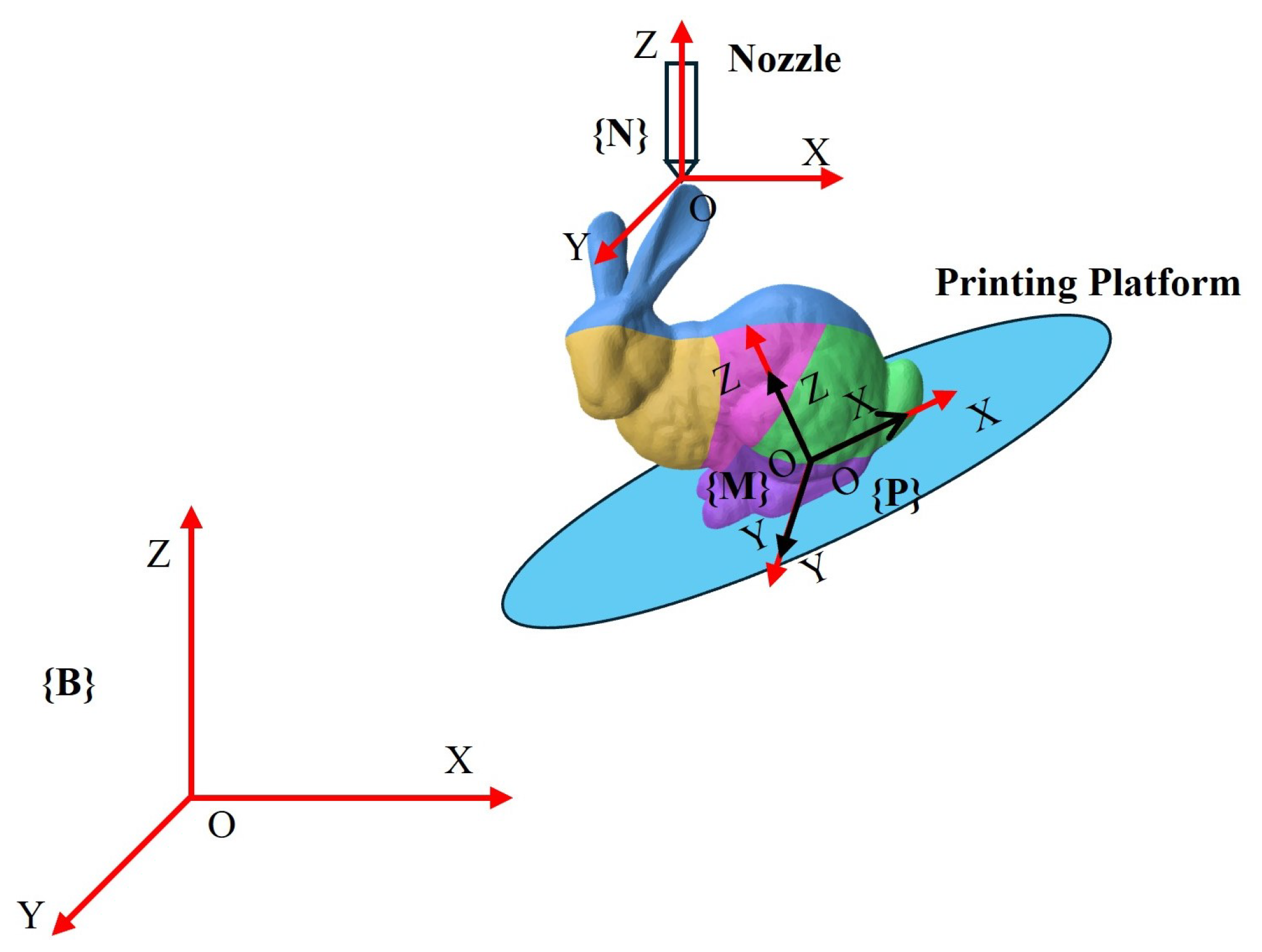
Coordinate Transformation
- Base Coordinate System : Fixed on the robotic arm base.
- Model Coordinate System : Defines the geometry of the 3D model.
- Platform Coordinate System : Origin located at the center of the printing platform.
- Nozzle Coordinate System : Fixed at the nozzle tip, with its Z-axis upward ().
- Direction Alignment: The platform is rotated so that the normal of the current print point is aligned with the nozzle’s z-axis direction:can be obtained using the standard axis-angle (Rodrigues) formula.
- Safety Adjustment: The system itself has redundant degrees of freedom. We added a rotation about the Z-axis to orient the platform from the robotic arm position toward the nozzle (see Figure 5b), while preventing the robotic arm from exceeding the joint movement limits and collisions between the link and the nozzle support:where .
- Position Calculation: The platform is translated so that the print point coincides with the nozzle tip:This transformation ensures that the print platform deposits material correctly and achieves collision-free movement throughout the printing process.
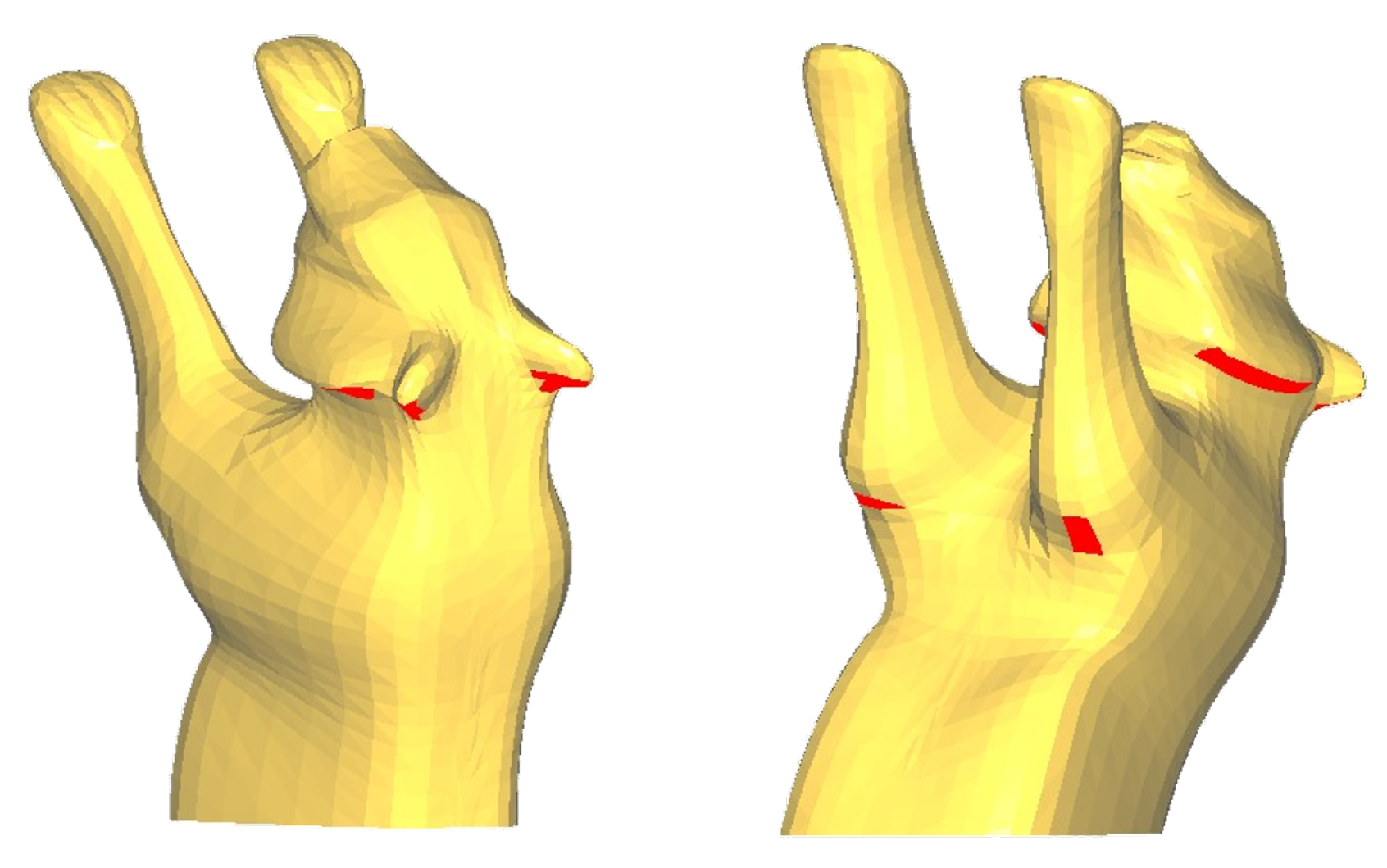
4. Results and Discussion
5. Conclusions and Future Work
- Our algorithm discretizes the cutting planes. Although beam search can avoid local optima, it is essentially an improved extension of the greedy algorithm. It cannot guarantee finding the global optimum, and there may be better solutions. We note that the current objective function (Equation (9)) is constructed based on the surface patches of the initial model and cannot dynamically update the internal geometric representation during iterative decomposition, which limits the construction of an accurate continuous optimization model. Future research will consider more suitable residual model representation methods, such as converting the preceding cutting planes into patches and then dynamically updating A, B, and mask in the algorithm to establish a functional relationship between the residual overhang area and each cutting plane in the cutting sequence. Based on this, gradient-based optimization algorithms can be used to improve the optimal solution obtained by the current discrete search, thus combining the robustness of discrete sampling with the accuracy of continuous optimization.
- This algorithm does not consider the trimming range of the cutting plane. While this can prevent collisions between the print head and the printed part, it also limits the exploration of the solution space. Future research could consider the trimming range as an optimization variable. When a cutting plane cuts the model, multiple components may be generated. By performing overhang analysis on each component separately and determining the trimming range of the cutting plane based on this analysis, we can better explore the solution space. However, this may introduce collision risks. To ensure printability, an interference detection algorithm between the print head and the model (e.g., fast collision detection based on bounding volume hierarchy) needs to be introduced to automatically and safely determine the maximum effective range of each cutting plane during the optimization process, thereby fully exploring better decomposition schemes without causing collisions.
- As discussed in Section 4 (The limitations of plane decomposition), the planar decomposition method, while efficient, has inherent limitations in handling locally complex geometries. To overcome this without sacrificing print efficiency, a promising future direction is to develop a hybrid decomposition approach. This strategy would maintain planar decomposition for the model’s main body to ensure efficiency, while selectively applying curved-layer decomposition only to locally complex areas where supports are otherwise unavoidable. This approach aims to eliminate the need for supports without significantly increasing manufacturing time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, J.; Newman, S.T.; Zhong, R.Y. A review of multiple degrees of freedom for additive manufacturing machines. Int. J. Comput. Integr. Manuf. 2021, 34, 195–211. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Nadagouda, M.N.; Rastogi, V.; Ginn, M. A review on 3D printing techniques for medical applications. Curr. Opin. Chem. Eng. 2020, 28, 152–157. [Google Scholar] [CrossRef]
- Radhika, C.; Shanmugam, R.; Ramoni, M.; BK, G. A review on additive manufacturing for aerospace application. Mater. Res. Express 2024, 11, 022001. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, L.; Yan, D.-M.; Nan, L. Near support-free multi-directional 3D printing via global-optimal decomposition. Graph. Model. 2019, 104, 101034. [Google Scholar] [CrossRef]
- Hu, K.; Jin, S.; Wang, C.C.L. Support slimming for single material based additive manufacturing. Comput.-Aided Des. 2015, 65, 1–10. [Google Scholar] [CrossRef]
- Pan, Y.; Zhou, C.; Chen, Y.; Partanen, J. Multitool and multi-axis computer numerically controlled accumulation for fabricating conformal features on curved surfaces. J. Manuf. Sci. Eng. 2014, 136, 031007. [Google Scholar] [CrossRef]
- Keating, S.; Oxman, N. Compound fabrication: A multi-functional robotic platform for digital design and fabrication. Robot. Comput.-Integr. Manuf. 2013, 29, 439–448. [Google Scholar] [CrossRef]
- Song, X.; Pan, Y.; Chen, Y. Development of a low-cost parallel kinematic machine for multidirectional additive manufacturing. J. Manuf. Sci. Eng. 2015, 137, 021005. [Google Scholar] [CrossRef]
- Wu, C.; Dai, C.; Fang, G.; Liu, Y.-J.; Wang, C.C.L. RoboFDM: A robotic system for support-free fabrication using FDM. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1175–1180. [Google Scholar] [CrossRef]
- Wu, R.; Peng, H.; Guimbretière, F.; Marschner, S. Printing arbitrary meshes with a 5DOF wireframe printer. ACM Trans. Graph. 2016, 35, 1–9. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.; Hu, X.; Song, G.; Liu, Z.; Yu, L.; Liu, L. FrameFab: Robotic fabrication of frame shapes. ACM Trans. Graph. 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Xu, K.; Li, Y.; Chen, L.; Tang, K. Curved layer based process planning for multi-axis volume printing of freeform parts. Comput.-Aided Des. 2019, 114, 51–63. [Google Scholar] [CrossRef]
- Xie, F.; Jing, X.; Zhang, C.; Chen, S.; Bi, D.; Li, Z.; He, D.; Tang, K. Volume decomposition for multi-axis support-free and gouging-free printing based on ellipsoidal slicing. Comput.-Aided Des. 2022, 143, 103135. [Google Scholar] [CrossRef]
- Shan, Y.; Shui, Y.; Hua, J.; Mao, H. Additive manufacturing of non-planar layers using isothermal surface slicing. J. Manuf. Process. 2023, 86, 326–335. [Google Scholar] [CrossRef]
- Zhang, T.; Fang, G.; Huang, Y.; Dutta, N.; Lefebvre, S.; Kilic, Z.M.; Wang, C.C.L. S3-Slicer: A general slicing framework for multi-axis 3D printing. ACM Trans. Graph. 2022, 41, 1–15. [Google Scholar] [CrossRef]
- Luo, L.; Baran, I.; Rusinkiewicz, S.; Matusik, W. Chopper: Partitioning models into 3D-printable parts. ACM Trans. Graph. 2012, 31, 1–9. [Google Scholar] [CrossRef]
- Wei, X.; Qiu, S.; Zhu, L.; Feng, R.; Tian, Y.; Xi, J.; Zheng, Y. Toward support-free 3D printing: A skeletal approach for partitioning models. IEEE Trans. Vis. Comput. Graph. 2018, 24, 2799–2812. [Google Scholar] [CrossRef]
- Hu, R.; Li, H.; Zhang, H.; Cohen-Or, D. Approximate pyramidal shape decomposition. ACM Trans. Graph. 2014, 33, 1–12. [Google Scholar] [CrossRef]
- Bi, D.; Duan, M.; Lau, T.Y.; Xie, F.; Tang, K. Strength-enhanced volume decomposition for multi-directional additive manufacturing. Addit. Manuf. 2023, 69, 103529. [Google Scholar] [CrossRef]
- Wu, C.; Dai, C.; Fang, G.; Liu, Y.-J.; Wang, C.C.L. General support-effective decomposition for multi-directional 3D printing. arXiv 2019, arXiv:1812.00606. [Google Scholar] [CrossRef]
- Wu, C.; Liu, Y.-J.; Wang, C.C.L. Learning to accelerate decomposition for multi-directional 3D printing. IEEE Robot. Autom. Lett. 2020, 5, 5897–5904. [Google Scholar] [CrossRef]
- Hannay, J.H.; Nye, J.F. Fibonacci spirals and the upper hemisphere. J. Phys. A Math. Gen. 2004, 37, 11591–11601. [Google Scholar] [CrossRef]
- Gunantara, N. A Review of Multi-Objective Optimization: Methods and Its Applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Lemons, S.; Linares López, C.; Holte, R.C.; Ruml, W. Beam Search: Faster and Monotonic. Proc. Int. Conf. Autom. Plan. Sched. 2022, 32, 222–230. [Google Scholar] [CrossRef]



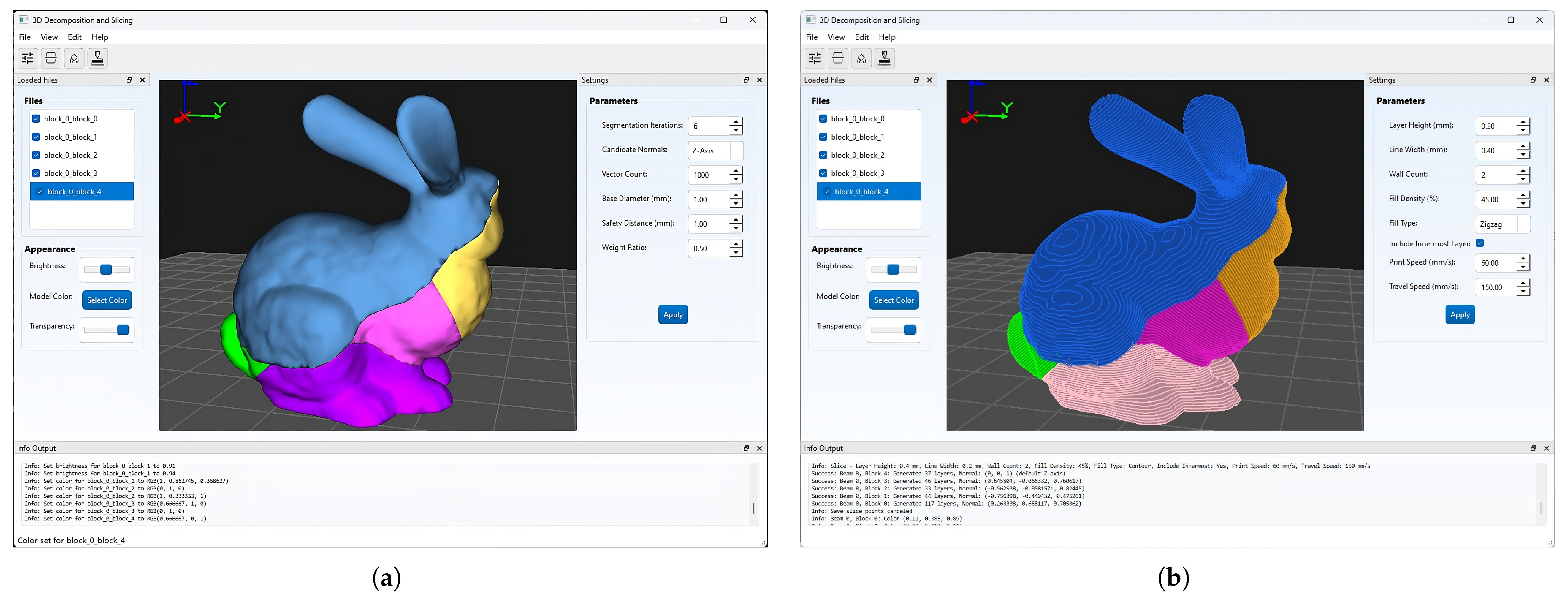
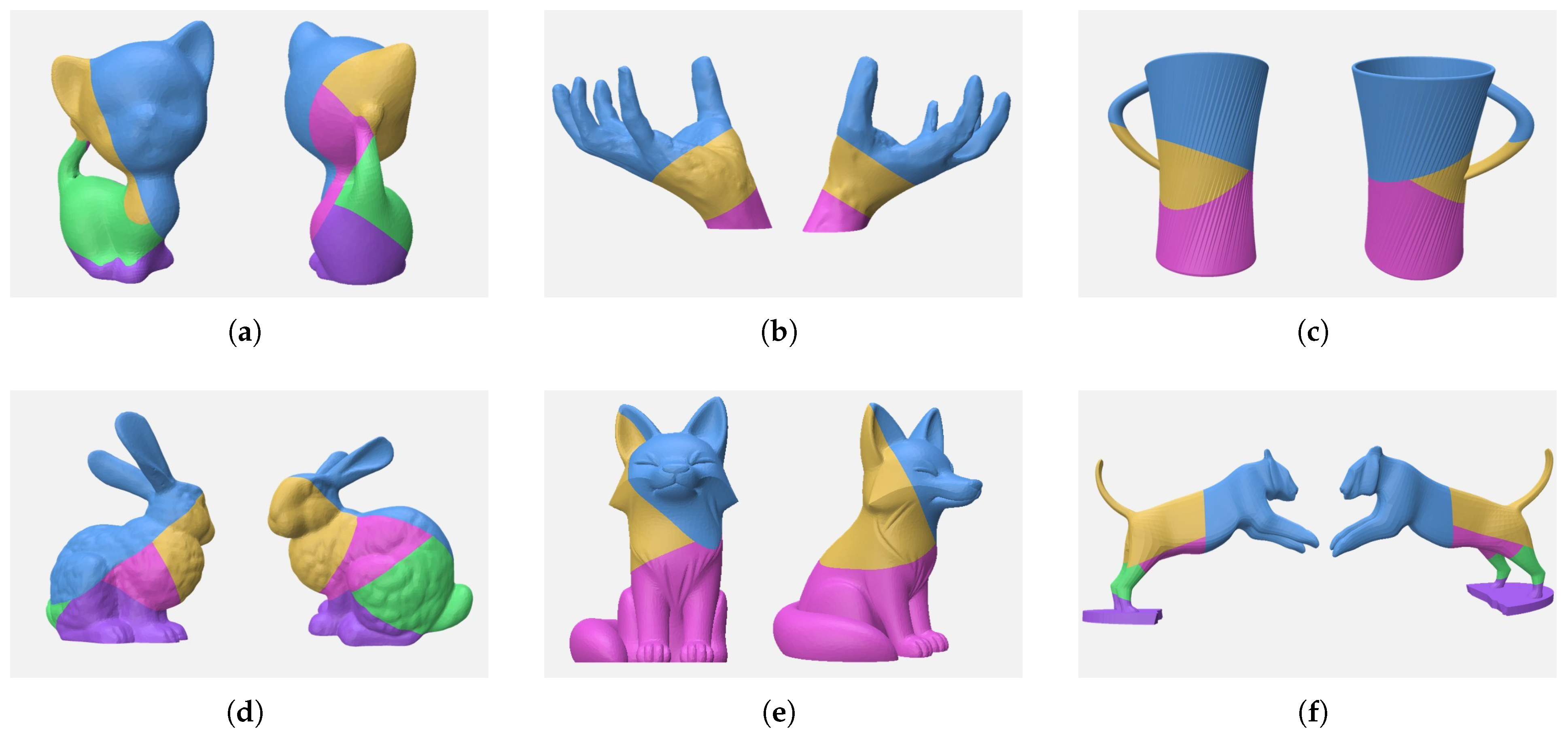
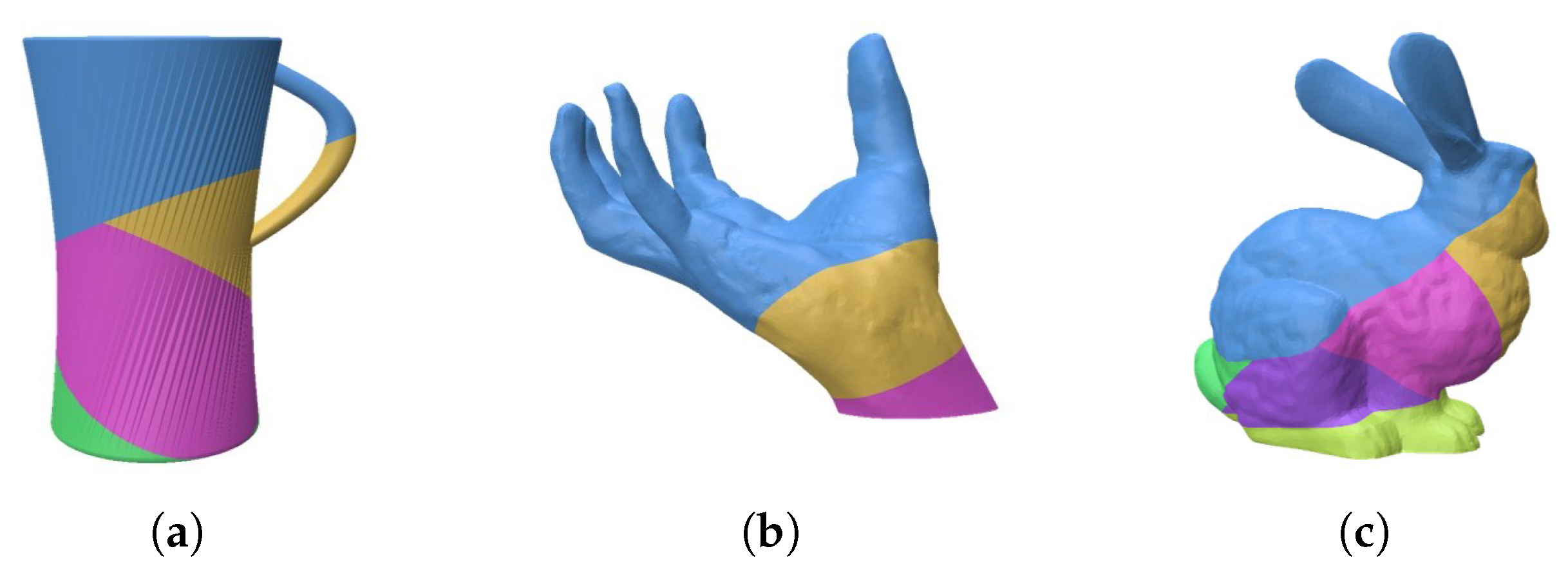

| Model | Faces | Part | Computing Time (s) | Overhanging Area (mm2) | |
|---|---|---|---|---|---|
| Before | After | ||||
| Bunny | 20,000 | 5 | 10.3 | 266.05 | 0 |
| Kitten | 10,000 | 5 | 4.6 | 321.09 | 0.71 |
| Cup | 16,462 | 3 | 3.6 | 114.01 | 0 |
| Hand | 34,198 | 3 | 5.3 | 798.91 | 0 |
| Fox | 14,282 | 3 | 5.5 | 58.51 | 0.87 |
| Tiger | 9052 | 5 | 6.2 | 426.81 | 17.30 |
| Model | Layer Thickness (mm) | Filament Length (mm) | Print Time (min) | ||
|---|---|---|---|---|---|
| Fixed Dir | Multi-Dir | Fixed Dir | Multi-Dir | ||
| Fox | 0.25 | 2425.30 | 1891.41 | 43 | 31 |
| Bunny | 0.25 | 6443.68 | 5319.68 | 98 | 78 |
| Hand | 0.25 | 6569.17 | 4996.85 | 112 | 79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Qin, Q.; Chen, S.; Liu, X.; Cui, L. Support-Free 3D Printing Based on Model Decomposition. Micromachines 2025, 16, 1316. https://doi.org/10.3390/mi16121316
Han X, Qin Q, Chen S, Liu X, Cui L. Support-Free 3D Printing Based on Model Decomposition. Micromachines. 2025; 16(12):1316. https://doi.org/10.3390/mi16121316
Chicago/Turabian StyleHan, Xingguo, Qijin Qin, Shizheng Chen, Xuan Liu, and Lixiu Cui. 2025. "Support-Free 3D Printing Based on Model Decomposition" Micromachines 16, no. 12: 1316. https://doi.org/10.3390/mi16121316
APA StyleHan, X., Qin, Q., Chen, S., Liu, X., & Cui, L. (2025). Support-Free 3D Printing Based on Model Decomposition. Micromachines, 16(12), 1316. https://doi.org/10.3390/mi16121316




