Piezoelectric Energy Harvester with Zigzag Root Section for Self-Powered Transformer Monitoring
Abstract
1. Introduction
2. System Configuration and Modeling
2.1. System Configuration
2.2. Mathematical Modeling
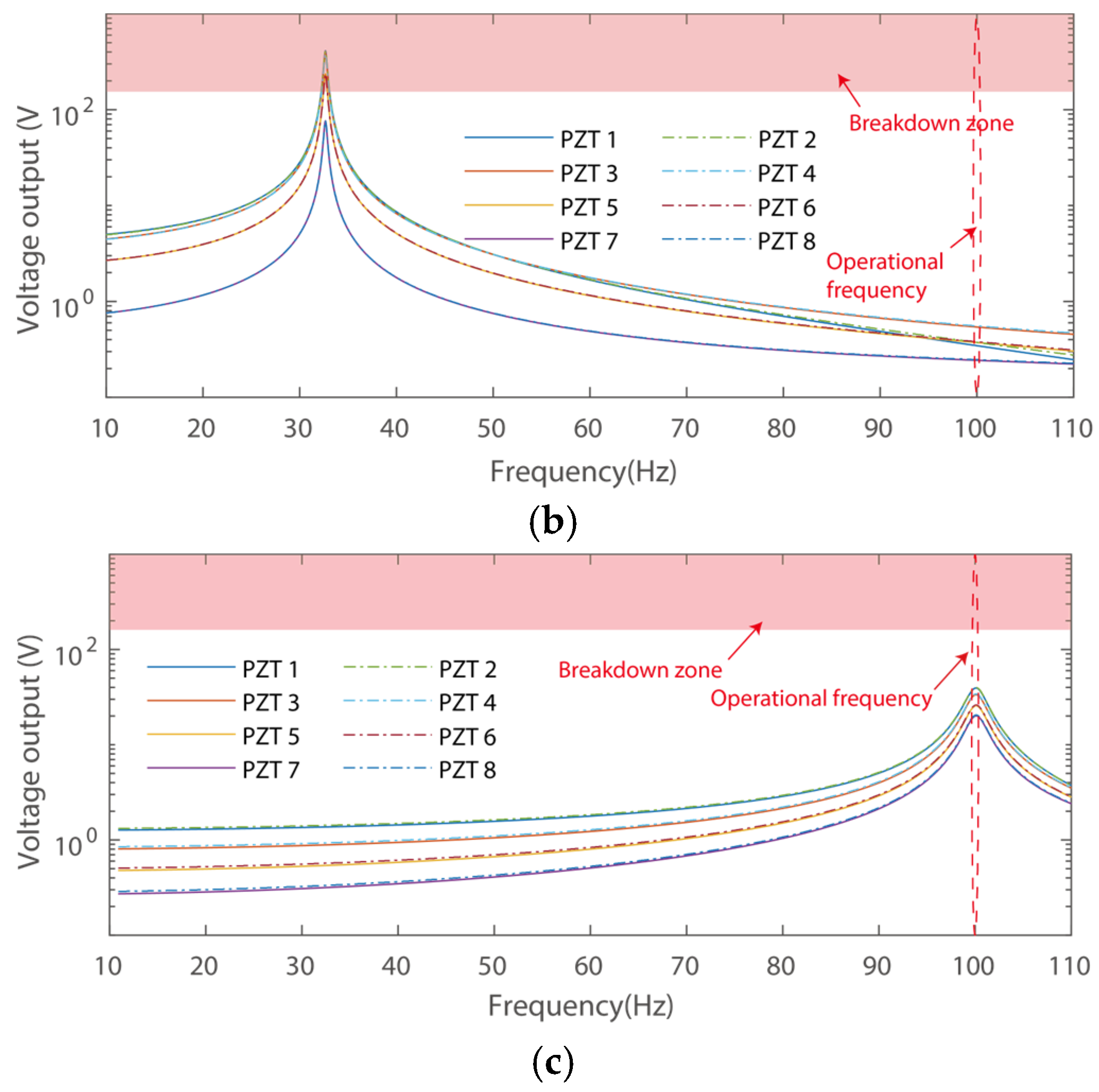
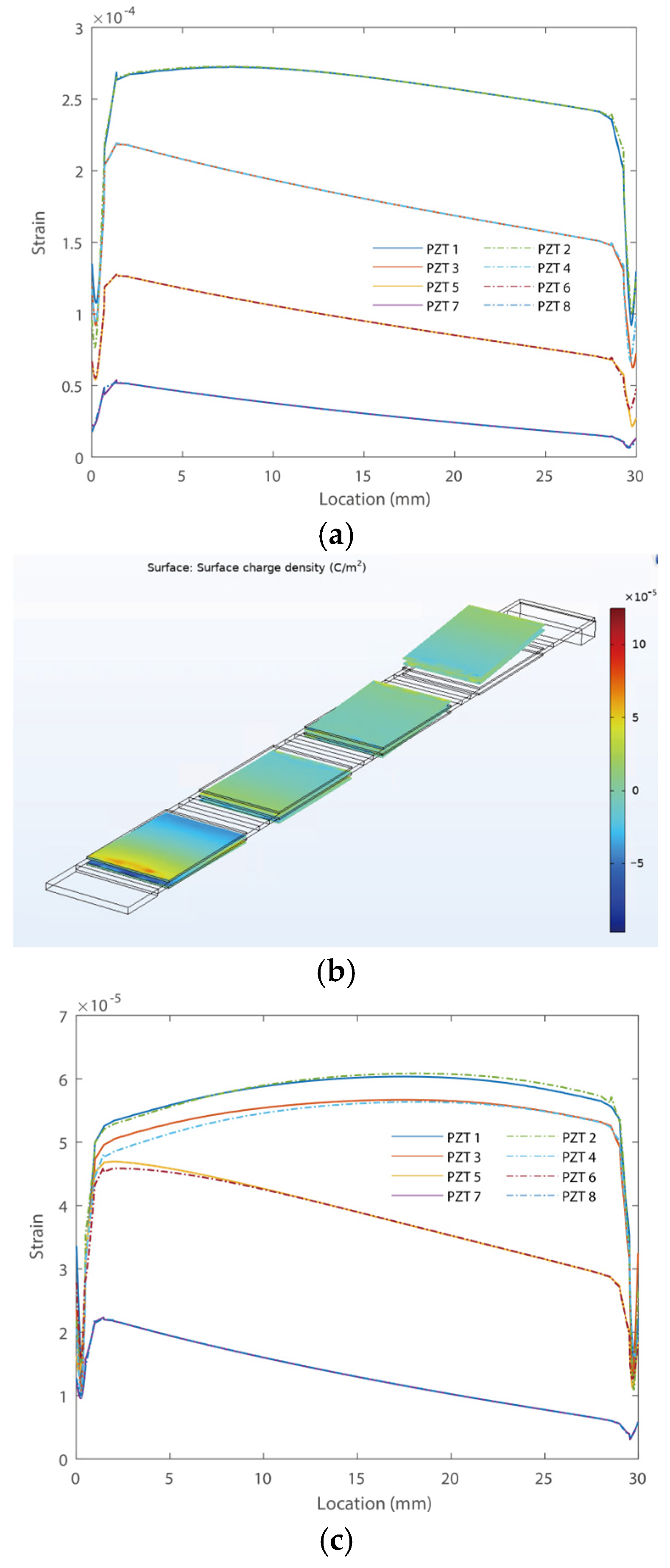
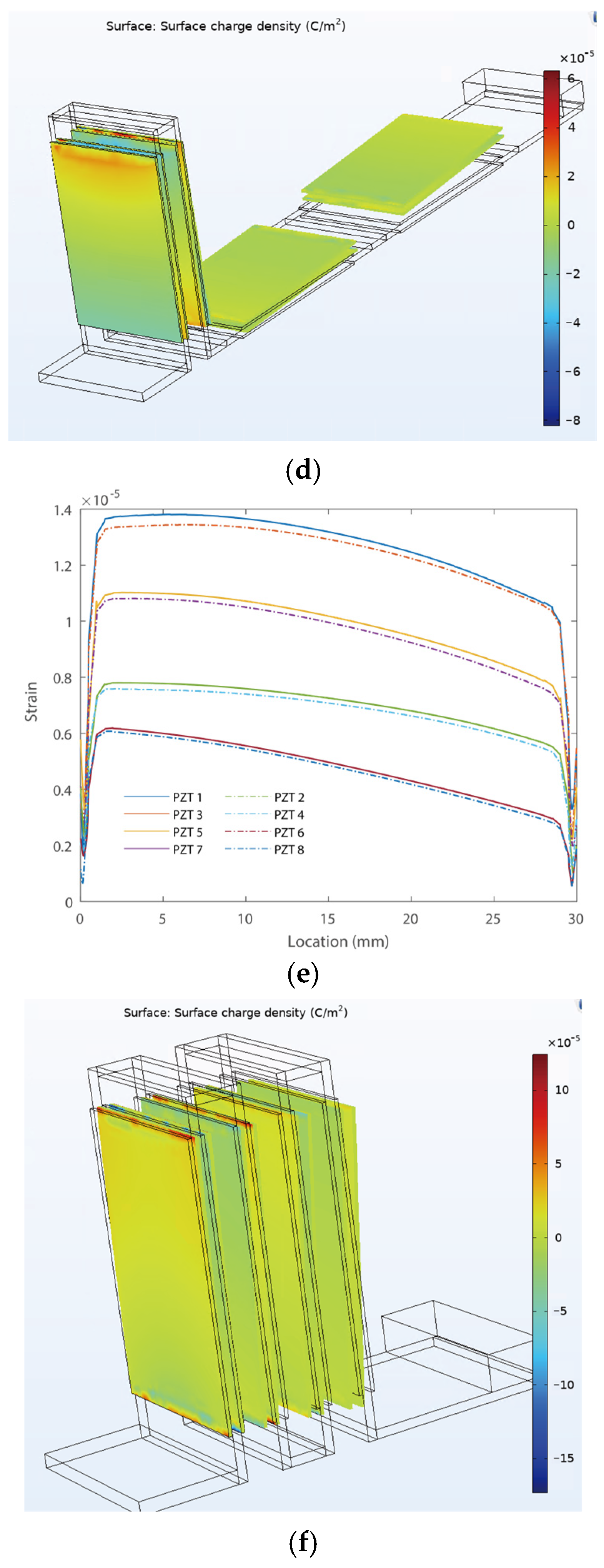
3. Case Studies
4. Experimental Results and Discussion
4.1. Experimental Setup
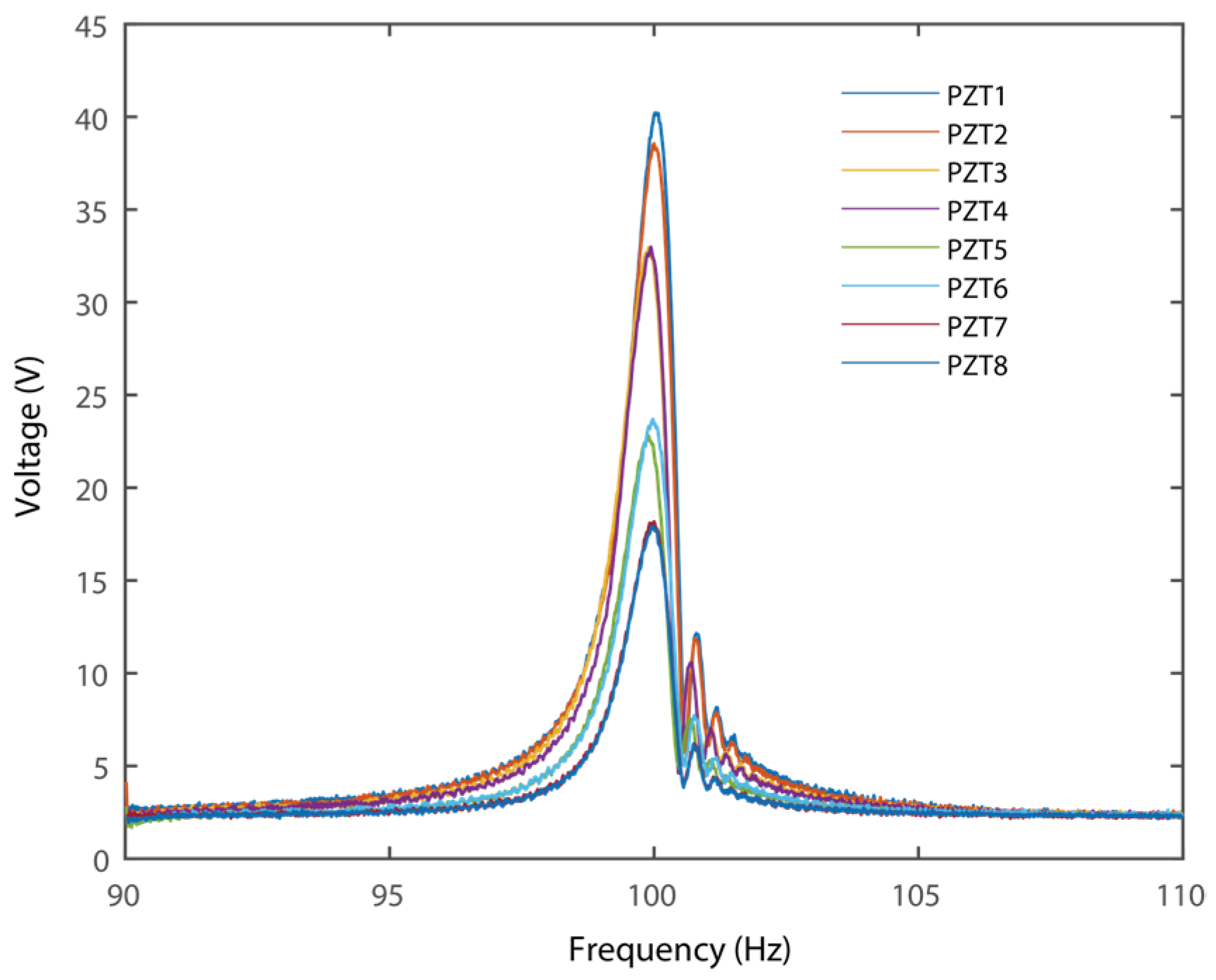
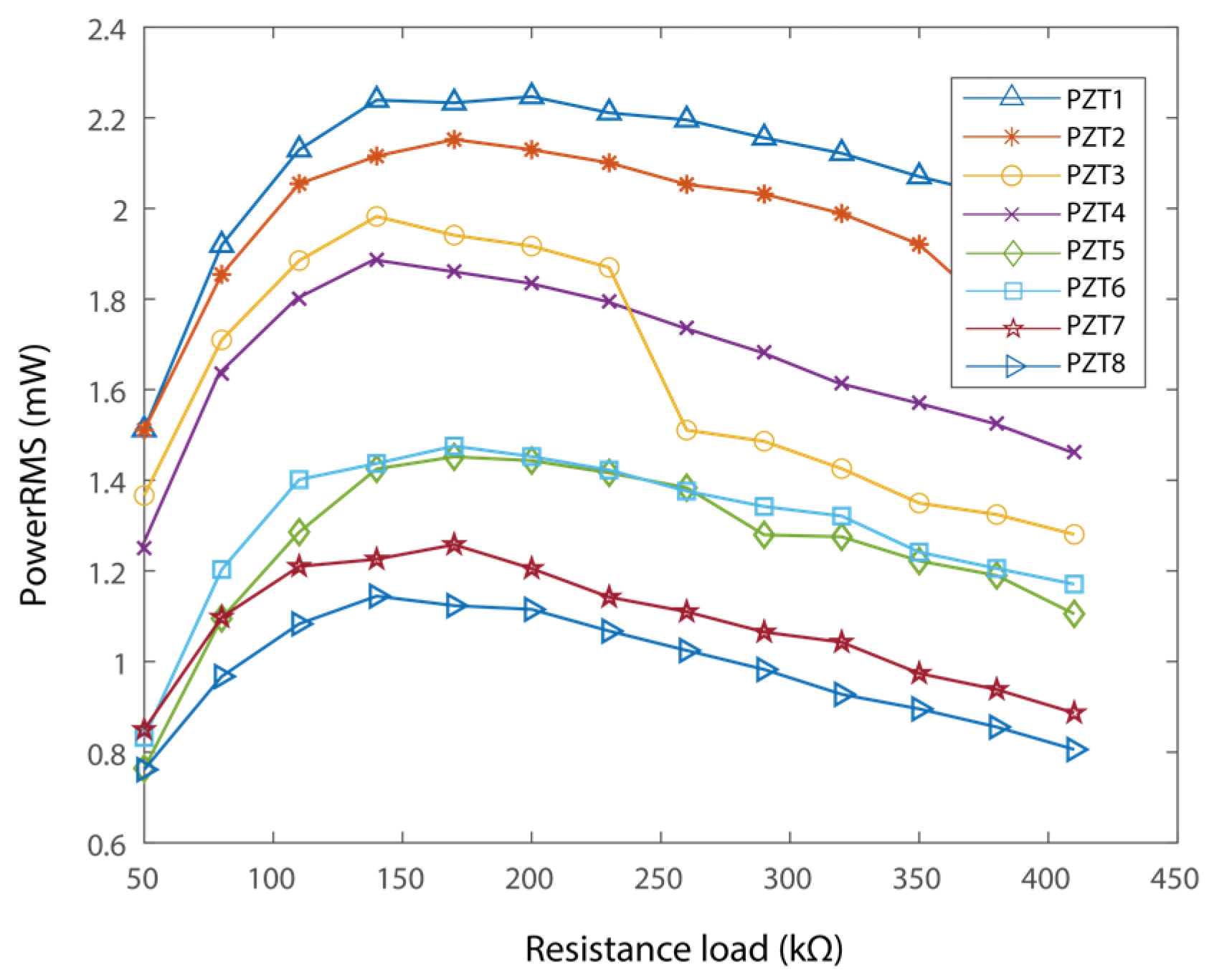
4.2. Output Performance
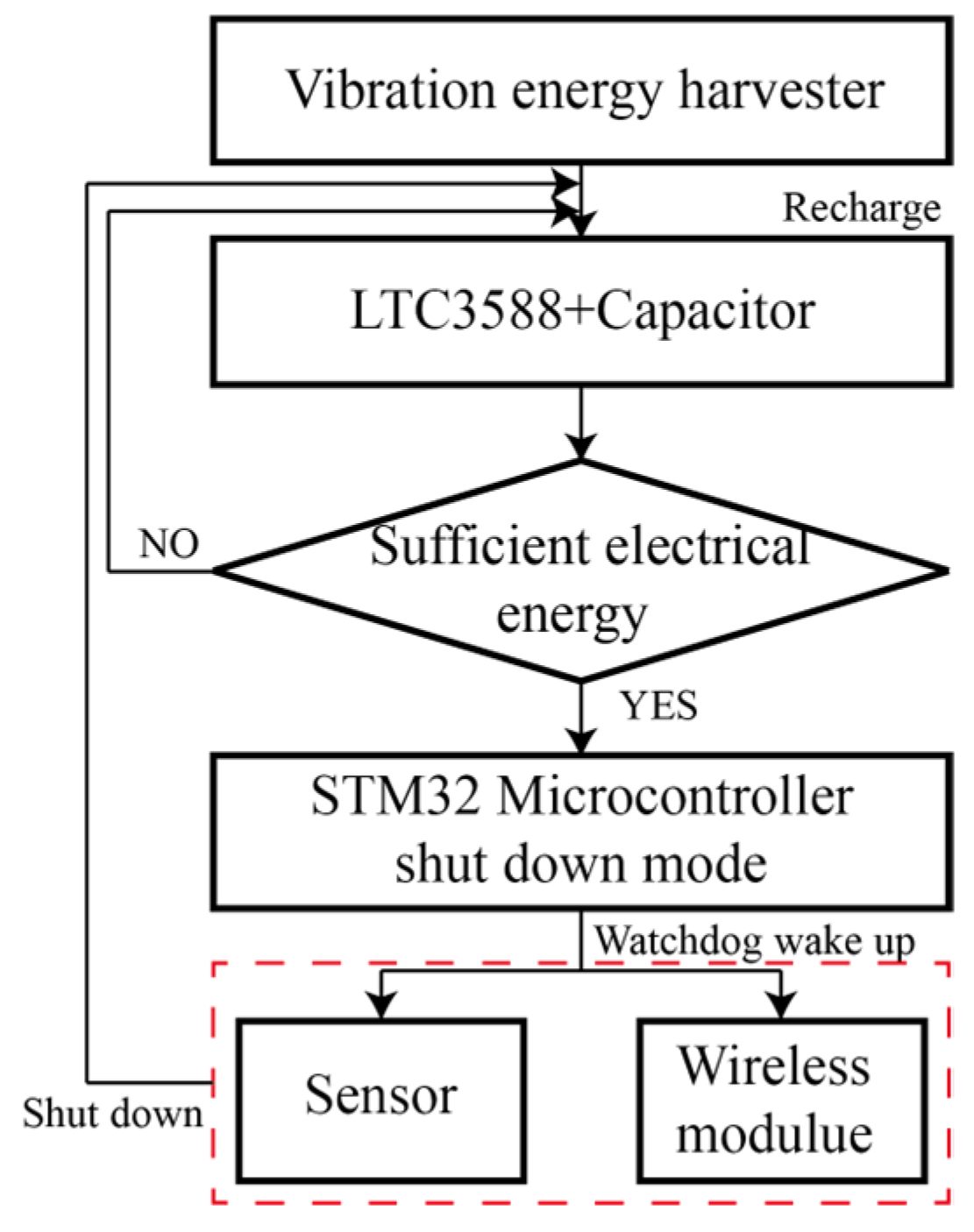
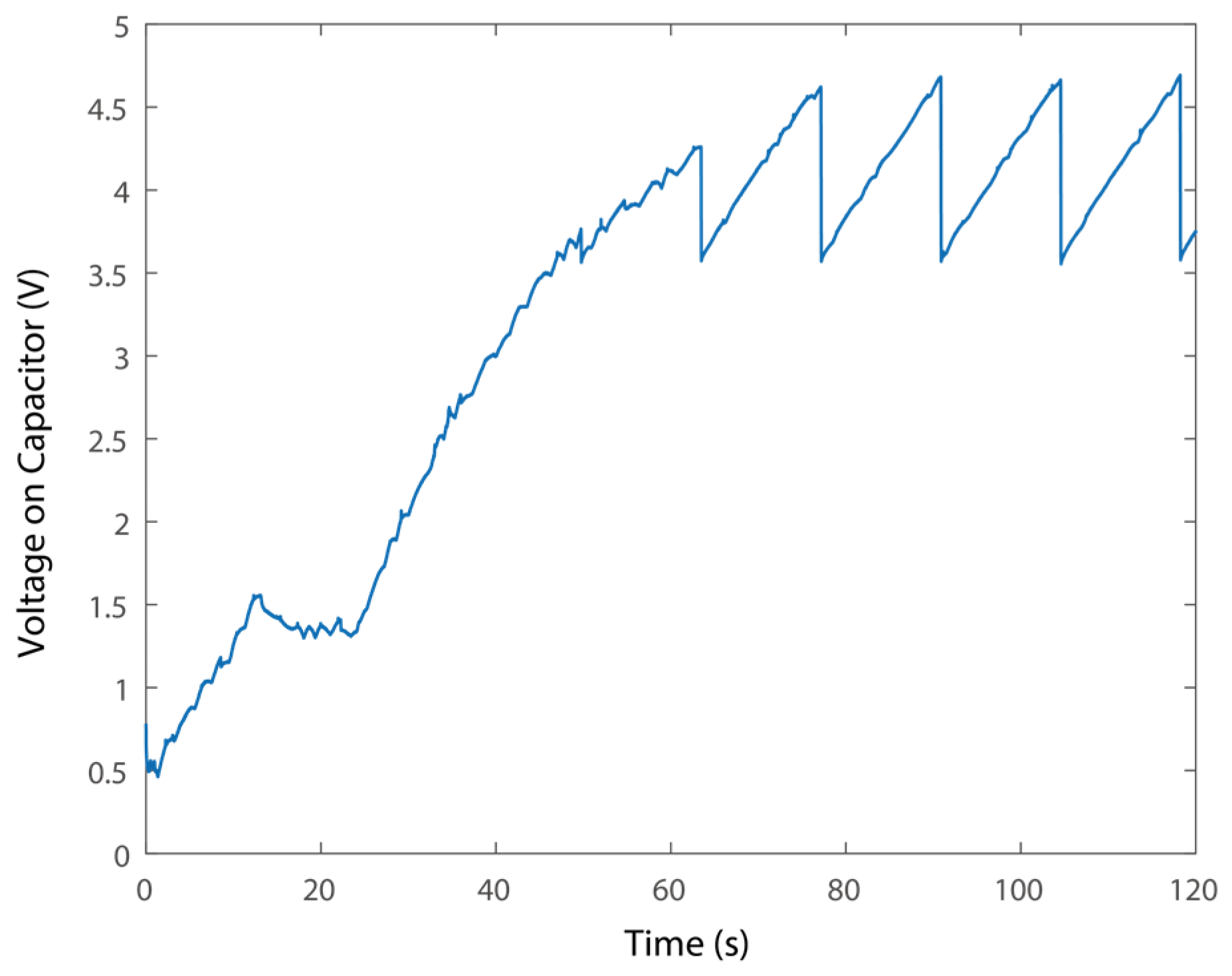
4.3. Self-Powered Sensing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, H.S.; Kim, J.H.; Kim, J. A Review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2018, 96, 1457–1486. [Google Scholar] [CrossRef]
- Paradiso, J.; Starner, T. Energy scavenging for mobile and wireless electronics. IEEE Pervas. Comput. 2005, 4, 18–27. [Google Scholar] [CrossRef]
- Priya, S. Advances in energy harvesting using low profile piezoelectric transducers. J. Electroceram. 2007, 19, 165–182. [Google Scholar] [CrossRef]
- Emine, Z.; Fehmi, N.; Najib, K. Nonlinear dynamics of a double pendulum energy harvesting device for continuously rotating systems. Phys. Scr. 2024, 99, 065273. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Dariusz, G.; Piotr, M. Piezoelectric energy harvesting based on macro fiber composite from a rotating shaft. Phys. Scr. 2019, 94, 095802. [Google Scholar] [CrossRef]
- Jiang, S.N.; Hu, Y.T. Analysis of a piezoelectric bimorph plate with a central-attached mass as an energy harvester. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007, 54, 1463–1469. [Google Scholar] [CrossRef]
- Xu, J.W.; Xia, D.W.; Lai, Z.H.; Chen, G.; Dai, W.X.; Wang, J.X.; Yang, H.X. Experimental study of vibration modes switching based triple frequency-up converting energy harvesting with pre-biased displacement. Smart Mater. Struct. 2024, 33, 045035. [Google Scholar] [CrossRef]
- Kim, H.W. Energy harvesting using a piezoelectric ‘cymbal’ transducer in dynamic environment Japan. J. Appl. Phys. 2004, 1, 6178–6183. [Google Scholar] [CrossRef]
- Shenck, N.S.; Paradiso, J.A. Energy scavenging with shoe-mounted piezoelectrics. IEEE Micro 2001, 21, 30–42. [Google Scholar] [CrossRef]
- Xu, J.W.; Liu, Y.B.; Shao, W.W.; Feng, Z. Optimization of a right-angle piezoelectric cantilever using auxiliary beams with different stiffness levels for vibration energy harvesting. Smart Mater. Struct. 2012, 21, 065017. [Google Scholar] [CrossRef]
- Xu, J.W.; Shao, W.W.; Kong, F.R.; Feng, Z.H. Right-angle piezoelectric cantilever with improved energy harvesting efficiency. Appl. Phys. Lett. 2010, 96, 152904. [Google Scholar] [CrossRef]
- Baker, J.; Roundy, S.; Wright, P. Alternatives geometries for increasing power density in vibration energy scavenging for wireless sensor networks. In Proceedings of the 3rd International Energy Conversion Engineering Conference, San Francisco, CA, USA, 15–18 August 2005; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005; pp. 959–970. [Google Scholar]
- Goldschmidtboeing, F.; Woias, P. Characterization of different beam shapes for piezoelectric energy harvesting. J. Micromech. Microeng. 2008, 18, 104013. [Google Scholar] [CrossRef]
- Friswell, M.I.; Adhikari, S. Sensor shape design for piezoelectric cantilever beams to harvest vibration energy. J. Appl. Phys. 2010, 108, 014901. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, Q.; Zhao, Y.P. Modeling analysis of surface stress on a rectangular cantilever beam. J. Phys. D Appl. Phys. 2004, 37, 2140. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Toward Broadband Vibration-based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1867–1897. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Frequency tuning of piezoelectric energy harvesters by magnetic force. Smart Mater. Struct. 2012, 21, 035019. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X. Nonlinear vibration energy harvesting with adjustable stiffness, damping and inertia. Nonlinear Dyn. 2017, 88, 79–95. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.; Kobayashi, T.; Tay, C.J.; Quan, C. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers. Smart Mater. Struct. 2012, 21, 035005. [Google Scholar] [CrossRef]
- Xu, J.; Tang, J. Multi-directional vibration energy harvesting by internal resonance. Appl. Phys. Lett. 2015, 107, 21. [Google Scholar] [CrossRef]
- Xu, J.; Tang, J. Modeling and analysis of piezoelectric cantilever-pendulum system for multi-directional energy harvesting. J. Intel. Mat. Syst. Str. 2017, 28, 323–338. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, W. Internal resonance energy harvesting. J. Appl. Mech. 2015, 28, 031004. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, L. Investigation on the characteristics of a novel internal resonance galloping oscillator for concurrent aeroelastic and base vibratory energy harvesting. Mech. Syst. Signal Process. 2022, 173, 109022. [Google Scholar] [CrossRef]
- Shahruz, S.M. Design of mechanical band-pass filters for energy scavenging. J. Sound Vib. 2006, 292, 987–998. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y. A nonlinear piezoelectric energy harvester with magnetic oscillator. Appl. Phys. Lett. 2012, 101, 094102. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal Process. 2017, 85, 71–81. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, W.; Zhou, Z.; Zhu, P.; Du, Q. Piezomagnetoelastic energy harvesting from bridge vibrations using bi-stable characteristics. Energy 2023, 263, 125859. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. D Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Masana, R.; Daqaq, M.F. Relative performance of a vibratory energy harvester in mono- and bi-stable potential. J. Sound Vib. 2011, 330, 6036–6052. [Google Scholar] [CrossRef]
- Shao, N.; Chen, Z.; Wang, X.; Zhang, C.; Xu, J.; Xu, X.; Yan, R. Modeling and analysis of magnetically coupled piezoelectric dual-beam with an annular potential energy function for broadband vibration energy harvesting. Nonlinear Dyn. 2023, 111, 11911–11937. [Google Scholar] [CrossRef]
- Shao, N.; Yang, H.; Huang, Z.; Xu, J.; Xu, X.; Yan, R. Improving energy harvesting by nonlinear dualbeam energy harvester with an annular potential energy function. Smart Mater. Struct. 2023, 32, 015018. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Liu, S.; Wang, W.; Lin, J. Impact-induced high-energy orbits of nonlinear energy harvesters. Appl. Phys. Lett. 2015, 106, 093901. [Google Scholar] [CrossRef]
- Zhu, W.; Morandini, M. Nonlinear Smart Beam Model for Energy Harvesting. J. Vib. Acoust. 2021, 143, 051008. [Google Scholar] [CrossRef]
- Zou, D.; Liu, G.; Rao, Z.; Tan, T.; Zhang, W.; Liao, W.-H. Design of a multi-stable piezoelectric energy harvester with programmable equilibrium point configurations. Appl. Energy 2021, 302, 117585. [Google Scholar] [CrossRef]
- Zou, D.; Liu, G.; Rao, Z.; Tan, T.; Zhang, W.; Liao, W.-H. A device capable of customizing nonlinear forces for vibration energy harvesting, vibration isolation, and nonlinear energy sink. Mech. Syst. Signal Process. 2021, 147, 107101. [Google Scholar] [CrossRef]
- Yang, H.; Shao, N.; Wang, J.; Xu, J.; Xu, H.; Zhang, Y. Experimental analysis of hybrid multiple-layer piezoelectric-solar energy harvester for self-powered wireless sensing. Sustain. Energy Technol. Ass. 2025, 73, 104157. [Google Scholar]
- Wang, M.; Yin, P.; Li, Z.; Sun, Y.; Ding, J.; Luo, J.; Xie, S.; Peng, Y.; Pu, H. Harnessing energy from spring suspension systems with a compressive-mode high-power-density piezoelectric transducer. Energy Convers. Manag. 2020, 220, 113050. [Google Scholar] [CrossRef]
- Lee, S.; Youn, B.D. A New Piezoelectric Energy Harvesting Design Concept: Multimodal Energy Harvesting Skin. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011, 58, 629–645. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, M.; Wu, P.; Gao, L.; Chen, X.; Mu, X. Self-powered transformer intelligent wireless temperature monitoring system based on an ultra-low acceleration piezoelectric vibration energy harvester. Nano Energy 2023, 114, 108662. [Google Scholar] [CrossRef]
- Daniel, J.; Shaun, K.; Richardt, H. Energy Harvesting for a Condition Monitoring Mote. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008. [Google Scholar]
- Li, P.; Wen, Y.; Zhang, Z.; Pan, S. A High-Efficiency Management Circuit Using Multiwinding Upconversion Current Transformer for Power-Line Energy Harvesting. IEEE Trans. Ind. Electron. 2015, 62, 6327–6335. [Google Scholar] [CrossRef]
- Karami, M.A.; Inman, D.J. Analytical modeling and experimental verification of the vibrations of the zigzag microstructure for energy harvesting. J. Vib. Acoust. 2011, 133, 011002. [Google Scholar] [CrossRef]
- Karami, M.A.; Inman, D.J. Electromechanical modeling of the low-frequency zigzag micro-energy harvester. J. Intel. Mater. Syst. Struct. 2011, 22, 271–282. [Google Scholar] [CrossRef]
- Berdy, D.F.; Srisungsitthisunti, P.; Jung, B.; Xu, X.; Rhoads, J.F.; Peroulis, D. Low-frequency meandering piezoelectric vibration energy harvester. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 846–858. [Google Scholar] [CrossRef]
- Bai, X.; Wen, Y.; Li, P.; Yang, J.; Peng, X.; Yue, X. Multi-modal vibration energy harvesting utilizing spiral cantilever with magnetic coupling. Sens. Actuators A Phys. 2014, 209, 78–86. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Sharpes, N.; Abdelkefi, A.; Lee, H.; Priya, S. Low-frequency Zigzag energy harvesters operating in torsion-dominant mode. Appl. Energy 2017, 204, 413–419. [Google Scholar] [CrossRef]
- Shi, C.; Li, F.; Zhao, J. An advanced folded piezoelectric vibration energy harvester with low resonant frequency and high power density. AIP Adv. 2020, 10, 065231. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, M.; Xu, Z.; Chen, H.; Xu, J. A Multiple-Cantilever Piezoelectric Vibration Energy Harvester for Self-Powered CO2 Monitoring in Transformer Substations. Appl. Sci. 2024, 14, 10805. [Google Scholar] [CrossRef]
- Erturk, A.; Renno, J.M.; Inman, D.J. Piezoelectric energy harvesting from an L-shaped beam-mass structure. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 9–13 March 2008; p. 69280I. [Google Scholar]
- Xu, J.; Li, S.; Tang, J. Customized Shaping of Vibration Modes by Acoustic Metamaterial Synthesis. Smart Mater. Struct. 2018, 27, 045001. [Google Scholar] [CrossRef]
- Li, H.; Liu, D.; Wang, J.; Shang, X. Energy Harvesting Using a Torsional Mode L-Shaped Unimorph Structure: Modeling and Experimental Investigations. J. Vib. Acoust. 2020, 142, 011008. [Google Scholar] [CrossRef]
- Tan, T.; Yan, Z.; Ma, K.; Liu, F.; Zhang, W. Nonlinear characterization and performance optimization for broadband bistable energy harvester. Acta Mech. Sin. 2020, 36, 578–591. [Google Scholar] [CrossRef]
- Wang, J.; Wu, B.; Shao, N.; Pu, X.; Xu, J.; Yan, R. Multi-layer annular-stable piezoelectric energy harvester for bi-directional human motion energy harvesting and ECG monitoring. Thin Walled Struct. 2026, 219, 114235. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Y.; Wang, J.; Xia, Z.; Xu, J.; Yan, R. Optimized Variable Reluctance Energy Harvester with Dual Magnet Arrays for Self-Powered Multimodal Monitoring of Rotating Machinery. Mech. Syst. Signal Process. 2026, 242, 113603. [Google Scholar] [CrossRef]

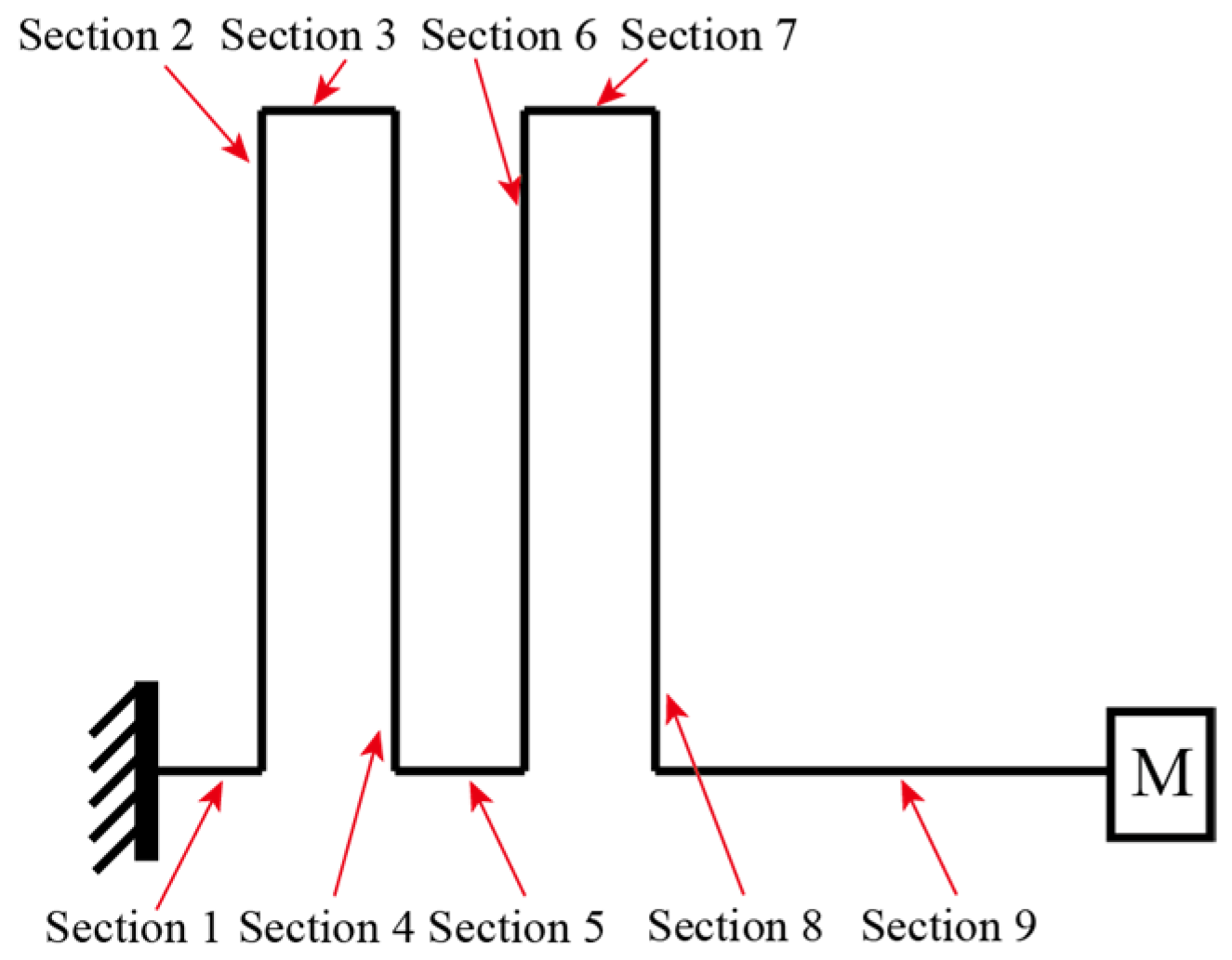






| Physical Length in Longitude Direction | Fully Extended Length | Resonant Frequency | |
|---|---|---|---|
| Case 1 | 188 mm | 188 mm | 22.5 Hz |
| Case 2 | 112 mm | 188 mm | 32.4 Hz |
| Case 3 | 36 mm | 188 mm | 100 Hz |
| Power Output at Resonances (mW) | Power Output at 100 Hz (mW) | |
|---|---|---|
| Case 1 | 526.48 (break down) | 0.069 |
| Case 2 | 248.38 (break down) | 0.013 |
| Case 3 | 15.47 | 15.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Xia, Z.; Xia, Y.; Zhang, R.; Ge, J. Piezoelectric Energy Harvester with Zigzag Root Section for Self-Powered Transformer Monitoring. Micromachines 2025, 16, 1314. https://doi.org/10.3390/mi16121314
Xu J, Xia Z, Xia Y, Zhang R, Ge J. Piezoelectric Energy Harvester with Zigzag Root Section for Self-Powered Transformer Monitoring. Micromachines. 2025; 16(12):1314. https://doi.org/10.3390/mi16121314
Chicago/Turabian StyleXu, Jiawen, Zixuan Xia, Yebao Xia, Ru Zhang, and Jianjun Ge. 2025. "Piezoelectric Energy Harvester with Zigzag Root Section for Self-Powered Transformer Monitoring" Micromachines 16, no. 12: 1314. https://doi.org/10.3390/mi16121314
APA StyleXu, J., Xia, Z., Xia, Y., Zhang, R., & Ge, J. (2025). Piezoelectric Energy Harvester with Zigzag Root Section for Self-Powered Transformer Monitoring. Micromachines, 16(12), 1314. https://doi.org/10.3390/mi16121314





