Femtosecond Laser Polishing of AlN Ceramics and Numerical Simulation of Ablated Morphology
Abstract
1. Introduction
2. Materials and Methods
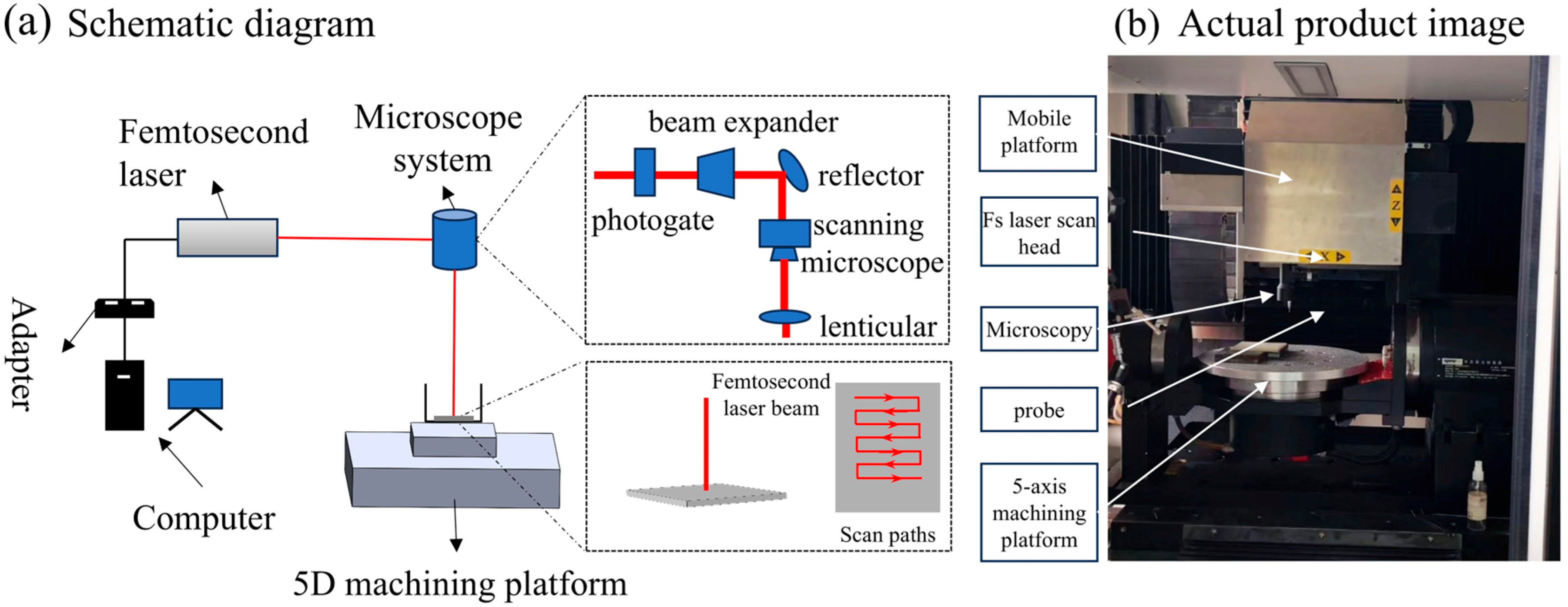
2.1. Experimental Setup and Polishing Experiments
2.2. Numerical Simulation
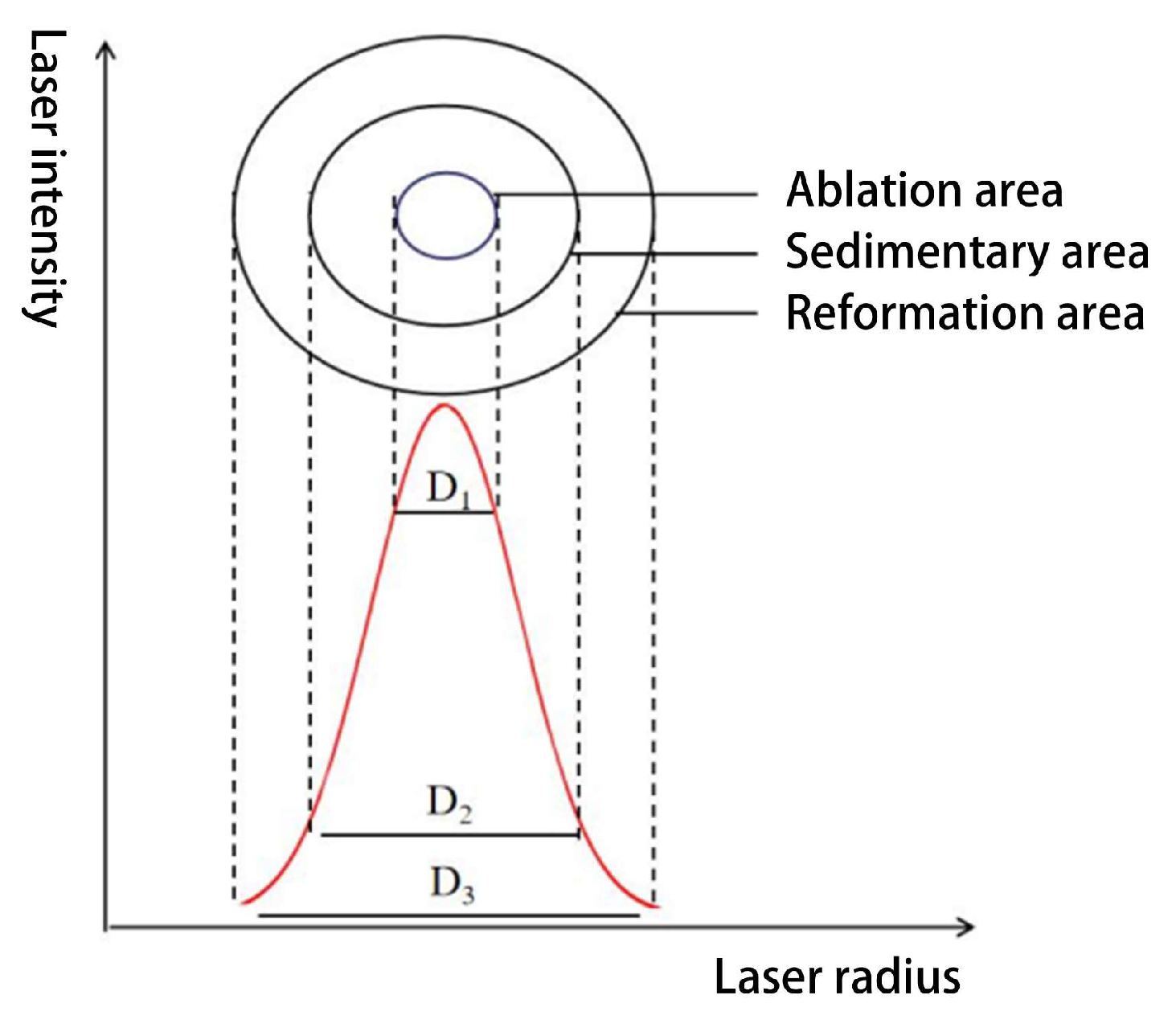
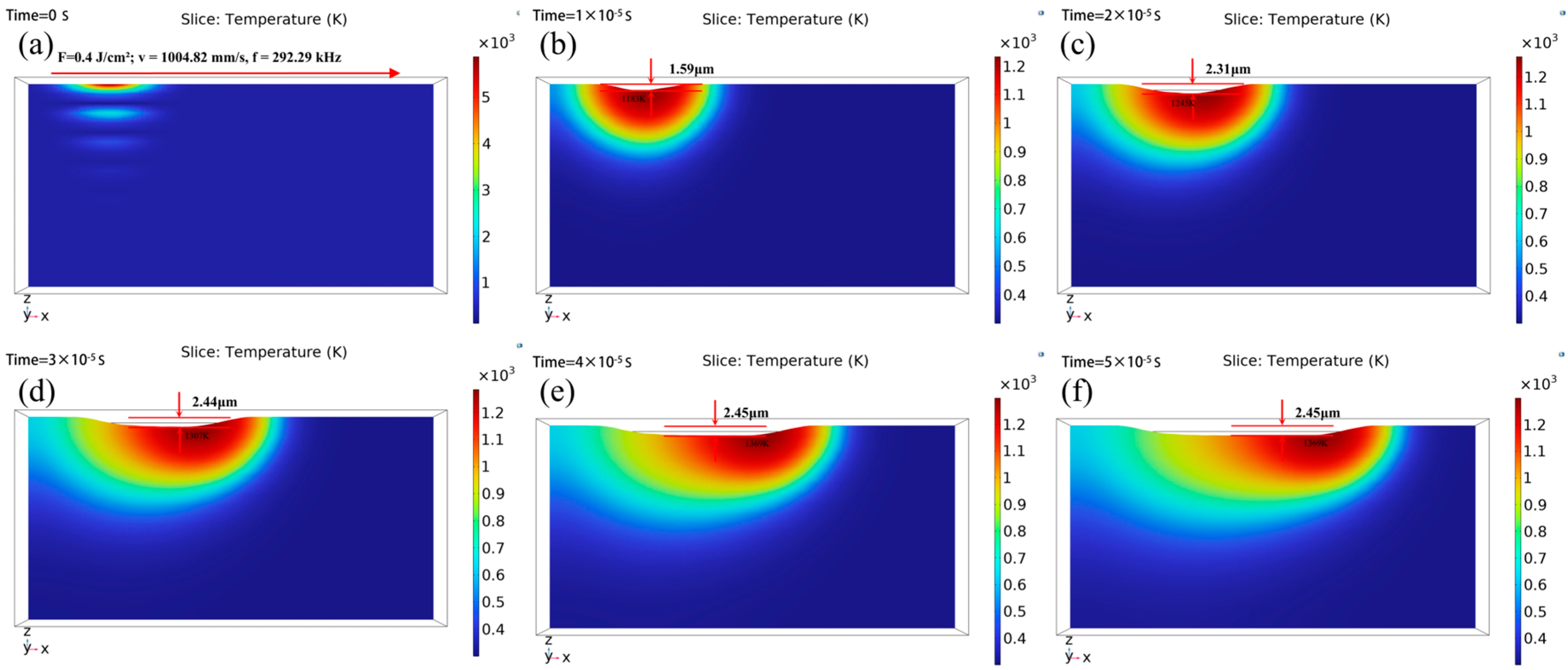
2.2.1. Physical Models and Assumptions
- The laser beam energy follows a Gaussian spatial distribution, ignoring its distortion and fluctuations;
- The substrate is treated as a continuous homogeneous medium, ignoring internal microdefects and anisotropy;
- The processing interface is simplified to an ideal plane, ignoring the influence of surface morphology on energy absorption.
2.2.2. Setting of Laser Heat Source
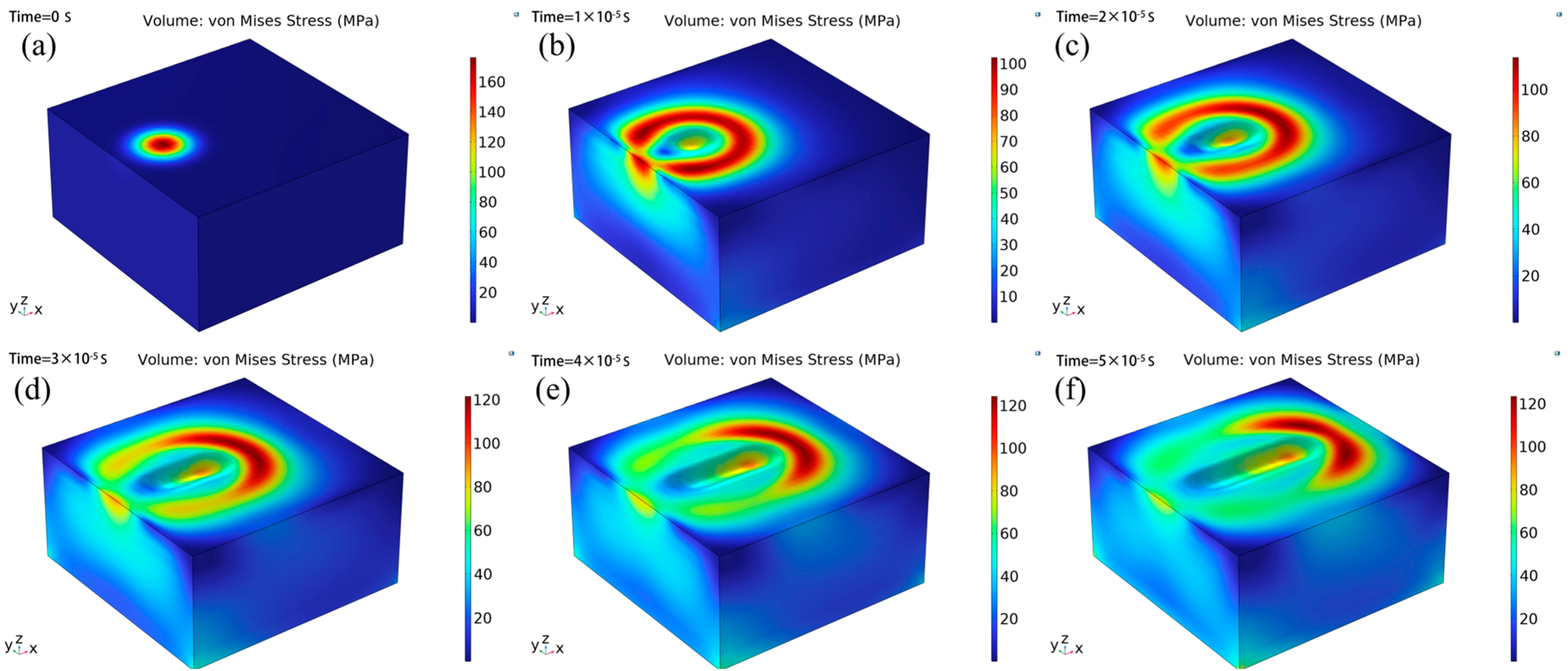
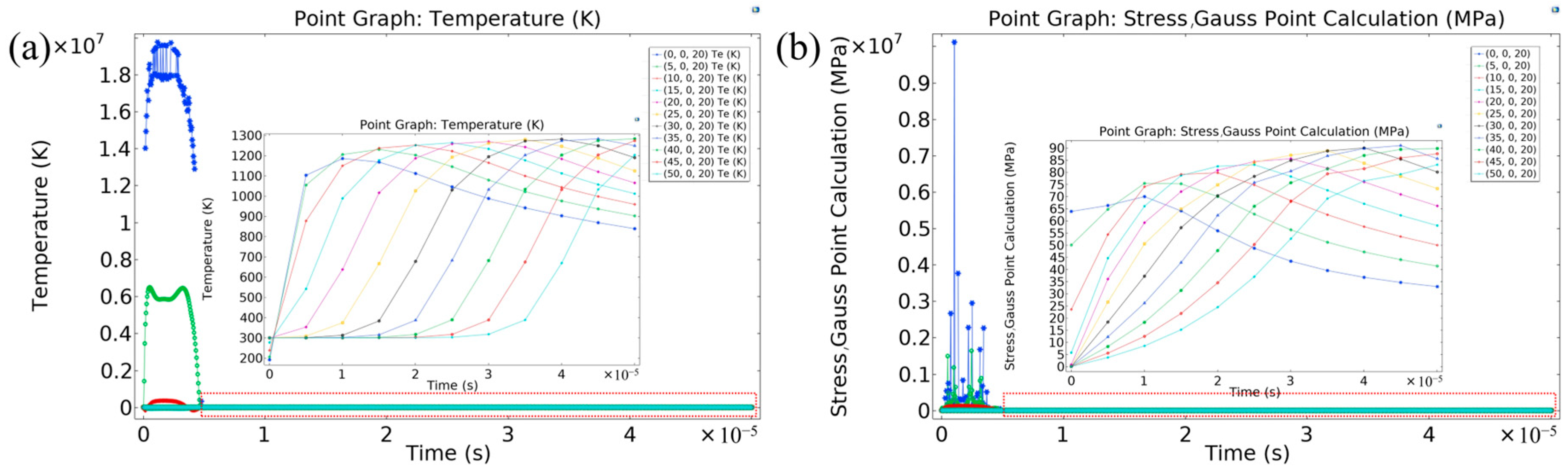
2.2.3. Stress Field Setup
3. Results and Discussion
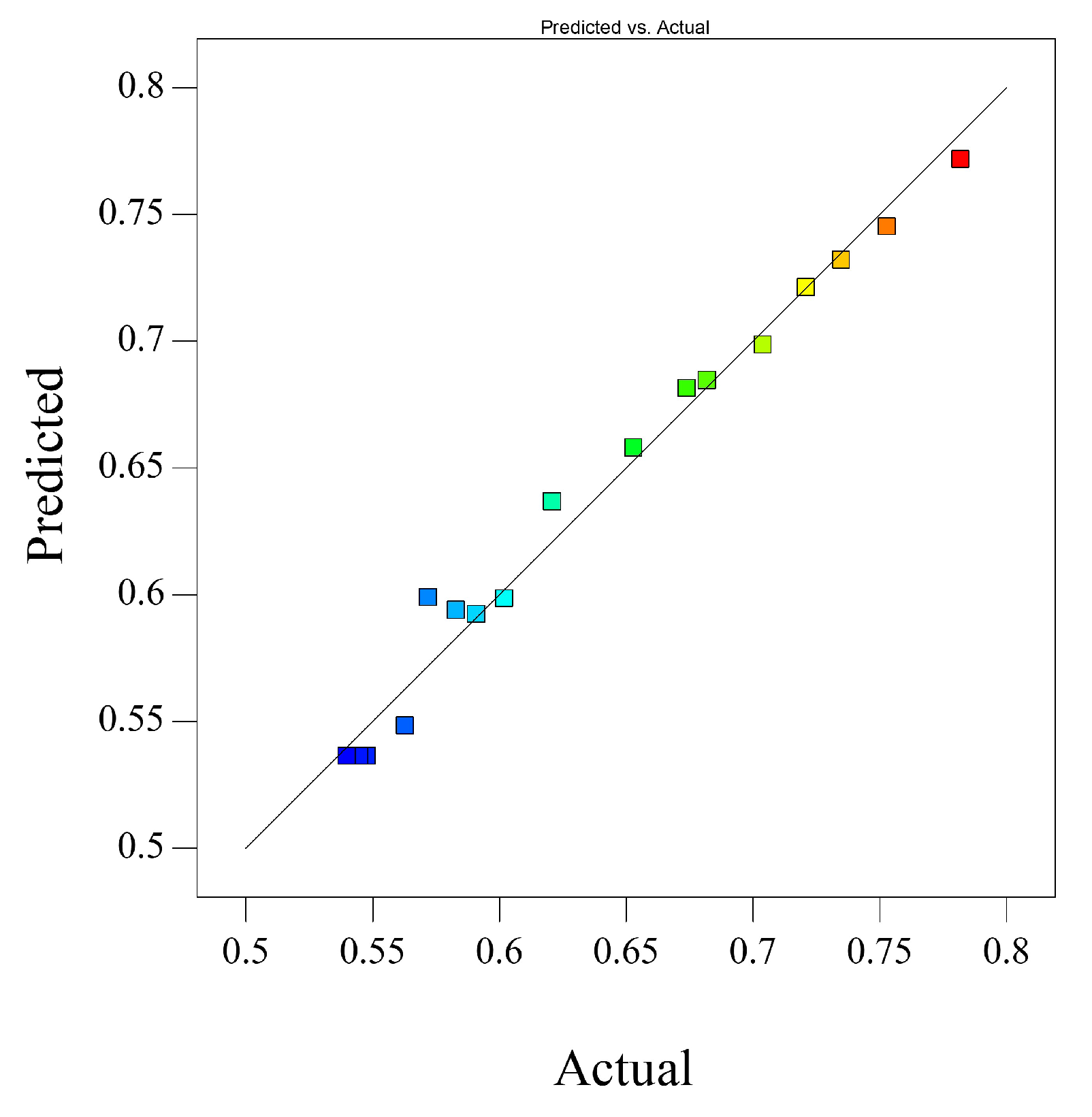
3.1. Construction of a Surface Roughness Prediction Model Using the Response Surface Method
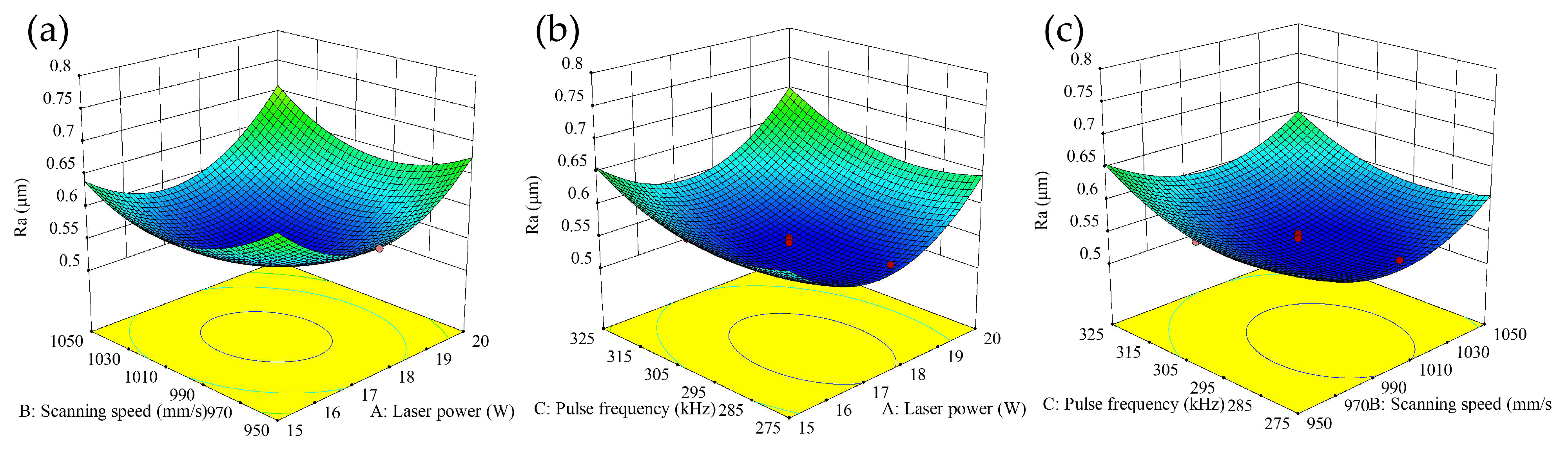
3.2. Mechanism of Influence of Parameter Interaction on Surface Morphology
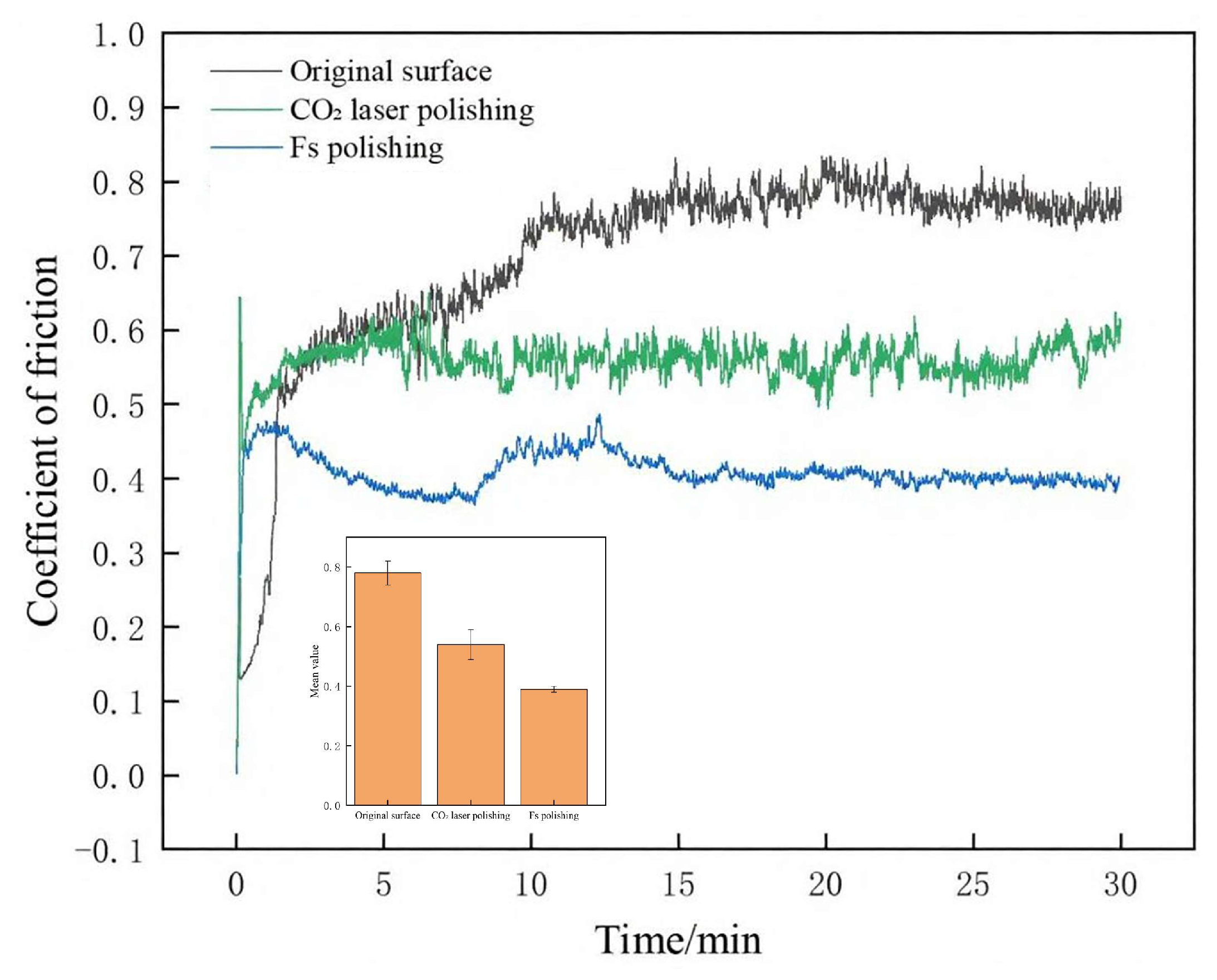
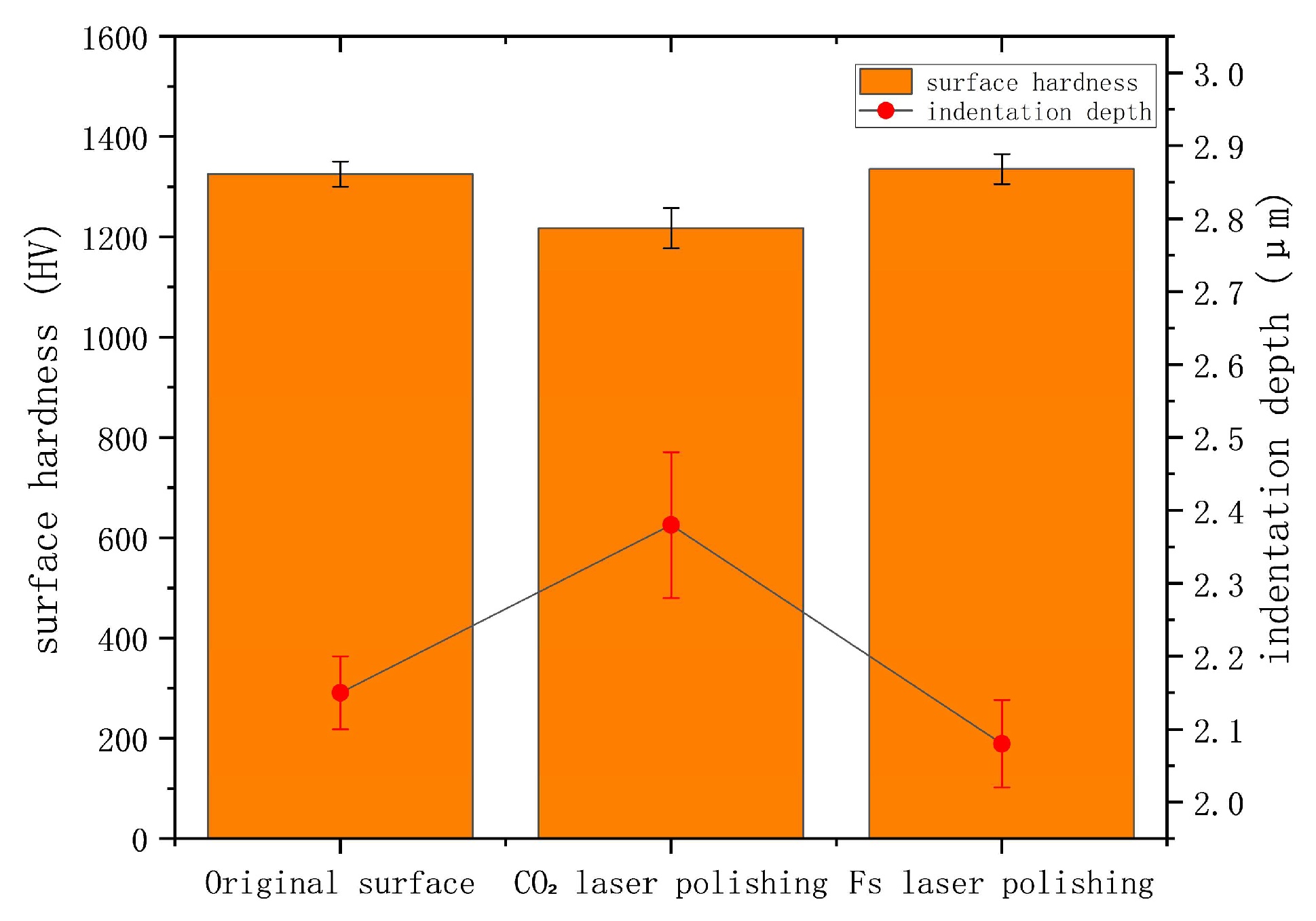
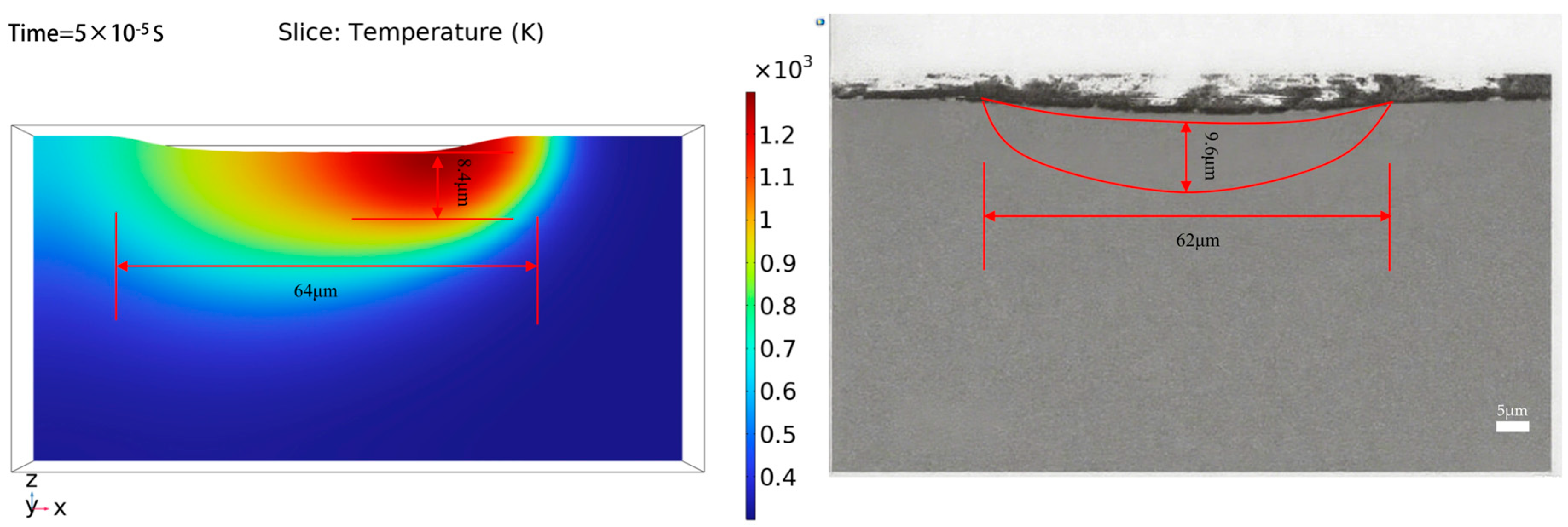
3.3. Characterization of Polished Surface Features and Analysis of Performance Evolution
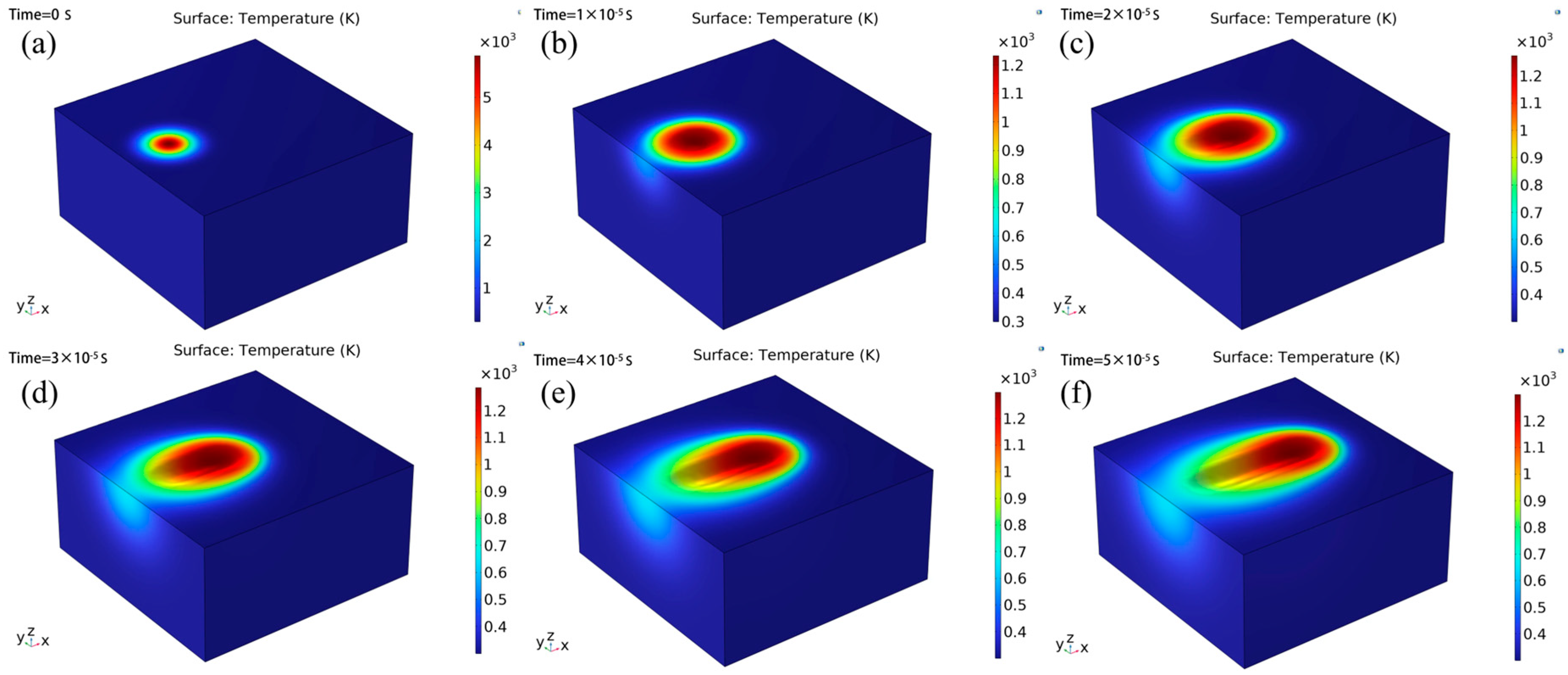
3.4. Simulation Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miyashiro, F.; Iwase, N.; Tsuge, A.; Ueno, F.; Nakahashi, M.; Takahashi, T. High thermal conductivity aluminum nitride ceramic substrates and packages. IEEE Trans. Compon. Hybrids Manuf. Technol. 1990, 13, 313–319. [Google Scholar] [CrossRef]
- Lee, R.R. Development of high thermal conductivity aluminum nitride ceramic. J. Am. Ceram. Soc. 1991, 74, 2242–2249. [Google Scholar] [CrossRef]
- Werdecker, W.; Aldinger, F. Aluminum nitride-an alternative ceramic substrate for high power applications in microcircuits. IEEE Trans. Compon. Hybrids Manuf. Technol. 1984, 7, 399–404. [Google Scholar] [CrossRef]
- Li, H.G. Research on Material Removal Mechanism in Ultra-Precision Grinding of LED Package Substrate. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar] [CrossRef]
- Zhu, P.F. Study of Ultrafast Laser Polishing Technology. Ph.D. Thesis, Xi’an Technological University, Xi’an, China, 2014. [Google Scholar] [CrossRef]
- Sun, R.; Yang, X.; Arima, K.; Kawai, K.; Yamamura, K. High-quality plasma-assisted polishing of aluminum nitride ceramic. CIRP Ann. 2020, 69, 301–304. [Google Scholar] [CrossRef]
- Zhao, L.; Feng, K.; Wang, J.; Xu, L.; Zhao, T.; Lyu, B. Material removal mechanism in Fenton based AlN ceramic substrate polishing process. Ceram. Int. 2025, 51, 8674–8689. [Google Scholar] [CrossRef]
- Krishnan, A.; Fang, F. Review on mechanism and process of surface polishing using lasers. Front. Mech. Eng. 2019, 14, 299–319. [Google Scholar] [CrossRef]
- Chen, B.W.; Sun, S.F.; Wang, X.; Zhang, F.; Shao, Y.; Zhang, L.; Zhao, D.; Wang, P.; Chen, X.; Liu, J.; et al. Research Progress of Laser Polishing Technology for Material Surface. China Surf. Eng. 2021, 34, 74–89. [Google Scholar] [CrossRef]
- Long, Y.; Chen, X.; Jiang, J.; Ji, C.; Feng, S.; Wang, C. Research progress of ultrafast laser ceramic polishing and texturing technology. Aeronaut. Manuf. Technol. 2022, 65, 50–62, 71. [Google Scholar] [CrossRef]
- Vorobyev, A.Y.; Guo, C. Direct femtosecond laser surface nano/microstructuring and its applications. Laser Photonics Rev. 2013, 7, 385–407. [Google Scholar] [CrossRef]
- Hirayama, Y.; Yabe, H.; Obara, M. Selective ablation of AlN ceramic using femtosecond, nanosecond, and microsecond pulsed laser. J. Appl. Phys. 2001, 89, 2943–2949. [Google Scholar] [CrossRef]
- Ihlemann, J.; Scholl, A.; Schmidt, H.; Wolff-Rottke, B. Nanosecond and femtosecond excimer-laser ablation of oxide ceramics. Appl. Phys. A 1995, 60, 411–417. [Google Scholar] [CrossRef]
- Taylor, L.L.; Qiao, J.; Qiao, J. Femtosecond laser polishing of optical materials. In Proceedings of the Optifab 2015, Rochester, NY, USA, 12–15 October 2015; Volume 9633, pp. 165–172. [Google Scholar] [CrossRef]
- Chen, B.C.; Ho, C.Y.; Wen, M.Y.; Chen, C.S.; Ma, C.; Tsai, Y.H. Ultrashort-laser-pulse machining characteristics of aluminum nitride and aluminum oxide. Ceram. Int. 2015, 41, S191–S196. [Google Scholar] [CrossRef]
- Preusch, F.; Adelmann, B.; Hellmann, R. Micromachining of AlN and Al2O3 using fiber laser. Micromachines 2014, 5, 1051–1060. [Google Scholar] [CrossRef]
- Posthumus, J.H. The dynamics of small molecules in intense laser fields. Rep. Prog. Phys. 2004, 67, 623. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, A.-D.; Li, B.; Cui, T.-H.; Lu, Y.-F. Electrons dynamics control by shaping femtosecond laser pulses in micro/nanofabrication: Modeling, method, measurement and application. Light Sci. Appl. 2018, 7, 17134. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.K.; Latham, W.P.; Beraun, J.E. The role of electron–phonon coupling in ultrafast laser heating. J. Laser Appl. 2005, 17, 63–68. [Google Scholar] [CrossRef]
- Jiang, L.; Tsai, H.L. A plasma model combined with an improved two-temperature equation for ultrafast laser ablation of dielectrics. J. Appl. Phys. 2008, 104, 093101. [Google Scholar] [CrossRef]
- Bulgakova, N.M.; Stoian, R.; Rosenfeld, A.; Hertel, I.V.; Campbell, E.E.B. Electronic transport and consequences for material removal in ultrafast pulsed laser ablation of materials. Phys. Rev. B 2004, 69, 054102. [Google Scholar] [CrossRef]
- Cheng, Y.; Bulgakov, A.V.; Bulgakova, N.M.; Bulgakova, N.M.; Beránek, J.; Zukerstein, M.; Milekhin, I.A.; Popov, A.A.; Volodin, V.A. Ultrafast infrared laser crystallization of amorphous Ge films on glass substrates. Micromachines 2023, 14, 2048. [Google Scholar] [CrossRef]
- Volodin, V.A.; Cheng, Y.; Bulgakov, A.; Levy, Y.; Beránek, J.; Nagisetty, S.; Zukerstein, M.; Popov, A.; Bulgakova, N. Single-shot selective femtosecond and picosecond infrared laser crystallization of an amorphous Ge/Si multilayer stack. Opt. Laser Technol. 2023, 161, 109161. [Google Scholar] [CrossRef]
- Jiang, L.; Tsai, H.L. Energy transport and material removal in wide bandgap materials by a femtosecond laser pulse. Int. J. Heat Mass Transf. 2005, 48, 487–499. [Google Scholar] [CrossRef]
- Hu, W.; Shin, Y.C.; King, G. Modeling of multi-burst mode pico-second laser ablation for improved material removal rate. Appl. Phys. A 2010, 98, 407–415. [Google Scholar] [CrossRef]
- Jackson, T.B.; Virkar, A.V.; More, K.L.; Dinwiddie, R.B.; Cutler, R.A. High-thermal-conductivity aluminum nitride ceramics: The effect of thermodynamic, kinetic, and microstructural factors. J. Am. Ceram. Soc. 1997, 80, 1421–1435. [Google Scholar] [CrossRef]
- Kuramoto, N.; Takada, K. Applications of aluminum nitride (AlN) ceramics. Key Eng. Mater. 2003, 247, 467. [Google Scholar] [CrossRef]
- Kurokawa, Y.; Utsumi, K.; Takamizawa, H. Development and microstructural characterization of high-thermal-conductivity aluminum nitride ceramics. J. Am. Ceram. Soc. 1988, 71, 588–594. [Google Scholar] [CrossRef]
- Nakano, H.; Watari, K.; Hayashi, H.; Urabe, K. Microstructural characterization of high-thermal-conductivity aluminum nitride ceramic. J. Am. Ceram. Soc. 2002, 85, 3093–3095. [Google Scholar] [CrossRef]
- He, X.; Shi, L.; Guo, Y.; Liu, J.; Ye, F. Study on microstructure and dielectric properties of aluminum nitride ceramics. Mater. Charact. 2015, 106, 404–410. [Google Scholar] [CrossRef]
- Taylor, K.M.; Lenie, C. Some properties of aluminum nitride. J. Electrochem. Soc. 1960, 107, 308. [Google Scholar] [CrossRef]
- Franco Júnior, A.; Shanafield, D.J. Thermal conductivity of polycrystalline aluminum nitride (AlN) ceramics. Ceramica 2004, 50, 247–253. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, R.; Han, S.; Dong, H.; Sun, S. The activation threshold evaluation of metallization for aluminum nitride ceramic under nanosecond laser pulses in air. Ceram. Int. 2021, 47, 24707–24712. [Google Scholar] [CrossRef]




| AlN | Y2O3 | CaO | Al2O3 | Si | Other |
|---|---|---|---|---|---|
| 94.7% | 4.8% | 0.32% | 0.008% | 0.007% | 0.165% |
| Factor | Level | ||
|---|---|---|---|
| High | Medium | Low | |
| laser power P/W | 20 | 17.5 | 15 |
| scanning speed ν/(mm/s) | 1050 | 1000 | 950 |
| pulse frequency f/kHz | 325 | 300 | 275 |
| Parameter (Unit) | Symbol | Value |
|---|---|---|
| Ambient temperature (K) | T0 | 300 |
| Density (kg/m3) | 3340 | |
| Laser spot radius (μm) | r0 | 10 |
| Pulse duration (fs) | tp | 500 |
| Electron lattice coupling coefficient (W/m3·K) | G | 2.11 × 1011 |
| Bandgap energy (eV) | Eg | 6.2 |
| Electron mobility (cm2/V·s) | ue | 100 |
| Original valence electron density (m−3) | n0 | 1.92 × 1029 |
| Evaporation temperature (K) | Tv | 2723.15 |
| Heat of evaporation (J/kg) | Hs | 2.27 × 107 |
| Electronic thermal conductivity (W/m·K) | Ke | 0.14 |
| Lattice heat capacity coefficient (J/m3·K) | Kl | 1701 |
| Thermal conductivity (W/m·K) | 188 | |
| Electron heat capacity coefficient (J/m3·K2) | 700 | |
| Laser reflectivity | R | 0.3 |
| Laser absorption coefficient (cm−1) | α | 5.2 × 105 |
| Material constant for electron relaxation time (K−2·s−1) | Ae | 1.2 × 10−13 |
| Material constant for electron relaxation time (K−1·s−1) | Bl | 3.5 × 10−9 |
| No. | Parameters | Result | No. | Parameters | Result | ||||
|---|---|---|---|---|---|---|---|---|---|
| P/W | v/(mm/s) | f/kHz | Ra/μm | P/W | v/(mm/s) | f/kHz | Ra/μm | ||
| 1 | 20 | 1050 | 325 | 0.782 | 10 | 15 | 1000 | 300 | 0.602 |
| 2 | 20 | 1050 | 275 | 0.721 | 11 | 17.5 | 1050 | 300 | 0.583 |
| 3 | 20 | 950 | 325 | 0.753 | 12 | 17.5 | 950 | 300 | 0.591 |
| 4 | 20 | 950 | 275 | 0.682 | 13 | 17.5 | 1000 | 325 | 0.572 |
| 5 | 15 | 1050 | 325 | 0.704 | 14 | 17.5 | 1000 | 275 | 0.563 |
| 6 | 15 | 1050 | 275 | 0.653 | 15 | 17.5 | 1000 | 300 | 0.548 |
| 7 | 15 | 950 | 325 | 0.735 | 16 | 17.5 | 1000 | 300 | 0.545 |
| 8 | 15 | 950 | 275 | 0.674 | 17 | 17.5 | 1000 | 300 | 0.541 |
| 9 | 20 | 1000 | 300 | 0.621 | |||||
| Source | Sum of Squares | df | Mean Square | F Value | p Value | |
|---|---|---|---|---|---|---|
| Model | 0.099 | 9 | 0.011 | 42.18 | <0.0001 | significant |
| A | 3.648 × 10−3 | 1 | 3.648 × 10−3 | 13.94 | 0.0073 | |
| B | 6.400 × 10−6 | 1 | 6.400 × 10−6 | 0.024 | 0.8802 | |
| C | 6.401 × 10−3 | 1 | 6.401 × 10−3 | 24.45 | 0.0017 | |
| AB | 1.800 × 10−3 | 1 | 1.800 × 10−3 | 6.88 | 0.0343 | |
| AC | 5.000 × 10−5 | 1 | 5.000 × 10−5 | 0.19 | 0.6752 | |
| BC | 5.000 × 10−5 | 1 | 5.000 × 10−5 | 0.19 | 0.6752 | |
| A2 | 0.018 | 1 | 0.018 | 67.54 | <0.0001 | |
| B2 | 8.623 × 10−3 | 1 | 8.623 × 10−3 | 32.94 | 0.0007 | |
| C2 | 3.714 × 10−3 | 1 | 3.714 × 10−3 | 14.19 | 0.0070 | |
| Residual | 1.832 × 10−3 | 7 | 2.618 × 10−4 | |||
| Lack of Fit | 1.800 × 10−3 | 5 | 3.599 × 10−4 | 22.04 | 0.0440 | not significant |
| Pure Error | 3.267 × 10−5 | 2 | 1.633 × 10−5 | |||
| R2 = 0.98189341080968 | R2adj = 0.95861351042213 | R2pre = 0.87284828300123 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, R.; Zhao, Z.; Zhou, H.; He, J. Femtosecond Laser Polishing of AlN Ceramics and Numerical Simulation of Ablated Morphology. Micromachines 2025, 16, 1303. https://doi.org/10.3390/mi16121303
Shi R, Zhao Z, Zhou H, He J. Femtosecond Laser Polishing of AlN Ceramics and Numerical Simulation of Ablated Morphology. Micromachines. 2025; 16(12):1303. https://doi.org/10.3390/mi16121303
Chicago/Turabian StyleShi, Ruikang, Zhenyu Zhao, Houming Zhou, and Jin He. 2025. "Femtosecond Laser Polishing of AlN Ceramics and Numerical Simulation of Ablated Morphology" Micromachines 16, no. 12: 1303. https://doi.org/10.3390/mi16121303
APA StyleShi, R., Zhao, Z., Zhou, H., & He, J. (2025). Femtosecond Laser Polishing of AlN Ceramics and Numerical Simulation of Ablated Morphology. Micromachines, 16(12), 1303. https://doi.org/10.3390/mi16121303





