Analytical Modelling of Orthotropic Transient Heat Conduction in the Thermal Therapy Mask Within the Symplectic Framework
Abstract
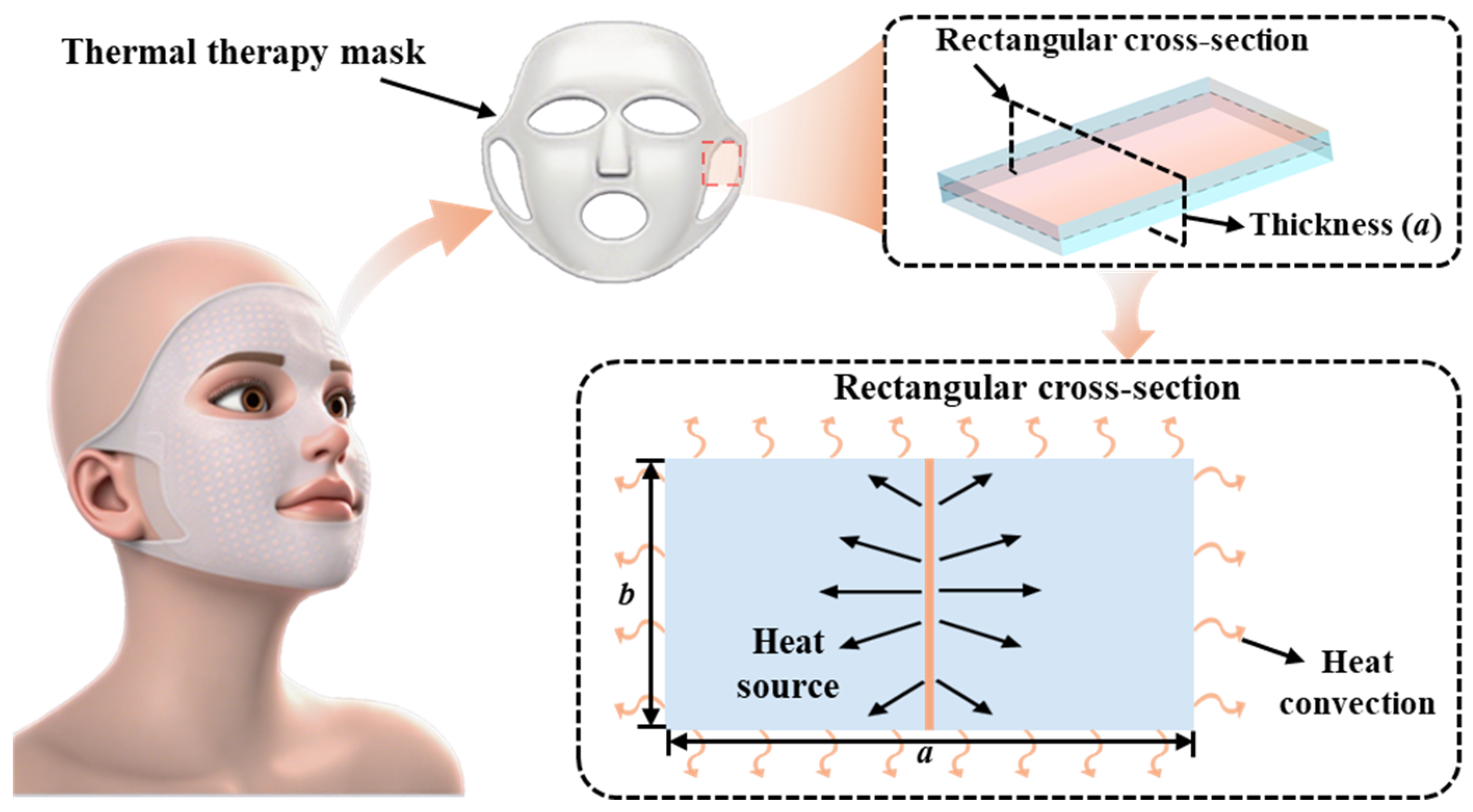
1. Introduction
2. Governing Equation of 2D Orthotropic Transient Heat Conduction Within the Symplectic Framework
3. Solution Procedure of 2D Orthotropic Transient Heat Conduction Within Symplectic Framework
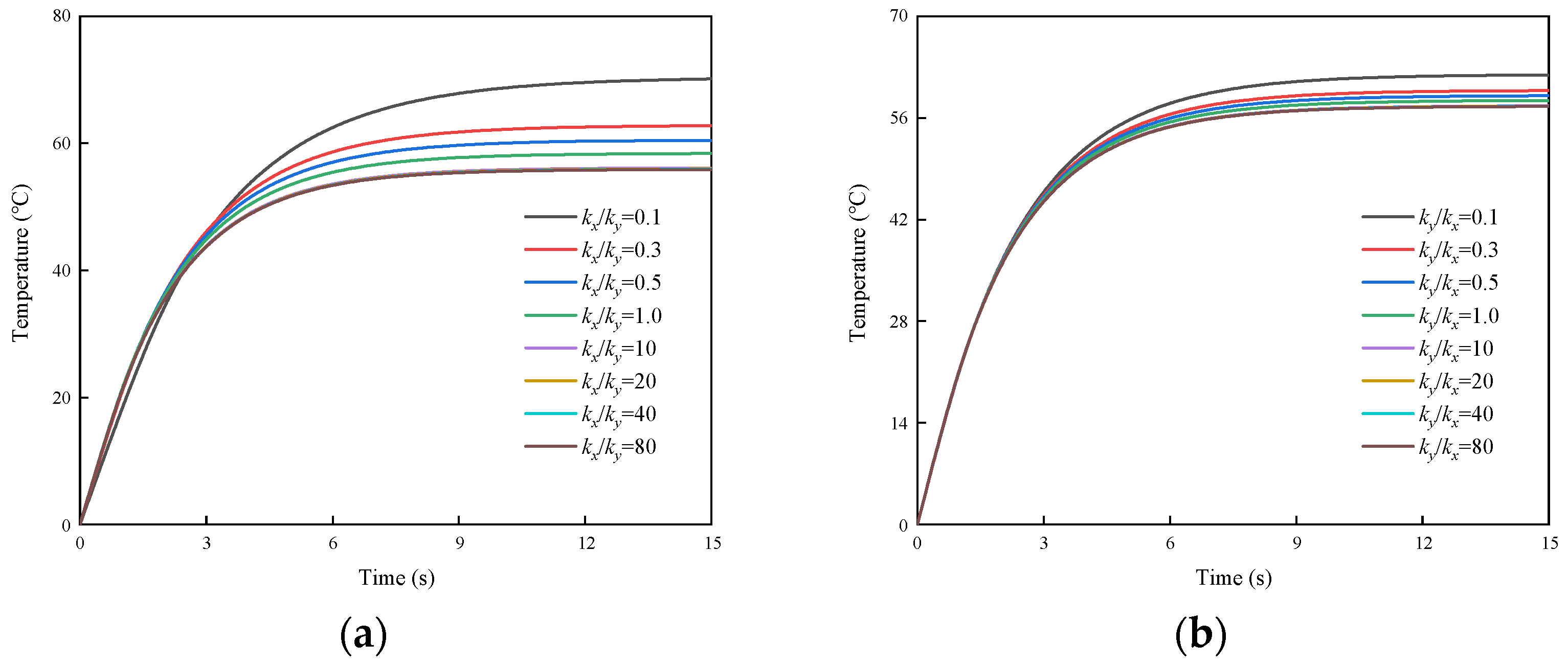
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| , | Length and width along the Ox and Oy axis direction |
| , | Thermal conductivity along the Ox and Oy axis direction |
| , | Temperature in the time domain |
| , | Temperature in the frequency domain |
| Time | |
| Frequency parameters | |
| Specific heat capacity | |
| Density | |
| Heat source strength | |
| Ambient temperature | |
| Heat convection coefficient | |
| , | State vector matrix |
| Hamiltonian operator matrix | |
| Symplectic matrix | |
| Eigenvector matrix | |
| Eigenvalue | |
| Characteristic root |
References
- Chen, S.; Fan, S.; Qiao, Z.; Wu, Z.; Lin, B.; Li, Z.; Riegler, M.A.; Wong, M.Y.H.; Opheim, A.; Korostynska, O.; et al. Transforming Healthcare: Intelligent Wearable Sensors Empowered by Smart Materials Artificial, Intelligence. Adv. Mater. 2025, 37, 2500412. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Song, Y. Wearable healthcare monitoring and therapeutic bioelectronics. Wearable Electron. 2025, 2, 18–22. [Google Scholar] [CrossRef]
- Khoshmanesh, F.; Thurgood, P.; Pirogova, E.; Nahavandi, S.; Baratchi, S. Wearable sensors: At the frontier of personalised health monitoring, smart prosthetics and assistive technologies. Biosens. Bioelectron. 2021, 176, 112946. [Google Scholar] [CrossRef]
- Ghazizadeh, E.; Naser, Z.; Deigner, H.; Rahimi, H.; Altintas, Z. Approaches of wearable and implantable biosensor towards of developing in precision medicine. Front. Med. 2024, 11, 1390634. [Google Scholar] [CrossRef] [PubMed]
- Ghazizadeh, E.; Deigner, H.; Al-Bahrani, M.; Muzammil, K.; Daneshmand, N.; Naseri, Z. DNA bioinspired by polyvinyl alcohol -MXene-borax hydrogel for wearable skin sensors. Sens. Actuators A Phys. 2025, 386, 116331. [Google Scholar] [CrossRef]
- Zhang, Q.; He, Z.; Fang, X.; Zhang, X.; Zhang, Z. Experimental and numerical investigations on a flexible paraffin/fiber composite phase change material for thermal therapy mask. Energy Storage Mater. 2017, 6, 36–45. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, Y.; Jia, L.; Mathewson, K.E.; Jang, K.-I.; Kim, J.; Fu, H.; Huang, X.; Chava, P.; Wang, R.; et al. Soft Microfluidic Assemblies of Sensors, Circuits, and Radios for the Skin. Science 2014, 344, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and Mechanics for Stretchable Electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef]
- Beybalaev, V.D.; Aliverdiev, A.A.; Hristov, J. Transient Heat Conduction in a Semi-Infinite Domain with a Memory Effect: Analytical Solutions with a Robin Boundary Condition. Fractal Fract. 2023, 7, 770. [Google Scholar] [CrossRef]
- Xu, D.; Li, J.; Wang, Z.; Xiong, S.; He, Q.; Li, R. Analytic Modeling of Two-Dimensional Transient Heat Conduction With Heat Source Under Mixed Boundary Constraints by Symplectic Superposition. ASME J. Heat Mass Transf. 2024, 146, 121401. [Google Scholar] [CrossRef]
- Xu, D.; Xiong, S.; Meng, F.; Wang, B.; Li, R. An analytic model of transient heat conduction for Bi-layered flexible electronic heaters by symplectic superposition. Micromachines 2022, 13, 1627. [Google Scholar] [CrossRef]
- Li, J.; He, Y.; Chen, F.; Guo, X.; Yang, H. A hybrid shape functions based temporal finite element method to solve transient heat conduction problems. Numer. Heat Transf. Part B Fundam. 2024, 1–16. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Y.; Xu, S.; Cui, X.; An, Q.; Chen, Y.; Jia, D.; Zhang, C.; Li, C. Modelling and heat transfer mechanism of coated tool temperature field in sustainable turning based on the finite difference method. Appl. Therm. Eng. 2025, 267, 125803. [Google Scholar] [CrossRef]
- Li, T.; Cheng, C.; Wang, F.; Hu, Z.; Li, J. Analytical evaluation of nearly singular integrals in the heat conduction boundary integral equations with heat source. Eng. Comput. 2025, 42, 951–968. [Google Scholar] [CrossRef]
- Zhou, L.; Feng, W.Z.; Sun, C.B.; Peng, H.F.; Cui, M.; Gao, X.W. A general analytical PBEM for solving three-dimensional transient inhomogeneous heat conduction problems with spatially varying heat generation. Int. Commun. Heat Mass Transf. 2022, 137, 106227. [Google Scholar] [CrossRef]
- Bartwal, N.; Shahane, S.; Roy, S.; Vanka, S.P. Simulation of heat conduction in complex domains of multi-material composites using a meshless method. Appl. Math. Comput. 2023, 457, 128208. [Google Scholar] [CrossRef]
- Huang, Z.; Lei, D.; Han, Z.; Xie, H.; Zhu, J. The Boundary Mapped Collocation Method for Heat Conduction Problems with Heat Generation Spatially Varying Conductivity. Adv. Appl. Math. Mech. 2025, 17, 240–262. [Google Scholar] [CrossRef]
- Wang, J.; Qiu, L.; Liang, Y.; Wang, F. A spatio-temporal radial basis function collocation method based on Hausdorff fractal distance for Hausdorff derivative heat conduction equations in three-dimensional anisotropic materials. Appl. Math. Comput. 2025, 502, 129501. [Google Scholar] [CrossRef]
- Yin, Y.; Li, M.; Yuan, W.; Chen, X.; Li, Y. A widely adaptable analytical method for thermal analysis of flexible electronics with complex heat source structures. Proc. R. Soc. A 2019, 475, 20190402. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Shi, Y.; Shen, Y.; Shen, Z.; Zhang, T.; Zhao, Z. Transient Heat Conduction in the Orthotropic Model with Rectangular Heat Source. Micromachines 2022, 13, 1324. [Google Scholar] [CrossRef]
- Jain, A.; Krishnan, G. Exact analytical solution for thermal conduction in a Cartesian body with heat-generating regions of arbitrary shapes and thermal properties. Int. J. Heat Mass Transf. 2025, 246, 126968. [Google Scholar] [CrossRef]
- Yao, W.; Zhong, W.; Lim, C. Symplectic Elasticity; World Scientific: Singapore, 2009. [Google Scholar]
- Li, R.; Zhong, Y.; Li, M. Analytic bending solutions of free rectangular thin plates resting on elastic foundations by a new symplectic superposition method. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20120681. [Google Scholar] [CrossRef]
- Li, R.; Wang, P.; Zheng, X.; Wang, B. New benchmark solutions for free vibration of clamped rectangular thick plates and their variants. Appl. Math. Lett. 2018, 78, 88–94. [Google Scholar] [CrossRef]
- Li, R.; Wang, H.; Zheng, X.; Xiong, S.; Hu, Z.; Yan, X.; Xiao, Z.; Xu, H.; Li, P. New analytic buckling solutions of rectangular thin plates with two free adjacent edges by the symplectic superposition method. Eur. J. Mech. A/Solids 2019, 76, 247–262. [Google Scholar] [CrossRef]
- Zhao, Z.; Nan, J.; Li, M. Thermal Management of Serpentine Flexible Heater Based on the Orthotropic Heat Conduction Model. Micromachines 2022, 13, 622. [Google Scholar] [CrossRef]
- Doetsch, G. Introduction to the Theory and Application of the Laplace Transformation; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Haarsa, P.; Pothat, S. On heaviside step function with a bulge function by using laplace transform. Appl. Math. Sci. 2015, 9, 1107–1112. [Google Scholar] [CrossRef]




| Location | Mesh Size | Time Increment/s | |||
|---|---|---|---|---|---|
| 1 | 0.1 | 0.01 | 0.005 | ||
| 25.55 | 25.78 | 25.80 | 25.80 | ||
| 25.55 | 25.78 | 25.80 | 25.80 | ||
| 25.55 | 25.78 | 25.80 | 25.80 | ||
| 24.02 | 24.23 | 24.24 | 24.24 | ||
| 24.01 | 24.22 | 24.24 | 24.24 | ||
| 24.01 | 24.22 | 24.24 | 24.24 | ||
| Case | Location | Number of Series Terms | |||||
|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | ||
| 1 | 25.60 | 25.60 | 25.60 | 25.60 | 25.60 | 25.60 | |
| 25.47 | 25.47 | 25.47 | 25.47 | 25.47 | 25.47 | ||
| 24.84 | 24.84 | 24.84 | 24.84 | 24.84 | 24.84 | ||
| 24.71 | 24.71 | 24.71 | 24.71 | 24.71 | 24.71 | ||
| 2 | 57.15 | 57.19 | 57.18 | 57.18 | 57.18 | 57.18 | |
| 56.21 | 56.25 | 56.25 | 56.24 | 56.24 | 56.24 | ||
| 55.97 | 56.01 | 56.00 | 56.00 | 56.00 | 56.00 | ||
| 55.05 | 55.09 | 55.08 | 55.08 | 55.08 | 55.08 | ||
| Time (s) | Method | Case 1 | Case 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | Present | 23.65 | 23.57 | 22.91 | 22.84 | 52.80 | 51.99 | 51.68 | 50.88 |
| FEM | 23.66 | 23.58 | 22.92 | 22.84 | 52.79 | 51.97 | 51.66 | 50.87 | |
| 10 | Present | 25.47 | 25.33 | 24.70 | 24.58 | 55.87 | 55.94 | 55.69 | 54.78 |
| FEM | 25.47 | 25.34 | 24.70 | 24.58 | 55.86 | 55.93 | 55.69 | 54.78 | |
| 15 | Present | 25.60 | 25.47 | 24.84 | 24.71 | 57.18 | 56.24 | 56.00 | 55.08 |
| FEM | 25.60 | 25.47 | 24.84 | 24.71 | 57.17 | 56.24 | 56.00 | 55.08 | |
| 20 | Present | 25.60 | 25.47 | 24.84 | 24.71 | 57.20 | 56.27 | 56.02 | 55.10 |
| FEM | 25.62 | 25.48 | 24.85 | 24.72 | 57.20 | 56.26 | 56.02 | 55.10 | |
| 25 | Present | 25.61 | 25.48 | 24.85 | 24.72 | 57.20 | 56.27 | 56.03 | 55.11 |
| FEM | 25.62 | 25.48 | 24.85 | 24.72 | 57.20 | 56.26 | 56.02 | 55.10 | |
| 30 | Present | 25.61 | 25.48 | 24.85 | 24.72 | 57.20 | 56.27 | 56.03 | 55.11 |
| FEM | 25.62 | 25.48 | 24.85 | 24.72 | 57.20 | 56.26 | 56.02 | 55.10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xu, D.; Guo, C.; Chen, Z.; Jiang, L.; Li, R. Analytical Modelling of Orthotropic Transient Heat Conduction in the Thermal Therapy Mask Within the Symplectic Framework. Micromachines 2025, 16, 1277. https://doi.org/10.3390/mi16111277
Li J, Xu D, Guo C, Chen Z, Jiang L, Li R. Analytical Modelling of Orthotropic Transient Heat Conduction in the Thermal Therapy Mask Within the Symplectic Framework. Micromachines. 2025; 16(11):1277. https://doi.org/10.3390/mi16111277
Chicago/Turabian StyleLi, Jinbao, Dian Xu, Chengjie Guo, Zhishan Chen, Linchi Jiang, and Rui Li. 2025. "Analytical Modelling of Orthotropic Transient Heat Conduction in the Thermal Therapy Mask Within the Symplectic Framework" Micromachines 16, no. 11: 1277. https://doi.org/10.3390/mi16111277
APA StyleLi, J., Xu, D., Guo, C., Chen, Z., Jiang, L., & Li, R. (2025). Analytical Modelling of Orthotropic Transient Heat Conduction in the Thermal Therapy Mask Within the Symplectic Framework. Micromachines, 16(11), 1277. https://doi.org/10.3390/mi16111277







