Reconfigurable Dual-Band SIW Bandpass Filter with Tunable Passbands and Enhanced Stopband Suppression
Abstract
1. Introduction
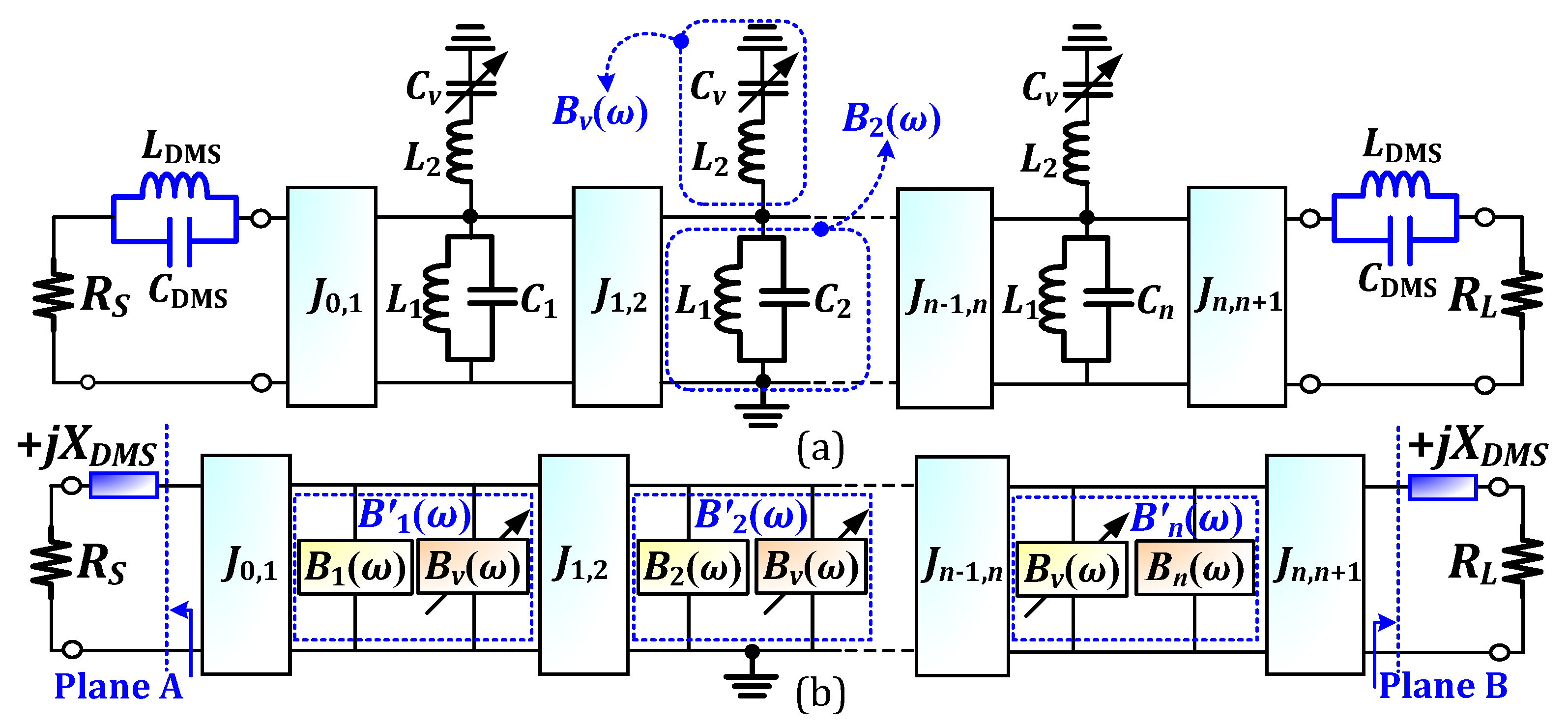
2. Design Concepts and Equations
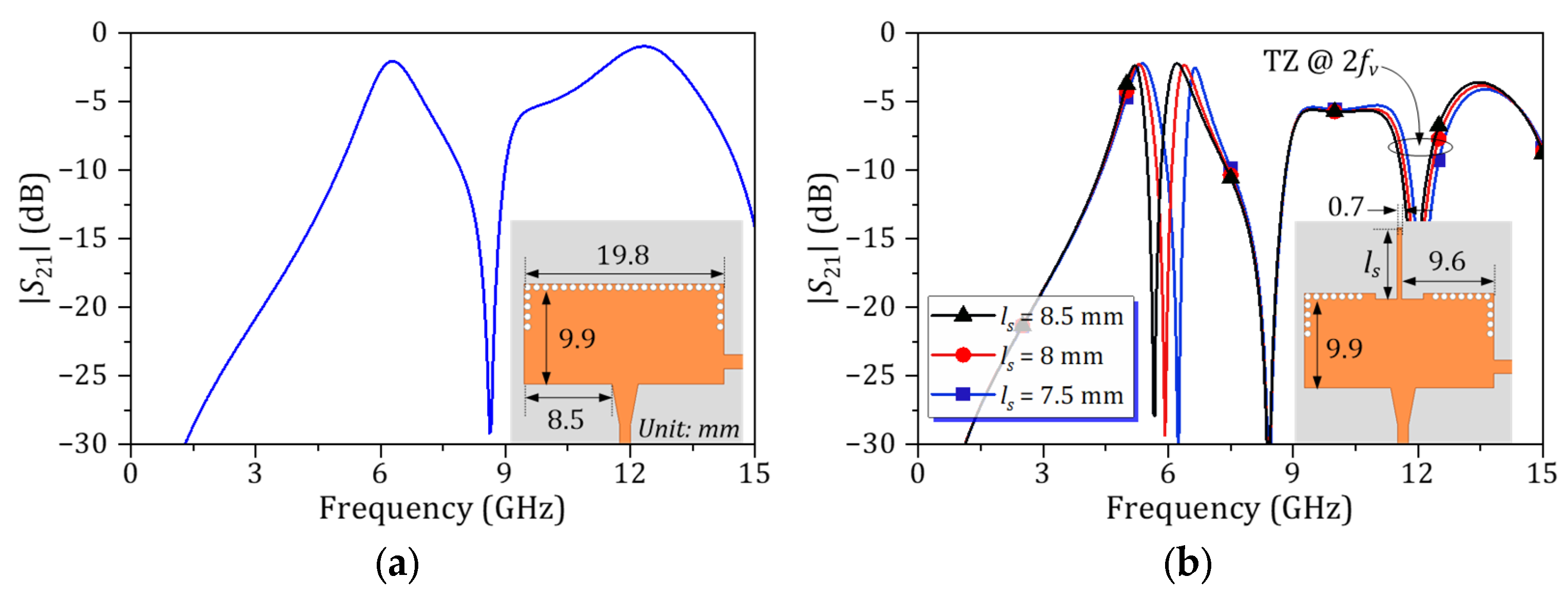
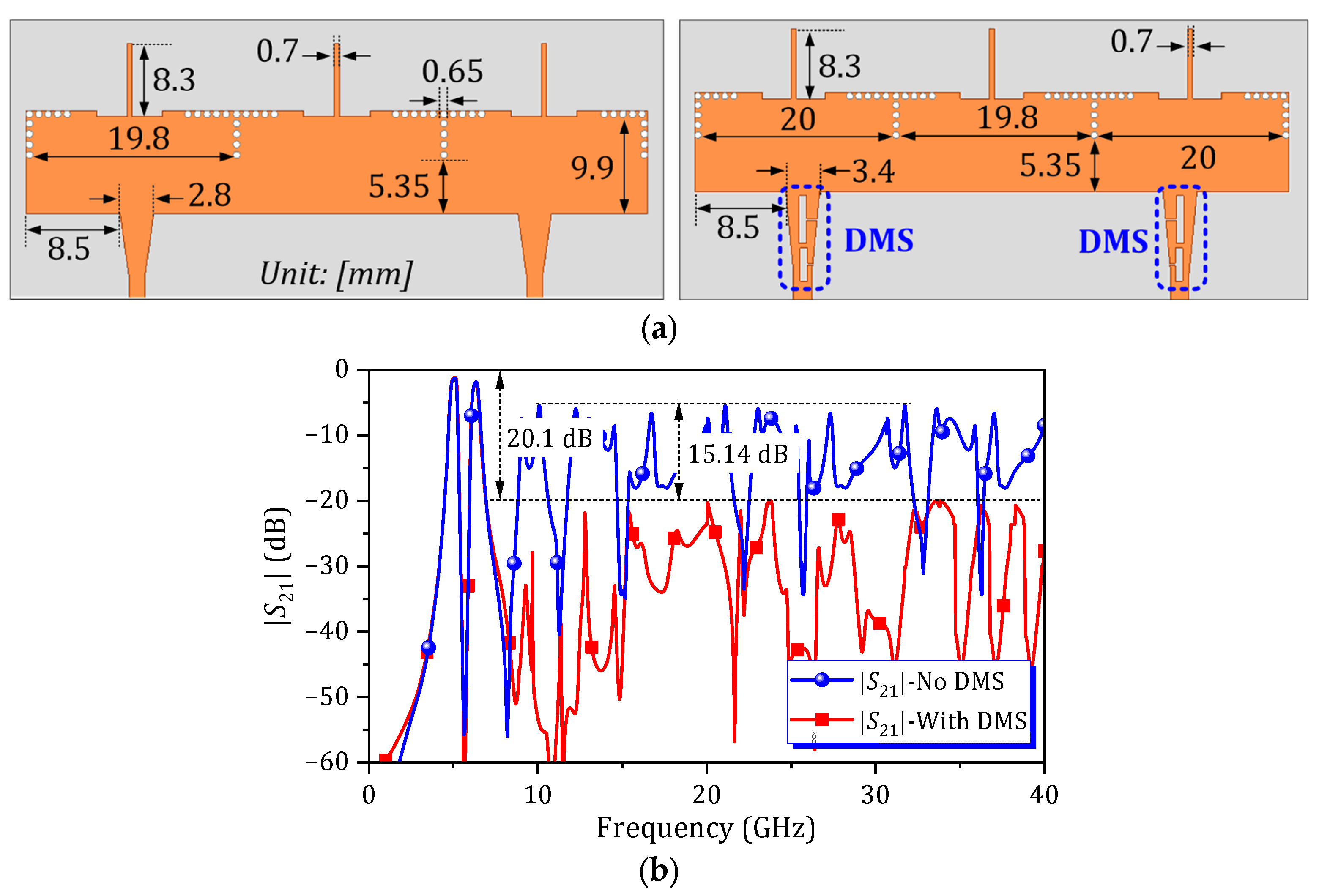
3. Design and Implementation of Proposed Dual-Band SIW BPF
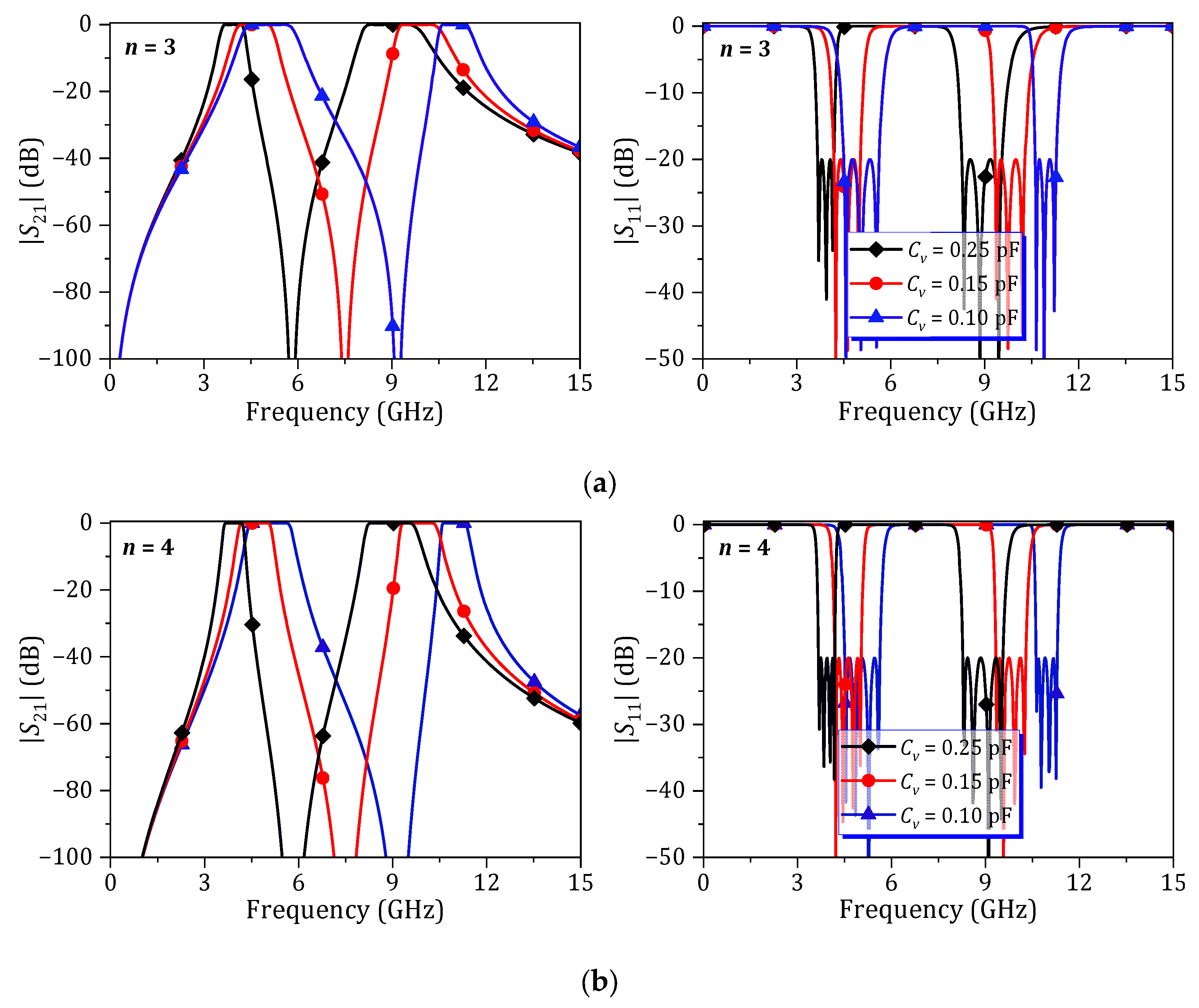
4. Simulation and Measurement Results
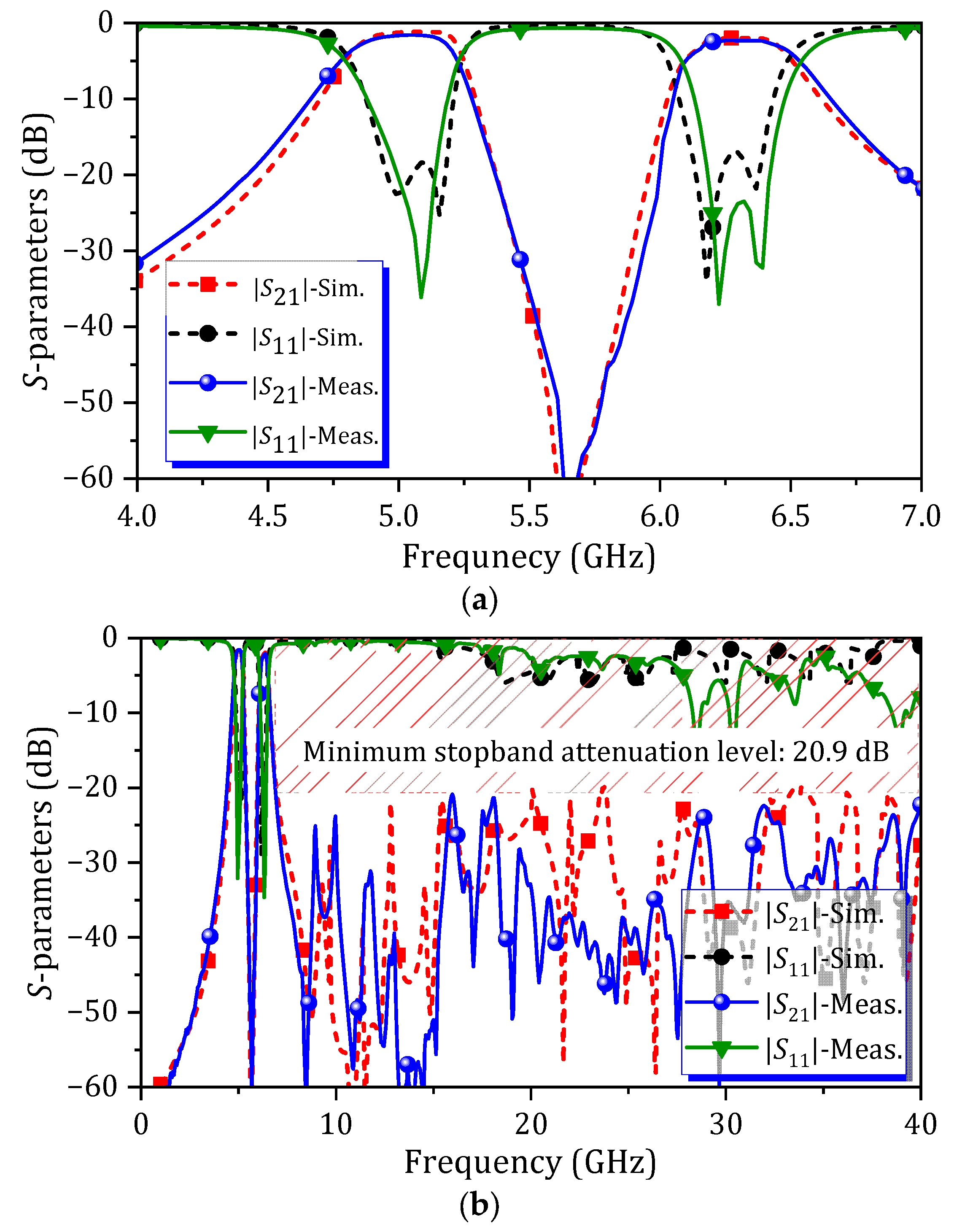
4.1. Dual-Band HM SIW BPF with Fixed Passband
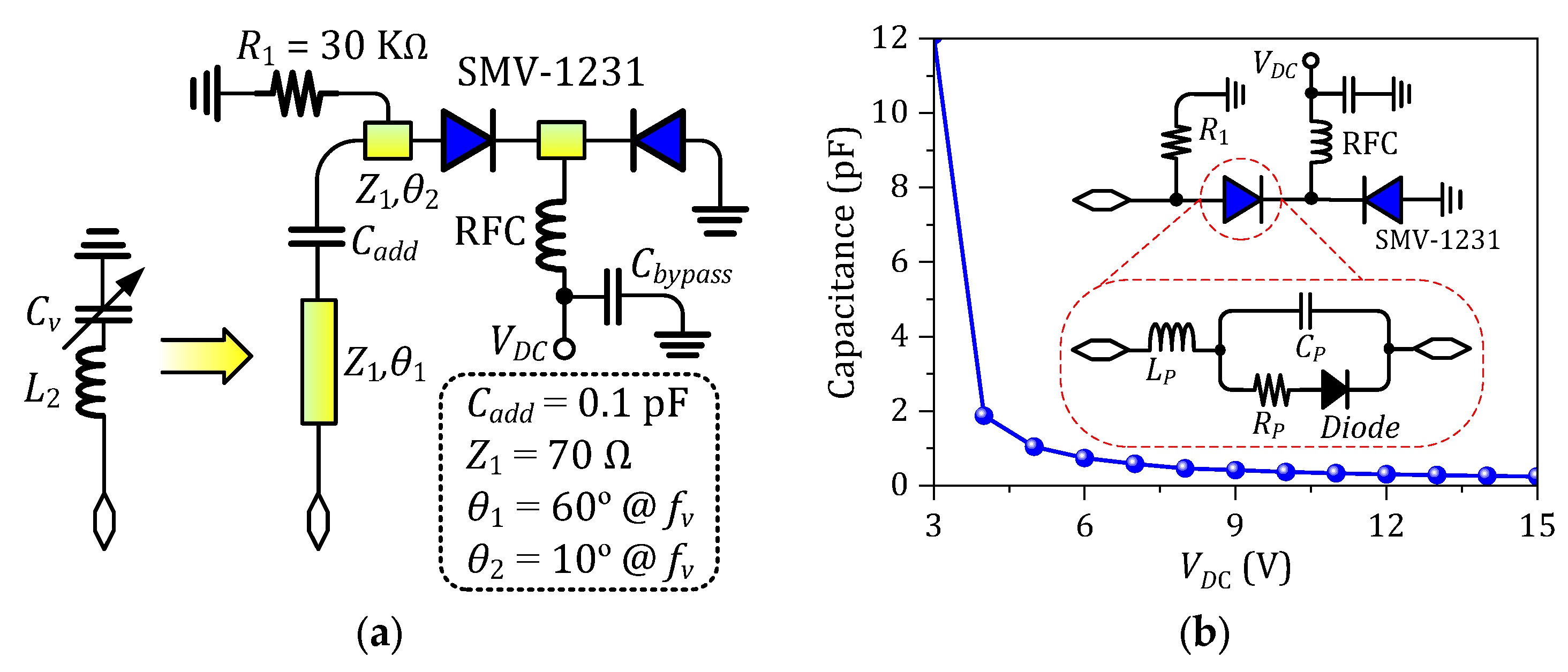
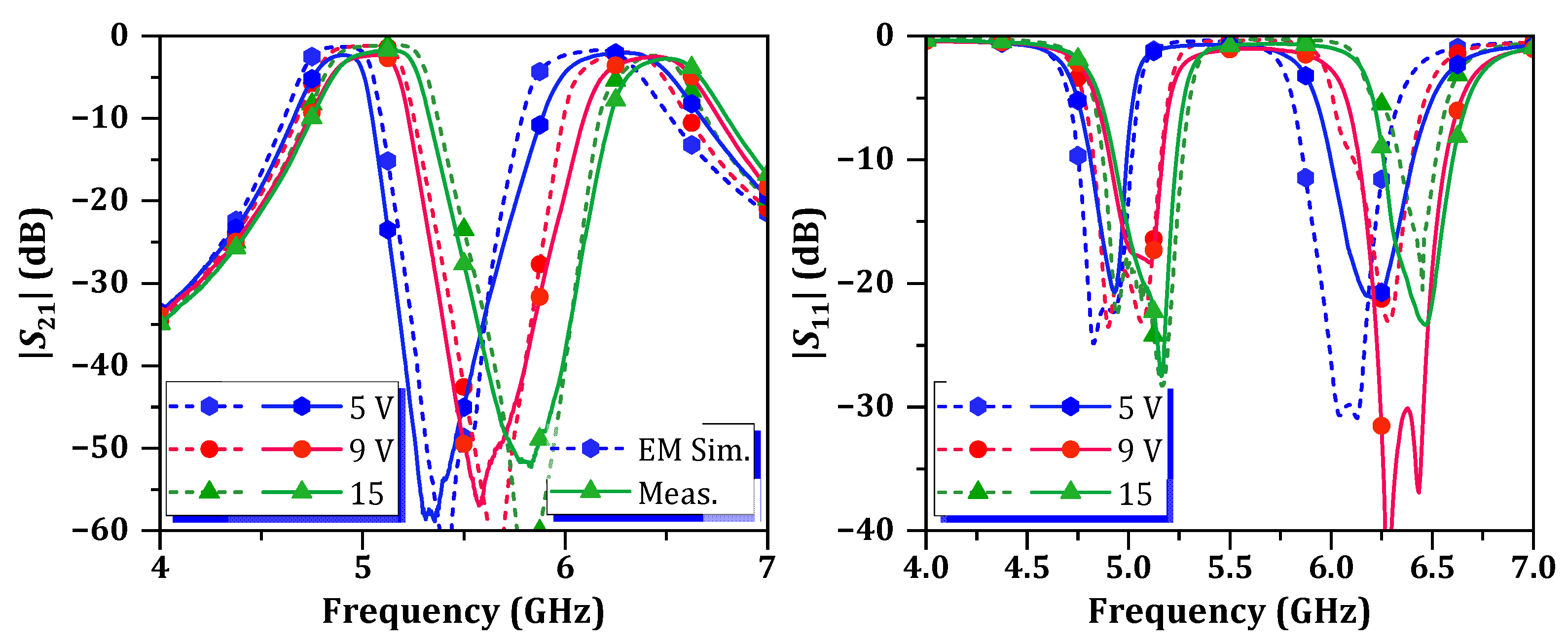
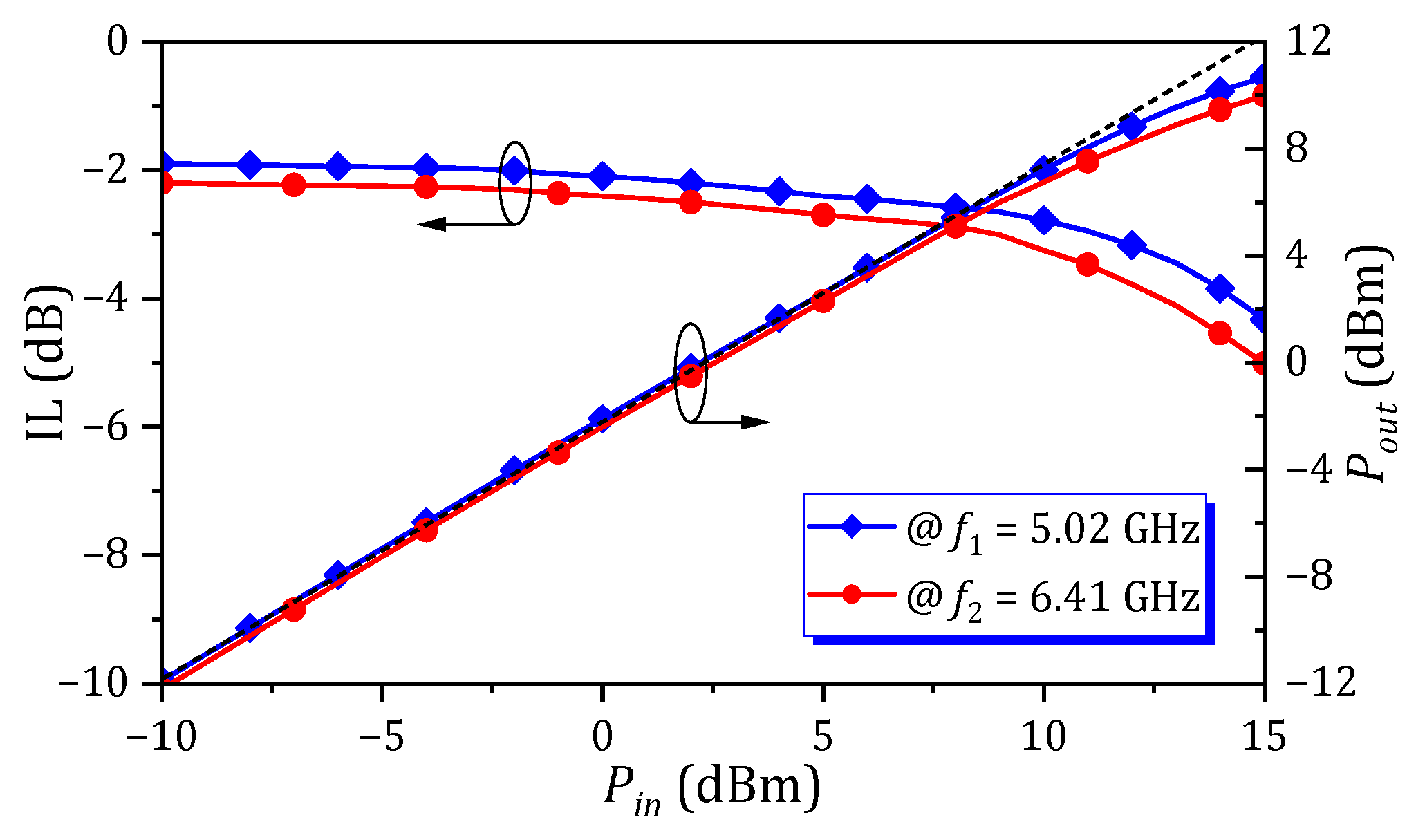
4.2. Dual-Band HM SIW BPF with Passband Tunability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BPF | Bandpass filter |
| CSRR | Complementary split-ring resonator |
| DMS | Defected microstrip structure |
| HM | Half-mode |
| IL | Insertion loss |
| PCB | Printed circuit board |
| RL | Return loss |
| SIW | Substrate integrated waveguide |
| TL | Transmission line |
| TSR | Tunable stopband resonator |
| TZ | Transmission zero |
References
- Chen, X.P.; Wu, K.; Li, Z.L. Dual-band and triple-band substrate integrated waveguide filters with Chebyshev and quasi-elliptic responses. IEEE Trans. Microw. Theory Technol. 2007, 55, 2569–2578. [Google Scholar] [CrossRef]
- Chen, F.; Song, K.; Hu, B.; Fan, Y. Compact dual-band bandpass filter using HMSIW resonator and slot perturbation. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 686–688. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C.X.; Wu, W. Dual-mode characteristics of half-mode SIW rectangular cavity and applications to dual-band filters with widely separated passbands. IEEE Trans. Microw. Theory Technol. 2018, 66, 4820–4829. [Google Scholar] [CrossRef]
- Fu, W.; Li, Z.; Liu, P.; Cheng, J.; Qiu, X. Modeling and analysis of novel CSRRs-loaded dual-band bandpass SIW filters. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2352–2356. [Google Scholar] [CrossRef]
- Han, K.; Jiang, X.; Wang, Z.; Mao, Z.; Wang, Y.; Tian, L.; Yu, Q. High-Performance Dual-Band Bandpass Filter Using SIPW and CSRRs. IEEE Trans. Plasma Sci. 2025, 53, 382–388. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, G.; Feng, S.; Tam, K.W.; Zhang, Z.; Tang, W.; Yang, J. Design of 3-D integrated SIW multiband bandpass filter with split-type extended doublet topology. IEEE Trans. Compon. Packag. Manuf. Technol. 2022, 12, 1681–1691. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, D.W.; Gong, K.; Qian, H.; Qu, W.Z.; An, N. Single-and dual-band bandpass filters based on multiple-mode folded substrate-integrated waveguide cavities. IEEE Trans. Microw. Theory Technol. 2023, 71, 5335–5345. [Google Scholar] [CrossRef]
- Chu, P.; Luo, M.; Zhang, W.; Zhu, F.; Liu, L.; Wu, K. Dual band dual mode substrate integrated waveguide filter with mixed coupling. IEEE Microw. Wirel. Technol. Lett. 2024, 34, 1239–1242. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, L.S.; Zhou, D.F.; Gong, K.; Zhang, D.W. Self-shielded single-and dual-band quad-mode substrate integrated waveguide bandpass filters based on mixed-mode cavity. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 3098–3109. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, X.; Hu, J.; Tam, K.W.; Li, D.; Zhang, Z.; Ma, T.; Yang, J. Multilayer packaged single- and dual-band dual-channel bandpass filters based on substrate integrated waveguide cavities. IEEE Trans. Compon. Packag. Manuf. Technol. 2024, 14, 114–121. [Google Scholar] [CrossRef]
- Liu, B.G.; Liu, L.; Bao, S.J.; Ju, Z.; Hu, L.; Yu, T.T.; Cheng, C.H. Ultracompact single- and dual-band FSIW filters with wide stopband based on multiple embedded hybrid resonant modes. IEEE Trans. Microw. Theory Technol. 2025, 73, 5248–5259. [Google Scholar] [CrossRef]
- Wu, G.; Jin, Y.; Zhang, W.; Jiang, R.; Shi, J. Dual bandpass filters with full band reflectionless response and enhanced upper stopband suppression. Sci. Rep. 2025, 15, 22520. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Jin, Y.; Wu, H.; Zhang, W.; Jiang, R.; Shil, J. Compact broadband input-reflectionless filtering power divider with high-isolation and extended out-of-band suppression. Int. J. Circuit Theory Appl. 2025, 1–11. [Google Scholar] [CrossRef]
- Ren, B.; Yuan, W.; Guan, X.; Liu, X.; Zhang, X.; Liu, H. High-order superconducting dual-band differential bandpass filter using symmetrical composite right-/left-handed resonator with wide stopband. IEEE Microw. Wirel. Technol. Lett. 2024, 34, 979–982. [Google Scholar] [CrossRef]
- Zhou, C.X.; Zhu, C.M.; Wu, W. Tunable dual-band filter based on stub-capacitor-loaded half-mode substrate integrated waveguide. IEEE Trans. Microw. Theory Technol. 2017, 65, 147–155. [Google Scholar] [CrossRef]
- Iqbal, A.; Tiang, J.J.; Lee, C.K.; Mallat, N.K.; Wong, S.W. Dual-band half mode substrate integrated waveguide filter with independently tunable bands. IEEE Trans. Circuits Syst. II Express Briefs. 2020, 67, 285–289. [Google Scholar] [CrossRef]
- Zhu, A.; Li, Z.; Cheng, L.; Hu, C.; Mahapatra, R.N. An amplitude tunable dual-band bandpass filter with perfect absorption and its sensing applications. IEEE Sens. Counc. 2024, 24, 4387–4399. [Google Scholar] [CrossRef]
- Hong, J.S. Microstrip Filter for RF/Microwave Applications, 2nd ed.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Pech, P.; Jeong, Y. Co-design of class-F-1 microwave amplifier and bandpass filtering matching network with harmonics control functionality. Int. J. Circuit Theory Appl. 2025, 1–14. [Google Scholar] [CrossRef]
- The Ideal Band for 6G. 2022. Available online: https://www.microwavejournal.com/articles/38670-the-ideal-band-for-6g (accessed on 10 September 2025).
- Nokia. Spectrum for 6G Explained. 2023. Available online: https://www.nokia.com/aboutus/newsroom/articles/spectrum-for-6G-explained/ (accessed on 10 September 2025).
- GSM Association. Setting the Stage for 6G. 2023. Available online: https://www.gsma.com/connectivity-for-good/spectrum/setting-the-stage-for-6g/ (accessed on 10 September 2025).
- 6G World. Prototyping the Future of 6G with SDR. 2024. Available online: https://6gworld.com/europe-updates-vision-for-6g-network-ecosystem-whitepaper/ (accessed on 10 September 2025).
- Pech, P.; Kim, P.; Jeong, Y. Microwave amplifier with substrate integrated waveguide bandpass filter matching network. IEEE Microw. Wirel. Technol. Lett. 2021, 31, 401–404. [Google Scholar] [CrossRef]
- Lai, Q.; Fumeaux, C.; Hong, W.; Vahldieck, R. Characterization of the propagation properties of the half-mode substrate integrated waveguide. IEEE Trans. Microw. Theory Technol. 2009, 57, 1996–2004. [Google Scholar] [CrossRef]
- Pech, P.; Saron, S.; Chaudhary, G.; Jeong, Y. Ultra-compact substrate integrated waveguide bandpass filter with unequal termination impedance. In Proceedings of the 2023 Asia-Pacific Microwave Conference (APMC), Taipei, Taiwan, 5–8 December 2023; pp. 134–136. [Google Scholar] [CrossRef]
- Chaudhary, G.; Jeong, Y.; Lim, J.; Kim, C.D.; Kim, D.; Kim, J.C.; Park, J.C. DMS harmonic termination load network for high efficiency power amplifier applications. In Proceedings of the 40th European Microwave Conference, Paris, France, 28–30 September 2010; pp. 946–949. [Google Scholar]
- Skyworks. SMV123x Series: Hyper Abrupt Junction Tuning Varactors; Skyworks Solutions, Inc.: Irvine, CA, USA, 2012. [Google Scholar]



| First Passband | Second Passband | |||||
|---|---|---|---|---|---|---|
| VDC (V) | 5 | 9 | 15 | 5 | 9 | 15 |
| fc (GHz) | 4.88 | 5.02 | 5.12 | 6.19 | 6.41 | 6.5 |
| IL (dB) | 2.2 | 2.1 | 1.7 | 2.1 | 2.4 | 2.5 |
| RL (dB) | 19.2 | 18 | 20.9 | 20.9 | 31.3 | 22.6 |
| Ref. | f1/f2 (GHz) | 3 dB-FBW (%) | IL (dB) | Δf/f0 (%) | Copper Layers | Possibility for n-Stage | Rejection | Size (λg × λg) |
|---|---|---|---|---|---|---|---|---|
| [3] | 5/7.5 | 5.46/4.75 | 1.7/2.3 | No | 2 | Yes | ≈20 dB up to 1.7f1 | 1.65 × 0.93 |
| 5/8.5 | 6.26/7.75 | 2/1.8 | No | 2 | Yes | ≈20 dB up to 2f1 | 1.31 × 0.84 | |
| [7] | 8.71/10.1 | 1.9/2.7 | 2.8/2 | No | 5 | Difficult | ≈20 dB up to 1.3f1 | 0.87 × 0.87 |
| [9] | 6.97/7.46 | 2.04/3.26 | 2.8/2.3 | No | 5 | Difficult | ≈20 dB up to 1.3f1 | 0.83 × 0.83 |
| [11] | 1.85~2.67/ 3.84~5.34 | 14.9~19.2/ 10.3~17.2 | 1.3~2.3/ 1.7~3.3 | 36.4 32.7 | 2 | Difficult | ≈20 dB up to 3f1 */ ≈10 dB up to 1.8f1 ** | 0.19 × 0.15 |
| [12] | 3.26~3.47/ 5.47~6.13 | N/A | 0.2~2.9/ 0.1~2.1 | 6.2 11.4 | 2 | Yes | ≈10 dB up to 2f1 */ ≈12 dB up to 1.2f1 ** | N/A |
| This Work | 4.88~5.12/ 6.19~6.5 | 3.2~6.64/ 2.62~5.8 | 1.7~2.2/ 2.1~2.5 | 4.8 4.9 | 2 | Yes | ≈20.6 dB up to 8.2f1 | 1.13 × 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, Y.; Pech, P. Reconfigurable Dual-Band SIW Bandpass Filter with Tunable Passbands and Enhanced Stopband Suppression. Micromachines 2025, 16, 1206. https://doi.org/10.3390/mi16111206
Jeong Y, Pech P. Reconfigurable Dual-Band SIW Bandpass Filter with Tunable Passbands and Enhanced Stopband Suppression. Micromachines. 2025; 16(11):1206. https://doi.org/10.3390/mi16111206
Chicago/Turabian StyleJeong, Yongchae, and Phanam Pech. 2025. "Reconfigurable Dual-Band SIW Bandpass Filter with Tunable Passbands and Enhanced Stopband Suppression" Micromachines 16, no. 11: 1206. https://doi.org/10.3390/mi16111206
APA StyleJeong, Y., & Pech, P. (2025). Reconfigurable Dual-Band SIW Bandpass Filter with Tunable Passbands and Enhanced Stopband Suppression. Micromachines, 16(11), 1206. https://doi.org/10.3390/mi16111206





