Study on Microdroplets Generation and Detection Method in Four-Way Microfluid Structure (FWMS) by Double Photoresist Method Pulses
Abstract
1. Introduction
2. Materials and Methods
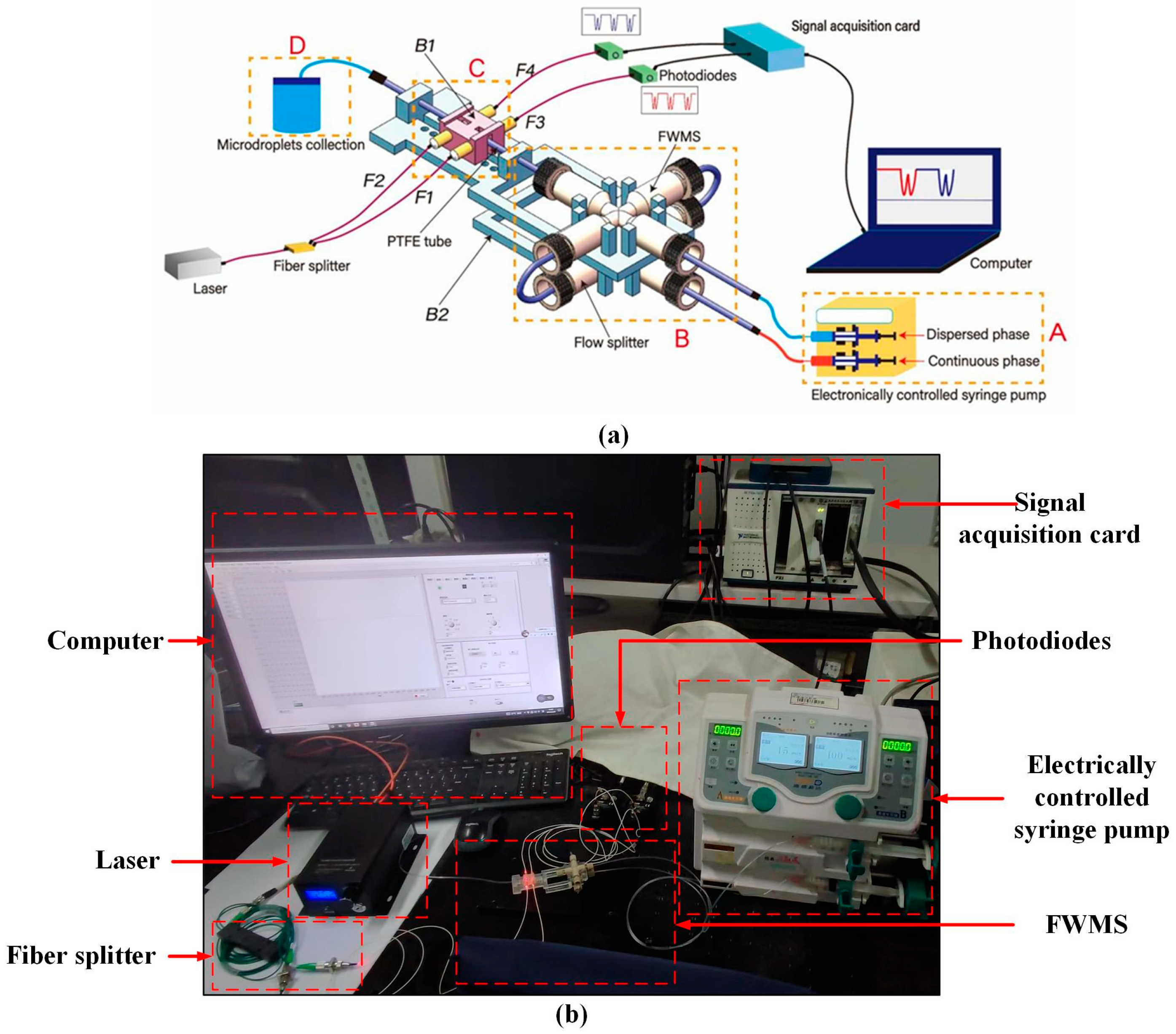
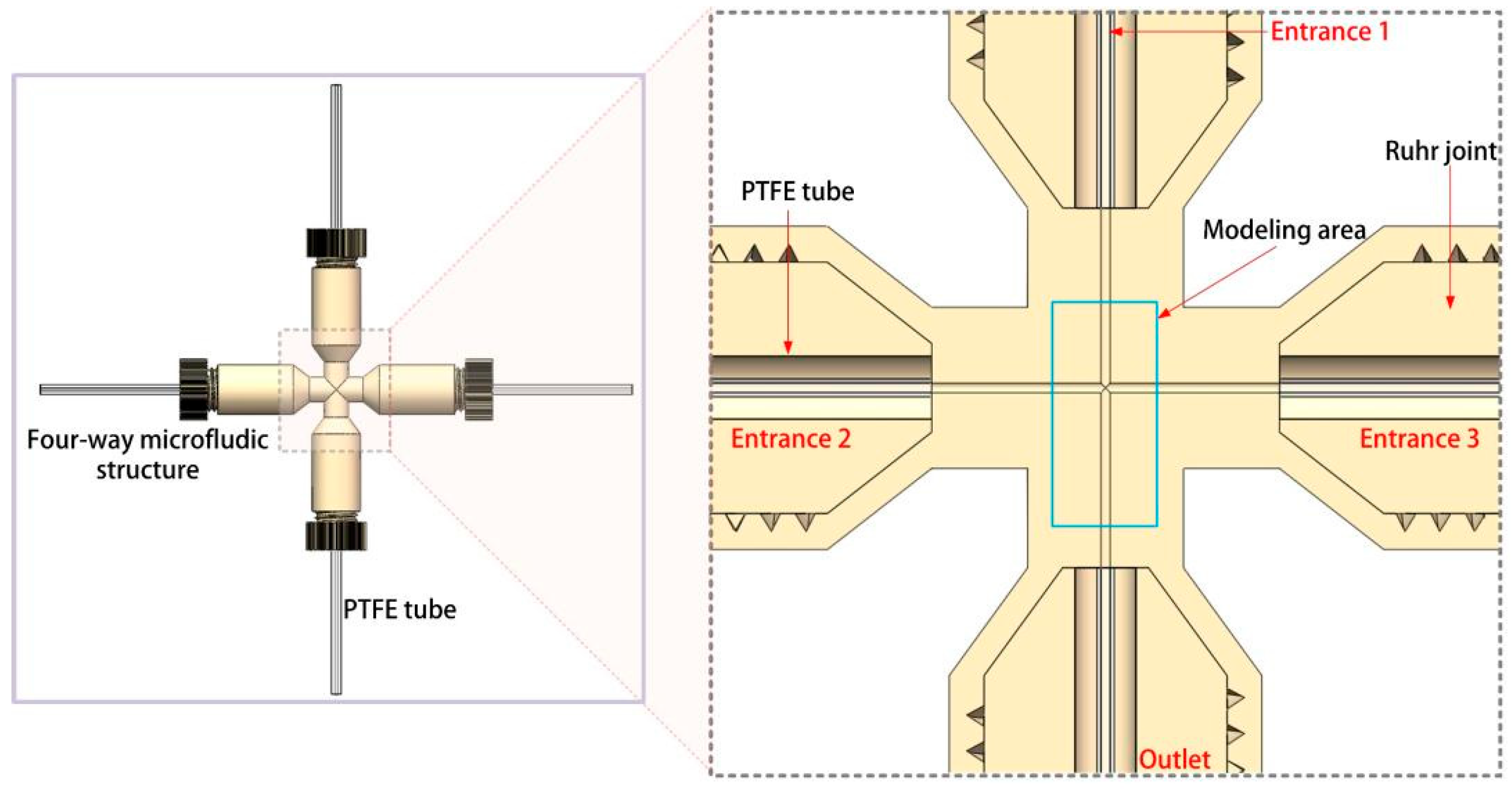
2.1. System Design
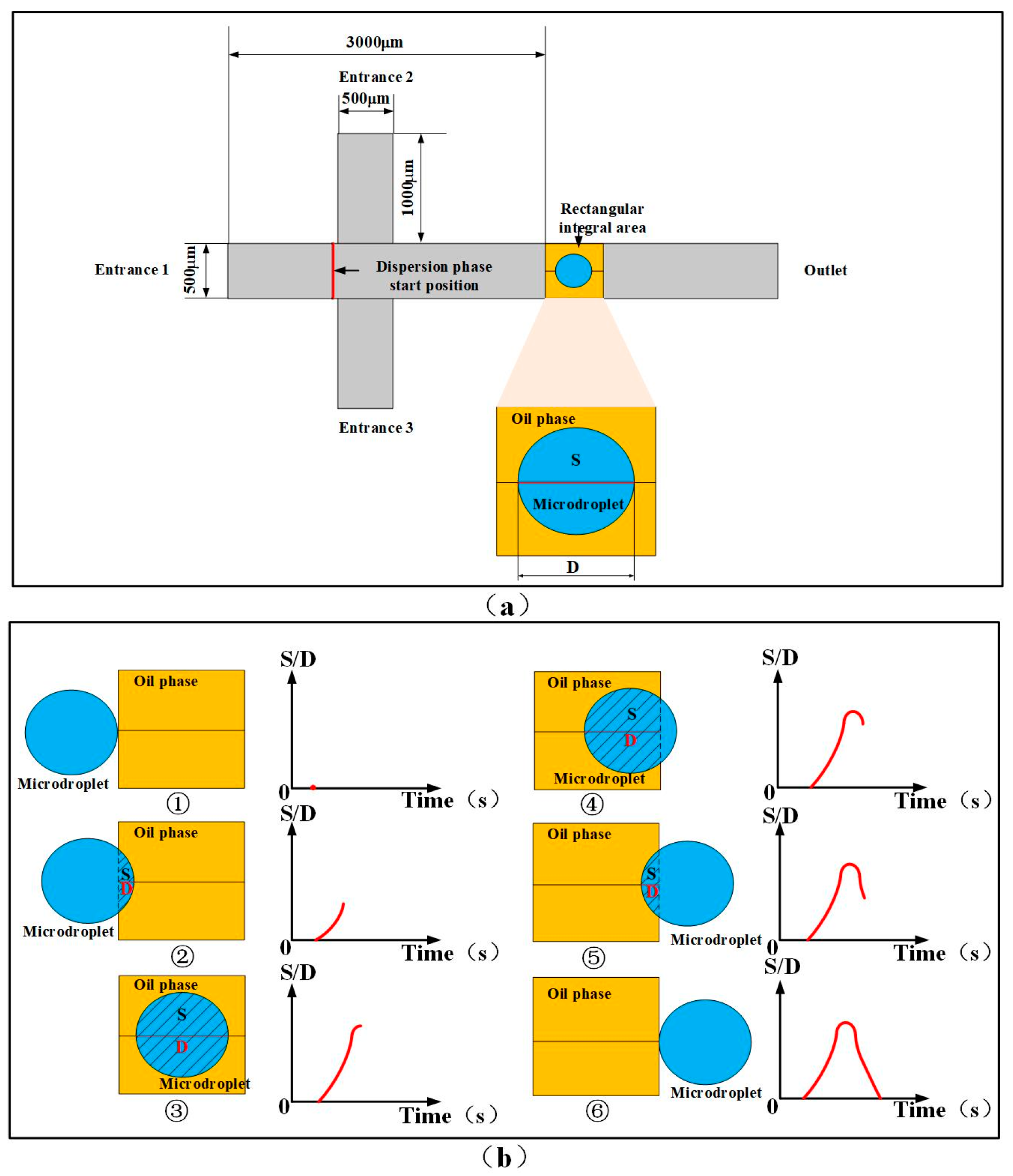
2.2. Principle
2.3. Simulation
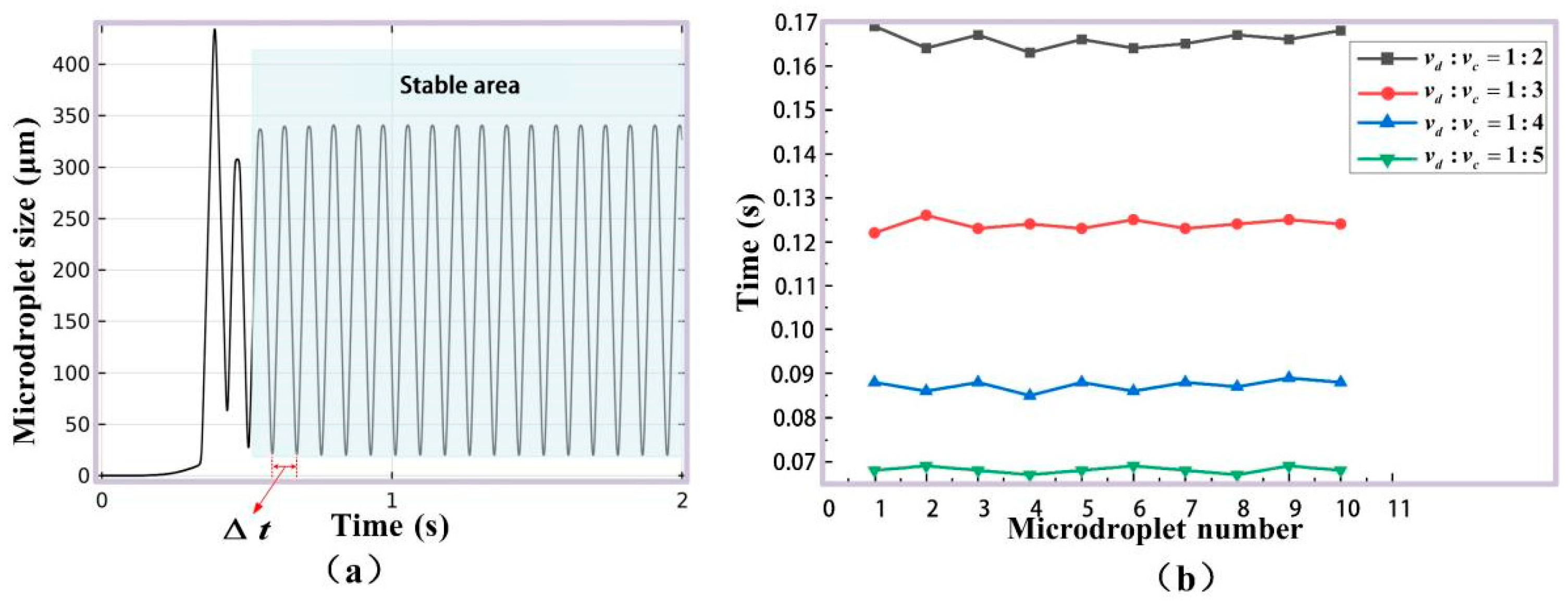
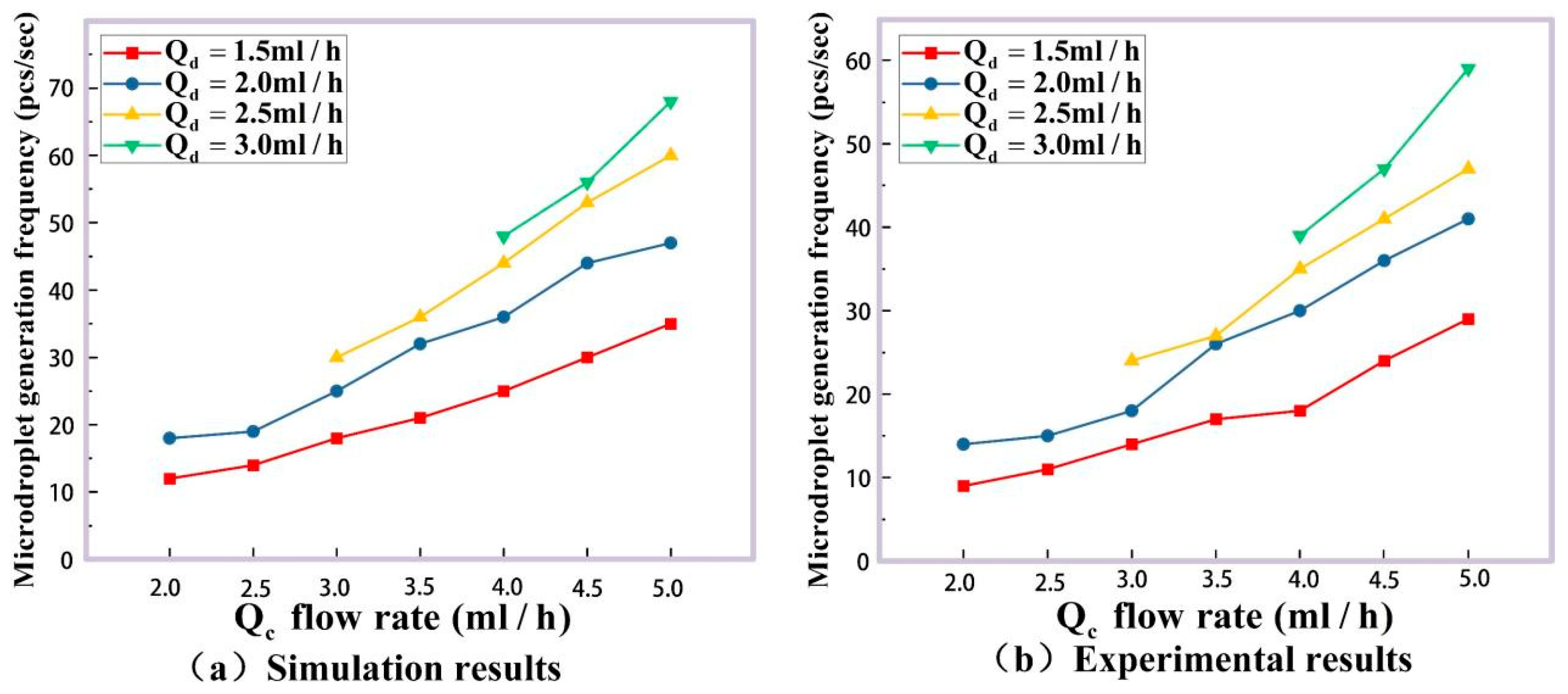
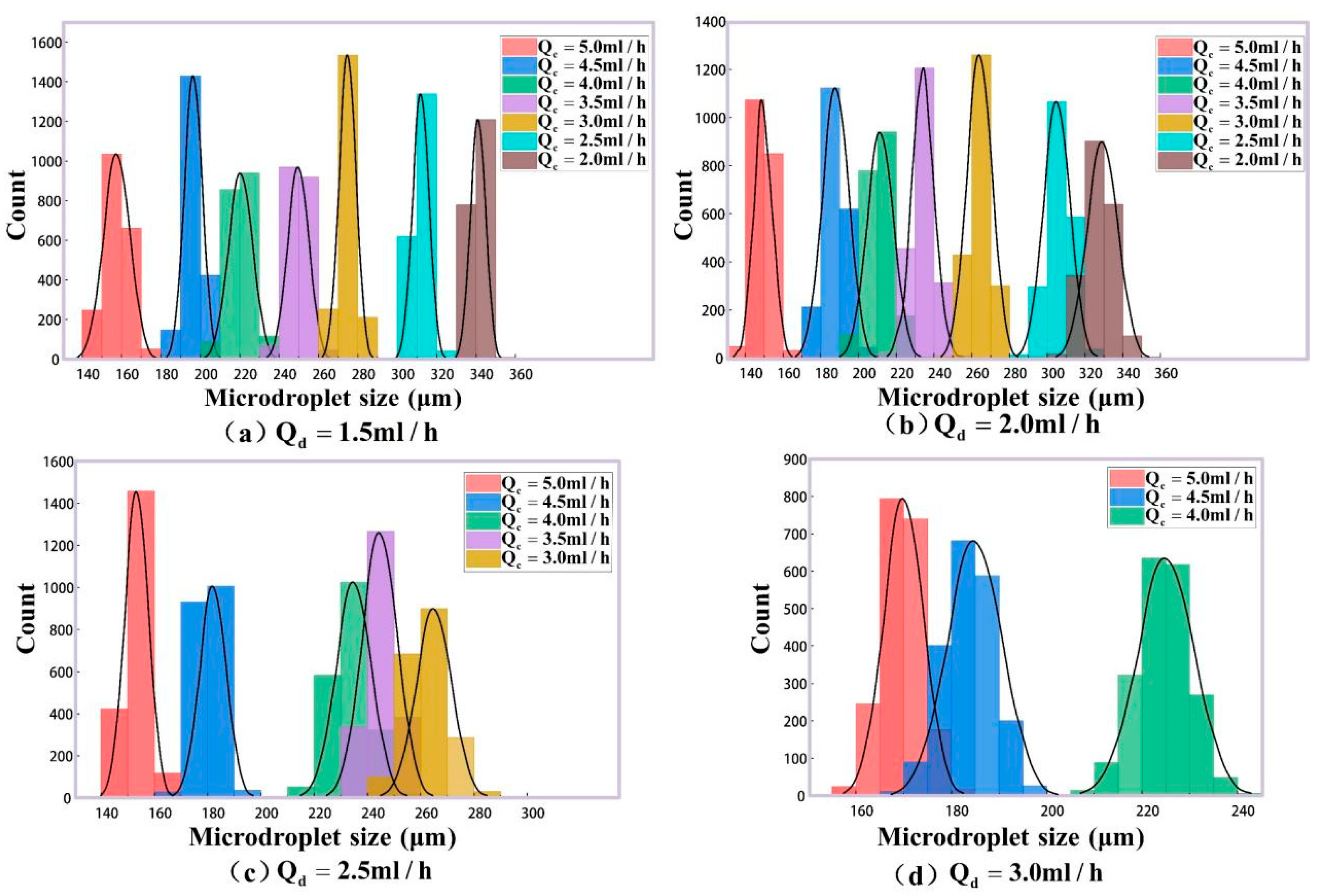
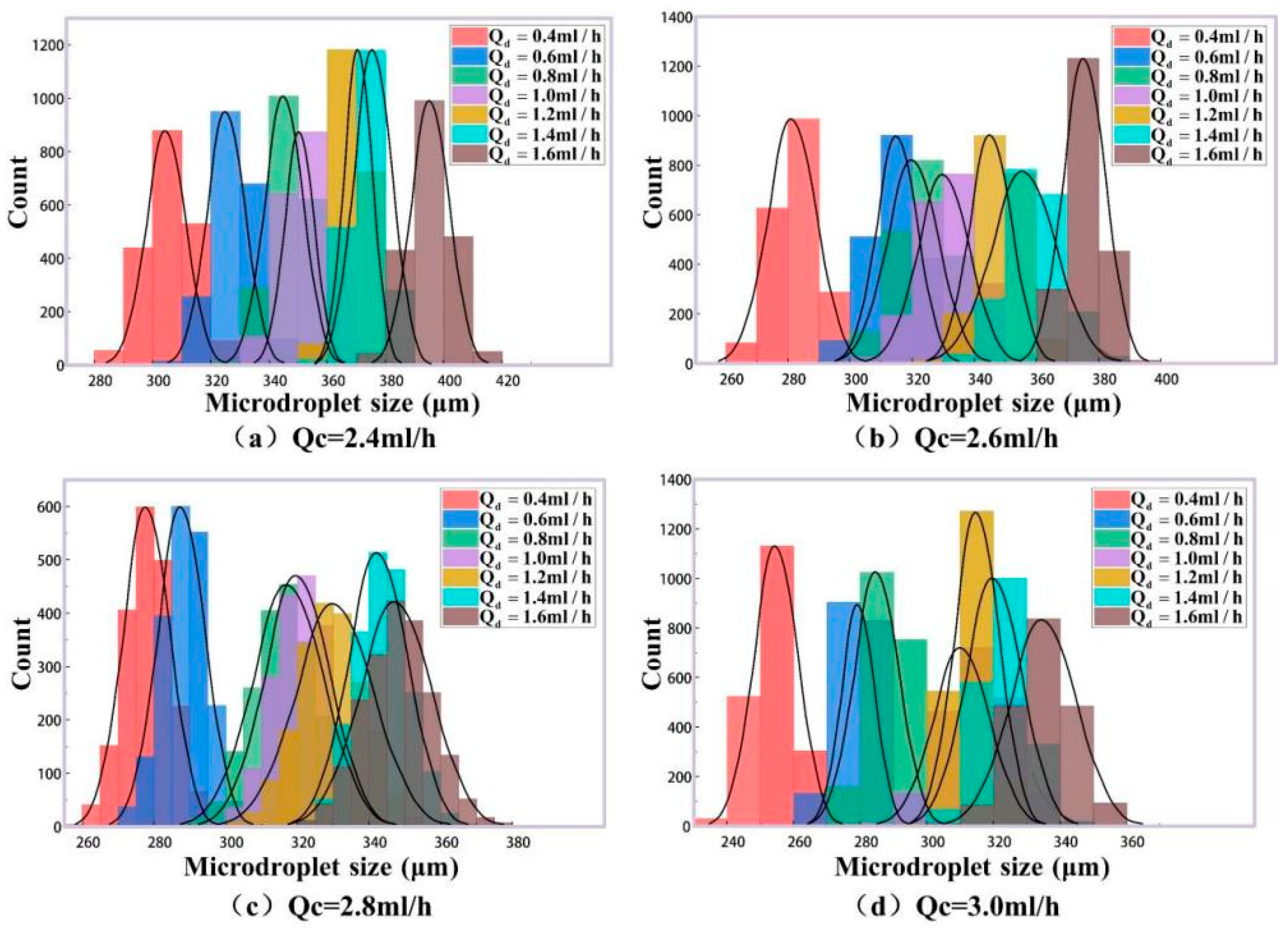
2.3.1. Microdroplet Generation Simulation
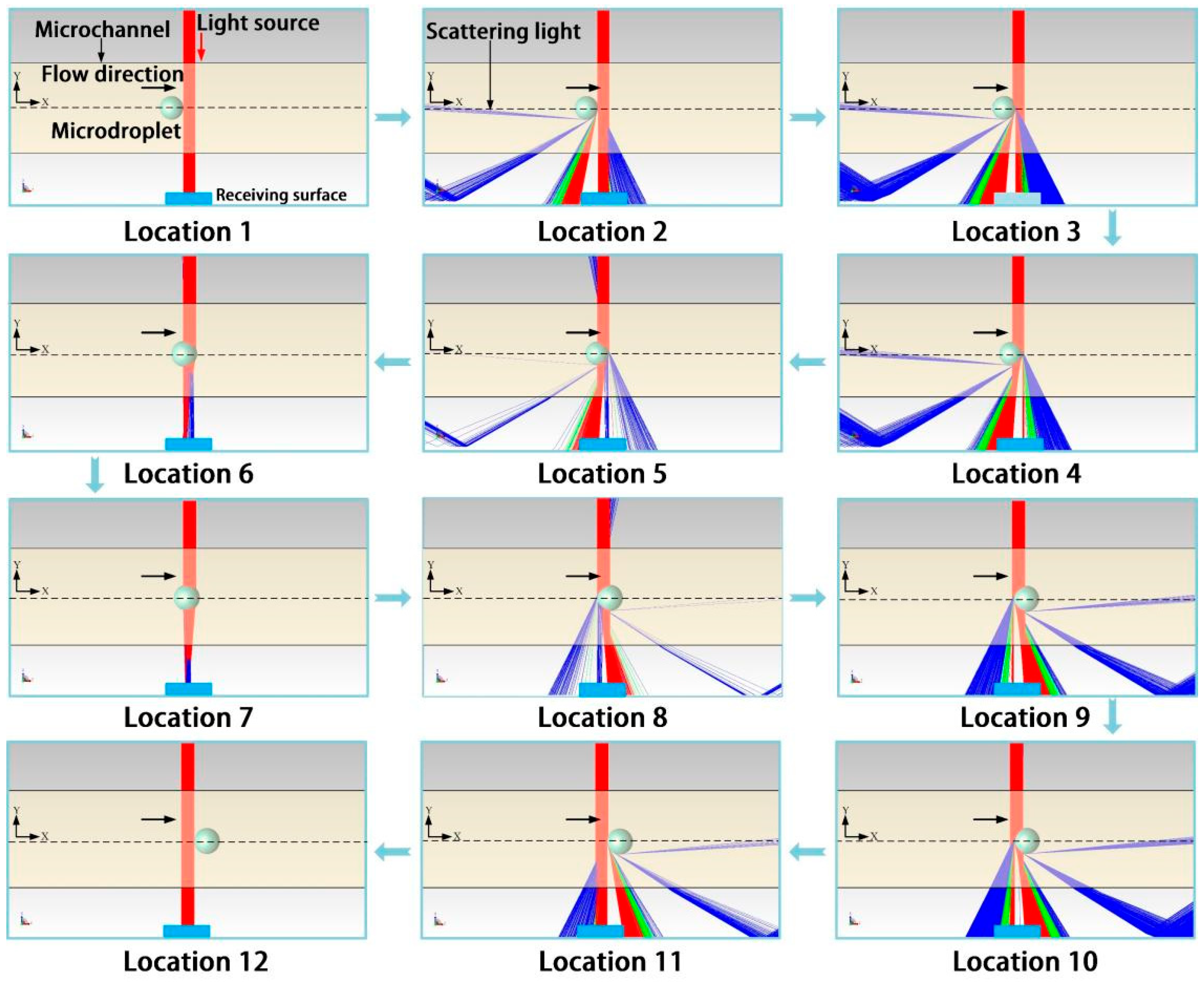
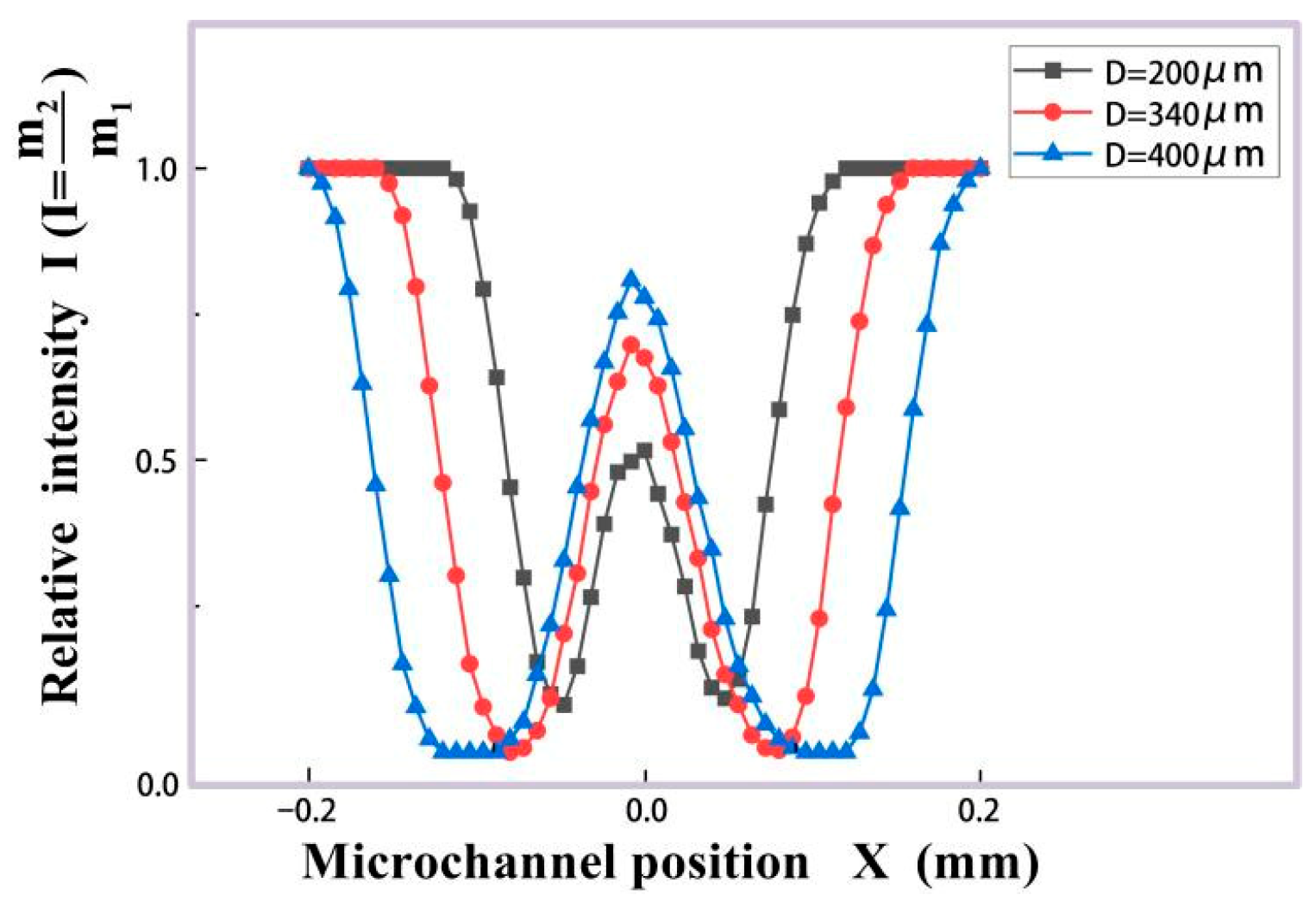
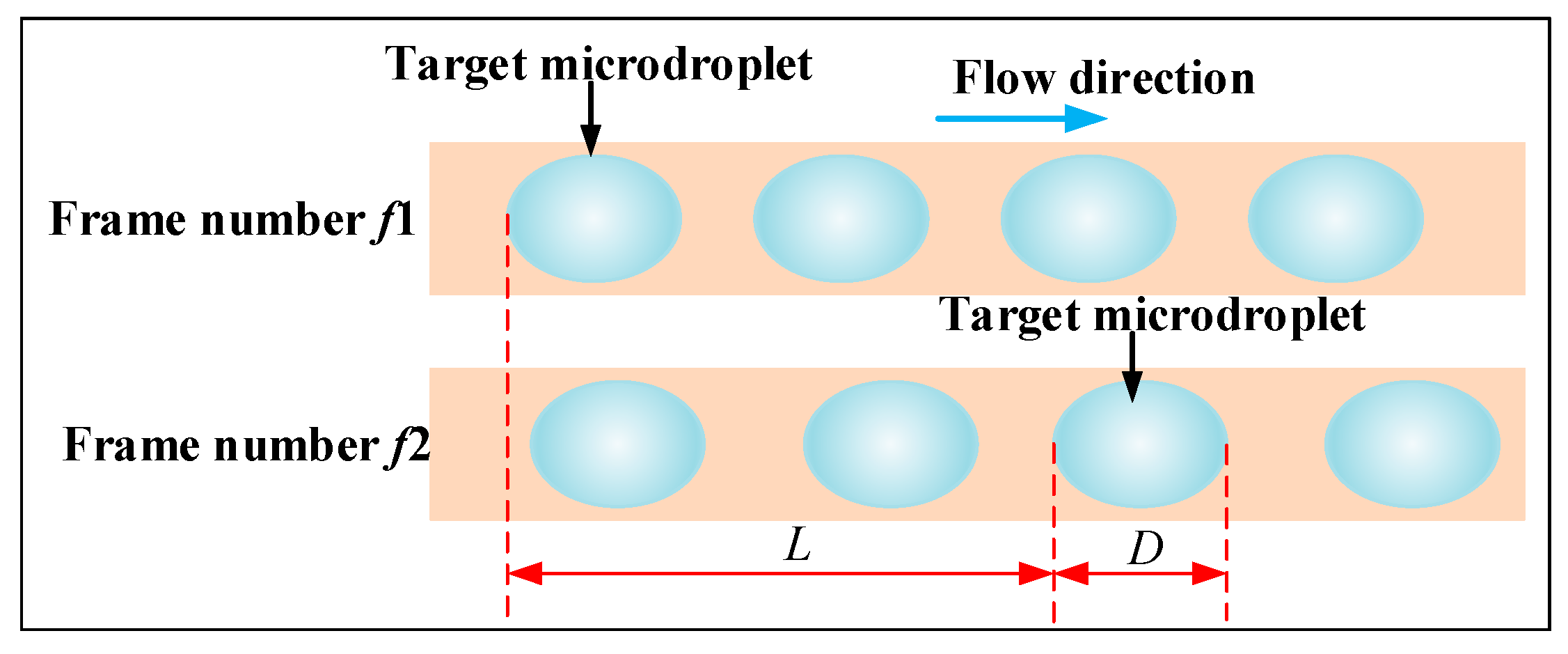
2.3.2. Microdroplet Detection Simulation
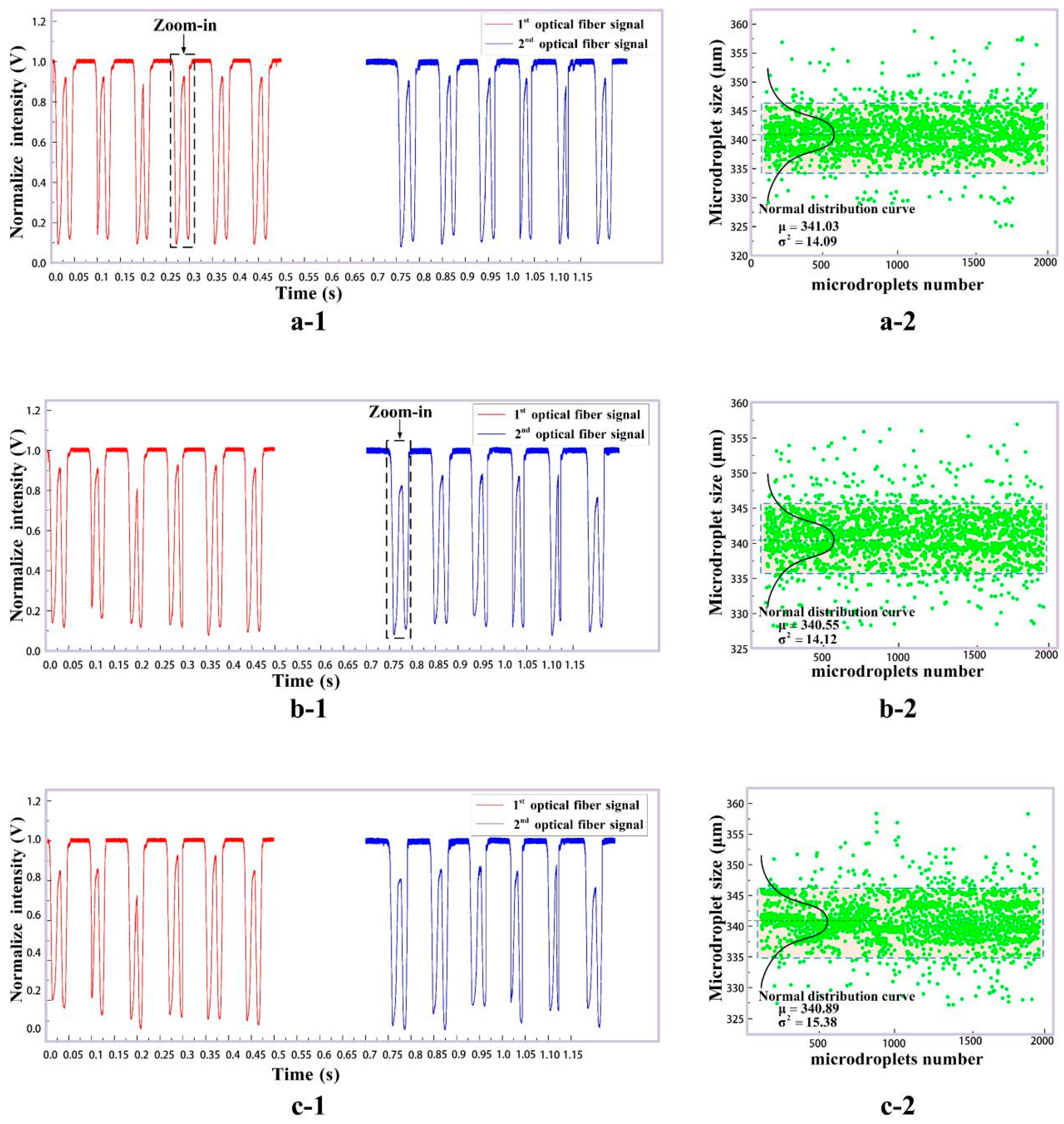
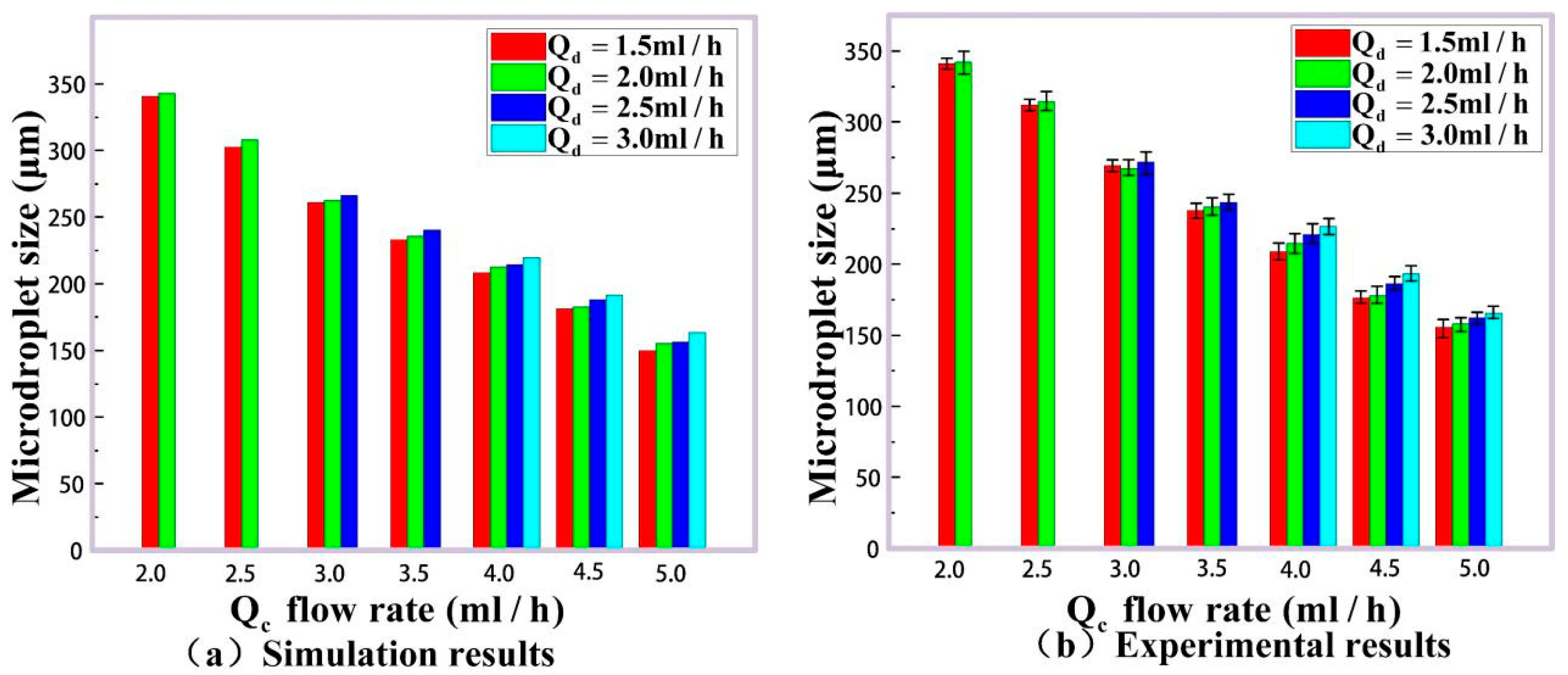
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Z.-M.; Yang, Y.; Du, Y.; Pang, Y. Advances in Droplet-Based Microfluidics Technology and Its Applications. Chin. J. Anal. Chem. 2017, 45, 282–296. [Google Scholar] [CrossRef]
- Cunha, A.G.; Mougel, J.-B.; Cathala, B. Preparation of Double Pickering Emulsions Stabilized by Chemically Tailored Nanocelluloses. Langmuir 2014, 30, 9327–9335. [Google Scholar] [CrossRef]
- Tao, Y.; Rotem, A.; Zhang, H.; Chang, C.B.; Basu, A.; Kolawole, A.O.; Koehler, S.A.; Ren, Y.; Lin, J.S.; Pipas, J.M.; et al. Rapid, targeted and culture-free viral infectivity assay in drop-based microfluidics. Lab Chip 2015, 15, 3934–3940. [Google Scholar] [CrossRef]
- Hu, H.; Eustace, D.; Merten, C.A. Efficient cell pairing in droplets using dual-color sorting. Lab Chip 2015, 15, 3989. [Google Scholar] [CrossRef]
- Akbari, S.; Pirbodaghi, T. Microfluidic encapsulation of cells in alginate particles via an improved internal gelation approach. Microfluid. Nanofluid. 2014, 16, 773–777. [Google Scholar] [CrossRef]
- Ma, J.; Tran, G.; Wan, A.M.D.; Young, E.W.K.; Kumacheva, E.; Iscove, N.N.; Zandstra, P.W. Microdroplet—based one—step RT—PCR for ultrahigh throughput single—cell multiplex gene expression analysis and rare cell detection. Sci. Rep. 2021, 11, 6777. [Google Scholar] [CrossRef]
- Yan, X. Emerging microdroplet chemistry for synthesis and analysis. Int. J. Mass Spectrom. 2021, 468, 116639. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; Chen, H.; Zare, R.N. Scale-up of microdroplet reactions by heated ultrasonic nebulization. Chem. Sci. 2019, 10, 9367. [Google Scholar] [CrossRef] [PubMed]
- Mashaghi, S.; van Oijen, A.M. External control of reactions in microdroplets. Sci. Rep. 2015, 5, 11837. [Google Scholar] [CrossRef]
- Li, K.; Gong, K.; Liu, J.; Ohnoutek, L.; Ao, J.; Liu, Y.; Chen, X.; Xu, G.; Ruan, X.; Cheng, H.; et al. Significantly accelerated photochemical and photocatalytic reactions in microdroplets. Cell Rep. Phys. Sci. 2022, 3, 100917. [Google Scholar] [CrossRef]
- van Tatenhove-Pel, R.J.; Hernandez-Valdes, J.A.; Teusink, B.; Kuipers, O.P.; Fischlechner, M.; Bachmann, H. Microdroplet screening and selection for improved microbial production of extracellular compounds. Curr. Opin. Biotechnol. 2020, 61, 72–81. [Google Scholar] [CrossRef]
- Neethirajan, S.; Kobayashi, I.; Nakajima, M.; Wu, D.; Nandagopal, S.; Lin, F. Microfluidics for food, agriculture and biosystems industries. Lab Chip 2011, 11, 1574. [Google Scholar] [CrossRef]
- Orabi, M.; Lo, J.F. Emerging Advances in Microfluidic Hydrogel Droplets for Tissue Engineering and STEM Cell Mechanobiology. Gels 2023, 9, 790. [Google Scholar] [CrossRef]
- Raveshi, M.R.; Halim, M.S.A.; Agnihotri, S.N.; O’bRyan, M.K.; Neild, A.; Nosrati, R. Curvature in the reproductive tract alters sperm–surface interactions. Nat. Commun. 2021, 12, 3446. [Google Scholar] [CrossRef]
- Vafaie, A.; Shahali, S.; Raveshi, M.R.; Nosrati, R.; Neild, A. Repeated pulses of ultrasound maintain sperm motility. Lab Chip 2024, 25, 16–27. [Google Scholar] [CrossRef] [PubMed]
- Sart, S.; Ronteix, G.; Jain, S.; Amselem, G.; Baroud, C.N. Cell Culture in Microfluidic Droplets. Chem. Rev. 2022, 122, 7061–7096. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-López, M.F.; Martins-Costa, M.T. Disentangling reaction rate acceleration in Microdroplets. Phys. Chem. Chem. Phys. 2022, 24, 29700. [Google Scholar] [CrossRef]
- Moragues, T.; Arguijo, D.; Beneyton, T.; Modavi, C.; Simutis, K.; Abate, A.R.; Baret, J.-C.; DeMello, A.J.; Densmore, D. Droplet-based microfluidics. Nat. Rev. Methods Primers 2023, 3, 32. [Google Scholar] [CrossRef]
- Xi, H.D.; Zheng, H.; Guo, W.; Gañán-Calvo, A.M.; Ai, Y.; Tsao, C.W.; Zhou, J.; Li, W.; Huang, Y.; Nguyen, N.-T. Active droplet sorting in microfluidics: A review. Lab Chip 2017, 17, 751–771. [Google Scholar] [CrossRef]
- Agnihotri, S.N.; Raveshi, M.R.; Nosrati, R.; Bhardwaj, R.; Neild, A. Droplet splitting in microfluidics: A review. Phys. Fluids 2025, 37, 051304. [Google Scholar] [CrossRef]
- Han, W.; Chen, X. A review on microdroplet generation in microfluidics. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 247. [Google Scholar] [CrossRef]
- Yang, W. Impedance Detection of Droplets in Microfludic Chip; Dalian University of Technology: Dalian, China, 2013; pp. 5–52. [Google Scholar]
- Moiseeva, E.V.; Fletcher, A.A.; Harnett, C.K. Thin-film electrode based droplet detection for microfluidic systems. Sens. Actuators B 2011, 155, 408–414. [Google Scholar] [CrossRef]
- Elbuken, C.; Glawdel, T.; Chan, D.; Ren, C.L. Detection of microdroplet size and speed using capacitive sensors. Sens. Actuators A 2011, 171, 55–62. [Google Scholar] [CrossRef]
- Fu, H.; Zeng, W.; Li, S.; Yuan, S. Electrical-detection droplet microfluidic closed-loop control system for precise droplet production. Sens. Actuators A 2017, 267, 142–149. [Google Scholar] [CrossRef]
- Kim, J.; Cho, H.; Han, K.-H. Disposable capacitive electrical droplet measurement (DisC-EDM) based on a film-chip technique. Sens. Actuators B Chem. 2021, 344, 130192. [Google Scholar] [CrossRef]
- Saateh, A.; Kalantarifard, A.; Celik, O.T.; Asghari, M.; Serhatlioglu, M.; Elbuken, C. Real-time impedimetric droplet measurement (iDM). Lab Chip 2019, 19, 3815. [Google Scholar] [CrossRef]
- Lombardo, T.; Lancellotti, L.; Souprayen, C.; Sella, C.; Thouin, L. Electrochemical Detection of Droplets in Microfluidic Devices: Simultaneous Determination of Velocity, Size and Content. Electroanalysis 2019, 31, 2103–2111. [Google Scholar] [CrossRef]
- Liu, Y.; Banerjee, A.; Papautsky, I. Precise droplet volume measurement and electrode-based volume metering in digital microfluidics. Microfluid. Nanofluid. 2014, 17, 295–303. [Google Scholar] [CrossRef]
- Dong, T.; Barbosa, C. Capacitance Variation Induced by Microfluidic Two-Phase Flow across Insulated Interdigital Electrodes in Lab-On-Chip Devices. Sensors 2015, 15, 2694–2708. [Google Scholar] [CrossRef] [PubMed]
- Ocvirk, G.; Tang, T.; Harrison, D.J. Optimization of confocal epifluorescence microscopy for microchip-based miniaturized total analysis systems. Analyst 1998, 123, 1429–1434. [Google Scholar] [CrossRef]
- Zhang, S.; Liang, X.; Huang, X.; Wang, K.; Qiu, T. Precise and fast microdroplet size distribution measurement using deep learning. Chem. Eng. Sci. 2022, 247, 116926. [Google Scholar] [CrossRef]
- Sibirtsev, S.; Zhai, S.; Neufang, M.; Seiler, J.; Jupke, A. Mask R-CNN based droplet detection in liquid–liquid systems, Part2: Methodology for determining training and image processing parameter values improving droplet detection accuracy. Chem. Eng. J. 2023, 473, 144826. [Google Scholar] [CrossRef]
- Farzi, G.A.; Parsian Nejad, A. An Image-Based Technique for Measuring Droplet Size Distribution: The Use of CNN Algorithm. J. Dispers. Sci. Technol. 2015, 37, 1444–1452. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, D.; Hu, Z. Application of Image Analysis in Droplet Detection Techniques. Transducer Microsyst. Technol. 2016, 35, 157–160. [Google Scholar] [CrossRef]
- Basu, A.S. Droplet morphometry and velocimetry (DMV): A video processing software for time-resolved, label-free tracking of droplet parameters. Lab Chip 2013, 13, 1892. [Google Scholar] [CrossRef]
- Hsieh, Y.-W.; Wang, A.-B.; Lu, X.-Y.; Wang, L.A. High-throughput on-line multi-detection for refractive index, velocity, size, and concentration measurements of micro-two-phase flow using optical microfibers. Sens. Actuators B 2016, 237, 841–848. [Google Scholar] [CrossRef]


| SI | Parameter | |
|---|---|---|
| Density | g/mL | 0.764 |
| Refractive Index | a.u. | 1.40 |
| Vapor Pressure (20 °C) | Mm Hg | 5 |
| Viscosity | mm2/s | 100 ± 8 |
| Freezing Point | °C | −55 |
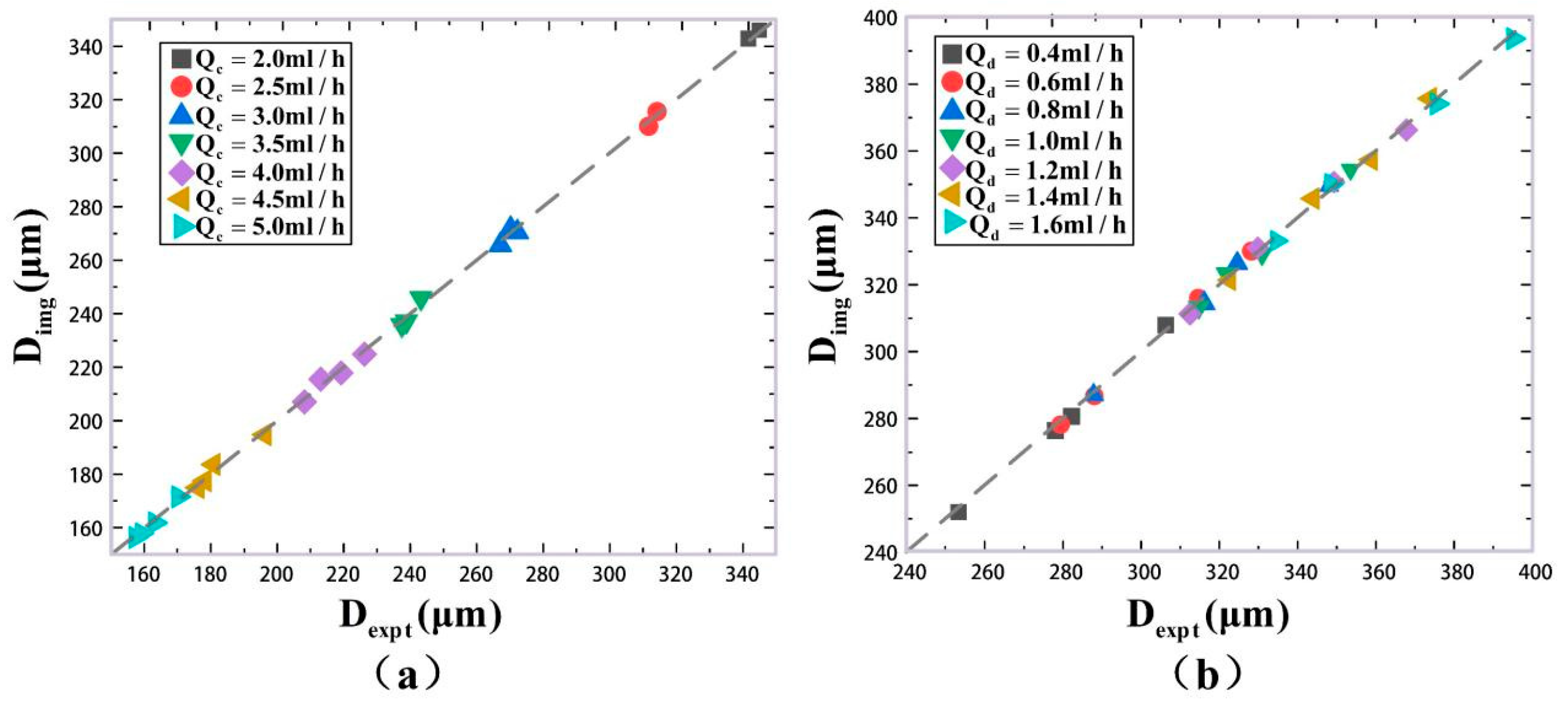
| (mL/h) | (mL/h) | Mean Size by Imaging Method ) | Mean Size by Our Results ) | Maximum Error (%) for 2000 Samples |
|---|---|---|---|---|
| 2.0 | 1.5 | 343.51 | 341.03 | 0.68 |
| 2.0 | 346.77 | 344.22 | 0.74 | |
| 2.5 | 1.5 | 309.50 | 311.94 | 0.78 |
| 2.0 | 315.99 | 313.73 | 0.73 | |
| 3.0 | 1.5 | 271.93 | 269.75 | 0.87 |
| 2.0 | 265.18 | 267.29 | 0.81 | |
| 2.5 | 270.03 | 272.38 | 0.74 | |
| 3.5 | 1.5 | 235.47 | 237.71 | 0.93 |
| 2.0 | 236.92 | 239.09 | 0.95 | |
| 2.5 | 245.58 | 243.46 | 0.88 | |
| 4.0 | 1.5 | 206.57 | 208.39 | 0.82 |
| 2.0 | 215.06 | 213.29 | 0.79 | |
| 2.5 | 217.43 | 219.39 | 0.88 | |
| 3.0 | 224.42 | 226.42 | 0.71 | |
| 4.5 | 1.5 | 174.45 | 176.39 | 1.22 |
| 2.0 | 176.97 | 178.57 | 0.92 | |
| 2.5 | 183.05 | 181.24 | 0.86 | |
| 3.0 | 194.23 | 196.59 | 0.93 | |
| 5.0 | 1.5 | 155.73 | 157.46 | 1.03 |
| 2.0 | 157.15 | 159.38 | 0.82 | |
| 2.5 | 161.25 | 163.37 | 1.42 | |
| 3.0 | 172.02 | 169.64 | 0.97 |
| (mL/h) | (mL/h) | Mean Size by Imaging Method ) | Mean Size by Our Results ) | Maximum Error (%) for 2000 Samples |
|---|---|---|---|---|
| 0.4 | 2.4 | 308.30 | 305.88 | 0.90 |
| 2.6 | 280.16 | 282.54 | 0.82 | |
| 2.8 | 276.00 | 278.37 | 0.77 | |
| 3.0 | 251.48 | 253.74 | 0.93 | |
| 0.6 | 2.4 | 330.37 | 327.88 | 0.84 |
| 2.6 | 316.56 | 314.11 | 0.83 | |
| 2.8 | 286.14 | 288.48 | 0.78 | |
| 3.0 | 277.55 | 279.87 | 0.79 | |
| 0.8 | 2.4 | 350.00 | 347.33 | 0.82 |
| 2.6 | 326.62 | 324.09 | 0.76 | |
| 2.8 | 313.91 | 316.41 | 0.83 | |
| 3.0 | 286.17 | 288.51 | 0.71 | |
| 1.0 | 2.4 | 355.41 | 352.77 | 0.78 |
| 2.6 | 328.90 | 331.41 | 0.75 | |
| 2.8 | 323.82 | 321.38 | 0.82 | |
| 3.0 | 312.85 | 315.28 | 0.73 | |
| 1.2 | 2.4 | 365.58 | 368.34 | 0.79 |
| 2.6 | 351.38 | 348.70 | 0.80 | |
| 2.8 | 331.71 | 329.21 | 0.71 | |
| 3.0 | 310.57 | 313.01 | 0.85 | |
| 1.4 | 2.4 | 376.00 | 373.68 | 0.76 |
| 2.6 | 356.79 | 359.27 | 0.82 | |
| 2.8 | 346.14 | 343.67 | 0.81 | |
| 3.0 | 320.70 | 323.15 | 0.84 | |
| 1.6 | 2.4 | 393.08 | 395.33 | 0.76 |
| 2.6 | 373.60 | 375.86 | 0.78 | |
| 2.8 | 350.47 | 348.10 | 0.78 | |
| 3.0 | 332.41 | 334.92 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Zhang, L. Study on Microdroplets Generation and Detection Method in Four-Way Microfluid Structure (FWMS) by Double Photoresist Method Pulses. Micromachines 2025, 16, 1205. https://doi.org/10.3390/mi16111205
Luo L, Zhang L. Study on Microdroplets Generation and Detection Method in Four-Way Microfluid Structure (FWMS) by Double Photoresist Method Pulses. Micromachines. 2025; 16(11):1205. https://doi.org/10.3390/mi16111205
Chicago/Turabian StyleLuo, Lele, and Lu Zhang. 2025. "Study on Microdroplets Generation and Detection Method in Four-Way Microfluid Structure (FWMS) by Double Photoresist Method Pulses" Micromachines 16, no. 11: 1205. https://doi.org/10.3390/mi16111205
APA StyleLuo, L., & Zhang, L. (2025). Study on Microdroplets Generation and Detection Method in Four-Way Microfluid Structure (FWMS) by Double Photoresist Method Pulses. Micromachines, 16(11), 1205. https://doi.org/10.3390/mi16111205





