Analysis of Dynamic Stability Control of Light Source in Immersion DUV Lithography
Abstract
1. Introduction
2. Theoretical Model
2.1. Lithographic Imaging Model
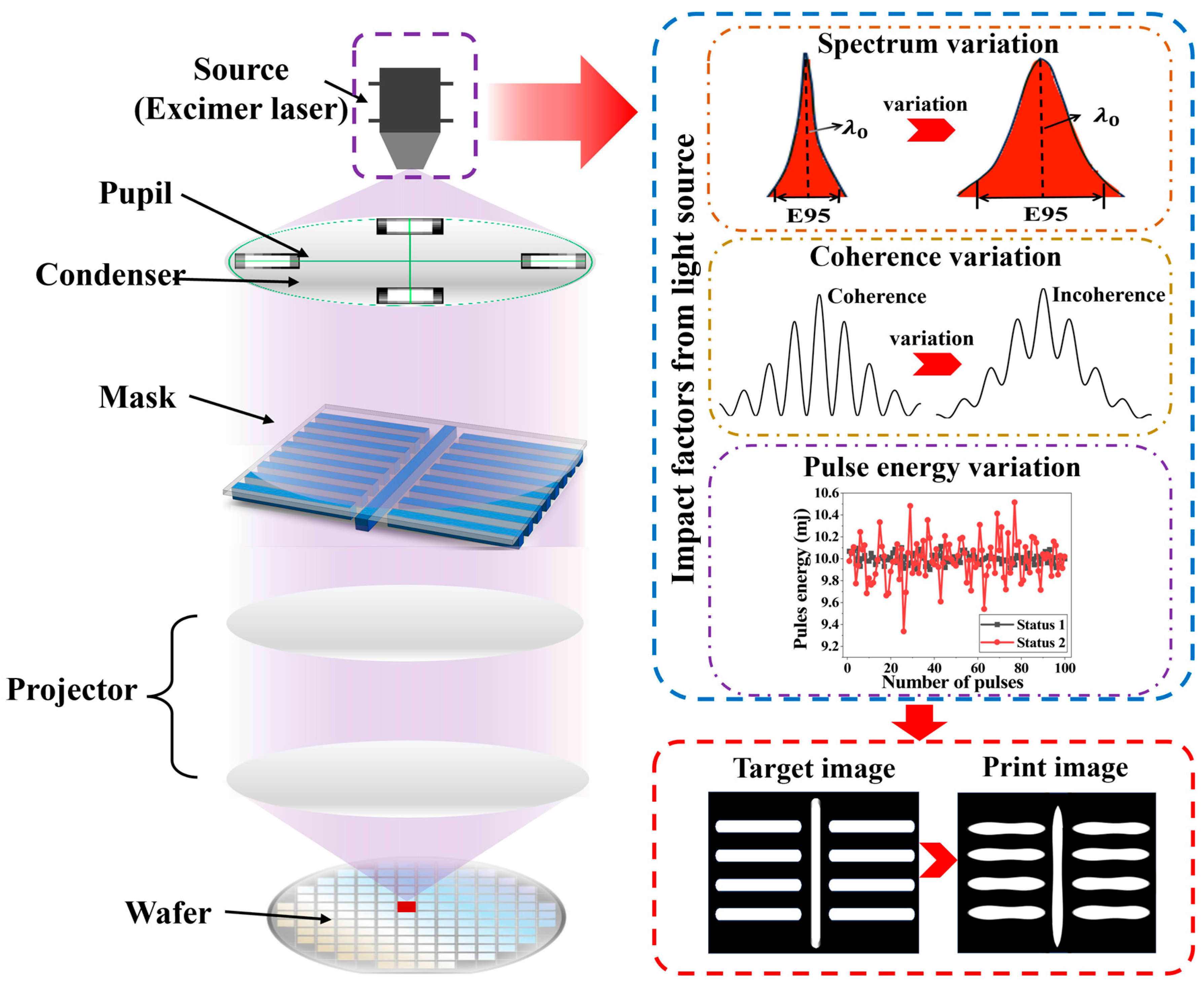
2.2. Impact of Light Source System Stability on Lithographic Imaging
2.2.1. Analysis of Spectral Characteristic Stability Variations
2.2.2. Analysis of Coherence-Induced Imaging Effects
2.2.3. Analysis of Pulse Energy Stability-Induced Imaging Effects
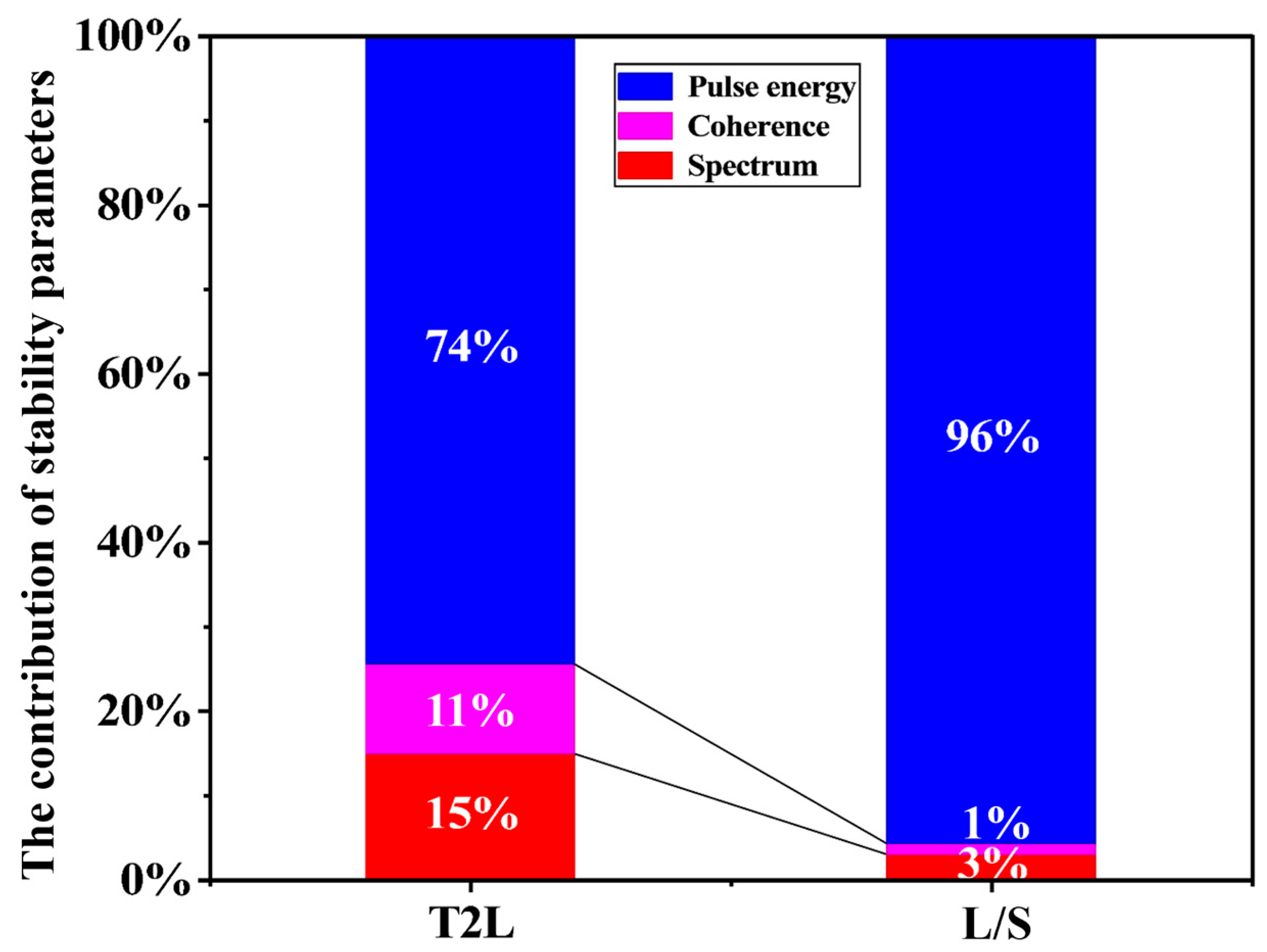
3. Results and Discussion
3.1. Simulation Scheme Design
- (1)
- Exposure Settings and Test Patterns
- (2)
- Laser Stability Parameters
3.2. Simulation and Analysis
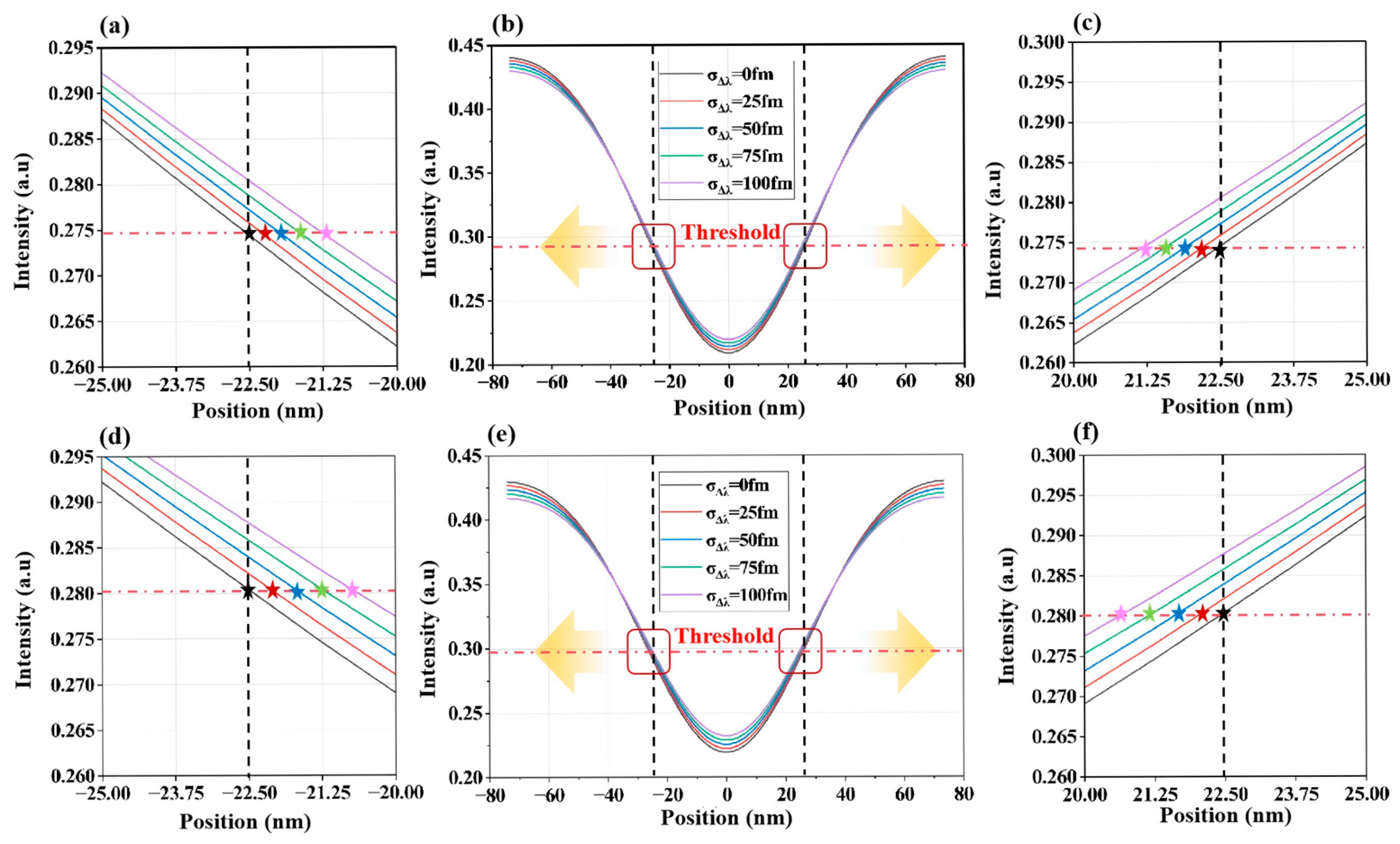
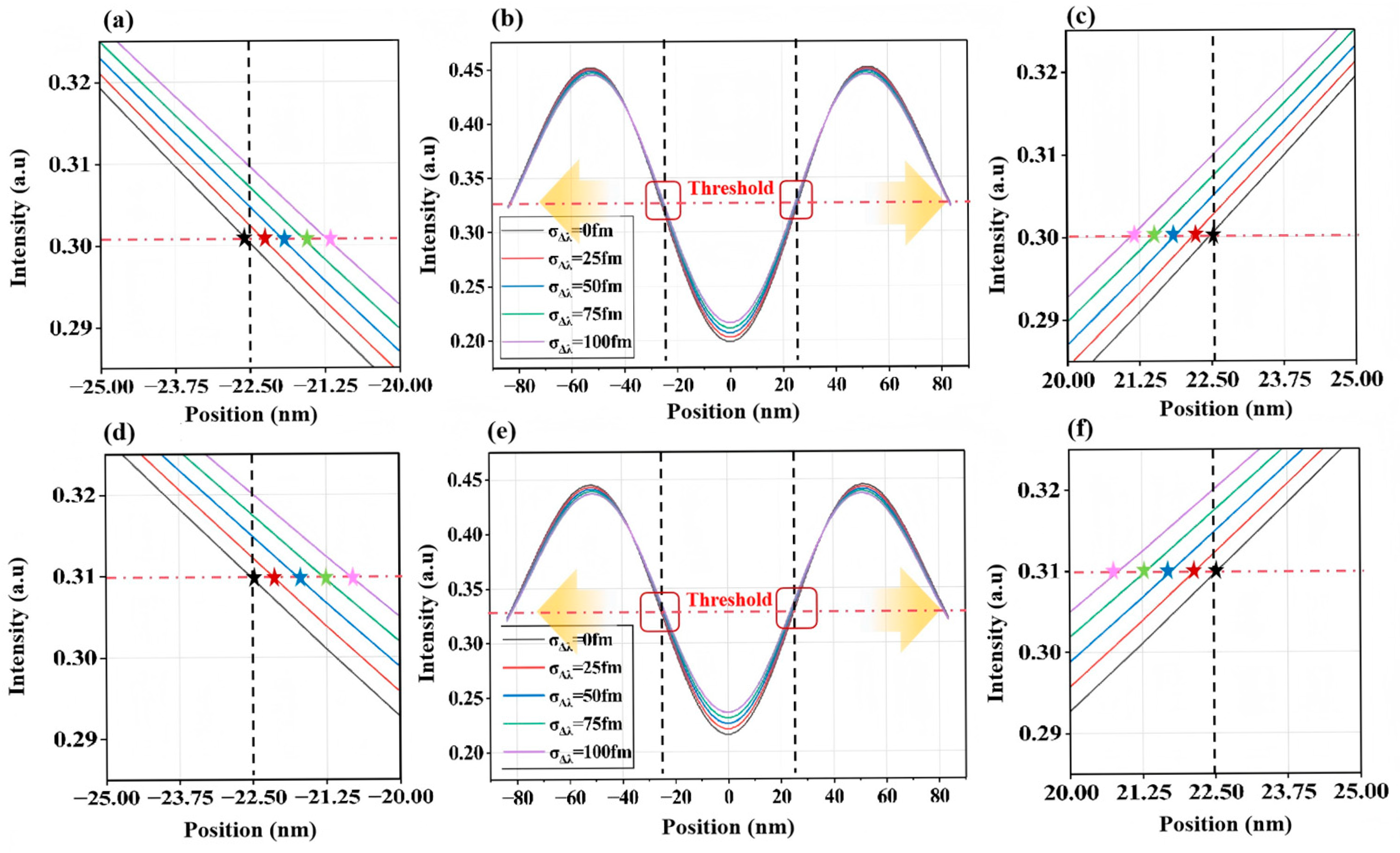
3.2.1. Impact of Spectral Parameter Fluctuations on Aerial Images
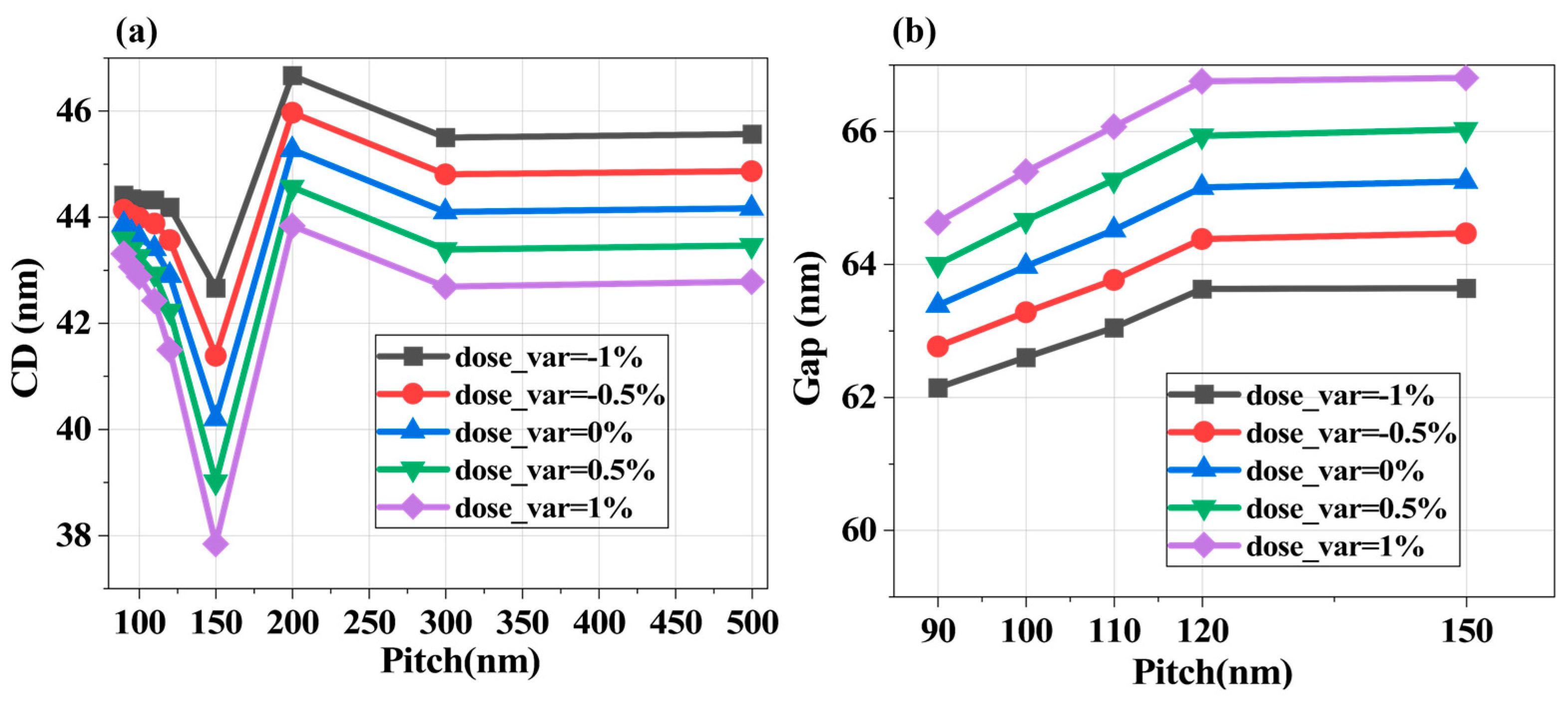
3.2.2. Impact of Pulse Stability on Lithographic Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Van Den Brink, M.; Yen, A.; Van Wijnen, P.; Lercel, M.; Sluijk, B. Holistic Patterning to Advance Semiconductor Manufacturing in the 2020s and Beyond. In Proceedings of the 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Honolulu, HI, USA, 13–17 June 2022; pp. 3–7. [Google Scholar]
- Awad, A.; Brendel, P.; Evanschitzky, P.; Woldeamanual, D.S.; Rosskopf, A.; Erdmann, A. Accurate Prediction of EUV Lithographic Images and 3D Mask Effects Using Generative Networks. J. Micro/Nanopatterning Mater. Metrol. 2021, 20, 043201. [Google Scholar] [CrossRef]
- Pan, D.Z.; Liebmann, L.; Yu, B.; Xu, X.; Lin, Y. Pushing Multiple Patterning in Sub-10nm: Are We Ready? In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 7–11 June 2015; pp. 1–6. [Google Scholar]
- Ohta, T.; Ishida, K.; Kumazaki, T.; Tsushima, H.; Kurosu, A.; Kakizaki, K.; Matsunaga, T.; Mizoguchi, H. 120 W ArF Laser with High-Wavelength Stability and Efficiency for the next-Generation Multiple-Patterning Immersion Lithography. In Proceedings of the Optical Microlithography XXVIII, San Jose, CA, USA, 18 March 2015; p. 94261J. [Google Scholar]
- Cacouris, T.; Conley, W.; Thornes, J.; Bibby, T.; Melchior, J.; Aggarwal, T.; Gross, E. New ArF Immersion Light Source Introduces Technologies for High-Volume 14nm Manufacturing and Beyond. In Proceedings of the Optical Microlithography XXVIII, San Jose, CA, USA, 18 March 2015; p. 942618. [Google Scholar]
- Ishida, K.; Ohta, T.; Miyamoto, H.; Kumazaki, T.; Tsushima, H.; Kurosu, A.; Matsunaga, T.; Mizoguchi, H. The ArF Laser for the Next-Generation Multiple-Patterning Immersion Lithography Supporting Green Operations. In Proceedings of the Optical Microlithography XXIX, San Jose, CA, USA, 15 March 2016; p. 978010. [Google Scholar]
- Cao, D.; Dong, H.; Zeng, Z.; Zhang, W.; Li, X.; Yu, H. Thermal Control Systems in Projection Lithography Tools: A Comprehensive Review. Micromachines 2025, 16, 880. [Google Scholar] [CrossRef] [PubMed]
- Kurosu, A.; Nakano, M.; Yashiro, M.; Yoshino, M.; Tsushima, H.; Masuda, H.; Kumazaki, T.; Matsumoto, S.; Kakizaki, K.; Matsunaga, T.; et al. A Reliable Higher Power ArF Laser with Advanced Functionality for Immersion Lithography. In Proceedings of the Optical Microlithography XXV, San Jose, CA, USA, 13 March 2012; p. 83261F. [Google Scholar]
- Alagna, P.; Biesemans, S.; Nafus, K.; Lorusso, G.F.; Rechtsteiner, G.; Conley, W. Tunable Bandwidth for Application-Specific SAxP Process Enhancement. In Proceedings of the Optical Microlithography XXXI, San Jose, CA, USA, 20 March 2018; p. 1058705. [Google Scholar]
- Trintchouk, F.; Ishihara, T.; Gillespie, W.; Ness, R.; Bergstedt, R.; Wittak, C.; Perkins, R. XLA-300: The Fourth-Generation ArF MOPA Light Source for Immersion Lithography. In Proceedings of the Optical Microlithography XIX, San Jose, CA, USA, 15 March 2006; p. 615423. [Google Scholar]
- Burdt, R.; Thornes, J.; Duffey, T.; Bibby, T.; Rokitski, R.; Mason, E.; Melchior, J.; Aggarwal, T.; Haran, D.; Wang, J.; et al. Flexible Power 90 W to 120 W ArF Immersion Light Source for Future Semiconductor Lithography. In Proceedings of the Optical Microlithography XXVII, San Jose, CA, USA, 31 March 2014; p. 90522K. [Google Scholar]
- Rokitski, R.; Ishihara, T.; Rao, R.; Jiang, R.; Haviland, M.; Cacouris, T.; Brown, D. High Reliability ArF Light Source for Double Patterning Immersion Lithography. In Proceedings of the Optical Microlithography XXIII, San Jose, CA, USA, 3 March 2010; p. 76401Q. [Google Scholar]
- Feng, Y.; Liu, J.; Song, Z.; Jiang, H.; Liu, S. Efficient Measurement and Optical Proximity Correction Modeling to Catch Lithography Pattern Shift Issues of Arbitrarily Distributed Hole Layer. Front. Mech. Eng. 2024, 19, 24. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Chang, K.-H.; Cheng, W.-L.; Tang, Y.-P. Curvilinear Mask Handling in OPC Flow. J. Micro/Nanopatterning Mater. Metrol. 2023, 23, 011203. [Google Scholar] [CrossRef]
- Wu, R.; Dong, L.; Wei, Y. Method for Optical Proximity Correction Based on a Vector Imaging Model. Appl. Opt. 2024, 63, 2719. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wu, Q.; Li, Y.; Liu, X.; Li, Y. Patterning Fidelity Enhancement and Aberration Mitigation in EUV Lithography Through Source–Mask Optimization. Micromachines 2025, 16, 1166. [Google Scholar] [CrossRef]
- Peng, F.; Xu, Y.; Song, Y.; Gui, C.; Zhao, Y. Source and Mask Optimizing with a Defocus Antagonism for Process Window Enhancement. Opt. Express 2022, 30, 36429. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhou, J.; Yu, D.; Sun, H.; Hu, S.; Wang, J. The Inverse Optimization of an Optical Lithographic Source with a Hybrid Genetic Algorithm. Appl. Sci. 2023, 13, 5708. [Google Scholar] [CrossRef]
- Sun, H.; Du, J.; Jin, C.; Quan, H.; Li, Y.; Tang, Y.; Wang, J.; Hu, S.; Liu, J. Global Optimisation of Source and Mask in Inverse Lithography via Tabu Search Combined with Genetic Algorithm. Opt. Express 2022, 30, 24166. [Google Scholar] [CrossRef] [PubMed]
- Granik, Y. Qualification of Structured Curvilinear ILT Assist Features for Production. J. Micro/Nanopatterning Mater. Metrol. 2024, 23, 021302. [Google Scholar] [CrossRef]
- Peng, R.C.; Lee, H.J.; Lin, J.; Lin, A.; Chang, A.; Lin, B.S.-M. Laser Spectrum Requirements for Tight CD Control at Advanced Logic Technology Nodes. In Proceedings of the Optical Microlithography XXIII, San Jose, CA, USA, 3 March 2010; p. 76402C. [Google Scholar]
- Conley, W.; Hsieh, S.; Alagna, P.; Hou, Y.; Martinez, P. Impact of Bandwidth on Contrast Sensitive Structures for Low K1 Lithography. In Proceedings of the Optical Microlithography XXVIII, San Jose, CA, USA, 18 March 2015; p. 942607. [Google Scholar]
- Bengtsson, J. Dynamic Laser Speckle as a Detrimental Phenomenon in Optical Projection Lithography. J. Micro/Nanolithography MEMS MOEMS 2006, 5, 033004. [Google Scholar] [CrossRef]
- Rokitski, R.; Rafac, R.; Melchior, J.; Dubi, R.; Thornes, J.; Cacouris, T.; Haviland, M.; Brown, D. High Power 120 W ArF Immersion XLR Laser System for High Dose Applications. In Proceedings of the Optical Microlithography XXVI, San Jose, CA, USA, 12 April 2013; p. 86831H. [Google Scholar]
- Smith, M.; Bendik, J.; Lalovic, I.; Farrar, N.; Howard, W.; Sallee, C. Modeling and Performance Metrics for Longitudinal Chromatic Aberrations, Focus-Drilling, and Z-Noise: Exploring Excimer Laser Pulse-Spectra. In Proceedings of the Optical Microlithography XX, San Jose, CA, USA, 27 March 2007; p. 65203E. [Google Scholar]
- Lalovic, I. Impact of Finite Laser Bandwidth on the Critical Dimension of L/S Structures. J. Micro/Nanolithography MEMS MOEMS 2008, 7, 033001. [Google Scholar] [CrossRef]
- Ma, X.; Han, C.; Li, Y.; Dong, L.; Arce, G.R. Pixelated Source and Mask Optimization for Immersion Lithography. J. Opt. Soc. Am. A 2013, 30, 112. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Su, X.; Dong, L.; Fan, T.; Wei, Y. Dynamic Budget Analysis of Multiple Parameters in a Lithography System Based on the Superposition of Light Intensity Fluctuations. Opt. Express 2024, 32, 5323. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Hu, P.; Tolani, V.; Dam, T.; Tyminski, J.; Slonaker, S. Toward a Consistent and Accurate Approach to Modeling Projection Optics. In Proceedings of the Optical Microlithography XXIII, San Jose, CA, USA, 11 March 2010; p. 76402Y. [Google Scholar]
- Farahiyan, M.; Aalipour, R. Assessing the Impact of Spatial Coherence on the Sinusoidal Linear Fresnel Zone Plate’s Depth of Focus. Sci. Rep. 2024, 14, 29896. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Yessenov, M.; Padgett, M.J. The Propagation Speed of Optical Speckle. Sci. Rep. 2023, 13, 9071. [Google Scholar] [CrossRef] [PubMed]
- Buijs, J.; Gucht, J.V.D.; Sprakel, J. Fourier Transforms for Fast and Quantitative Laser Speckle Imaging. Sci. Rep. 2019, 9, 13279. [Google Scholar] [CrossRef] [PubMed]





| Process Parameters | |
|---|---|
| Illimitation condition | cQuad: σout = 0.96, σinner = 0.65, blade angle = 20 |
| NA | 1.35 |
| Process | PTD |
| Mask type | Bright field and 6% attenuated PSM |
| Test pattern: Line/Space | |
 | CD: 45 nm; Pitch: 90, 95, 100, 110, 120, 150, 200, 300, 500 nm |
| Test pattern: Tip to Line | |
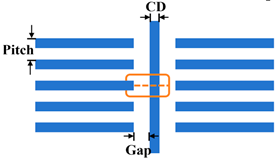 | CD: 45 nm; Gap: 60, 65, 70 nm; Pitch: 90, 100, 110, 120, 150 nm; |
| Laser Parameter Stability | ||
|---|---|---|
| Bandwidth distribution change | 300, 200 fm | |
| 0, 25, 50, 75, 100 fm | ||
| Central wavelength change | 193 nm | |
| 0, 1, 2 pm | ||
| Pulse energy variation | 102% (Assume that the deviation caused by the dose control of the light source system is 2%) | |
| 0.5, 1, 1.5, 2% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Han, D.; Wu, C.; Deng, S.; Wei, Y. Analysis of Dynamic Stability Control of Light Source in Immersion DUV Lithography. Micromachines 2025, 16, 1207. https://doi.org/10.3390/mi16111207
Zhu Y, Han D, Wu C, Deng S, Wei Y. Analysis of Dynamic Stability Control of Light Source in Immersion DUV Lithography. Micromachines. 2025; 16(11):1207. https://doi.org/10.3390/mi16111207
Chicago/Turabian StyleZhu, Yihua, Dandan Han, Chuang Wu, Sen Deng, and Yayi Wei. 2025. "Analysis of Dynamic Stability Control of Light Source in Immersion DUV Lithography" Micromachines 16, no. 11: 1207. https://doi.org/10.3390/mi16111207
APA StyleZhu, Y., Han, D., Wu, C., Deng, S., & Wei, Y. (2025). Analysis of Dynamic Stability Control of Light Source in Immersion DUV Lithography. Micromachines, 16(11), 1207. https://doi.org/10.3390/mi16111207






