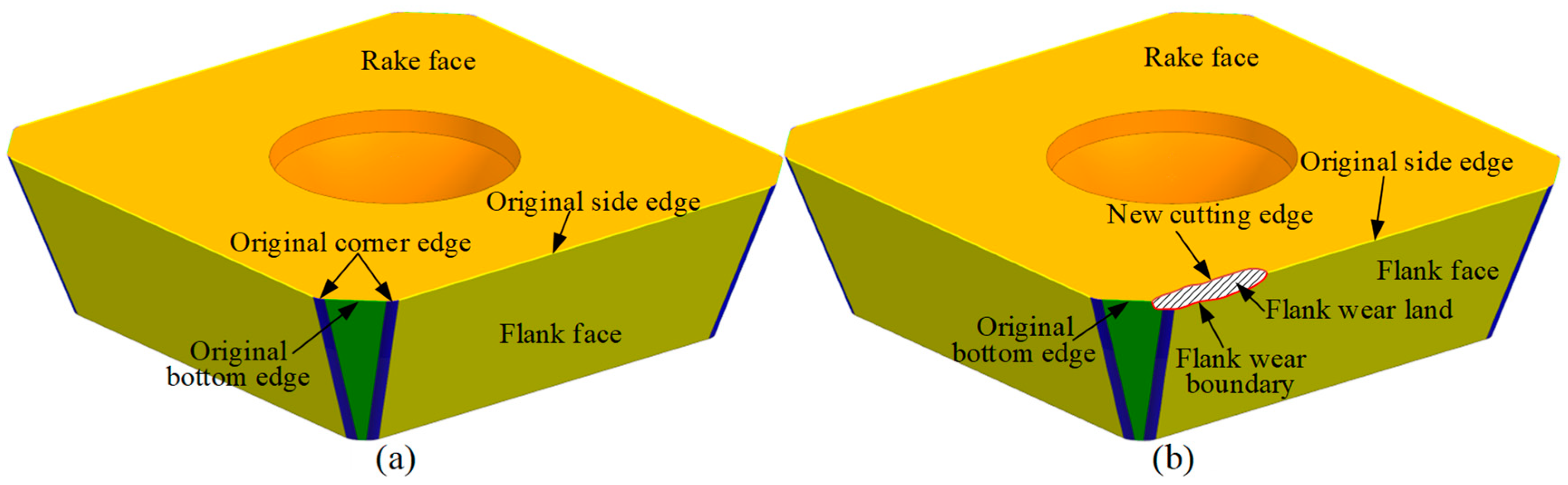
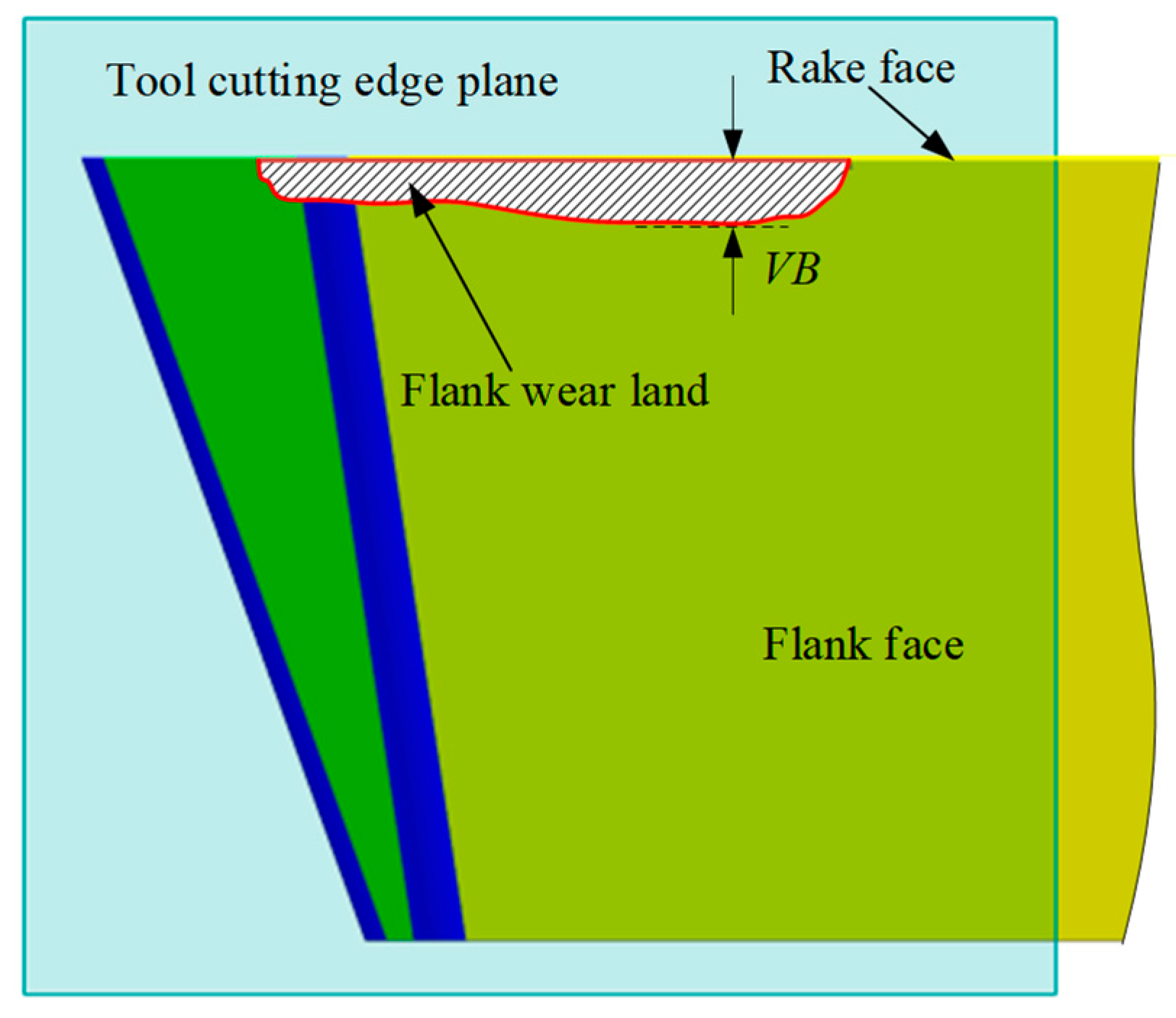
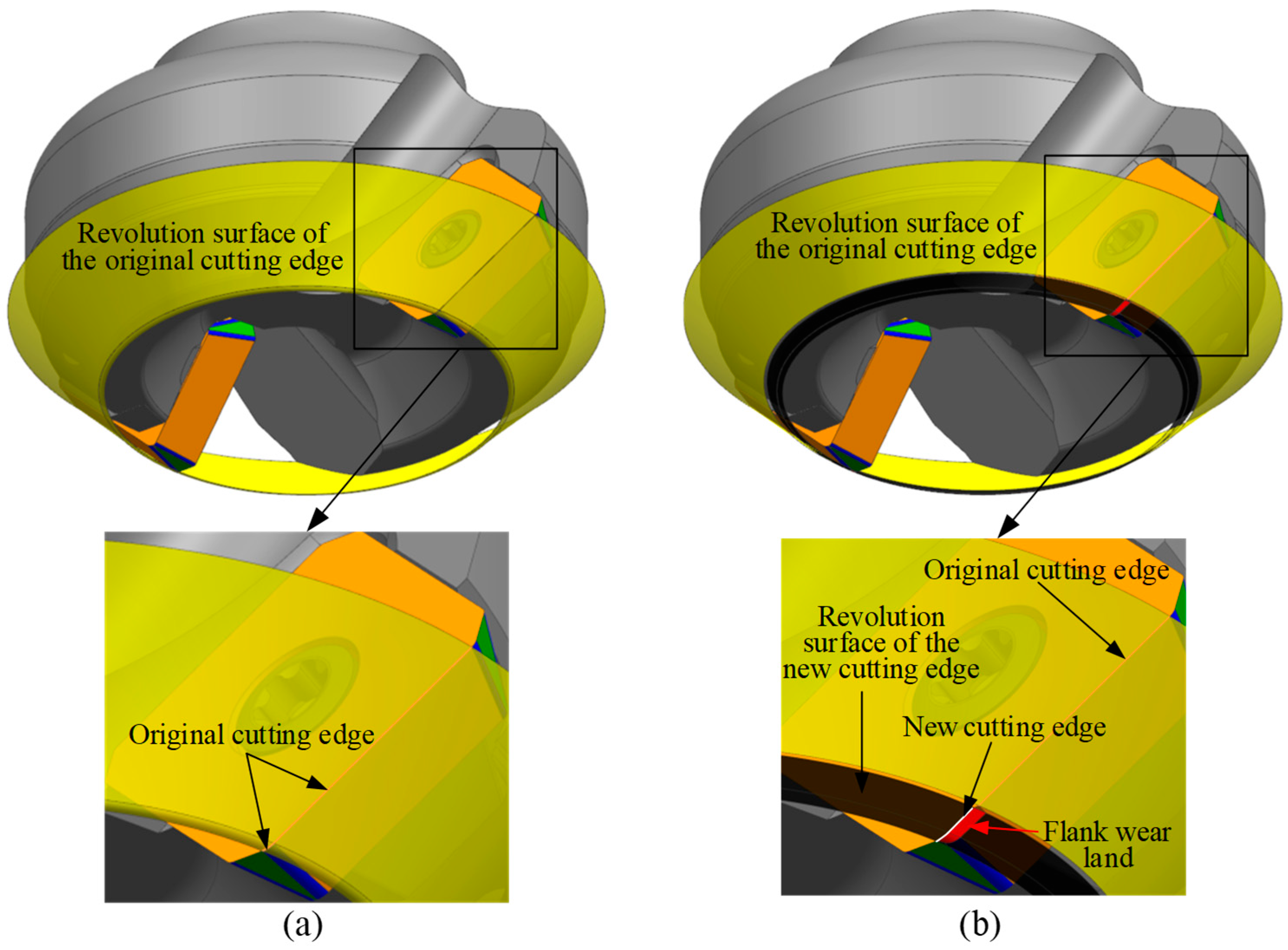
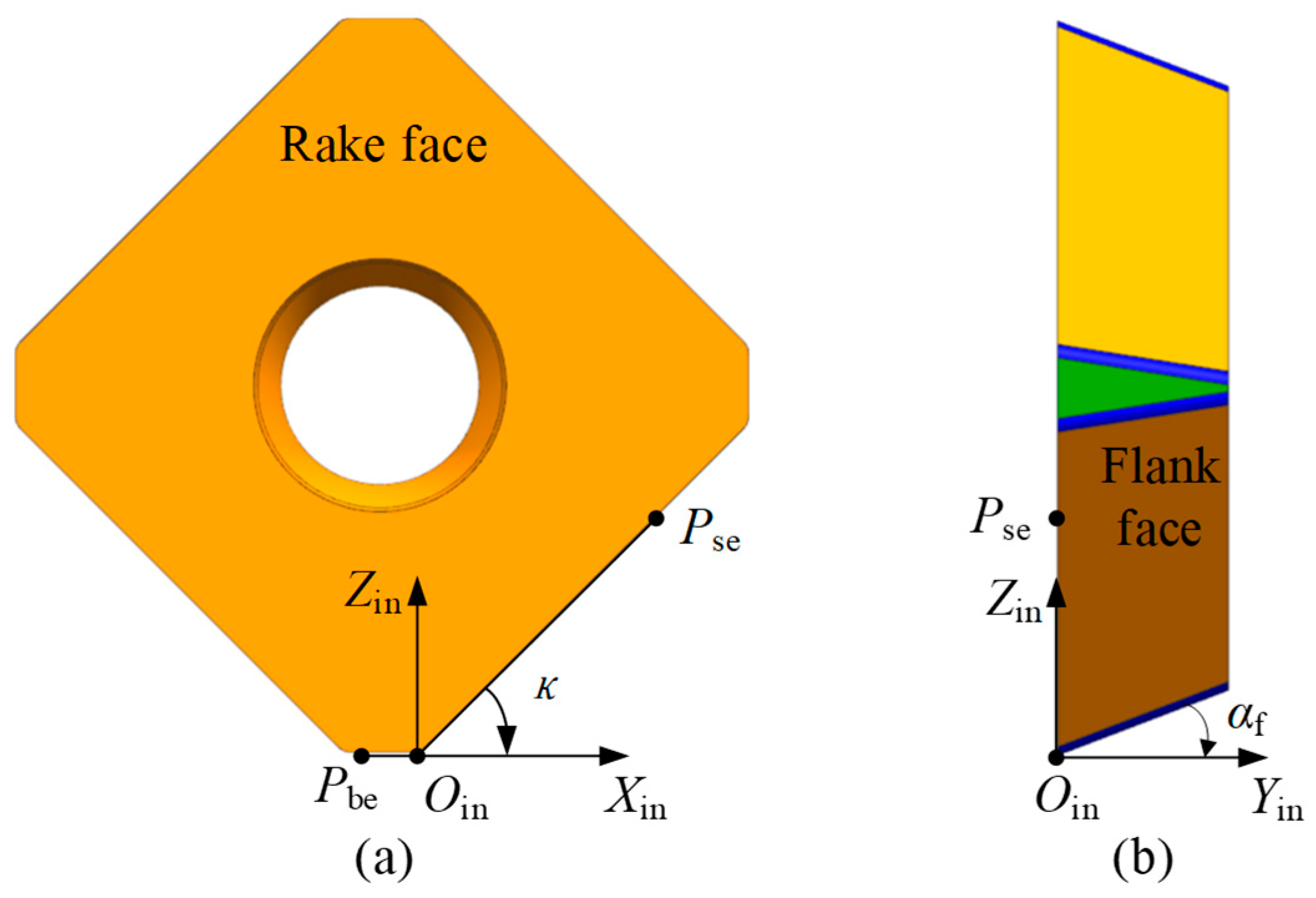
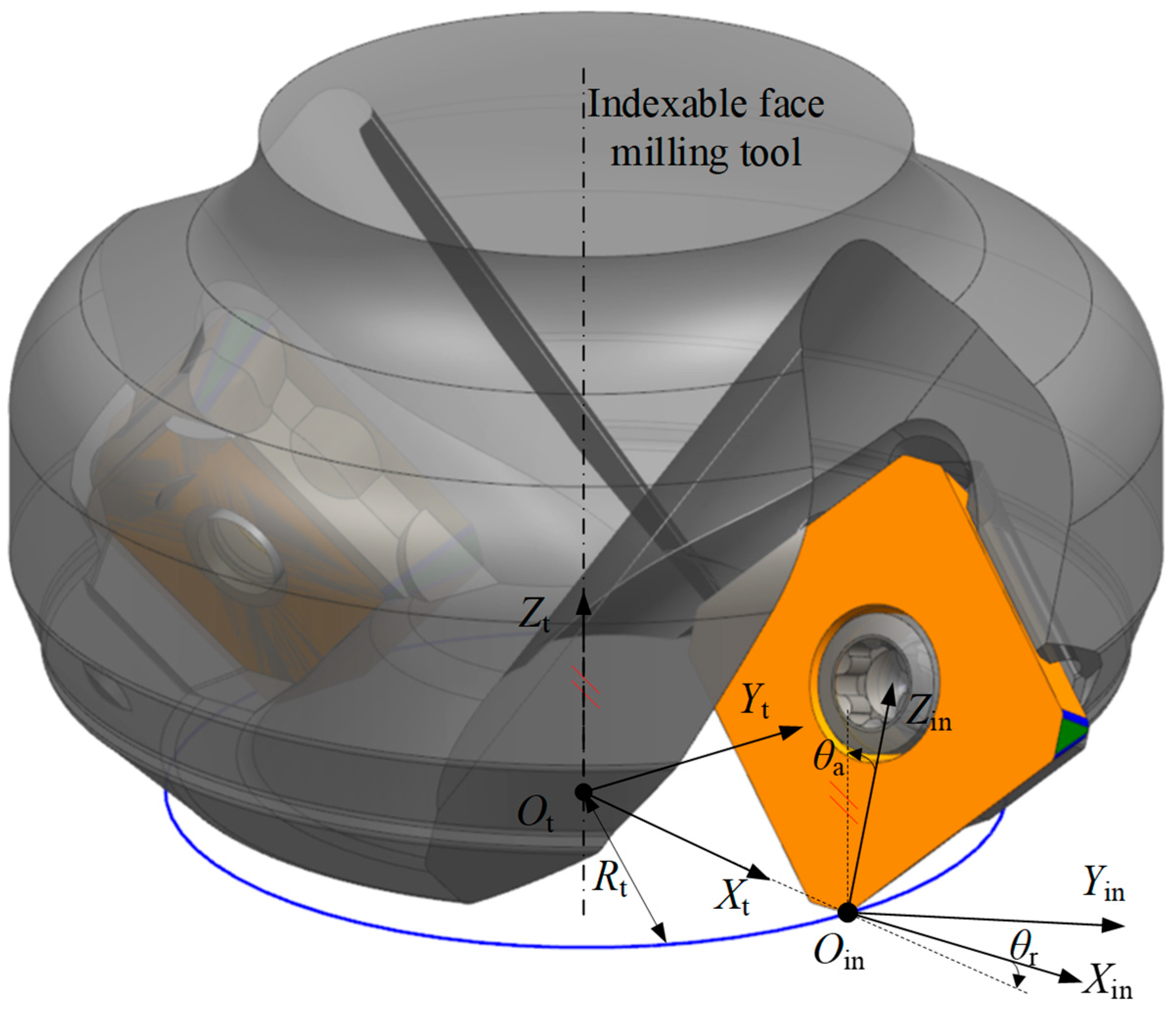
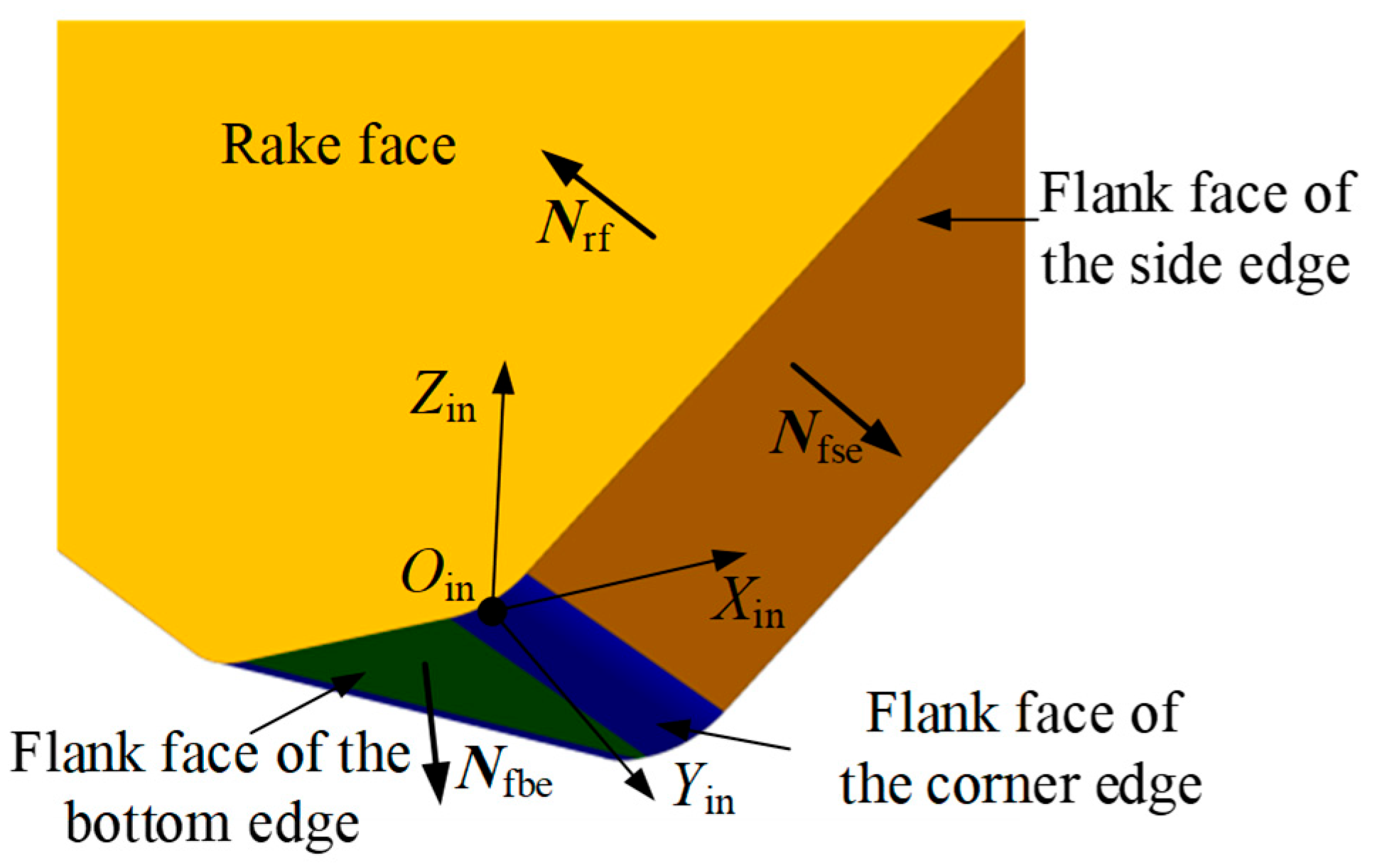
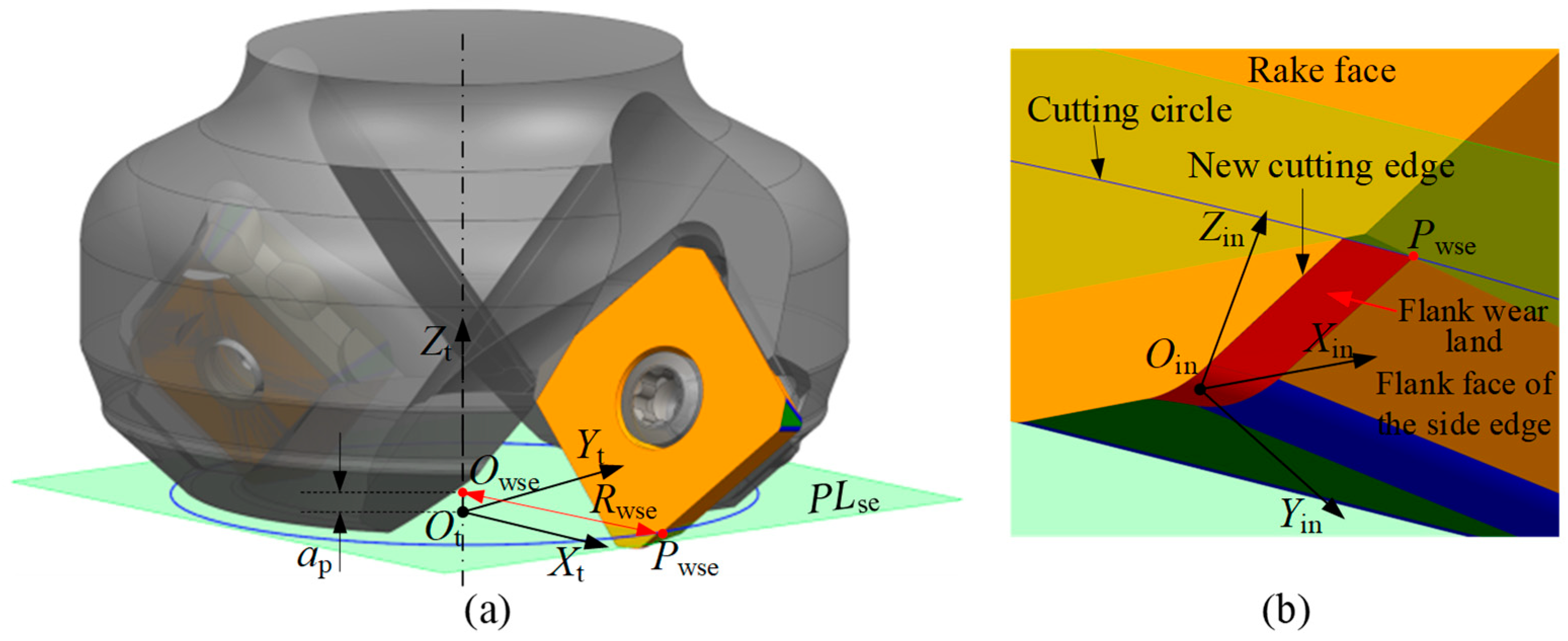
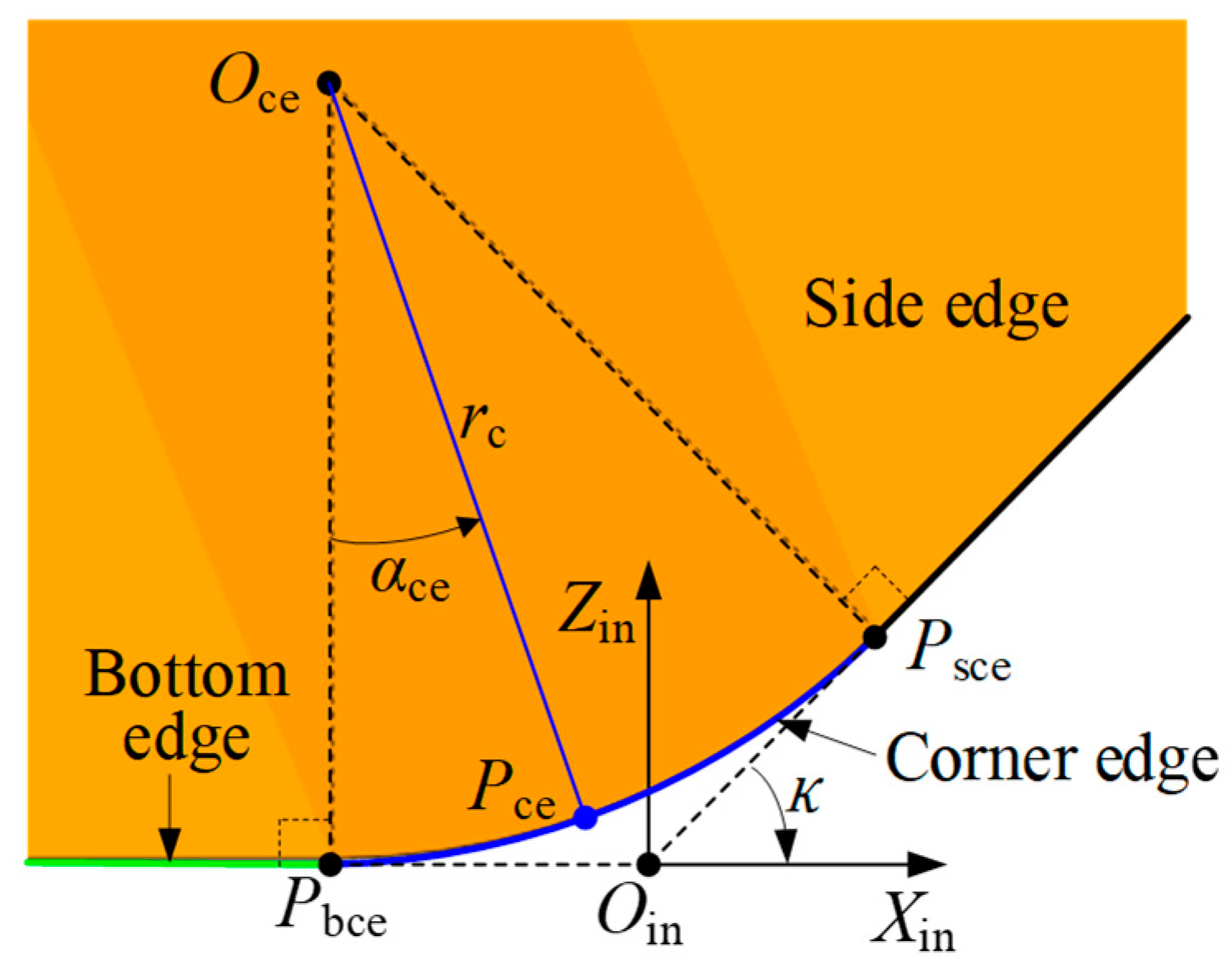
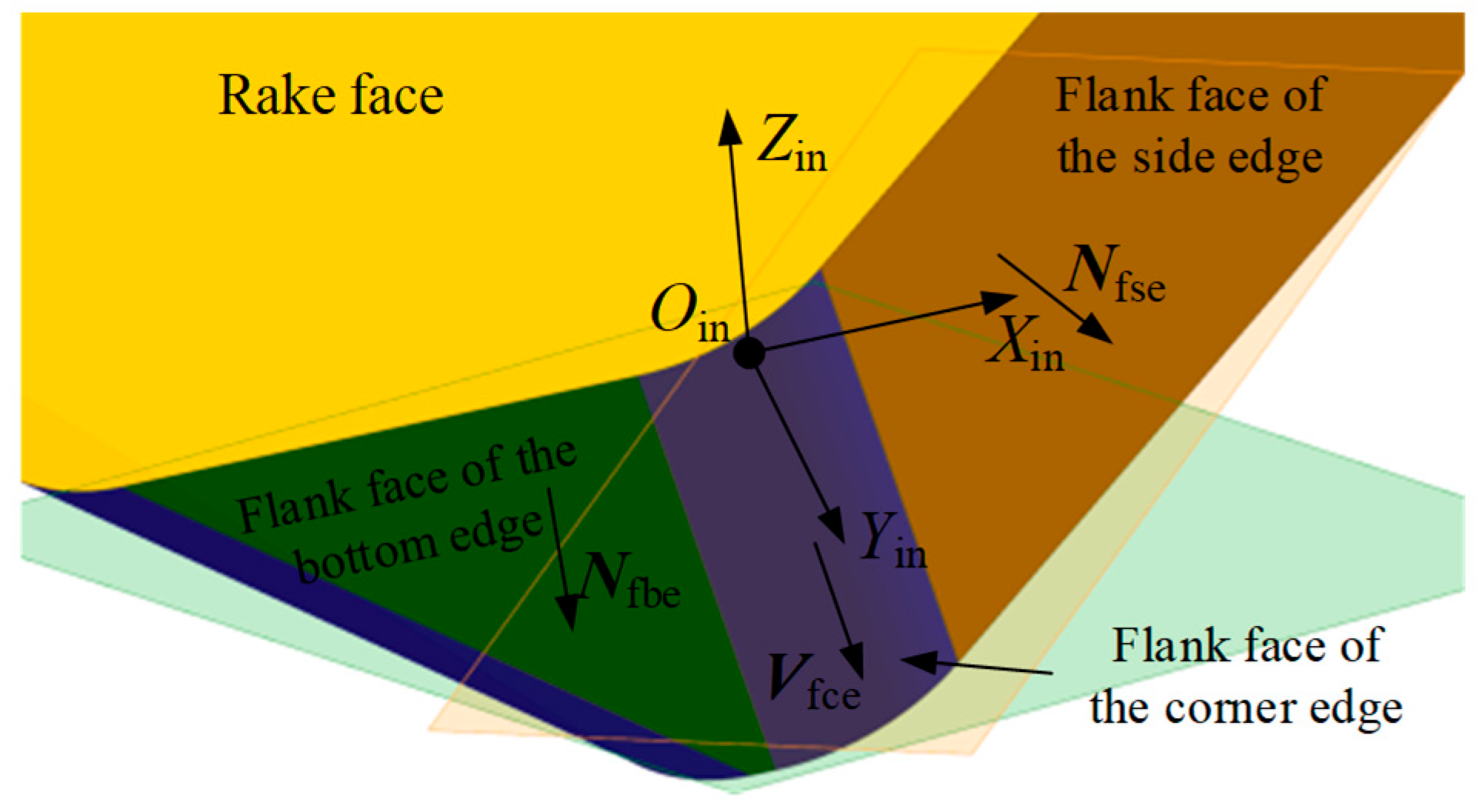
1. Introduction
A kernel technique of smart (or intelligent) machining is on-machine tool measurement for tool wear compensation and tool condition monitoring. Specifically, radii and lengths of the cutting tools should be regularly, automatically, and precisely measured with the laser tool setter on the machine table; no machinist is needed. After measuring the cutting tool, its radius and length wear is compensated in the subsequent machining so that the workpiece accuracy remains high as before. Tool wear compensation is realized. At the same time, the tool wear amount is calculated and compared to its threshold so that it can be automatically changed right before it becomes invalid. Therefore, the tool can effectively cut qualified workpieces with its best longevity, and the tool cost is reduced. Tool condition monitoring is realized. However, in the conventional machining, machinists do not regularly measure the tool radius and length with manual tool setters outside the CNC machines during machining; the tool wear compensation cannot be conducted. When mechanists physically notice the tool wears out, they pause machining and manually measure the tool to determine whether to replace the tool or not. This tool condition monitoring is ineffective. It is in high demand in industry to conduct the tool wear compensation and the tool condition monitoring in machining.
Tool condition monitoring is critical to workpiece quality and the maximum extent of using tools [
1]. During the machining process, the cutting tool continuously removes material from the workpiece and gradually undergoes wear. The wear pattern of the tool is influenced by numerous factors, primarily including cutting parameters (cutting speed, feed rate, and depth of cut), tool material and geometry (carbide and coatings), workpiece material and geometry, machine tool conditions, and the cooling methods (dry machining, minimum quantity lubrication, and minimum quantity cooling lubrication) employed [
2]. Tool wear patterns are typically categorized into several types, including flank wear, crater wear, plastic deformation, notch wear, thermal cracking, chipping, and built-up edge (BUE) [
3]. It has been found that the main wear pattern for coated cemented carbide tools when cutting steel materials is flank wear [
4]. During machining, the flank face of the tool remains in continuous contact with the machined surface of the workpiece. This contact generates significant frictional heat on the workpiece surface, which leads to gradual wear on the flank face [
5].
The influence of tool wear on cutting forces is significant and cannot be ignored. Gao et al. [
6] developed a cutting force prediction model that comprehensively considers tool flank wear and tool runout. Milling experiments showed that as the flank wear increases, the engagement between the tool and the workpiece becomes greater, resulting in a sharp rise in cutting forces. Ding et al. [
7] constructed a real-time cutting force monitoring model that integrates tool deformation, tool runout, and tool wear. They proposed a tool wear prediction method based on temporal convolutional networks, bi-directional long short-term memory networks, and multi-objective optimization algorithms, achieving a maximum prediction error of 12.02%. Wang et al. [
8] considered the impact of tool wear on the actual milling cutter radius and developed a stainless steel milling force prediction model that accounts for tool wear. The experimental results show that during the rapid wear stage, the milling force generated by a worn tool is more than twice that of a new tool. Song et al. [
9], aiming to reveal the mechanism by which vibration affects cutting force and tool wear in ultrasonic-assisted machining, established a two-dimensional ultrasonic-assisted scratching force model that incorporates tool wear, confirming the inhibitory effect of ultrasonic vibration technology on tool wear. A worn cutting tool leads to progressive deterioration of the cutting edge, which can result in “chip-like burr” forming on the workpiece surface, severely affecting surface quality [
10]. As is well known, tool wear directly determines both tool life and workpiece machining quality. Worn cutting tools increase the surface roughness of the workpiece and reduce machining accuracy. As tool wear intensifies, both the tool diameter and length continue to decrease. The purpose of tool condition monitoring is to measure the reduction in tool dimensions and thereby calculate the extent of tool wear.
Face milling is one of the primary types of milling processing and is widely used in the machining of large components [
11]. Face milling involves high material removal rates and significant energy consumption, which generates substantial cutting heat and leads to severe tool wear [
12]. The wear distribution on the tool is non-uniform [
13], primarily concentrated near the cutting edge due to the combined effects of extrusion deformation and shear deformation imposed by the tool on the workpiece [
14]. Pozzato et al. [
15] used round ceramic inserts to machine Inconel 718 superalloy and found that the central region of the insert flank face experienced the most severe tool wear. Zhao et al. [
16] developed a non-uniform flank wear model considering the real cutting length (RCL) of the tool, and based on this, proposed a tool orientation optimization method to reduce the maximum flank wear and thereby extend tool life. Jin et al. [
17] machined unidirectional CFRP composites using indexable milling tools and observed non-uniform wear distribution caused by the different fiber orientations in the UD layers. Therefore, to accurately measure tool wear and improve measurement efficiency, it is essential to identify the region where maximum tool wear occurs.
As a new technology, on-machine measurement (OMM) enables automatic measurement of tool radius and length during machining by using tool setters mounted on the machine table, allowing for tool path compensation in subsequent processes. Liu et al. [
18] developed a non-contact automated tool setter for micro-milling machines using a fiber optic sensor composed of a laser emitter and receiver. The sensor calculates the tool position by detecting the change in light intensity as the tool passes through the beam, and compares it with the beam location to determine the tool dimensions. The system achieved a measurement accuracy of 2 µm and repeatability of 0.6 µm for micro-tools of various sizes, with each measurement taking approximately 10 s, and an 80% improvement in efficiency compared to manual tool setting. In ultra-precision machining, laser diffraction-based micro-tool measurement techniques offer significant application value. Khajornrungruang et al. [
19] utilized laser diffraction fringe characteristics to precisely measure the dimensions of rotating micro end mills and drills on the machine tool. The accuracy of tool setter measurements depends on factors such as calibration accuracy and measurement parameters. Fang et al. [
20] developed a new calibration method by establishing a laser beam axis calibration mechanism, which accurately determined the position of the laser tool setter in the machine coordinate system and significantly improved its calibration accuracy. Vieira Junior et al. [
21] conducted a series of experiments to thoroughly investigate the effects of spindle speed and feed rate on the measurement accuracy of tool dimensions using a laser tool setter. The optimal measurement parameters were determined to achieve precise tool size measurement. Although the above-mentioned laser tool setter can directly measure the tool radius and length, it is incapable of measuring flank wear on the tool and therefore cannot achieve the objective of tool condition monitoring.
Accurately measuring tool wear is a challenging task, especially in finishing processes where tool wear typically occurs on the micron scale, making measurement even more difficult [
22]. Moreover, tool wear is inherently uncertain and presents in complex and varied patterns, which adds to the difficulty of tool wear measurement. The measurement methods of tool wear can be classified into two main categories: direct and indirect measurement methods. Direct measurement methods involve directly capturing the geometric features and dimensions of the worn region to assess the wear condition of the tool. This approach primarily focuses on evaluating parameters such as the width [
23], area [
24], and volume [
25] of the tool wear regions. Meanwhile, indirect measurement methods assess tool wear by capturing dynamic signals generated during the cutting process that are correlated with the tool wear condition. These signals include vibration, current and power signals, cutting force, temperature, and acoustic emission, among others [
26]. Saha et al. [
27] investigated progressive tool wear indicators in micro-milling processes, such as the increase in cutting edge radius, the reduction in tool radius, and the increase in flank wear land width. And established a geometric relationship between the change in cutting edge radius and the corresponding reduction in tool radius. By directly measuring these three wear-related indicators on worn-out tools and conducting an in-depth analysis, they concluded that the reduction in tool radius is the most suitable indicator for plotting tool life curves. Li et al. [
28] pointed out that, unlike progressive tool wear, tool breakage is sudden and random, posing a more severe threat to workpiece quality, machine tool integrity, and operator safety. The impact of data imbalance on tool breakage monitoring models is explored, and feasible solutions are proposed at both the data and algorithm levels. Liu et al. [
29] proposed a vision-based method for precise measurement of tool geometry and established a multi-zone light source illumination model considering multiple incident angles to improve lighting uniformity. Experimental results show that image uniformity increases by 1.5 times, with a relative measurement error of less than 0.35%. Zhu et al. [
30] developed a single-image super-resolution method for on-machine measurement of tool wear. By reconstructing high-resolution tool wear images, the tool wear region is measured accurately, and the goal of online evaluation of tool condition has been achieved. Zhang et al. [
31] integrated multiple advanced image processing techniques and proposed a visual measurement method for flank wear volume. Using Accelerated-KAZE (AKAZE) feature matching for image registration, the flank wear region is extracted, allowing a precise assessment of the flank wear condition. Wang et al. [
32], under minimum quantity lubrication (MQL) cutting conditions, eliminated interface acoustic emission (AE) burst signals by configuring appropriate AE parameters (including threshold, rise time, and duration time), and performed clustering of AE energy to establish the relationship between flank wear and AE burst signals for accurate assessment of tool flank wear. Akhtar et al. [
33] utilized infrared sensors to monitor the machining process, including workpiece deflection, chatter, and tool wear, enabling estimation of tool wear at different machining stages. Cheng et al. [
34] designed a multi-level parallel convolutional neural network (parallel CNN) framework based on a bi-directional long short-term memory network (BiLSTM) to monitor tool wear conditions under various working scenarios.
Compared with methods relying on a single sensor, most current studies adopt multi-sensor signal fusion for tool wear monitoring [
35]. This approach enables information complementation, overcoming the limitations of single-sensor signals that fail to fully characterize tool wear features, thus improving the accuracy of tool wear monitoring. He et al. [
36] investigated a deep learning method based on a Stacked Sparse Autoencoder (SSAE) and multi-sensor signal feature fusion. Cutting force, vibration, and acoustic emission signals collected during milling were analyzed in the time domain, frequency domain, and time-frequency domain, respectively. The most sensitive features were selected through correlation analysis, which were input into the SSAE model for deep feature learning to build a predictive model for tool wear. Sun et al. [
37] proposed a hybrid-driven, physics-informed Gaussian process regression model to predict tool wear, primarily using cutting force and vibration signals. The model achieved a prediction accuracy of 99.7%. Liu et al. [
38] developed an indirect tool wear monitoring system for online measurement of cutting force and cutting temperature. An analytical model was established to relate the flank wear rate of WC-Co cemented carbide tools to cutting force and temperature during the milling process. Zhang et al. [
39] introduced a tool wear monitoring method based on multi-channel hybrid information and deep transfer learning. This method integrates six-dimensional sensor data, including cutting force, acoustic emission, vibration signals, and so on. The features extracted from the multi-channel hybrid information showed stronger correlation with tool wear compared to those from single-channel sensor data.
With the rapid advancement of machine learning technologies, many researchers have recently applied machine learning algorithms to tool condition monitoring (TCM). For instance, Cheng et al. [
40] proposed an intrinsic information-constrained unsupervised domain adaptation approach to achieve robust feature extraction and transfer learning of tool wear under varying cutting conditions. Tang et al. [
41] developed a hybrid learning model to perform time–sequence prediction based on fused sensor features, thereby improving wear prediction accuracy. Similarly, Sun et al. [
42] presented a parallel neural network framework for intelligent tool wear monitoring under variable machining conditions, demonstrating strong adaptability in feature learning and state classification. These studies indicate that machine learning-based approaches can effectively mine latent features from complex signals and capture nonlinear degradation trends, providing valuable support for tool wear prediction and remaining useful life estimation. However, most existing studies primarily focus on tool wear condition classification, such as distinguishing between initial wear, severe wear, and tool breakage, rather than achieving precise wear quantification. In addition, it often requires expensive sensors and strict installation conditions, which limit their applicability in real industrial environments [
43].
To address the limitations of existing insert flank wear width cannot be measured on the on-machine laser tool setter, this study proposes a novel tool condition monitoring technique capable of determining the flank wear width of indexable face milling tools using on-machine laser tool setters. The remainder of this paper is organized as follows.
Section 2 introduces the mechanism of flank wear formation in indexable face milling tools.
Section 3 establishes the geometric model of the flank wear land width based on the insert and tool coordinate systems.
Section 4 presents the flank wear land width measurement method using on-machine laser tool setters.
Section 5 reports the experimental verification and industrial application of the proposed approach. Finally,
Section 6 concludes the paper with the main findings.
4. Flank Wear Land Width Measurement Method Based on Laser Tool Setters
This core purpose of this study is to achieve real-time compensation and condition monitoring of cutting tools during machining by utilizing on-machine tool measurement systems. Specifically, flank wear width is used as the primary indicator for assessing tool condition. To this end, a novel monitoring approach based on the laser tool setter is proposed, comprising two main tasks.
First, the focus is on monitoring tool size variations throughout the machining process using the laser tool setter, while simultaneously acquiring tool wear images and measuring wear values with a tool microscope, to identify wear patterns and determine the critical wear threshold. In actual machining environments, due to errors in tool manufacturing and installation, as well as variations in material properties and unreasonable cutting parameters, flank wear on the cutting edge often displays non-uniform characteristics. The wear amount of the cutting edge varies greatly at different heights, with some positions along the axial direction exhibit significantly greater wear than others. It is known that these severely worn areas tend to degrade more rapidly, accelerating the overall deterioration of the tool performance and leading to premature failure. The laser tool setter, known for its high precision and on-machine measurement capability, is widely adopted in CNC machining. It enables efficient measurement of tool radius at specific axial positions. In theory, the cutting edge within the range of the axial depth of cut experiences wear. By measuring the tool radius at each height within this range, a comprehensive profile of the tool wear can be obtained, enabling accurate determination of the tool wear condition. However, measuring the tool radius at all heights would significantly increase machining time and production costs, making this approach not feasible in practice. Therefore, it is essential to optimize the measurement positions along the tool axis to balance accuracy in wear evaluation with measurement efficiency. Moreover, the wear status and wear threshold are often influenced by multiple factors and thus cannot be assumed fixed. To determine the optimal heights for radius measurement and the corresponding wear threshold, dedicated cutting experiments are carried out. In these experiments, actual cutting tools and workpiece materials are employed. The tool radius measurements are conducted at various heights at regular intervals. Simultaneously, wear images are collected using tool microscope until tool failure occurs. By analyzing these images of tool wear conditions, the dominant wear pattern of the tool is identified. Particular attention is given to the quantitative analysis of the flank wear land width, aiming to reveal the spatial distribution characteristics of flank wear, to optimize the height of the tool radius measurement. Meanwhile, the calculated flank wear land widths are obtained using the calculation method proposed in
Section 3, which is compared with the measurement results to verify the accuracy of the calculation method. Based on the experimental results, the dominant wear pattern is summarized, and the axial heights with the largest flank wear and leading to tool failure were selected as the optimized height of the tool radius measurement. The flank wear land width at tool failure is then used to define a wear threshold, which serves as a criterion for real-time TCM.
Second, with the optimized height identified, the laser tool setter is used to measure the radius at that specific axial location and update the tool dimension in the machine controller’s tool offset list. Specifically, the tool radius is measured at the optimized height, and the corresponding flank wear land width is calculated using the method proposed in
Section 3. The wear widths obtained at all measured heights are comprehensively evaluated and compared with the predefined wear threshold. If all calculated wear widths are below the threshold, the tool is considered to be in valid condition. However, if any calculated width exceeds the threshold, the tool is judged to be invalid, indicating that the insert or cutting edge needs to be replaced.
5. Experimental Verification and Application
To verify the accuracy of the proposed flank wear land width calculation method and evaluate the practicality of the TCM approach presented in this study, a series of cutting experiments were conducted under representative conditions that reflect typical milling operations. The experiments are divided into two parts: The objective of Experiment I is to identify the wear pattern of the experimental tools, optimize the height of the tool radius measurement, validate the accuracy of the flank wear land width calculation method, and determine the corresponding wear threshold. Experiment II is an application-oriented test designed to assess the feasibility and effectiveness of the TCM method developed based on the results of Experiment I.
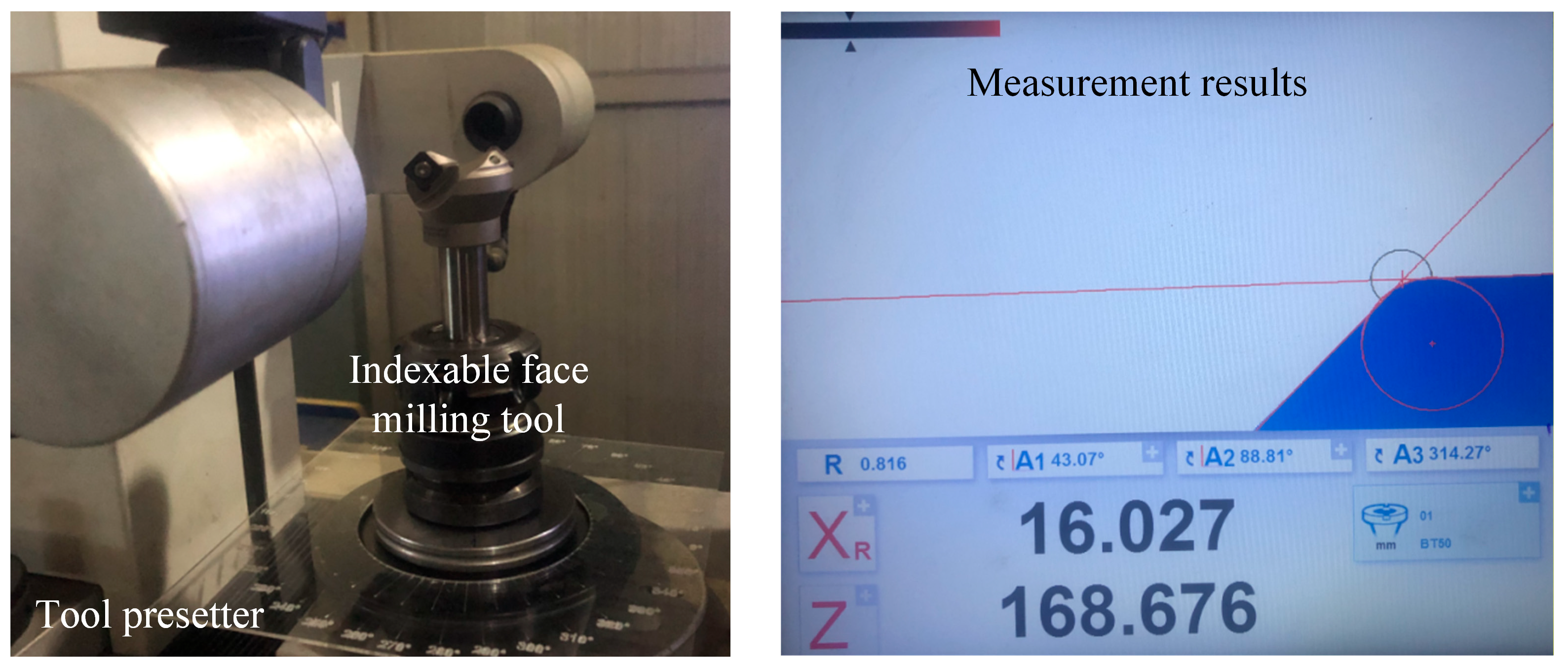
All experiments were conducted on a four-axis vertical machining center, model YHVT850Z, and its manufacturer is Shandong Yonghua Machinery Co., Ltd. in Jining, China. The machining center is equipped with a Siemens 840D sl CNC system and a BT40 spindle tool holder. The non-contact laser tool setter used in the experiments was the NC4 system from Renishaw, Wales, UK, specifically the modular fixed model F300. The indexable face milling tool used in the experiment is model TSE12-C20-32-120-2T, with an overall shank length of 120 mm, a shank diameter of 20 mm, and a nominal tool diameter of 32 mm. This milling tool is equipped with two square inserts. The insert model is SEKT1204, made of cemented carbide with a TiAlN coating. The manufacturer of the indexable face milling tool and insert is Dongguan Yiyang Precision Hardware Co., Ltd. in Dongguan, China. Detailed specifications of the indexable face milling tool and inserts are listed in
Table 1. The workpiece material is 2Cr13 stainless steel with a hardness of HRC 20 and dimensions of 110 mm × 110 mm × 35 mm. The manufacturer is Jiangsu Hengshuntai Steel Co., Ltd., Wuxi, China. Meanwhile, the tool wear condition images were captured and measured via the YW2300 tool microscope manufactured by Shenzhen Yangwang Technology Co., Ltd., Shenzhen, China, and the device evaluates the flank wear width (
VB), which is used as the reference value for the experiments. The main equipment used in the experiment is shown in
Figure 13.
5.1. Experiment I
Through cutting experiments, wear images of the tool at different machining stages were captured using a tool microscope to identify the primary wear pattern. The flank wear data were measured to study the distribution characteristics of the wear land and determine the position of maximum wear. The tool radius at different heights was measured using a laser tool setter, and the flank wear land width was calculated. By comparing the calculated wear land results with the measured values to verify the accuracy of the wear land width calculation model. Based on the experimental results, a threshold for wear band width was established to provide a quantitative basis for TCM.
The cutting experiments were conducted using face milling to machine stainless steel blocks, with a reciprocating milling strategy (see
Figure 14) under dry cutting conditions. Based on the tool manufacturer’s catalog, the selected cutting parameters are listed in
Table 2. In order to eliminate surface irregularities of the workpiece and ensure consistent cutting depth during the experiment, a preprocessing step was performed before the cutting experiment by machining a depth of 0.5 mm from the workpiece surface.
Due to manufacturing and installation errors of the indexable face milling tool and its inserts, the actual tool radius of the insert mounted on the milling tool may deviate from the nominal radius. Therefore, before the cutting experiments, the actual tool radius was measured using an offline tool presetter. The inserts were then manually adjusted to ensure that both axial and radial runout remained within 0.005 mm, in order to minimize the influence of tool length and radius variations on the experimental results, as shown in
Figure 15.
During the entire cutting experiment, the tool length and radius were measured using a laser tool setter. The tool was removed from the machine spindle to capture images of the insert wear condition and to measure the tool wear using a tool microscope. The experimental setup is shown in
Figure 16.
The experimental procedure was as follows:
Inspecting the inserts: A tool microscope was used to inspect the inserts, and only those without defects or damage were selected for use.
Mounting and adjusting inserts: Two inserts were installed onto the face milling tool. Each insert was marked with an oil-based marker as Insert 1 and Insert 2, respectively, for identification. The inserts were then manually adjusted to ensure that both axial and radial runout remained within 0.005 mm, and the actual tool radius was measured using an offline tool presetter.
Workpiece setup: The workpiece was clamped onto the machine tool table using a machine vise, and the workpiece coordinate system was aligned and set.
Installing the tool and measuring tool length: The tool was installed into the machine spindle. The tool length and radius were measured using a Renishaw non-contact laser tool setter. Specifically, five points on the tool bottom edge were selected for length measurement, labeled ML1 to ML5, with radial distances from the tool axis of 15.6, 15.4, 14.8, 14.4, and 14 mm, respectively.
Measuring cutting edge radius: For radius measurements, five height positions were defined: MR1 to MR5. Based on the maximum tool length, tool geometry, and cutting depth, the height levels were set at 0.1, 0.2, 0.4, 0.65, and 0.9 mm. Theoretically, MR1 and MR2 lie on the corner cutting edge, while MR3, MR4, and MR5 lie on the side cutting edge of the insert.
Conducting the cutting experiment: Face milling was performed in a reciprocating milling strategy to eliminate the effects of up and down milling. One complete back-and-forth pass was considered a single cutting segment, totaling a length of 220 mm. After completing one or more cutting segments as per the experimental design, cutting was paused. The tool length and radius were measured again using the same strategies in steps 4 and 5, and data were recorded.
Tool wear image acquisition and flank wear measurement: The tool was removed from the spindle, and wear images of the two inserts were captured using the tool microscope. Only the wear land on the flank face of the corner and side cutting edges was measured. The measurement heights corresponded to those in step 5. Since it was difficult to determine the tool end face and axis in the microscope, the side cutting edge was placed parallel to the microscope viewing plane, and the line of sight was aligned parallel to the rake face. Using the midpoint of the corner edge as a reference point, measurement positions along the side edge were offset accordingly. The calculated offset distances corresponding to the measurement heights were 0.144, 0.288, 0.574, 0.933, and 1.292 mm, with point intervals of 0.144, 0.286, 0.359, and 0.359 mm, respectively, as shown in
Figure 17.
Insert replacement decision: Based on the tool wear condition, a decision was made whether to replace the insert. If chipping was observed, the insert was replaced, and the experiment resumed from step 2. If the insert remained valid, the experiment continued from step 4 until the tool was invalidated by chipping.
To determine the tool wear pattern and the height positions for radius measurement, cutting experiments are conducted following the steps described above. After completing two cutting segments, the tool is removed to capture flank wear images and measure flank wear land width. To enhance the stability of the experiment, two tools are used, denoted as Tool 1 and Tool 2. The experimental results are presented in
Table 3 and
Table 4, and
Figure 18,
Figure 19,
Figure 20 and
Figure 21.
For Tool 1, the tool radius is 16.054 mm.
Table 3 presents the data of tool length, cutting edge radius, and flank wear land width for Tool 1.
Figure 18 and
Figure 19 show the wear images of Insert 1 and Insert 2 of Tool 1, including the wear conditions on the bottom flank, rake face, and side flank. From
Table 3, with the increasing number of cutting segments, the variation in tool length remains within the range of 5 μm, indicating that wear on the bottom cutting edge is almost not worn. This is further supported by the images from the subgraphs (a) and (d) of
Figure 18 and
Figure 19, where the bottom edge wear appears very slight. In contrast, the variation in cutting edge radius reaches up to 70 μm, revealing significant wear on the corner and side cutting edges. Therefore, attention should be paid to flank wear on these edges. As shown in the subgraphs (c) and (f) of
Figure 18 and
Figure 19, flank wear on the corner and side cutting edges is more obvious. According to the flank wear data in
Table 3, it can be seen that under the same cutting length, there are differences in wear amounts between the two inserts, as well as at different heights on the same insert. This indicates that during actual cutting, wear distribution is non-uniform both between inserts and along the height of a single insert. Hence, it is necessary to determine the location where wear failure is prone to occur through cutting experiments. Specifically, when the Insert 1 completes two and four cutting segments, the maximum wear occurs at point
MR5, with wear amounts of 0.09 mm and 0.11 mm, respectively. The wear at point
MR3 is the second highest. The point
MR1 shows the smallest wear of 0.04 mm and 0.05 mm, respectively. In comparison, Insert 2 shows a more uniform wear distribution and the overall wear amount is relatively small, with a maximum wear of 0.10 mm, also occurring at point
MR5.
Based on the wear conditions of the two inserts on Tool 1 (see
Figure 18 and
Figure 19), the primary wear pattern of the tool is flank wear on the corner and side cutting edges. Insert 1 shows more severe wear than Insert 2, possibly due to runout introduced during insert installation. Insert 1 has a larger radius, removes more material during cutting, and is subjected to greater cutting force, which leads to greater wear. In addition, after two cutting segments, both inserts remain in a normal wear state and can still continue cutting workpieces without any obvious clear characteristics of failure. However, after four cutting segments, chipping occurs on Insert 1 at point
MR5, and chipping occurs on Insert 2 at point
MR5 and a location somewhere between
MR2 and
MR3, indicating that the inserts are already in a failed state and can no longer continue effective cutting.
According to the analysis of Tool 1 above, it can be concluded that the two locations with the most severe wear and chipping are at points MR3 and MR5. Among them, point MR5 is located near the cutting depth, where a hardened layer may exist on the workpiece or its machined surface, resulting in increased stress and greater tool wear. Point MR3 is located on the side cutting edge near the corner cutting edge, which is the transition area between the two edges. Due to geometric discontinuity and stress concentration, this area is more prone to wear and chipping. Based on the above analysis, points MR3 and MR5 are identified as key positions for tool condition monitoring.
For Tool 2, its tool radius is 16.019 mm.
Table 4 presents the data on tool length, cutting edge radius, and flank wear land width for Tool 2.
Figure 20 and
Figure 21 show the wear condition images of Insert 1 and Insert 2, respectively. Similarly to Tool 1, the variation in tool length for Tool 2 is also very small, indicating that there is almost no wear on the bottom cutting edge of the inserts. However, the change in cutting edge radius is relatively large, reaching 71 μm, which suggests that the corner cutting edge and side cutting edge experience significant wear. As shown in
Table 4, it can be seen that Tool 2 has already experienced significant wear after only two cutting segments. Specifically, the maximum wear on Insert 1 occurs at point
MR5, with a wear value of 0.11 mm. For Insert 2, the maximum wear appears at point
MR4, also measuring 0.11 mm, while the wear amount at point
MR5 is also relatively large, reaching 0.10 mm. In addition, from
Figure 20 and
Figure 21, obvious chipping is observed. Insert 1 shows chipping near point
MR3, and Insert 2 exhibits chipping at point
MR5, with the latter showing a larger chipped area.
Based on the previous experimental results, it has been identified the primary wear pattern of the tool is flank wear occurring on the corner cutting edge and side cutting edge. To further validate the accuracy of the proposed method for calculating the flank wear land width on these edges, and to determine the threshold value of the wear land width, two new inserts (referred to as Tool 3) were installed to conduct another cutting experiment following the same procedure as described above. In order to collect more experimental sample data before tool failure occurs, the tool is measured and wear images are carried out after each cutting segment, continuing until chipping failure of the inserts is observed. After completing the cutting experiment, the flank wear land widths are calculated using the proposed method in this study, based on the tool radius values measured by the laser tool setter at five different heights. The radius of Tool 3 is 16.004 mm, and the experimental results are presented in
Table 5.
Since the laser tool setter can only measure insert sizes with larger radii, the measured data recorded in
Table 5 represent the wear values of inserts with greater wear. As shown in
Table 5, Tool 3 experiences tool failure due to chipping after machining four cutting segments, with the chipping occurring at point
MR5. The wear images of Tool 3 of the failed insert with chipping are shown in
Figure 22. Furthermore, the calculated wear values exhibit good consistency with the measured wear values. After one cutting segment, the maximum error percentage is 14.00%, which occurs at measurement point
MR3. After completing two, three, and four cutting segments, the maximum error percentages are 5.00%, 8.57%, and 3.33%, respectively, occurring at measurement points
MR1,
MR2, and
MR2. These results indicate that the flank wear land width calculation method proposed in this study demonstrates high accuracy and provides reliable theoretical support for tool condition monitoring.
After completing three cutting segments, the maximum measured flank wear land width is 0.09 mm, and no chipping is observed on the tool. However, after four cutting segments, the tool fails due to chipping at point MR5. The measured wear values at the other four points are 0.07, 0.09, 0.09, and 0.09 mm, while the calculated wear values at the five measurement points are 0.070, 0.093, 0.092, 0.089, and 0.104 mm, respectively. Therefore, based on the above results, the threshold for flank wear land width is set to 0.10 mm to determine whether the tool is invalid.
In summary, through the cutting experiment of Experiment I, it was determined that the main wear pattern of the tool is flank wear on the corner and side cutting edges, and the failure form is mainly manifested as insert chipping. Based on wear characteristic analysis, the heights for measuring tool radius are set at the inflection point between the corner and side cutting edges, as well as near the cutting depth. In addition, the experimental data verified the effectiveness and high accuracy of the flank wear land width calculation method proposed in this study. At the same time, a critical wear threshold of 0.10 mm for flank wear land width is set to determine tool failure.
5.2. Experiment II
Experiment II is conducted to verify the practicality of the tool condition monitoring method. A new tool, referred to as Tool 4, is prepared and the cutting process is performed following the same steps as in Experiment I. After completing two cutting segments, the laser tool setter is used to measure the tool radii at points
MR3 and
MR5. These radius values are substituted into the flank wear land width calculation method to obtain the calculated wear values. The calculated values are then compared with the predetermined critical wear threshold of 0.10 mm to determine whether the tool has failed. Additionally, the tool radius at point
MR5 is updated in the tool list to compensate for the tool path. The radius of Tool 4 is 16.035 mm, and the experimental results are listed in
Table 6, and the wear images are shown in
Figure 23.
According to the experimental results in
Table 6, after machining two cutting segments, the measured tool radii at points
MR3 and
MR5 are 16.355 mm and 16.830 mm, respectively. The corresponding calculated flank wear land widths are 0.069 mm and 0.076 mm, both of which are below the predetermined critical wear threshold of 0.10 mm. Therefore, the tool is considered valid and can continue machining. Before continuing with the machining, the tool radius is updated to 16.830 mm. After completing four cutting segments, the measured tool radii are 16.336 mm and 16.811 mm, and the calculated flank wear land widths are 0.102 mm and 0.110 mm, respectively. Both exceeded the predetermined critical wear threshold. As a result, the tool is determined to be in an invalid state. To confirm tool failure, the insert is placed under a tool microscope for wear image acquisition. As shown in
Figure 23, severe chipping occurs at both points
MR3 and
MR5 on the larger worn insert. This result strongly demonstrates the practicality of the proposed tool condition monitoring method, which effectively predicts tool conditions and ensures machining quality.
The method proposed in this paper primarily involves a purely geometric calculation of the tool flank wear width based on the measured reduction in tool radius. The calculated wear value is then compared with a defined critical wear threshold. These calculations are minimal, requiring only a few milliseconds on a standard CNC controller or external PC. On our equipment (a Siemens 840D sl), the computation time for a single wear width calculation is approximately 20–30 milliseconds, negligible compared to the cycle time of a laser tool setter for tool dimension measurement (approximately 1–2 min). Therefore, this method can be applied in real time for on-machine tool condition monitoring without compromising machining efficiency. And, compared with the tool condition monitoring (TCM) method based on multi-sensor fusion and machine learning, the method proposed in this study has the following advantages. Specifically, (1) Unlike multi-sensor fusion systems (e.g., vibration, acoustic emission, and current), which require additional sensors hardware and complex signal processing, the proposed method leverages the existing on-machine laser tool setter, thus incurring no extra hardware cost. (2) The proposed method is deterministic and physically interpretable, eliminating the need for data-driven model training or large labeled datasets. (3) Integration into CNC systems is straightforward, as laser tool setters are already standard in many modern machine tools. Consequently, the proposed method does not rely on statistical learning, thereby avoiding issues such as overfitting or retraining when machining conditions change.