Quantitative Analysis of Droplet Evaporation Based on Wedge Prism Digital Holographic Microscope
Abstract
1. Introduction
2. Methods
3. Results and Discussion
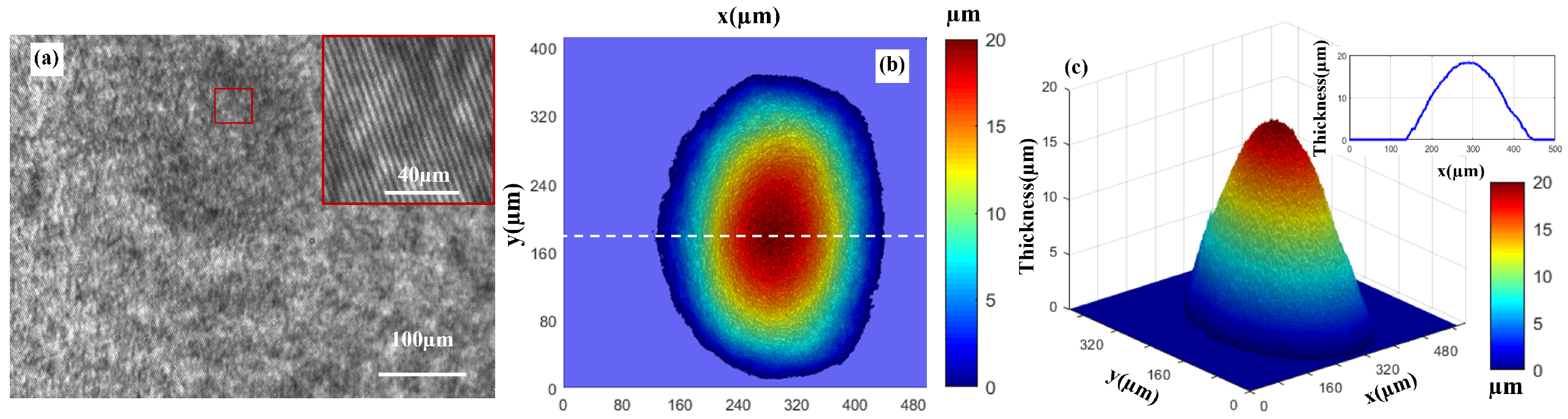
3.1. Liquid Droplet Experiment
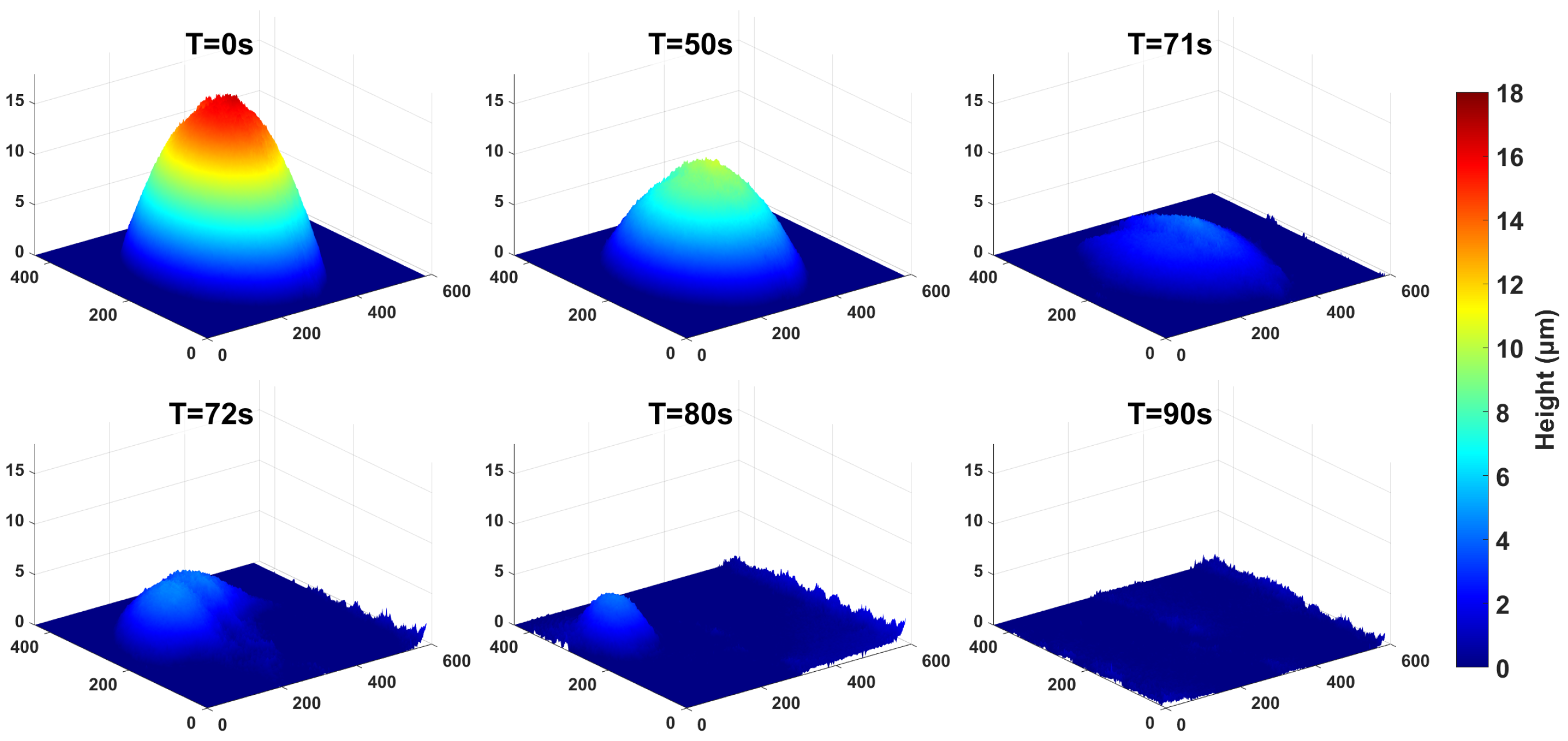
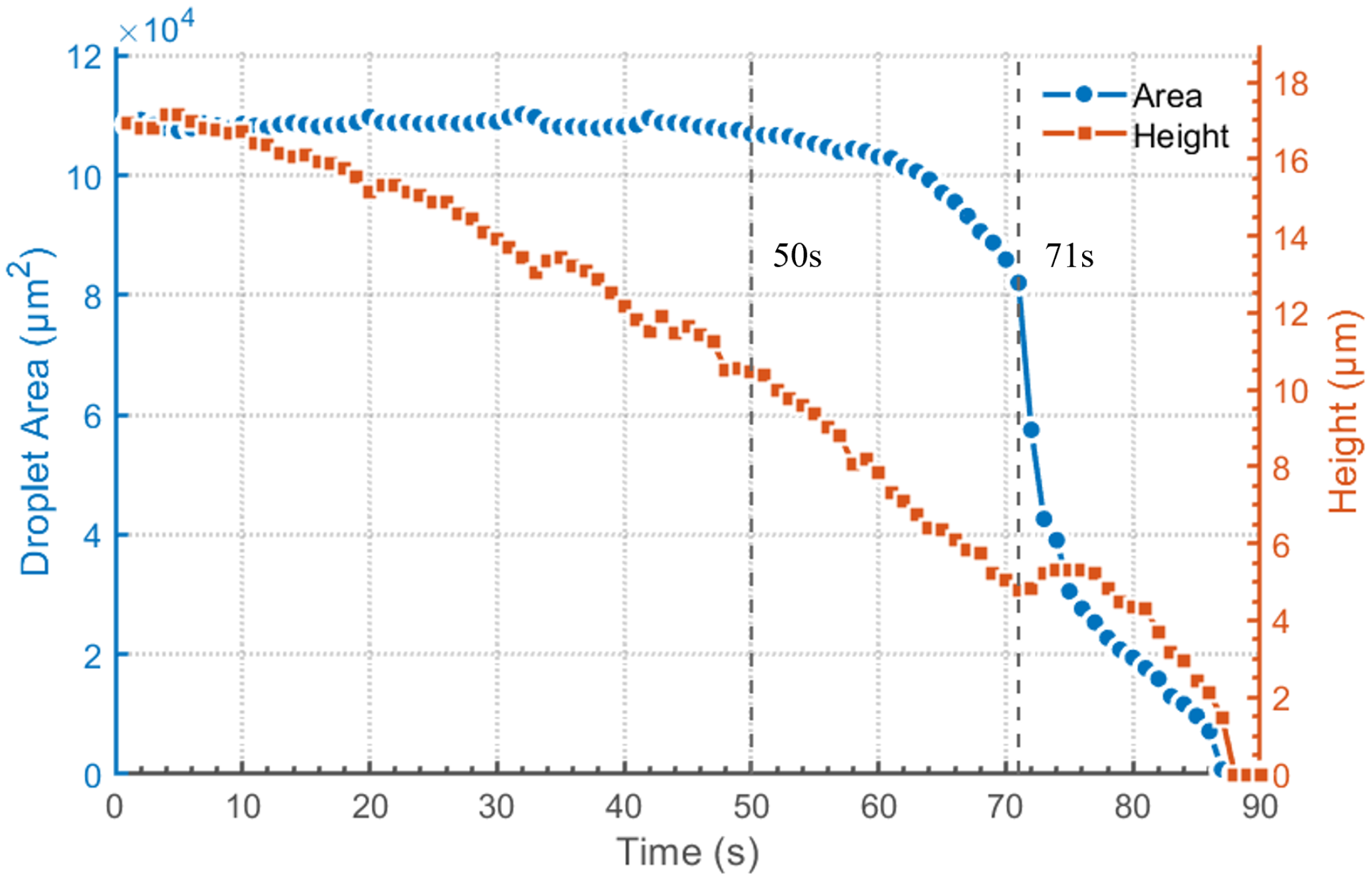
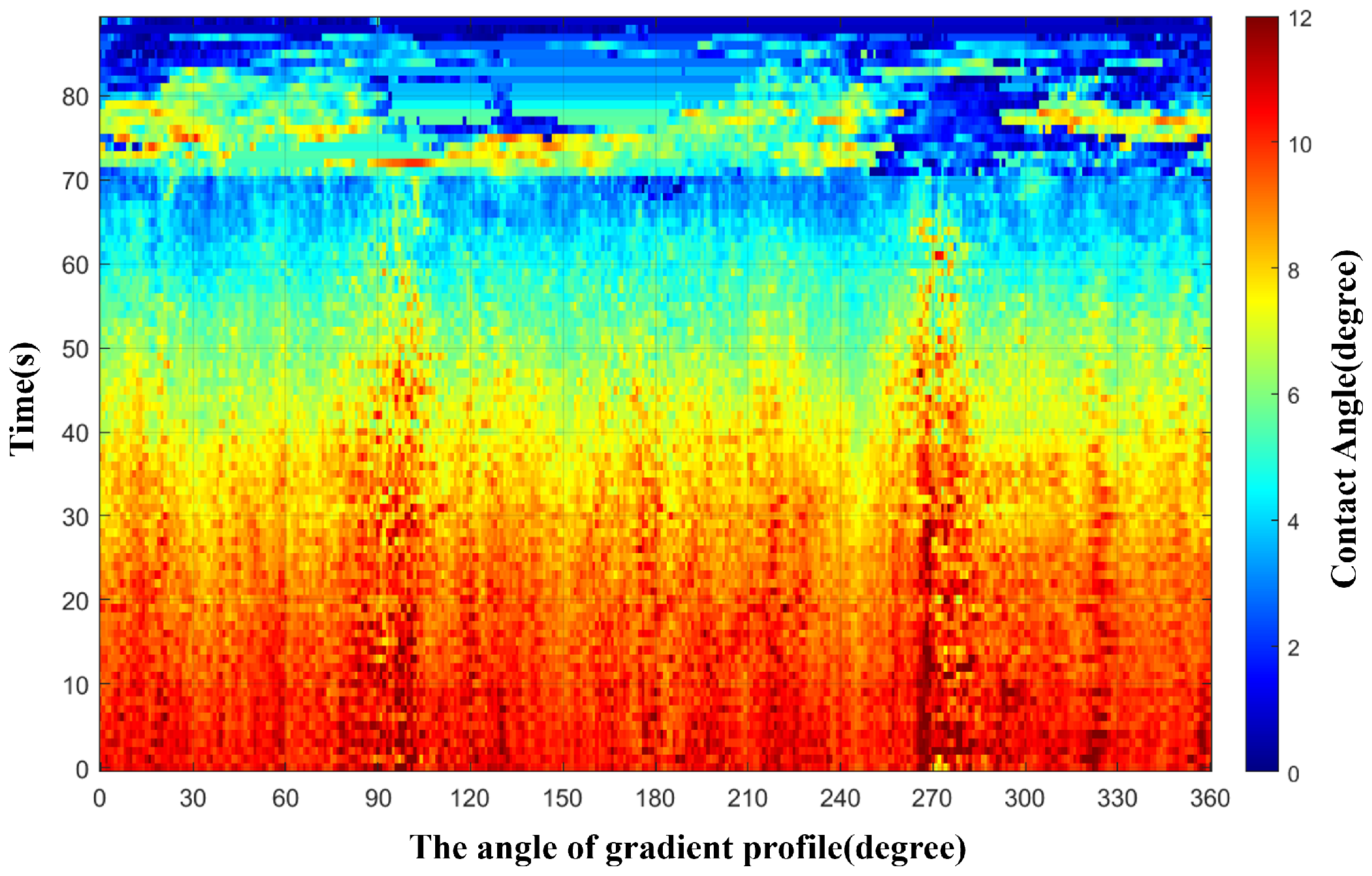
3.2. Droplet Evaporation Experiment
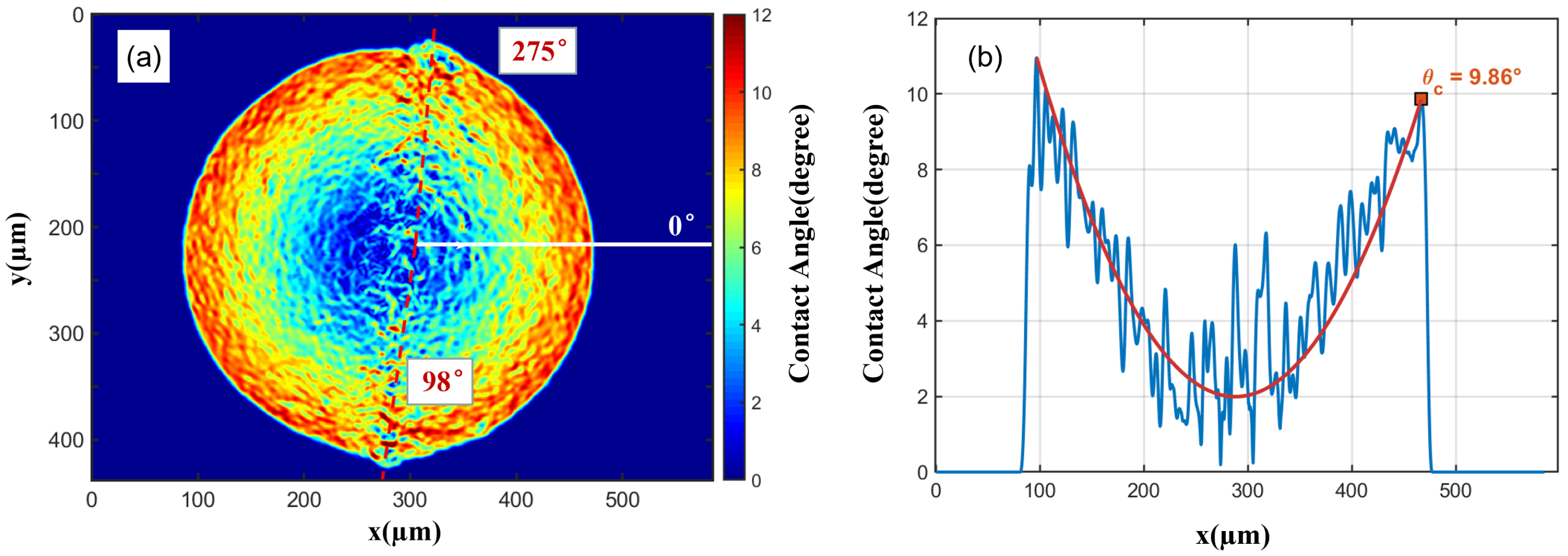
3.3. Device Performance and Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DHM | digital holographic microscopy |
| PSDHM | prism-based self-referencing digital holographic microscopy |
| OPD | optical path difference |
| BS | beam splitter |
| PBS | polarization beam splitter |
| FOV | field of view |
| RH | relative humidity |
| AT | temperature |
| CCR | constant contact radius |
| SS | stick-slip |
| SJ | stick-jump |
| PMMA | polymethyl methacrylate |
References
- Mir, M.; Tangella, K.; Popescu, G. Blood Testing at the Single Cell Level Using Quantitative Phase and Amplitude Microscopy. Biomed. Opt. Express 2011, 2, 3259. [Google Scholar] [CrossRef]
- Chhaniwal, V.; Singh, A.S.G.; Leitgeb, R.A.; Javidi, B.; Anand, A. Quantitative Phase-Contrast Imaging with Compact Digital Holographic Microscope Employing Lloyd’s Mirror. Opt. Lett. 2012, 37, 5127. [Google Scholar] [CrossRef] [PubMed]
- Anand, A.; Faridian, A.; Chhaniwal, V.K.; Mahajan, S.; Trivedi, V.; Dubey, S.K.; Pedrini, G.; Osten, W.; Javidi, B. Single Beam Fourier Transform Digital Holographic Quantitative Phase Microscopy. Appl. Phys. Lett. 2014, 104, 103705. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, C.; Chen, L.; Chen, G.; Zheng, G. A Novel Approach for Measurement of Free-Form Optical Elements with Digital Holographic Microscopy. Micromachines 2022, 13, 1719. [Google Scholar] [CrossRef]
- Shaked, N.T. Quantitative Phase Microscopy of Biological Samples Using a Portable Interferometer. Opt. Lett. 2012, 37, 2016. [Google Scholar] [CrossRef]
- Singh, A.S.; Anand, A.; Leitgeb, R.A.; Javidi, B. Lateral Shearing Digital Holographic Imaging of Small Biological Specimens. Opt. Express 2012, 20, 23617. [Google Scholar] [CrossRef] [PubMed]
- Utadiya, S.; Trivedi, V.; Bhanderi, K.; Joglekar, M.; Limberkar, C.; Patel, K.; Sheoran, G.; Cabrera, H.; Javidi, B.; Anand, A. Thickness and Surface Profiling of Optically Transparent and Reflecting Samples Using Lens-Less Self-Referencing Digital Holographic Microscopy. Appl. Surf. Sci. Adv. 2023, 18, 100484. [Google Scholar] [CrossRef]
- Ganjkhani, Y.; Calabuig, A.; Pedrini, G.; Moradi, A.R. Oblique Illumination Lateral Shearing Digital Holographic Microscopy. J. Opt. 2020, 22, 095601. [Google Scholar] [CrossRef]
- Asl, M.M.Z.; Dorao, C.A.; Giacomello, A.; Fernandino, M. Digital Holographic Microscopy for Measurement of Instantaneous Contact Angle of an Evaporating Droplet. Exp. Fluids 2023, 64, 152. [Google Scholar] [CrossRef]
- Semenov, S.; Starov, V.; Rubio, R.; Agogo, H.; Velarde, M. Evaporation of Sessile Water Droplets in Presence of Contact Angle Hysteresis. Math. Model. Nat. Phenom. 2012, 7, 82–98. [Google Scholar] [CrossRef]
- Debuisson, D.; Merlen, A.; Senez, V.; Arscott, S. Stick–Jump (SJ) Evaporation of Strongly Pinned Nanoliter Volume Sessile Water Droplets on Quick Drying, Micropatterned Surfaces. Langmuir 2025, 32, 2679–2686. [Google Scholar] [CrossRef]
- Anand, A.; Moon, I.; Javidi, B. Automated Disease Identification with 3-D Optical Imaging: A Medical Diagnostic Tool. Proc. IEEE 2017, 105, 924–946. [Google Scholar] [CrossRef]
- Grare, S. Compact, Low-Cost Blu-Ray Pickup-Based Digital Holographic Microscope. Opt. Lasers Eng. 2023, 160, 107272. [Google Scholar] [CrossRef]
- Joglekar, M.; Trivedi, V.; Bhatt, R.; Chhaniwal, V.; Dubey, S.; Claus, D.; Pedrini, G.; Leitgeb, R.; Javidi, B.; Anand, A. Compact, Low Cost, Large Field-of-View Self-Referencing Digital Holographic Interference Microscope. Optik 2021, 245, 167615. [Google Scholar] [CrossRef]
- Joglekar, M.; Trivedi, V.; Chhaniwal, V.; Claus, D.; Javidi, B.; Anand, A. LED Based Large Field of View Off-Axis Quantitative Phase Contrast Microscopy by Hologram Multiplexing. Opt. Express 2022, 30, 29234. [Google Scholar] [CrossRef]
- Kumar, M.; Pensia, L.; Kumar, R. Single-Shot off-Axis Digital Holographic System with Extended Field-of-View by Using Multiplexing Method. Sci. Rep. 2022, 12, 16462. [Google Scholar] [CrossRef]
- Yaghoubi, S.H.S.; Ebrahimi, S.; Dashtdar, M. Structured Illumination in Fresnel Biprism-Based Digital Holographic Microscopy. Opt. Lasers Eng. 2022, 159, 107215. [Google Scholar] [CrossRef]
- Javed, I.; Hassan, M.B.; Khalid, R.; Dashtdar, M.; Garcia, L.G.; Fonda, C.; Crespo, M.L.; Danailov, M.; Cojoc, D.; Zubair, M.; et al. Compact Inverted Digital Holographic Microscope Based on Common-Path Configuration. Appl. Opt. 2025, 64, B65. [Google Scholar] [CrossRef]
- Javed, I.; Khalid, R.; Hassan, M.B.; Dashtdar, M.; Danailov, M.; Zubair, M.; Cabrera, H.; Mehmood, M.Q. HoloLume: Point-of-Application Holographic Imaging Solution. Meas. Sci. Technol. 2025, 36, 015708. [Google Scholar] [CrossRef]
- Kumari, V.; Barak, N.; Sharma, A.K.; Anand, A.; Sheoran, G. Telecentric Phase Imaging at Extended Depth of Focus Using Digital Holographic Microscopy. Precis. Eng. 2024, 87, 23–32. [Google Scholar] [CrossRef]
- Wang, D. Snapshot Phase-Shifting Lateral Shearing Interferometer. Opt. Lasers Eng. 2020, 128, 106032. [Google Scholar] [CrossRef]
- Tsai, C.M.; Vyas, S.; Luo, Y. Common-Path Digital Holographic Microscopy Based on a Volume Holographic Grating for Quantitative Phase Imaging. Opt. Express 2024, 32, 7919. [Google Scholar] [CrossRef] [PubMed]
- Shalev, A.N.; Misura, A.A.; Georgieva, A.O.; Chernykh, A.V.; Petrov, N.V.; Orlova, T.; Lobanov, I.S.; Aksenova, E.V.; Uzdin, V.M.; Kiselev, A.D. Polarization-Controlled Orbital Angular Momentum of Light Passing through a Cholesteric Spherulite. Opt. Lett. 2025, 50, 4866. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, Z.; Deng, Z.; Jin, Q.; Wu, Y.; Zheng, C.; Wang, Z.; Wu, X. Compact Dual-Wavelength Common-Path Digital Holographic Microscope for Dynamic Topography Reconstruction. Opt. Lasers Eng. 2025, 194, 109156. [Google Scholar] [CrossRef]
- Chaudhari, H.; Das, A.; Singh, H.V.; Ghosh, A.; Kulkarni, R.; Bhuyan, M.K.; Thummer, R.P. Lateral Shearing Common-Path Digital Holographic Microscopy with Iterative Reconstruction. Appl. Opt. 2025, 64, 6285. [Google Scholar] [CrossRef]
- Sardana, J.; Devinder, S.; Zhu, W.; Agrawal, A.; Joseph, J. Dielectric Metasurface Enabled Compact, Single-Shot Digital Holography for Quantitative Phase Imaging. Nano Lett. 2023, 23, 11112–11119. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, H.; Luo, Y.; Liang, Z.; Chen, G.; Wang, M.; Zheng, G.; Zhang, X. Quantitative Analysis of Droplet Evaporation Based on Wedge Prism Digital Holographic Microscope. Micromachines 2025, 16, 1114. https://doi.org/10.3390/mi16101114
Wang J, Wang H, Luo Y, Liang Z, Chen G, Wang M, Zheng G, Zhang X. Quantitative Analysis of Droplet Evaporation Based on Wedge Prism Digital Holographic Microscope. Micromachines. 2025; 16(10):1114. https://doi.org/10.3390/mi16101114
Chicago/Turabian StyleWang, Jiankun, Han Wang, Yang Luo, Zhuoji Liang, Gengliang Chen, Meng Wang, Guoliang Zheng, and Xuhui Zhang. 2025. "Quantitative Analysis of Droplet Evaporation Based on Wedge Prism Digital Holographic Microscope" Micromachines 16, no. 10: 1114. https://doi.org/10.3390/mi16101114
APA StyleWang, J., Wang, H., Luo, Y., Liang, Z., Chen, G., Wang, M., Zheng, G., & Zhang, X. (2025). Quantitative Analysis of Droplet Evaporation Based on Wedge Prism Digital Holographic Microscope. Micromachines, 16(10), 1114. https://doi.org/10.3390/mi16101114






