Achieving High-Quality Formed Hastelloy X Cladding Layers on Heterological 50CrVA Surface by Optimizing Process Parameters in Directed Energy Deposition
Abstract
1. Introduction
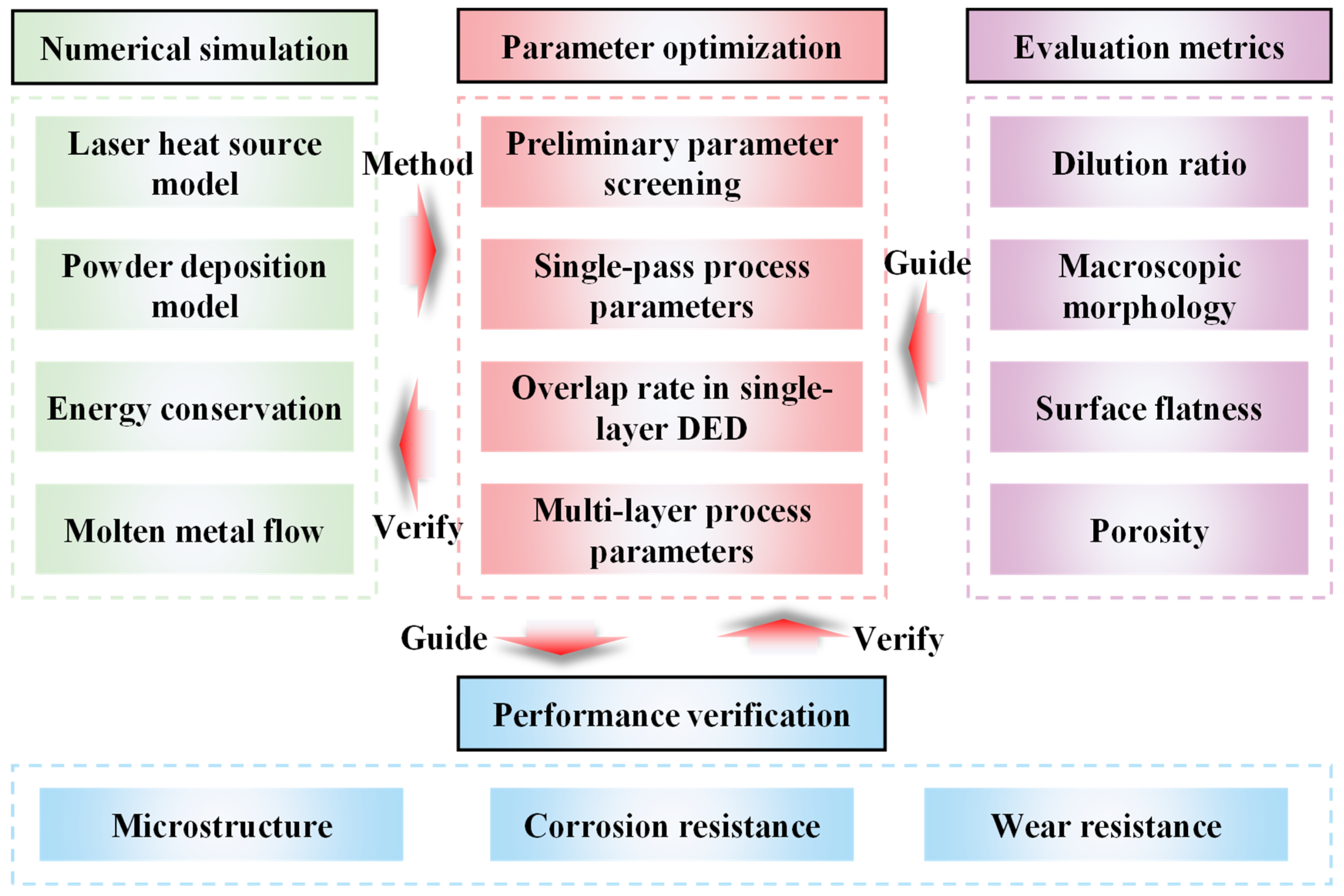
2. FE Modeling for the DED Process of Hastelloy X on 50CrVA Substrates
3. Experimental Details
3.1. Materials and DED Equipment
3.2. Method of Process Parameter Optimization
3.3. Corrosion and Wear Performance Verification
4. Results and Discussion
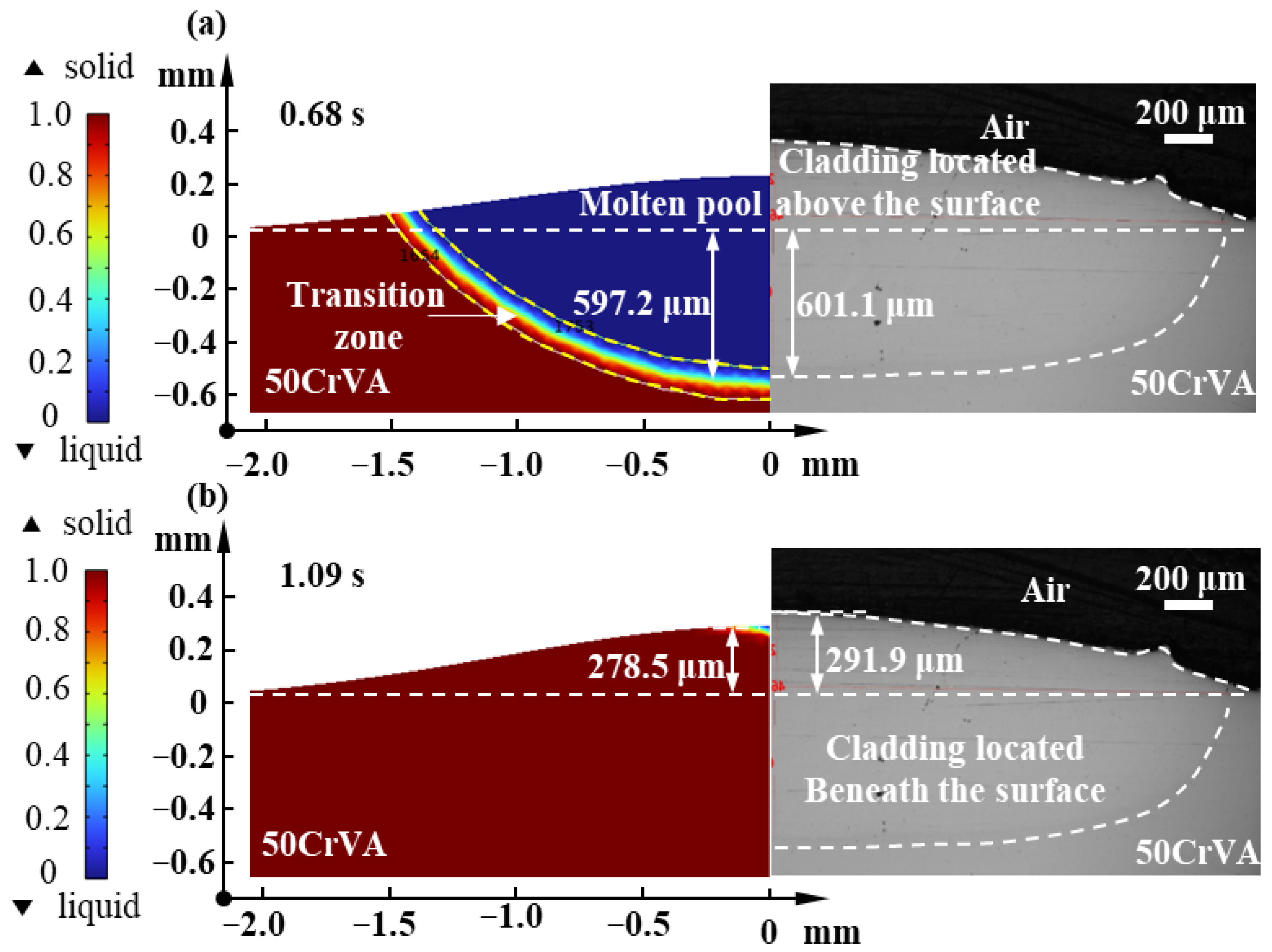
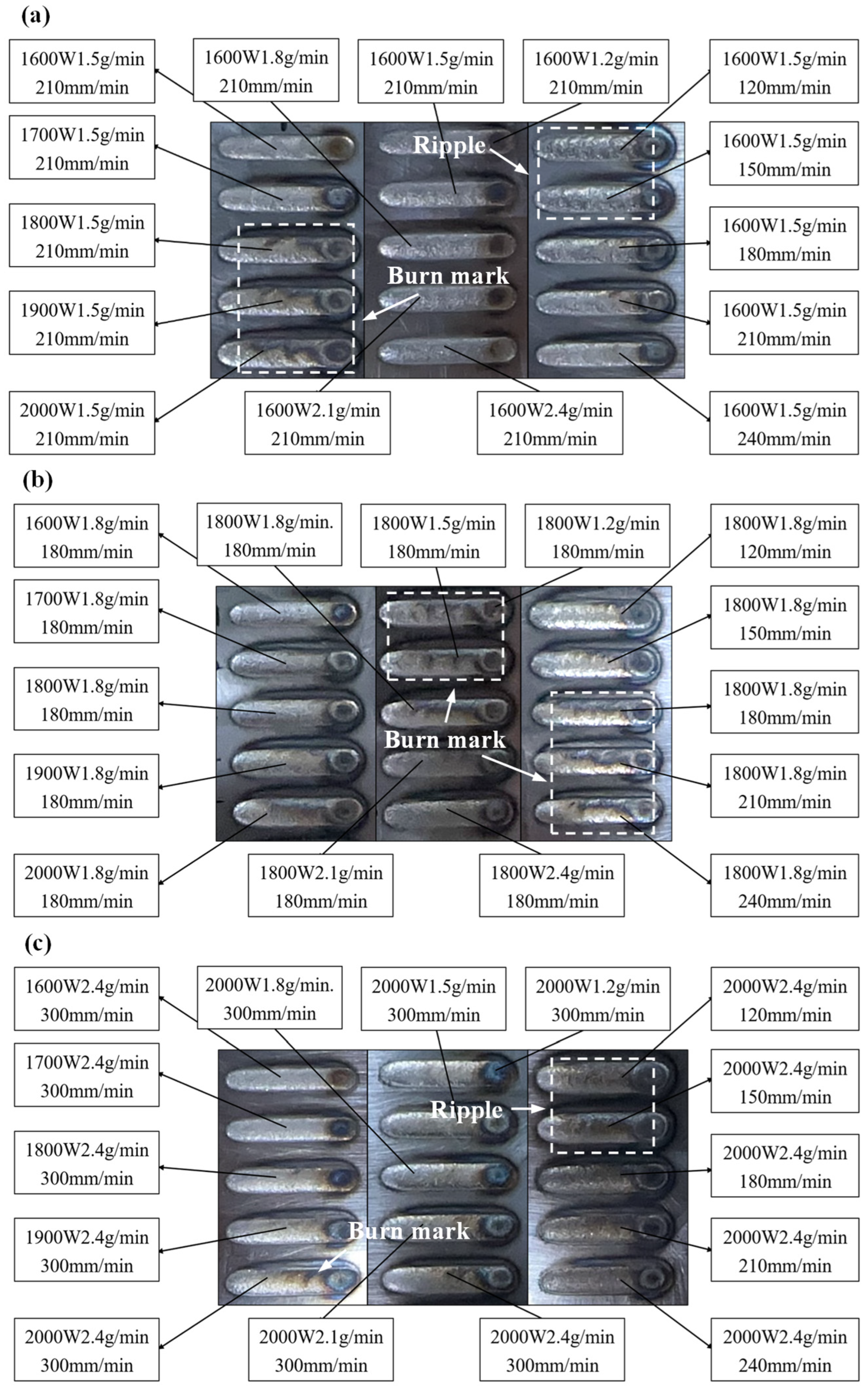
4.1. Determination of Process Parameters for High-Quality Single-Track Cladding Based on a Thermal–Flow Coupled Model and Single-Factor Experiments
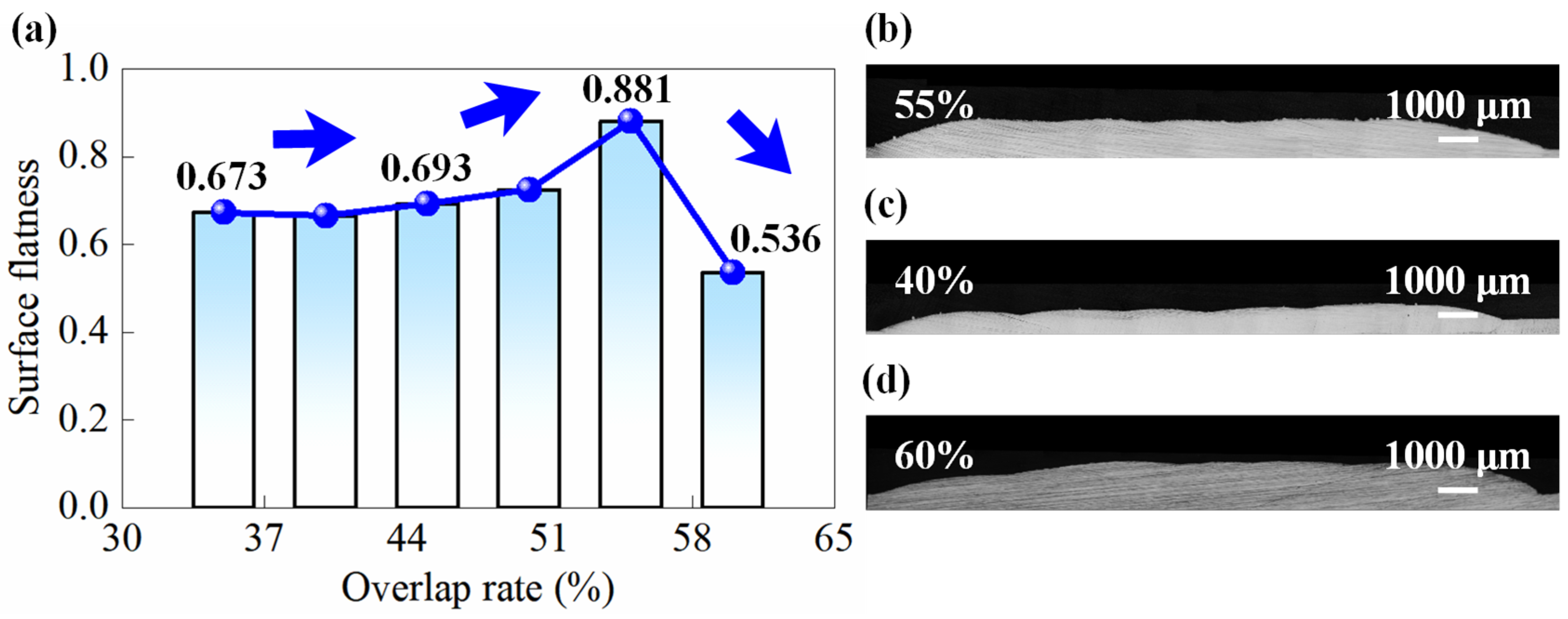
4.2. Optimization of Process Parameters for Multi-Layer Cladding by Considering Surface Flatness and Porosity
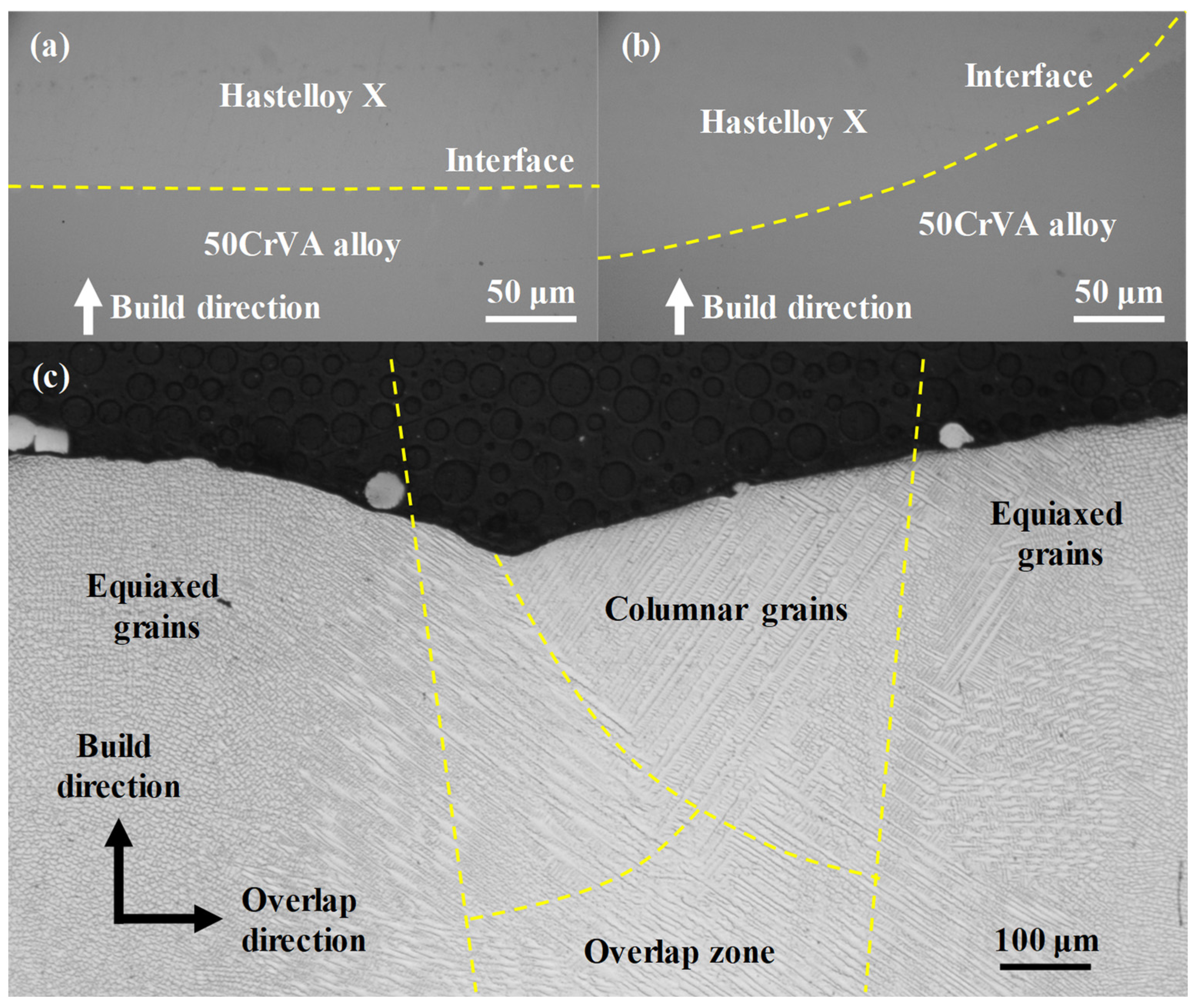
4.3. Performance Verification of Corrosion and Wear Resistance for Multi-Layer Cladding Fabricated by Optimized Process Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, J.; Chen, G.; Chen, M.J.; Zhao, L.J.; Xu, Q.; Yuan, X.D.; Liu, Z.C.; Wang, S.F.; Liao, W.; Liu, Q.; et al. Overview of advanced optical manufacturing techniques applied in regulating laser damage precursors in nonlinear functional KHxD2-xPO4 crystal. Light Adv. Manuf. 2025, 6, 48. [Google Scholar] [CrossRef]
- Yang, D.H.; Liu, Z.C.; Zhao, L.J.; Cheng, J.; Chen, M.J.; Wang, S.F.; Geng, F.; Sun, Y.Z.; Xu, Q. Role of atomic electronic structure defects in initiating laser-induced modification and failure of brittle-hard fused silica optics. Optica 2025, 12, 1291–1303. [Google Scholar] [CrossRef]
- Wilson, J.M.; Piya, C.; Shin, Y.C.; Zhao, F.; Ramani, K. Remanufacturing of turbine blades by laser direct deposition with its energy and environmental impact analysis. J. Clean. Prod. 2014, 80, 170–178. [Google Scholar] [CrossRef]
- Oh, W.J.; Son, J.Y.; Baek, G.Y.; Shim, D. Excess deposition for suppressing interfacial defects induced on parts repaired using direct energy deposition. Int. J. Adv. Manuf. Tech. 2020, 106, 1303–1316. [Google Scholar] [CrossRef]
- Smith, L.; Scott-Emuakpor, O.; Gockel, J.; Celli, D.; Johnson, P. Vibration bending fatigue analysis of Ti-6Al-4V airfoil blades repaired using additive manufacturing. Fatigue Fract. Eng. M. 2024, 47, 1417–1430. [Google Scholar] [CrossRef]
- Hamilton, J.D.; Rivero, I.V. Visualization of melt pool stability for wire- and powder-based directed energy deposition repair of gray cast iron. Int. J. Adv. Manuf. Tech. 2023, 129, 4399–4405. [Google Scholar] [CrossRef]
- Chang, T.Y.; Dong, E.J.; Zhao, L.J.; Xing, Y.H.; Chen, M.J.; Lu, J.W.; Cheng, J. Achieving low-porosity AlSi10Mg cladding layers for the additive repair of aluminum alloy parts by directed energy deposition. Opt. Laser Technol. 2025, 181, 111854. [Google Scholar] [CrossRef]
- Tan, J.C.; Looney, L.; Hashmi, M.S.J. Component repair using HVOF thermal spraying. J. Mater. Process. Tech. 1999, 93, 203–208. [Google Scholar] [CrossRef]
- Shen, S.P.; Chen, W.H.; Dow, W.P.; Kamitamari, T.; Cheng, E.; Lin, J.Y.; Chang, W.C. Copper seed layer repair using an electroplating process for through silicon via metallization. Microelectron. Eng. 2013, 105, 25–30. [Google Scholar] [CrossRef]
- Chen, Z.C.; Zhang, Y.K.; Chi, Y.Q.; Gou, J.F.; Lin, C.H.; Lin, Y.Q. Research on morphology, porosity, mechanical properties of 7075 aluminum alloy repaired by arc welding and laser shock forging. Heliyon 2023, 9, e22791. [Google Scholar] [CrossRef]
- Cheng, J.; Xing, Y.H.; Dong, E.J.; Zhao, L.J.; Liu, H.N.; Chang, T.Y.; Chen, M.J.; Wang, J.H.; Lu, J.W.; Wan, J. An overview of laser metal deposition for cladding: Defect formation mechanisms, defect suppression methods and performance improvements of laser-cladded layers. Materials 2022, 15, 5522. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.J.; Zhang, Y.S.; Yang, Z.S.; Cui, D.C.; He, F.; Li, J.J.; Wang, Z.J.; Lin, X.; Wang, J.C. Cracking mechanism of Hastelloy X superalloy during directed energy deposition additive manufacturing. Addit. Manuf. 2022, 55, 102792. [Google Scholar] [CrossRef]
- Zhang, W.J.; Liu, F.G.; Liu, F.C.; Huang, C.P.; Zheng, H.Z.; Zhang, Q.; Zheng, Y.S.; Gao, J.Y. Microstructural evolution and cracking behavior of Hastelloy X superalloy fabricated by laser directed energy deposition. J. Alloy. Compd. 2022, 905, 164179. [Google Scholar] [CrossRef]
- Chen, Y.; Rong, P.; Fang, X.; Liu, Y.; Wu, Y.; Zhang, Z.L.; Cao, S.T.; Chen, R.W.; Wen, T.; Cheng, S.X.; et al. Effects of Al/Ti additions on the corrosion behavior of laser-cladded Hastelloy C276 coatings. Coatings 2025, 15, 678. [Google Scholar] [CrossRef]
- Xia, Y.L.; Wu, H.R.; Liu, K.Y.; Lei, J.B.; Hu, Y.B.; Chen, H.N.; Zheng, C. Mechanical properties and corrosion behavior of circular oscillating laser direct energy deposited nickel-based superalloy after different heat-treatment processes. J. Mater. Res. Technol. 2025, 34, 1045–1056. [Google Scholar] [CrossRef]
- Wang, X.; Xu, L.Y.; Zhao, L.; Han, Y.D. Defect-related strain-controlled high-temperature fatigue behavior in additive manufacturing Hastelloy X assisted with ultrasonic micro-forging treatment. Int. J. Fatigue 2023, 172, 107607. [Google Scholar] [CrossRef]
- Lv, S.J.; Liu, F.G.; Huang, C.P.; Liu, F.C.; Qiu, C.; Liu, L.X.; Geng, Y.X.; Qiu, H.; Sun, Y.H. Investigation of the microstructure, high temperature oxidation and deformation behavior of Hastelloy X superalloy fabricated by ultrasonic vibration laser directed energy deposition. J. Alloy. Compd. 2025, 1010, 177799. [Google Scholar] [CrossRef]
- Jinoop, A.N.; Paul, C.P.; Bindra, K.S. Laser assisted direct energy deposition of Hastelloy-X. Opt. Laser Technol. 2019, 109, 14–19. [Google Scholar] [CrossRef]
- Gonnabattula, A.; Thanumoorthy, R.S.; Bontha, S.; Balan, A.S.S.; Kumar, V.A.; Kanjarla, A.K. Process parameter optimization for laser directed energy deposition (LDED) of Ti6Al4V using single-track experiments with small laser spot size. Opt. Laser Technol. 2024, 175, 110861. [Google Scholar] [CrossRef]
- Qiu, J.R.; Chen, Y.X.; Hwang, Y.K.; Chang, W.L.; Hwang, S.J. Directed energy deposition process optimization and factor interaction analysis by response surface methodology. Int. J. Adv. Manuf. Tech. 2024, 132, 5329–5350. [Google Scholar] [CrossRef]
- Shao, D.L.; Bi, X.L.; Hong, M.S.; Li, R.F. Optimization of process pparameters for laser-directed energy deposition coatings of FeCoNi + 1%Y2O3 high-entropy alloy based on response surface methodology. Materials 2025, 18, 883. [Google Scholar] [CrossRef]
- Feenstra, D.R.; Molotnikov, A.; Birbilis, N. Utilisation of artificial neural networks to rationalise processing windows in directed energy deposition applications. Mater. Design 2021, 198, 109342. [Google Scholar] [CrossRef]
- Ghasempour-Mouziraji, M.; Afonso, D.; de Sousa, R.A. On the prediction and optimisation of processing parameters in directed energy deposition of SS316L via finite element simulation and machine learning. Materials 2025, 18, 1039. [Google Scholar] [CrossRef]
- Chen, Y.X.; Qiu, J.R.; Chang, W.L.; Hwang, Y.K.; Hwang, S.J. Process optimization and mechanical properties analysis of Inconel 718/stainless steel 316 L multi-material via direct energy deposition. Sci. Rep. 2024, 14, 28927. [Google Scholar] [CrossRef]
- Chandra, S.; Cagirici, M.; Ramamurty, U. Process parameter optimisation for precision manufacturing of H13 tool steel via laser-based directed energy deposition. J. Manuf. Process. 2025, 149, 12–26. [Google Scholar] [CrossRef]
- Lee, Y.S.; Nordin, M.; Babu, S.S.; Farson, D.F. Influence of fluid convection on weld pool formation in laser cladding a transient 3D transport model was used to generate insight into details of melt pool formation, fluid convection, and solidification in Inconel 718 laser claddings. Weld. J. 2014, 93, 292S–300S. [Google Scholar]
- Chan, R.K.C. A generalized arbitrary Lagrangian-Eulerian method for incompressible flows with sharp interfaces. J. Comput. Phys. 1975, 17, 311–331. [Google Scholar] [CrossRef]
- He, X.; Fuerschbach, P.W.; DebRoy, T. Heat transfer and fluid flow during laser spot welding of 304 stainless steel. J. Phys. D Appl. Physics 2003, 36, 1388–1398. [Google Scholar] [CrossRef]
- Dong, E.J.; Chang, T.Y.; Li, G.; Liu, Z.; Xia, L.M.; Zhao, L.J.; Lu, J.W.; Chen, J.X.; Chen, M.J.; Cheng, J. A generalized model for predicting the optimal overlap rate and height of successive single-layer involved in laser metal deposition process based on the aspect ratio. Opt. Laser Technol. 2025, 191, 113364. [Google Scholar] [CrossRef]
- Chang, T.Y.; Dong, E.J.; Zhao, L.J.; Chen, M.J.; Cheng, J. Investigation of thermal and solidification behaviors to predict dendrite microstructure formation during directed energy deposition of AlSi10Mg. Cirp J. Manuf. Sci. Tec. 2025, 61, 222–232. [Google Scholar] [CrossRef]
- Hariharan, M.K.; Anderson, A.; Raghavan, K.; Nithya, S. Hot corrosion behaviour of Hastelloy X and Inconel 625 in an aggressive environment for superalloys for high-temperature energy applications. Appl. Nanosci. 2022, 13, 3359–3368. [Google Scholar] [CrossRef]
- Li, C.H.; Guan, J.H.; Zheng, L.; Yu, B.N.; Chang, D.X.; Zhu, H.W.; Wang, M.T.; Yu, B.Y. Study on the microstructure, wear, and corrosion resistance of GH3536 coatings prepared by laser-assisted Cold Spraying. Adv. Eng. Mater. 2025, 27, 2500051. [Google Scholar] [CrossRef]
- Dong, E.J.; Chang, T.Y.; Zhao, L.J.; Xing, Y.H.; Chen, J.X.; Chen, M.J.; Lu, J.W.; Cheng, J. Laser metal deposition of AlSi10Mg for aeroengine casing repair: Microhardness, wear and corrosion behavior. Mater. Today Commun. 2024, 38, 108412. [Google Scholar] [CrossRef]

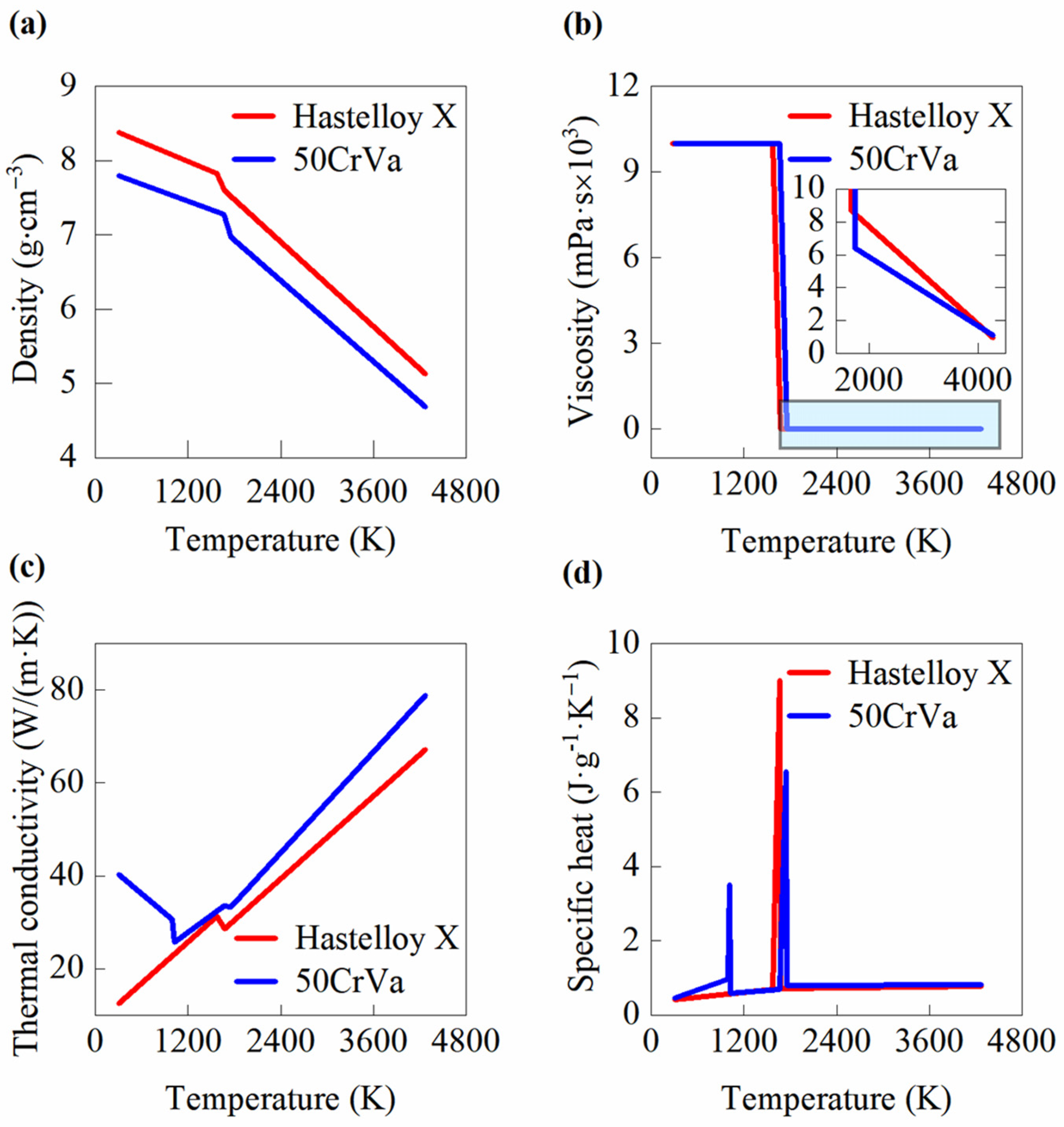




| Thermal Properties | Unit | Value |
|---|---|---|
| Solidus temperature of the powder | K | 1568.9 |
| Liquidus temperature of the powder | K | 1670.4 |
| Phase transformation temperature of the powder | K | 1619.7 |
| Transformation interval of the powder | K | 66.3 |
| Latent heat of the powder | J/g | 299.7 |
| Solidus temperature of the substrate | K | 1663.3 |
| Liquidus temperature of the substrate | K | 1752.6 |
| Phase transformation temperature of the substrate | K | 1707.9 |
| Transformation interval of the substrate | K | 89.3 |
| Latent heat of the substrate | J/g | 308.8 |
| Cr | Fe | Co | Mo | Al | W | Ti | Si | Mn | Cu | C | Ni |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 22.33 | 19.07 | 1.33 | 8.72 | 0.014 | 0.57 | 0.01 | 0.03 | 0.0054 | 0.005 | 0.069 | Bal. |
| Parameters | Temperature (K) | Load (N) | Rotational Speed (rpm) | Time (min) | Ball Diameter (mm) | Ball Material |
|---|---|---|---|---|---|---|
| Value | 293.15 | 5 | 100 | 10 | 2.38 | Si3N4 |
| Factors | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Laser power (W) | 1600 | 1700 | 1800 |
| Powder feed rate (g/min) | 1.8 | 2.1 | 2.4 |
| Scanning speed (mm/min) | 150 | 195 | 240 |
| No. | Factors | Porosity (%) | |||
|---|---|---|---|---|---|
| Laser Power (W) | Powder Feed Rate (g/min) | Scanning Speed (mm/min) | Average | Standard Deviation | |
| 1 | 1600 | 1.8 | 150 | 0.054 | 0.023 |
| 2 | 1600 | 2.1 | 195 | 0.066 | 0.067 |
| 3 | 1600 | 2.4 | 240 | 0.031 | 0.041 |
| 4 | 1700 | 1.8 | 195 | 0.071 | 0.059 |
| 5 | 1700 | 2.1 | 240 | 0.085 | 0.135 |
| 6 | 1700 | 2.4 | 150 | 0.063 | 0.065 |
| 7 | 1800 | 1.8 | 240 | 0.053 | 0.044 |
| 8 | 1800 | 2.1 | 150 | 0.083 | 0.122 |
| 9 | 1800 | 2.4 | 195 | 0.083 | 0.161 |
| Scheme. | Sum of Squares | Degrees of Freedom | Mean Square | F | P |
|---|---|---|---|---|---|
| Laser power | 0.001022742 | 2 | 0.000511371 | 21.301 | 0.045 |
| Powder feed rate | 0.000718039 | 2 | 0.000359020 | 19.113 | 0.050 |
| Scanning speed | 0.000436842 | 2 | 0.000218421 | 6.267 | 0.138 |
| Error | 0.000323292 | 2 | 0.000161646 | / | / |
| Total | 0.002500915 | 8 | / | / | / |
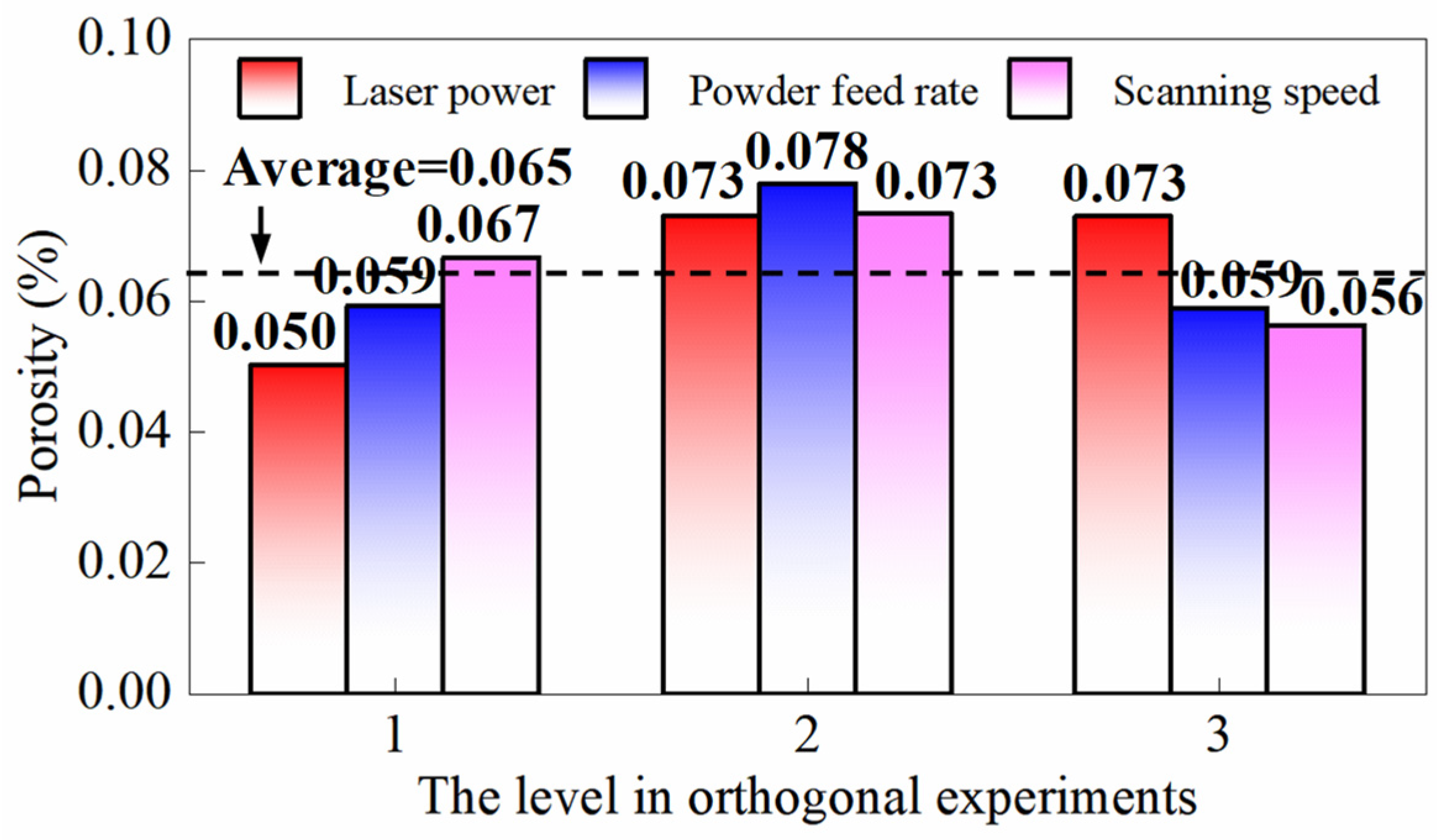
| Mean Value at Each Level | Laser Power (W) | Powder Feed Rate (g/min) | Scanning Speed (mm/min) |
|---|---|---|---|
| 1 | 0.05037 | 0.05912 | 0.06667 |
| 2 | 0.07344 | 0.07807 | 0.07329 |
| 3 | 0.07250 | 0.05912 | 0.05636 |
| Range | 0.02307 | 0.01895 | 0.01693 |
| Order | 1 | 2 | 3 |
| Samples | Average Hardness (HV0.5) |
|---|---|
| Pre-optimization cladding | 223.21 |
| Optimized cladding | 222.33 |
| Substrate | 288.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, L.; Lei, H.; Dong, E.; Chang, T.; Zhao, L.; Chen, M.; Lu, J.; Cheng, J. Achieving High-Quality Formed Hastelloy X Cladding Layers on Heterological 50CrVA Surface by Optimizing Process Parameters in Directed Energy Deposition. Micromachines 2025, 16, 1110. https://doi.org/10.3390/mi16101110
Xia L, Lei H, Dong E, Chang T, Zhao L, Chen M, Lu J, Cheng J. Achieving High-Quality Formed Hastelloy X Cladding Layers on Heterological 50CrVA Surface by Optimizing Process Parameters in Directed Energy Deposition. Micromachines. 2025; 16(10):1110. https://doi.org/10.3390/mi16101110
Chicago/Turabian StyleXia, Liming, Hongqin Lei, Enjie Dong, Tingyu Chang, Linjie Zhao, Mingjun Chen, Junwen Lu, and Jian Cheng. 2025. "Achieving High-Quality Formed Hastelloy X Cladding Layers on Heterological 50CrVA Surface by Optimizing Process Parameters in Directed Energy Deposition" Micromachines 16, no. 10: 1110. https://doi.org/10.3390/mi16101110
APA StyleXia, L., Lei, H., Dong, E., Chang, T., Zhao, L., Chen, M., Lu, J., & Cheng, J. (2025). Achieving High-Quality Formed Hastelloy X Cladding Layers on Heterological 50CrVA Surface by Optimizing Process Parameters in Directed Energy Deposition. Micromachines, 16(10), 1110. https://doi.org/10.3390/mi16101110







