Impact of Extrinsic Defects in Wavelength Separation Coatings on the Process of Laser-Induced Damage
Abstract
1. Introduction
2. Model Establishment and Experiment
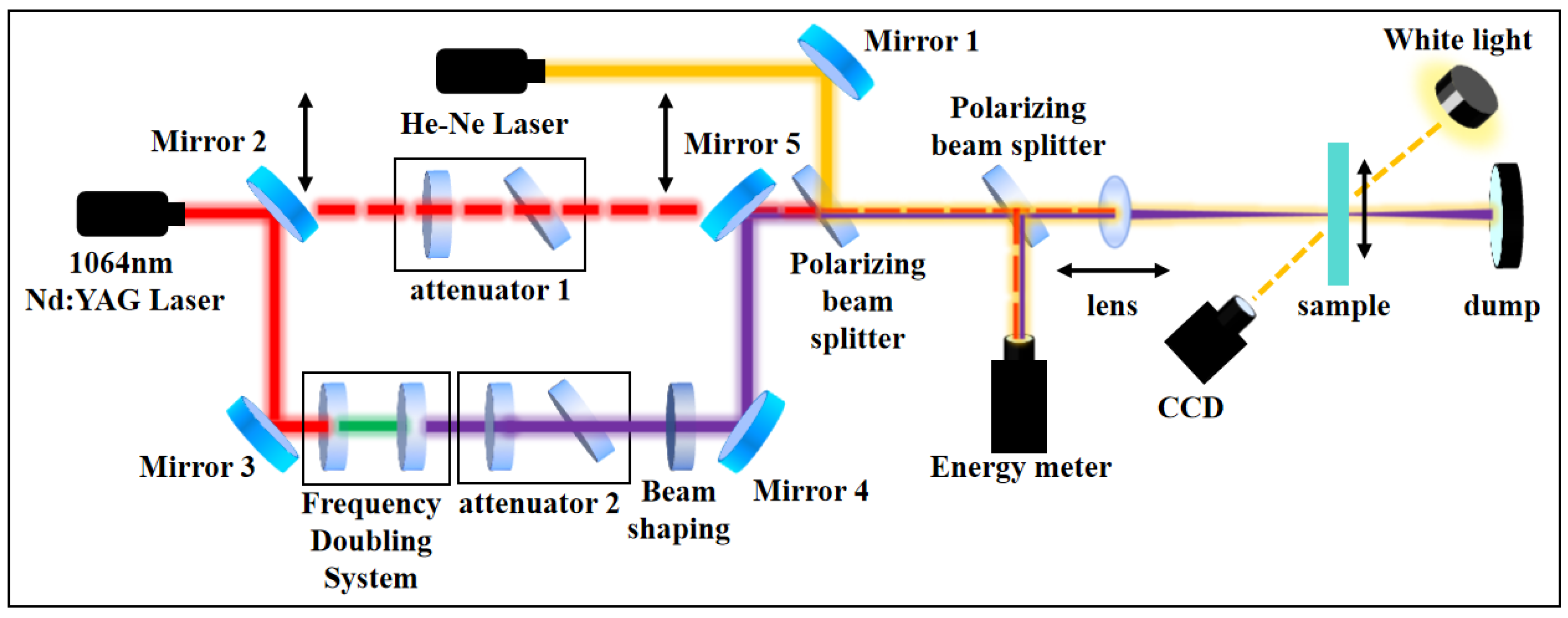
2.1. Sample Preparation and Damage Threshold Test
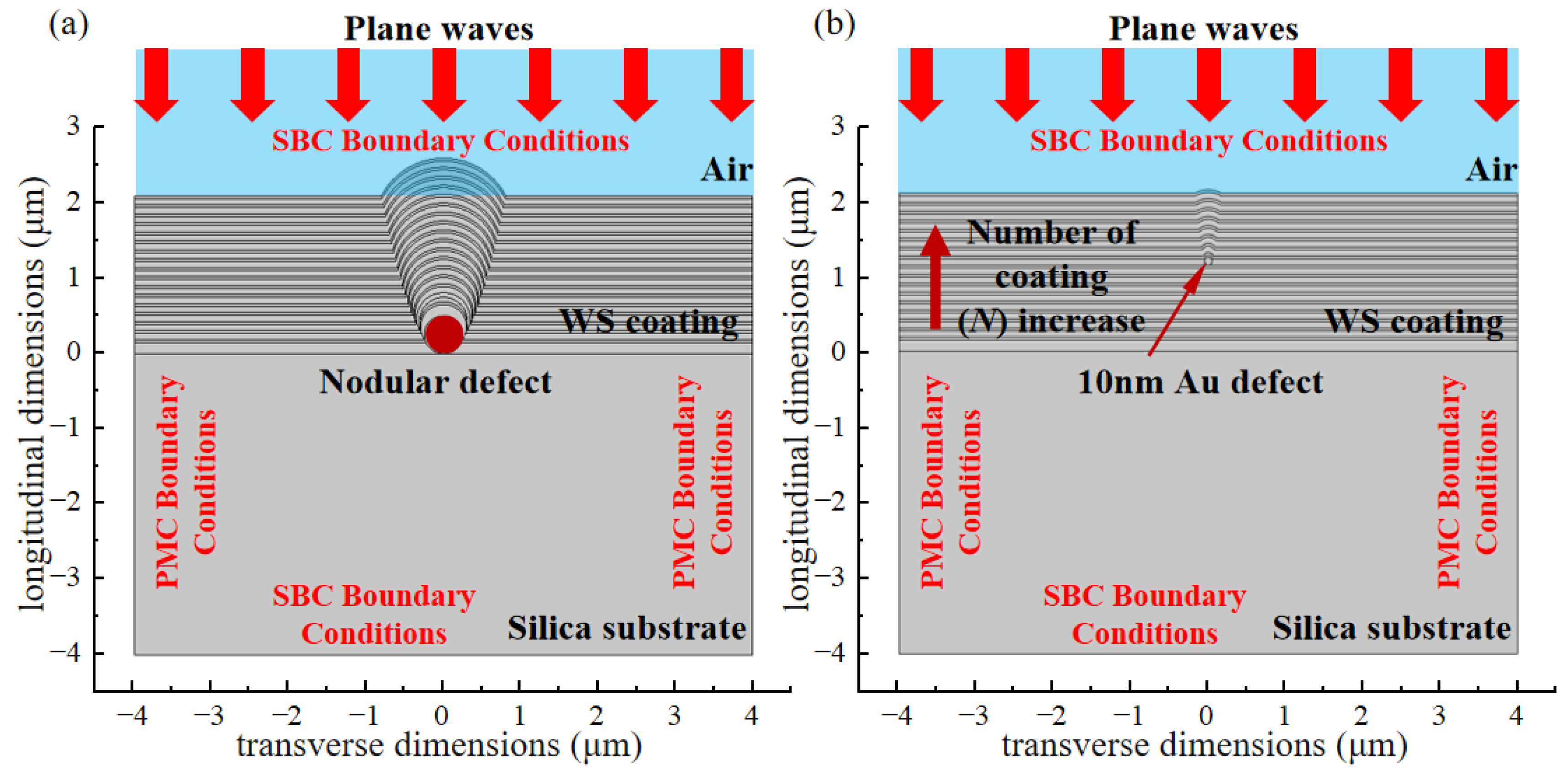
2.2. Establishment of the Multi-Physics Coupling Model
3. Results and Discussion
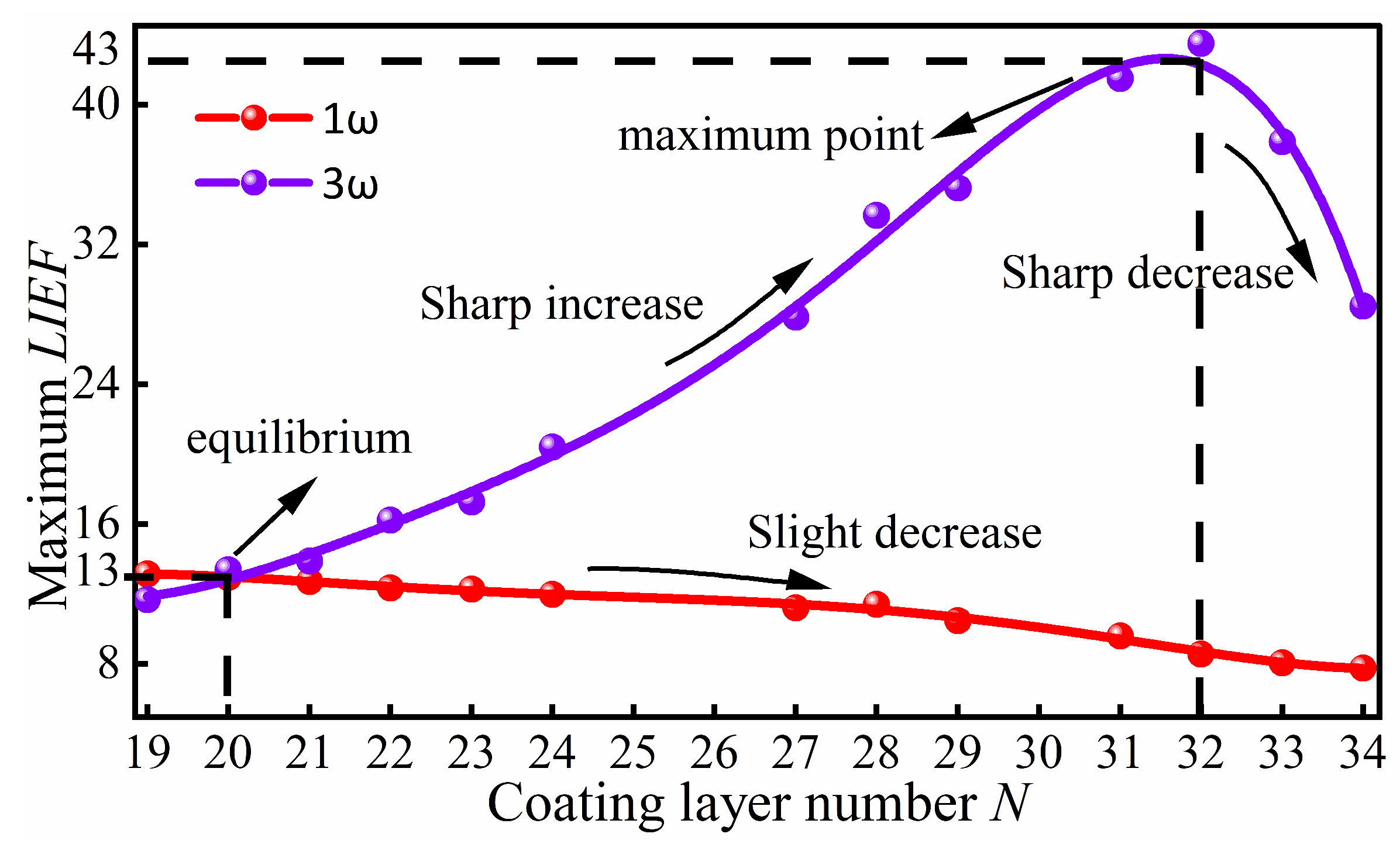
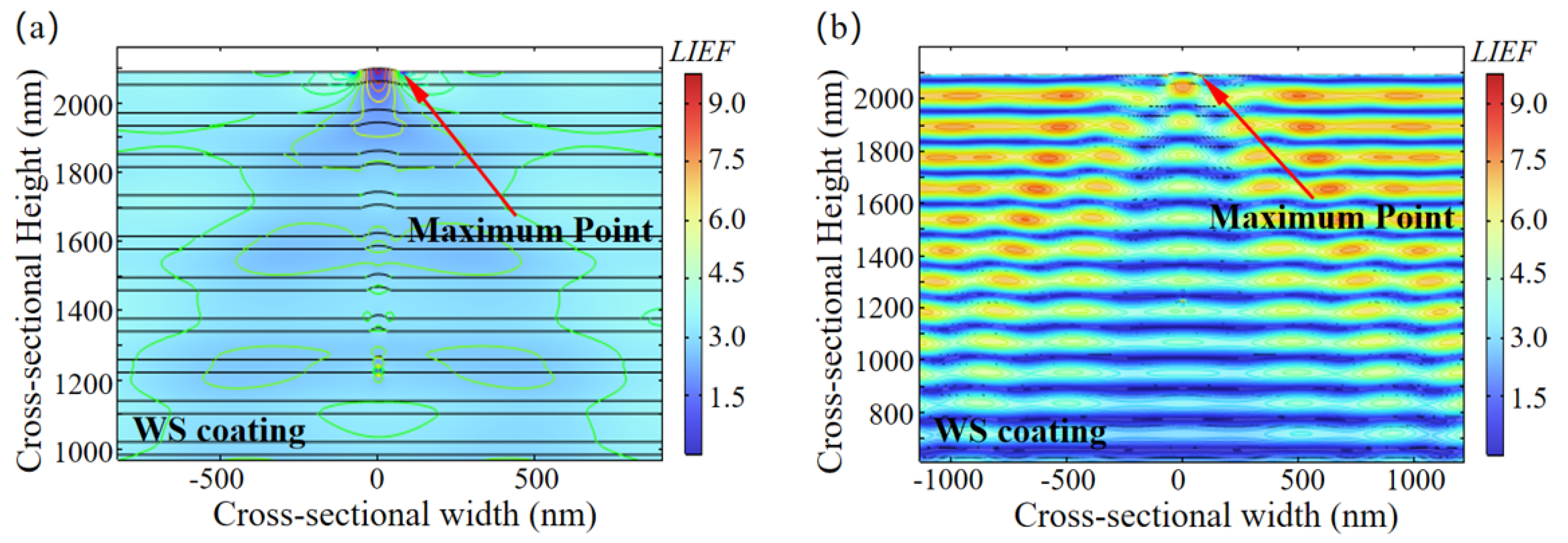
3.1. Influence of Nanoscale Defect Location on the Modulation Effect of Laser
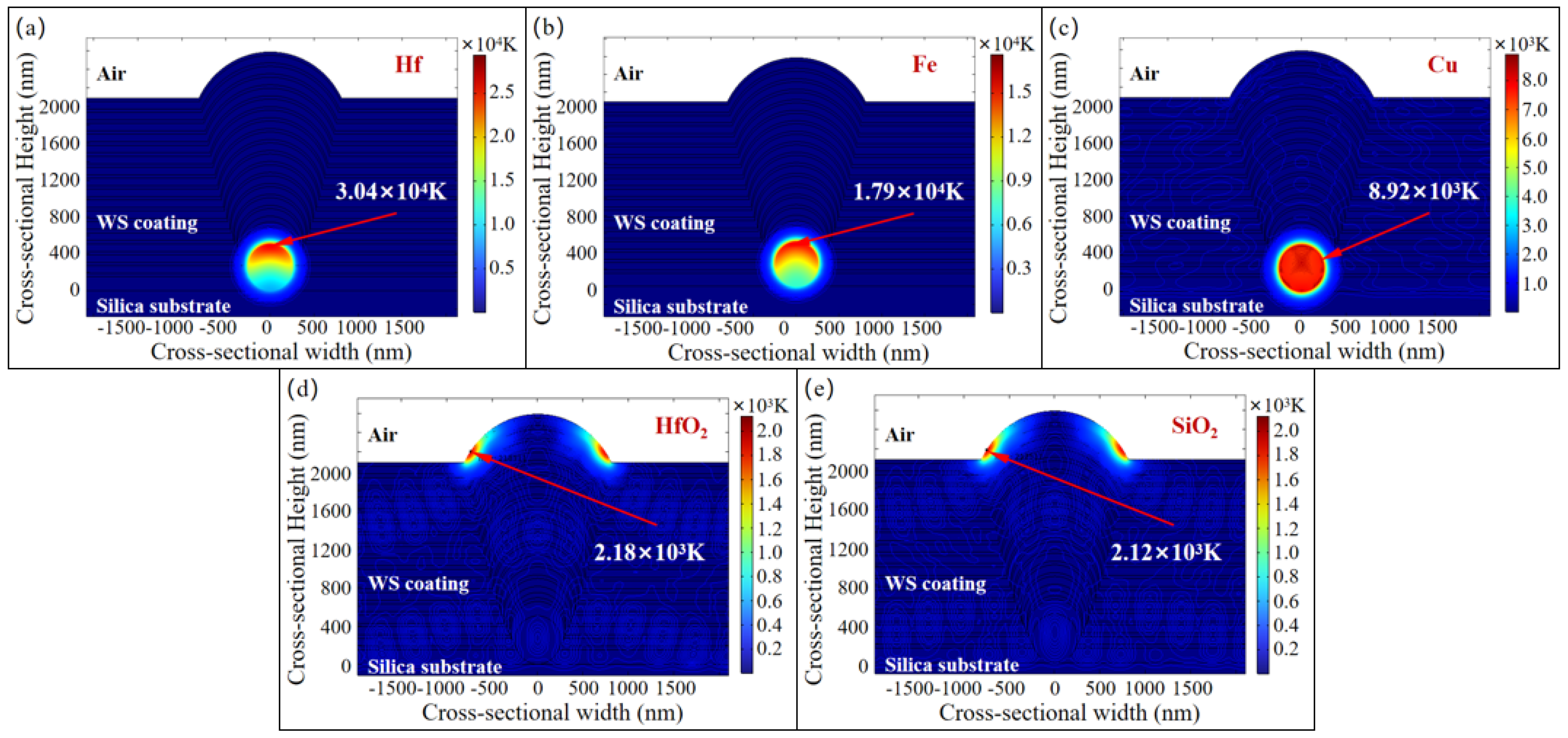
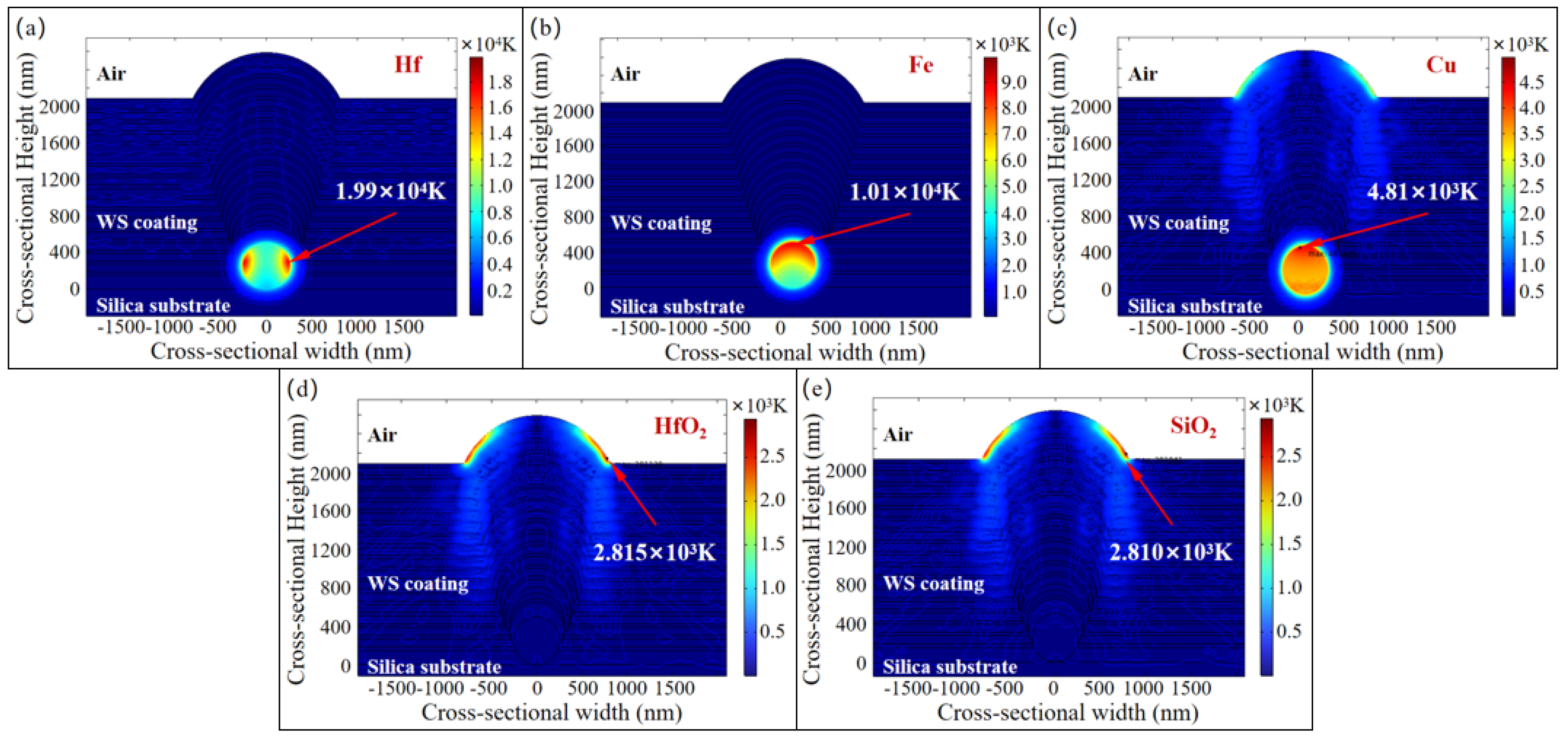
3.2. Influence of Nodule Defect Types on the Energy Deposition Process
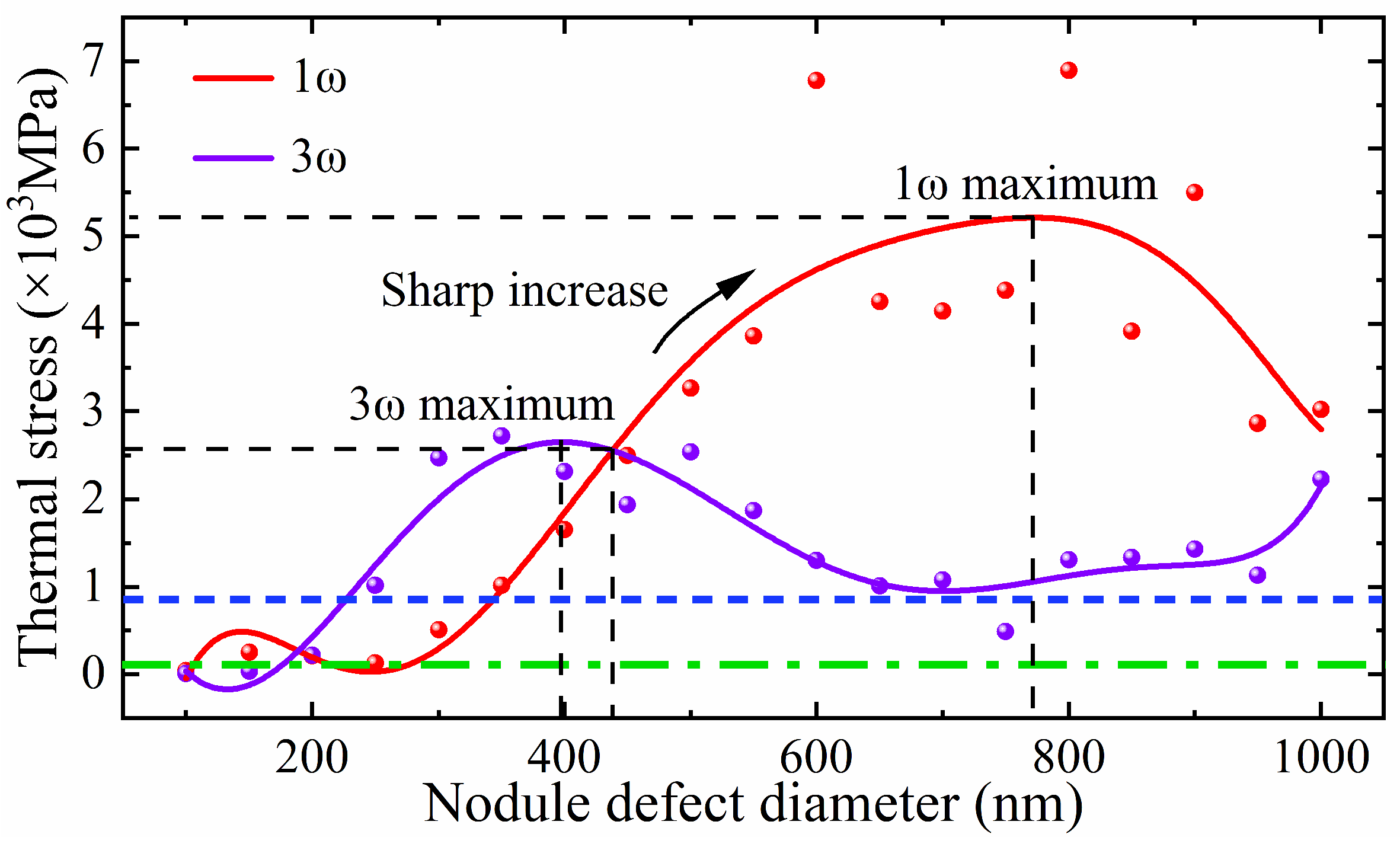
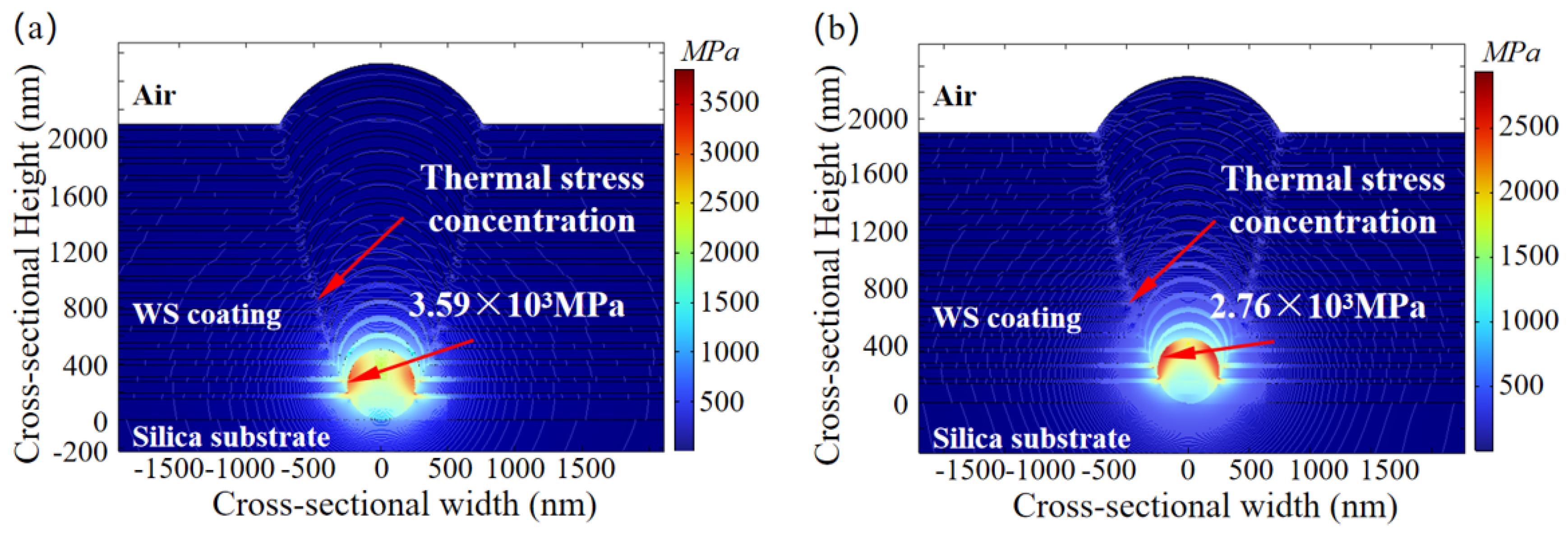
3.3. Influence of Nodular Defect Size on Thermal Stress Induced by Lasers
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, W.Y.; Zhu, M.P.; Shi, J.; Liu, T.B.; Zeng, T.T.; Sun, J.; Yi, K.; Shao, J.D. Plate laser beam splitter with mixture-based quarter-wave coating design. Opt. Laser Technol. 2022, 155, 108399. [Google Scholar] [CrossRef]
- Hu, G.; Kong, M.D.; Wei, M.; Gao, W.D.; Wang, B.; Li, M.; He, W.J. Effect of oxygen flow on micro-defects and laser damage resistance of ion-beam sputtered hafnium dioxide films. Vacuum 2025, 239, 114443. [Google Scholar] [CrossRef]
- He, J.S.; Wang, H.Y.; Wang, M.X.; Guo, M.; Liu, Y.C.; Qian, C.P.; Ye, X.S.; Peng, Y.J.; Yao, J.K.; Leng, Y.X.; et al. Damage mechanisms of mid-infrared coating components induced by 2.1μm nanosecond laser pulses. Opt. Laser Technol. 2025, 192, 113644. [Google Scholar] [CrossRef]
- Zhang, M.Z.; Qiu, F.M.; Qiao, Z.; Zhou, Q.; Pu, Y.T.; Xiong, B.C.; Die, J.; Lv, L.; Ma, P. High-repetition rate picosecond laser-induced damage properties of Ta2O5:SiO2 coatings. Front. Phys. 2022, 10, 981024. [Google Scholar] [CrossRef]
- Huang, Z.L.; Liu, L.Q.; Zeng, T.X.; Sun, H.; Liu, Q.Y.; Gao, X.Y.; Yang, D.Y.; Zhang, J.H.; Zhang, L.S.; Le, J.S. Investigation of the performance-enhancing effects of annealing on magnetron sputtered Ta2O5 high-power optical films. Opt. Mater. Express 2025, 15, 1738–1749. [Google Scholar] [CrossRef]
- Dong, S.Y.; Jiao, H.F.; Wang, Z.S.; Zhang, J.L.; Cheng, X.B. Interface and defects engineering for multilayer laser coatings. Prog. Surf. Sci. 2022, 97, 100663. [Google Scholar] [CrossRef]
- Qi, Y.N.; Guo, X.G.; Gao, X.; Zhou, P. Deep learning potential-assisted surface engineering for HfO2/SiO2 interface and enhanced laser damage resistance. Appl. Surf. Sci. 2025, 706, 163540. [Google Scholar] [CrossRef]
- Lin, Z.S.; Song, C.; Liu, T.B.; Shao, J.D.; Zhu, M.P. Comparative study of plasma-enhanced-atomic-layer-deposited Al2O3/HfO2/SiO2 and HfO2/Al2O3/SiO2 trilayers for ultraviolet laser applications. Acs Appl. Mater. Interfaces 2024, 16, 31756–31767. [Google Scholar] [CrossRef]
- Yang, Z.C.; Zhao, L.J.; Chen, M.J.; Yang, D.H.; Yin, Z.Y.; Yang, W.S.; Cheng, J.; Xu, Q.; Liu, Z.C.; Geng, F.; et al. Evolution of intrinsic defects and ring structures on the surface of fused silica optics after CO2 laser conditioning. Opt. Lett. 2024, 48, 5727–5730. [Google Scholar] [CrossRef]
- Yang, D.H.; Liu, Z.C.; Zhao, L.J.; Cheng, J.; Chen, M.J.; Wang, S.F.; Geng, F.; Sun, Y.Z.; Xu, Q. Role of atomic electronic structure defects in initiating laser-induced modification and failure of brittle-hard fused silica optics. Optica 2025, 12, 1291–1303. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, G.; Chen, M.J.; Zhao, L.J.; Xu, Q.; Yuan, X.D.; Liu, Z.C.; Wang, S.F.; Liao, W.; Liu, Q.; et al. Overview of advanced optical manufacturing techniques applied in regulating laser damage precursors in nonlinear functional KHxD2−xPO4 crystal. Light Adv. Manuf. 2025, 6, 546–574. [Google Scholar] [CrossRef]
- Shan, C.; Zhao, X.H.; Gao, Y.Q.; Zhao, Y.N.; Rao, D.X.; Cui, Y.; Li, C.; Hu, G.H.; Ma, W.X.; Sui, Z.; et al. Multi-wavelength coupling effect of laser-induced defect damage in beam splitter films captured by a three-dimensional spatially and temporally resolved method. Opt. Laser Technol. 2020, 130, 106368. [Google Scholar] [CrossRef]
- Liu, X.Y.; Feng, C.; Zhang, W.L.; Nasibli, H.; Zhao, Y.A.; Liu, X.F.; Shuai, K.; Shao, J.D. Nanosecond laser damage of 532nm thin film polarizers evaluated by different testing protocols. Opt. Mater. 2024, 149, 115124. [Google Scholar] [CrossRef]
- Gong, H.; Liu, X.F.; Tao, C.X.; Zhao, Y.A.; Shuai, K.; Li, D.W.; Zhang, W.L.; Sun, J.; Zhou, L.; Jiang, Y.E.; et al. Investigation on nano-absorbing precursors in the picosecond regime via the comparative study of HfO2/SiO2 and Ta2O5/SiO2 high-reflectivity coating damage. Opt. Mater. Express 2023, 13, 1820–1835. [Google Scholar] [CrossRef]
- Zhou, Q.; Ma, P.; Qiu, F.M.; Pu, Y.T.; Qiao, Z.; Lv, L.; Zhang, M.X.; Die, J.H. Material ejection and layer peeling-off in HfO2/SiO2 thin-film beam splitters induced by 1ω and 3ω lasers. Opt. Mater. 2022, 125, 111894. [Google Scholar] [CrossRef]
- Stolz, C.J.; Feigenbaum, E. Impact of high refractive coating material on the nodular-induced electric field enhancement for near infrared multilayer mirrors. Appl. Opt. 2020, 59, A20–A25. [Google Scholar] [CrossRef]
- Stolz, C.J.; Feigenbaum, E. Temporal and spatial laser intensification within nodular defects overcoated with multilayer dielectric mirrors over a wide range of defect geometries. Appl. Opt. 2023, 62, B25–B34. [Google Scholar] [CrossRef]
- Li, H.R.; Yang, R.S.; Xie, L.Y.; Wei, Z.Y.; Zhang, J.L.; Wang, Z.S.; Cheng, X.B. Scattering characteristics of various nodular defects in a dichroic beam splitter. Opt. Express 2024, 32, 949–958. [Google Scholar] [CrossRef]
- Guo, C.; Li, K.; Liu, Z.L.; Chen, Y.Y.; Xu, J.Y.; Li, Z.; Cui, W.D.; Song, C.Q.; Wang, C.; Jia, X.S.; et al. CW laser damage of ceramics induced by air filament. Opto-Electron. Adv. 2025, 8, 240296. [Google Scholar] [CrossRef]
- Chen, J.X.; Yin, C.Y.; Cheng, J.; Zhao, L.J.; Chen, M.J.; Chen, G.; Hu, J.R.; Lei, H.Q.; Zhang, Z.X.; Yang, D.H. Comparative study of the steady and transient photoluminescence induced by plastic and brittle surface defects and their correlation to the laser damage performance of KDP crystal optics. Opt. Mater. 2025, 159, 116657. [Google Scholar] [CrossRef]
- Papernov, S.; Schmid, A.W. Testing asymmetry in plasma-ball growth seeded by a nanoscale absorbing defect embedded in a SiO2 thin-film matrix subjected to UV pulsed-laser radiation. J. Appl. Phys. 2008, 104, 063101. [Google Scholar] [CrossRef]
- Ding, W.Y.; Zhao, L.J.; Chen, M.J.; Cheng, J.; Chen, G.; Lei, H.Q.; Liu, Z.C.; Geng, F.; Wang, S.F.; Xu, Q. Determination of stress waves and their effect on the damage extension induced by surface defects of KDP crystals under intense laser irradiation. Optica 2023, 10, 671–681. [Google Scholar] [CrossRef]
- Nunes, F.D.; Vasconcelos, T.C.; Bezerra, M.; Weiner, J. Electromagnetic energy density in dispersive and dissipative media. J. Opt. Soc. Am. B-Opt. Phys. 2011, 28, 1544–1552. [Google Scholar] [CrossRef]
- Han, Y.C.; Wan, S.L.; Peng, X.C.; Chen, H.; Wang, S.S.; Li, H.J.; Jiang, P.D.; Wei, C.Y.; Shao, J.D. Evolution mechanism of subsurface damage during laser machining process of fused silica. Opt. Express 2024, 32, 16273–16291. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.T.; Zheng, Y.H.; Wang, S.Y. Algorithm for accurate and efficient calculation of coating-induced effects. Opt. Express 2024, 32, 29279–29290. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, R.Z.; Chen, M. Analysis of composite wavelength multilayer dielectric film damage based on the field-thermal effect. J. Opt. Soc. Am. B-Opt. Phys. 2024, 41, 2589–2598. [Google Scholar] [CrossRef]
- Falmbigl, M.; Godin, K.; George, J.; Muhlig, C.; Rubin, B. Effect of annealing on properties and performance of HfO2/SiO2 optical coatings for UV-applications. Opt. Express 2022, 30, 12326–12336. [Google Scholar] [CrossRef]
- Wu, Y.L.; Xiang, X.; Yu, J.X.; Yuan, X.D.; Shen, H.H.; Zheng, W.G.; Zu, X.T. Review: Research progress on nanosecond laser irradiation damage of optical films. Nucl. Anal. 2022, 1, 1000045. [Google Scholar] [CrossRef]
- Wang, H.; Qi, H.J.; Zhang, W.L.; Sun, J.; Chai, Y.J.; Tu, F.F.; Zhao, J.L.; Yu, Z.; Wang, B.; Zhu, M.P.; et al. Suppression of nano-absorbing precursors and damage mechanism in optical coatings for 3ω mirrors. Opt. Lett. 2016, 41, 1209–1212. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, G.; Chen, M.J.; Zhao, L.J.; Xu, Q.; Yuan, X.D.; Liu, Z.C.; Wang, S.F.; Liao, W.; Liu, Q.; et al. Challenges of optical manufacturing techniques applied in improving the laser damage resistance of hard-brittle fused silica optics. Opt. Laser Technol. 2025, 192, 113475. [Google Scholar] [CrossRef]
- Lv, X.R.; Zhong, B.; Huang, Y.F.; Xing, Z.G.; Wang, H.D.; Guo, W.L.; Chang, X.T.; Zhang, Z.A. Research progress in preparation and application of photonic crystals. Chin. J. Mech. Eng. 2023, 36, 39. [Google Scholar] [CrossRef]
- Cheng, Z.P.; Liu, Z.Y.; Guo, D.M.; Xu, Q.; Gao, H. Material removal uniformity in water dissolution ultraprecision continuous polishing for large-size water-soluble crystals. Chin. J. Mech. Eng. 2024, 37, 145. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Mai, T.N.; Liu, J.W.; Zou, T. Regulating microstructure, mechanical properties and corrosion resistance of laser direct energy deposited Al0.5Mn0.5CoCrFeNi high-entropy alloy by annealing heat treatment. Virtual Phys. Prototyp. 2025, 20, e2458656. [Google Scholar] [CrossRef]
- Lin, Q.L.; Liu, L.; Zhu, W.Q. Formation mechanism of precursor films at high temperatures: A review. Chin. J. Mech. Eng. 2022, 35, 21. [Google Scholar] [CrossRef]
- Wang, B.; Dai, G.; Zhang, H.C.; Ni, X.W.; Shen, Z.H.; Lu, J. Damage performance of TiO2/SiO2 thin film components induced by a long-pulsed laser. Appl. Surf. Sci. 2011, 257, 9977–9981. [Google Scholar] [CrossRef]
- Shan, Y.G.; He, H.B.; Wei, C.Y.; Wang, Y.; Zhao, Y.A. Thermomechanical analysis of nodule damage in HfO2/SiO2 multilayer coatings. Chin. Opt. Lett. 2011, 9, 03101. [Google Scholar] [CrossRef]


| Parameter | Symbol/Unit | HfO2 | SiO2 | Au | Cu | Fe | Hf |
|---|---|---|---|---|---|---|---|
| Heat capacity | CP/(J/(Kg∙K)) | 270 | 750 | 129 | 380 | 440 | 140 |
| Density | ρ/(Kg/m3) | 9680 | 2203 | 19,300 | 8960 | 7870 | 13,310 |
| Thermal conductivity coefficient | k/(W/(m·K)) | 2 | 1.38 | 10 | 350 | 60 | 20 |
| Relative permittivity | εr | 3.9 | 2.25 | −10.4 | −10 | −10 | −5 |
| Refractive index | n | 1.97−0.000022i | 1.475−0.00002i | 0.18−3.1i | 0.14−3.2i | 2−3i | 2.5−1.5i |
| Young’s modulus | E/(GPa) | 170 | 190 | 79 | 120 | 211 | |
| Poisson’s ratio | υ | 0.27 | 0.17 | 0.42 | 0.34 | 0.29 | |
| Coefficient of thermal expansion | β/(10−6 K−1) | 5.6 | 0.5 | 14.2 | 16.5 | 11.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; Zhou, X.; Zheng, Y.; Li, J.; Zhang, T.; Zhao, L.; Chai, L.; Chen, M. Impact of Extrinsic Defects in Wavelength Separation Coatings on the Process of Laser-Induced Damage. Micromachines 2025, 16, 1191. https://doi.org/10.3390/mi16111191
Shen S, Zhou X, Zheng Y, Li J, Zhang T, Zhao L, Chai L, Chen M. Impact of Extrinsic Defects in Wavelength Separation Coatings on the Process of Laser-Induced Damage. Micromachines. 2025; 16(11):1191. https://doi.org/10.3390/mi16111191
Chicago/Turabian StyleShen, Shichen, Xinda Zhou, Yinbo Zheng, Jie Li, Tianhao Zhang, Linjie Zhao, Liqun Chai, and Mingjun Chen. 2025. "Impact of Extrinsic Defects in Wavelength Separation Coatings on the Process of Laser-Induced Damage" Micromachines 16, no. 11: 1191. https://doi.org/10.3390/mi16111191
APA StyleShen, S., Zhou, X., Zheng, Y., Li, J., Zhang, T., Zhao, L., Chai, L., & Chen, M. (2025). Impact of Extrinsic Defects in Wavelength Separation Coatings on the Process of Laser-Induced Damage. Micromachines, 16(11), 1191. https://doi.org/10.3390/mi16111191






