Robust and Compact Electrostatic Comb Drive Arrays for High-Performance Monolithic Silicon Photonics
Abstract
1. Introduction
1.1. Background
| Feature | Monolithic Devices | Segmented Devices | Refs. | ||
|---|---|---|---|---|---|
| Optical coupling and alignment |
|
| [15,17,20,22,23,24,25] | ||
| Fabrication |
|
| [5,6,24,25,27] | ||
| Actuation |
|
| [17,20,22,23,24,25,28,29,30] | ||
| Tuning Method and Applications | Waveguide Routing Control | 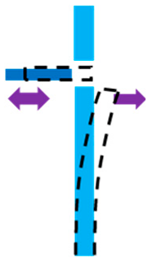 | Mechanical Modification of Waveguide Routing:
| Coupling/Decoupling Light Between Waveguides:
| [5,8,15,17,20,22,24,26,30,31,32,33,34,35,36,37,38,39,40] |
| Evanescent Field Interactions |  |
|
| [1,15,22,30,31,41,42,43] | |
| Waveguide Property Modification | 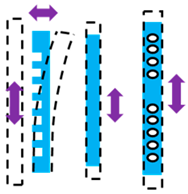 | Modifying Waveguide Properties (Strain/Stress/Deforming/Shortening Lengthening):
|
| [19,31,33,44,45,46,47,48] | |
1.2. Monolithic Device Actuation: The Need for High Force and Large Traveling Range
- Lower Loss: The absence of gaps eliminates optical losses due to diffraction, scattering, and reflections, ensuring higher optical efficiency and improved signal transmission.
- Reduced Polarization Extinction Ratio (PER): Continuous waveguides maintain a more consistent polarization state, leading to lower PER and enhanced polarization stability, which is critical for many photonic applications.
- Improved Performance: The combination of lower loss, reduced PER, and the ability to achieve mechanically and optically robust structure translates to significantly improved performance and broader functionality for tunable photonic devices.
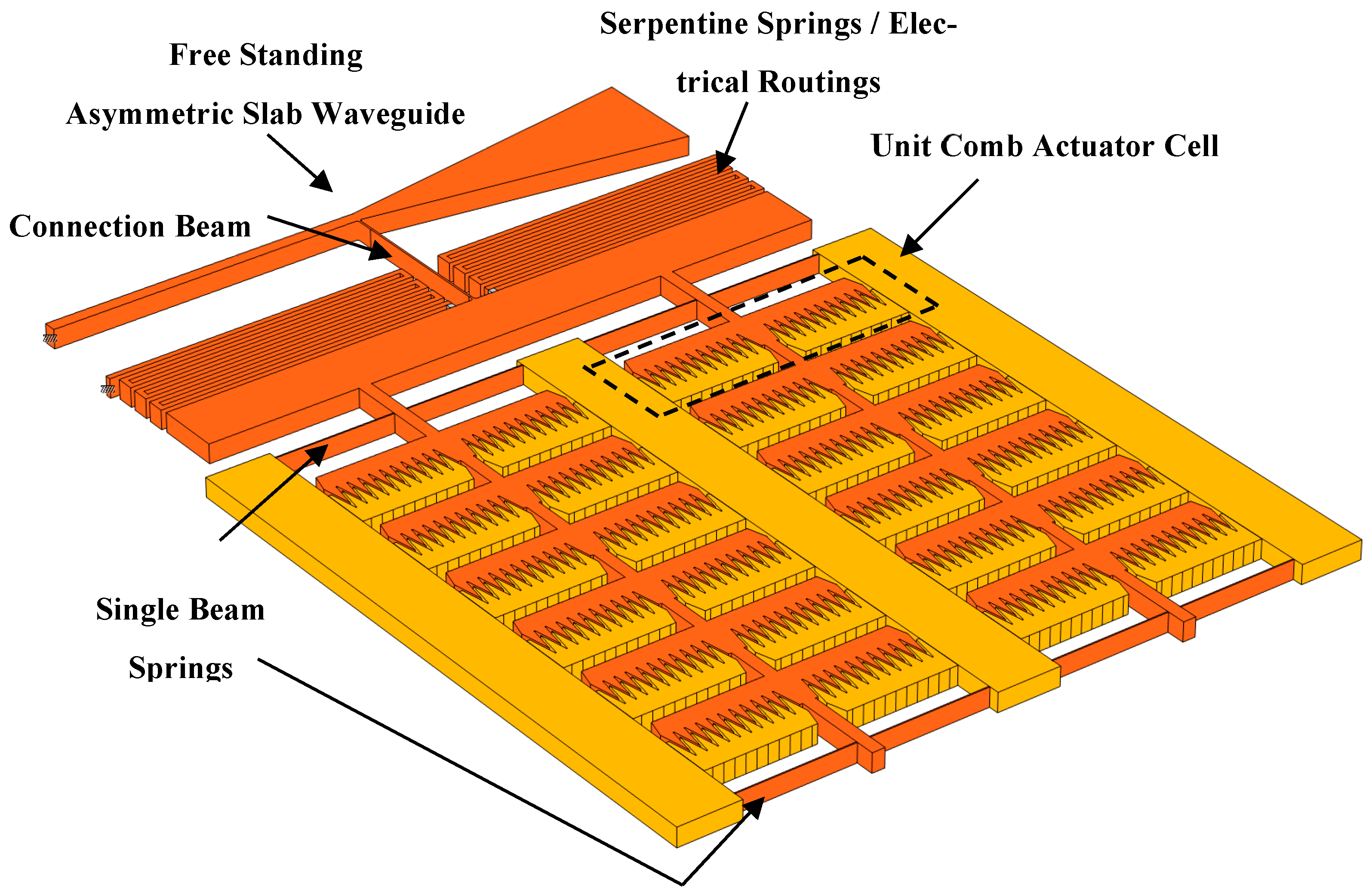
1.3. System Overview
1.4. Array-Level Optimization for Footprint and Force
2. Materials and Methods
2.1. Analytical and Parametric Study
2.2. Numerical Simulation
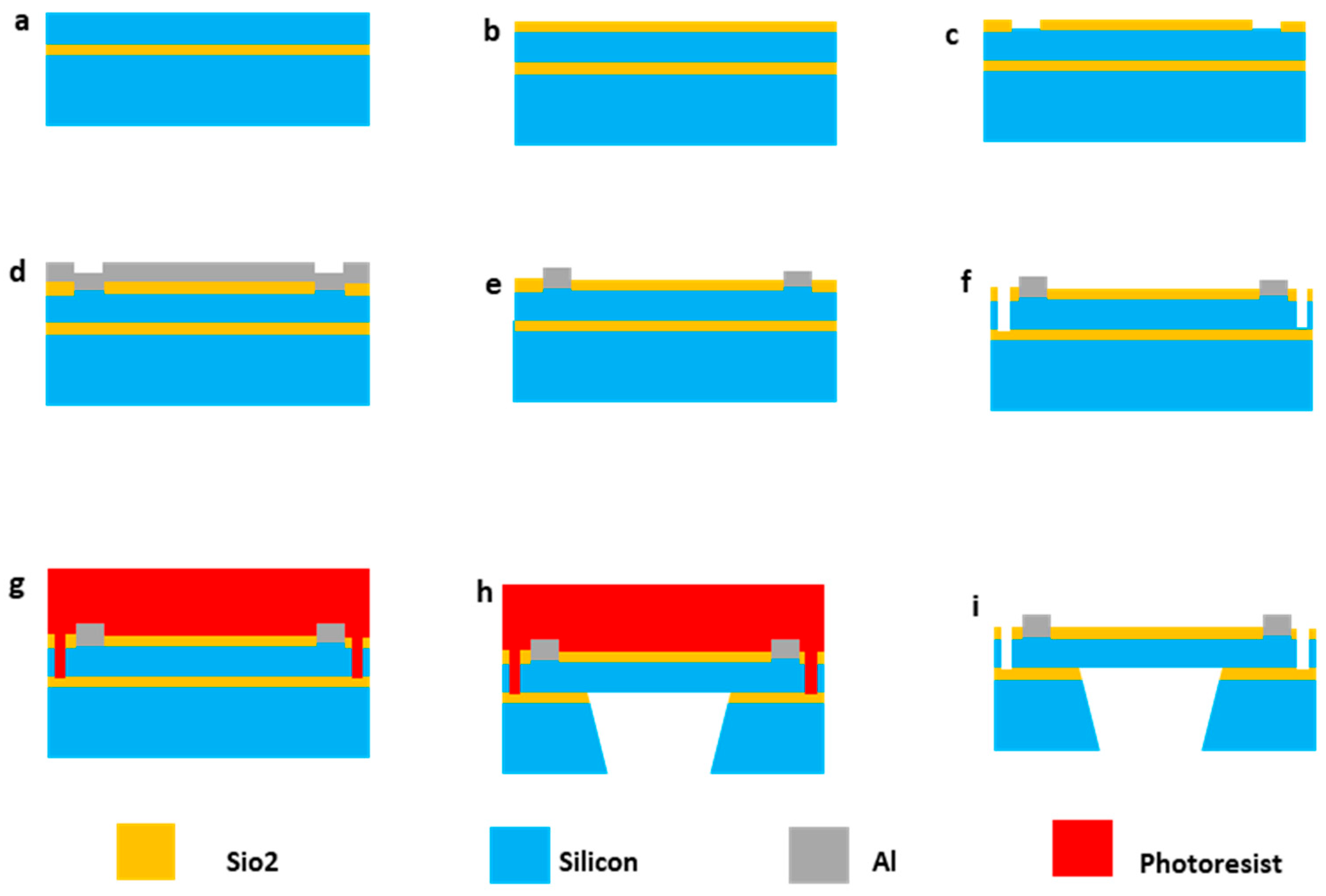
2.3. Fabrication Process
2.4. Data Analysis and Correction
2.5. Experimental Validation
Measurement Setup
3. Results
3.1. Analytical Calculations and Numerical Simulations
3.1.1. Design Configuration of Electrostatic Actuator Cell with Triangular Fingers
3.1.2. Mechanical Restoring Force and Traveling Range
3.1.3. Mechanical Stability and Arm Width Optimization: Travel Range Sacrifice Ratio
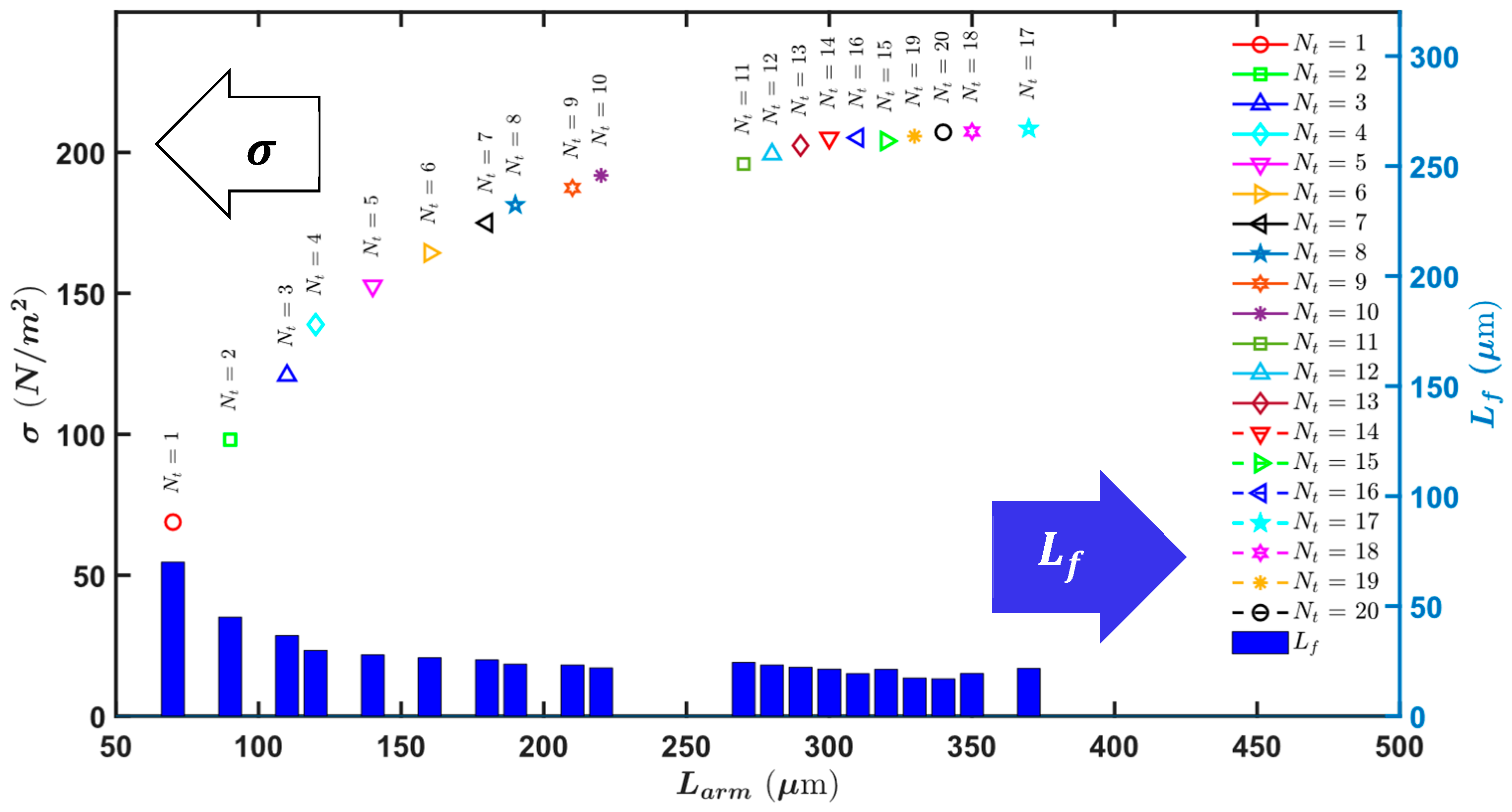
3.1.4. Force Intensity in Different Arm Lengths (Analytical Calculations)
3.2. Arm Geometry Optimization
3.3. Analytical Calculations and Numerical Simulation of Selected Design
3.3.1. Analytical Calculations
3.3.2. Numerical Simulations
3.4. Design Selection for Fabrication
3.5. Testing and Validation
3.5.1. SEM Characterization of Fabricated Electrostatic Comb Drive Actuators
3.5.2. Testing Results
3.6. Comparison of Simulation and Fabrication Results
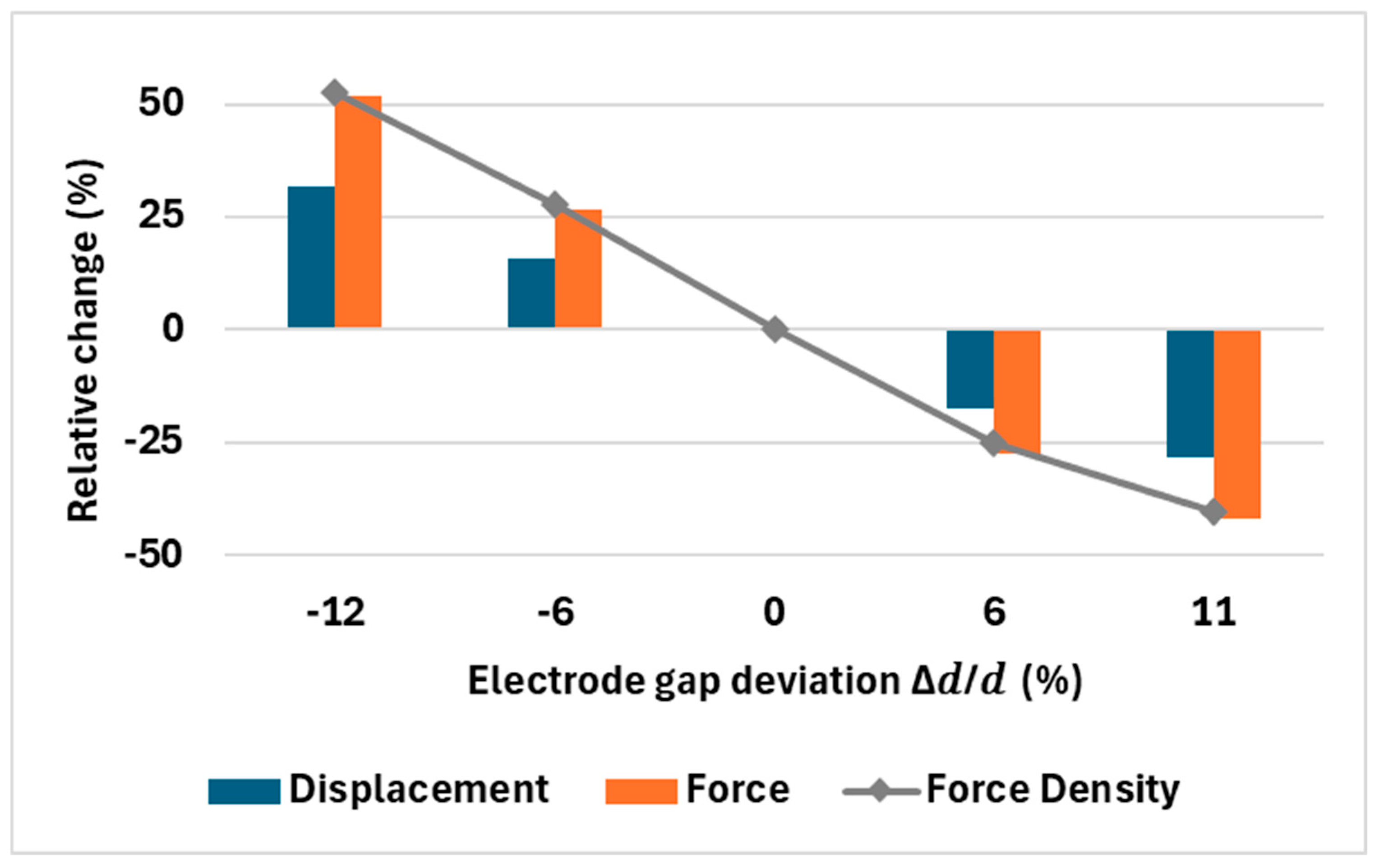
3.7. Fabrication Tolerances
4. Discussion
4.1. Comparison with Previous Studies
4.2. Detailed Analysis of Results
4.3. Fabrication Challenges and Solutions
4.4. Implications for Silicon Photonics
4.5. Limitations and Future Work
4.6. Conclusion of Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, H.; Chau, F.; Zhou, G. Mechanically-Tunable Photonic Devices with on-Chip Integrated MEMS/NEMS Actuators. Micromachines 2016, 7, 69. [Google Scholar] [CrossRef]
- Li, M.; Pernice, W.H.P.; Tang, H.X. Broadband All-Photonic Transduction of Nanocantilevers. Nat. Nanotechnol. 2009, 4, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Zhou, G.; Chew, X.; Sinha, S.K.; Chau, F.S. Nano-Tribometer Integrated with a Nano-Photonic Displacement-Sensing Mechanism. J. Micromech. Microeng. 2011, 21, 065014. [Google Scholar] [CrossRef]
- Briere, J.; Elsayed, M.Y.; Saidani, M.; Bérard, M.; Beaulieu, P.O.; Rabbani-Haghighi, H.; Nabki, F.; Ménard, M. Rotating Circular Micro-Platform with Integrated Waveguides and Latching Arm for Reconfigurable Integrated Optics. Micromachines 2017, 8, 354. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Kohli, N.; Brière, J.; Ménard, M.; Nabki, F. Translational MEMS Platform for Planar Optical Switching Fabrics. Micromachines 2019, 10, 435. [Google Scholar] [CrossRef]
- Quack, N.; Takabayashi, A.Y.; Sattari, H.; Edinger, P.; Jo, G.; Bleiker, S.J.; Errando-Herranz, C.; Gylfason, K.B.; Niklaus, F.; Khan, U.; et al. Integrated Silicon Photonic MEMS. Microsyst. Nanoeng. 2023, 9, 1–22. [Google Scholar] [CrossRef]
- Li, C.; Wu, H.; Tan, Y.; Wang, S.; Dai, D. Silicon-Based on-Chip Hybrid (de) Multiplexers. Sci. China Inf. Sci. 2018, 61, 080407. [Google Scholar] [CrossRef]
- Bulgan, E.; Kanamori, Y.; Hane, K. Submicron Silicon Waveguide Optical Switch Driven by Microelectromechanical Actuator. Appl. Phys. Lett. 2008, 92, 101110. [Google Scholar] [CrossRef]
- Bao, M. Chapter 4—Electrostatic Actuation. In Analysis and Design Principles of MEMS Devices; Bao, M., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2005; pp. 175–212. ISBN 978-0-444-51616-9. [Google Scholar]
- Kang, S.; Kim, H.C.; Chun, K. A Low-Loss, Single-Pole, Four-Throw RF MEMS Switch Driven by a Double Stop Comb Drive. J. Micromech. Microeng. 2009, 19, 035011. [Google Scholar] [CrossRef]
- Bian, W.; Zhao, J.; You, Z.; Sun, X. A Restoring Force Boosting Structure with Flexible Stiction Recovery Electrode for MEMS Relays/Switches. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Republic of Korea, 27–31 January 2019; pp. 986–989. [Google Scholar]
- Zhao, J.; Gao, Y. Electrostatic Comb-Drived Actuator for MEMS Relay/Switch. In Micro Electro Mechanical Systems; Huang, Q.-A., Ed.; Micro/Nano Technologies; Springer: Singapore, 2018; pp. 907–927. ISBN 978-981-10-5945-2. [Google Scholar]
- Gao, Y.; You, Z.; Zhao, J. Electrostatic Comb-Drive Actuator for MEMS Relays/Switches with Double-Tilt Comb Fingers and Tilted Parallelogram Beams. J. Micromech. Microeng. 2015, 25, 045003. [Google Scholar] [CrossRef]
- Rosa, M.A.; Dimitrijev, S.; Harrison, H.B. Improved Operation of Micromechanical Comb-Drive Actuators through the Use of a New Angled Comb Finger Design. J. Intell. Mater. Syst. Struct. 1998, 9, 283–290. [Google Scholar] [CrossRef]
- Fasihanifard, M.; Packirisamy, M. Design Regime of Electrostatic Actuators for Optical Microsystems. JOM 2024, 5, 014001. [Google Scholar] [CrossRef]
- Fasihanifard, M.; Packirisamy, M. Angled Electrode Comb Drives for Enhanced Actuator in Silicon Photonic Applications. Microsyst. Nanoeng. 2025, 11. [Google Scholar] [CrossRef]
- Fasihanifard, M.; Packirisamy, M. Mechanically Actuated Asymmetric Slab Waveguide: Optical and Mechanical Design Considerations. In Proceedings of the 2022 Photonics North (PN), Niagara Falls, ON, Canada, 24–26 May 2022; p. 1. [Google Scholar]
- Fasihanifard, M.; Pottier, P.; Packirisamy, M. Asymmetric Stiff Slab Waveguide Actuation with Footprint-Optimized Mechanical Platform. In Proceedings of the 2020 Photonics North (PN), Niagara Falls, ON, Canada, 26–28 May 2020; p. 1. [Google Scholar]
- Fasihanifard, M. Design and Verification of Optomechanical Actuation for Tunable Filters. PhD Thesis, Concordia University, Montreal, QC, Canada, 2024. [Google Scholar]
- Fasihanifard, M.; Packirisamy, M. Methods and Systems of Mechanical Tuning Multi Channel Optical Components. US20,230,384,579A1, 30 November 2023. [Google Scholar]
- Menard, F.; NABKI, F.; Menard, M.; Berard, M.; Aeponyx Inc. Methods and System for Microelectromechanical Packaging. United States patent US 11,125,948, 21 September 2021. [Google Scholar]
- Stepanovsky, M. A Comparative Review of MEMS-Based Optical Cross-Connects for All-Optical Networks from the Past to the Present Day. IEEE Commun. Surv. Tutor. 2019, 21, 2928–2946. [Google Scholar] [CrossRef]
- Menard, M.; NABKI, F.; Rahim, M.; Briere, J.; Beaulieu, P.O. Mirror Based Micromechanical Systems and Methods. United States patent US 10,067,293, 4 September 2018. [Google Scholar]
- Brière, J.; Beaulieu, P.-O.; Saidani, M.; Nabki, F.; Menard, M. Rotational MEMS Mirror with Latching Arm for Silicon Photonics. In Proceedings of the MOEMS and Miniaturized Systems XIV, San Francisco, CA, USA, 27 February 2015; International Society for Optics and Photonics: Bellingham, WA, USA; Volume 9375, p. 937507. [Google Scholar]
- Sharma, S.; Kohli, N.; Kohli, N.; Brière, J.; Nabki, F.; Ménard, M. Integrated 1 × 3 MEMS Silicon Nitride Photonics Switch. Opt. Express OE 2022, 30, 22200–22220. [Google Scholar] [CrossRef]
- Kharazmi, M.; Fasihanifard, M.; Packirisamy, M. Opto-Mechanical Interaction in Air-Gap Coupled System. In Proceedings of the 2025 Photonics North (PN), Ottawa, ON, Canada, 20–23 May 2025; pp. 1–2. [Google Scholar]
- Omran, H.; Sabry, Y.M.; Sadek, M.; Hassan, K.; Shalaby, M.Y.; Khalil, D. Deeply-Etched Optical MEMS Tunable Filter for Swept Laser Source Applications. IEEE Photonics Technol. Lett. 2014, 26, 37–39. [Google Scholar] [CrossRef]
- Xu, R.-J.; Lin, Y.-S. Actively MEMS-Based Tunable Metamaterials for Advanced and Emerging Applications. Electronics 2022, 11, 243. [Google Scholar] [CrossRef]
- Xia, J.; Qiao, Q.; Zhou, G.; Chau, F.S.; Zhou, G. Opto-Mechanical Photonic Crystal Cavities for Sensing Application. Appl. Sci. 2020, 10, 7080. [Google Scholar] [CrossRef]
- Errando-Herranz, C.; Takabayashi, A.Y.; Edinger, P.; Sattari, H.; Gylfason, K.B.; Quack, N. MEMS for Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 82200916. [Google Scholar] [CrossRef]
- Wu, M.C.; Solgaard, O.; Ford, J.E. Optical MEMS for Lightwave Communication. J. Light. Technol. 2006, 24, 4433–4454. [Google Scholar] [CrossRef]
- Zhou, G.; Lim, Z.H.; Qi, Y.; Chau, F.S.; Zhou, G. MEMS Gratings and Their Applications. Int. J. Optomechatronics 2021, 15, 61–86. [Google Scholar] [CrossRef]
- Chollet, F. Devices Based on Co-Integrated MEMS Actuators and Optical Waveguide: A Review. Micromachines 2016, 7, 18. [Google Scholar] [CrossRef]
- Bogaerts, W.; Sattari, H.; Edinger, P.; Takabayashi, A.Y.; Zand, I.; Wang, X.; Ribeiro, A.; Jezzini, M.; Errando-Herranz, C.; Talli, G.; et al. MORPHIC: Programmable Photonic Circuits Enabled by Silicon Photonic MEMS. In Proceedings of the Silicon Photonics XV, San Francisco, CA, USA, 26 February 2020; International Society for Optics and Photonics: Bellingham, WA, USA; Volume 11285, p. 1128503. [Google Scholar]
- Grade, J.D.; Yasumura, K.Y.; Jerman, H. Advanced, Vibration-Resistant, Comb-Drive Actuators for Use in a Tunable Laser Source. Sens. Actuators A Phys. 2004, 114, 413–422. [Google Scholar] [CrossRef]
- Akihama, Y.; Hane, K. Single and Multiple Optical Switches That Use Freestanding Silicon Nanowire Waveguide Couplers. Light. Sci. Appl. 2012, 1, e16. [Google Scholar] [CrossRef]
- Errando-Herranz, C.; Thomas, N.L.; Gylfason, K.B. Low-Power Optical Beam Steering by Microelectromechanical Waveguide Gratings. Opt. Lett. OL 2019, 44, 855–858. [Google Scholar] [CrossRef] [PubMed]
- Fasihanifard, M.; Pottier, P.; Packirisamy, M. MEMS Enabled Asymmetric Slab Waveguide for Continuously Tunable Filter. In Proceedings of the 2021 Photonics North (PN), Toronto, ON, Canada, 31 May–2 June 2021; p. 1. [Google Scholar]
- Packirisamy, M.; Pottier, P.; Valorbec, S.C. Wavelength Tunable Optical Sources, Filters and Detectors. United States patent US 10,816,792, 27 October 2020. [Google Scholar]
- Paul, S.; Gierl, C.; Cesar, J.; Le, Q.T.; Malekizandi, M.; Kögel, B.; Neumeyr, C.; Ortsiefer, M.; Küppers, F. 10-Gb/s Direct Modulation of Widely Tunable 1550-Nm MEMS VCSEL. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 436–443. [Google Scholar] [CrossRef]
- Quack, N.; Sattari, H.; Takabayashi, A.Y.; Zhang, Y.; Verheyen, P.; Bogaerts, W.; Edinger, P.; Errando-Herranz, C.; Gylfason, K.B. MEMS-Enabled Silicon Photonic Integrated Devices and Circuits. IEEE J. Quantum Electron. 2019, 56, 8400210. [Google Scholar] [CrossRef]
- Lee, M.-C.M.; Wu, M.C. Tunable Coupling Regimes of Silicon Microdisk Resonators Using MEMS Actuators. Opt. Express OE 2006, 14, 4703–4712. [Google Scholar] [CrossRef]
- Tu, X.; Song, C.; Huang, T.; Chen, Z.; Fu, H. State of the Art and Perspectives on Silicon Photonic Switches. Micromachines 2019, 10, 51. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Roels, J.; Mechet, P.; Claes, T.; Van Thourhout, D.; Baets, R. Ultracompact Phase Modulator Based on a Cascade of NEMS-Operated Slot Waveguides Fabricated in Silicon-on-Insulator. IEEE Photonics J. 2012, 4, 779–788. [Google Scholar] [CrossRef]
- Midolo, L.; Schliesser, A.; Fiore, A. Nano-Opto-Electro-Mechanical Systems. Nat. Nanotechnol. 2018, 13, 11. [Google Scholar] [CrossRef]
- Ayan, A.; Turkay, D.; Unlu, B.; Naghinazhadahmadi, P.; Oliaei, S.N.B.; Boztug, C.; Yerci, S. Strain Engineering of Germanium Nanobeams by Electrostatic Actuation. Sci. Rep. 2019, 9, 4963. [Google Scholar] [CrossRef]
- Fasihanifard, M.; Pottier, P.; Packirisamy, M. Design of an Integrated Multi-Band Continuous Optical Filter Using Mechanical Tuning. In Proceedings of the 2023 Photonics North (PN), Montreal, QC, Canada, 12–15 June 2023; p. 1. [Google Scholar]
- Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Ba Hashwan, S.S.; Junaid, M.M. A Review of Actuation and Sensing Mechanisms in MEMS-Based Sensor Devices. Nanoscale Res. Lett. 2021, 16, 16. [Google Scholar] [CrossRef]
- Gorecki, C.; Bargiel, S. MEMS Scanning Mirrors for Optical Coherence Tomography. Photonics 2021, 8, 6. [Google Scholar] [CrossRef]
- Piezo Standard Technology. Available online: https://science.xyz/docs/d/mems-piezo/index (accessed on 24 March 2024).
- Roark, R.J.; Young, W.C. Roark’s Formulas for Stress and Strain, 6th ed.; McGraw-Hill: New York, NY, USA, 1989; ISBN 978-0-07-072541-6. [Google Scholar]

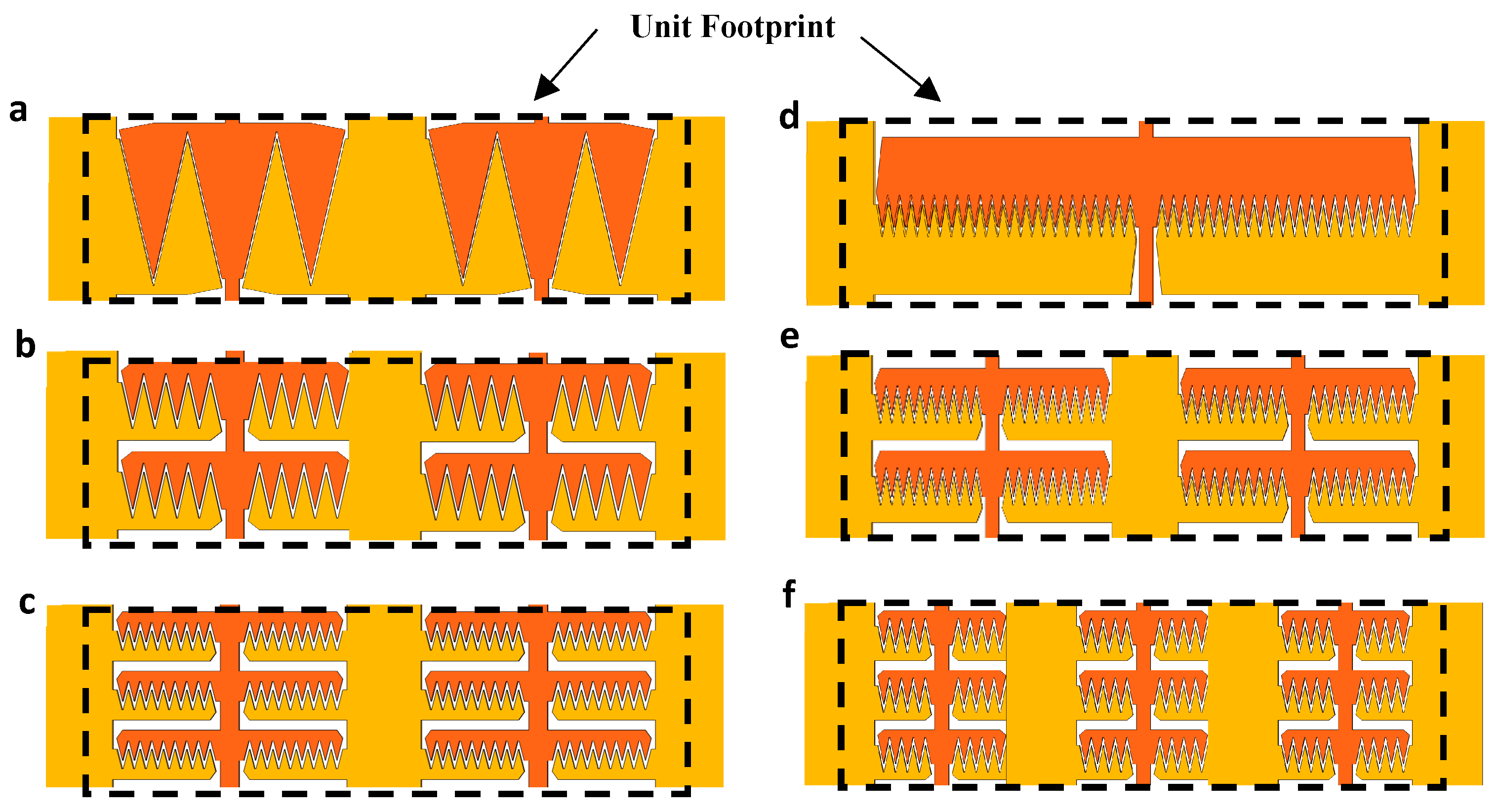

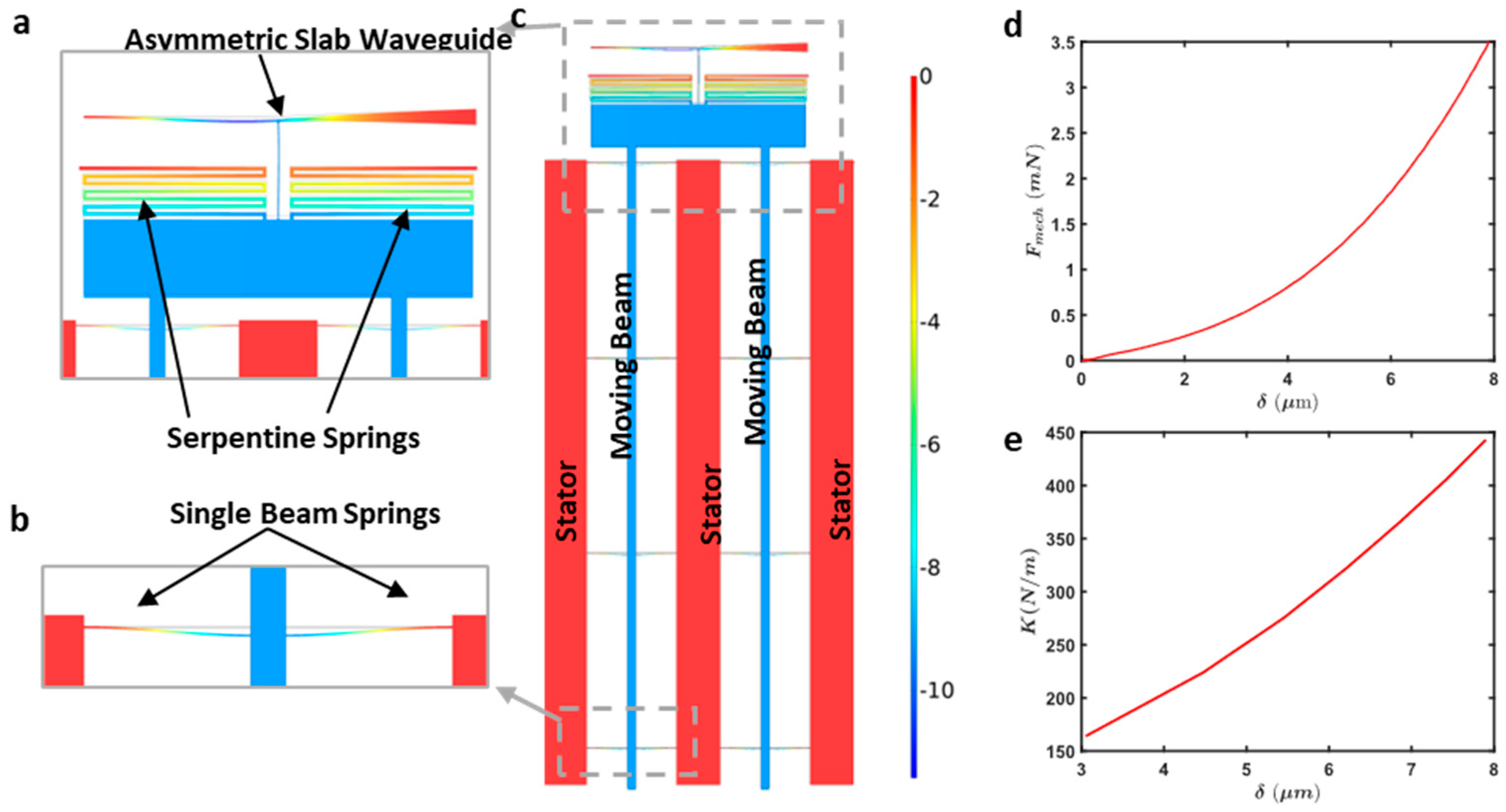
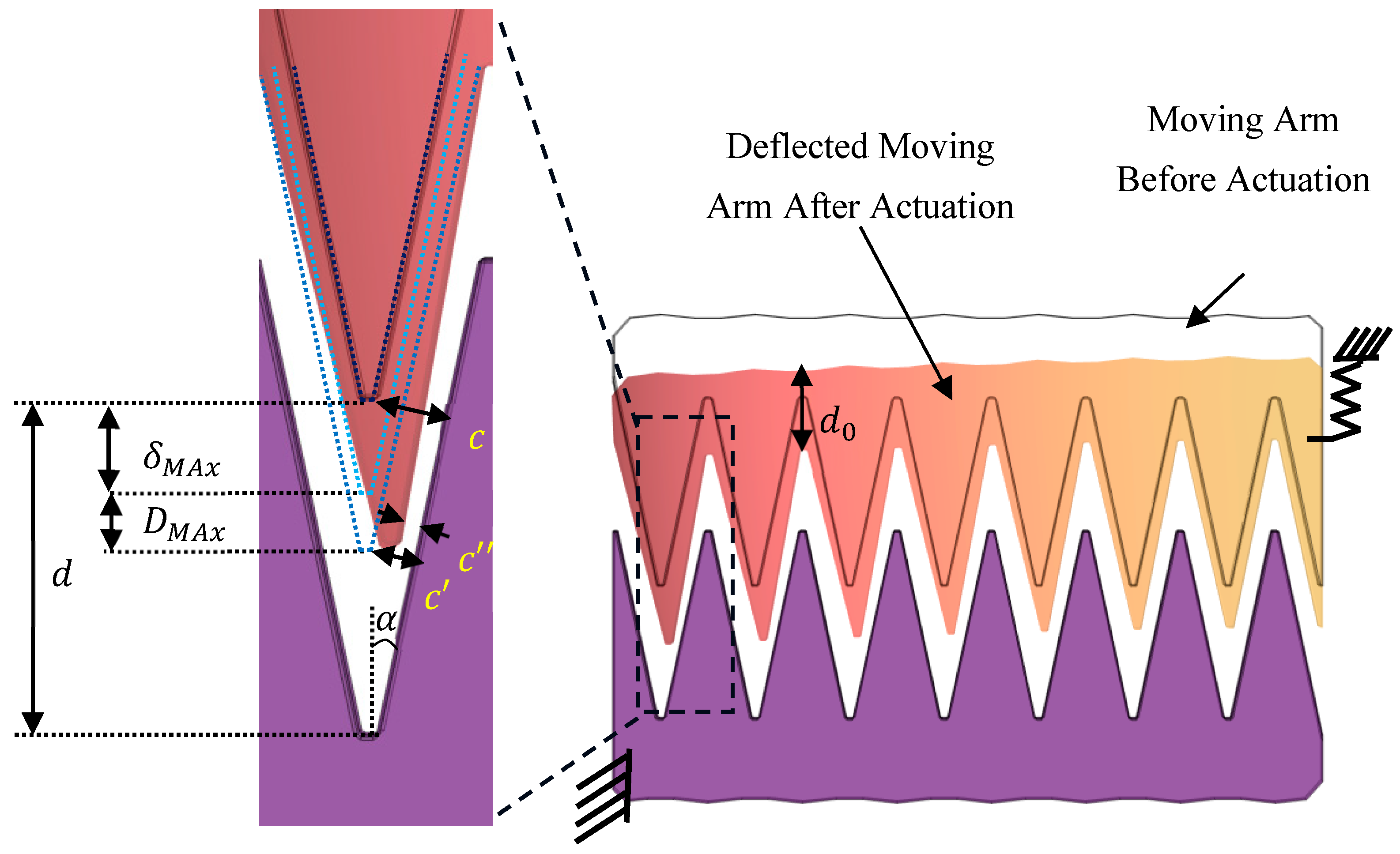

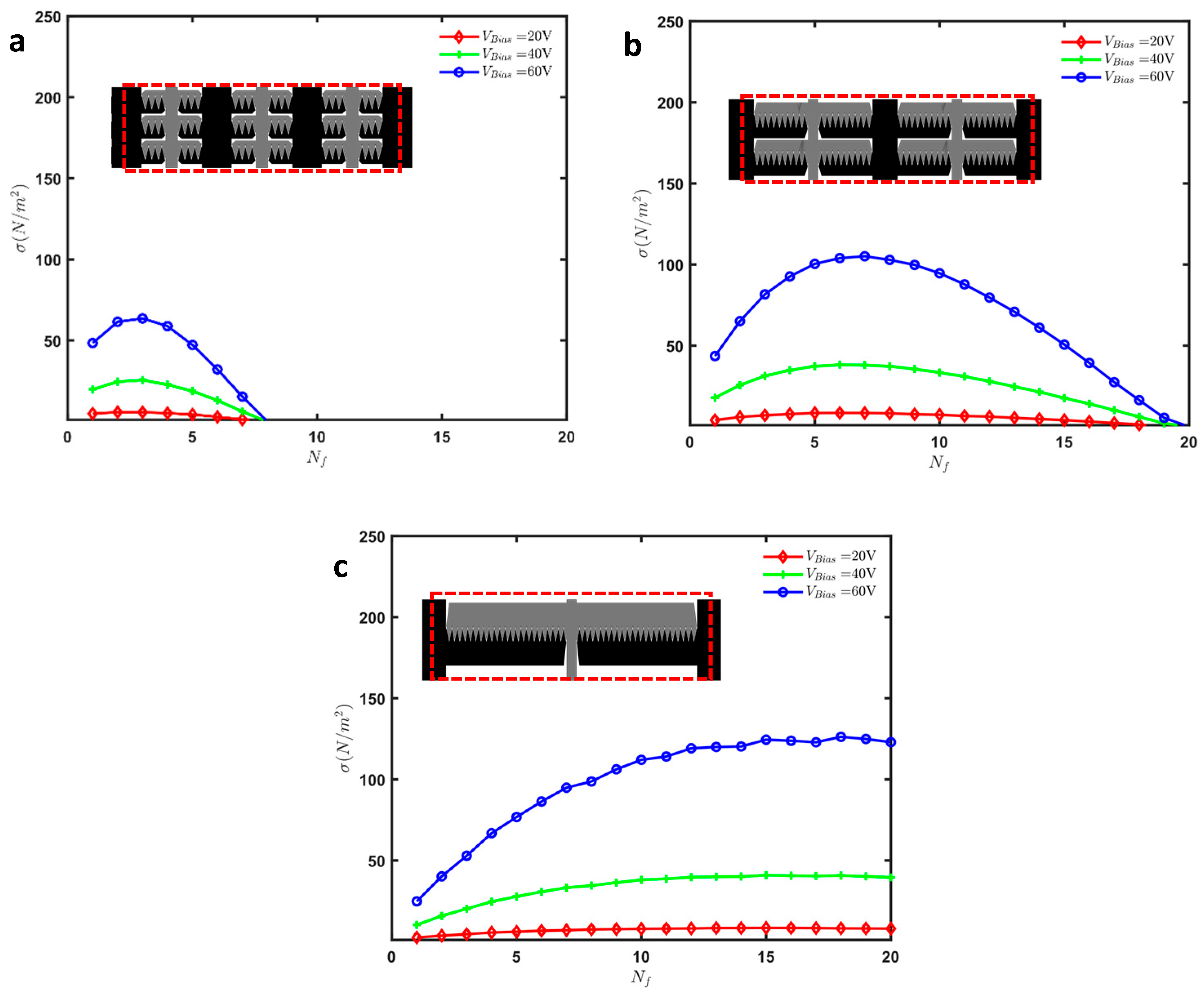

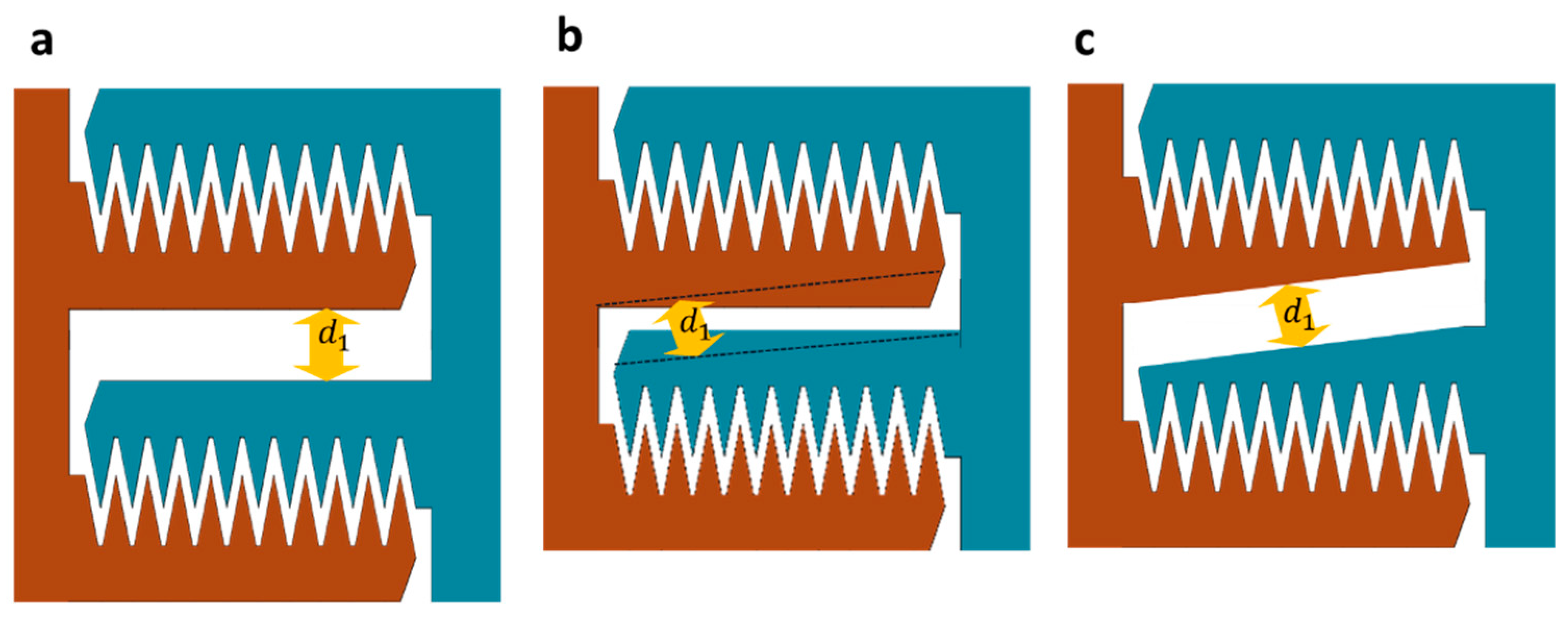
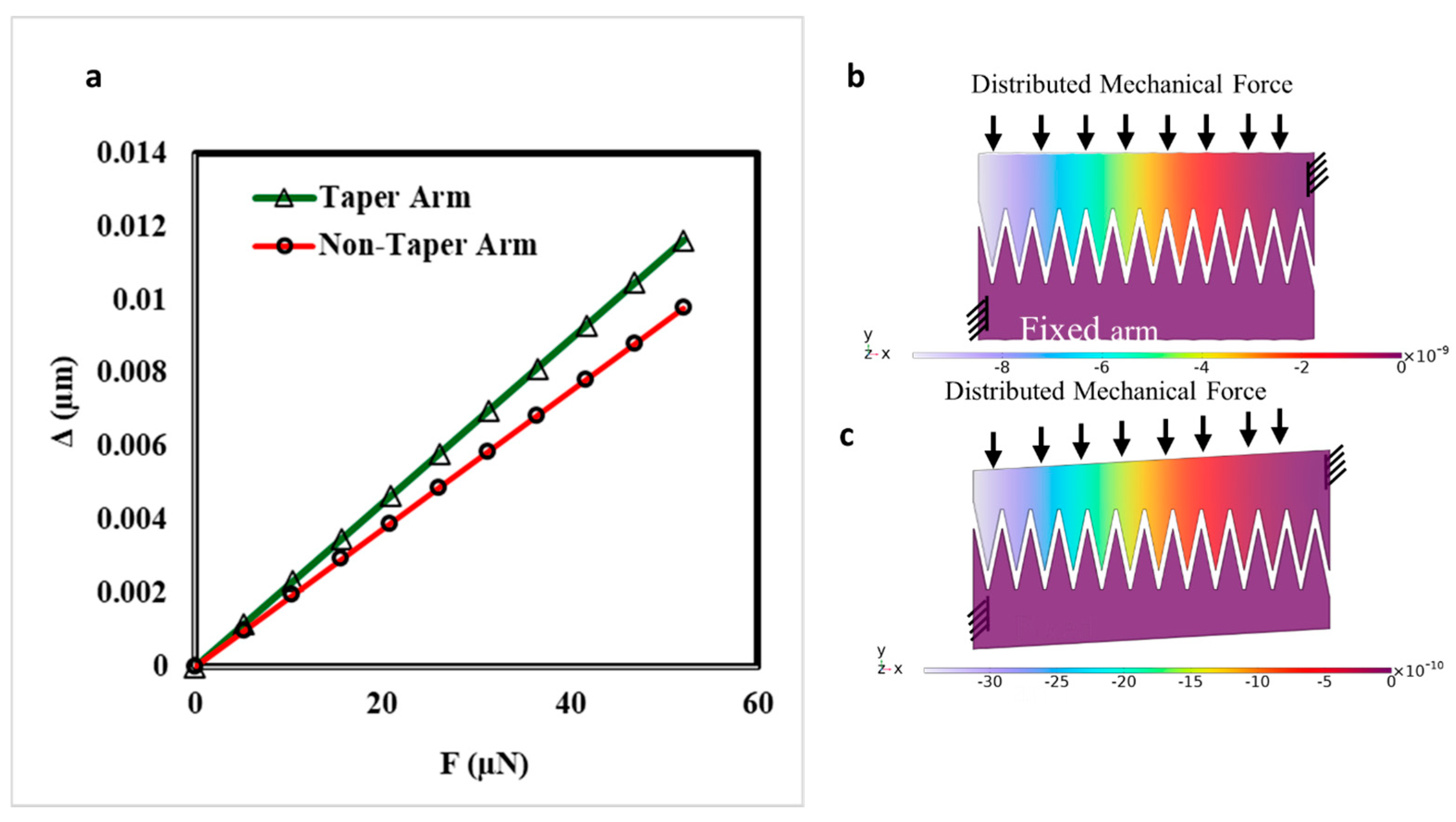
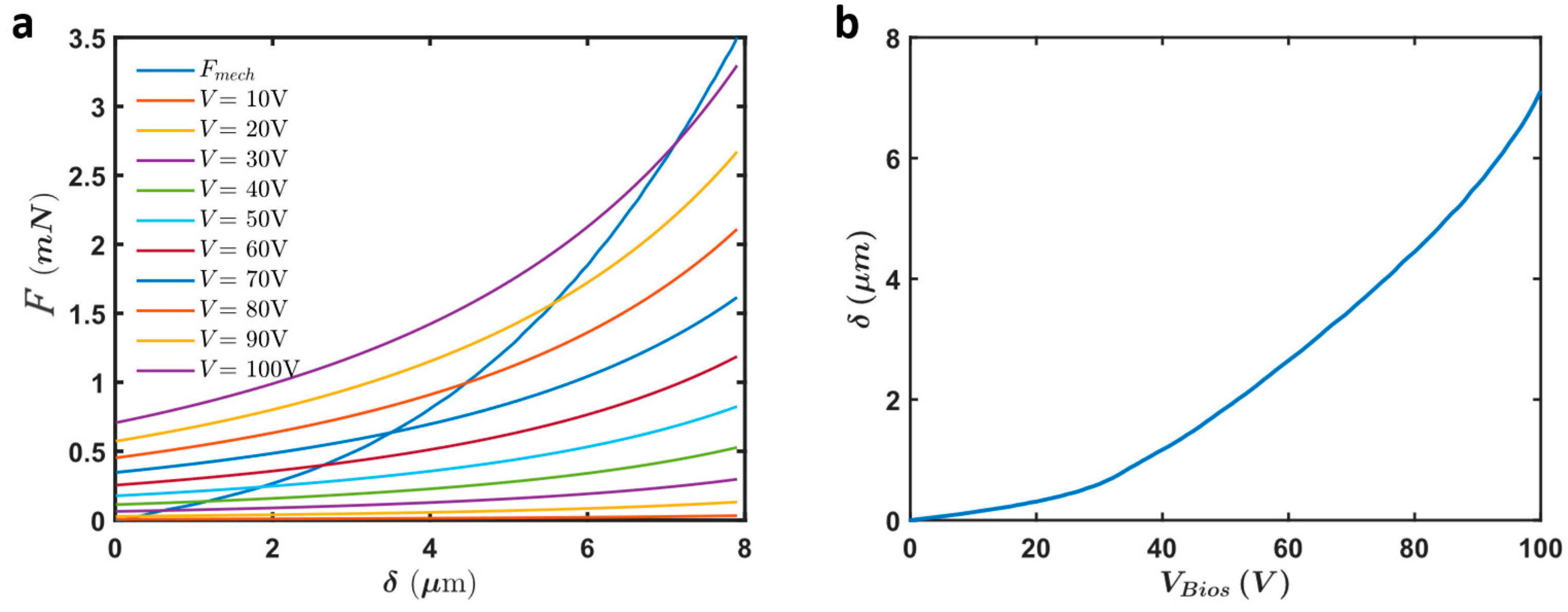
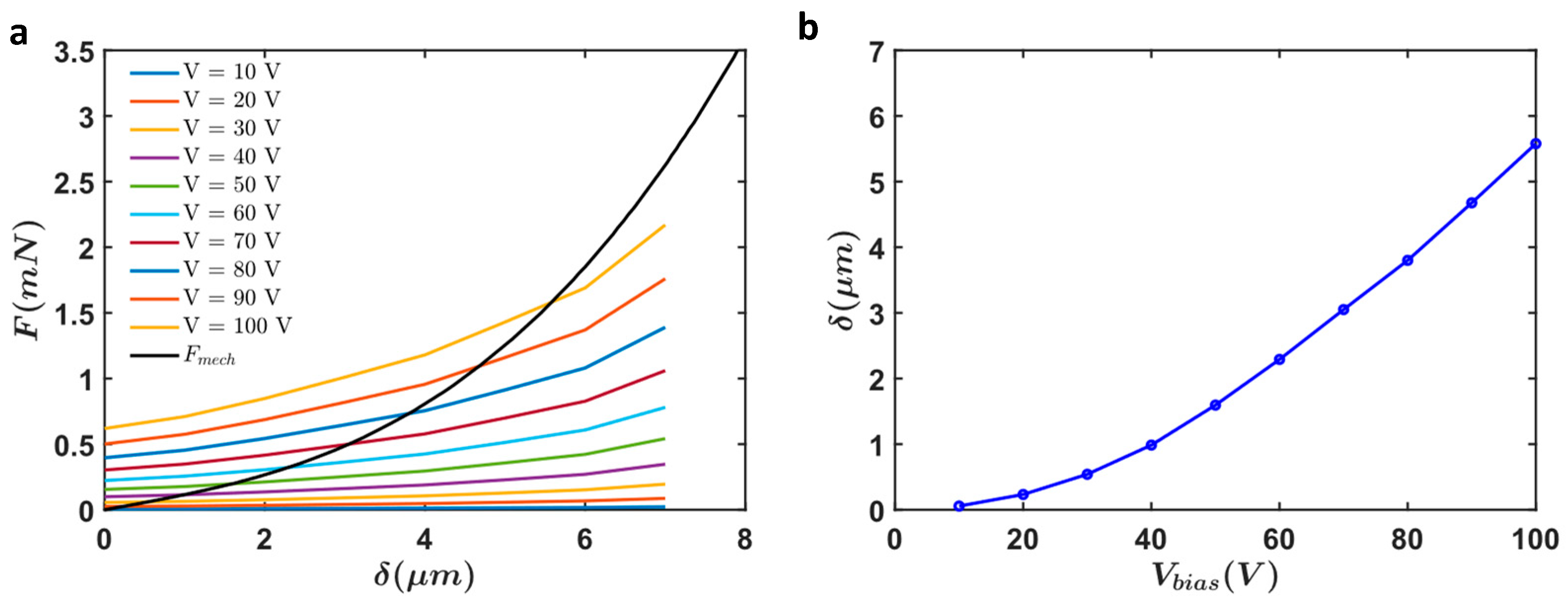

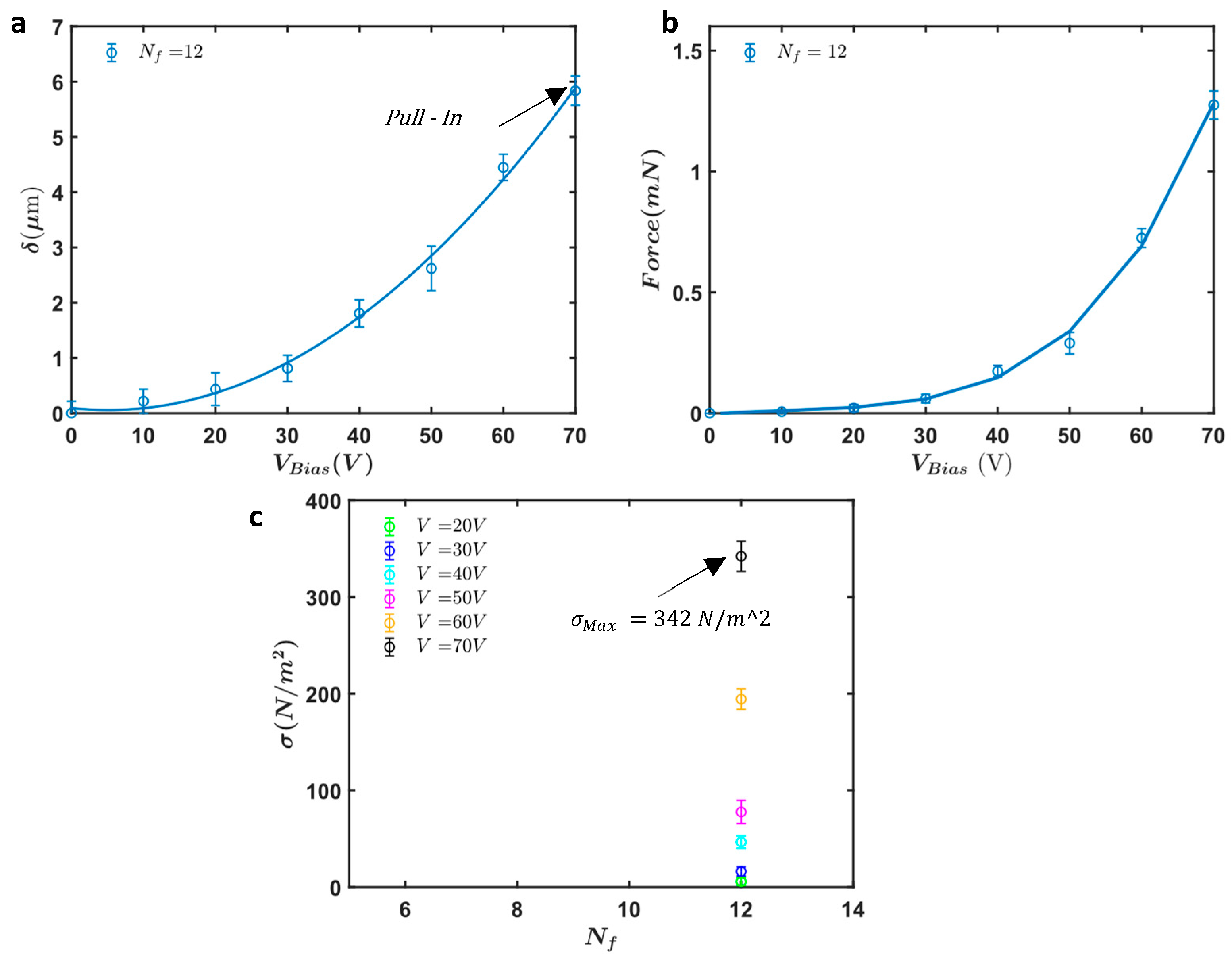
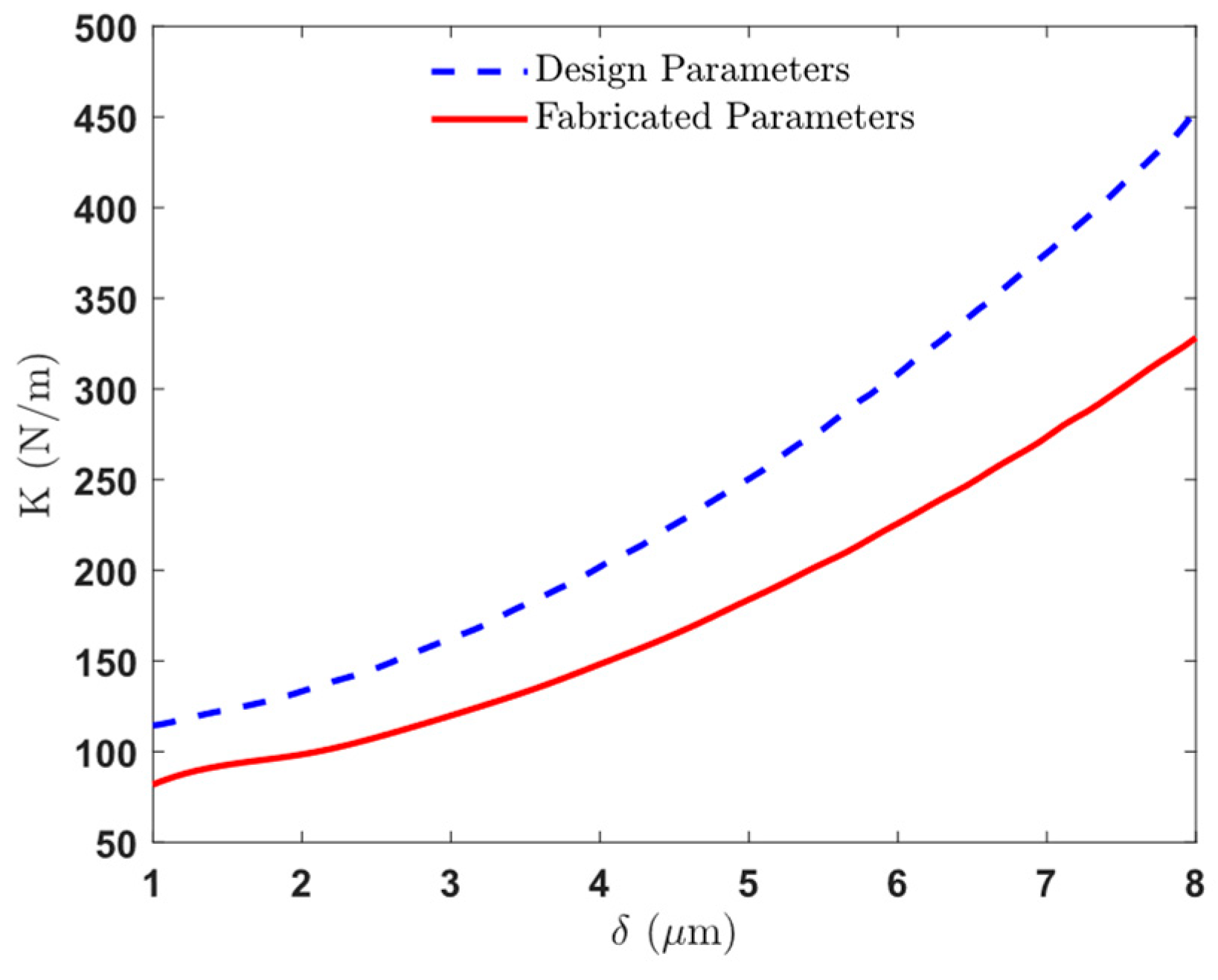
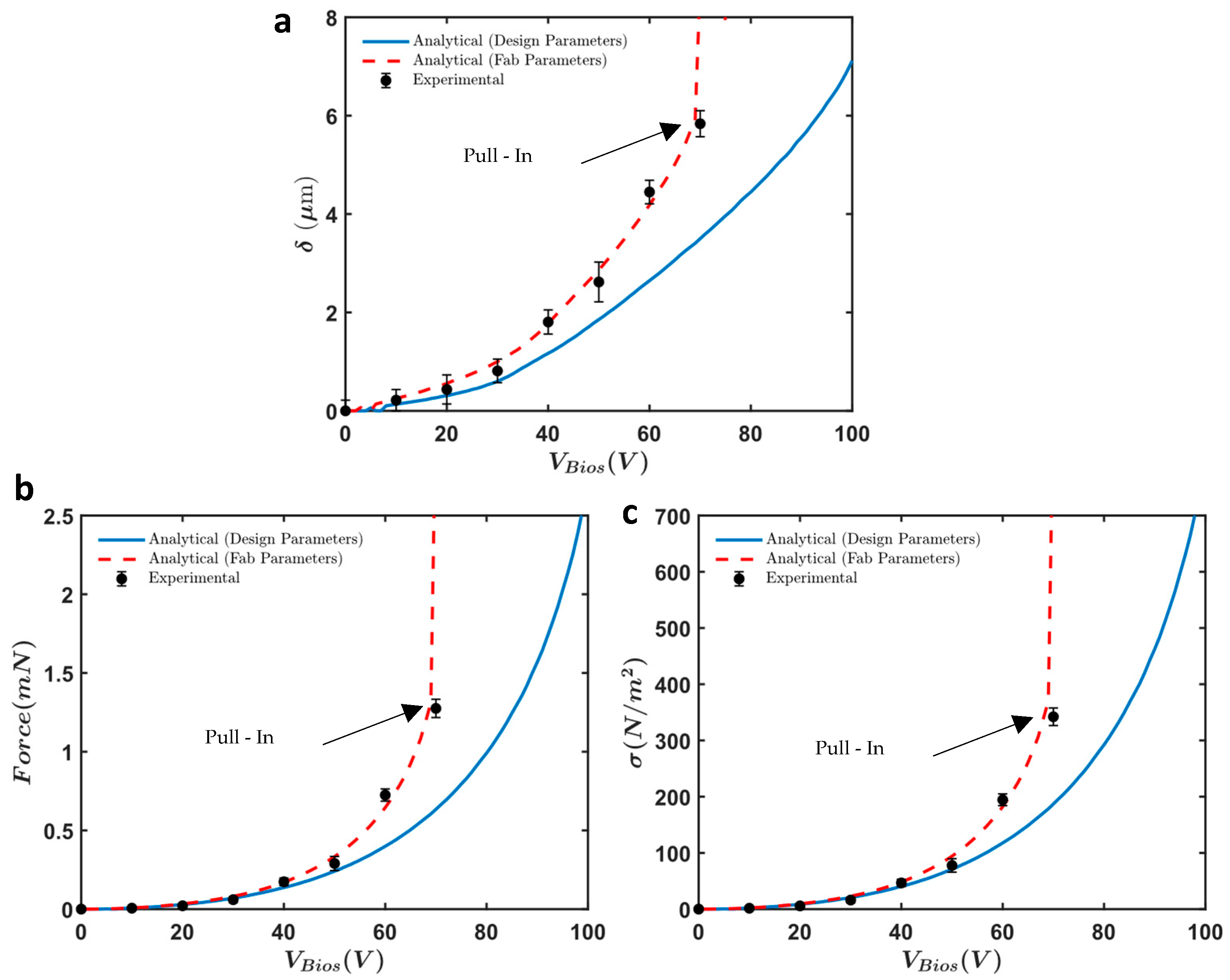
| Symbol | Description | Type | Limitations | Fabrication Value |
|---|---|---|---|---|
| h | Element thickness | FPC | SOI silicon layer thickness | 10 µm |
| c | Finger separation (Dependent) | FPC | 3.51 µm | |
| Connection beam length between arms and mobile or fixed beams | FPC | 5 µm | ||
| Stator length | FPC | Deep trench under etch | 200 µm | |
| Triangular finger half angle | FPC | Losing sharp tips | ||
| Electrode separation along the Y direction | DV | Proportional to the traveling range | 17 µm | |
| Arm Width | DR | Bending and side pull-in | 27–21 µm * | |
| Distance to the next pair of electrodes | DR | Minimize the Electrostatic Force | 17 µm | |
| Moving rail length | DR | Electrode lateral instability | 40 µm | |
| Maximum bending deflection | DR | Electrode lateral instability | 0.05 µm | |
| Finger pitch | OPT | - | ||
| Number of fingers in each arm | OPT | - | ||
| Arm Length | DP | |||
| projected TRI electrode length on Y-axis | DP | |||
| Cell length | DP | |||
| Cell width | DP | |||
| The number of cells in the comb drive | DR | Device maximum allowed footprint | 48 | |
| Description | Value | |
|---|---|---|
| Slab Waveguide | ||
| Rectangular beam width of the slab (left side) | 5 µm | |
| Trapezoid beam width of the slab (right side) | 40 µm | |
| Rectangular beam length | 500 µm | |
| Trapezoid beam length | 500 µm | |
| Beam thickness | 10 µm | |
| Deflection of the beam at middle | 5 µm | |
| Force applied at middle | 3.5 mN | |
| Young’s modulus (silicon <110>) | 169 GPa | |
| Comb Frame Structure | ||
| Width of single beam springs | 2 µm | |
| Width of serpentine springs | 9 µm | |
| length of serpentine springs | 467 µm | |
| Length of single-beam springs | 197 µm | |
| The pitch of the serpentine springs | 19 µm | |
| Stator beam length | 200 | |
| Mobile beam length | ||
| Element thickness | 10 µm |
| Larm [μm] | (Nf, Lf) [1, μm] | σ Range |
|---|---|---|
| 180 | (8,22.5), (9,20), (10,18), (11,16.4), (12,15), (13,13.8) | 181.0–187.7 |
| 190 | (8,23.8), (9,21.1), (10,19), (11,17.3), (12,15.8), (13,14.6), (14,13.6) | 181.4–191.4 |
| 200 | (8,25), (9,22.2), (10,20), (11,18.2), (12,16.7), (13,15.4), (14,14.3), (15,13.3) | 180.8–193.8 |
| 210 | (8,26.3), (9,23.3), (10,21), (11,19.1), (12,17.5), (13,16.2), (14,15), (15,14), (16,13.1) | 180.5–195.6 |
| 220 | (9,24.4), (10,22), (11,20), (12,18.3), (13,16.9), (14,15.7), (15,14.7), (16,13.8), (17,12.9), (18,12.2) | 181.0–197.7 |
| 230 | (9,25.6), (10,23), (11,20.9), (12,19.2), (13,17.7), (14,16.4), (15,15.3), (16,14.4), (17,13.5), (18,12.8) | 186.0–198.8 |
| 240 | (9,26.7), (10,24), (11,21.8), (12,20), (13,18.5), (14,17.1), (15,16), (16,15), (17,14.1), (18,13.3), (19,12.6) | 185.6–199.9 |
| 250 | (9,27.8), (10,25), (11,22.7), (12,20.8), (13,19.2), (14,17.9), (15,16.7), (16,15.6), (17,14.7), (18,13.9), (19,13.2), (20,12.5) | 184.4–201.3 |
| 260 | (9,28.9), (10,26), (11,23.6), (12,21.7), (13,20), (14,18.6), (15,17.3), (16,16.3), (17,15.3), (18,14.4), (19,13.7), (20,13) | 183.2–203.3 |
| 270 | (9,30), (10,27), (11,24.5), (12,22.5), (13,20.8), (14,19.3), (15,18), (16,16.9), (17,15.9), (18,15), (19,14.2), (20,13.5) | 181.3–203.3 |
| 280 | (9,31.1), (10,28), (11,25.5), (12,23.3), (13,21.5), (14,20), (15,18.7), (16,17.5), (17,16.5), (18,15.6), (19,14.7), (20,14) | 180.5–204.8 |
| 290 | (10,29), (11,26.4), (12,24.2), (13,22.3), (14,20.7), (15,19.3), (16,18.1), (17,17.1), (18,16.1), (19,15.3), (20,14.5) | 184.8–204.4 |
| 300 | (10,30), (11,27.3), (12,25), (13,23.1), (14,21.4), (15,20), (16,18.8), (17,17.6), (18,16.7), (19,15.8), (20,15) | 184.0–206.3 |
| 310 | (10,31), (11,28.2), (12,25.8), (13,23.8), (14,22.1), (15,20.7), (16,19.4), (17,18.2), (18,17.2), (19,16.3), (20,15.5) | 182.7–206.6 |
| 320 | (10,32), (11,29.1), (12,26.7), (13,24.6), (14,22.9), (15,21.3), (16,20), (17,18.8), (18,17.8), (19,16.8), (20,16) | 181.3–207.0 |
| 330 | (10,33), (11,30), (12,27.5), (13,25.4), (14,23.6), (15,22), (16,20.6), (17,19.4), (18,18.3), (19,17.4), (20,16.5) | 181.0–207.1 |
| 340 | (11,30.9), (12,28.3), (13,26.2), (14,24.3), (15,22.7), (16,21.3), (17,20), (18,18.9), (19,17.9), (20,17) | 185.0–207.4 |
| 350 | (11,31.8), (12,29.2), (13,26.9), (14,25), (15,23.3), (16,21.9), (17,20.6), (18,19.4), (19,18.4), (20,17.5) | 183.0–207.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fasihanifard, M.; Packirisamy, M. Robust and Compact Electrostatic Comb Drive Arrays for High-Performance Monolithic Silicon Photonics. Micromachines 2025, 16, 1102. https://doi.org/10.3390/mi16101102
Fasihanifard M, Packirisamy M. Robust and Compact Electrostatic Comb Drive Arrays for High-Performance Monolithic Silicon Photonics. Micromachines. 2025; 16(10):1102. https://doi.org/10.3390/mi16101102
Chicago/Turabian StyleFasihanifard, Mohammadreza, and Muthukumaran Packirisamy. 2025. "Robust and Compact Electrostatic Comb Drive Arrays for High-Performance Monolithic Silicon Photonics" Micromachines 16, no. 10: 1102. https://doi.org/10.3390/mi16101102
APA StyleFasihanifard, M., & Packirisamy, M. (2025). Robust and Compact Electrostatic Comb Drive Arrays for High-Performance Monolithic Silicon Photonics. Micromachines, 16(10), 1102. https://doi.org/10.3390/mi16101102







