Continuous Separation of Lithium Iron Phosphate and Graphite Microparticles via Coupled Electric and Magnetic Fields
Abstract
1. Introduction
2. Theory and Numerical Simulations
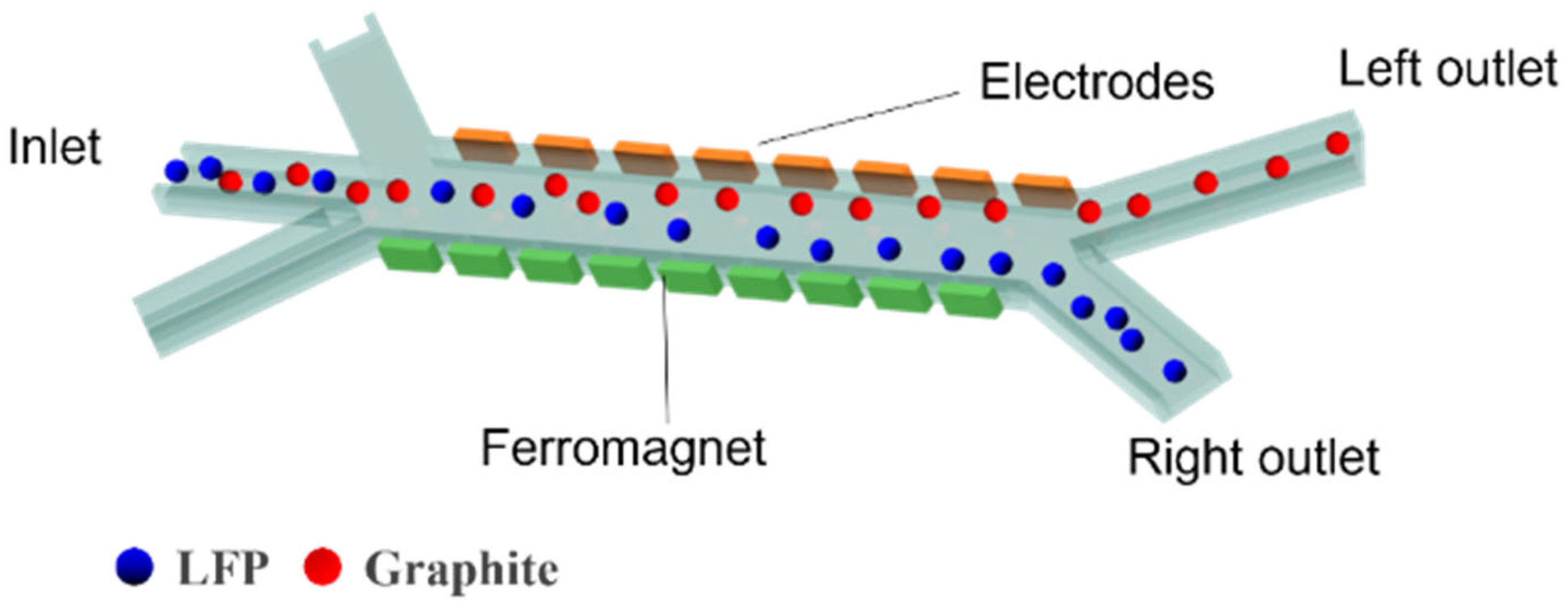
2.1. Separation Mechanism
2.2. Physical and Mathematical Models
2.2.1. Hydrodynamics
2.2.2. Magnetic Field
2.2.3. Electric Field
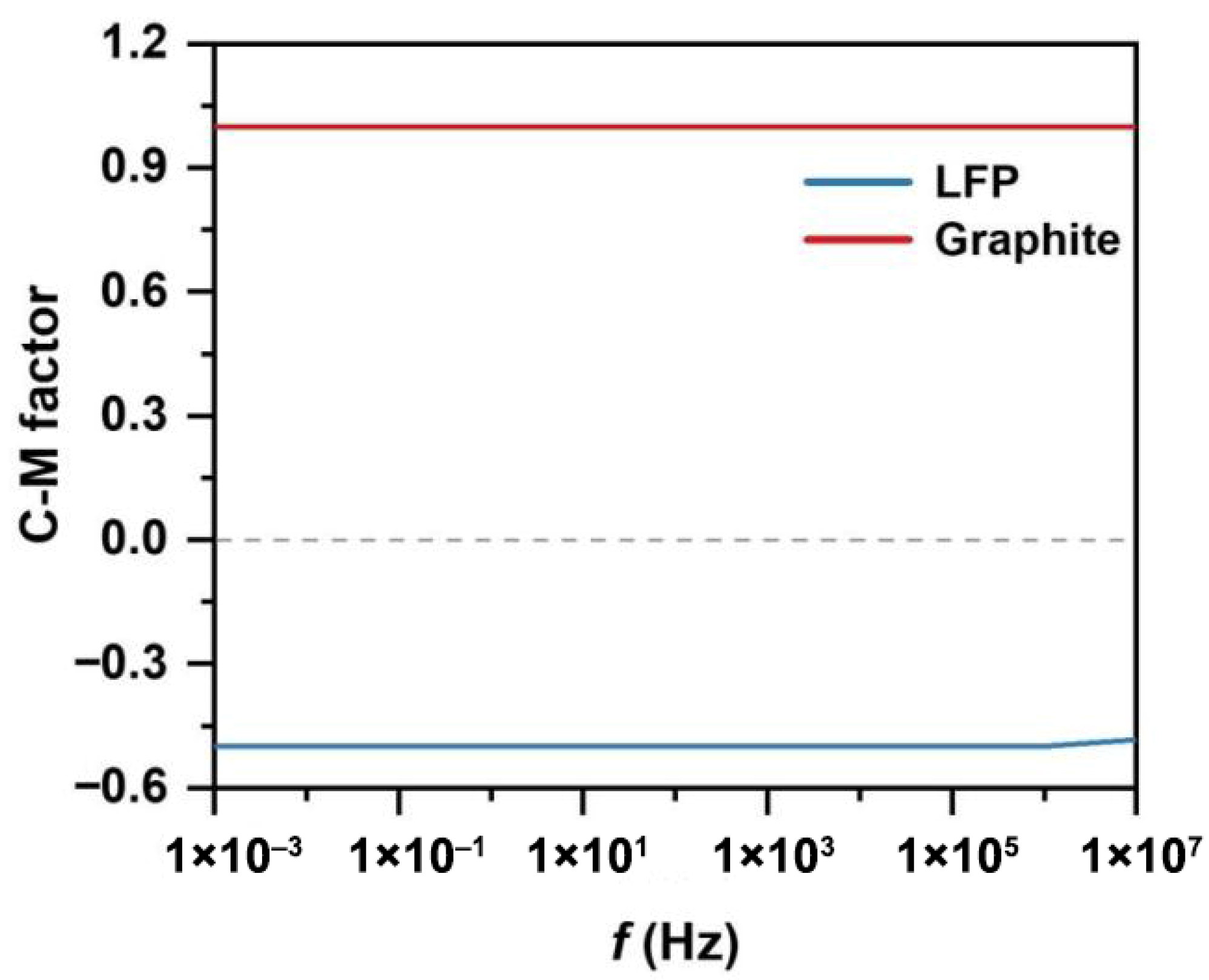
2.2.4. Particle Tracking
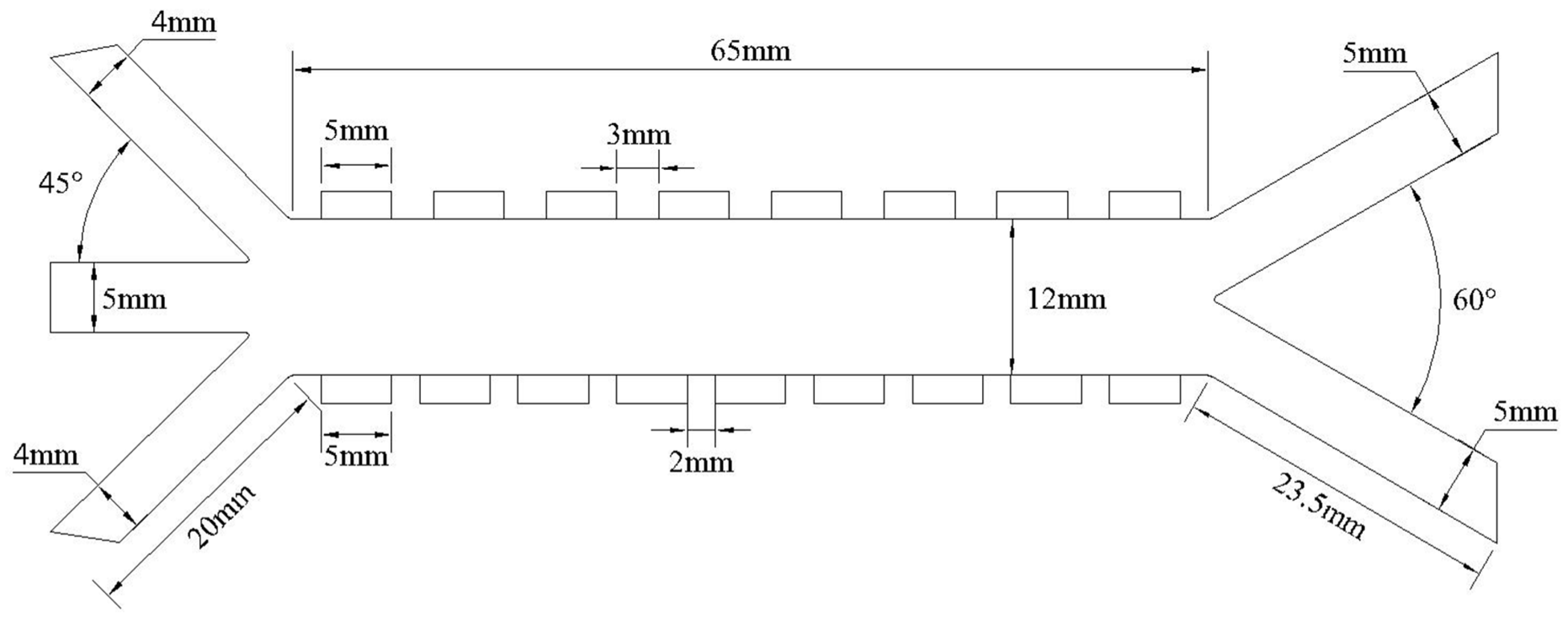
2.3. Computational Domain and Boundary Conditions
2.4. Numerical Simulation
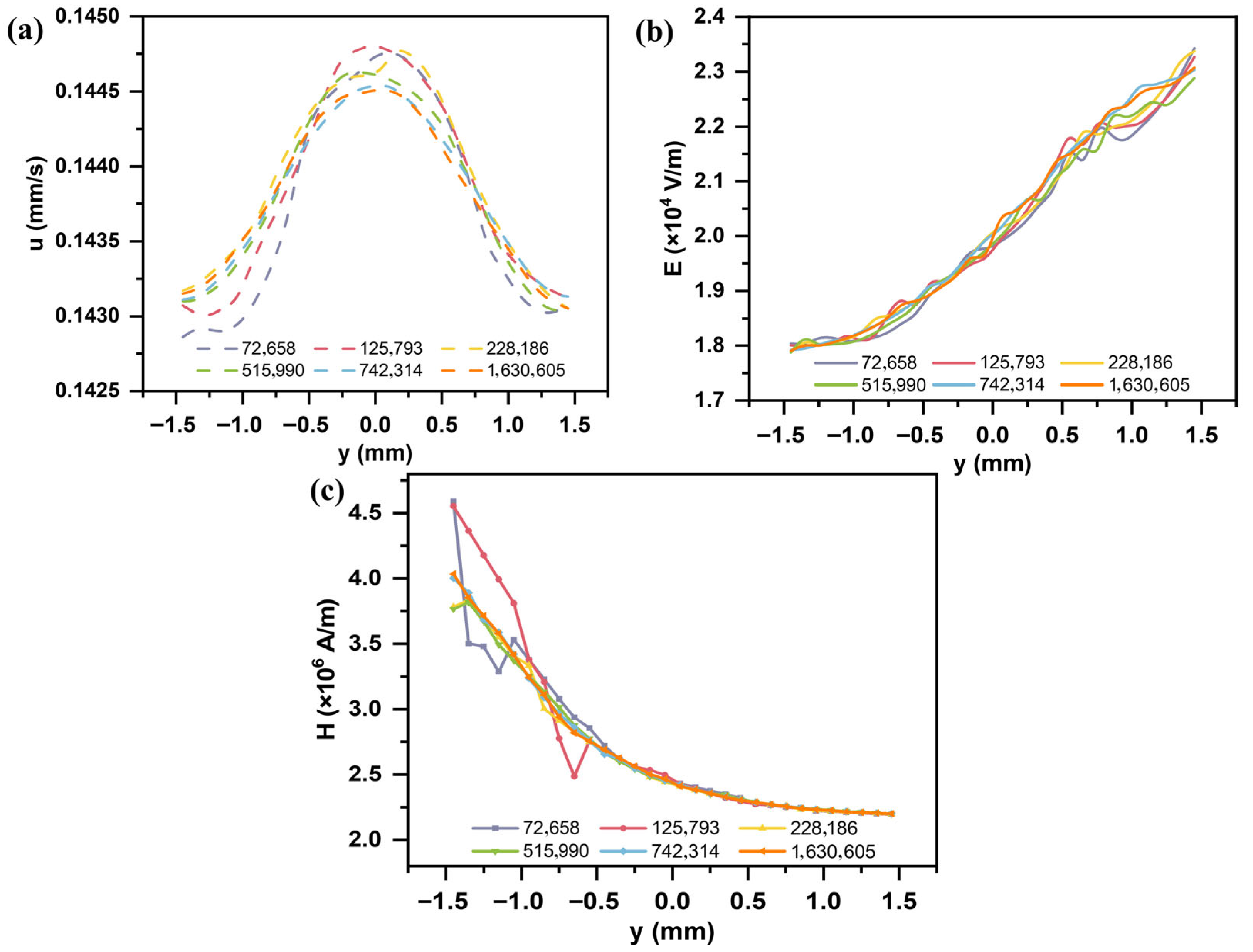
2.5. Grid Independence Verification
3. Results and Discussion
3.1. Influence of Electrode and Magnet Configuration
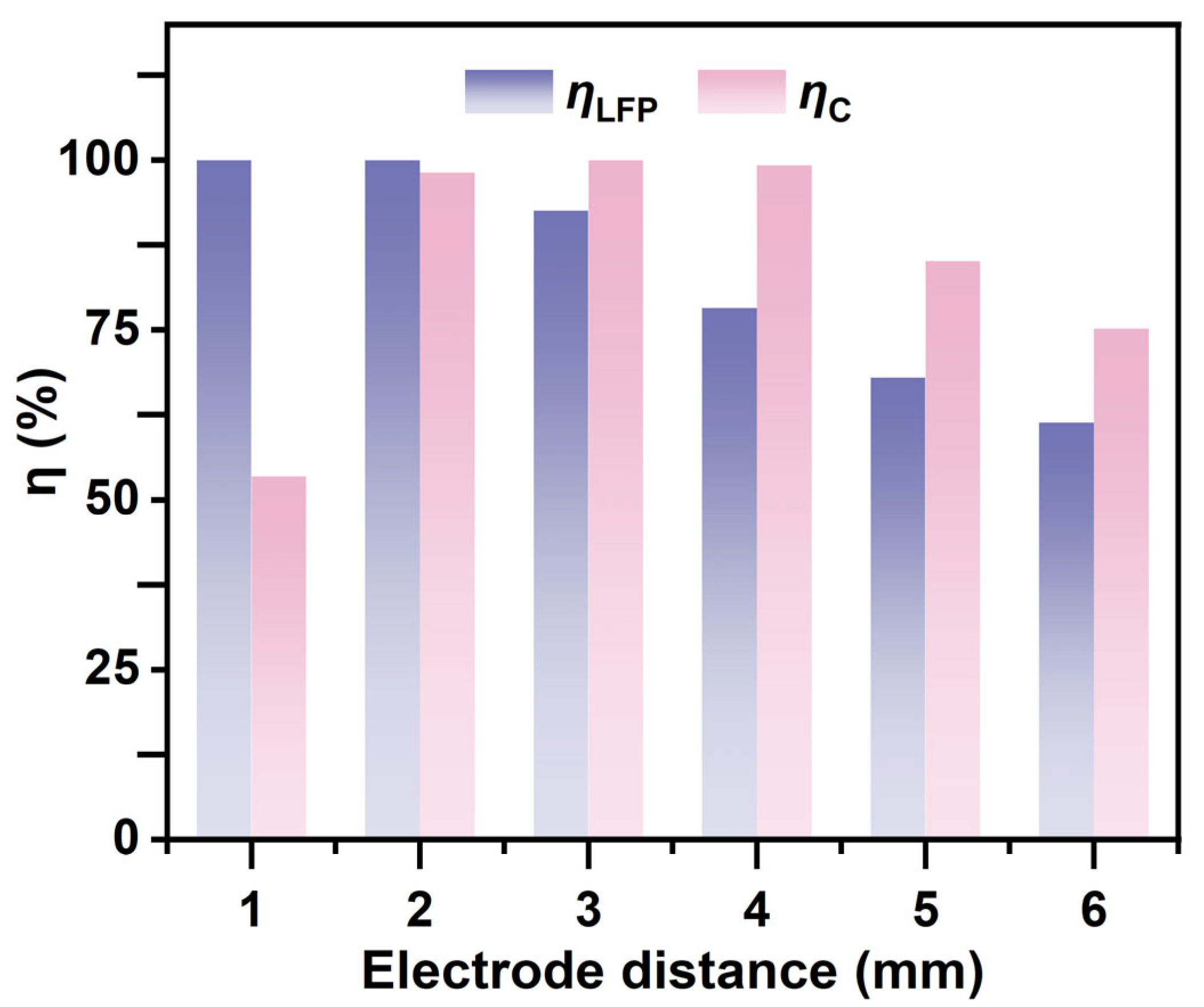
3.1.1. Effect of Electrode Spacing
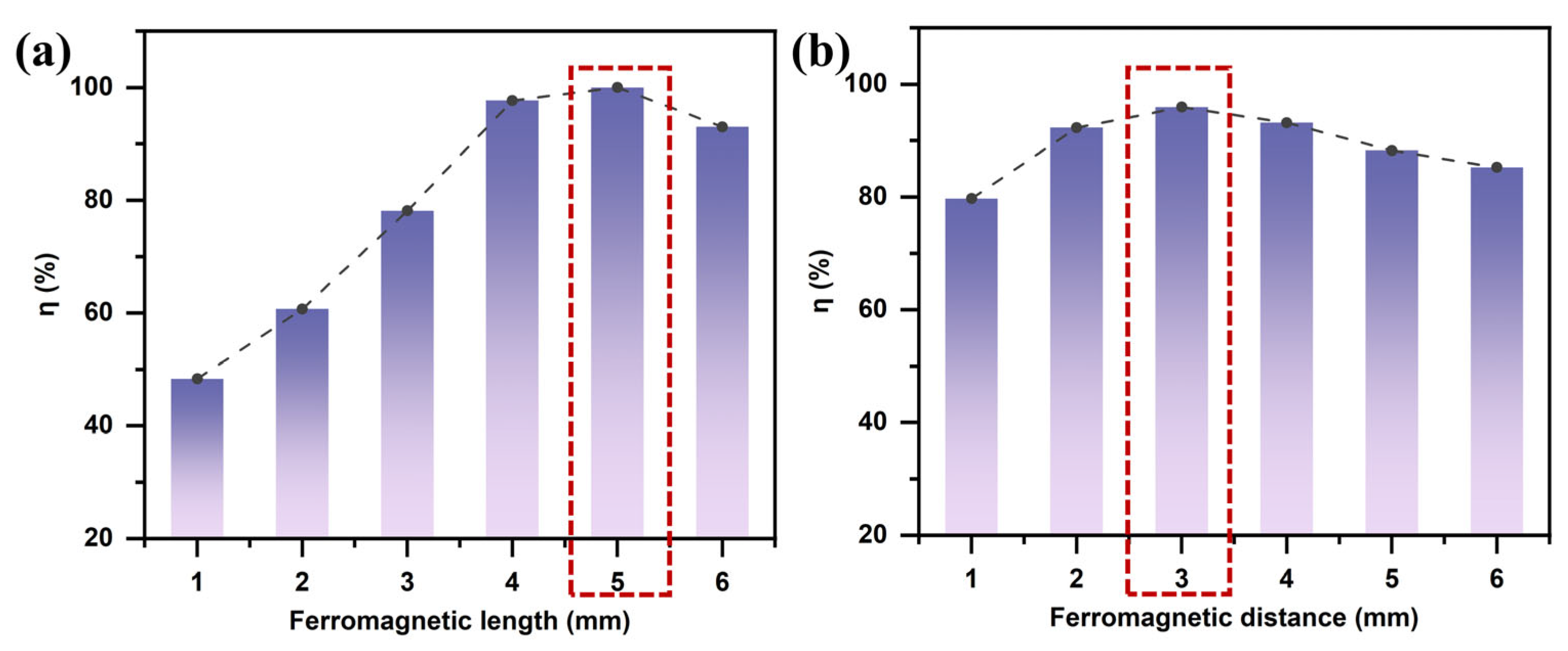
3.1.2. Effect of Ferromagnet Length
3.1.3. Effect of Ferromagnet Spacing
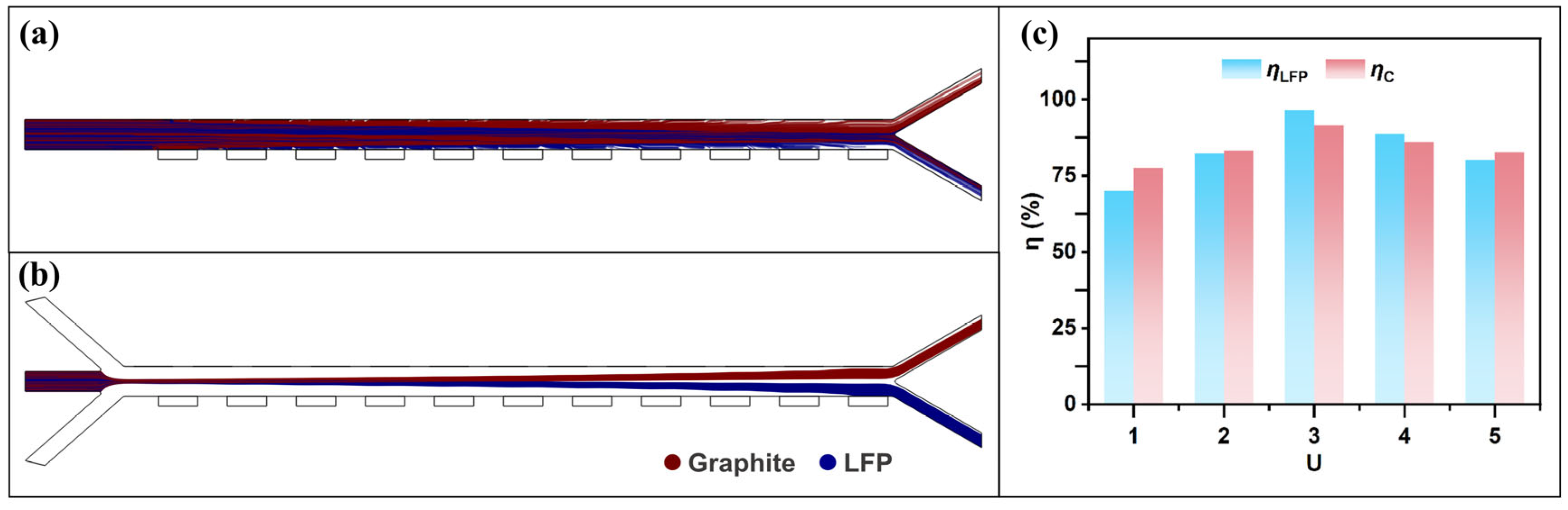
3.2. Sheath-to-Sample Flow Rate Ratio
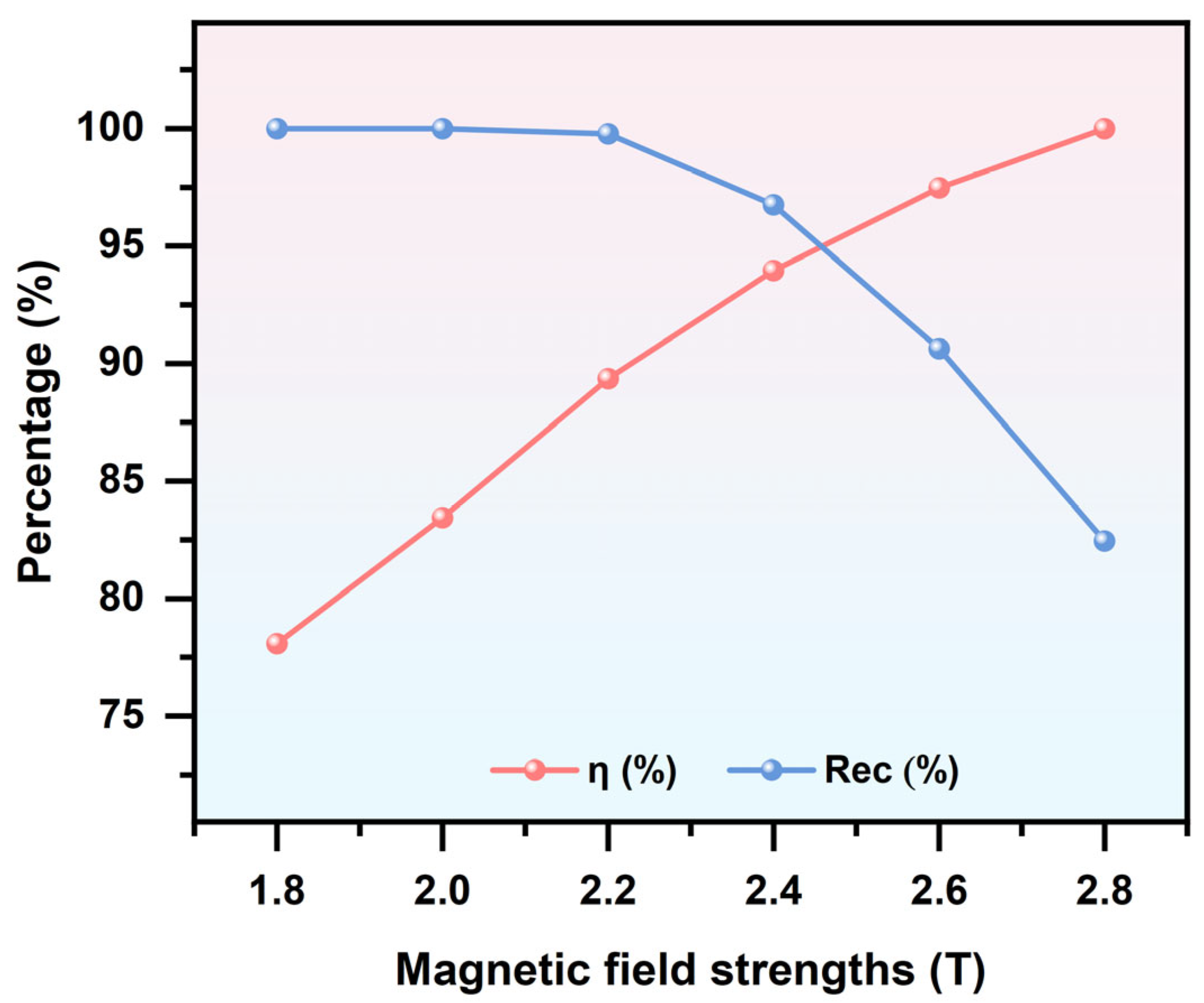
3.3. Effect of Applied Magnetic Field Strength
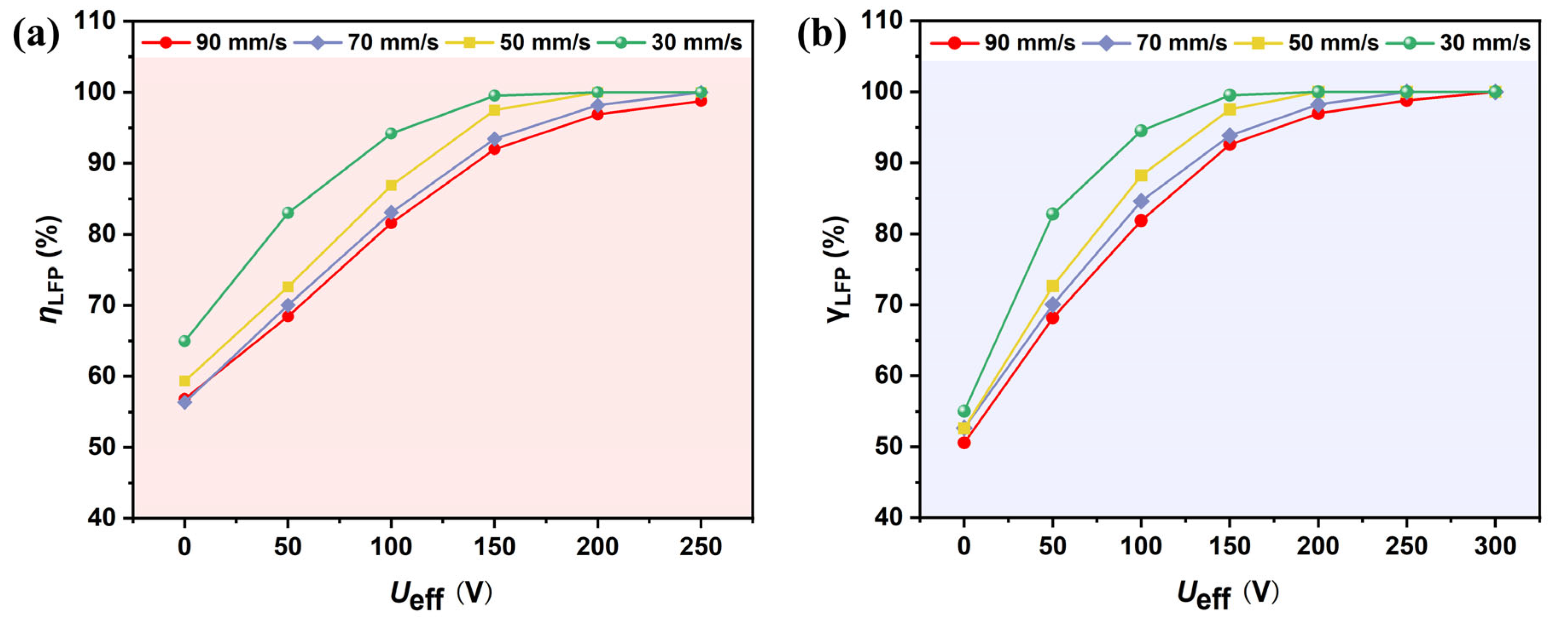
3.4. Relationship Between Voltage and Flow Rate
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eskander, S.M.S.U.; Fankhauser, S. Reduction in greenhouse gas emissions from national climate legislation. Nat. Clim. Change 2020, 10, 750–756. [Google Scholar] [CrossRef]
- Rogelj, J.; Den Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 2016, 534, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Zhang, X.; Fan, E.; Chen, R.; Wu, F.; Li, L. Carbon neutrality strategies for sustainable batteries: From structure, recycling, and properties to applications. Energy Environ. Sci. 2023, 16, 745–791. [Google Scholar] [CrossRef]
- Li, P.; Luo, S.; Lin, Y.; Xiao, J.; Xia, X.; Liu, X.; Wang, L.; He, X. Fundamentals of the recycling of spent lithium-ion batteries. Chem. Soc. Rev. 2024, 53, 11967–12013. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Q.; Zhang, X.; Ge, M.; Zhang, H.; Yin, Y.; Yang, S.-T. High Electrochemical Performance Recycling Spent LiFePO4 Materials through the Preoxidation Regeneration Strategy. ACS Sustain. Chem. Eng. 2023, 11, 14457–14466. [Google Scholar] [CrossRef]
- Yu, H.; Yang, H.; Chen, K.; Yang, L.; Huang, M.; Wang, Z.; Lv, H.; Xu, C.; Chen, L.; Luo, X. Non–closed–loop recycling strategies for spent lithium–ion batteries: Current status and future prospects. Energy Storage Mater. 2024, 67, 103288. [Google Scholar] [CrossRef]
- Liu, K.; Wang, M.; Zhang, Q.; Xu, Z.; Labianca, C.; Komarek, M.; Gao, B.; Tsang, D.C.W. A perspective on the recovery mechanisms of spent lithium iron phosphate cathode materials in different oxidation environments. J. Hazard. Mater. 2023, 445, 130502. [Google Scholar] [CrossRef]
- Huang, Z.; Qiu, R.; Lin, K.; Ruan, J.; Xu, Z. In Situ Recombination of Elements in Spent Lithium-Ion Batteries to Recover High-Value gamma-LiAlO2 and LiAl5O8. Environ. Sci. Technol. 2021, 55, 7643–7653. [Google Scholar] [CrossRef]
- Wang, J.; Ma, J.; Zhuang, Z.; Liang, Z.; Jia, K.; Ji, G.; Zhou, G.; Cheng, H.M. Toward Direct Regeneration of Spent Lithium-Ion Batteries: A Next-Generation Recycling Method. Chem. Rev. 2024, 124, 2839–2887. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Zhang, H.; Wang, Y.; Chen, Y.; Wang, C. Simultaneous anodic de-lithiation/cathodic lithium-embedded regeneration method for recycling of spent LiFePO4 battery. Energy Storage Mater. 2024, 65, 103081. [Google Scholar] [CrossRef]
- Chen, B.; Liu, M.; Cao, S.; Chen, G.; Guo, X.; Wang, X. Regeneration and performance of LiFePO4 with Li2CO3 and FePO4 as raw materials recovered from spent LiFePO4 batteries. Mater. Chem. Phys. 2022, 279, 125750. [Google Scholar] [CrossRef]
- Fan, E.; Li, L.; Wang, Z.; Lin, J.; Huang, Y.; Yao, Y.; Chen, R.; Wu, F. Sustainable Recycling Technology for Li-Ion Batteries and Beyond: Challenges and Future Prospects. Chem. Rev. 2020, 120, 7020–7063. [Google Scholar] [CrossRef]
- Sederholm, J.G.; Li, L.; Liu, Z.; Lan, K.W.; Cho, E.J.; Gurumukhi, Y.; Dipto, M.J.; Ahmari, A.; Yu, J.; Haynes, M.; et al. Emerging Trends and Future Opportunities for Battery Recycling. ACS Energy Lett. 2025, 10, 107–119. [Google Scholar] [CrossRef]
- Zhang, B.; Qu, X.; Chen, X.; Liu, D.; Zhao, Z.; Xie, H.; Wang, D.; Yin, H. A sodium salt-assisted roasting approach followed by leaching for recovering spent LiFePO4 batteries. J. Hazard. Mater. 2022, 424, 127586. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhang, F.-S.; Zhang, Z.-Y.; Zhang, C.-C. An environmentally friendly process for selective recovery of lithium and simultaneous synthesis of LiFe5O8 from spent LiFePO4 battery by mechanochemical. J. Clean. Prod. 2023, 396, 136504. [Google Scholar] [CrossRef]
- Ren, J.; Zhu, H.; Fang, Y.; Li, W.; Lan, S.; Wei, S.; Yin, Z.; Tang, Y.; Ren, Y.; Liu, Q. Typical cathode materials for lithium-ion and sodium-ion batteries: From structural design to performance optimization. Carbon Neutralization 2023, 2, 339–377. [Google Scholar] [CrossRef]
- Qiu, X.; Wang, C.; Xie, L.; Zhu, L.; Cao, X.; Ji, X. Challenges and perspectives towards direct regeneration of spent LiFePO4 cathode. J. Power Sources 2024, 602, 234365. [Google Scholar] [CrossRef]
- Xu, F.; He, H.; Liu, Y.; Dun, C.; Ren, Y.; Liu, Q.; Wang, M.-X.; Xie, J. Failure investigation of LiFePO4 cells under overcharge conditions. J. Electrochem. Soc. 2012, 159, A678. [Google Scholar] [CrossRef]
- Naseri, T.; Mousavi, S.M. Treatment of spent lithium iron phosphate (LFP) batteries. Curr. Opin. Green Sustain. Chem. 2024, 47, 100906. [Google Scholar] [CrossRef]
- Mahandra, H.; Ghahreman, A. A sustainable process for selective recovery of lithium as lithium phosphate from spent LiFePO4 batteries. Resour. Conserv. Recycl. 2021, 175, 105883. [Google Scholar] [CrossRef]
- Jung, J.C.-Y.; Sui, P.-C.; Zhang, J. A review of recycling spent lithium-ion battery cathode materials using hydrometallurgical treatments. J. Energy Storage 2021, 35, 102217. [Google Scholar] [CrossRef]
- Ding, Y.; Fu, J.; Zhang, S.; He, X.; Zhao, B.; Ren, J.; Zhong, J.; Liu, Z. Advances in recycling LiFePO4 from spent lithium batteries: A critical review. Sep. Purif. Technol. 2024, 338, 126551. [Google Scholar] [CrossRef]
- Dang, H.; Li, N.; Chang, Z.; Wang, B.; Zhan, Y.; Wu, X.; Liu, W.; Ali, S.; Li, H.; Guo, J.; et al. Lithium leaching via calcium chloride roasting from simulated pyrometallurgical slag of spent lithium ion battery. Sep. Purif. Technol. 2020, 233, 116025. [Google Scholar] [CrossRef]
- Li, N.; Guo, J.; Chang, Z.; Dang, H.; Zhao, X.; Ali, S.; Li, W.; Zhou, H.; Sun, C. Aqueous leaching of lithium from simulated pyrometallurgical slag by sodium sulfate roasting. RSC Adv. 2019, 9, 23908–23915. [Google Scholar] [CrossRef]
- Yang, X.; Wan, Z.; Lin, S.; Zhou, L. Recycling Strategy for Spent Lithium-Ion Batteries as an Ultra-efficiency Peroxymonosulfate Activator. Ind. Eng. Chem. Res. 2023, 62, 9104–9113. [Google Scholar] [CrossRef]
- Fan, E.; Yang, J.; Huang, Y.; Lin, J.; Arshad, F.; Wu, F.; Li, L.; Chen, R. Leaching Mechanisms of Recycling Valuable Metals from Spent Lithium-Ion Batteries by a Malonic Acid-Based Leaching System. ACS Appl. Energy Mater. 2020, 3, 8532–8542. [Google Scholar] [CrossRef]
- Al-Ali, A.; Waheed, W.; Abu-Nada, E.; Alazzam, A. A review of active and passive hybrid systems based on Dielectrophoresis for the manipulation of microparticles. J. Chromatogr. A 2022, 1676, 463268. [Google Scholar] [CrossRef]
- Viefhues, M.; Eichhorn, R. DNA dielectrophoresis: Theory and applications a review. Electrophoresis 2017, 38, 1483–1506. [Google Scholar] [CrossRef]
- Doh, I.; Cho, Y.-H. A continuous cell separation chip using hydrodynamic dielectrophoresis (DEP) process. Sens. Actuators A Phys. 2005, 121, 59–65. [Google Scholar] [CrossRef]
- Chen, D.F.; Du, H.; Li, W.H. Bioparticle separation and manipulation using dielectrophoresis. Sens. Actuators A Phys. 2007, 133, 329–334. [Google Scholar] [CrossRef]
- Neculae, A.; Biris, C.G.; Bunoiu, M.; Lungu, M. Numerical analysis of nanoparticle behavior in a microfluidic channel under dielectrophoresis. J. Nanoparticle Res. 2012, 14, 1154. [Google Scholar] [CrossRef]
- Yang, Y.; Biswas, S.; Xu, R.; Xiao, X.; Xu, X.; Zhang, P.; Gong, H.; Zheng, X.; Peng, Y.; Li, J.; et al. Capacity recovery by transient voltage pulse in silicon-anode batteries. Science 2024, 386, 322–327. [Google Scholar] [CrossRef]
- Munaz, A.; Shiddiky, M.J.; Nguyen, N.-T. Recent advances and current challenges in magnetophoresis based micro magnetofluidics. Biomicrofluidics 2018, 12, 031501. [Google Scholar] [CrossRef]
- Huang, S.; He, Y.-Q.; Jiao, F. Advances of Particles/Cells Magnetic Manipulation in Microfluidic Chips. Chin. J. Anal. Chem. 2017, 45, 1238–1246. [Google Scholar] [CrossRef]
- Wittmann, L.; Krucker-Velasquez, E.; Schaupp, J.; Westphal, L.; Swan, J.W.; Alexander-Katz, A.; Bazant, M.Z.; Schwaminger, S.P.; Berensmeier, S. Influence of magnetic convection on separation efficiency in magnetophoretic microfluidic processes: A combined simulation and experimental study. Nanoscale 2025, 17, 1574–1584. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Liu, J.; Gan, T.; Lu, D.; Wang, Y.; Zheng, X. High-intensity magnetic separation for recovery of LiFePO4 and graphite from spent lithium-ion batteries. Sep. Purif. Technol. 2022, 297, 121486. [Google Scholar] [CrossRef]
- Kepper, M.; Rother, A.; Thöming, J.; Pesch, G.R. Polarisability-dependent separation of lithium iron phosphate (LFP) and graphite in dielectrophoretic filtration. Results Eng. 2024, 21, 101854. [Google Scholar] [CrossRef]
- Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. AC Electrokinetics: A Review of Forces in Microelectrode Structures. J. Phys. D Appl. Phys. 1998, 31, 2338–2353. [Google Scholar] [CrossRef]
- Kua, C.H.; Lam, Y.C.; Rodriguez, I.; Yang, C.; Youcef-Toumi, K. Cell motion model for moving dielectrophoresis. Anal. Chem. 2008, 80, 5454–5461. [Google Scholar] [CrossRef]
- Giesler, J.; Weirauch, L.; Rother, A.; Thoming, J.; Pesch, G.R.; Baune, M. Sorting Lithium-Ion Battery Electrode Materials Using Dielectrophoresis. ACS Omega 2023, 8, 26635–26643. [Google Scholar] [CrossRef]
- Pesch, G.R.; Du, F. A review of dielectrophoretic separation and classification of non-biological particles. Electrophoresis 2021, 42, 134–152. [Google Scholar] [CrossRef]
- Lin, R.Z.; Ho, C.T.; Liu, C.H.; Chang, H.Y. Dielectrophoresis based-cell patterning for tissue engineering. Biotechnol. J. 2006, 1, 949–957. [Google Scholar] [CrossRef]
- Furlani, E.P. Analysis of Particle Transport in a Magnetophoretic Microsystem. J. Appl. Phys. 2006, 99, 024912. [Google Scholar] [CrossRef]
- Huang, K.-R.; Chang, J.-S.; Chao, S.D.; Wung, T.-S.; Wu, K.-C. Study of Active Micromixer Driven by Electrothermal Force. Jpn. J. Appl. Phys. 2012, 51, 047002. [Google Scholar] [CrossRef]
- Hatton, F.C.K.A.S.T.A. A dynamic buildup growth model for magnetic particle accumulation on single wires in high-gradient magnetic separation. Aiche J. 2012, 58, 2865–2874. [Google Scholar]
- Li, Y.; Wang, Y.; Pesch, G.R.; Baune, M.; Du, F.; Liu, X. Rational Design and Numerical Analysis of a Hybrid Floating cIDE Separator for Continuous Dielectrophoretic Separation of Microparticles at High Throughput. Micromachines 2022, 13, 582. [Google Scholar] [CrossRef] [PubMed]
- Xue, Z.; Wang, Y.; Zheng, X.; Lu, D.; Sun, Z.; Jing, Z. Mechanical entrainment study by separately collecting particle deposit on matrix in high gradient magnetic separation. Miner. Eng. 2022, 178, 107435. [Google Scholar] [CrossRef]
- Zhao, K.; Zhao, P.; Dong, J.; Wei, Y.; Chen, B.; Wang, Y.; Pan, X.; Wang, J. Implementation of an Integrated Dielectrophoretic and Magnetophoretic Microfluidic Chip for CTC Isolation. Biosensors 2022, 12, 757. [Google Scholar] [CrossRef] [PubMed]
- Rosaiah, P.; Jeevan Kumar, P.; Jayanth Babu, K.; Hussain, O.M. Electrical and electrochemical properties of nanocrystalline LiFePO4 cathode. Appl. Phys. A 2013, 113, 603–611. [Google Scholar] [CrossRef]
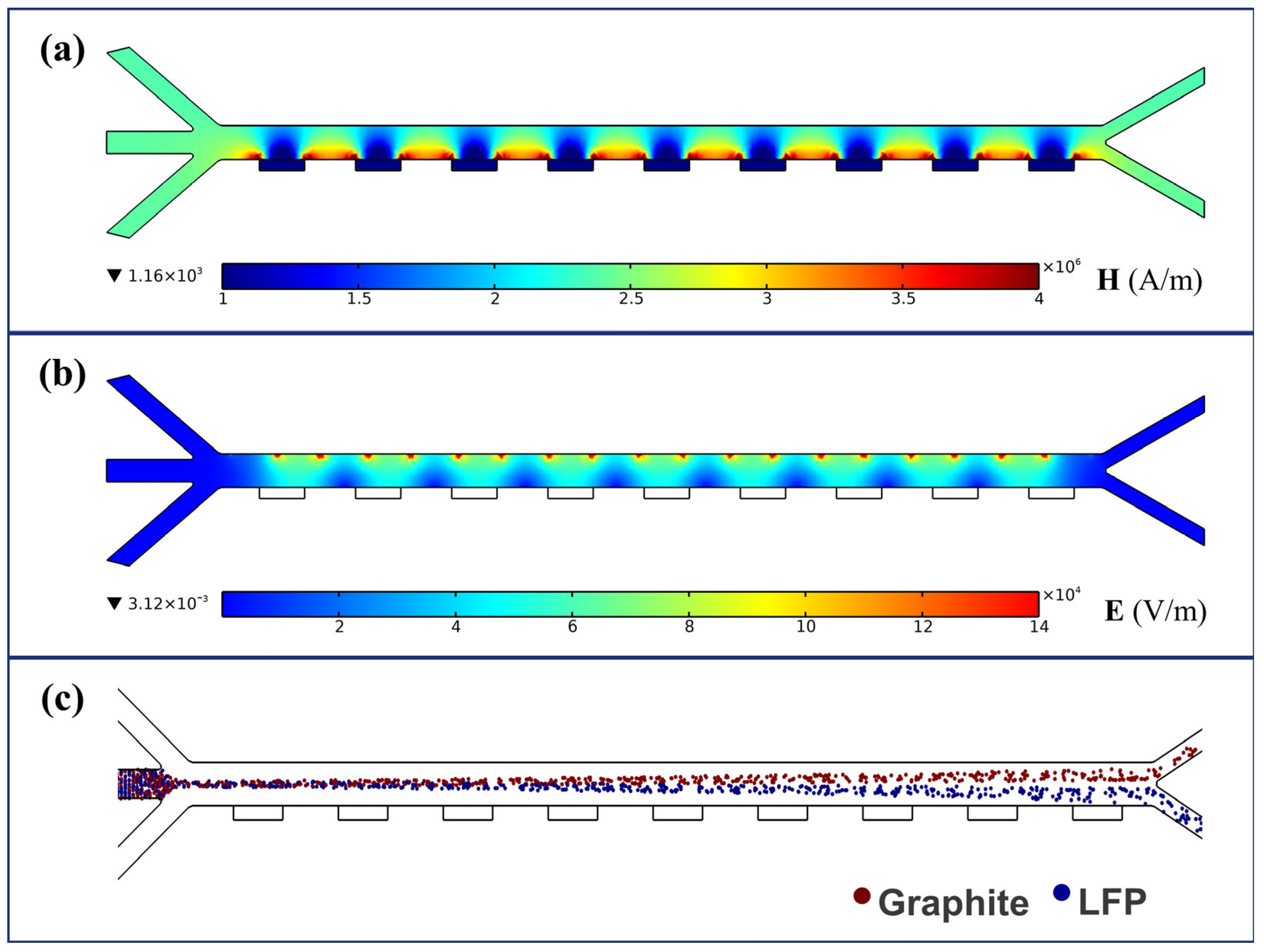
| Computation Domain/Boundary Conditions (Scope of Application) | Governing Conditions/Equations | |
|---|---|---|
| Laminar flow module | Entrance (Top to bottom) | , , |
| Export (Top to bottom) | ||
| Slip (walls, electrodes) | ||
| Current module | Conservation of current | |
| Electrical insulation (walls) | ||
| Initial values (domain 1) | ||
| Potential 1 (electrodes 1 and 2) | ||
| Potential 2 (electrodes 3 and 4) | − | |
| Magnetic module | Conservation of Magnetic | |
| Initial values (domain 1) | ||
| Particle tracking | Bounce (walls, electrodes) | |
| Entrance (entrance 2) | ||
| Freeze (exports 1, 2, and 3) |
| Parameters | Values |
|---|---|
| Dielectric constant of buffer liquid phase, | 80 |
| Permittivity of vacuum, | 8.85 × 10−12 |
| Vacuum permeability, | 4π × 10−7 |
| Density of buffer, | 1000 |
| Dynamic viscosity of buffer, | 1 × 10−3 |
| Electrical conductivity of buffer | 5.5 × 10−6 |
| Magnetic susceptibility of buffer, | −9.05 × 10−9 |
| Microchannel height | 6 |
| Relative Permittivity | Diameter (μm) | Density | Magnetic Susceptibility | ||
|---|---|---|---|---|---|
| LFP | 10 | 1.67 × 10−8 | 75 | 1523 | 7.41 × 10−7 |
| graphite | 12.35 | 2 × 105 | 75 | 2250 | −8.4 × 10−8 |
| water | 80 | 5.5 × 10−6 | - | 1000 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Chen, X.; Qi, P.; Liu, X.; Wang, Y. Continuous Separation of Lithium Iron Phosphate and Graphite Microparticles via Coupled Electric and Magnetic Fields. Micromachines 2025, 16, 1094. https://doi.org/10.3390/mi16101094
Liu W, Chen X, Qi P, Liu X, Wang Y. Continuous Separation of Lithium Iron Phosphate and Graphite Microparticles via Coupled Electric and Magnetic Fields. Micromachines. 2025; 16(10):1094. https://doi.org/10.3390/mi16101094
Chicago/Turabian StyleLiu, Wenbo, Xiaolei Chen, Pengfei Qi, Xiaomin Liu, and Yan Wang. 2025. "Continuous Separation of Lithium Iron Phosphate and Graphite Microparticles via Coupled Electric and Magnetic Fields" Micromachines 16, no. 10: 1094. https://doi.org/10.3390/mi16101094
APA StyleLiu, W., Chen, X., Qi, P., Liu, X., & Wang, Y. (2025). Continuous Separation of Lithium Iron Phosphate and Graphite Microparticles via Coupled Electric and Magnetic Fields. Micromachines, 16(10), 1094. https://doi.org/10.3390/mi16101094







