Advanced Modeling and Simulation of Multilayer Spin–Transfer Torque Magnetoresistive Random Access Memory with Interface Exchange Coupling
Abstract
1. Introduction
2. Micromagnetics Model
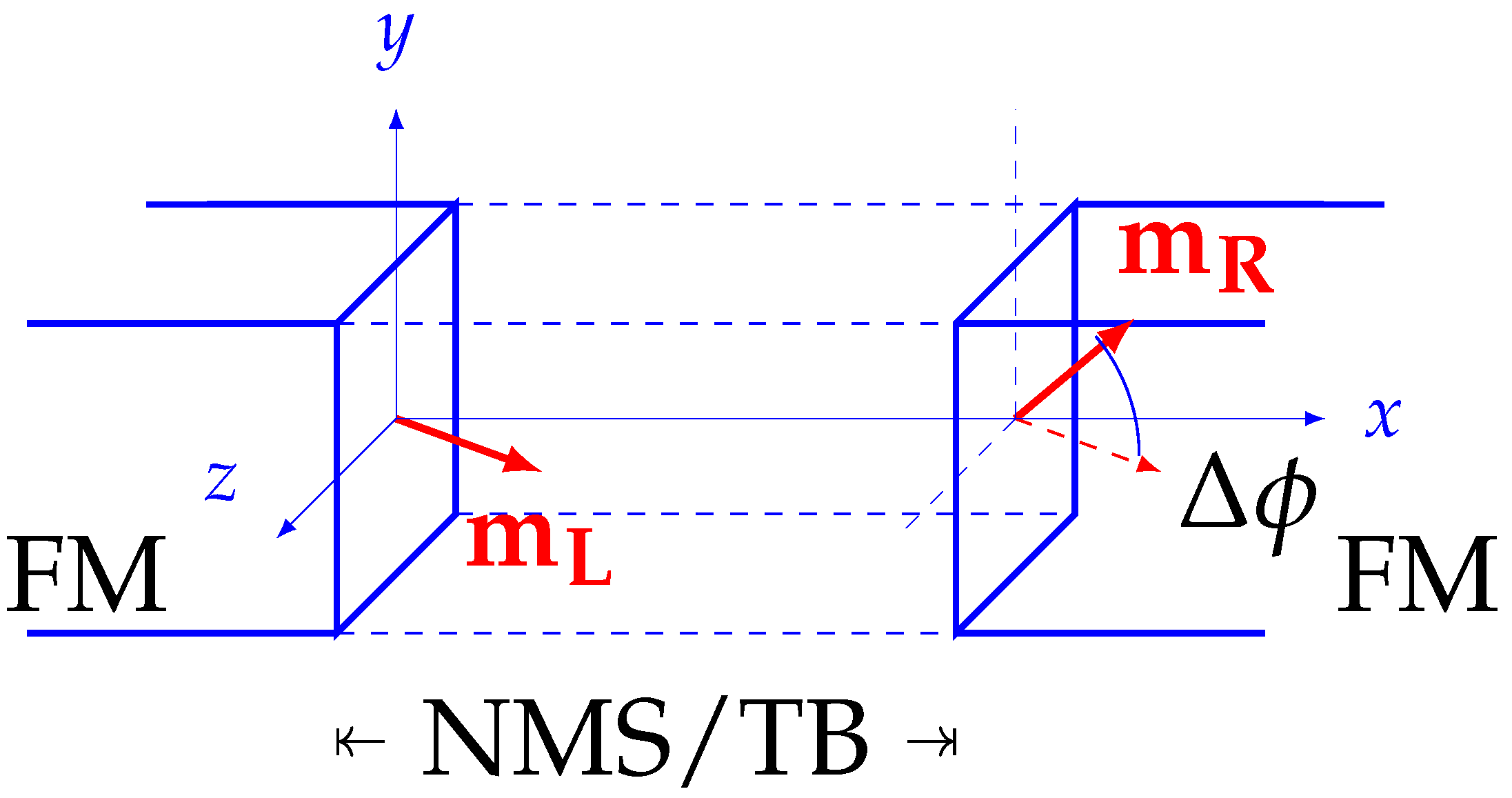
Interlayer Exchange Coupling
3. Results and Discussion
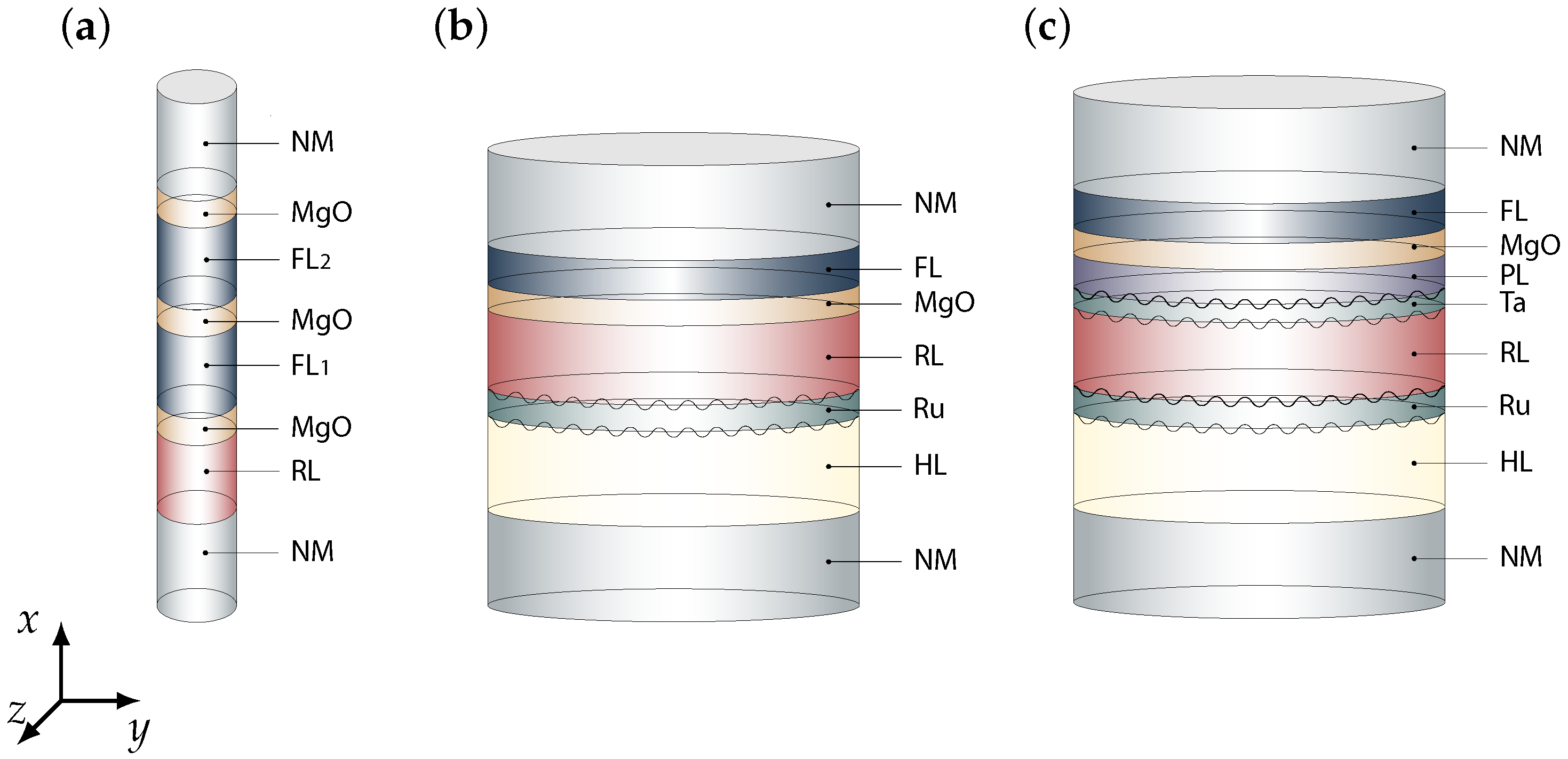
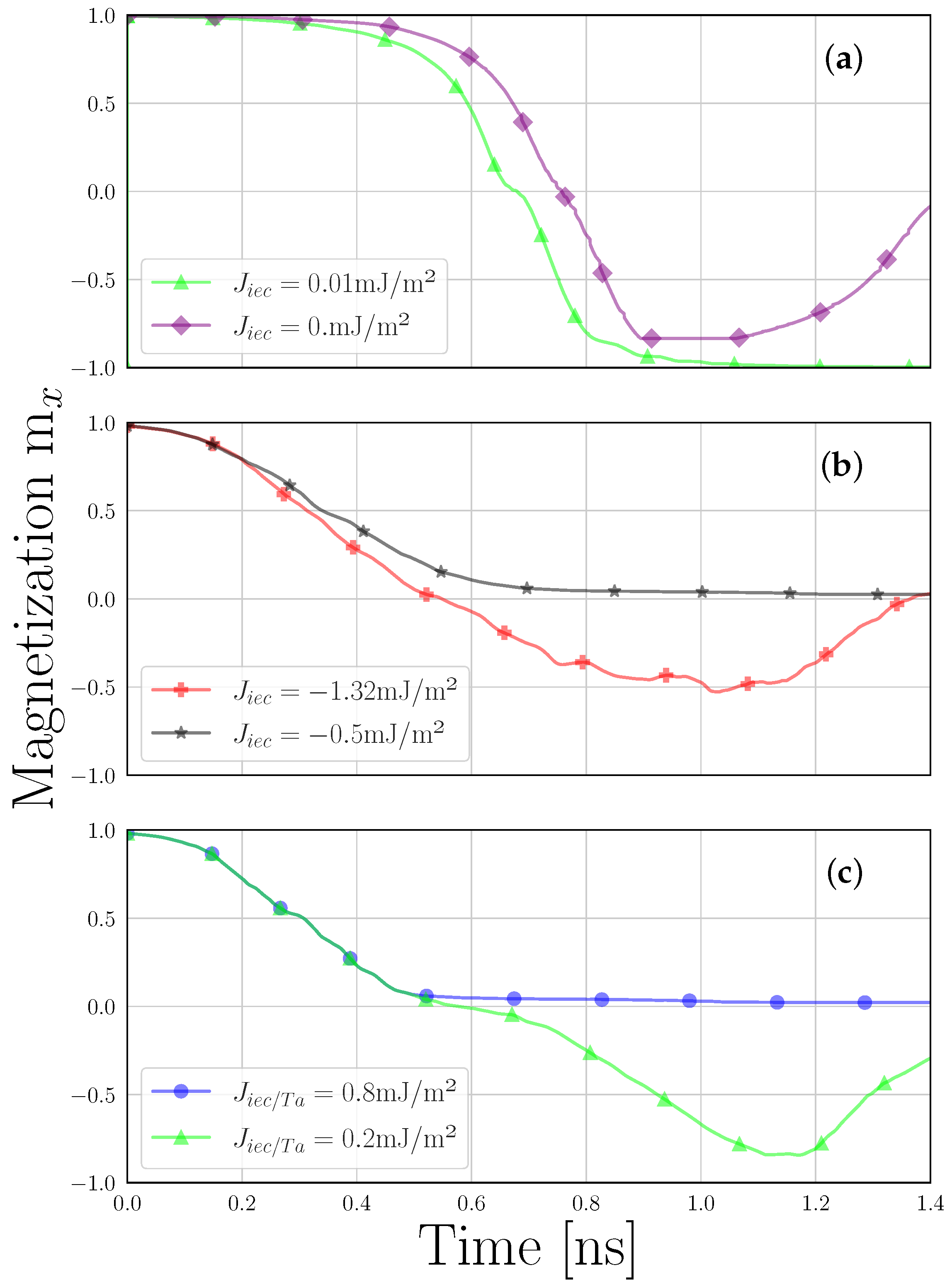
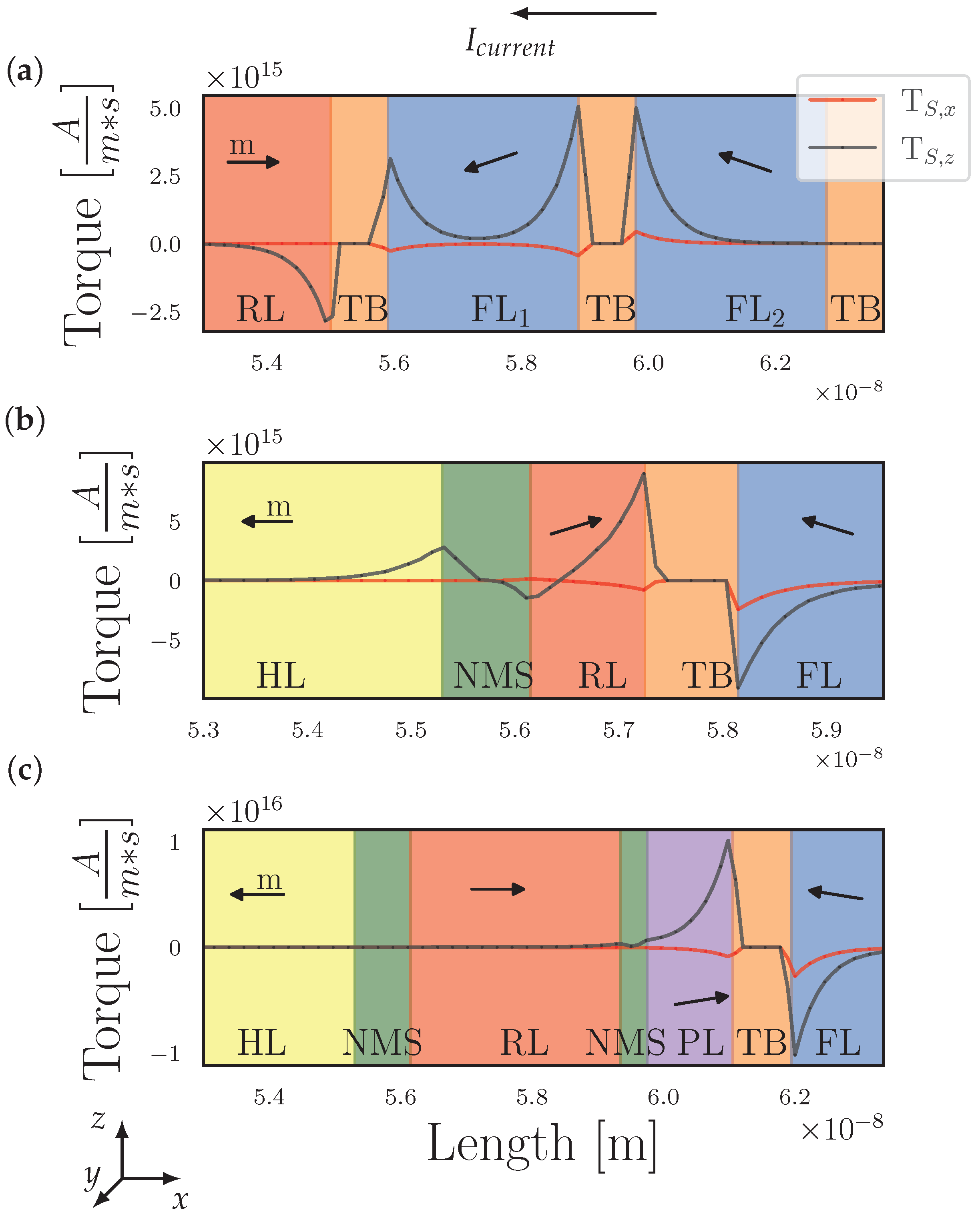
3.1. Stack A
3.2. Stack B
3.3. Stack C
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STT-MRAM | spin–transfer torque magnetoresistive random access memory |
| MTJ | magnetic tunnel junction |
| SRAM | static random-access memory |
| DRAM | dynamic random-access memory |
| RL | reference layer |
| FL | free layer |
| TB | tunnel barrier |
| NMS | non-magnetic spacer |
| NM | normal metal |
| IEC | interlayer exchange coupling |
| HL | hard layer |
| PL | spin–polarization layer |
| LLG | Landau–Lifshitz–Gilbert |
| FEM | finite element method |
| BEM | boundary element method |
| TMR | tunnel magnetoresistance |
| RKKY | Ruderman–Kittel–Kasuya–Yosida |
| FM | ferromagnetic |
| AFM | antiferromagnetic |
| SAF | synthetic antiferromagnetic |
References
- Jung, S.; Lee, H.; Myung, S.; Kim, H.; Yoon, S.K.; Kwon, S.-W.; Ju, Y.; Kim, M.; Yi, W.; Han, S.; et al. A Crossbar Array of Magnetoresistive Memory Devices for In-Memory Computing. Nature 2022, 601, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Naik, V.B.; Yamane, K.; Lee, T.; Kwon, J.; Chao, R.; Lim, J.H.; Chung, N.L.; Behin-Aein, B.; Hau, L.Y.; Zeng, D.; et al. JEDEC-Qualified Highly Reliable 22 nm FD-SOI Embedded MRAM For Low-Power Industrial-Grade, and Extended Performance Towards Automotive-Grade-1 Applications. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 12–18 December 2020; pp. 11.3.1–11.3.4. [Google Scholar] [CrossRef]
- Ikegawa, S.; Nagel, K.; Mancoff, F.B.; Alam, S.M.; Arora, M.; DeHerrera, M.; Lee, H.K.; Mukherjee, S.; Shimon, G.; Sun, J.J.; et al. High-Speed (400MB/s) and Low-BER STT-MRAM Technology for Industrial Applications. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2022; pp. 10.4.1–10.4.4. [Google Scholar] [CrossRef]
- Hu, G.; Safranski, C.; Sun, J.Z.; Hashemi, P.; Brown, S.L.; Bruley, J.; Buzi, L.; D’Emic, C.P.; Galligan, E.; Gottwald, M.G.; et al. Double Spin-Torque Magnetic Tunnel Junction Devices for Last-Level Cache Applications. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2022; pp. 10.2.1–10.2.4. [Google Scholar] [CrossRef]
- Seo, S.M.; Aikawa, H.; Kim, S.G.; Nagase, T.; Ito, Y.; Ha, T.J.; Yoshino, K.; Jung, B.K.; Oikawa, T.; Jung, K.Y.; et al. First Demonstration of Full Integration and Characterization of 4F2 1S1M Cells with 45 nm of pitch and 20 nm of MTJ Size. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2022; pp. 10.1.1–10.1.4. [Google Scholar] [CrossRef]
- Gebregiorgis, A.; Wu, L.; Münch, C.; Rao, S.; Tahoori, M.B.; Hamdioui, S. Special Session: STT-MRAMs: Technology, Design and Test. In Proceedings of the 2022 IEEE 40th VLSI Test Symposium (VTS), San Diego, CA, USA, 25–27 April 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Jinnai, B.; Igarashi, J.; Watanabe, K.; Funatsu, T.; Sato, H.; Fukami, S.; Ohno, H. High-Performance Shape-Anisotropy Magnetic Tunnel Junctions Down to 2.3 nm. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 12–18 December 2020; pp. 24.6.1–24.6.4. [Google Scholar] [CrossRef]
- Nishioka, K.; Honjo, H.; Ikeda, S.; Watanabe, T.; Miura, S.; Inoue, H.; Tanigawa, T.; Noguchi, Y.; Yasuhira, M.; Sato, H.; et al. Novel Quad Interface MTJ Technology and its First Demonstration with High Thermal Stability and Switching Efficiency for STT-MRAM Beyond 2Xnm. In Proceedings of the Symposium on VLSI Technology, Kyoto, Japan, 9–14 June 2019; pp. T120–T121. [Google Scholar] [CrossRef]
- Sato, H.; Yamanouchi, M.; Ikeda, S.; Fukami, S.; Matsukura, F.; Ohno, H. MgO/CoFeB/Ta/CoFeB/MgO Recording Structure in Magnetic Tunnel Junctions With Perpendicular Easy Axis. IEEE Trans. Magn. 2013, 49, 4437–4440. [Google Scholar] [CrossRef]
- Igarashi, J.; Jinnai, B.; Watanabe, K.; Shinoda, T.; Funatsu, T.; Sato, H.; Fukami, S.; Ohno, H. Single-Nanometer CoFeB/MgO Magnetic Tunnel Junctions with High-Retention and High-Speed Capabilities. Npj Spintron. 2024, 2, 211–216. [Google Scholar] [CrossRef]
- Watanabe, K.; Jinnai, B.; ukami, S.; Sato, H.; Ohno, H. Shape Anisotropy Revisited in Single-Digit Nanometer Magnetic Tunnel Junctions. Nat. Commun. 2018, 9, 663. [Google Scholar] [CrossRef]
- Phoomatna, R.; a pai, S.S.; Meo, A.; Chantrell, R.W.; Chureemart, J.; Chureemart, P. Dimensional Scaling Effects on Critical Current Density and Magnetization Switching in CoFeB-Based Magnetic Tunnel Junction. J. Phys. D Appl. Phys. 2024, 57, 185002. [Google Scholar] [CrossRef]
- Abert, C.; Sepehri-Amin, H.; Bruckner, F.; Vogler, C.; Hayashi, M.; Suess, D. Back-Hopping in Spin-Transfer-Torque Devices: Possible Origin and Countermeasures. Phys. Rev. Appl. 2018, 9, 054010. [Google Scholar] [CrossRef]
- Ahn, S. Antiferromagnetically Coupled CoFe/MgO/CoFe Stacks. Phys. Scr. 2023, 98, 105948. [Google Scholar] [CrossRef]
- Yoshikawa, M.; Kitagawa, E.; Nagase, T.; Daibou, T.; Nagamine, M.; Nishiyama, K.; Kishi, T.; Yoda, H. Tunnel Magnetoresistance Over 100% in MgO-Based Magnetic Tunnel Junction Films With Perpendicular Magnetic L10-FePt Electrodes. IEEE Trans. Magn. 2008, 44, 2573–2576. [Google Scholar] [CrossRef]
- Zhao, X.P.; Lu, J.; Mao, S.W.; Yu, Z.F.; Wei, D.H.; Zhao, J.H. Spin-Orbit Torque Induced Magnetization Switching in Ferrimagnetic Heusler Alloy D22-Mn3Ga with Large Perpendicular Magnetic Anisotropy. Appl. Phys. Lett. 2019, 115, 142405. [Google Scholar] [CrossRef]
- Ren, L.; Liu, L.; Shu, X.; Lin, W.; Yang, P.; Chen, J.; Teo, K.L. Spin Orbit Torque Switching of a High-Quality Perpendicularly Magnetized Ferrimagnetic Heusler Mn3Ge Film. ACS Appl. Mater. Interfaces 2021, 13, 18294–18300. [Google Scholar] [CrossRef] [PubMed]
- Balluff, J.; Schmalhorst, J.M.; Arenholz, E.; Meinert, M.; Reiss, G. Enhancing magnetic properties in Mn3Ge thin films by doping. Phys. Rev. B 2018, 97, 014403. [Google Scholar] [CrossRef]
- Chiu, Y.C.; Yang, C.S.; Teng, S.H.; Huang, H.Y.; Chang, F.C.; Wu, Y.; Chien, Y.A.; Hsieh, F.L.; Li, C.Y.; Lin, G.Y.; et al. A 22 nm 4 Mb STT-MRAM Data-Encrypted Near-Memory Computation Macro with a 192 GB/s Read-and-Decryption Bandwidth and 25.1-55.1TOPS/W 8b MAC for AI Operations. In Proceedings of the IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; Volume 65, pp. 178–180. [Google Scholar] [CrossRef]
- Cai, W.; Wang, M.; Cao, K.; Yang, H.; Peng, S.; Li, H. Stateful Implication Logic Based on Perpendicular Magnetic Tunnel Junctions. Sci. China Inf. Sci. 2022, 65, 122406. [Google Scholar] [CrossRef]
- Shinoda, T.; Igarashi, J.; Jinnai, B.; Fukami, S.; Ohno, H. Pitch Scaling Prospect of Ultra-Small Magnetic Tunnel Junctions for High-Density STT-MRAM: Effects of Magnetostatic Interference From Neighboring Bits. IEEE Electron Device Lett. 2024, 45, 184–187. [Google Scholar] [CrossRef]
- Naganuma, H. Spintronics Memory Using Magnetic Tunnel Junction for X nm-Generation. Jpn. J. Appl. Phys. 2023, 62, SG0811. [Google Scholar] [CrossRef]
- Kumar Yadav, M.; Kumar, R.; Kumar Ratnesh, R.; Singh, J.; Chandra, R.; Kumar, A.; Vishnoi, V.; Singh, G.; Kumar Singh, A. Revolutionizing Technology with Spintronics: Devices and Their Transformative Applications. Mater. Sci. Eng. B 2024, 303, 117293. [Google Scholar] [CrossRef]
- Garzón, E.; Lanuzza, M.; Teman, A.; Yavits, L. AM4: MRAM Crossbar Based CAM/TCAM/ACAM/AP for In-Memory Computing. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 408–421. [Google Scholar] [CrossRef]
- Ikeda, S.; Miura, K.; Yamamoto, H.; Mizunuma, K.; Gan, H.D.; Endo, M.; Hayakawa, L.; Matsukura, F. A Perpendicular-Anisotropy CoFeB–MgO Magnetic Tunnel Junction. Nat. Mater. 2010, 9, 721–724. [Google Scholar] [CrossRef] [PubMed]
- Bin Hamid, S.; Dutta, R.; Hassan, O.; Baten, M.Z. Implementing Bidirectional Logic with Backhopping in Magnetic Tunnel Junctions. AIP Adv. 2024, 14, 025224. [Google Scholar] [CrossRef]
- Devolder, T.; Kim, J.V.; Garcia-Sanchez, F.; Swerts, J.; Kim, W.; Couet, S.; Kar, G.; Furnemont, A. Time-Resolved Spin-Torque Switching in MgO-Based Perpendicularly Magnetized Tunnel Junctions. Phys. Rev. B 2016, 93, 024420. [Google Scholar] [CrossRef]
- Lepadatu, S. Boris Computational Spintronics Online Materials Database. Available online: http://www.boris-spintronics.uk/online-materials-database/ (accessed on 24 March 2024).
- Khodadadi, B.; Mohammadi, J.B.; Jones, J.M.; Srivastava, A.; Mewes, C.; Mewes, T.; Kaiser, C. Interlayer Exchange Coupling in Asymmetric Co-Fe/Ru/Co-Fe Trilayers Investigated with Broadband Temperature-Dependent Ferromagnetic Resonance. Phys. Rev. Appl. 2017, 8, 014024. [Google Scholar] [CrossRef]
- Mouhoub, A.; Millo, F.; Chappert, C.; Kim, J.V.; Létang, J.; Solignac, A.; Devolder, T. Exchange Energies in CoFeB/Ru/CoFeB Synthetic Antiferromagnets. Phys. Rev. Mater. 2023, 7, 044404. [Google Scholar] [CrossRef]
- Katayama, T.; Yuasa, S.; Velev, J.; Zhuravlev, M.Y.; Jaswal, S.S.; Tsymbal, E.Y. Interlayer Exchange Coupling in Fe/MgO/Fe Magnetic Tunnel Junctions. Appl. Phys. Lett. 2006, 89, 112503. [Google Scholar] [CrossRef]
- ViennaSpinMag. An Open Access Finite Element-Based Application for Calculating the Magnetization Dynamics of Multi-Layered Structures Composed of Ferromagnets, Metal Spacers and Tunnel Barriers. Available online: https://www.iue.tuwien.ac.at/viennaspinmag/ (accessed on 24 March 2024).
- Kolev, T.; Dobrev, V. MFEM: Modular Finite Element Methods Library. Available online: http://mfem.org (accessed on 24 March 2024).
- Ender, J.; Mohamedou, M.; Fiorentini, S.; de Orio, R.L.; Selberherr, S.; Goes, W.; Sverdlov, V. Efficient Demagnetizing Field Calculation for Disconnected Complex Geometries in STT-MRAM Cells. In Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Piscataway, NJ, USA, 23 September 2020; pp. 213–216. [Google Scholar] [CrossRef]
- ViennaDemag. An Open Access Demagnetization Field Solver. Available online: https://www.iue.tuwien.ac.at/viennademag/ (accessed on 24 March 2024).
- Petitjean, C.; Luc, D.; Waintal, X. Unified Drift-Diffusion Theory for Transverse Spin Currents in Spin Valves, Domain Walls, and Other Textured Magnets. Phys. Rev. Lett. 2012, 109, 117204. [Google Scholar] [CrossRef] [PubMed]
- Abert, C.; Ruggeri, M.; Bruckner, F.; Vogler, C.; Manchon, A.; Praetorius, D.; Suess, D. A Self-Consistent Spin-Diffusion Model for Micromagnetics. Sci. Rep. 2016, 6, 16. [Google Scholar] [CrossRef] [PubMed]
- Valet, T.; Fert, A. Theory of the Perpendicular Magnetoresistance in Magnetic Multilayers. Phys. Rev. B 1993, 48, 7099–7113. [Google Scholar] [CrossRef] [PubMed]
- Fiorentini, S.; Bendra, M.; Ender, J.; de Orio, R.L.; Goes, W.; Selberherr, S.; Sverdlov, V. Spin and Charge Drift-Diffusion in Ultra-Scaled MRAM Cells. Sci. Rep. 2022, 12, 20958. [Google Scholar] [CrossRef] [PubMed]
- Fiorentini, S.; Jørstad, N.P.; Ender, J.; de Orio, R.L.; Selberherr, S.; Bendra, M.; Goes, W.; Sverdlov, V. Finite Element Approach for the Simulation of Modern MRAM Devices. Micromachines 2023, 14, 898. [Google Scholar] [CrossRef]
- Slonczewski, J.C. Currents, torques, and polarization factors in magnetic tunnel junctions. Phys. Rev. B 2005, 71, 024411. [Google Scholar] [CrossRef]
- Julliere, M. Tunneling between Ferromagnetic Films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Chshiev, M.; Manchon, A.; Kalitsov, A.; Ryzhanova, N.; Vedyayev, A.; Strelkov, N.; Butler, W.H.; Dieny, B. Analytical Description of Ballistic Spin Currents and Torques in Magnetic Tunnel Junctions. Phys. Rev. B 2015, 92, 104422. [Google Scholar] [CrossRef]
- ViennaSCDD. An Open Access Spin-Charge Drift-Diffusion Solver. Available online: https://www.iue.tuwien.ac.at/viennascdd/ (accessed on 24 March 2024).
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Inomata, K.; Yusu, K.; Saito, Y. Magnetoresistance Associated with Antiferromagnetic Interlayer Coupling Spaced by a Semiconductor in Fe/Si Multilayers. Phys. Rev. Lett. 1995, 74, 1863–1866. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Wei, G.; Lin, X.; Wang, X.; Si, Z.; Zhang, X.; Shao, Q.; Mangin, S.; Fullerton, E.; Jiang, L.; et al. Reversible Switching of Interlayer Exchange Coupling through Atomically Thin VO2 via Electronic State Modulation. Matter 2020, 2, 1582–1593. [Google Scholar] [CrossRef]
- Bruno, P. Theory of Interlayer Exchange Interactions in Magnetic Multilayers. J. Phys. Condens. Matter 1999, 11, 9403–9419. [Google Scholar] [CrossRef]
- Xu, T.; Liu, J.; Zhang, X.; Zhang, Q.; Zhou, H.A.; Dong, Y.; Gargiani, P.; Valvidares, S.; Zhou, Y.; Jiang, W. Systematic Control of the Interlayer Exchange Coupling in Perpendicularly Magnetized Synthetic Antiferromagnets. Phys. Rev. Appl. 2022, 18, 054051. [Google Scholar] [CrossRef]
- McKinnon, T.; Heinrich, B.; Girt, E. Spacer Layer Thickness and Temperature Dependence of Interlayer Exchange Coupling in Co/Ru/Co Trilayer Structures. Phys. Rev. B 2021, 104, 024422. [Google Scholar] [CrossRef]
- Nunn, Z.R.; Abert, C.; Suess, D.; Girt, E. Control of the Noncollinear Interlayer Exchange Coupling. Sci. Adv. 2020, 6, eabd8861. [Google Scholar] [CrossRef] [PubMed]
- Flauger, P.; Abert, C.; Suess, D. Computational Assessment of Possible Origins of the Back-Hopping Effect in Magnetic Tunnel Junctions. Phys. Rev. B 2023, 108, 014430. [Google Scholar] [CrossRef]
- Bendra, M.; Orio, d.L.R.; Goes, W.; Sverdlov, V.; Selberherr, S. Modeling of Ultra-Scaled Magnetoresistive Random Access Memory. Microelectron. Devices Technol. 2023, 12, 28–30. [Google Scholar] [CrossRef]
- Weng, Y.C.; Cheng, C.W.; Chern, G. Interlayer Exchange Coupling and Perpendicular Magnetic Anisotropy in Co40Fe40B20/MgO/Co20Fe60B20 Tunnel Junction Structures. IEEE Trans. Magn. 2013, 49, 4425–4428. [Google Scholar] [CrossRef]
- Warnatz, T.; Skovdal, B.E.; Magnus, F.; Stopfel, H.; Primetzhofer, D.; Stein, A.; Brucas, R.; Hjörvarsson, B. The Influence of Diameter on the magnetic Saturation in Fe84Cu16/MgO [001] multilayered islands. J. Magn. Magn. Mater. 2020, 496, 165864. [Google Scholar] [CrossRef]
- Faure-Vincent, J.; Tiusan, C.; Bellouard, C.; Popova, E.; Hehn, M.; Montaigne, F.; Schuhl, A. Interlayer Magnetic Coupling Interactions of Two Ferromagnetic Layers by Spin Polarized Tunneling. Phys. Rev. Lett. 2002, 89, 107206. [Google Scholar] [CrossRef] [PubMed]
- Warnatz, T.; Magnus, F.; Strandqvist, N.; Sanz, S.; Ali, H.; Leifer, K.; Vorobiev, A.; Hjörvarsson, B. The Impact of Number of Repeats N on the Interlayer Exchange in [Fe/MgO]N (001) Superlattices. Sci. Rep. 2021, 11, 1942. [Google Scholar] [CrossRef] [PubMed]
- Devolder, T.; Bultynck, O.; Bouquin, P.; Nguyen, V.D.; Rao, S.; Wan, D.; Sorée, B.; Radu, I.P.; Kar, G.S.; Couet, S. Back Hopping in Spin Transfer Torque Switching of Perpendicularly Magnetized Tunnel Junctions. Phys. Rev. B 2020, 102, 184406. [Google Scholar] [CrossRef]
- Le Goff, A.; Garcia, K.; Vernier, N.; Tahmasebi, T.; Cornelissen, S.; Min, T.; Devolder, T. Effect of Ta Insertion in Reference Layers of MTJs With Perpendicular Anisotropy. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
| LLG Parameters | Stack A | Stack B | Stack C |
|---|---|---|---|
| Saturation magnetization (, HL) | |||
| Saturation magnetization (, RL) | |||
| Saturation magnetization (, PL) | |||
| Saturation magnetization (, FL) | |||
| Exchange constant (, HL) | |||
| Exchange constant (, RL) | |||
| Exchange constant (, PL) | |||
| Exchange constant (, FL) | |||
| Shape anisotropy (, HL) | |||
| Shape anisotropy (, RL) | |||
| Shape anisotropy (, PL) | |||
| Shape anisotropy (, FL) | |||
| Gilbert damping constant (, HL) | |||
| Gilbert damping constant (, RL) | |||
| Gilbert damping constant (, PL) | |||
| Gilbert damping constant (, FL) | |||
| IEC (, Ru) | |||
| IEC (, Ta) | |||
| Resistance parallel () | |||
| Resistance parallel () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bendra, M.; Orio, R.L.d.; Selberherr, S.; Goes, W.; Sverdlov, V. Advanced Modeling and Simulation of Multilayer Spin–Transfer Torque Magnetoresistive Random Access Memory with Interface Exchange Coupling. Micromachines 2024, 15, 568. https://doi.org/10.3390/mi15050568
Bendra M, Orio RLd, Selberherr S, Goes W, Sverdlov V. Advanced Modeling and Simulation of Multilayer Spin–Transfer Torque Magnetoresistive Random Access Memory with Interface Exchange Coupling. Micromachines. 2024; 15(5):568. https://doi.org/10.3390/mi15050568
Chicago/Turabian StyleBendra, Mario, Roberto Lacerda de Orio, Siegfried Selberherr, Wolfgang Goes, and Viktor Sverdlov. 2024. "Advanced Modeling and Simulation of Multilayer Spin–Transfer Torque Magnetoresistive Random Access Memory with Interface Exchange Coupling" Micromachines 15, no. 5: 568. https://doi.org/10.3390/mi15050568
APA StyleBendra, M., Orio, R. L. d., Selberherr, S., Goes, W., & Sverdlov, V. (2024). Advanced Modeling and Simulation of Multilayer Spin–Transfer Torque Magnetoresistive Random Access Memory with Interface Exchange Coupling. Micromachines, 15(5), 568. https://doi.org/10.3390/mi15050568








