Tailoring the Coefficient of Friction by Direct Laser Writing Surface Texturing
Abstract
1. Introduction
2. Lubrication Regimes and Tribological Characteristics of Microstructured Surfaces
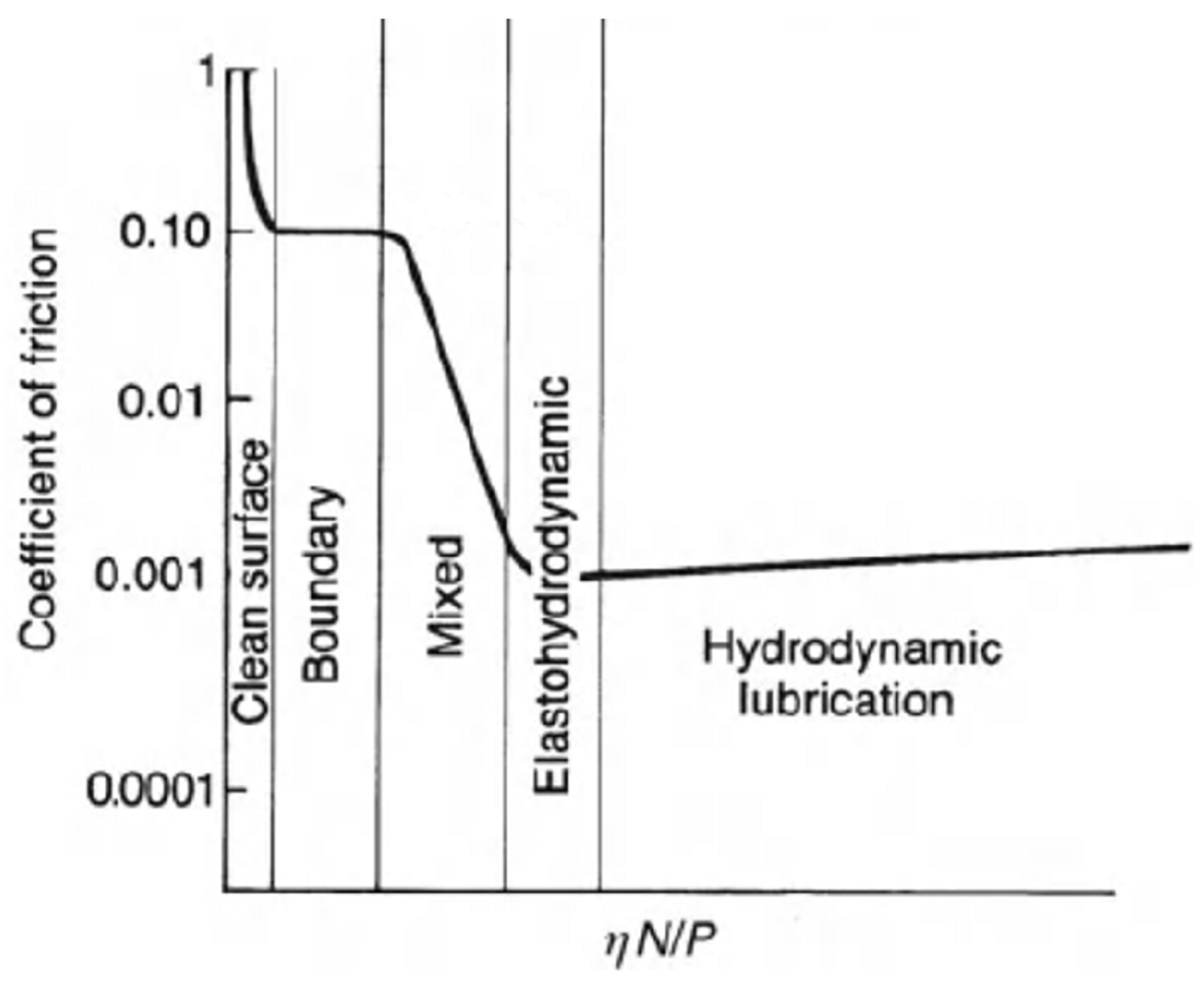
2.1. Stribeck Curve for Fluid Lubrication Description
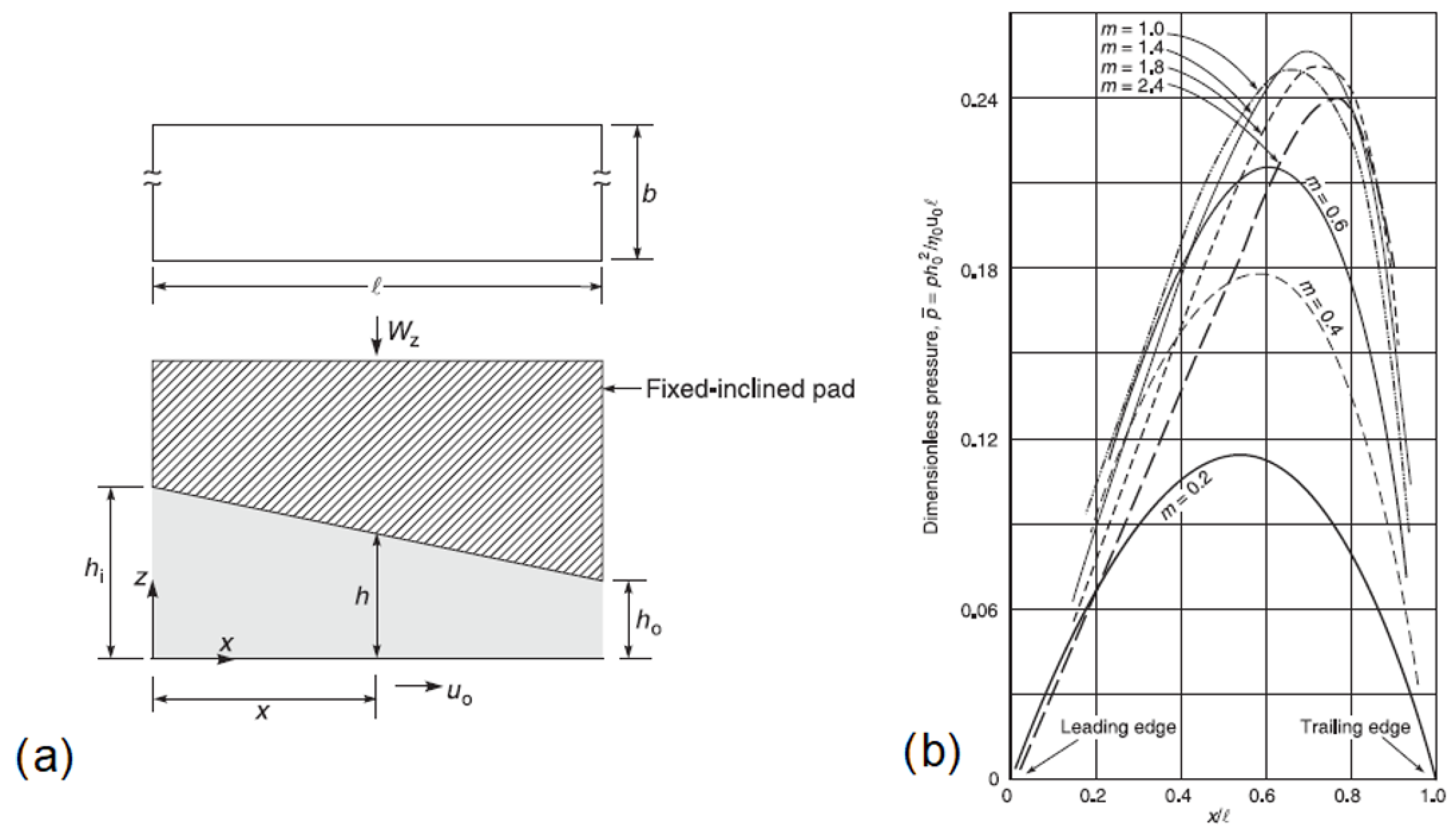
2.2. Controlling of Friction Properties through Surface Microstructuring
3. Direct Laser Writing with Ultrashort Pulses for Surface Topography Modification
4. Laser Surface Texturing for Friction Reduction
4.1. Conformal Contacts
4.1.1. Homogeneous
4.1.2. Non-Uniform
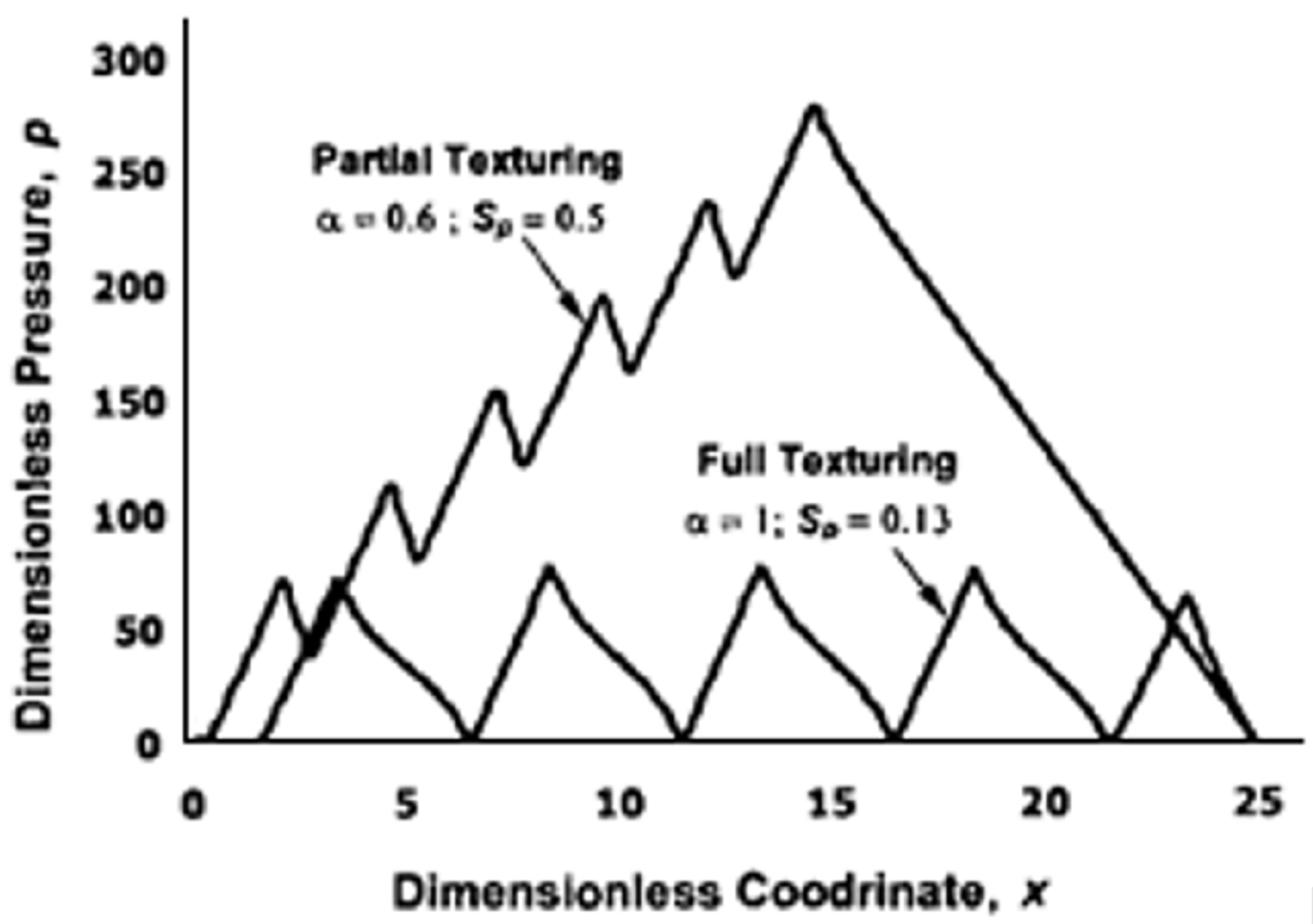
4.2. Non-Conformal Contacts
5. Conclusions
- (1)
- Homogeneous arrangements of circular dimples allow a significant reduction the COF, the extent of the decrease being dependent on the geometry of the dimples (of the order of 20% with circular dimples with a diameter around 100 μm and an optimized depth around 6–7 μm; of the order of 80% with dimples with a diameter of 40 μm and depth of 4 μm. The specific arrangement of such micro-defects generated by direct laser writing over the sample surface revealed no to be significant especially in hydrodynamic lubrication regime, where cavitation played a more important role on the definition of the final tribological behavior.
- (2)
- Directional textures of circular dimples (diameter of 180 μm and depth of 6.5 μm) highlighting the presence of equivalent convergent or divergent wedge, depending on the direction of the tests, reveal the possibility to dynamically switch between different frictional properties behavior, i.e., increase up to or reduction in the COF.
- (3)
- Non-uniform textures consisting of elliptical or rectangular dimples (dimensions of 30 μm × 170 μm) having varying depth, give the possibility to obtain an important increase in the load capacity and the redirection of the lubricant fluid in the desired region of the surface.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blau, P.J. Friction Science and Technology From Concept to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Marian, M.; Weikert, T.; Tremmel, S. On Friction Reduction by Surface Modifications in the TEHL Cam/Tappet-Contact-Experimental and Numerical Studies. Coatings 2019, 9, 843. [Google Scholar] [CrossRef]
- Hamilton, D.B.; Walowit, J.A.; Allen, C.M. A Theory of Lubrication by Micro- irregularities. Trans. ASME, J. Basic Eng. 1966, 88, 177–185. [Google Scholar] [CrossRef]
- Anno, J.N.; Walowit, J.A.; Allen, C.M. Microasperity Lubrication. J. Lubr. Technol. 1968, 90, 5–9. [Google Scholar] [CrossRef]
- Pratap, T.; Patra, K. Mechanical micro-texturing of Ti-6Al-4V surfaces for improved wettability and bio-tribological performances. Surf. Coat. Technol. 2018, 349, 71–81. [Google Scholar] [CrossRef]
- Denkena, B.; Grove, T.; Schmidt, C. Machining of Micro Dimples for Friction Reduction in Cylinder Liners. Procedia CIRP 2018, 78, 318–322. [Google Scholar] [CrossRef]
- Greco, A.; Raphaelson, S.; Ehmann, K.; Wang, Q.J. Surface Texturing of Tribological Vibromechanical Texturing Method. J. Manuf. Sci. Eng. Trans. 2016, 131, 0610051. [Google Scholar]
- Wang, X.; Kato, K.; Adachi, K.; Aizawa, K. Loads carrying capacity map for the surface texture design of SiC thrust bearing sliding in water. Tribol. Int. 2003, 36, 189–197. [Google Scholar] [CrossRef]
- Etsion, I. State of the art in laser surface texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Gaudiuso, C.; Fanelli, F.; Mezzapesa, F.P.; Volpe, A.; Ancona, A. Tailoring the wettability of surface-textured copper using sub-THz bursts of femtosecond laser pulses. Appl. Surf. Sci. 2023, 638, 158032. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G.; Brizmer, V.; Kligerman, Y. Experimental investigation of laser surface textured parallel thrust bearings. Tribol. Lett. 2004, 17, 295–300. [Google Scholar] [CrossRef]
- Ronen, A.; Etsion, I.; Kligerman, Y. Friction-reducing surface-texturing in reciprocating automotive components. Tribol. Trans. 2001, 44, 359–366. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; Von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A Mater. Sci. Process. 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Gaudiuso, C.; Giannuzzi, G.; Volpe, A.; Lugarà, P.M.; Choquet, I.; Ancona, A. Incubation during laser ablation with bursts of femtosecond pulses with picosecond delays. Opt. Express 2018, 26, 3801. [Google Scholar] [CrossRef] [PubMed]
- Kerse, C.; Kalaycloĝ Lu, H.; Elahi, P.; Çetin, B.; Kesim, D.K.; Akçaalan, Ö.; Yavaş, S.; Aşlk, M.D.; Öktem, B.; Hoogland, H.; et al. Ablation-cooled material removal with ultrafast bursts of pulses. Nature 2016, 537, 84–88. [Google Scholar] [CrossRef] [PubMed]
- Bonamis, G.; Audouard, E.; Hönninger, C.; Lopez, J.; Mishchik, K.; Mottay, E.; Manek-Hönninger, I. Systematic study of laser ablation with GHz bursts of femtosecond pulses. Opt. Express 2020, 28, 27702. [Google Scholar] [CrossRef] [PubMed]
- Mishchik, K.; Bonamis, G.; Qiao, J.; Lopez, J.; Audouard, E.; Mottay, E.; Hönninger, C.; Manek-Hönninger, I. High-efficiency femtosecond ablation of silicon with GHz repetition rate laser source. Opt. Lett. 2019, 44, 2193. [Google Scholar] [CrossRef]
- Bauer, F.; Michalowski, A.; Kiedrowski, T.; Nolte, S. Heat accumulation in ultra-short pulsed scanning laser ablation of metals. Opt. Express 2015, 23, 1035. [Google Scholar] [CrossRef]
- Gaudiuso, C.; Terekhin, P.N.; Volpe, A.; Nolte, S.; Rethfeld, B.; Ancona, A. Laser ablation of silicon with THz bursts of femtosecond pulses. Sci. Rep. 2021, 11, 13321. [Google Scholar] [CrossRef]
- Gaudiuso, C.; Stampone, B.; Trotta, G.; Volpe, A.; Ancona, A. Investigation of the micro-milling process of steel with THz bursts of ultrashort laser pulses. Opt. Laser Technol. 2023, 162, 109301. [Google Scholar] [CrossRef]
- Hu, J.; Xu, H. Friction and wear behavior analysis of the stainless steel surface fabricated by laser texturing underwater. Tribol. Int. 2016, 102, 371–377. [Google Scholar] [CrossRef]
- Schille, J.; Schneider, L.; Mauersberger, S.; Szokup, S.; Höhn, S.; Pötschke, J.; Reiß, F.; Leidich, E.; Löschner, U. High-Rate laser surface texturing for advanced tribological functionality. Lubricants 2020, 8, 33. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, W.; Zhou, Y.; Qiao, T.; Lin, W.; Xu, S.; Yang, Z. 5 GHz fundamental repetition rate, wavelength tunable, all-fiber passively mode-locked Yb-fiber laser. Opt. Express 2017, 25, 27646. [Google Scholar] [CrossRef] [PubMed]
- Bharat Bhushan Introduction to Tribology, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 9781119944539.
- Hamrock, B.J.; Schmid, S.R.; Bo, O. Jacobson Fundamental of Fluid Film Lubrication; Marcel Dekker, I., Ed.; NASA: Washington, DC, USA, 2004; ISBN 0824753712.
- Lu, P.; Wood, R.J.K.; Gee, M.G.; Wang, L.; Pfleging, W. A Novel Surface Texture Shape for Directional Friction Control. Tribol. Lett. 2018, 66, 51. [Google Scholar] [CrossRef]
- Lu, P.; Wood, R.J.K.; Gee, M.G.; Wang, L.; Pfleging, W. The use of anisotropic texturing for control of directional friction. Tribol. Int. 2017, 113, 169–181. [Google Scholar] [CrossRef]
- Scaraggi, M.; Mezzapesa, F.P.; Carbone, G.; Ancona, A.; Tricarico, L. Friction Properties of Lubricated Laser-MicroTextured-Surfaces: An Experimental Study from Boundary- to Hydrodynamic- Lubrication. Tribol. Lett. 2013, 49, 117–125. [Google Scholar] [CrossRef]
- Handbook of Micro/Nano Tribology; Bhushan, B. (Eds.) CRC Mechanics and Materials Science Series; CRC Press: Boca Raton, FL, USA, 1999; ISBN 0849384028. [Google Scholar]
- Schneider, J.; Braun, D.; Greiner, C. Laser textured surfaces for mixed lubrication: Influence of aspect ratio, textured area and dimple arrangement. Lubricants 2017, 5, 32. [Google Scholar] [CrossRef]
- Hsu, S.M.; Jing, Y.; Hua, D.; Zhang, H. Friction reduction using discrete surface textures: Principle and design. J. Phys. D. Appl. Phys. 2014, 47, 335307. [Google Scholar] [CrossRef]
- Yu, H.; Wang, X.; Zhou, F. Geometric Shape Effects of Surface Texture on the Generation of Hydrodynamic Pressure Between Conformal Contacting Surfaces. Tribol. Lett. 2010, 37, 123–130. [Google Scholar] [CrossRef]
- Qiu, M.; Delic, A.; Raeymaekers, B. The Effect of Texture Shape on the Load-Carrying Capacity of Gas-Lubricated Parallel Slider Bearings. Tribol. Lett. 2012, 48, 315–327. [Google Scholar] [CrossRef]
- Putignano, C.; Parente, G.; Profito, F.J.; Gaudiuso, C.; Ancona, A.; Carbone, G. Laser Microtextured Surfaces for Friction Reduction: Does the Pattern Matter? Materials 2020, 13, 4915. [Google Scholar] [CrossRef]
- Zhong, Y.; Zheng, L.; Gao, Y.; Liu, Z. Numerical simulation and experimental investigation of tribological performance on bionic hexagonal textured surface. Tribol. Int. 2019, 129, 151–161. [Google Scholar] [CrossRef]
- Scaraggi, M. Partial surface texturing: A mechanism for local flow reconditioning in lubricated contacts. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2015, 229, 493–504. [Google Scholar] [CrossRef]
- Ancona, A.; Carbone, G.; Filippis, M.D.; Volpe, A.; Lugarà, P.M. Femtosecond laser full and partial texturing of steel surfaces to reduce friction in lubricated contact. Adv. Opt. Technol. 2014, 3, 539–547. [Google Scholar] [CrossRef]
- Ryk, G.; Kligerman, Y.; Etsion, I.; Shinkarenko, A. Experimental investigation of partial laser surface texturing for piston-ring friction reduction. Tribol. Trans. 2005, 48, 583–588. [Google Scholar] [CrossRef]
- Etsion, I. Improving tribological performance of mechanical components by laser surface texturing. Tribol. Lett. 2004, 17, 733–737. [Google Scholar] [CrossRef]
- Scaraggi, M.; Mezzapesa, F.P.; Carbone, G.; Ancona, A.; Sorgente, D.; Lugarà, P.M. Minimize friction of lubricated laser-microtextured-surfaces by tuning microholes depth. Tribol. Int. 2014, 75, 123–127. [Google Scholar] [CrossRef]
- Etsion, I. Handbook of Lubrication and Tribology, Volume II: Theory and Design, 2nd ed.; Bruce, R.W., Ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Brizmer, V.; Kligerman, Y.; Etsion, I. A laser surface textured parallel thrust bearing. Tribol. Trans. 2003, 46, 397–403. [Google Scholar] [CrossRef]
- Scaraggi, M. Optimal Textures for Increasing the Load Support in a Thrust Bearing Pad Geometry. Tribol. Lett. 2014, 53, 127–143. [Google Scholar] [CrossRef]
- Costa, H.L.; Schille, J.; Rosenkranz, A. Tailored surface textures to increase friction—A review. Friction 2022, 10, 1285–1304. [Google Scholar] [CrossRef]
- Scaraggi, M. Textured surface hydrodynamic lubrication: Discussion. Tribol. Lett. 2012, 48, 375–391. [Google Scholar] [CrossRef]
- Ancona, A.; Joshi, G.S.; Volpe, A.; Scaraggi, M.; Lugarà, P.M.; Carbone, G. Non-uniform laser surface texturing of an un-tapered square pad for tribological applications. Lubricants 2017, 5, 41. [Google Scholar] [CrossRef]
- Stark, T.; Alamri, S.; Aguilar-Morales, A.I.; Kiedrowski, T.; Lasagni, A.F. Positive effect of laser structured surfaces on tribological performance. J. Laser Micro Nanoeng. 2019, 14, 13–18. [Google Scholar]
- Stark, T.; Kiedrowski, T.; Marschall, H.; Lasagni, A.F. Avoiding starvation in tribocontact through active lubricant transport in laser textured surfaces. Lubricants 2019, 7, 54. [Google Scholar] [CrossRef]
- Nolte, S.; Momma, C.; Jacobs, H.; Tünnermann, A.; Chickov, B.N.; Wellegehausen, B.; Welling, H. Ablation of metals by ultrashort laser pulses. J. Opt. Soc. Am. B 1997, 14, 2716–2722. [Google Scholar] [CrossRef]
- Moradi, S.; Kamal, S.; Englezos, P.; Hatzikiriakos, S.G. Femtosecond laser irradiation of metallic surfaces: Effects of laser parameters on superhydrophobicity. Nanotechnology 2013, 24, 415302. [Google Scholar] [CrossRef] [PubMed]
- Romano, J.; Garcia-giron, A.; Penchev, P.; Dimov, S. Triangular laser-induced submicron textures for functionalising stainless steel surfaces. Appl. Surf. Sci. 2018, 440, 162–169. [Google Scholar] [CrossRef]
- Belloni, V.V.; Bollani, M.; Eaton, S.M.; Di Trapani, P.; Jedrkiewicz, O. Micro-hole generation by high-energy pulsed bessel beams in different transparent materials. Micromachines 2021, 12, 455. [Google Scholar] [CrossRef]
- Gaudiuso, C.; Volpe, A.; Ancona, A. One-Step Femtosecond Laser Stealth Dicing of Quartz. Micromachines 2020, 11, 327. [Google Scholar] [CrossRef]
- Lasagni, A.F. Laser interference patterning methods: Possibilities for high-throughput fabrication of periodic surface patterns. Adv. Opt. Technol. 2017, 6, 265–275. [Google Scholar] [CrossRef]
- Aguilar-Morales, A.I.; Alamri, S.; Lasagni, A.F. Micro-fabrication of high aspect ratio periodic structures on stainless steel by picosecond direct laser interference patterning. J. Mater. Process. Technol. 2018, 252, 313–321. [Google Scholar] [CrossRef]
- Bieda, M.; Siebold, M.; Lasagni, A.F. Fabrication of sub-micron surface structures on copper, stainless steel and titanium using picosecond laser interference patterning. Appl. Surf. Sci. 2016, 387, 175–182. [Google Scholar] [CrossRef]
- Lasagni, A.; Benke, D.; Kunze, T.; Bieda, M.; Eckhardt, S.; Roch, T.; Langheinrich, D.; Berger, J. Bringing the direct laser interference patterning method to industry: A one tool-complete solution for surface functionalization. J. Laser Micro Nanoeng. 2015, 10, 340–344. [Google Scholar] [CrossRef]
- Mezera, M.; Florian, C.; Römer, G.W.; Krüger, J.; Bonse, J. Creation of Material Functions by Nanostructuring; Springer: Berlin/Heidelberg, Germany, 2023; Volume 239, ISBN 9783031147524. [Google Scholar]
- Bonse, J.; Hohm, S.; Kirner, S.V.; Rosenfeld, A.; Kruger, J. Laser-Induced Periodic Surface Structures— A Scientific Evergreen. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 9000615. [Google Scholar] [CrossRef]
- Giannuzzi, G.; Gaudiuso, C.; Franco, C.D.; Scamarcio, G.; Lugarà, P.M.; Ancona, A. Large area laser-induced periodic surface structures on steel by bursts of femtosecond pulses with picosecond delays. Opt. Lasers Eng. 2019, 114, 15–21. [Google Scholar] [CrossRef]
- Giannuzzi, G.; Gaudiuso, C.; Di Mundo, R.; Mirenghi, L.; Fraggelakis, F.; Kling, R.; Lugarà, P.M.; Ancona, A. Short and long term surface chemistry and wetting behaviour of stainless steel with 1D and 2D periodic structures induced by bursts of femtosecond laser pulses. Appl. Surf. Sci. 2019, 494, 1055–1065. [Google Scholar] [CrossRef]
- Bonse, J.; Gräf, S. Ten open questions about laser-induced periodic surface structures. Nanomaterials 2021, 11, 3326. [Google Scholar] [CrossRef] [PubMed]
- Römer, G.R.B.E.; Skolski, J.Z.P.; Oboňa, J.V.; Ocelík, V.; de Hosson, J.T.M. Laser-induced periodic surface structures, modeling, experiments, and applications. Laser-Based Micro-Nanoprocessing VIII 2014, 8968, 89680D. [Google Scholar]
- Mao, B.; Siddaiah, A.; Liao, Y.; Menezes, P.L. Laser surface texturing and related techniques for enhancing tribological performance of engineering materials: A review. J. Manuf. Process. 2020, 53, 153–173. [Google Scholar] [CrossRef]
- Boidi, G.; Grützmacher, P.G.; Kadiric, A.; Profito, F.J.; Machado, I.F.; Gachot, C.; Dini, D. Fast laser surface texturing of spherical samples to improve the frictional performance of elasto-hydrodynamic lubricated contacts. Friction 2021, 9, 1227–1241. [Google Scholar] [CrossRef]
- Mannion, P.T.; Magee, J.; Coyne, E.; O’Connor, G.M.; Glynn, T.J. The effect of damage accumulation behaviour on ablation thresholds and damage morphology in ultrafast laser micro-machining of common metals in air. Appl. Surf. Sci. 2004, 233, 275–287. [Google Scholar] [CrossRef]
- Di Niso, F.; Gaudiuso, C.; Sibillano, T.; Mezzapesa, F.P.; Ancona, A.; Lugarà, P.M. Role of heat accumulation on the incubation effect in multi-shot laser ablation of stainless steel at high repetition rates. Opt. Express 2014, 22, 12200. [Google Scholar] [CrossRef] [PubMed]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Gachot, C.; Rosenkranz, A.; Hsu, S.M.; Costa, H.L. A critical assessment of surface texturing for friction and wear improvement. Wear 2017, 372–373, 21–41. [Google Scholar] [CrossRef]
- Sudeep, U.; Tandon, N.; Pandey, R.K. Performance of Lubricated Rolling/Sliding Concentrated Contacts With Surface Textures: A Review. J. Tribol. 2015, 137, 031501. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Grützmacher, P.G.; Gachot, C.; Costa, H.L. Surface Texturing in Machine Elements − A Critical Discussion for Rolling and Sliding Contacts. Adv. Eng. Mater. 2019, 21, 1900194. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Profito, F.J.; Rosenkranz, A. Multi-scale surface texturing in tribology-current knowledge and future perspectives. Lubricants 2019, 7, 95. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; He, M.; Zhang, W. Effect of micro grooves on lubrication performance of friction pairs. Meccanica 2021, 56, 351–364. [Google Scholar] [CrossRef]
- Joshi, G.S.; Putignano, C.; Gaudiuso, C.; Stark, T.; Kiedrowski, T.; Ancona, A.; Carbone, G. Effects of the micro surface texturing in lubricated non-conformal point contacts. Tribol. Int. 2018, 127, 296–301. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Tong, Z.; Ma, Q.; Ni, Y.; Dong, G. Enhanced lubrication effect of gallium-based liquid metal with laser textured surface. Tribol. Int. 2019, 129, 407–415. [Google Scholar] [CrossRef]
- Yan, S.; Wei, C.; Zou, H.; Chen, J.; Li, Y.; Shen, T.; Wang, A.; Sui, T.; Lin, B. Fabrication and tribological characterization of laser textured engineering ceramics: Si3N4, SiC and ZrO2. Ceram. Int. 2021, 47, 13789–13805. [Google Scholar] [CrossRef]
- Putignano, C.; Scarati, D.; Gaudiuso, C.; Di Mundo, R.; Ancona, A.; Carbone, G. Soft matter laser micro-texturing for friction reduction: An experimental investigation. Tribol. Int. 2019, 136, 82–86. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Szurdak, A.; Grützmacher, P.G.; Hirt, G.; Mücklich, F. Friction Reduction Induced by Elliptical Surface Patterns under Lubricated Conditions. Adv. Eng. Mater. 2018, 20, 1700731. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Q.; Li, Y.; Guo, M.; Li, P.; Li, Y. Numerical and experimental study on the effect of surface texture with roughness orientation considered under a mixed lubrication state. Ind. Lubr. Tribol. 2021, 73, 1333–1341. [Google Scholar] [CrossRef]
- Shinkarenko, A.; Kligerman, Y.; Etsion, I. The effect of elastomer surface texturing in soft elasto-hydrodynamic lubrication. Tribol. Lett. 2009, 36, 95–103. [Google Scholar] [CrossRef]
- Ramesh, A.; Akram, W.; Mishra, S.P.; Cannon, A.H.; Polycarpou, A.A.; King, W.P. Friction characteristics of microtextured surfaces under mixed and hydrodynamic lubrication. Tribol. Int. 2013, 57, 170–176. [Google Scholar] [CrossRef]
- Peng, X.D.; Sheng, S.E.; Li, J.Y.; Pan, X.M.; Bai, S.X. Effects of dimple geometric parameters on the performance of a laser-textured mechanical seal. Key Eng. Mater. 2008, 373–374, 766–769. [Google Scholar] [CrossRef]
- Braun, D.; Greiner, C.; Schneider, J.; Gumbsch, P. Efficiency of laser surface texturing in the reduction of friction under mixed lubrication. Tribol. Int. 2014, 77, 142–147. [Google Scholar] [CrossRef]
- Greiner, C.; Merz, T.; Braun, D.; Codrignani, A.; Magagnato, F. Optimum dimple diameter for friction reduction with laser surface texturing: The effect of velocity gradient. Surf. Topogr. Metrol. Prop. 2015, 3, 044001. [Google Scholar] [CrossRef]
- Yan, D.; Qu, N.; Li, H.; Wang, X. Significance of dimple parameters on the friction of sliding surfaces investigated by orthogonal experiments. Tribol. Trans. 2010, 53, 703–712. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The effect of laser surface texturing on transitions in lubrication regimes during unidirectional sliding contact. Tribol. Int. 2005, 38, 219–225. [Google Scholar] [CrossRef]
- Vlădescu, S.; Medina, S.; Olver, A.V.; Pegg, I.G.; Reddyhoff, T. The Transient Friction Response of a Laser-Textured, Reciprocating Contact to the Entrainment of Individual Pockets. Tribol. Lett. 2016, 62, 19. [Google Scholar] [CrossRef]
- Segu, D.Z.; Choi, S.G.; Choi, J.H.; Kim, S.S. The effect of multi-scale laser textured surface on lubrication regime. Appl. Surf. Sci. 2013, 270, 58–63. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Costa, H.L.; Profito, F.; Gachot, C.; Medina, S.; Dini, D. Influence of surface texturing on hydrodynamic friction in plane converging bearings—An experimental and numerical approach. Tribol. Int. 2019, 134, 190–204. [Google Scholar] [CrossRef]
- Wos, S.; Koszela, W.; Dzierwa, A.; Pawlus, P. Friction reduction in unidirectional lubricated sliding due to disc surface texturing. Coatings 2020, 10, 221. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of powdery rubber wear. J. Phys. Condens. Matter 2009, 21, 485001. [Google Scholar] [CrossRef] [PubMed]
- Gaudiuso, C. Applied Sciences Laser Fabrication: A Solid Present for the Brightest Future. Appl. Sci. 2023, 13, 10831. [Google Scholar] [CrossRef]
- Lawrence, J.; Waugh, D.G. Creating superhydrophobic surface structures via the rose petal effect on stainless steel with a picosecond laser. Lasers Eng. 2017, 37, 125–134. [Google Scholar]
- Cardoso, J.T.; Aguilar-Morales, A.I.; Alamri, S.; Huerta-Murillo, D.; Cordovilla, F.; Lasagni, A.F.; Ocaña, J.L. Superhydrophobicity on hierarchical periodic surface structures fabricated via direct laser writing and direct laser interference patterning on an aluminium alloy. Opt. Lasers Eng. 2018, 111, 193–200. [Google Scholar] [CrossRef]
- Sackfield, A.; Dini, D.; Hills, D.A. Contact of a rotating wheel with a flat. Int. J. Solids Struct. 2007, 44, 3304–3316. [Google Scholar] [CrossRef][Green Version]
- Vlădescu, S.; Ciniero, A.; Tufail, K.; Reddyhoff, T. Optimization of Pocket Geometry for Friction Reduction in Piston—Liner Contacts. Tribol. Trans. 2018, 61, 522–531. [Google Scholar] [CrossRef]
- Nakashima, K.; Matsunaga, K.; Uchiyama, Y.; Yoshida, M. Development of measurement apparatus of piston assembly friction in a small motorcycle engine. Combust. Engines 2023, 194, 32–37. [Google Scholar] [CrossRef]




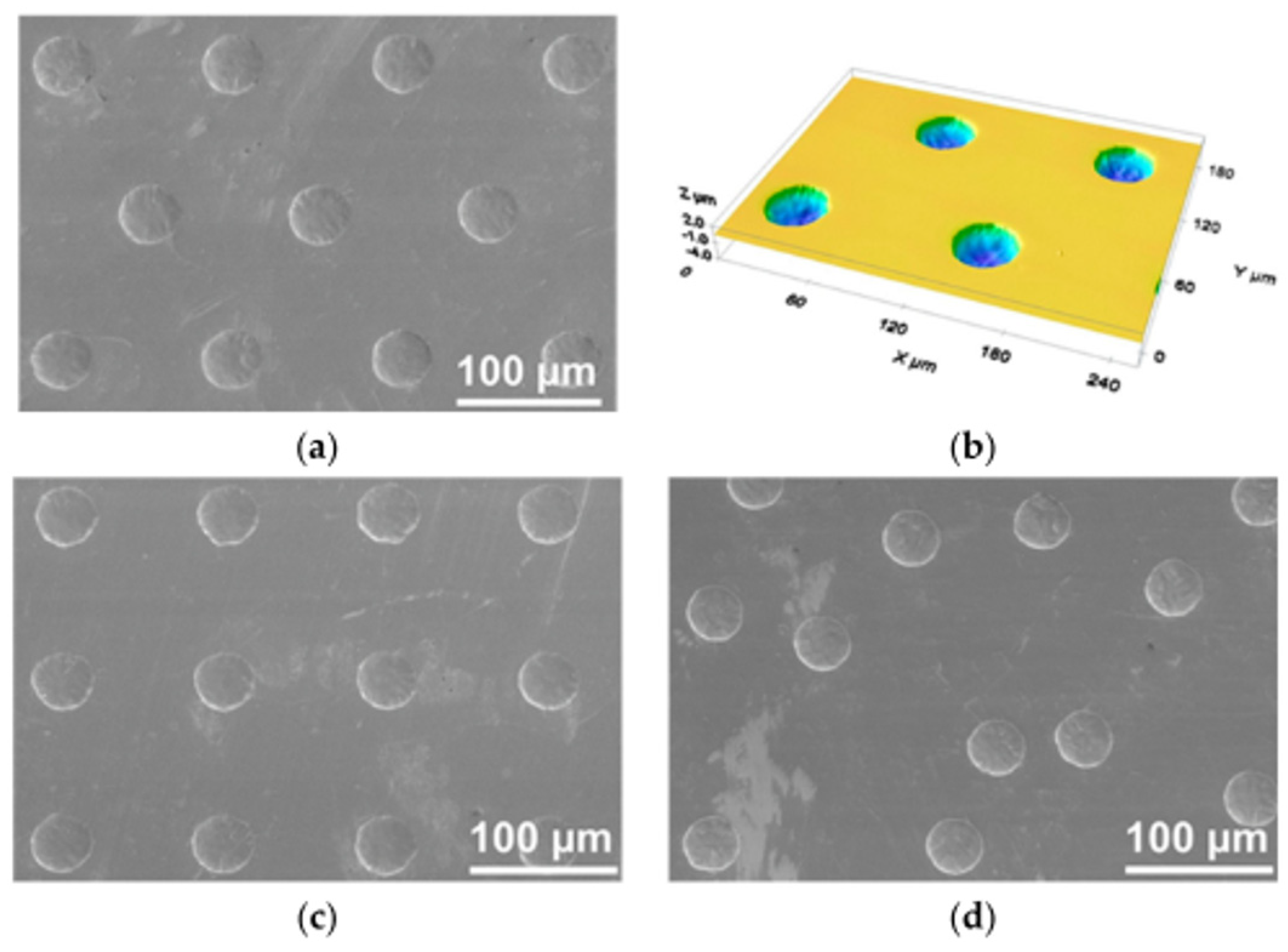
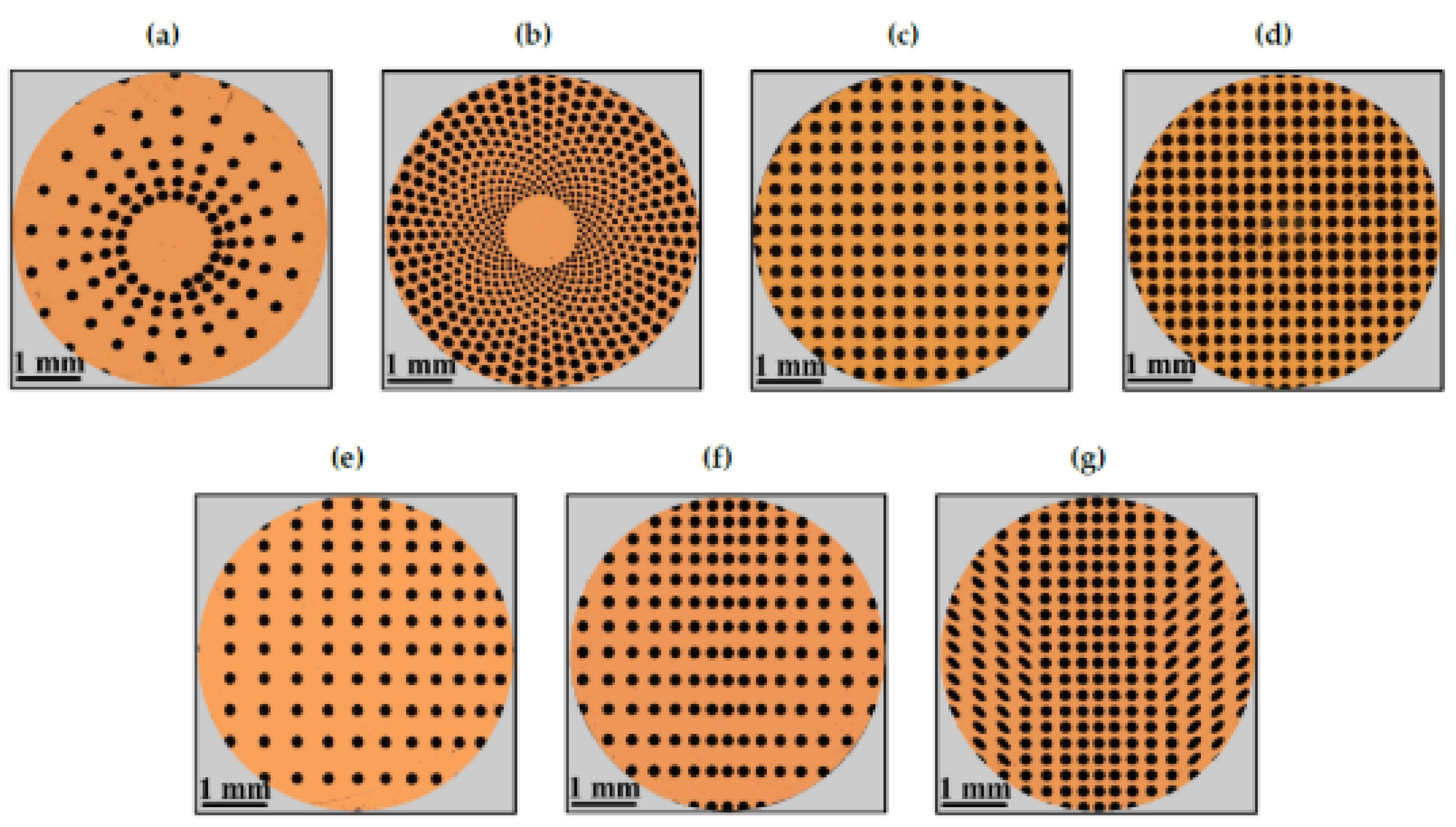

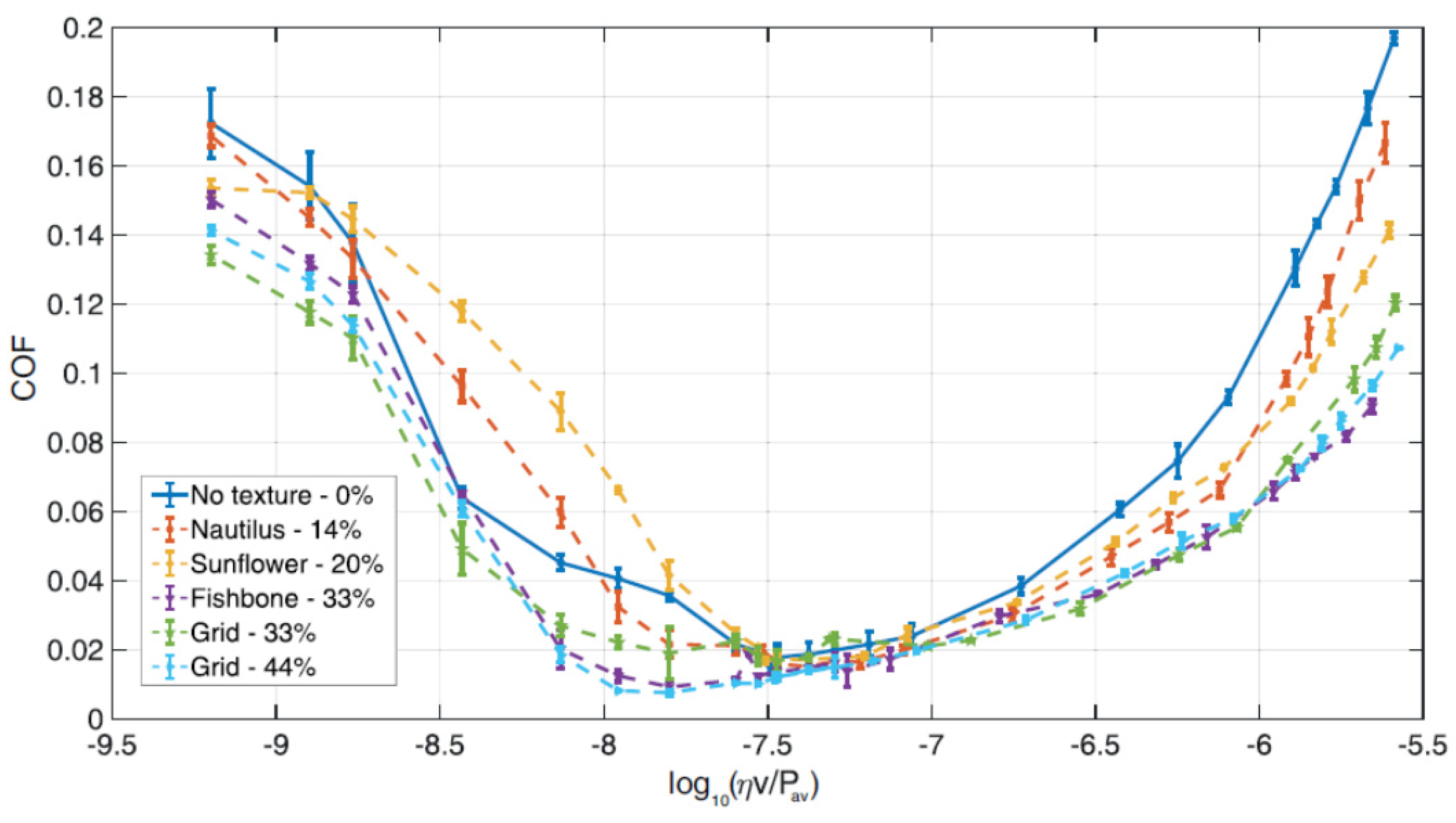
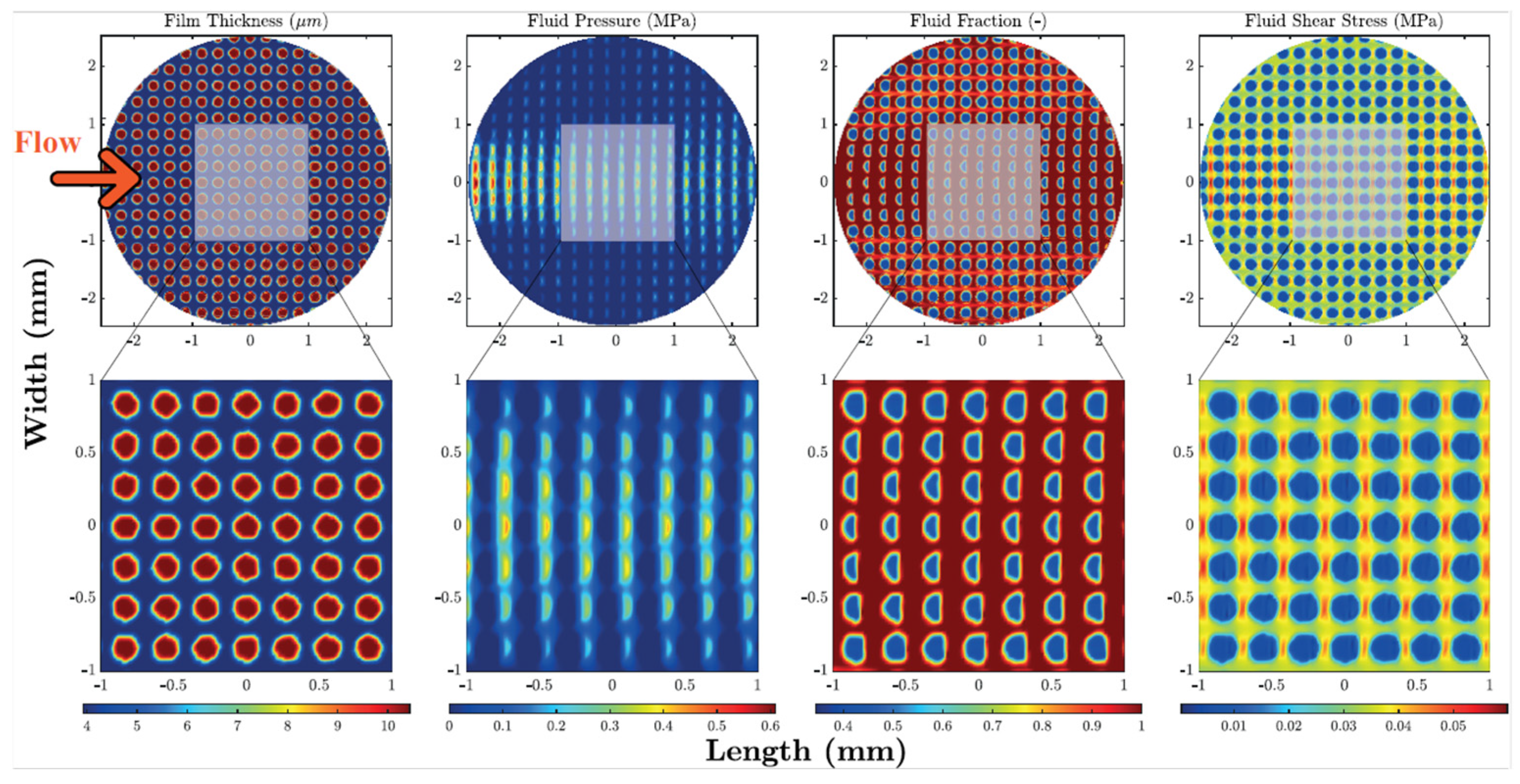
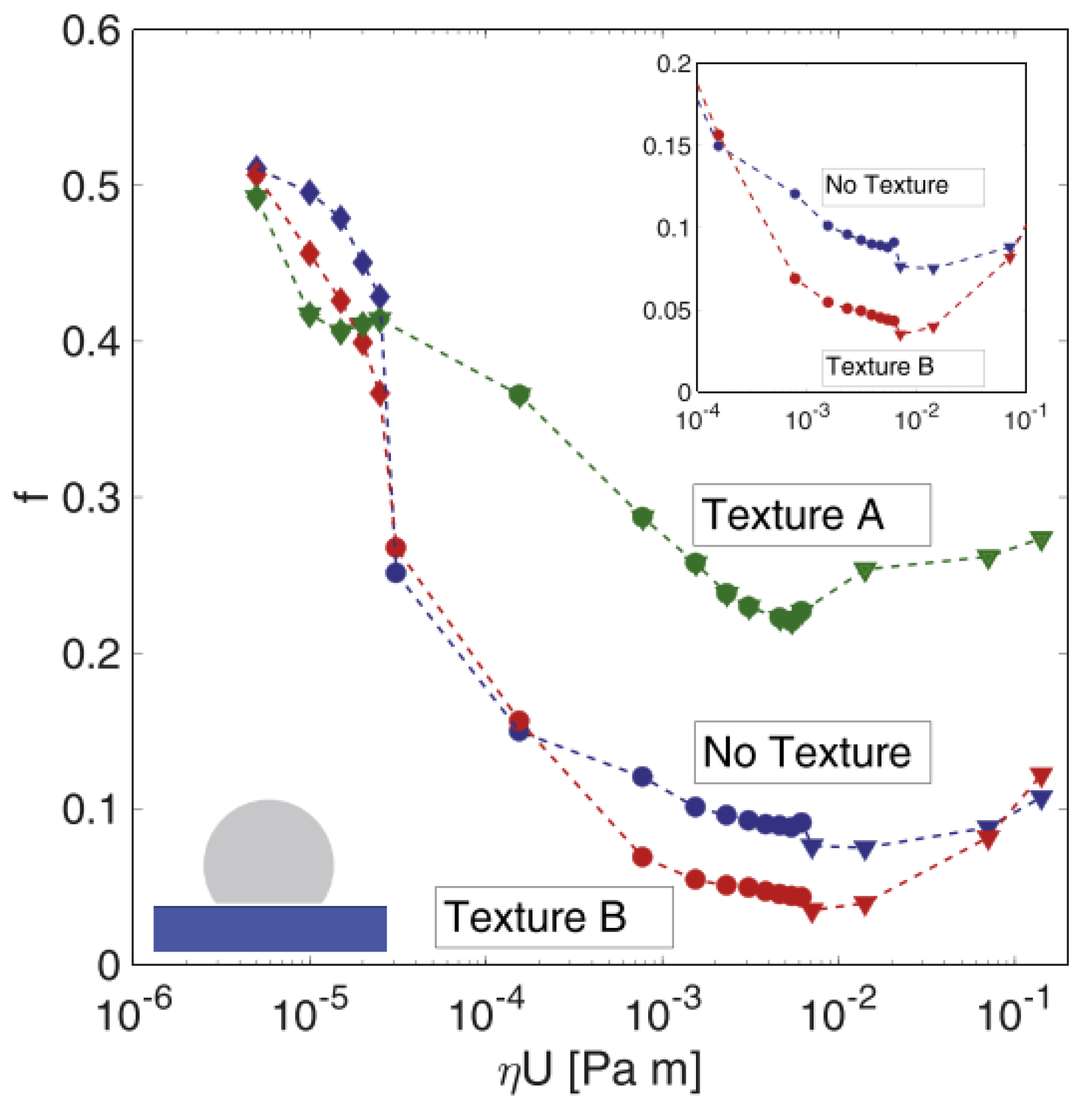
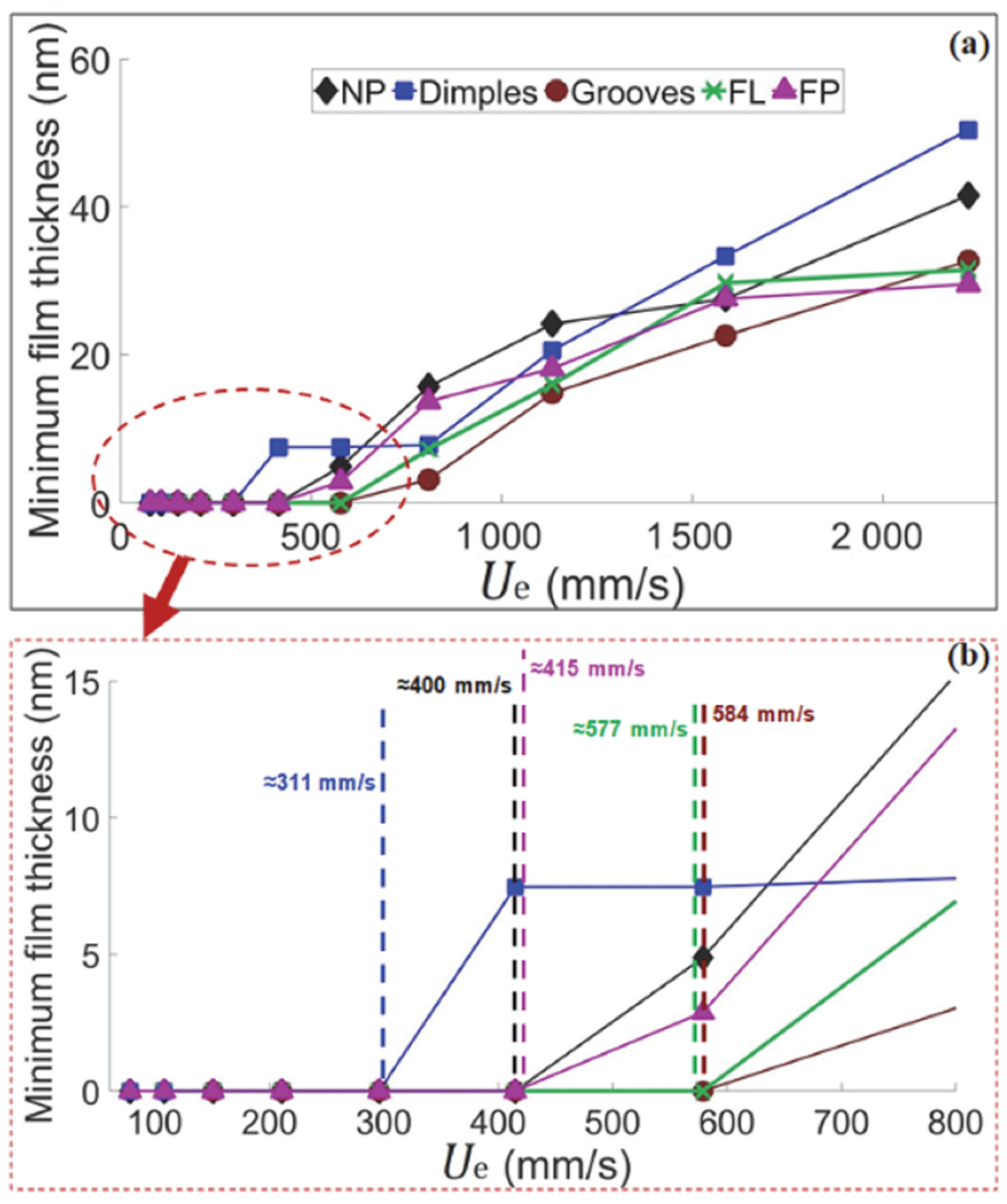
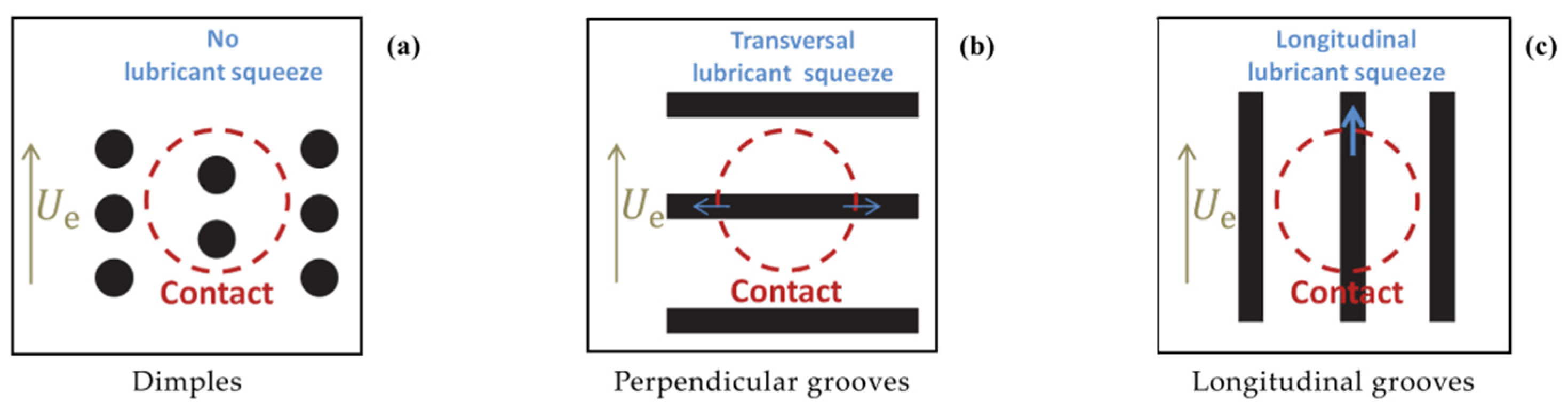
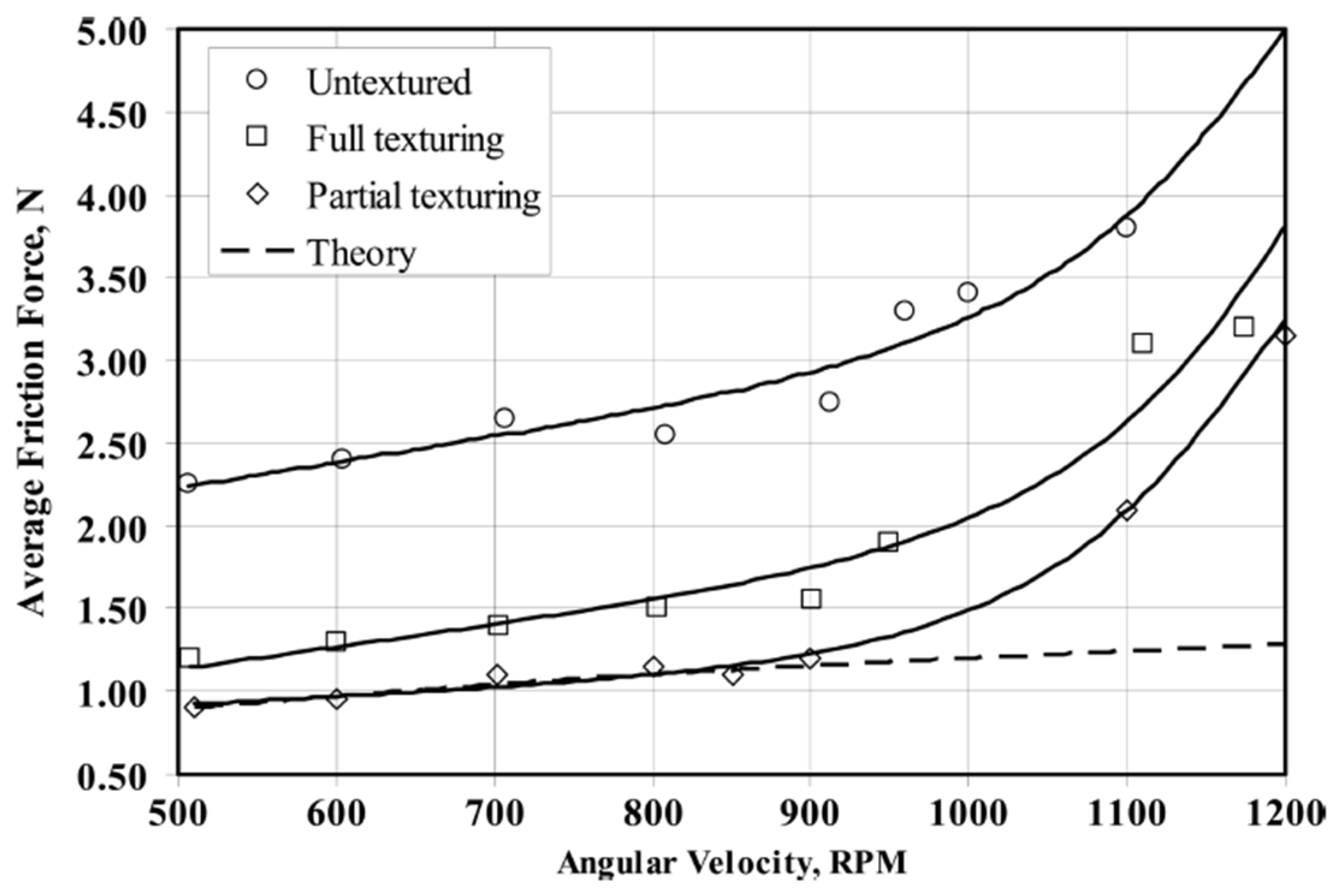





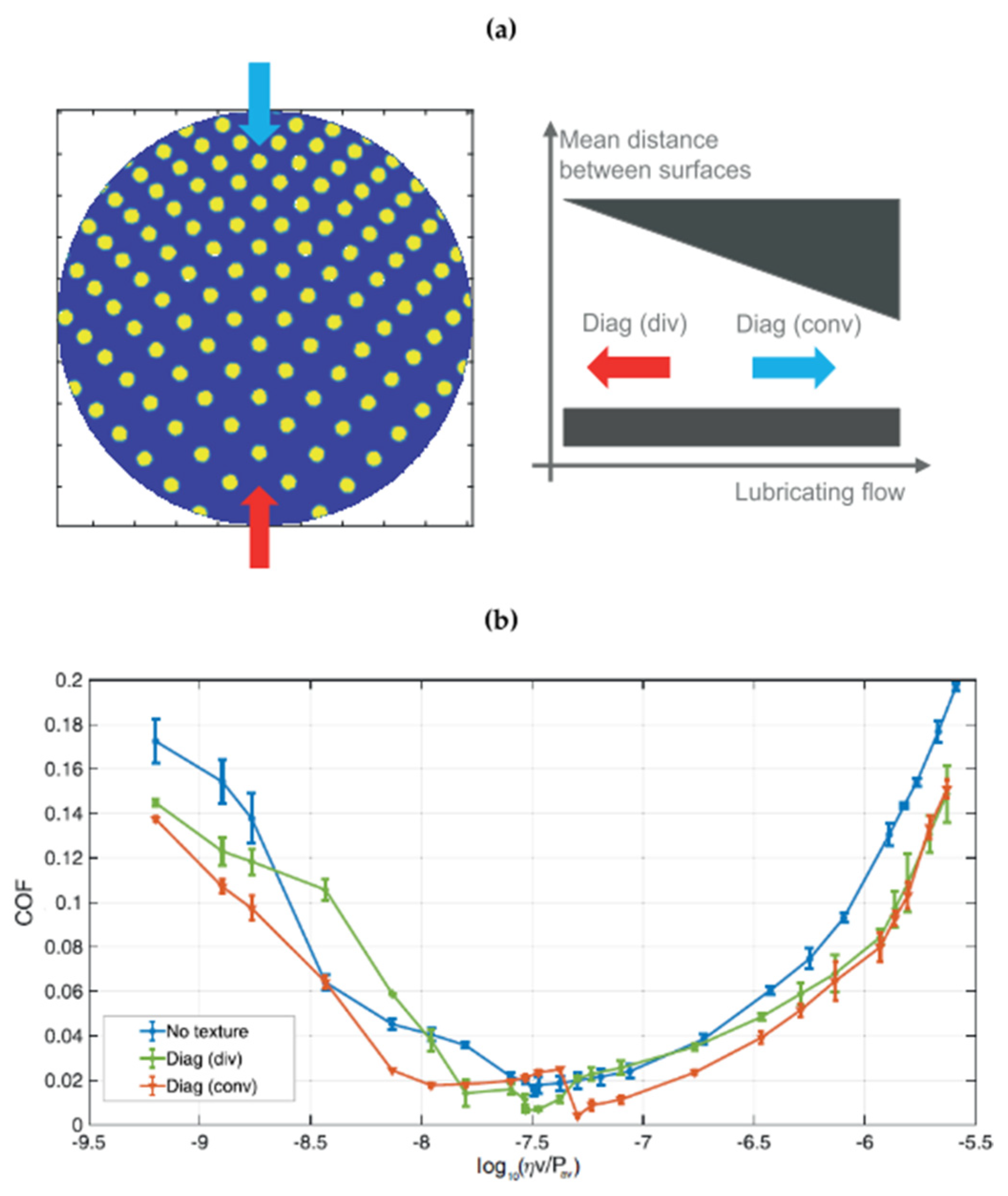
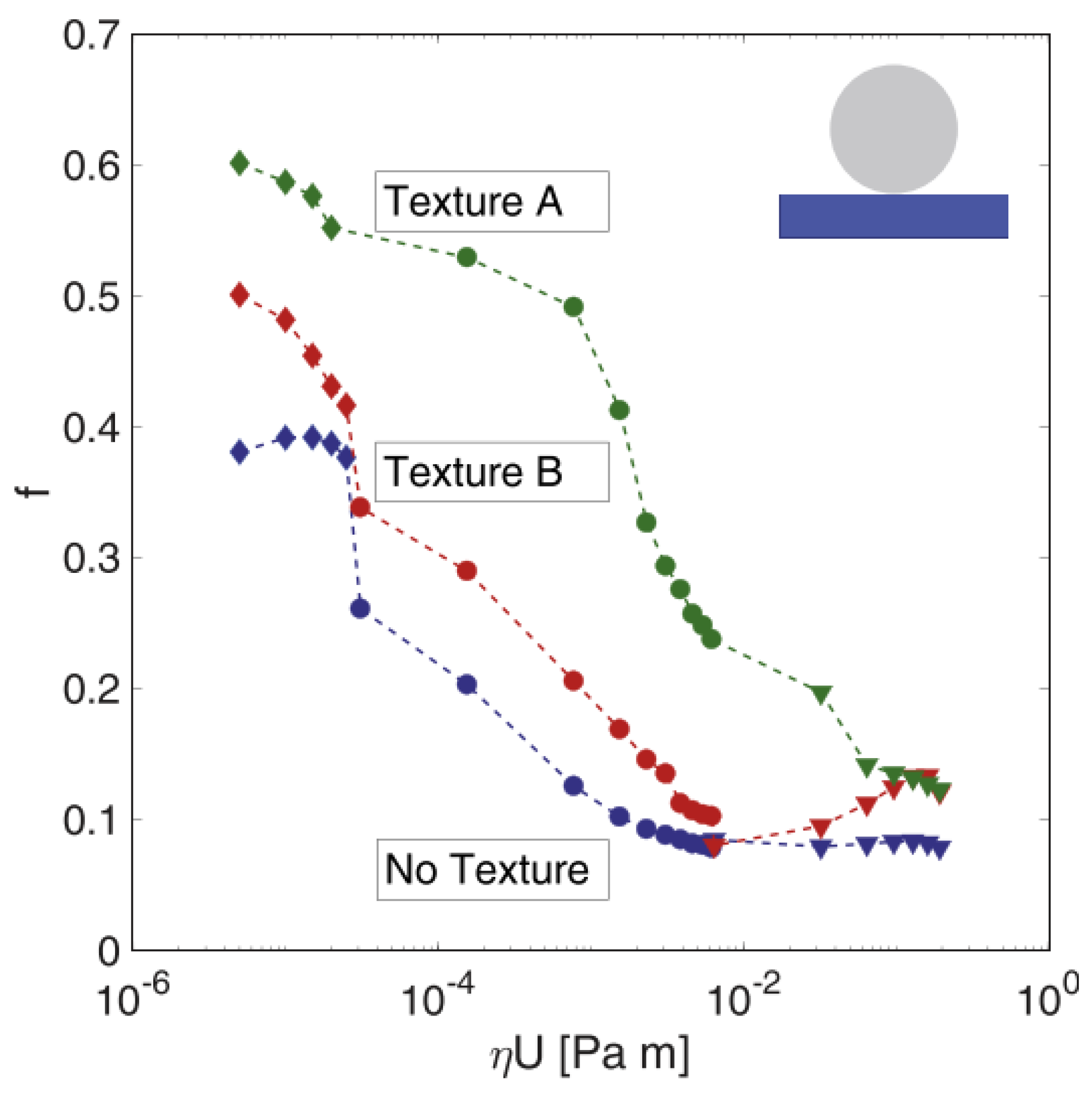
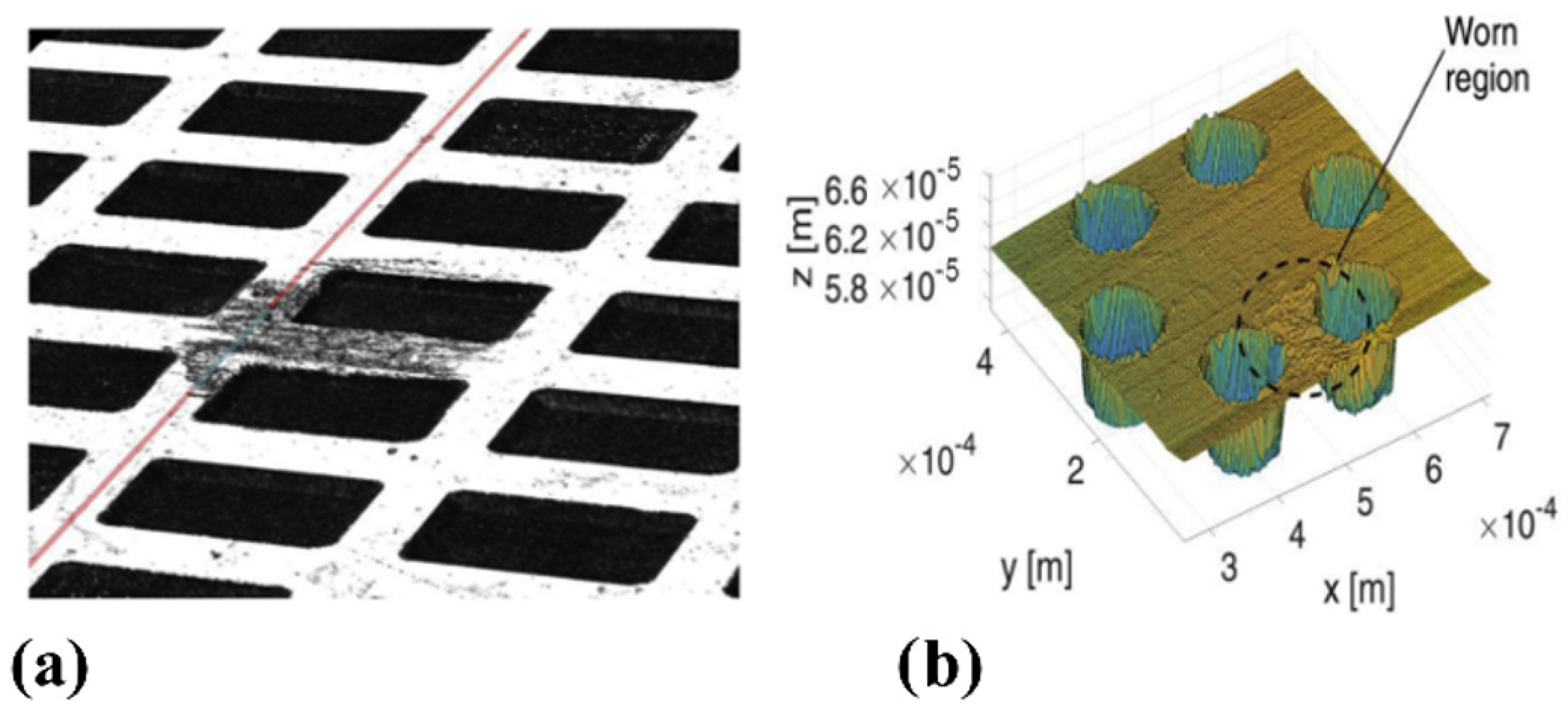
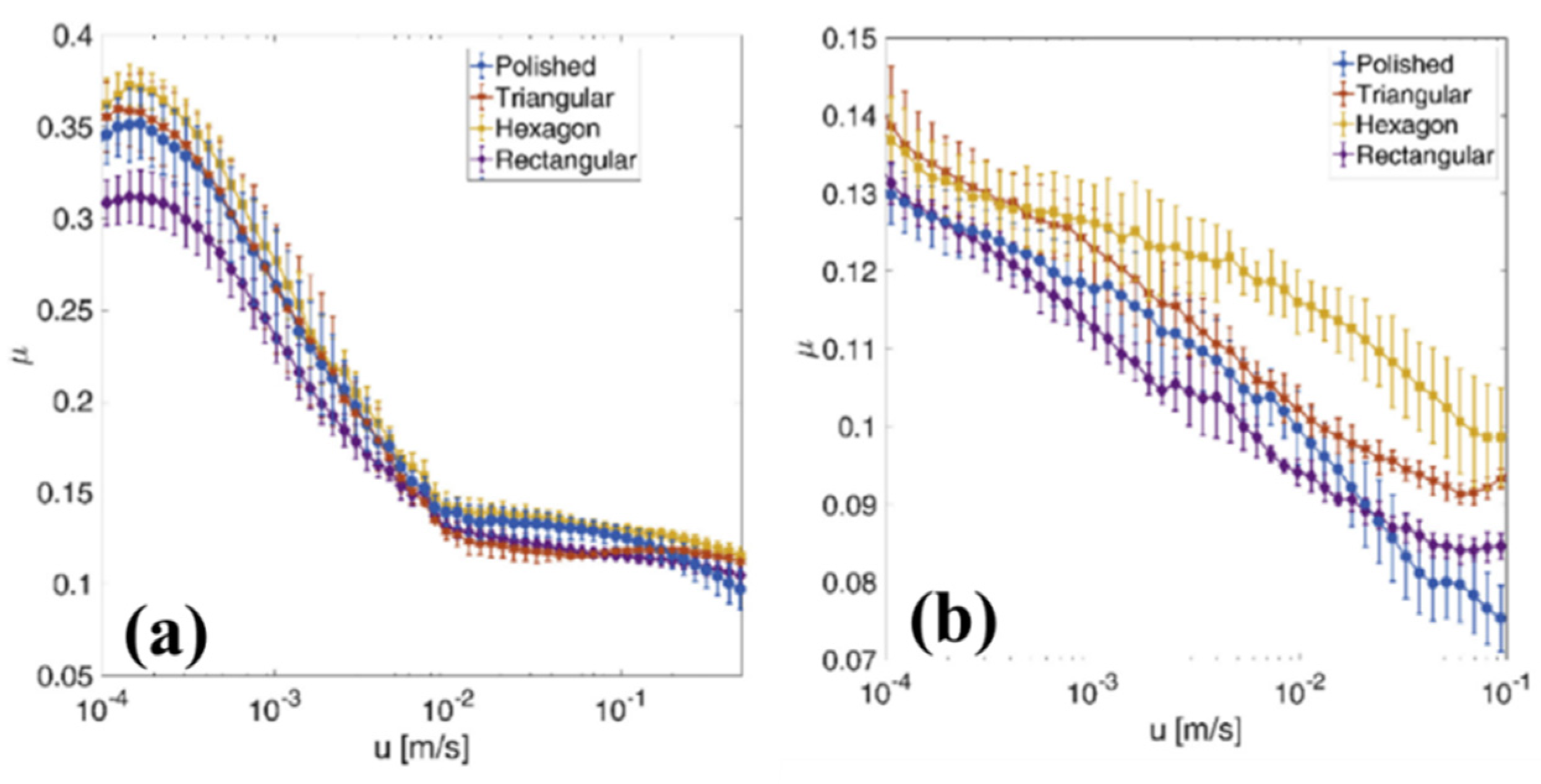
| Sample | Texture Design | Contact Type | Influence on COF | Reference |
|---|---|---|---|---|
| Martensitic stainless steel X90CrMoV18 (1.4112) | Crossed grooves | Conformal | Reduction Up to 33% | [47] |
| Steel C85 | Hexagonal matrix circular dimples VR = 10% | Conformal | Reduction Up to 82% | [30] |
| Steel C85 | Uniform grid Circular dimples VR = 10% | Conformal | Reduction Up to 82% | [30] |
| 100Cr6 steel | Uniform grid Circular dimples VR = 33% and 44% | Conformal | Reduction Up to 60% | [34] |
| Fluoroelastomer (commercial name Viton) | Uniform grid Circular dimples VR = 35% | Non-conformal | Increase Up to 325% | [77] |
| Fluoroelastomer (commercial name Viton) | Uniform grid Circular dimples VR = 35% | Conformal | Reduction Up to 22% | [77] |
| Fluoroelastomer (commercial name Viton) | Uniform grid Circular dimples VR = 20% | Non-conformal | Increase Up to 28% | [77] |
| Fluoroelastomer (commercial name Viton) | Uniform grid Circular dimples VR = 20% | Conformal | Reduction Up to 60% | [77] |
| Stainless steel (1.4112) | Unifrom grid Rectangular dimples VR = 53% | Non-conformal | Reduction Up to 20% | [74] |
| Chromium-hardened steel (AISI 52100) balls | Uniform grid Circular dimples VR = 14% | Conformal | Reduction Up to 20% | [65] |
| Steel C85 | Random matrix Circular dimples VR = 10% | Conformal | Reduction Up to 48% | [47] |
| Chrome-coated steel | Partial Texturing (symmetrical, at the ends of the sample) Circular dimples VR = 50% | Conformal | Directional Reduction Up to 29% | [38] |
| 100Cr6 steel | Non -uniform design Five groups of inclined micro-grooved dimples with different depths | Conformal | Directional Reduction Up to 20% | [46] |
| 100Cr6 steel | Fishbone design Circular dimples VR = 30% | Conformal | Directional Reduction Up to 55% Increase Up to 75% | [34] |
| 100Cr6 steel | Diagonal matrix Circular dimples | Conformal | Directional Reduction Up to 25% Increase Up to 83% | [34] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaudiuso, C.; Volpe, A.; Mezzapesa, F.P.; Putignano, C.; Ancona, A. Tailoring the Coefficient of Friction by Direct Laser Writing Surface Texturing. Micromachines 2024, 15, 7. https://doi.org/10.3390/mi15010007
Gaudiuso C, Volpe A, Mezzapesa FP, Putignano C, Ancona A. Tailoring the Coefficient of Friction by Direct Laser Writing Surface Texturing. Micromachines. 2024; 15(1):7. https://doi.org/10.3390/mi15010007
Chicago/Turabian StyleGaudiuso, Caterina, Annalisa Volpe, Francesco Paolo Mezzapesa, Carmine Putignano, and Antonio Ancona. 2024. "Tailoring the Coefficient of Friction by Direct Laser Writing Surface Texturing" Micromachines 15, no. 1: 7. https://doi.org/10.3390/mi15010007
APA StyleGaudiuso, C., Volpe, A., Mezzapesa, F. P., Putignano, C., & Ancona, A. (2024). Tailoring the Coefficient of Friction by Direct Laser Writing Surface Texturing. Micromachines, 15(1), 7. https://doi.org/10.3390/mi15010007










