An Active Vibration Isolation and Compensation System for Improving Optical Image Quality: Modeling and Experiment
Abstract
1. Introduction
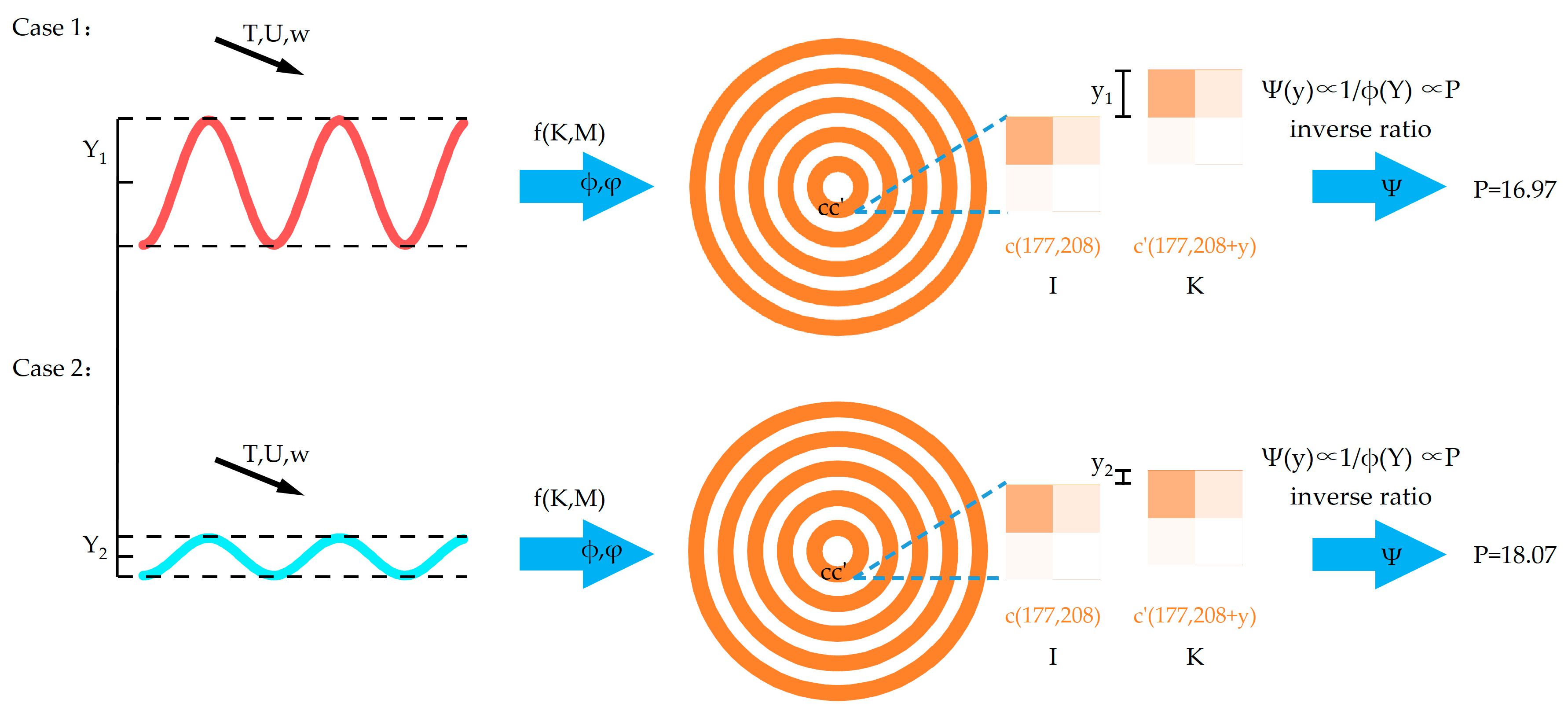
2. Design of the Image Performance Evaluation Index (IPEI)
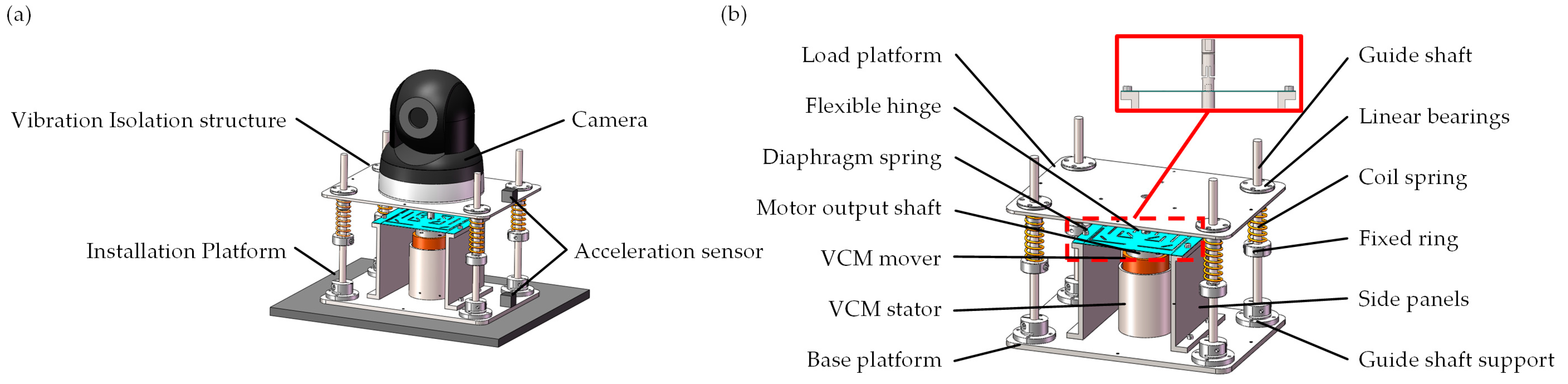
3. Design of an Active VICS for the ODE
4. Modeling and Active Control Algorithm Strategies
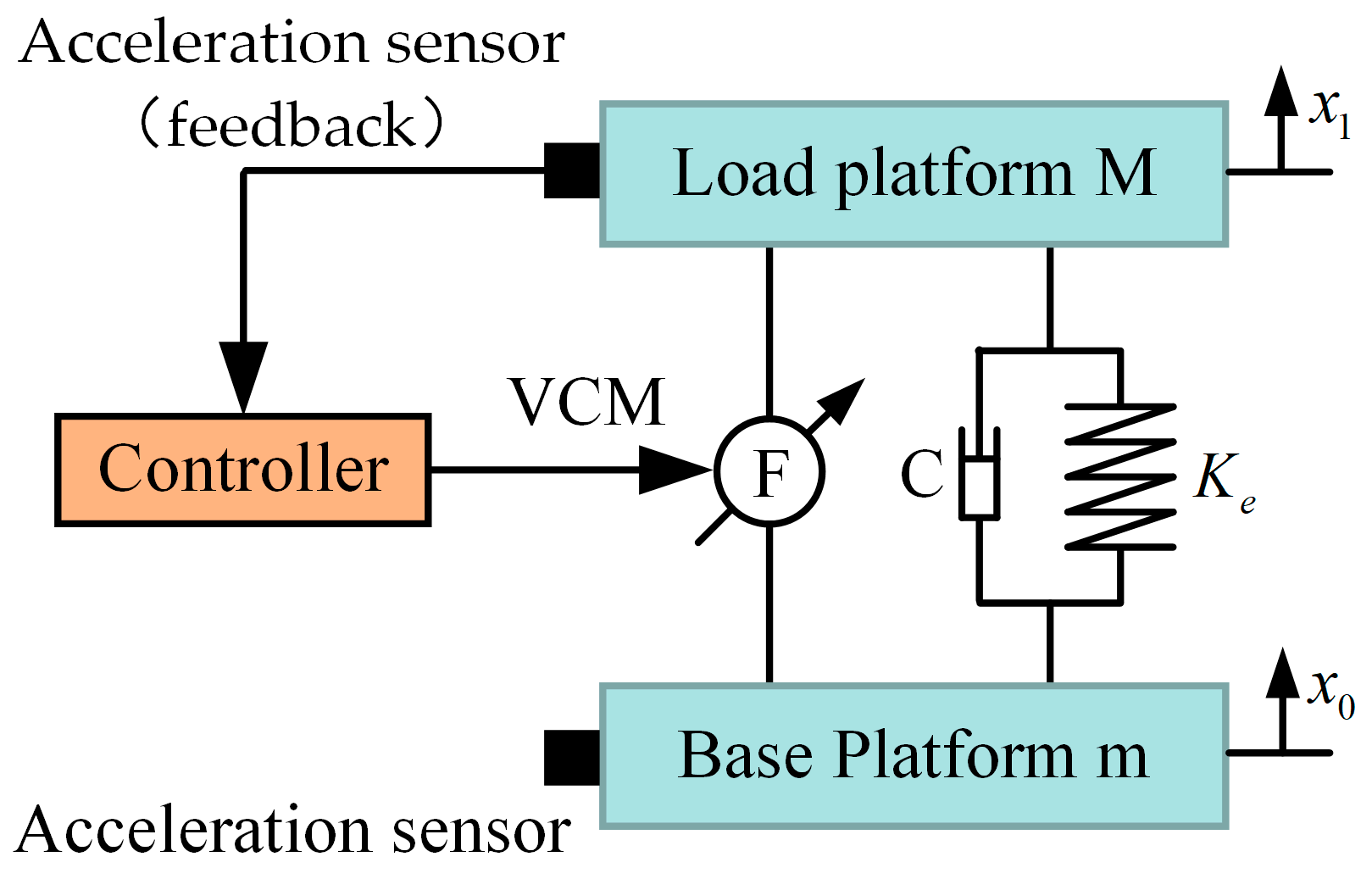
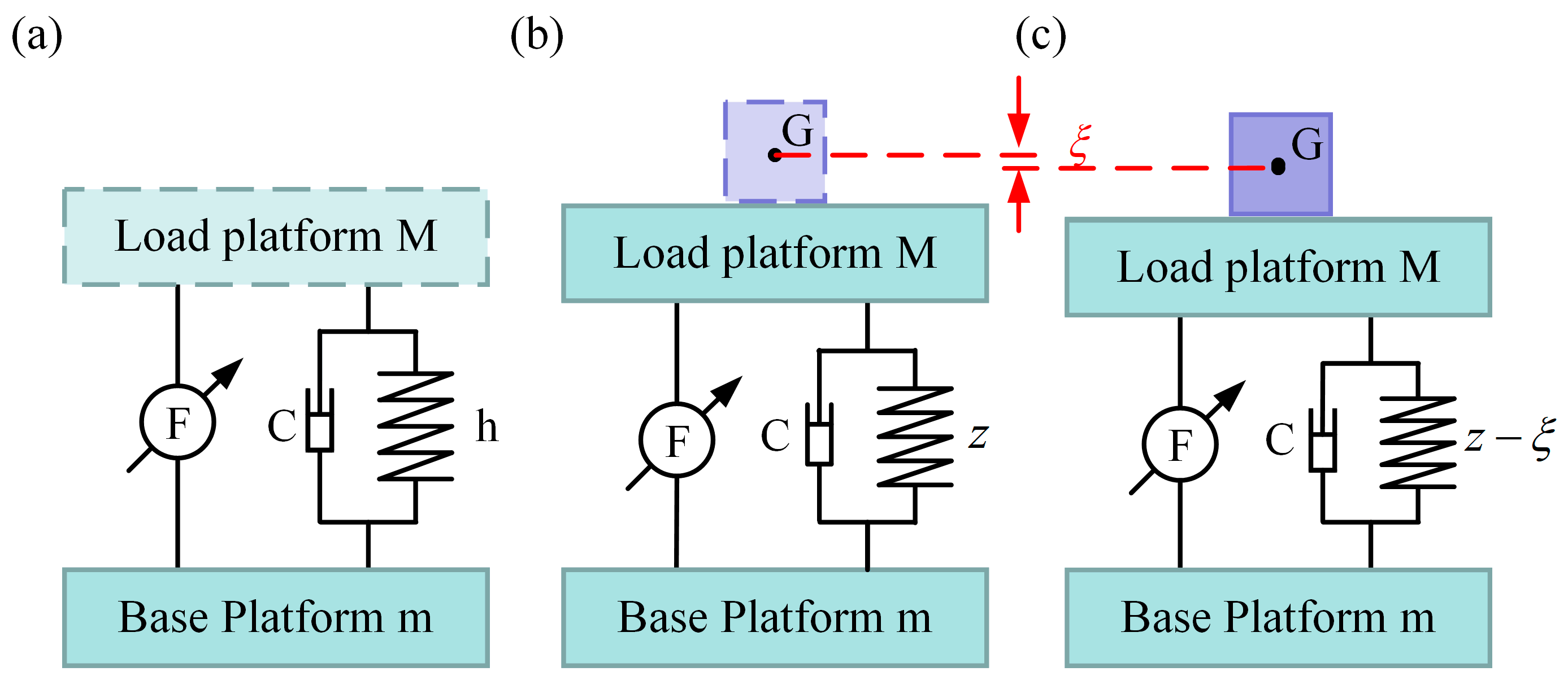
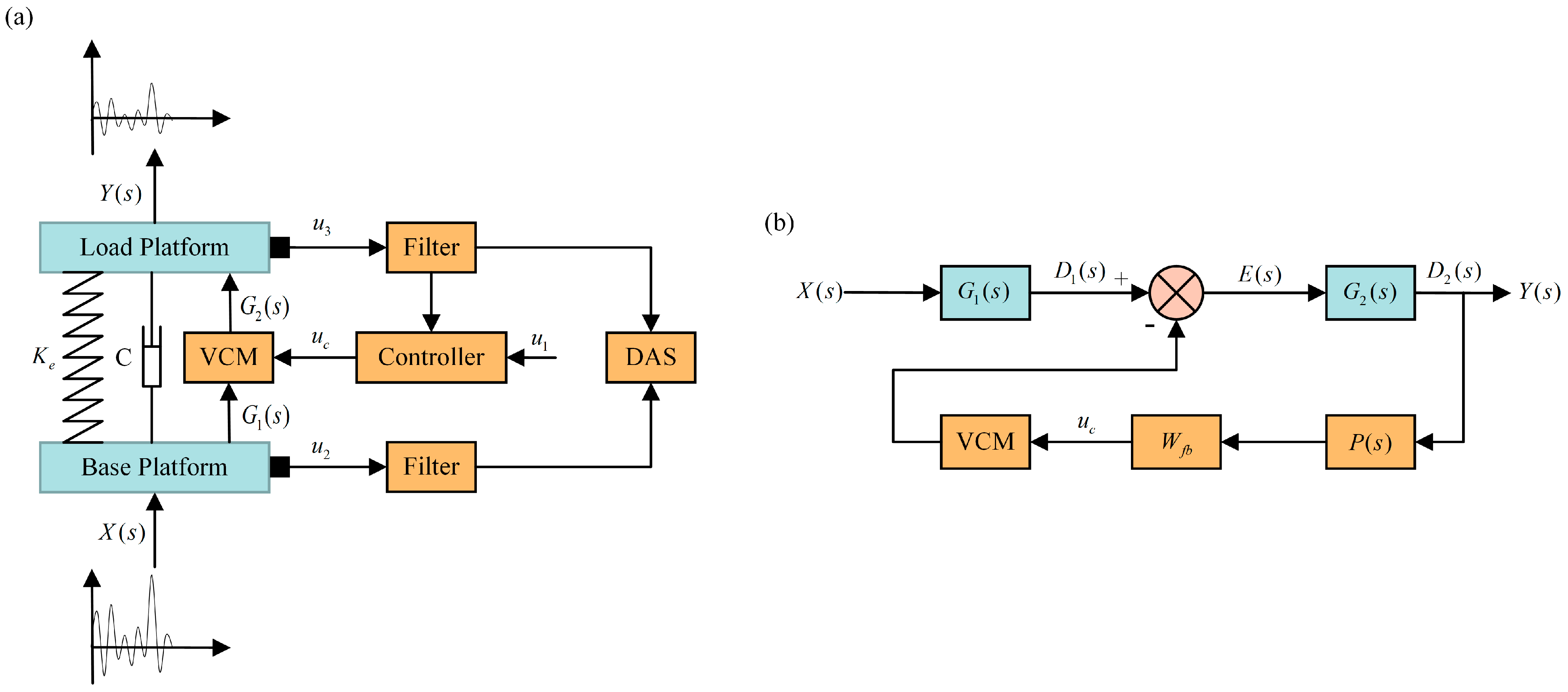
4.1. Modeling of the VICS for the ODE
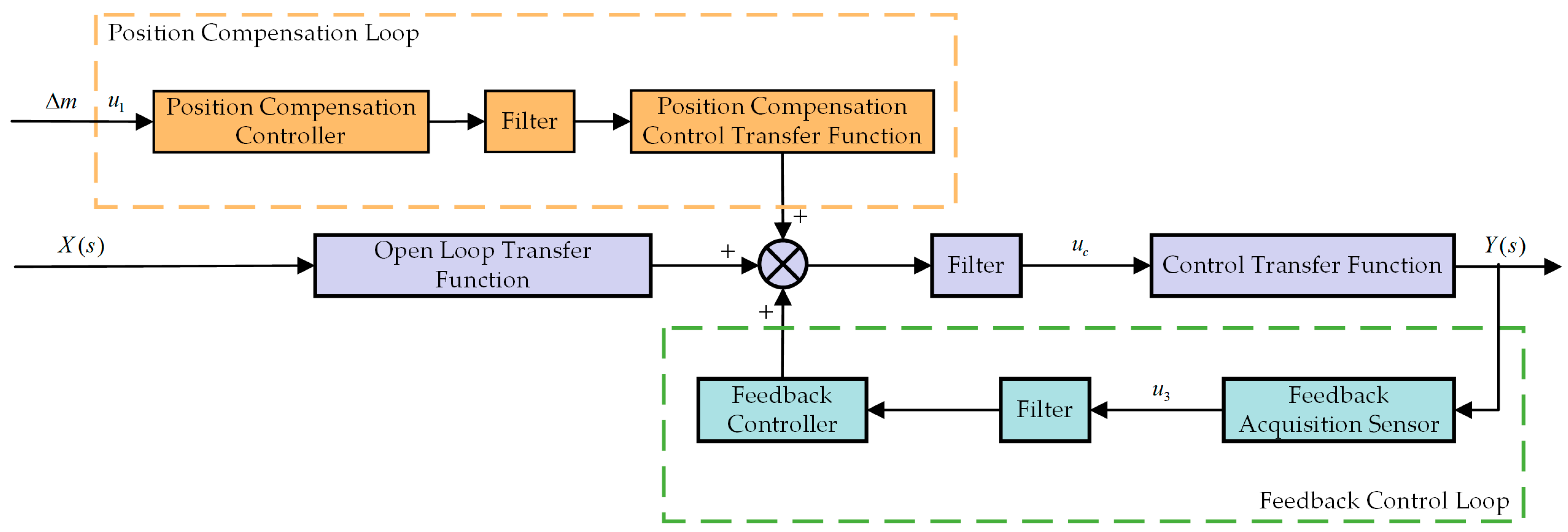
4.2. Dual-Loop Control Strategy of the ODE
5. Experiment
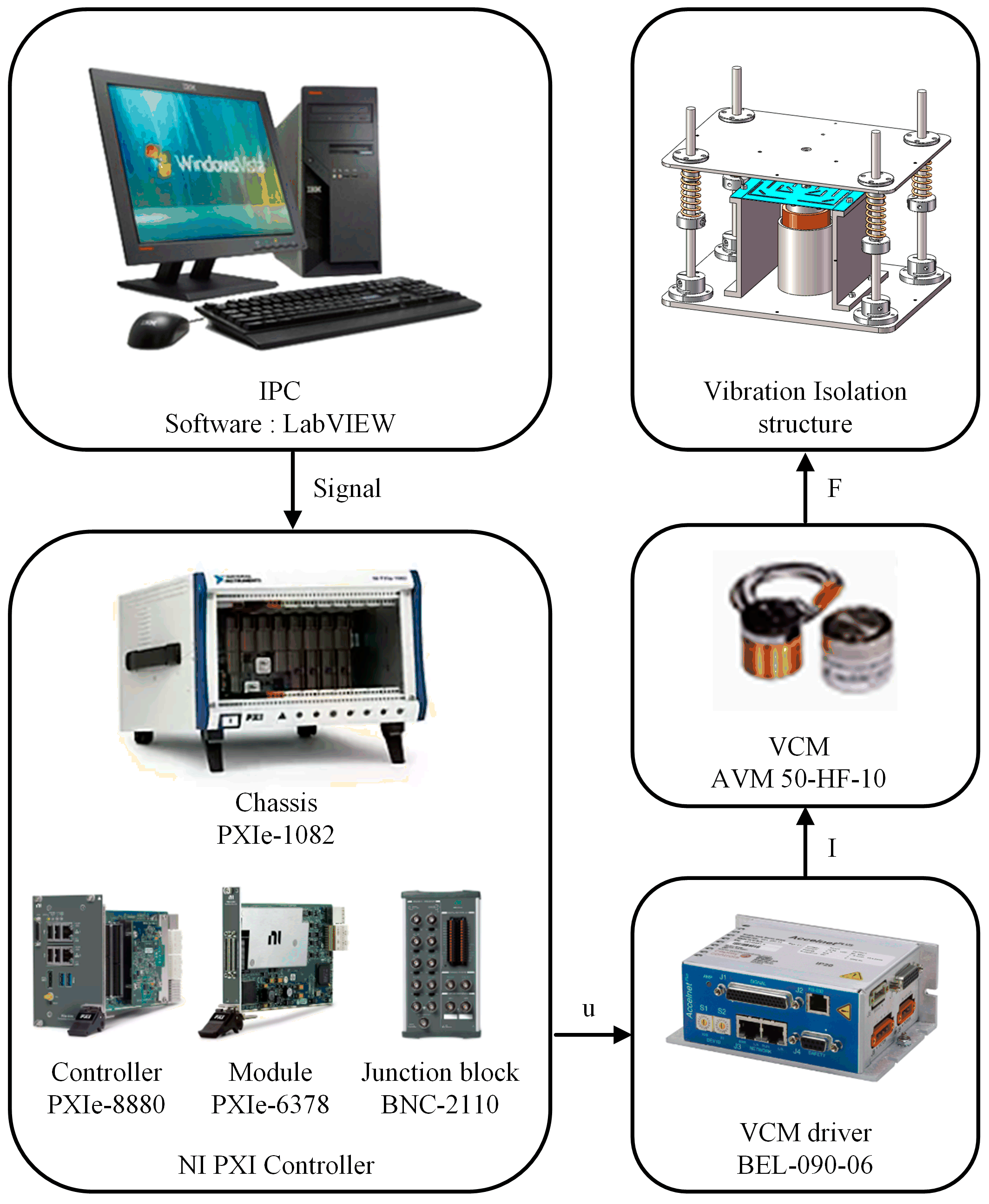
5.1. Experimental Platform Construction
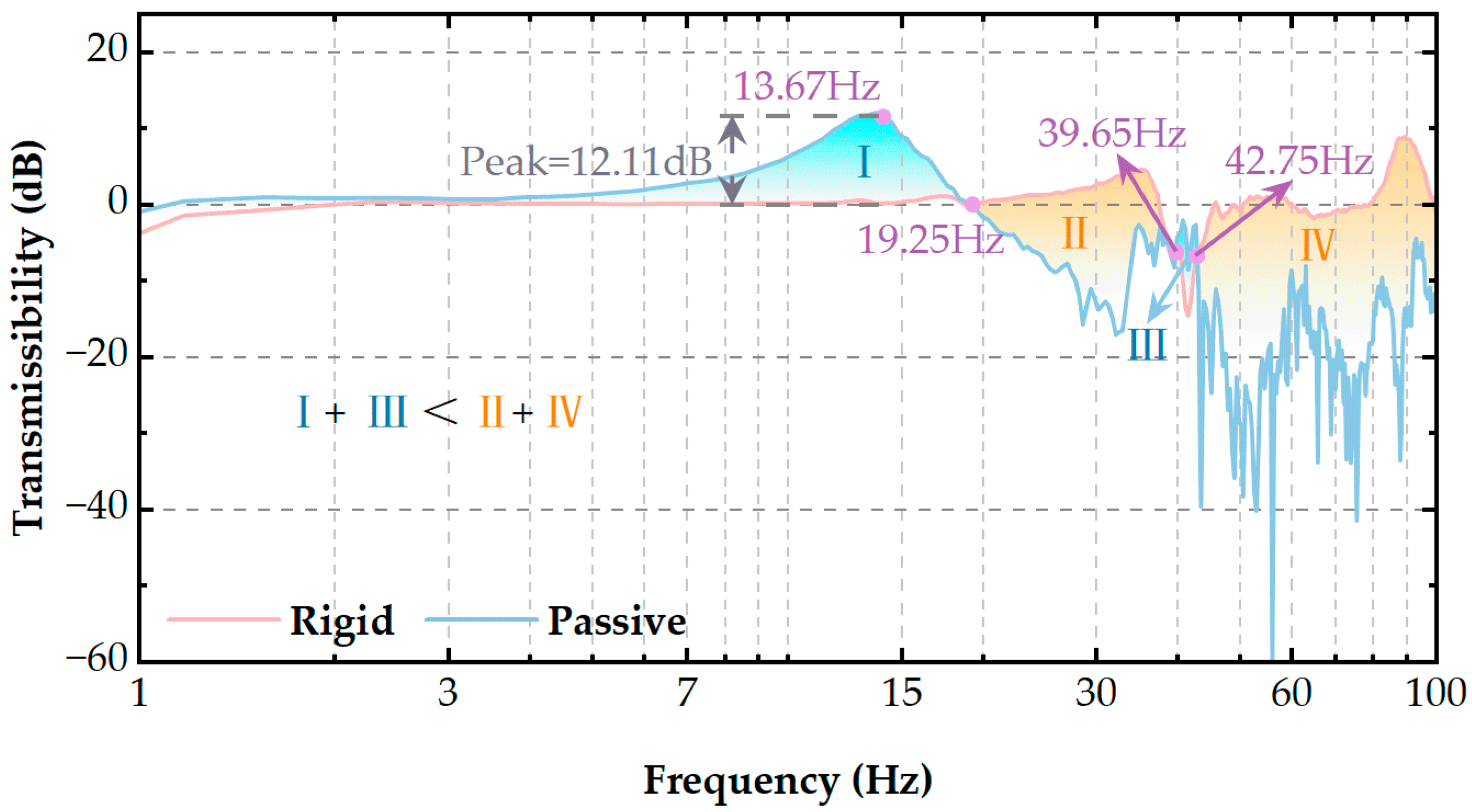
5.2. Experiment of the Vibration Isolation Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rahmaniar, W.; Rakhmania, A.E. Online Digital Image Stabilization for an Unmanned Aerial Vehicle (UAV). J. Robot. Control JRC 2021, 2, 234–239. [Google Scholar] [CrossRef]
- Shao, Z.; Luo, J.; Yu, F. Design and Simulation of a Damping Platform for Image Data Collecting Device on an Intelligent Vehicle. Noise Vib. Control 2021, 41, 230–235. [Google Scholar]
- Lv, Z.; Liu, T.; Benediktsson, J.A.; Falco, N. Land Cover Change Detection Techniques: Very-High-Resolution Optical Images: A Review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 44–63. [Google Scholar] [CrossRef]
- Li, B.; Xie, X.; Wei, X.; Tang, W. Ship Detection and Classification from Optical Remote Sensing Images: A Survey. Chin. J. Aeronaut. 2021, 34, 145–163. [Google Scholar] [CrossRef]
- Gerstmair, M.; Gschwandtner, M.; Findenig, R.; Lang, O.; Melzer, A.; Huemer, M. Miniaturized Advanced Driver Assistance Systems: A Low-Cost Educational Platform for Advanced Driver Assistance Systems and Autonomous Driving. IEEE Signal Process. Mag. 2021, 38, 105–114. [Google Scholar] [CrossRef]
- Rodin, C.D.; de Alcantara Andrade, F.A.; Hovenburg, A.R.; Johansen, T.A. A Survey of Practical Design Considerations of Optical Imaging Stabilization Systems for Small Unmanned Aerial Systems. Sensors 2019, 19, 4800. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Cao, D.; Yu, T. Decentralized Vibration Control of a Voice Coil Motor-Based Stewart Parallel Mechanism: Simulation and Experiments. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2019, 233, 132–145. [Google Scholar] [CrossRef]
- Li, C.; Tan, F. Effect of UAV Vibration on Imaging Quality of Binary Optical Elements. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1693–1698. [Google Scholar]
- Erturk, S. Real-Time Digital Image Stabilization Using Kalman Filters. Real-Time Imaging 2002, 8, 317–328. [Google Scholar] [CrossRef]
- Ljubicic, R.; Strelnikova, D.; Perks, M.T.; Eltner, A.; Pena-Haro, S.; Pizarro, A.; Dal Sasso, S.F.; Scherling, U.; Vuono, P.; Manfreda, S. A Comparison of Tools and Techniques for Stabilising Unmanned Aerial System (UAS) Imagery for Surface Flow Observations. Hydrol. Earth Syst. Sci. 2021, 25, 5105–5132. [Google Scholar] [CrossRef]
- Gurtner, A.; Walker, R.; Boles, W. Vibration Compensation for Fisheye Lenses in UAV Applications. In Proceedings of the 9th Biennial Conference of the Australian Pattern Recognition Society on Digital Image Computing Techniques and Applications (DICTA 2007), Glenelg, Australia, 3–5 December 2007; pp. 218–225. [Google Scholar]
- Doan, N.V.; Goo, N.S.; Ko, Y.; Seo, S.; Chung, M. Design and Analysis of Micro-Vibration Isolation System for Digital Image Correlation System-Based Structural Health Monitoring. Int. J. Aeronaut. Space Sci. 2022, 23, 711–722. [Google Scholar] [CrossRef]
- Kumar, R.; Dwivedi, G.; Singh, O. Portable Digital Holographic Camera Featuring Enhanced Field of View and Reduced Exposure Time. Opt. Lasers Eng. 2021, 137, 106359. [Google Scholar] [CrossRef]
- Rawat, P.; Singhai, J. Review of Motion Estimation and Video Stabilization Techniques For Hand Held Mobile Video. Signal Image Process. Int. J. SIPIJ 2011, 2, 159–168. [Google Scholar] [CrossRef]
- Li, Z.; Lao, M.; Phang, S.K.; Hamid, M.R.A.; Tang, K.Z.; Lin, F. Development and Design Methodology of an Anti-Vibration System on Micro-UAVs. In Proceedings of the International Micro Air Vehicle Conference and Flight Competition (IMAV), Toulouse, France, 18–21 September 2017; pp. 223–228. [Google Scholar]
- Li, L.; Tan, L.; Lin, K.; Wang, D.; Yang, H. The Influence of Flywheel Micro Vibration on Space Camera and Vibration Suppression. Mech. Syst. Signal Process. 2018, 100, 360–370. [Google Scholar] [CrossRef]
- Verma, M.; Lafarga, V.; Dehaeze, T.; Collette, C. Multi-Degree of Freedom Isolation System with High Frequency Roll-Off for Drone Camera Stabilization. IEEE Access 2020, 8, 176188–176201. [Google Scholar] [CrossRef]
- Wang, M.; Hu, Y.; Sun, Y.; Ding, J.; Pu, H.; Yuan, S.; Zhao, J.; Peng, Y.; Xie, S.; Luo, J. An Adjustable Low-Frequency Vibration Isolation Stewart Platform Based On Electromagnetic Negative Stiffness. Int. J. Mech. Sci. 2020, 181, 105714. [Google Scholar] [CrossRef]
- Yan, B.; Wang, Z.; Ma, H.; Bao, H.; Wang, K.; Wu, C. A Novel Lever-Type Vibration Isolator with Eddy Current Damping. J. Sound Vib. 2021, 494, 115862. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wang, Z.; Wu, C.; Wang, S.; Zhang, W. Lever-Type Quasi-Zero Stiffness Vibration Isolator with Magnetic Spring. J. Sound Vib. 2022, 527, 116865. [Google Scholar] [CrossRef]
- Wang, M.; Fu, S.; Ding, J.; Sun, Y.; Peng, Y.; Luo, J.; Pu, H. Analytical and Experimental Validation of Vibration Isolation System with Complementary Stiffness and Composite Control. Aerosp. Sci. Technol. 2023, 133, 108117. [Google Scholar] [CrossRef]
- Shin, Y.-H.; Kim, D.; Son, S.; Ham, J.-W.; Oh, K.-Y. Vibration Isolation of a Surveillance System Equipped in a Drone with Mode Decoupling. Appl. Sci.-Basel 2021, 11, 1961. [Google Scholar] [CrossRef]
- Jiang, G.; Jing, X.; Guo, Y. A Novel Bio-Inspired Multi-Joint Anti-Vibration Structure and Its Nonlinear HSLDS Properties. Mech. Syst. Signal Process. 2020, 138, 106552. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Wu, Z.-Y.; Zhang, W.-M. Bio-Inspired Toe-like Structure for Low-Frequency Vibration Isolation. Mech. Syst. Signal Process. 2022, 162, 108010. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Kovacic, I.; Waters, T.P. On the Force Transmissibility of a Vibration Isolator with Quasi-Zero-Stiffness. J. Sound Vib. 2009, 322, 707–717. [Google Scholar] [CrossRef]
- Virgin, L.N.; Santillan, S.T.; Plaut, R.H. Vibration Isolation Using Extreme Geometric Nonlinearity. J. Sound Vib. 2008, 315, 721–731. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kumar, A. Disturbance Rejection and Force-Tracking Controller of Nonlinear Lateral Vibrations in Passenger Rail Vehicle Using Magnetorheological Fluid Damper. J. Intell. Mater. Syst. Struct. 2018, 29, 279–297. [Google Scholar] [CrossRef]
- Ortiz Batista, E.L.; Barghouthi, M.R.; de Oliveira Lopes, E.M. A Novel Adaptive Scheme to Improve the Performance of Feedforward Active Vibration Control Systems. IEEE/Asme Trans. Mechatron. 2022, 27, 2322–2332. [Google Scholar] [CrossRef]
- Gawryluk, J.; Mitura, A.; Teter, A. Dynamic Control of Kinematically Excited Laminated, Thin-Walled Beam Using Macro Fibre Composite Actuator. Compos. Struct. 2020, 236, 111898. [Google Scholar] [CrossRef]
- Jamshidifar, H.; Khosravani, S.; Fidan, B.; Khajepour, A. Vibration Decoupled Modeling and Robust Control of Redundant Cable-Driven Parallel Robots. IEEE/Asme Trans. Mechatron. 2018, 23, 690–701. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Shaw, J. Low-Frequency Vibration Control of a Pan/Tilt Platform with Vision Feedback. J. Sound Vib. 2007, 302, 716–727. [Google Scholar] [CrossRef]
- Zhao, F.; Dong, M.; Qin, Y.; Gu, L.; Guan, J. Adaptive Neural-Sliding Mode Control of Active Suspension System for Camera Stabilization. Shock Vib. 2015, 2015, 542364. [Google Scholar] [CrossRef]
- Negash, B.A.; You, W.; Lee, J.; Lee, C.; Lee, K. Semi-Active Control of a Nonlinear Quarter-Car Model of Hyperloop Capsule Vehicle with Skyhook and Mixed Skyhook-Acceleration Driven Damper Controller. Adv. Mech. Eng. 2021, 13, 1687814021999528. [Google Scholar] [CrossRef]
- Cheng, M.; Xing, J.; Chen, Z.; Pan, Z. Design, Analysis and Experimental Investigation on the Whole-Spacecraft Vibration Isolation Platform with Magnetorheological Dampers. Smart Mater. Struct. 2019, 28, 075016. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Z.; Zheng, G. Policy Optimization for Vibration Isolator Stiffness Control during Agile Attitude Maneuvers. Mech. Syst. Signal Process. 2022, 165, 108279. [Google Scholar] [CrossRef]
- Sun, M.; Feng, Y.; Wang, Y.; Huang, W.; Su, S. Design, Analysis and Experiment of a Bridge-Type Piezoelectric Actuator for Infrared Image Stabilization. Micromachines 2021, 12, 1197. [Google Scholar] [CrossRef]
- Hyde, T.T.; Ha, K.Q.; Johnston, J.D.; Howard, J.M.; Mosier, G.E. Integrated Modeling Activites for the James Webb Space Telescope Opticle Jitter Analysis. In Optical, Infrared, and Millimeter Space Telescopes, Pts 1-3; Mather, J.C., Ed.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2004; Volume 5487, pp. 588–599. [Google Scholar]
- Lee, J.H.; Yoon, S.; Kim, B.; Gwon, G.-H.; Kim, I.-H.; Jung, H.-J. A New Image-Quality Evaluating and Enhancing Methodology for Bridge Inspection Using an Unmanned Aerial Vehicle. Smart Struct. Syst. 2021, 27, 209–226. [Google Scholar] [CrossRef]
- Ali, M.A.; Eltohamy, F.; Abd-Elrazek, A.; Hanafy, M.E. Assessment of Micro-Vibrations Effect on the Quality of Remote Sensing Satellites Images. Int. J. Image Data Fusion 2023. ahead-of-print. [Google Scholar] [CrossRef]
- Satapathy, S.C.; Raja, N.S.M.; Rajinikanth, V.; Ashour, A.S.; Dey, N. Multi-Level Image Thresholding Using Otsu and Chaotic Bat Algorithm. Neural Comput. Appl. 2018, 29, 1285–1307. [Google Scholar] [CrossRef]
- Hao, R.-B.; Lu, Z.-Q.; Ding, H.; Chen, L.-Q. A Nonlinear Vibration Isolator Supported on a Flexible Plate: Analysis and Experiment. Nonlinear Dyn. 2022, 108, 941–958. [Google Scholar] [CrossRef]
- Chai, Y.; Jing, X.; Chao, X. X-Shaped Mechanism Based Enhanced Tunable QZS Property for Passive Vibration Isolation. Int. J. Mech. Sci. 2022, 218, 107077. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Ma, H.; Wu, C. A Theory for Bistable Vibration Isolators. Mech. Syst. Signal Process. 2022, 167, 108507. [Google Scholar] [CrossRef]






| Parameter | Specifications |
|---|---|
| Model | DS-2DE2204IW-DE3/W/XM |
| Size | 125 × 137.6 mm |
| Weight | 650 g |
| Parameters | Values |
|---|---|
| Payload Mass M (Kg) | 1.5 |
| System stiffness (N/m) | 11,066 |
| System damping C (N S/m) | 33 |
| Name | Material |
|---|---|
| Load platform, base platform, flexible hinge, side panels, motor output shaft, fixed ring. | Al6061 |
| Guide shaft support | S45C |
| Linear bearings, guide shaft | GCr15 |
| Diaphragm spring, coil spring | 65Mn |
| System Composition | Equipment Model |
|---|---|
| Data acquisition system | LMS SCADAS Mobile SCM205 |
| Power amplifier | SA-PA050 |
| Vibration exciter | SA-JZ020 |
| Acceleration sensor | PCB-356A17 |
| Sensor signal conditioner | PCB-482C05 |
| NI controller | NI PXIe-1082, PXIe-8880, PXIe-6378, BNC-2110 |
| DC power supply | MAISHENG MT-152D |
| VCM driver | BEL-090-06 |
| VCM | AVM 50-HF-10 |
| Upper computer | LMS Testlab software |
| NI LabVIEW software | |
| HIKVCSION SADP |
| Resonance Peak at Natural Frequency (13.67 Hz) | Acceleration Amplitude | Decrease | ||
|---|---|---|---|---|
| Random | Passive | 12.11 dB | / | 13.95 dB |
| IFF | −1.84 dB | |||
| 10 Hz | Passive | / | ±0.254 g | 0.160 g |
| IFF | / | ±0.094 g | ||
| 14 Hz | Passive | / | ±0.410 g | 0.300 g |
| IFF | / | ±0.110 g | ||
| 20 Hz | Passive | / | ±0.119 g | 0.053 g |
| IFF | / | ±0.066 g | ||
| 60 Hz | Passive | / | ±0.025 g | 0.009 g |
| IFF | / | ±0.016 g |
| Conditions | White Noise | 10 Hz | 14 Hz | 20 Hz | 60 Hz |
|---|---|---|---|---|---|
| Passive | 23.36274 | 19.63535 | 16.31451 | 27.28037 | 28.13014 |
| IFF | 25.53195 | 23.12428 | 23.82355 | 27.54754 | 28.11190 |
| Performance improvement | 9.28% | 17.77% | 46.03% | 0.98% | −0.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Xiong, J.; Fu, S.; Ding, J.; Sun, Y.; Peng, Y.; Xie, S.; Luo, J.; Pu, H.; Shao, S. An Active Vibration Isolation and Compensation System for Improving Optical Image Quality: Modeling and Experiment. Micromachines 2023, 14, 1387. https://doi.org/10.3390/mi14071387
Wang M, Xiong J, Fu S, Ding J, Sun Y, Peng Y, Xie S, Luo J, Pu H, Shao S. An Active Vibration Isolation and Compensation System for Improving Optical Image Quality: Modeling and Experiment. Micromachines. 2023; 14(7):1387. https://doi.org/10.3390/mi14071387
Chicago/Turabian StyleWang, Min, Jing Xiong, Shibo Fu, Jiheng Ding, Yi Sun, Yan Peng, Shaorong Xie, Jun Luo, Huayan Pu, and Shilin Shao. 2023. "An Active Vibration Isolation and Compensation System for Improving Optical Image Quality: Modeling and Experiment" Micromachines 14, no. 7: 1387. https://doi.org/10.3390/mi14071387
APA StyleWang, M., Xiong, J., Fu, S., Ding, J., Sun, Y., Peng, Y., Xie, S., Luo, J., Pu, H., & Shao, S. (2023). An Active Vibration Isolation and Compensation System for Improving Optical Image Quality: Modeling and Experiment. Micromachines, 14(7), 1387. https://doi.org/10.3390/mi14071387






