An Experimental Study of Dislocation Dynamics in GaN
Abstract
1. Introduction
2. Materials and Methods
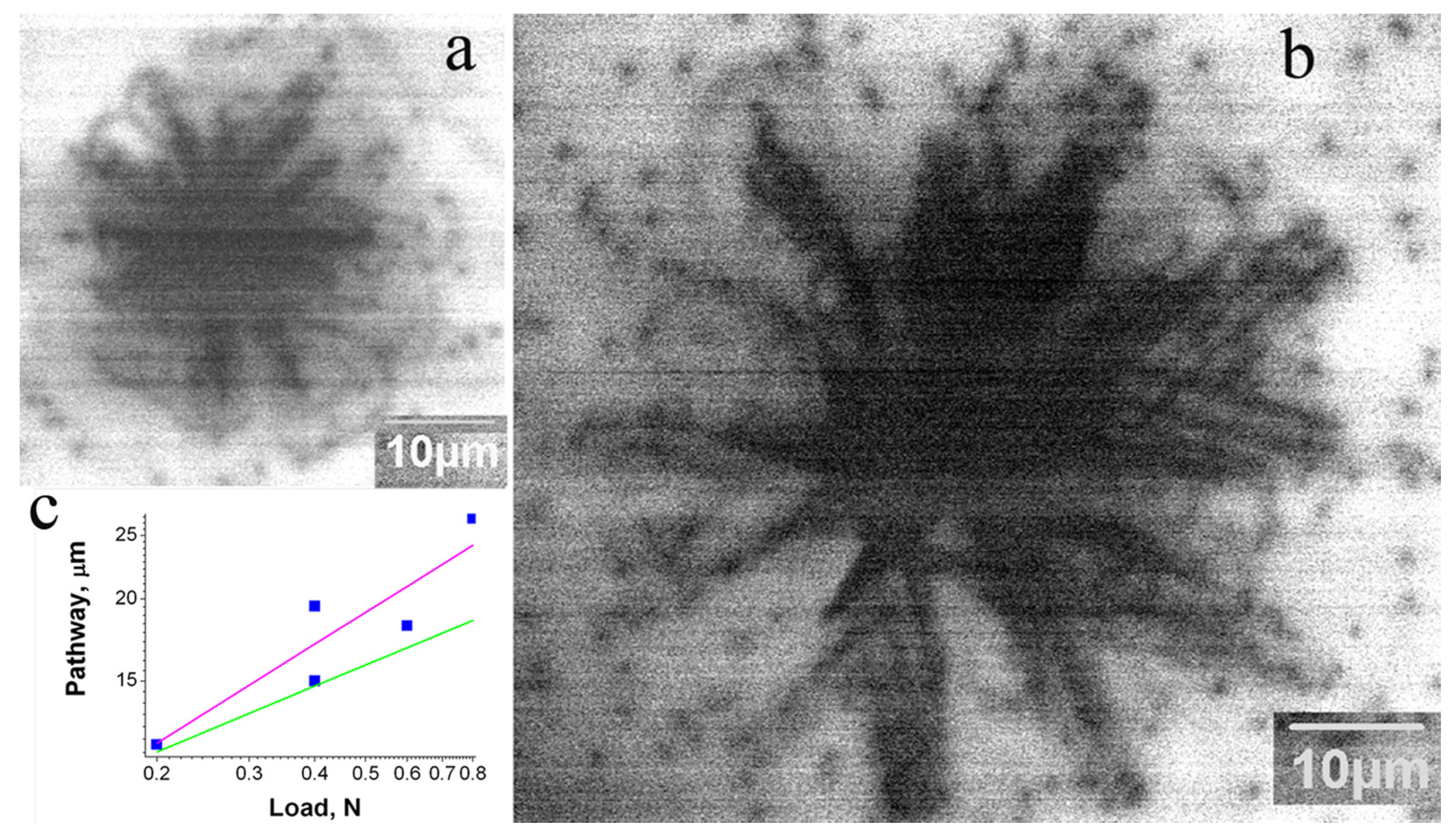
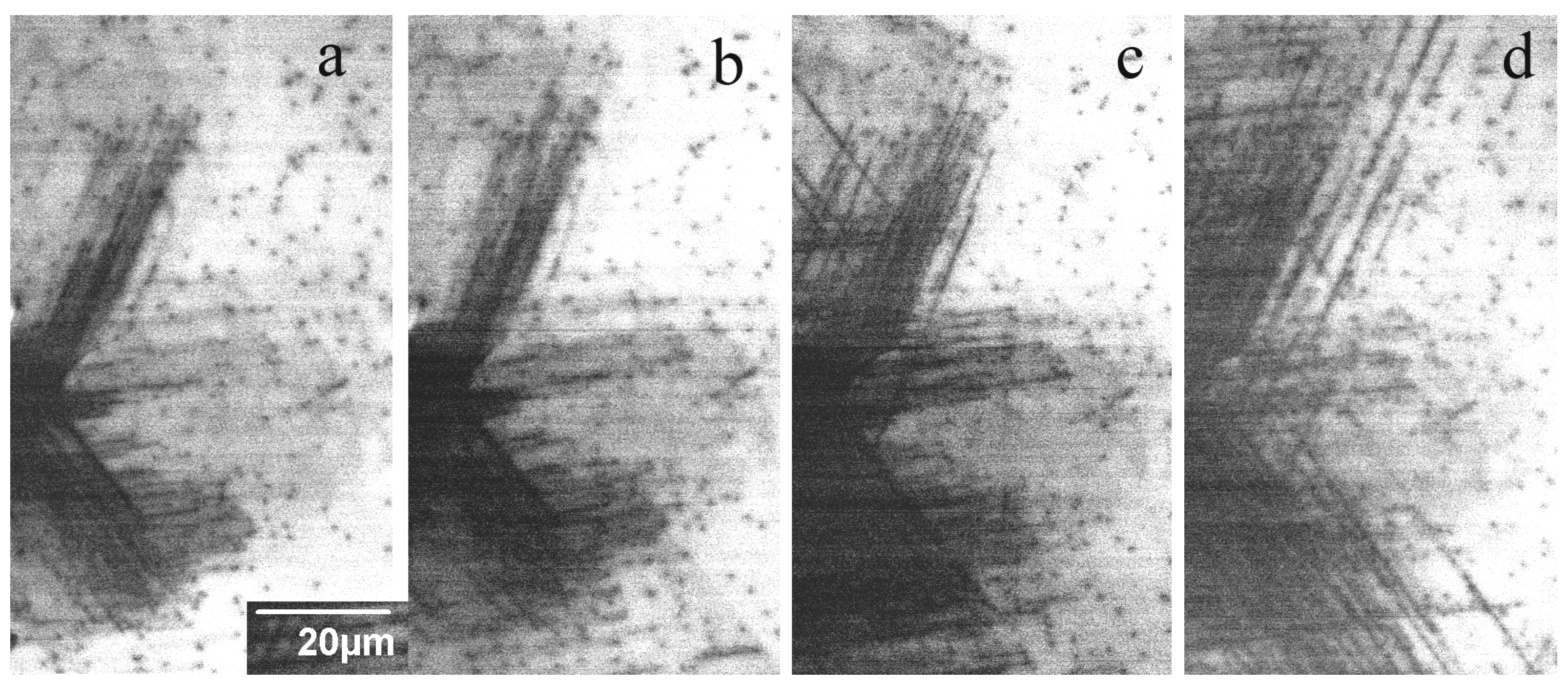
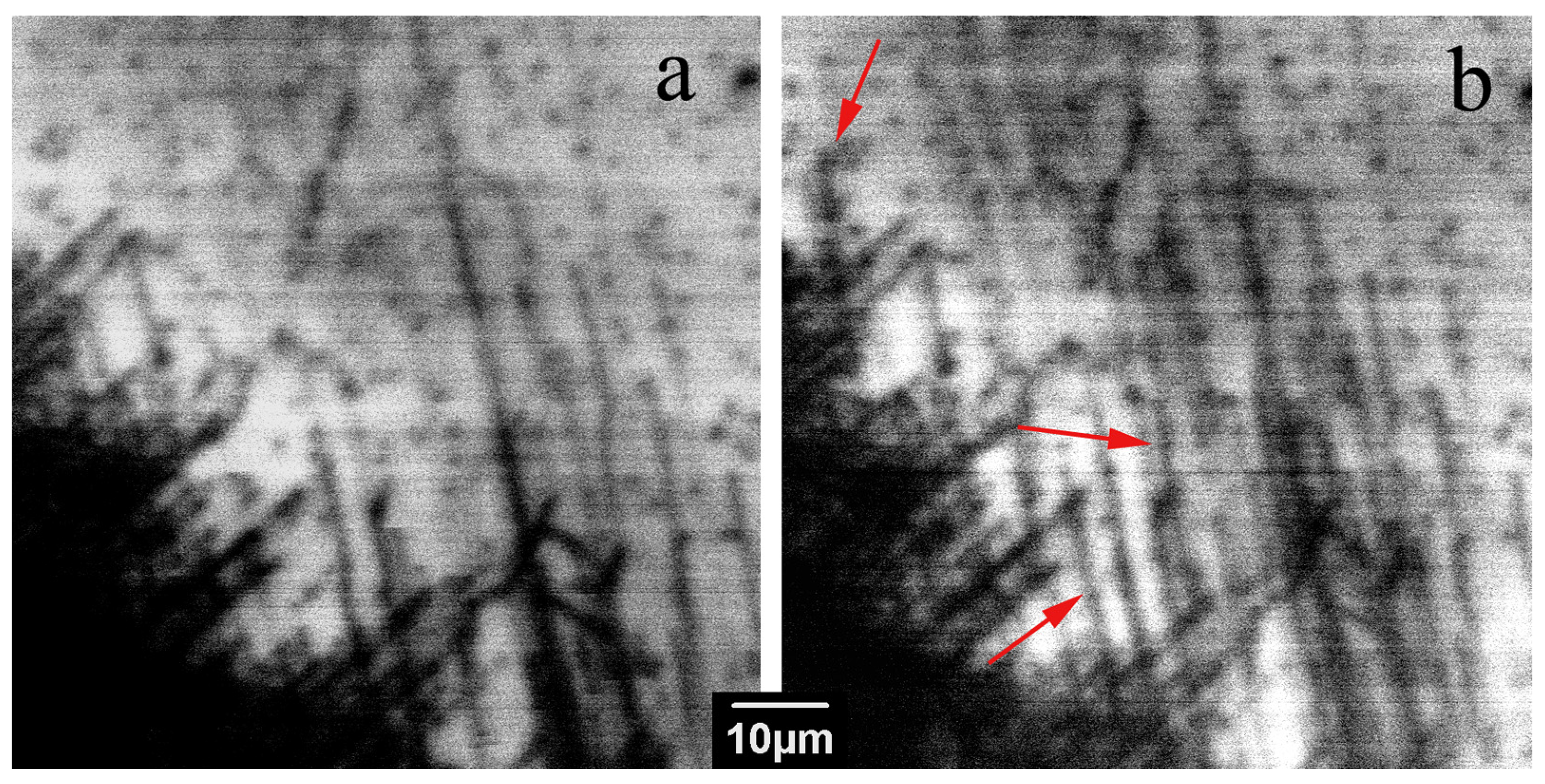
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bradby, E.; Kucheyev, S.O.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P.; Li, G.; Philips, M.R. Indentation-induced damage in GaN epilayers. Appl. Phys. Lett. 2002, 80, 383–385. [Google Scholar] [CrossRef]
- Jahn, U.; Trampert, A.; Wagner, T.; Brandt, O.; Ploog, K.H. Indentation of GaN: A Study of the Optical Activity and Strain State of Extended Defects. Phys. Status Solidi A 2002, 192, 79–84. [Google Scholar] [CrossRef]
- Jian, S.R. Berkovich indentation-induced deformation behaviors of GaN thin films observed using cathodoluminescence and cross-sectional transmission electron microscopy. Appl. Surf. Sci. 2008, 254, 6749–6753. [Google Scholar] [CrossRef]
- Huang, J.; Xu, K.; Gong, X.J.; Wang, J.F.; Fan, Y.M.; Liu, J.Q.; Zeng, X.H.; Ren, G.Q.; Zhou, T.F.; Yang, H. Dislocation cross-slip in GaN single crystals under nanoindentation. Appl. Phys. Lett. 2011, 98, 221906. [Google Scholar] [CrossRef]
- Ratschinski, I.; Leipner, H.S.; Heyroth, F.; Fränzel, W.; Hammer, R.; Jurisch, M. Dislocations and cracks at vickers indentations in (0001) GaN single Crystals. Philos. Mag. Lett. 2011, 90, 565–571. [Google Scholar] [CrossRef]
- Medvedev, O.S.; Vyvenko, O.F.; Bondarenko, A.S. On the luminescence of freshly introduced a-screw dislocation in low-resistance GaN. Semiconductors 2015, 49, 1181–1186. [Google Scholar] [CrossRef]
- Vergeles, P.S.; Orlov, V.I.; Polyakov, A.Y.; Yakimov, E.B.; Kim, T.; Lee, I.-H. Recombination and optical properties of dislocations gliding at room temperature in GaN under applied stress. J. Alloys Compd. 2019, 776, 181. [Google Scholar] [CrossRef]
- Orlov, V.I.; Vergeles, P.S.; Yakimov, E.B.; Li, X.; Yang, J.; Lv, G.; Dong, S. Estimations of Low Temperature Dislocation Mobility in GaN. Phys. Status Solidi A 2019, 216, 1900163. [Google Scholar] [CrossRef]
- Vergeles, P.S.; Yakimov, E.B.; Orlov, V.I. Comparative Study of Optical and Electrical Properties of Grown-In and Freshly Introduced Dislocations in GaN by SEM Methods. J. Electr. Mater. 2020, 49, 5173–5177. [Google Scholar] [CrossRef]
- Orlov, V.I.; Polyakov, A.Y.; Vergeles, P.S.; Yakimov, E.B.; Kim, G.C.; Lee, I.-H. Estimations of Activation Energy for Dislocation Mobility in p-GaN. ECS J. Solid State Sci. Technol. 2021, 10, 026004. [Google Scholar] [CrossRef]
- Vergeles, P.S.; Kulanchikov, Y.O.; Polyakov, A.Y.; Yakimov, E.B.; Pearton, S.J. Communication—Electron-Beam Stimulated Release of Dislocations from Pinning Sites in GaN. ECS J. Solid State Sci. Technol. 2022, 11, 015003. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; John Wiley & Sons: Toronto, ON, Canada, 1982. [Google Scholar]
- Alexander, H.; Teichler, H. Dislocations. In Handbook of Semiconductor Technology, 1st ed.; Jackson, K.A., Schroter, W., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2000; pp. 291–376. [Google Scholar]
- Schröter, W.; Labusch, R. Electrical Properties of Dislocations in Ge and Si. Phys. Stat. Sol. B 1969, 36, 539–550. [Google Scholar] [CrossRef]
- Hirsch, P.B. The Structure and Electrical Properties of Dislocations in Semiconductors. J. Microsc. 1980, 118, 3–12. [Google Scholar] [CrossRef]
- Reiche, M.; Kittler, M.; Uebensee, H.; Pippel, E.; Haehnel, A.; Birner, S. Electronic properties of dislocations. Appl. Phys. A 2016, 122, 389. [Google Scholar] [CrossRef]
- Termentzidis, K.; Isaiev, M.; Salnikova, A.; Belabbas, I.; Lacroix, D.; Kioseoglou, J. Impact of screw and edge dislocations on the thermal conductivity of individual nanowires and bulk GaN: A molecular dynamics study. Phys. Chem. Chem. Phys. 2018, 20, 5159–5172. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W.; Bilhmayer, G.; Waser, R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3. Nature Mater. 2006, 5, 312–320. [Google Scholar] [CrossRef]
- Yakimov, E.B. What is the real value of diffusion length in GaN? J. Alloys Compd. 2015, 627, 344–351. [Google Scholar] [CrossRef]
- Lee, I.-H.; Polyakov, A.Y.; Smirnov, N.B.; Yakimov, E.B.; Tarelkin, S.A.; Turutin, A.V.; Shemerov, I.V.; Pearton, S.J. Studies of deep level centers determining the diffusion length in epitaxial layers and crystals of undoped n-GaN. J. Appl. Phys. 2016, 119, 205109. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Smirnov, N.B.; Yakimov, E.B.; Tarelkin, S.A.; Turutin, A.V.; Shemerov, I.V.; Pearton, S.J.; Bae, K.-B.; Lee, I.-H. Deep traps determining the non-radiative lifetime and defect band yellow luminescence in n-GaN. J. Alloys Compd. 2016, 686, 1044–1052. [Google Scholar] [CrossRef]
- Lee, I.-H.; Polyakov, A.Y.; Yakimov, E.B.; Smirnov, N.B.; Shemerov, I.V.; Tarelkin, S.A.; Didenko, S.I.; Tapero, K.I.; Zinovyev, R.A.; Pearton, S.J. Defects responsible for lifetime degradation in electron irradiated n-GaN grown by hydride vapor phase epitaxy. Appl. Phys. Lett. 2017, 110, 112102. [Google Scholar] [CrossRef]
- Rosner, S.J.; Carr, E.C.; Ludowise, M.J.; Girolami, G.; Erikson, H.I. Correlation of cathodoluminescence inhomogeneity with microstructural defects in epitaxial GaN grown by metalorganic chemical-vapor deposition. Appl. Phys. Lett. 1997, 70, 420–422. [Google Scholar] [CrossRef]
- Yakimov, E.B. Electron-beam-induced-current study defects in GaN; experiments and simulation. J. Phys. Condens. Matter 2002, 14, 13069. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Polyakov, A.Y.; Lee, I.-H.; Pearton, S.J. Recombination properties of dislocation in GaN. J. Appl. Phys. 2018, 123, 161543. [Google Scholar] [CrossRef]
- Nakano, T.; Harashima, Y.; Chokawa, K.; Shiraishi, K.; Oshiyama, A.; Kangawa, Y.; Usami, S.; Mayama, N.; Toda, K.; Tanaka, A.; et al. Screw dislocation that converts p-type GaN to n-type: Microscopic study on Mg condensation and leakage current in p–n diodes. Appl. Phys. Lett. 2020, 117, 012105. [Google Scholar] [CrossRef]
- Usami, S.; Tanaka, A.; Fukushima, H.; Ando, Y.; Deki, M.; Nitta, S.; Honda, Y.; Amano, H. Correlation between nanopipes formed from screw dislocations during homoepitaxial growth by metal-organic vapor-phase epitaxy and reverse leakage current in vertical p–n diodes on a free-standing GaN substrates. Jpn. J. Appl. Phys. 2019, 58, SCCB24. [Google Scholar]
- Ohta, H.; Asai, N.; Horikiri, F.; Narita, Y.; Yoshida, T.; Mishima, T. Impact of threading dislocations in GaN p–n diodes on forward I–V characteristics. Jpn. J. Appl. Phys. 2020, 59, 106503. [Google Scholar] [CrossRef]
- Hinoki, A.; Kikawa, J.; Yamada, T.; Tsuchiya, T.; Kamiya, S.; Kurouchi, M.; Kosaka, K.; Araki, T.; Suzuki, A.; Nanishi, Y. Effects of Traps Formed by Threading Dislocations on Off-State Breakdown Characteristics in GaN Buffer Layer in AlGaN/GaN Heterostructure Field-Effect Transistors. Appl. Phys. Express 2008, 1, 011103. [Google Scholar] [CrossRef]
- Law, J.J.M. Low defect-mediated reverse-bias leakage in (0001) GaN via high-temperature molecular beam epitaxy. Appl. Phys. Lett. 2010, 96, 102111. [Google Scholar]
- Gao, F.; Lu, B.; Li, L.; Kaun, S.; Speck, J.S.; Thompson, C.V.; Palacios, T. Role of oxygen in the OFF-state degradation of AlGaN/GaN high electron mobility transistors. Appl. Phys. Lett. 2011, 99, 223506. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Lee, I.H. Deep traps in GaN-based structures as affecting the performance of GaN devices. Mater. Sci. Eng. R 2015, 94, 1–56. [Google Scholar] [CrossRef]
- Benzarti, Z.; Sekrafi, T.; Bougrioua, Z.; Khalfallah, A.; El Jani, B. Effect of SiN Treatment on Optical Properties of InxGa1-xN/GaN MQW Blue LEDs. J. Electron. Mater. 2017, 46, 4312–4320. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Vergeles, P.S.; Polyakov, A.Y.; Shchemerov, I.V.; Chernyh, A.V.; Vasilev, A.A.; Kochkova, A.I.; Lee, I.-H.; Pearton, S.J. Dislocations introduced in n-GaN at room temperature cause conductivity inversion. J. Alloys Compd. 2021, 877, 160281. [Google Scholar] [CrossRef]
- Boughrara, N.; Benzarti, Z.; Khalfallah, A.; Evaristo, M.; Cavaleiro, A. Comparative study on the nanomechanical behavior and physical properties influenced by the epitaxial growth mechanisms of GaN thin films. Appl. Surf. Sci. 2022, 579, 152188. [Google Scholar] [CrossRef]
- Weyher, J.L.; Albrecht, M.; Wosinski, T.; Nowak, G.; Strunk, H.P.; Porowski, S. Study of individual grown-in and indentation-induced dislocations in GaN by defect-selective etching and transmission electron microscopy. Mater. Sci. Eng. B 2001, 80, 318–321. [Google Scholar] [CrossRef]
- Caldas, P.G.; Silva, E.M.; Prioli, R.; Huang, J.Y.; Juday, R.; Fischer, A.M.; Ponce, F.A. Plasticity and optical properties of GaN under highly localized nanoindentation stress fields. J. Appl. Phys. 2017, 121, 125105. [Google Scholar] [CrossRef]
- Medvedev, O.S.; Vyvenko, O.F.; Bondarenko, A.S.; Mikhailovskii, V.Y.; Ubyivovk, E.V.; Peretzki, P.; Seibt, M. Recombination-Related Properties of a-Screw Dislocations in GaN: A Combined CL, EBIC, TEM Study. AIP Conf. Proc. 2016, 1748, 020011. [Google Scholar]
- Medvedev, O.; Vyvenko, O.; Ubyivovk, E.; Shapenkov, S.; Bondarenko, A.; Saring, P.; Seibt, M. Intrinsic luminescence and core structure of freshly introduced a-screw dislocations in n-GaN. J. Appl. Phys. 2018, 123, 161427. [Google Scholar] [CrossRef]
- Yonenaga, I.; Itoh, S.; Goto, T. Dislocation mobility and photoluminescence of plastically deformed GaN. Phys. B Condens. Matter 2003, 340–342, 484–487. [Google Scholar] [CrossRef]
- Harafuji, K.; Tsuchiya, T.; Kawamura, K. Molecular dynamics simulation of dislocations in wurtzite-type GaN crystal. J. Appl. Phys. 2004, 96, 2513–2524. [Google Scholar] [CrossRef]
- Weingarten, N.S.; Chung, P.W. a-Type edge dislocation mobility in wurtzite GaN using molecular dynamics. Scripta Mater. 2013, 69, 311–314. [Google Scholar] [CrossRef]
- Weingarten, N.S. Dislocation Mobilities in GaN from Molecular Dynamics Simulations. MRS Online Proc. Libr. 2015, 1741, 1324. [Google Scholar] [CrossRef]
- Belabbas, I.; Chen, J.; Heggie, M.I.; Latham, C.D.; Rayson, M.J.; Briddon, P.R.; Nouet, G. Core properties and mobility of the basal screw dislocation in wurtzite GaN: A density functional theory study. Modelling Simul. Mater. Sci. Eng. 2016, 24, 075001. [Google Scholar] [CrossRef]
- Weingarten, N.S. Dislocation mobility and Peierls stress of c-type screw dislocations in GaN from molecular dynamics. Comput. Mater. Sci. 2018, 153, 409–416. [Google Scholar] [CrossRef]
- Sugiura, L. Dislocation motion in GaN light-emitting devices and its effect on device lifetime. J. Appl. Phys. 1997, 81, 1633–1638. [Google Scholar] [CrossRef]
- Yonenaga, I. Hardness, Yield Strength, and Dislocation Velocity in Elemental and Compound Semiconductors. Mater. Trans. 2005, 46, 1979–1985. [Google Scholar] [CrossRef]
- Yonenaga, I. Atomic structures and dynamic properties of dislocations in semiconductors: Current progress and stagnation. Semicond. Sci. Technol. 2020, 35, 043001. [Google Scholar] [CrossRef]
- Messerschmidt, U. Dislocation Dynamics during Plastic Deformation; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 113–116. [Google Scholar]
- Yonenaga, I.; Motoki, K. Yield strength and dislocation mobility in plastically deformed bulk single-crystal GaN. J. Appl. Phys. 2001, 90, 6539–6541. [Google Scholar] [CrossRef]
- Alexander, H. Dislocations in covalent crystals. In Dislocations in Solids; Nabarro, F.R.N., Ed.; Elseiver Science Publ.: Amsterdam, The Netherlands, 1986; Volume 7, Chapter 35. [Google Scholar]
- Hirsch, P.B. A mechanism for the effect of doping on dislocation mobility. J. Physiq. 1979, 40, C6-117–C6-121. [Google Scholar] [CrossRef]
- Maeda, K.; Suzuki, K.; Ichihara, M.; Nishiguchi, S.; Ono, K.; Mera, Y.; Takeuchi, S. Electronically induced dislocation glide motion in hexagonal GaN single crystals. Phys. B Condens. Matter 1999, 273, 134–139. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Vergeles, P.S.; Polyakov, A.Y.; Lee, I.-H.; Pearton, S.J. Movement of basal plane dislocation in GaN during electron beam irradiation. Appl. Phys. Lett. 2015, 106, 132101. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Vergeles, P.S.; Polyakov, A.Y.; Lee, I.-H.; Pearton, S.J. Radiation enhanced basal plane dislocation glide in GaN. Jpn. J. Appl. Phys. 2016, 55, 05FM03. [Google Scholar] [CrossRef]
- Yakimov, E.E.; Yakimov, E.B. Kink Migration along 30° Si-Core Partial Dislocations in 4H-SiC. Phys. Status Solidi A 2022, 219, 2200119. [Google Scholar] [CrossRef]
- Yakimov, E.E.; Yakimov, E.B. Cathodoluminescence and EBIC investigations of stacking fault expansion in 4H-SiC due to e-beam irradiation at fixed points. J. Phys. D: Appl. Phys. 2022, 55, 245101. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Smirnov, N.B.; Govorkov, A.V.; Markov, A.V.; Yakimov, E.B.; Vergeles, P.S.; Lee, I.-H.; Lee, C.R.; Pearton, S.J. Effects of laterally overgrown n-GaN thickness on defect and deep level concentrations. J. Vac. Sci. Technol. B 2008, 26, 990–994. [Google Scholar] [CrossRef]
- Albrecht, M.; Lymperakis, L.; Neugebauer, O. Origin of the unusually strong luminescence of a-type screw dislocations in GaN. Phys. Rev. B 2014, 90, 241201. [Google Scholar] [CrossRef]
- Huang, J.; Xu, K.; Fan, Y.M.; Wang, J.F.; Zhang, J.C.; Ren, G.Q. Dislocation luminescence in GaN single crystals under nanoindentation. Nanoscale Res. Lett. 2014, 9, 649. [Google Scholar] [CrossRef] [PubMed]
- Bondarenko, I.E.; Eremenko, V.G.; Farber, B.Y.; Nikitenko, V.I.; Yakimov, E.B. On the Real Structure of Monocrystalline Silicon near Dislocation Slip Planes. Phys. Status Solidi A 1981, 68, 53–60. [Google Scholar] [CrossRef]
- Bondarenko, I.E.; Blumtritt, H.; Heydenreich, J.; Kazmiruk, V.V.; Yakimov, E.B. Recombination Properties of Dislocation Slip Planes. Phys. Status Solidi A 1986, 95, 173–177. [Google Scholar] [CrossRef]
- Kveder, V.; Khorosheva, M.; Seibt, M. Concerning vacancy defects generated by moving dislocations in Si. Mater. Today Proc. 2018, 5, 14757–14764. [Google Scholar] [CrossRef]
- Yakimov, E.B. Study of Wide-Gap Semiconductors Using Electron-Beam Induced Current Method. Crystallogr. Rep. 2021, 66, 581–593. [Google Scholar] [CrossRef]
- Maniatty, A.; Karvani, P. Constitutive Relations for Modeling Single Crystal GaN at Elevated Temperatures. J. Eng. Mater. Technol. 2015, 137, 011002. [Google Scholar] [CrossRef]
- Gridneva, I.V.; Milman, Y.V.; Trefilov, V.I.; Chugunova, S.I. Analysis of Dislocation Mobility under Concentrated Loads at Indentations of Single Crystals. Phys. Status Solidi A 1979, 54, 195–206. [Google Scholar] [CrossRef]
- Maeda, K. Radiation-Enhanced Dislocation Glide: The Current Status of Research. In Materials and Reliability Handbook for Semiconductor Optical and Electron Devices; Ueda, O., Pearton, S.J., Eds.; Springer Science+Business Media: New York, NY, USA, 2013; pp. 263–281. [Google Scholar]
- Krimsky, E.; Jones, K.A.; Tompkins, R.P.; Rotella, P.; Ligda, J.; Schuster, B.E. Nano-indentation used to study pyramidal slip in GaN single crystals. J. Appl. Phys. 2018, 123, 065701. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Sugawara, Y.; Yokoe, D.; Yao, Y. Screw dislocations on {1 12} pyramidal planes induced by Vickers indentation in HVPE GaN. Jpn. J. Appl. Phys. 2020, 59, 091005. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Sugawara, Y.; Yao, Y.; Takeda, H.; Aida, H.; Tadatomo, K. Size of dislocation patterns induced by Vickers indentation in hydride vapor-phase epitaxy GaN. J. Appl. Phys. 2022, 131, 225303. [Google Scholar] [CrossRef]
- Bondarenko, I.E.; Eremenko, V.G.; Nikitenko, V.I.; Yakimov, E.B. The Effect of Thermal Treatment on the Electrical Activity and Mobility of Dislocations in Si. Phys. Status Solidi A 1980, 60, 341–349. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakimov, E.B.; Kulanchikov, Y.O.; Vergeles, P.S. An Experimental Study of Dislocation Dynamics in GaN. Micromachines 2023, 14, 1190. https://doi.org/10.3390/mi14061190
Yakimov EB, Kulanchikov YO, Vergeles PS. An Experimental Study of Dislocation Dynamics in GaN. Micromachines. 2023; 14(6):1190. https://doi.org/10.3390/mi14061190
Chicago/Turabian StyleYakimov, Eugene B., Yury O. Kulanchikov, and Pavel S. Vergeles. 2023. "An Experimental Study of Dislocation Dynamics in GaN" Micromachines 14, no. 6: 1190. https://doi.org/10.3390/mi14061190
APA StyleYakimov, E. B., Kulanchikov, Y. O., & Vergeles, P. S. (2023). An Experimental Study of Dislocation Dynamics in GaN. Micromachines, 14(6), 1190. https://doi.org/10.3390/mi14061190





