Paper-Based Bi-Material Cantilever Actuator Bending Behavior and Modeling
Abstract
1. Introduction
2. Experimental Section
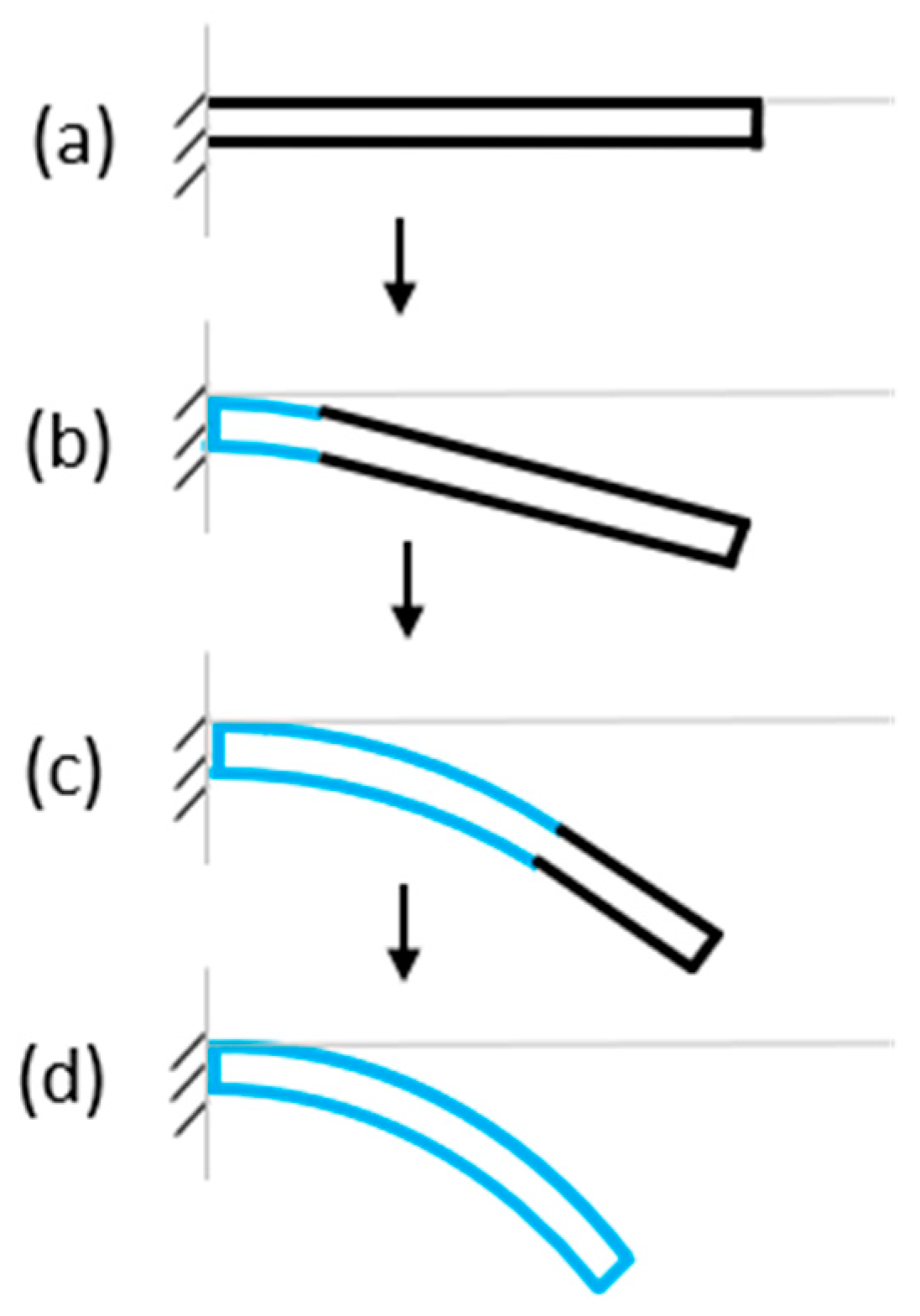
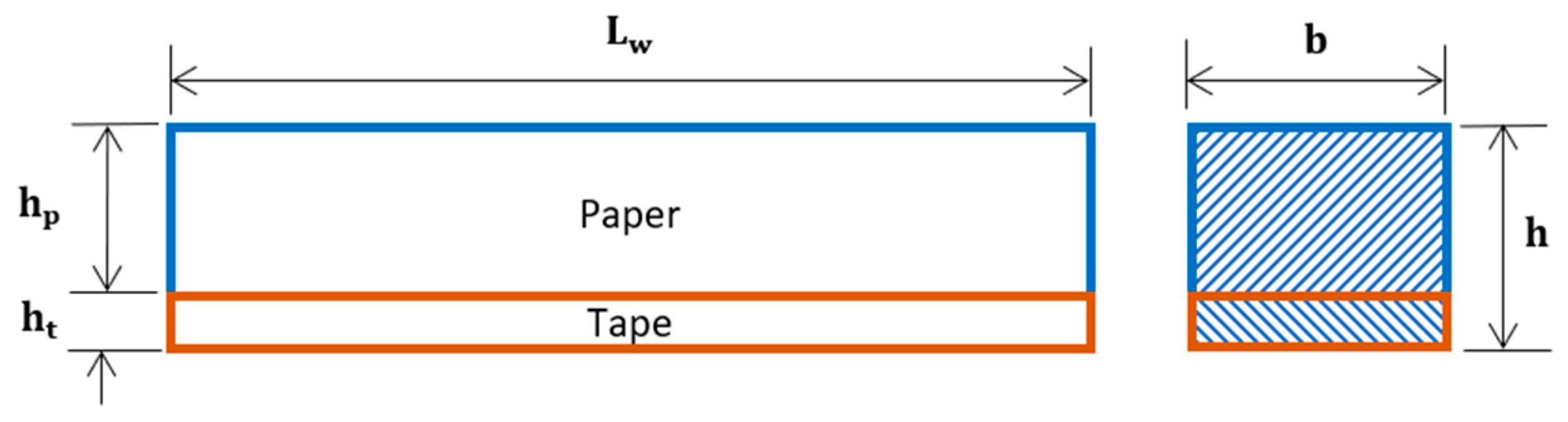
2.1. B-MaC Concept of Design
2.2. Visual Experiments
2.2.1. Paper Orientation
2.2.2. Paper Type
2.2.3. Tape Type
2.2.4. B-MaC Length, Support Location, Orientation
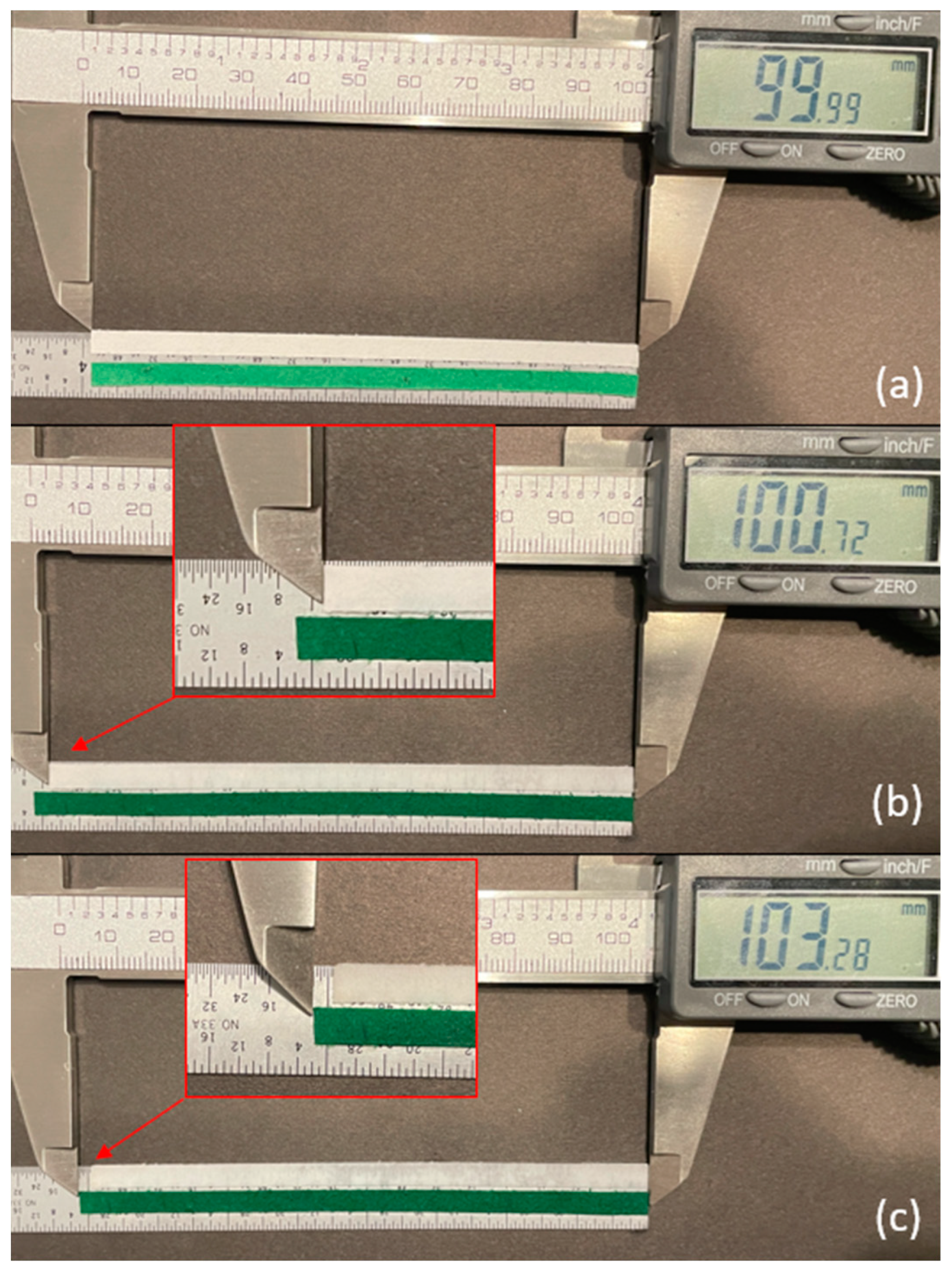
2.3. Laboratory Experiment
3. Theoretical Model
- Static Deformation: The response deflection of a B-MaC is the sole function of wetted length, and time dependence is not considered.
- The fluidic loading is determined by the wetted length of the bilayer, governed by the Lucas-Washburn equation.
- The cross-section of the bilayer remains normal to the neutral axis before and after deformation.
- The thickness of the bilayer is negligible in comparison to the radius of curvature.
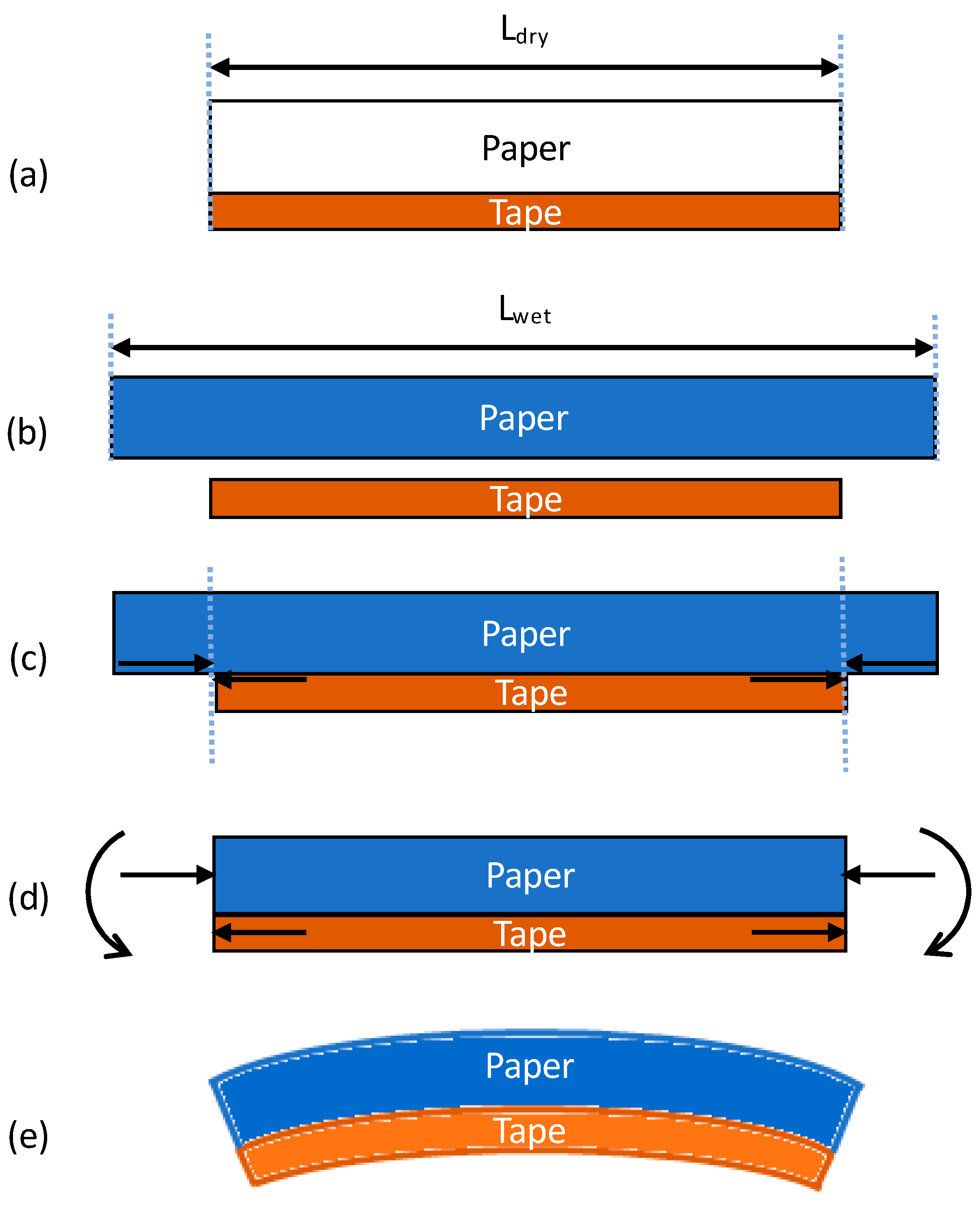
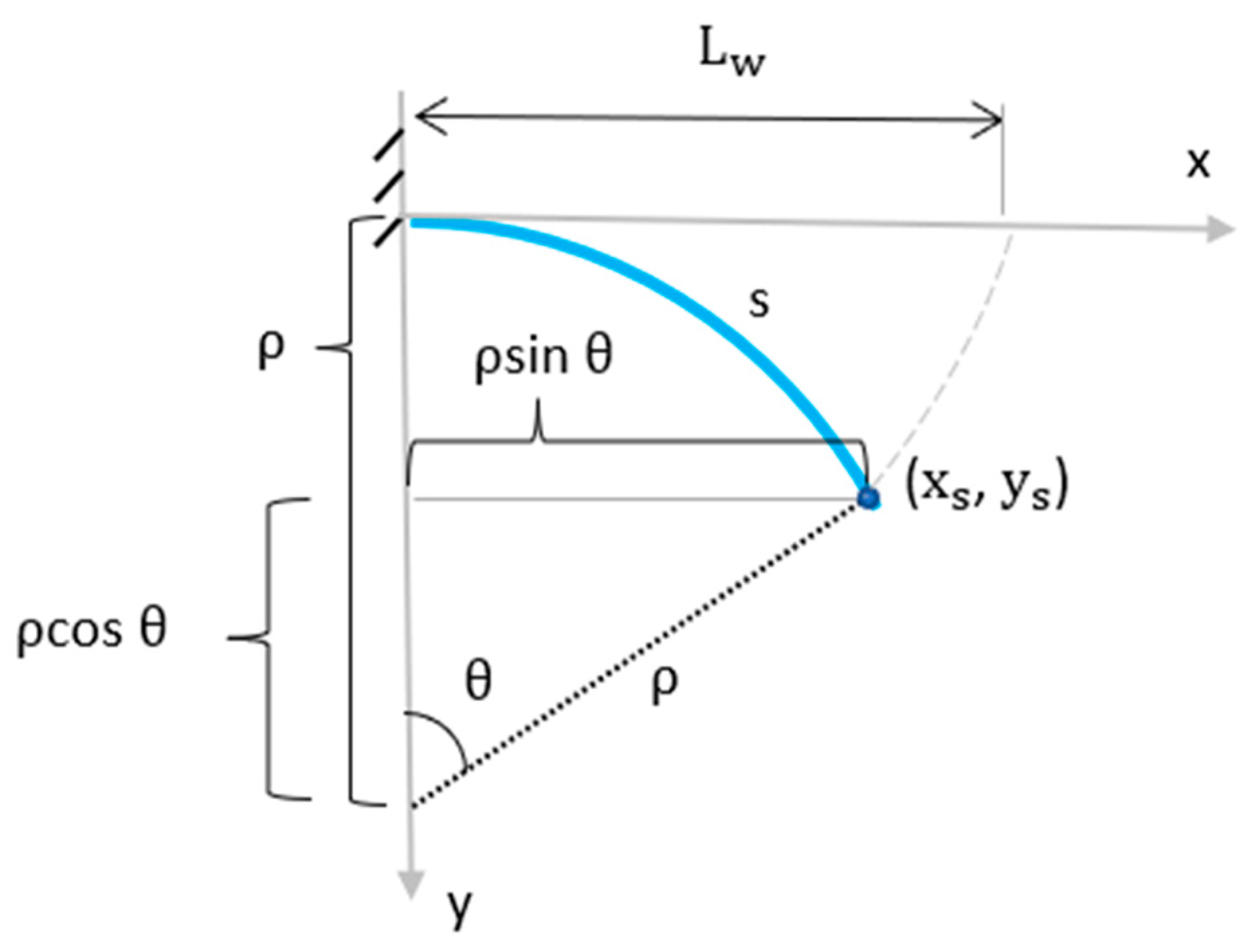
3.1. Wetted Length
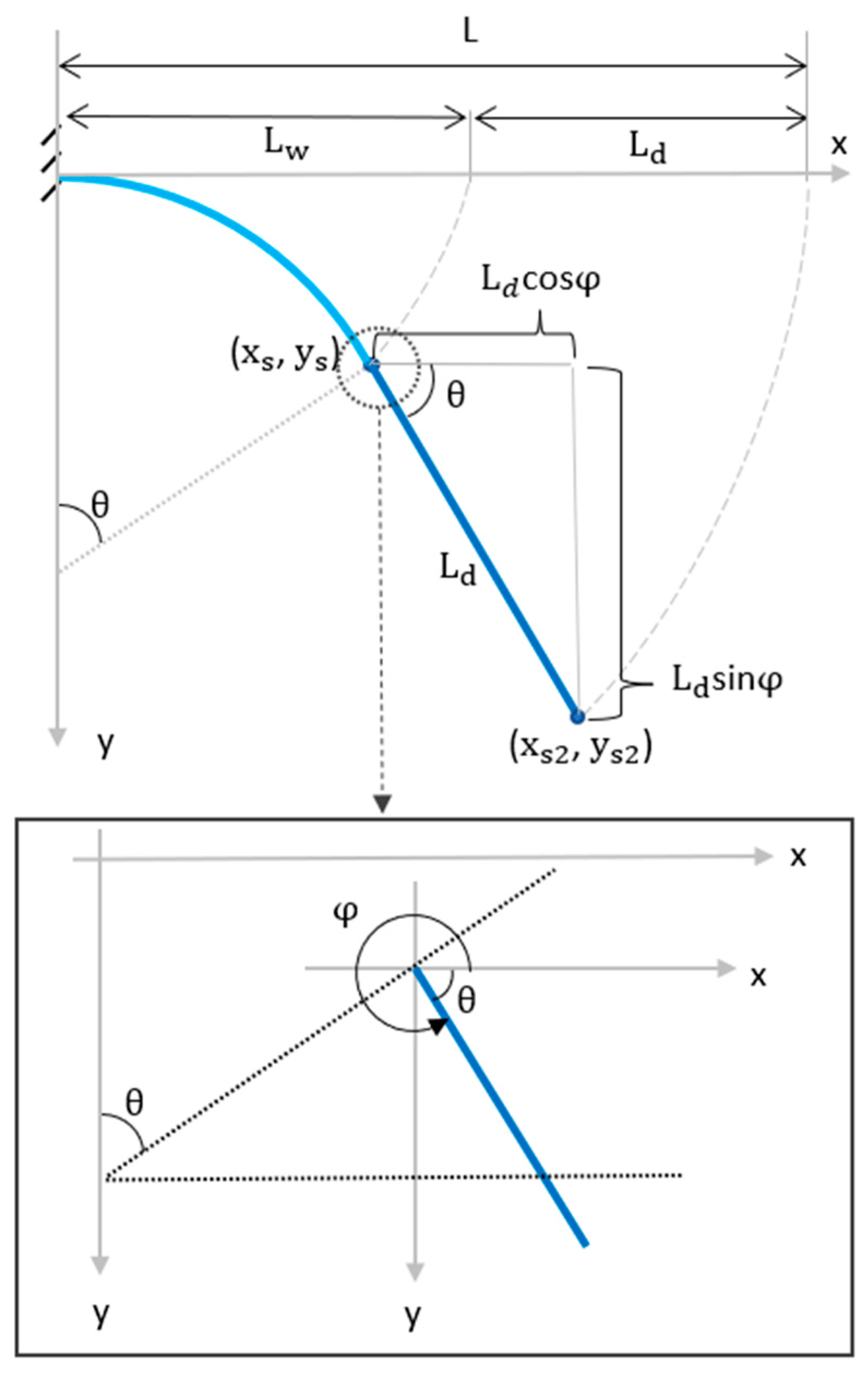
3.2. Dry Length
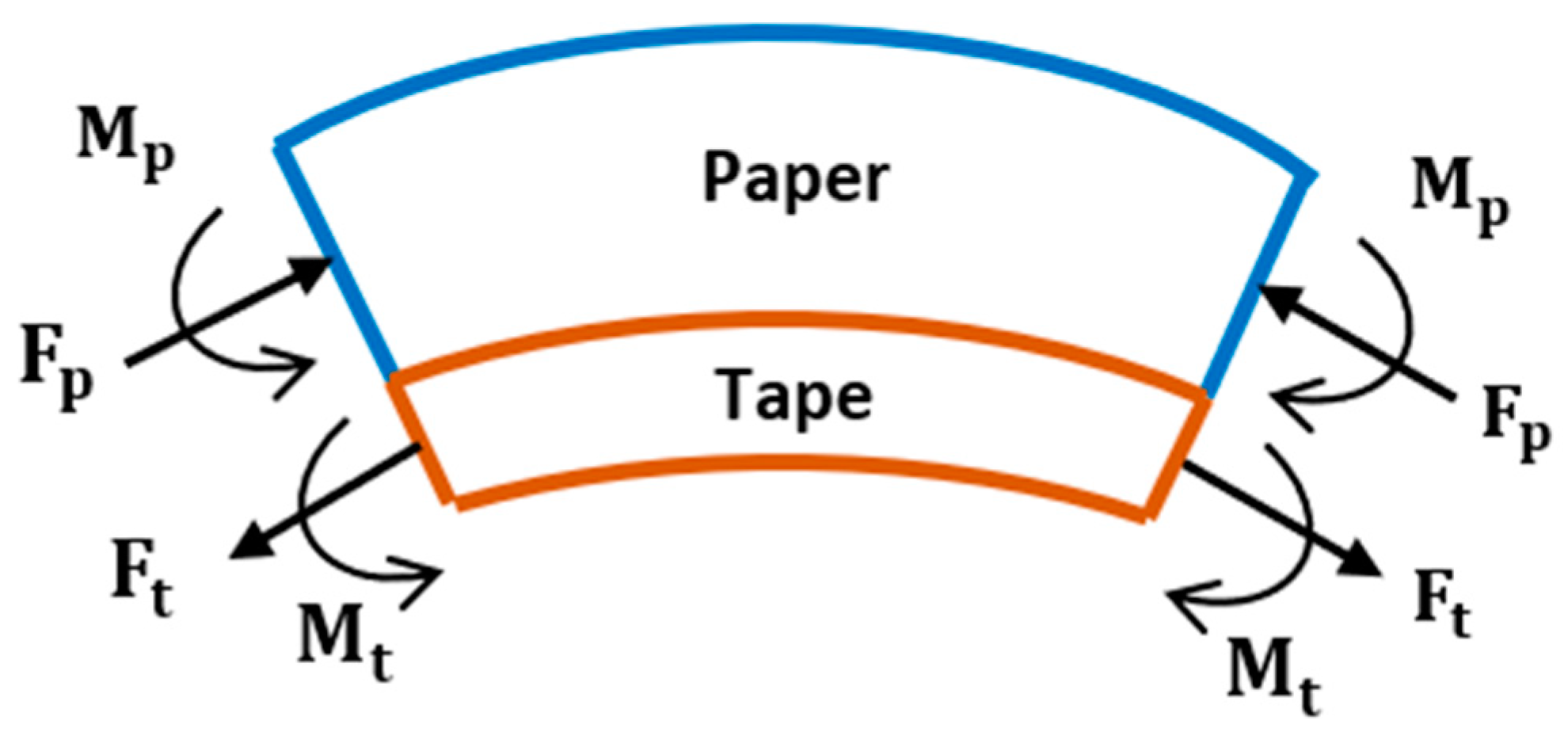
3.3. Final Combined Model
4. Results and Discussion
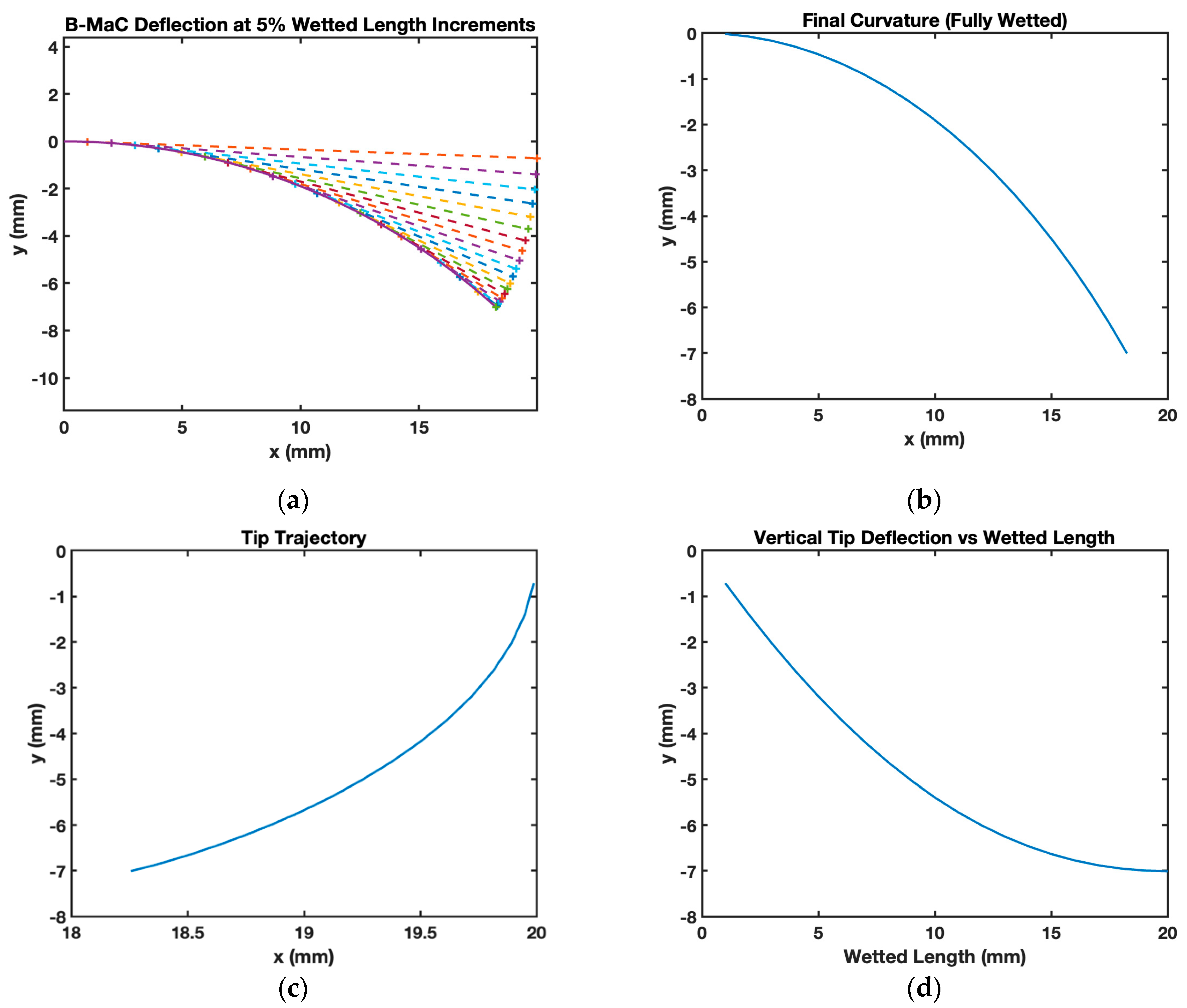
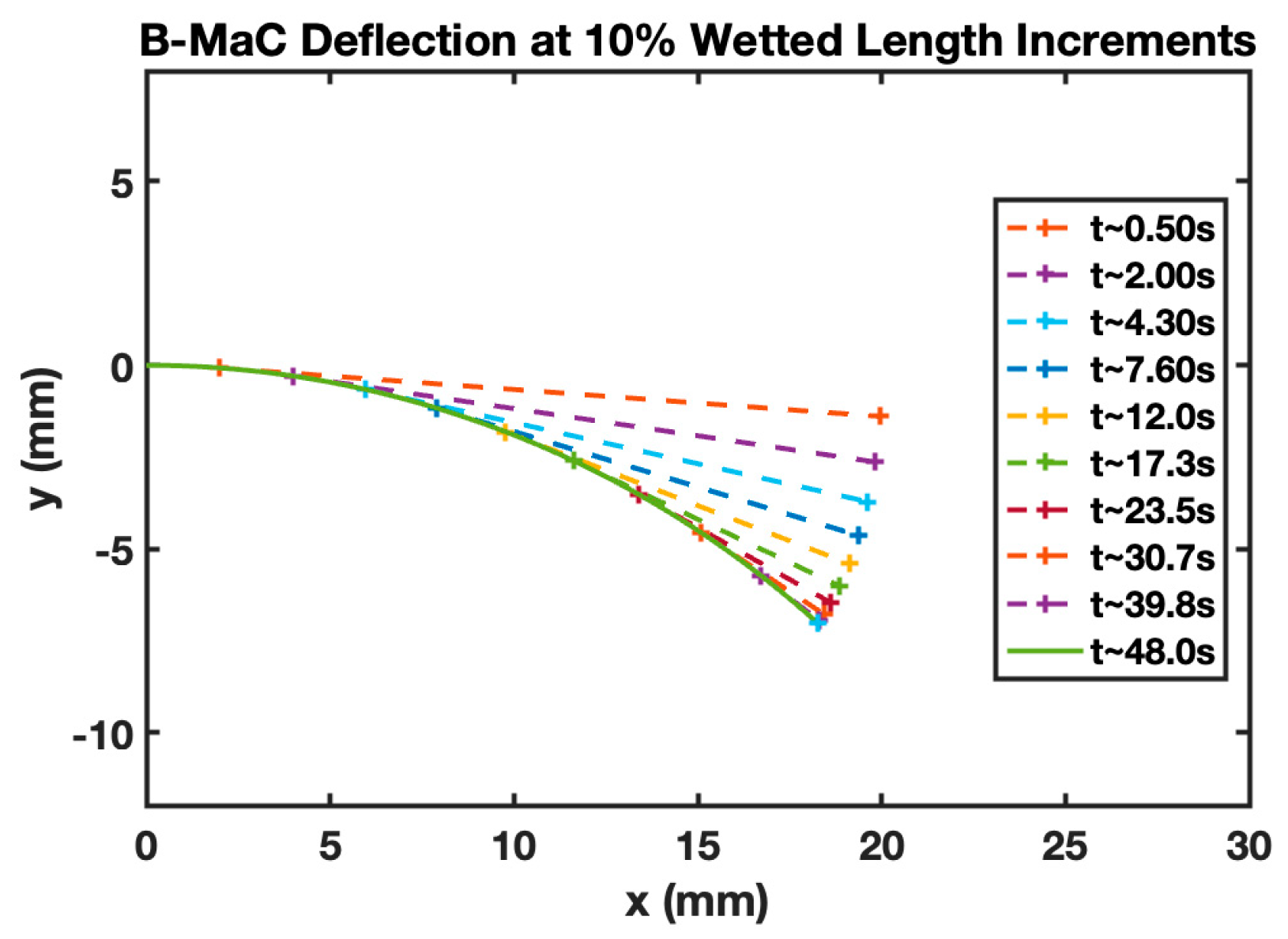
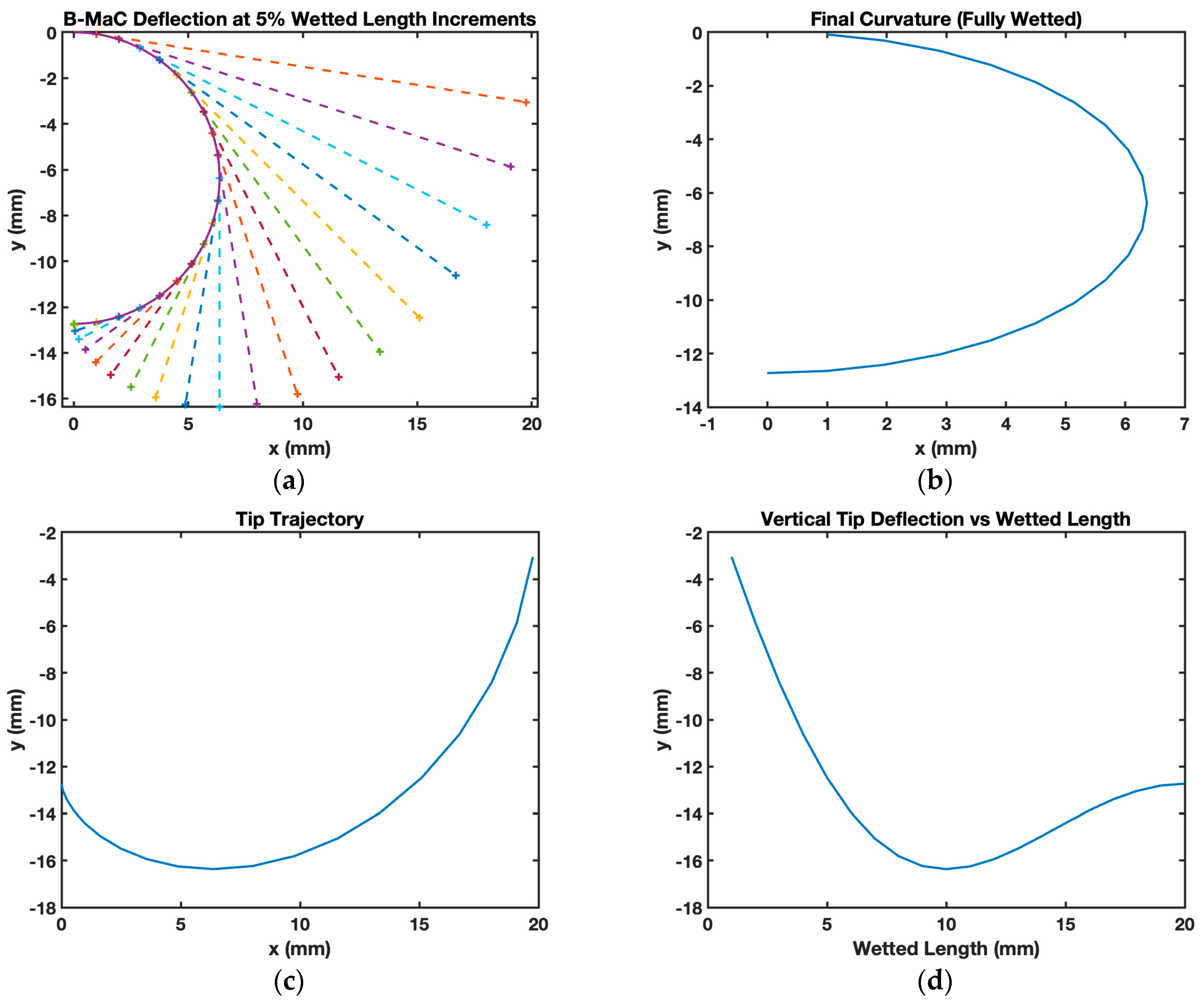
4.1. Analytical Model Plots
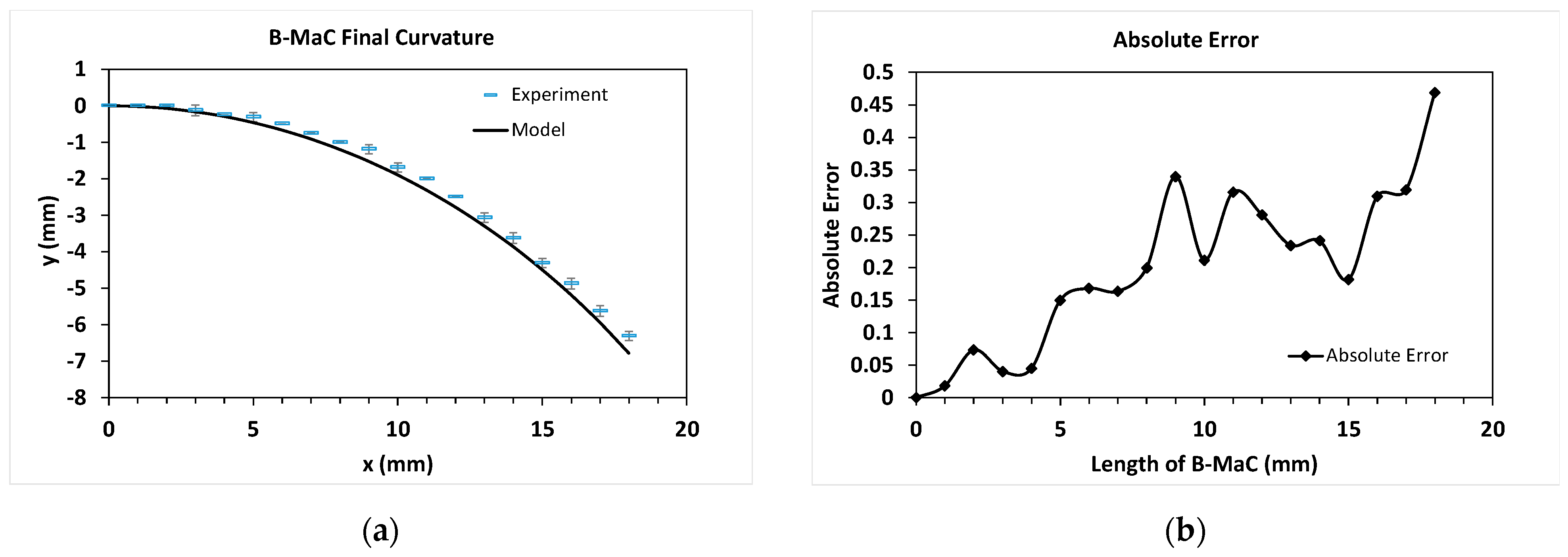
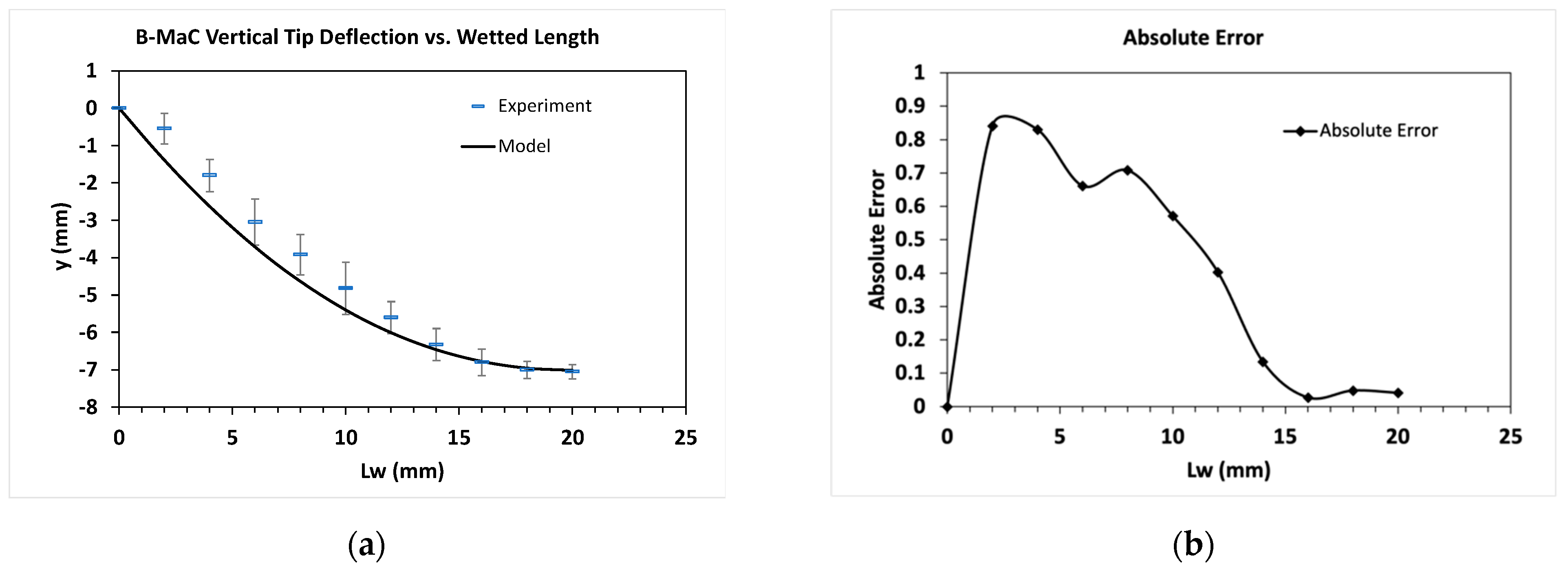
4.2. Comparison between Experiment and Model
4.3. Model Limitation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, R.; Lee, J.W.; Pan, T.; Ma, S.; Wang, J.; Han, J.H.; Ma, Y.; Rogers, J.A.; Huang, Y. Designing Thin, Ultrastretchable Electronics with Stacked Circuits and Elastomeric Encapsulation Materials. Adv. Funct. Mater. 2017, 27, 1604545. [Google Scholar] [CrossRef] [PubMed]
- Quirion, D.; Manna, M.; Hidalgo, S.; Pellegrini, G. Manufacturability and Stress Issues in 3D Silicon Detector Technology at IMB-CNM. Micromachines 2020, 11, 1126. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Pan, J.; Liu, Y.; Xu, Y.; Zhang, A. NIR–UV Responsive Actuator with Graphene Oxide/Microchannel-Induced Liquid Crystal Bilayer Structure for Biomimetic Devices. ACS Appl. Mater. Interfaces 2020, 12, 6727–6735. [Google Scholar] [CrossRef]
- Wang, L.; Wang, D.; Huang, S.; Guo, X.; Wan, G.; Fan, J.; Chen, Z. Controllable Shape Changing and Tristability of Bilayer Composite. ACS Appl. Mater. Interfaces 2019, 11, 16881–16887. [Google Scholar] [CrossRef] [PubMed]
- Mortezam, A. Functional Nanomaterial Composites for Soft Sensing and Actuation. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2019. [Google Scholar] [CrossRef]
- Timoshenko, S. Analysis of Bi-Metal Thermostats. J. Opt. Soc. Am. 1925, 11, 233–255. [Google Scholar] [CrossRef]
- Agarwal, S.; Jiang, S.; Chen, Y. Progress in the Field of Water- and/or Temperature-Triggered Polymer Actuators. Macromol. Mater. Eng. 2019, 304, 1800548. [Google Scholar] [CrossRef]
- Cui, J.; Adams, J.G.M.; Zhu, Y. Controlled bending and folding of a bilayer structure consisting of a thin stiff film and a heat-shrinkable polymer sheet. Smart Mater. Struct. 2018, 27, 055009. [Google Scholar] [CrossRef]
- Morales, D.; Podolsky, I.; Mailen, R.; Shay, T.; Dickey, M.; Velev, O. Ionoprinted Multi-Responsive Hydrogel Actuators. Micromachines 2016, 7, 98. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, N.; Du, J. Thermally controlled large deformation in temperature-sensitive hydrogels bilayers. Int. J. Smart Nano Mater. 2021, 12, 450–471. [Google Scholar] [CrossRef]
- Wu, Y.; Hao, X.; Xiao, R.; Lin, J.; Wu, Z.L.; Yin, J.; Qian, J. Controllable Bending of Bi-hydrogel Strips with Differential Swelling. Acta Mech. Solida Sin. 2019, 32, 652–662. [Google Scholar] [CrossRef]
- Grönquist, P.; Wittel, F.K.; Rüggeberg, M. Modeling and design of thin bending wooden bilayers. PLoS ONE 2018, 13, e0205607. [Google Scholar] [CrossRef] [PubMed]
- Rüggeberg, M.; Burgert, I. Bio-inspired wooden actuators for large scale applications. PLoS ONE 2015, 10, e0120718. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Lee, H.; Yoon, J. Highly bendable bilayer-type photo-actuators comprising of reduced graphene oxide dispersed in hydrogels. Sci. Rep. 2016, 6, 20921. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Fox, C.H.J.; Mcwilliam, S. Optimization of a Cantilever Microswitch with Piezoelectric Actuation. J. Intell. Mater. Syst. Struct. 2004, 15, 823–834. [Google Scholar] [CrossRef]
- Techawanitchai, P.; Ebara, M.; Idota, N.; Asoh, T.-A.; Kikuchi, A.; Aoyagi, T. Photo-switchable control of pH-responsive actuators via pH jump reaction. Soft Matter. 2012, 8, 2844–2851. [Google Scholar] [CrossRef]
- Khoshtinat, S.; Carvelli, V.; Marano, C. Characterization and modeling the hygroscopic behavior of cellulose acetate membranes. Cellulose 2022, 29, 2175–2186. [Google Scholar] [CrossRef]
- Zhang, F.; Fan, J.; Zhang, P.; Liu, M.; Meng, J.; Jiang, L.; Wang, S. A monolithic hydro/organic macro copolymer actuator synthesized via interfacial copolymerization. NPG Asia Mater. 2017, 9, e380. [Google Scholar] [CrossRef]
- Krüger, F.; Thierer, R.; Tahouni, Y.; Sachse, R.; Wood, D.; Menges, A.; Bischoff, M.; Rühe, J. Development of a Material Design Space for 4D-Printed Bio-Inspired Hygroscopically Actuated Bilayer Structures with Unequal Effective Layer Widths. Biomimetics 2021, 6, 58. [Google Scholar] [CrossRef]
- Le Duigou, A.; Castro, M. Moisture-Induced Self-Shaping Flax-Reinforced Polypropylene Biocomposite Actuator. Ind. Crops Prod. 2015, 71, 1–6. [Google Scholar] [CrossRef]
- Smith, W.; Rahmani, N.; Charbaji, A.; Lemos, N.; Anagnostopoulos, C.; Faghri, M.; Hong, C. A Fluidically Controlled Bi-Material Actuator For Automation of Paper-based Assay. In Proceedings of the International Symposium on Thermal Effects in Gas Flows in Microscale, Ettlingen, Germany, 24–25 October 2019. [Google Scholar]
- Heidari-Bafroui, H.; Kumar, A.; Charbaji, A.; Smith, W.; Rahmani, N.; Anagnostopoulos, C.; Faghri, M. A Parametric Study on a Paper-Based Bi-Material Cantilever Valve. Micromachines 2022, 13, 1502. [Google Scholar] [CrossRef]
- Vyas, A.; Staaf, H.; Rusu, C.; Ebefors, T.; Liljeholm, J.; Smith, A.D.; Lundgren, P.; Enoksson, P. A Micromachined Coupled-Cantilever for Piezoelectric Energy Harvesters. Micromachines 2018, 9, 252. [Google Scholar] [CrossRef]
- Kumar, A.; Heidari-Bafroui, H.; Charbaji, A.; Rahmani, N.; Anagnostopoulos, C.; Faghri, M. Numerical and Experimental Modeling of Paper-Based Actuators. Chem. Proc. 2021, 5, 15. [Google Scholar] [CrossRef]
- Department of Materials Science and Metallurgy—University of Cambridge. The Concept of a Misfit Strain. Misfit Strains. 26 November 2020. Available online: www.doitpoms.ac.uk/tlplib/coating_mechanics/misfit_Strain.php (accessed on 23 April 2023).
- Freund, L.B.; Floro, J.A.; Chason, E. Extensions of the Stoney formula for substrate curvature to configurations with thin substrates or large deformations. Appl. Phys. Lett. 1999, 74, 1987–1989. [Google Scholar] [CrossRef]
- Lee, M.; Kim, S.; Kim, H.-Y.; Mahadevan, L. Bending and buckling of wet paper. Phys. Fluids 2016, 28, 042101. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Kumar, A.; Heidari-Bafroui, H.; Smith, W.; Charbaji, A.; Rahmani, N.; Anagnostopoulos, C.; Faghri, M. Paper-Based Bi-Material Cantilever Actuator Bending Behavior and Modeling. Micromachines 2023, 14, 924. https://doi.org/10.3390/mi14050924
Chen G, Kumar A, Heidari-Bafroui H, Smith W, Charbaji A, Rahmani N, Anagnostopoulos C, Faghri M. Paper-Based Bi-Material Cantilever Actuator Bending Behavior and Modeling. Micromachines. 2023; 14(5):924. https://doi.org/10.3390/mi14050924
Chicago/Turabian StyleChen, Gordon, Ashutosh Kumar, Hojat Heidari-Bafroui, Winfield Smith, Amer Charbaji, Nassim Rahmani, Constantine Anagnostopoulos, and Mohammad Faghri. 2023. "Paper-Based Bi-Material Cantilever Actuator Bending Behavior and Modeling" Micromachines 14, no. 5: 924. https://doi.org/10.3390/mi14050924
APA StyleChen, G., Kumar, A., Heidari-Bafroui, H., Smith, W., Charbaji, A., Rahmani, N., Anagnostopoulos, C., & Faghri, M. (2023). Paper-Based Bi-Material Cantilever Actuator Bending Behavior and Modeling. Micromachines, 14(5), 924. https://doi.org/10.3390/mi14050924







