Finite Element Approach for the Simulation of Modern MRAM Devices
Abstract
1. Introduction

2. Micromagnetic Modeling
Spin and Charge Transport
3. Finite Element Implementation
3.1. Charge Current Solution
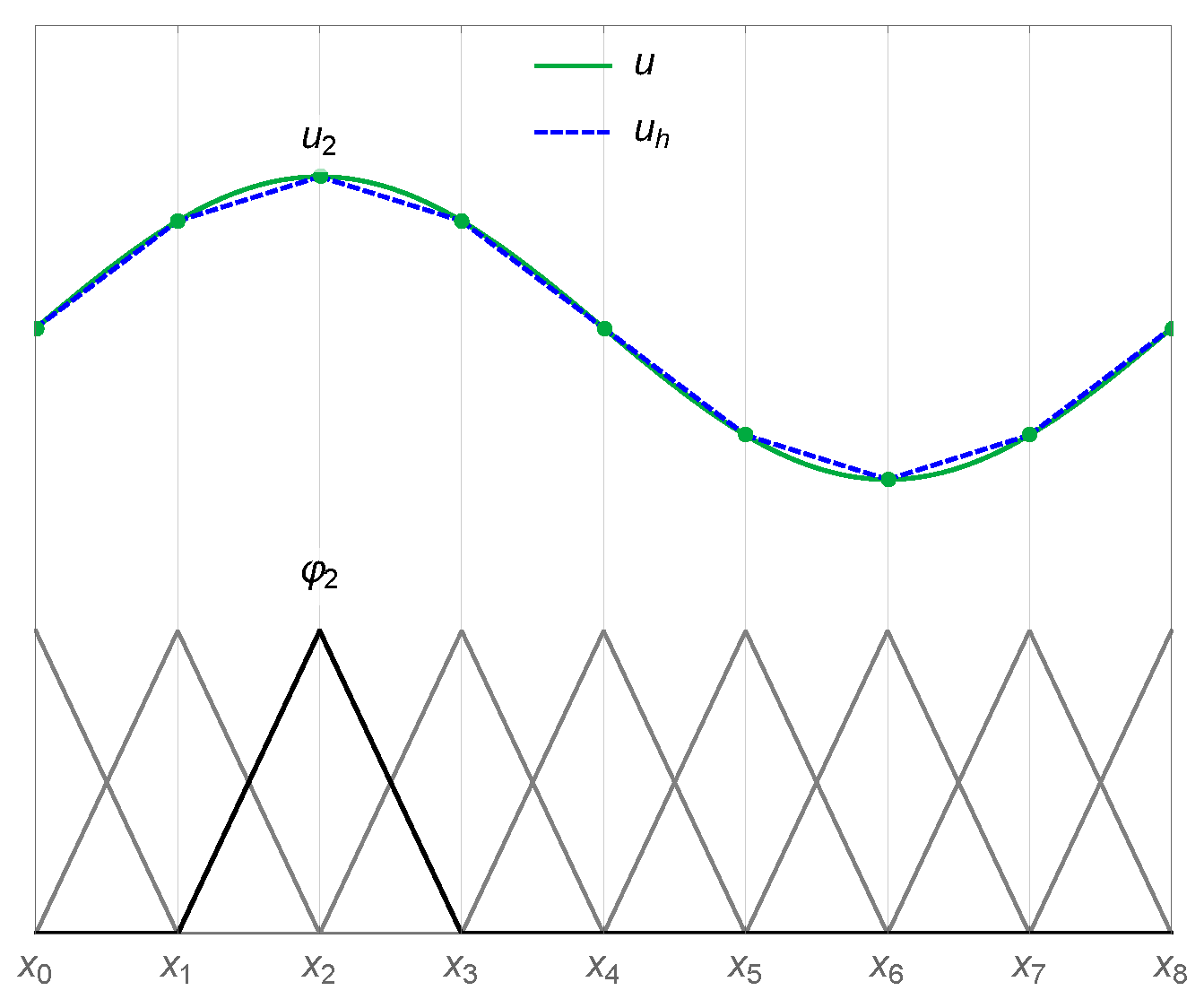
- For each point inside the TB where the conductivity needs to be computed, referred to as an integration point, the solver loops through the integration points of the RL and FL elements closer to the interfaces.
- The RL and FL points near to or at the interface with coordinates closest to the TB point are selected.
- The integration point number and element number associated with the nearest RL and FL points are mapped to the coordinates of the TB points.
3.2. Spin Accumulation Solution
3.2.1. Tunneling Spin Current
3.2.2. Spin Hall Effect
3.2.3. Complete Weak Formulation
- For each integration point on the RL|TB interface requiring the computation of the tunneling spin current, the solver loops through the integration points of the TB|FL interface.
- The TB|FL point with coordinates closest to the RL|TB one is selected.
- The integration point number and the element number associated with the found TB|FL point are mapped to the coordinates of the RL|TB one.
- The mapping procedure is repeated for the TB|FL interface.
3.3. Magnetization Dynamics Solution
3.4. Demagnetizing Field
4. Device Simulation
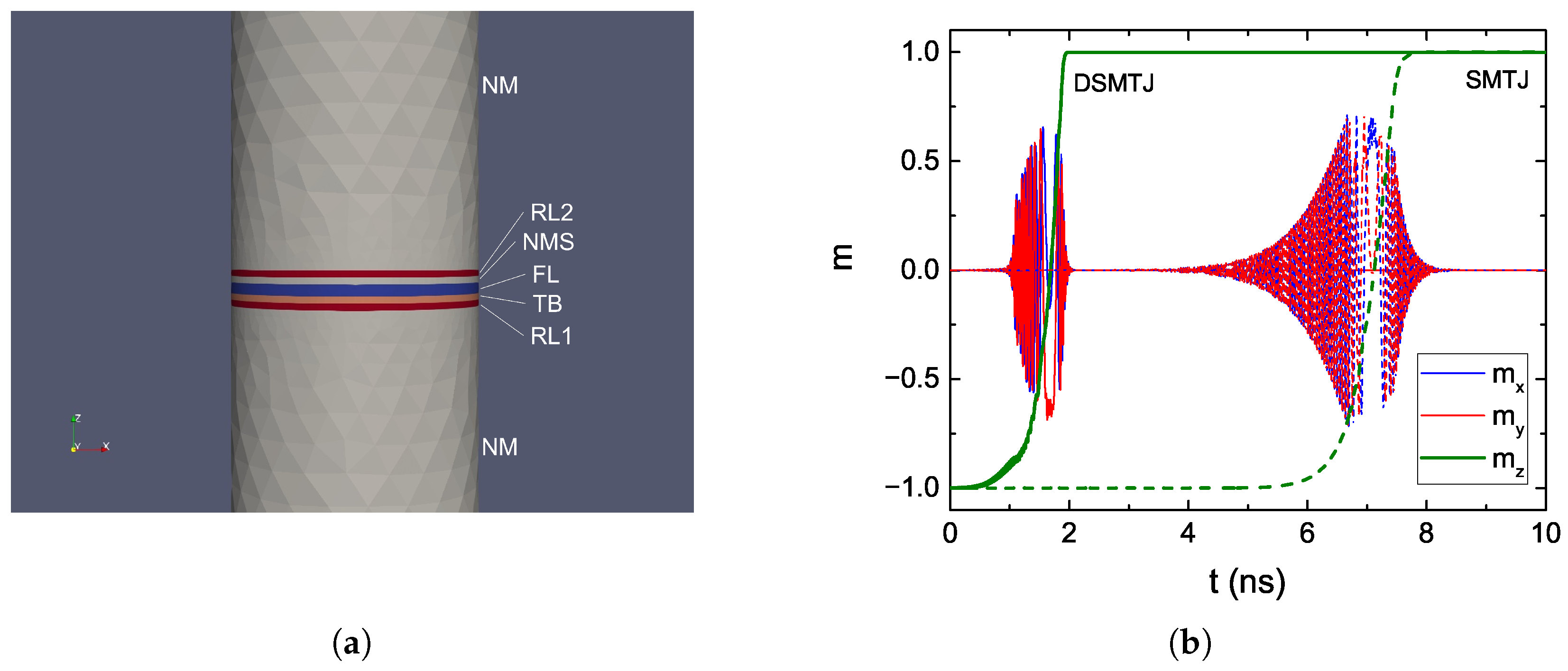
4.1. Double RL STT-MRAM
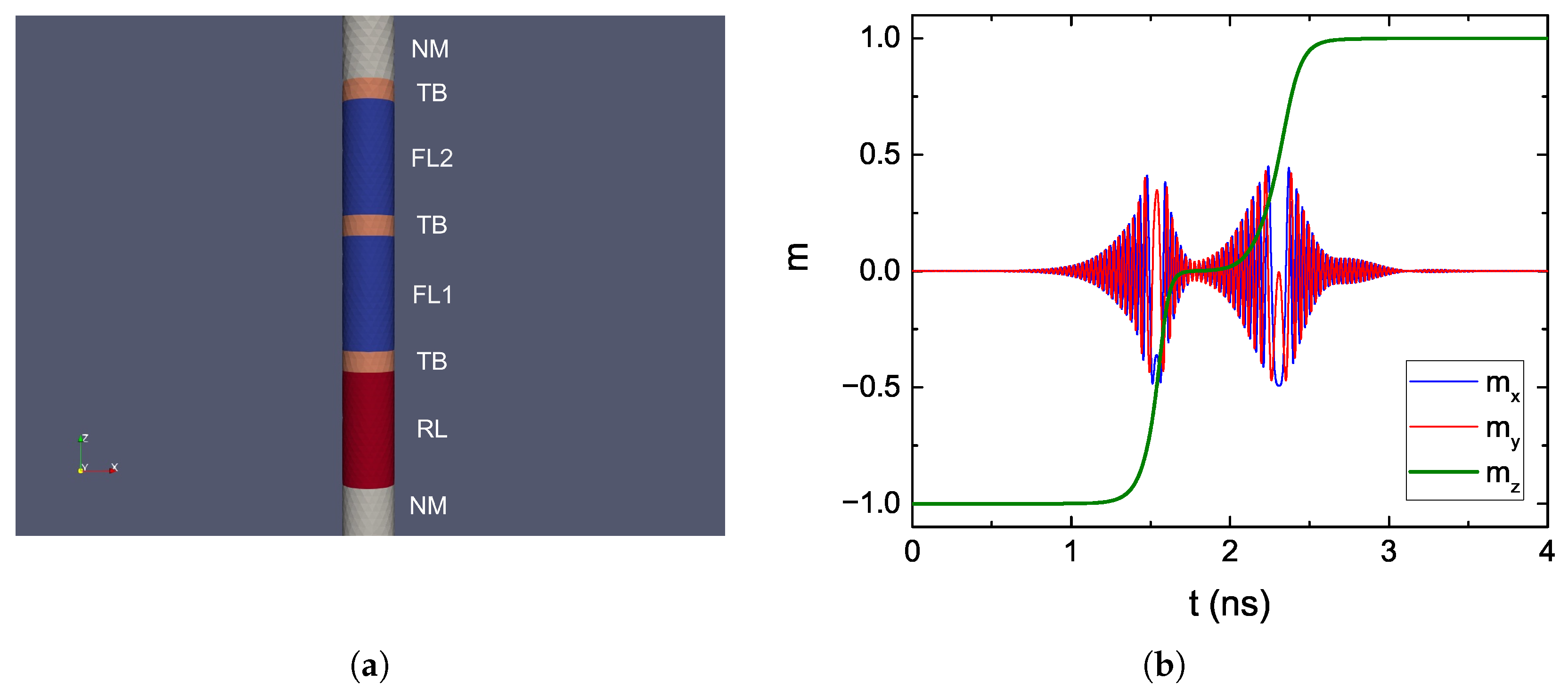
4.2. Ultra-Scaled STT-MRAM
4.3. SOT Assisted STT-MRAM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MRAM | Magnetoresistive random access memory |
| CMOS | Complementary metal-oxide semiconductor |
| SRAM | Static random access memory |
| MTJ | Magnetic tunnel junction |
| FM | Ferromagnetic |
| NM | Non-magnetic |
| RL | Reference layer |
| FL | Free layer |
| TB | Tunnel barrier |
| NMS | Non-magnetic spacer |
| HM | Heavy metal |
| P | Parallel |
| AP | Anti-parallel |
| TMR | Tunneling magnetoresistance ratio |
| STT | Spin-transfer torque |
| SOT | Spin-orbit torque |
| SHE | Spin Hall effect |
| LLG | Landau–Lifshitz–Gilbert |
| FE | Finite element |
| CRMT | Continuous random matrix theory |
| BEM | Boundary element method |
| LHS | Left-hand side |
| RHS | Right-hand side |
| DSMTJ | Double spin torque MTJ |
References
- Hanyu, T.; Endoh, T.; Suzuki, D.; Koike, H.; Ma, Y.; Onizawa, N.; Natsui, M.; Ikeda, S.; Ohno, H. Standby-Power-Free Integrated Circuits Using MTJ-based VLSI Computing. Proc. IEEE 2016, 104, 1844–1863. [Google Scholar] [CrossRef]
- Gallagher, W.J.; Chien, E.; Chiang, T.; Huang, J.; Shih, M.; Wang, C.Y.; Weng, C.; Chen, S.; Bair, C.; Lee, G.; et al. 22nm STT-MRAM for Reflow and Automotive Uses with High Yield, Reliability, and Magnetic Immunity and with Performance and Shielding Options. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 2.7.1–2.7.4. [Google Scholar] [CrossRef]
- Han, S.H.; Lee, J.M.; Shin, H.M.; Lee, J.H.; Suh, K.S.; Nam, K.T.; Kwon, B.S.; Cho, M.K.; Lee, J.; Jeong, J.H.; et al. 28-nm 0.08 mm2/Mb Embedded MRAM for Frame Buffer Memory. In Proceedings of the IEDM Conference, San Francisco, CA, USA, 12–18 December 2020; pp. 11.2.1–11.2.4. [Google Scholar] [CrossRef]
- Shih, Y.C.; Lee, C.F.; Chang, Y.A.; Lee, P.H.; Lin, H.J.; Chen, Y.L.; Lo, C.P.; Lin, K.F.; Chiang, T.W.; Lee, Y.J.; et al. A Reflow-Capable, Embedded 8Mb STT-MRAM Macro with 9ns Read Access Time in 16nm FinFET Logic CMOS Process. In Proceedings of the IEDM Conference, San Francisco, CA, USA, 12–18 December 2020; pp. 11.4.1–11.4.4. [Google Scholar] [CrossRef]
- Naik, V.B.; Yamane, K.; Lee, T.; Kwon, J.; Chao, R.; Lim, J.; Chung, N.; Behin-Aein, B.; Hau, L.; Zeng, D.; et al. JEDEC-Qualified Highly Reliable 22nm FD-SOI Embedded MRAM For Low-Power Industrial-Grade, and Extended Performance Towards Automotive-Grade-1 Applications. In Proceedings of the IEDM Conference, San Francisco, CA, USA, 12–18 December 2020; pp. 11.3.1–11.3.4. [Google Scholar] [CrossRef]
- Yau, J.B.; Fung, Y.K.K.; Gibson, G.W. Hybrid Cryogenic Memory Cells for Superconducting Computing Applications. In Proceedings of the ICRC Conference, Washington, DC, USA, 8–9 November 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Rowlands, G.E.; Ryan, C.A.; Ye, L.; Rehm, L.; Pinna, D.; Kent, A.D.; Ohki, T.A. A Cryogenic Spin-Torque Memory Element with Precessional Magnetization Dynamics. Sci. Rep. 2019, 9, 803. [Google Scholar] [CrossRef]
- Lang, L.; Jiang, Y.; Lu, F.; Wang, C.; Chen, Y.; Kent, A.D.; Ye, L. A Low Temperature Functioning CoFeB/MgO-Based Perpendicular Magnetic Tunnel Junction for Cryogenic Nonvolatile Random Access Memory. Appl. Phys. Lett. 2020, 116, 022409. [Google Scholar] [CrossRef]
- Slonczewski, J.C. Current-Driven Excitation of Magnetic Multilayers. J. Magn. Magn. Mater. 1996, 159, L1–L7. [Google Scholar] [CrossRef]
- Berger, L. Emission of Spin Waves by a Magnetic Multilayer Traversed by a Current. Phys. Rev. B 1996, 54, 9353–9358. [Google Scholar] [CrossRef] [PubMed]
- Slonczewski, J.C. Currents, Torques, and Polarization Factors in Magnetic Tunnel Junctions. Phys. Rev. B 2005, 71, 024411. [Google Scholar] [CrossRef]
- Dyakonov, M.I.; Perel, V.I. Current-Induced Spin Orientation of Electrons in Semiconductors. Phys. Lett. A 1971, 35, 459–460. [Google Scholar] [CrossRef]
- Ando, K.; Takahashi, S.; Harii, K.; Sasage, K.; Ieda, J.; Maekawa, S.; Saitoh, E. Electric Manipulation of Spin Relaxation Using the Spin Hall Effect. Phys. Rev. Lett. 2008, 101, 036601. [Google Scholar] [CrossRef]
- Abert, C.; Ruggeri, M.; Bruckner, F.; Vogler, C.; Hrkac, G.; Praetorius, D.; Suess, D. A Three-Dimensional Spin-Diffusion Model for Micromagnetics. Sci. Rep. 2015, 5, 14855. [Google Scholar] [CrossRef]
- Abert, C.; Ruggeri, M.; Bruckner, F.; Vogler, C.; Manchon, A.; Praetorius, D.; Suess, D. A Self-Consistent Spin-Diffusion Model for Micromagnetics. Sci. Rep. 2016, 6, 16. [Google Scholar] [CrossRef] [PubMed]
- Lepadatu, S. Unified Treatment of Spin Torques Using a Coupled Magnetisation Dynamics and Three-Dimensional Spin Current Solver. Sci. Rep. 2017, 7, 12937. [Google Scholar] [CrossRef]
- Anderson, R.; Andrej, J.; Barker, A.; Bramwell, J.; Camier, J.S.; Dobrev, J.C.V.; Dudouit, Y.; Fisher, A.; Kolev, T.; Pazner, W.; et al. MFEM: A Modular Finite Element Library. Comp. Math. Appl. 2020, 81, 42–74. [Google Scholar] [CrossRef]
- MFEM: Modular Finite Element Methods [Software]. Available online: https://mfem.org (accessed on 19 April 2023). [CrossRef]
- Ender, J.; Fiorentini, S.; de Orio, R.L.; Hadámek, T.; Bendra, M.; Jørstad, N.P.; Loch, W.J. ViennaSpinMag. 2023. Available online: https://www.iue.tuwien.ac.at/viennaspinmag (accessed on 19 April 2023).
- Hu, G.; Lauer, G.; Sun, J.Z.; Hashemi, P.; Safranski, C.; Brown, S.L.; Buzi, L.; Edwards, E.R.J.; D’Emic, C.P.; Galligan, E.; et al. 2X Reduction of STT-MRAM Switching Current Using Double Spin-Torque Magnetic Tunnel Junction. In Proceedings of the IEDM Conference, San Francisco, CA, USA, 11–16 December 2021; pp. 2.5.1–2.5.4. [Google Scholar] [CrossRef]
- Jinnai, B.; Igarashi, J.; Watanabe, K.; Funatsu, T.; Sato, H.; Fukami, S.; Ohno, H. High-Performance Shape-Anisotropy Magnetic Tunnel Junctions down to 2.3 nm. In Proceedings of the IEDM Conference, San Francisco, CA, USA, 12–18 December 2020; pp. 24.6.1–24.6.4. [Google Scholar] [CrossRef]
- Wang, M.; Cai, W.; Zhu, D.; Wang, Z.; Kan, J.; Zhao, Z.; Cao, K.; Wang, Z.; Zhang, Y.; Zhang, T.; et al. Field-Free Switching of a Perpendicular Magnetic Tunnel Junction Through the Interplay of Spin–Orbit and Spin-Transfer Torques. Nat. Electron. 2018, 1, 582–588. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. On the Theory of the Dispersion of Magnetic Permeability in Ferromagnetic Bodies. Phys. Z. Sowjetunion 1935, 8, 153–164. [Google Scholar]
- Gilbert, T.L. A Phenomenological Theory of Damping in Ferromagnetic Materials. IEEE Trans. Magn. 2004, 40, 3443–3449. [Google Scholar] [CrossRef]
- Martinez, E.; Lopez-Diaz, L.; Torres, L.; Garcia-Cervera, C. Micromagnetic Simulations with Thermal Noise: Physical and Numerical Aspects. J. Magn. Magn. Mater. 2007, 316, 269–272. [Google Scholar] [CrossRef]
- Torres, L.; Lopez-Diaz, L.; Martinez, E.; Carpentieri, M.; Finocchio, G. Micromagnetic Computations of Spin Polarized Current-Driven Magnetization Processes. J. Magn. Magn. Mater. 2005, 286, 381–385. [Google Scholar] [CrossRef]
- Xiao, Z.H.; Ma, X.Q.; Wu, P.P.; Zhang, J.X.; Chen, L.Q.; Shi, S.Q. Micromagnetic Simulations of Current-Induced Magnetization Switching in Co/Cu/Co Nanopillars. J. Appl. Phys. 2007, 102, 093907. [Google Scholar] [CrossRef]
- Finocchio, G.; Azzerboni, B.; Fuchs, G.D.; Buhrman, R.A.; Torres, L. Micromagnetic Modeling of Magnetization Switching Driven by Spin-Polarized Current in Magnetic Tunnel Junctions. J. Appl. Phys. 2007, 101, 063914. [Google Scholar] [CrossRef]
- Carpentieri, M.; Finocchio, G.; Torres, L.; Azzerboni, B. Modeling of Fast Switching Processes in Nanoscale Spin Valves. J. Appl. Phys. 2008, 103, 07B117. [Google Scholar] [CrossRef]
- Petitjean, C.; Luc, D.; Waintal, X. Unified Drift-Diffusion Theory for Transverse Spin Currents in Spin Valves, Domain Walls, and Other Textured Magnets. Phys. Rev. Lett. 2012, 109, 117204. [Google Scholar] [CrossRef] [PubMed]
- Graczyk, P.; Krawczyk, M. Nonresonant Amplification of Spin Waves Through Interface Magnetoelectric Effect and Spin-Transfer Torque. Sci. Rep. 2021, 11, 15692. [Google Scholar] [CrossRef] [PubMed]
- Haney, P.; Lee, H.W.; Lee, K.J.; Manchon, A.; Stiles, M. Current Induced Torques and Interfacial Spin-Orbit Coupling: Semiclassical Modeling. Phys. Rev. B 2013, 87, 174411. [Google Scholar] [CrossRef]
- Abert, C. Micromagnetics and Spintronics: Models and Numerical Methods. Eur. Phys. J. B 2019, 92, 120. [Google Scholar] [CrossRef]
- Zhang, S.; Levy, P.M.; Fert, A. Mechanisms of Spin-Polarized Current-Driven Magnetization Switching. Phys. Rev. Lett. 2002, 88, 236601. [Google Scholar] [CrossRef]
- Luc, D. Théorie Unifiée du Transport de Spin, Charge et Chaleur. Ph.D. Thesis, Université Grenoble Alpes, Grenoble, France, 2016. [Google Scholar]
- Ruggeri, M.; Abert, C.; Hrkac, G.; Suess, D.; Praetorius, D. Coupling of Dynamical Micromagnetism and a Stationary Spin Drift-Diffusion Equation: A Step Towards a Fully Self-Consistent Spintronics Framework. Physica B 2016, 486, 88–91. [Google Scholar] [CrossRef]
- Braess, D. Finite Elements: Theory, Fast Solvers, and Applications in Solid Mechanics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Larson, M.G.; Bengzon, F. The Finite Element Method: Theory, Implementation, and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Alouges, F.; Jaisson, P. Convergence of a Finite Element Discretization for the Landau-Lifshitz Equations in Micromagnetism. Math. Models Methods Appl. Sci. 2006, 16, 299–316. [Google Scholar] [CrossRef]
- Bartels, S.; Ko, J.; Prohl, A. Numerical Analysis of an Explicit Approximation Scheme for the Landau-Lifshitz-Gilbert Equation. Math. Comput. 2008, 77, 773–788. [Google Scholar] [CrossRef]
- Alouges, F. A New Finite Element Scheme for Landau-Lifchitz Equations. Discrete Contin. Dyn. Syst. S 2008, 1, 187–196. [Google Scholar] [CrossRef]
- Alouges, F.; Kritsikis, E.; Toussaint, J.C. A Convergent Finite Element Approximation for Landau–Lifschitz–Gilbert Equation. Physica B 2012, 407, 1345–1349. [Google Scholar] [CrossRef]
- Bruckner, F.; Suess, D.; Feischl, M.; Führer, T.; Goldenits, P.; Page, M.; Praetorius, D.; Ruggeri, M. Multiscale Modeling in Micromagnetics: Existence of Solutions and Numerical Integration. Math. Models Methods Appl. Sci. 2014, 24, 2627–2662. [Google Scholar] [CrossRef]
- Abert, C.; Hrkac, G.; Page, M.; Praetorius, D.; Ruggeri, M.; Suess, D. Spin-Polarized Transport in Ferromagnetic Multilayers: An Unconditionally Convergent FEM Integrator. Comp. Math. Appl. 2014, 68, 639–654. [Google Scholar] [CrossRef]
- Fiorentini, S.; Ender, J.; Selberherr, S.; de Orio, R.L.; Goes, W.; Sverdlov, V. Coupled Spin and Charge Drift-Diffusion Approach Applied to Magnetic Tunnel Junctions. Solid-State Electron. 2021, 186, 108103. [Google Scholar] [CrossRef]
- Fiorentini, S.; Bendra, M.; Ender, J.; de Orio, R.L.; Goes, W.; Selberherr, S.; Sverdlov, V. Spin and Charge Drift-Diffusion in Ultra-Scaled MRAM Cells. Sci. Rep. 2022, 12, 20958. [Google Scholar] [CrossRef]
- Chshiev, M.; Manchon, A.; Kalitsov, A.; Ryzhanova, N.; Vedyayev, A.; Strelkov, N.; Butler, W.; Dieny, B. Analytical Description of Ballistic Spin Currents and Torques in Magnetic Tunnel Junctions. Phys. Rev. B 2015, 92, 104422. [Google Scholar] [CrossRef]
- Julliere, M. Tunneling Between Ferromagnetic Films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Camsari, K.Y.; Ganguly, S.; Datta, D.; Datta, S. Physics-Based Factorization of Magnetic Tunnel Junctions for Modeling and Circuit Simulation. In Proceedings of the IEDM Conference, San Francisco, CA, USA, 15–17 December 2014; pp. 35.6.1–35.6.4. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Hrkac, G.; Pfeiler, C.M.; Praetorius, D.; Ruggeri, M.; Segatti, A.; Stiftner, B. Convergent Tangent Plane Integrators for the Simulation of Chiral Magnetic Skyrmion Dynamics. Adv. Comput. Math. 2019, 45, 1329–1368. [Google Scholar] [CrossRef]
- Abert, C.; Exl, L.; Bruckner, F.; Drews, A.; Suess, D. magnum.fe: A Micromagnetic Finite-Element Simulation Code Based on FEniCS. J. Magn. Magn. Mater. 2013, 345, 29–35. [Google Scholar] [CrossRef]
- Imhoff, J.; Meunier, G.; Brunotte, X.; Sabonnadiere, J. An Original Solution for Unbounded Electromagnetic 2D- and 3D-Problems Throughout the Finite Element Method. IEEE Trans. Magn. 1990, 26, 1659–1661. [Google Scholar] [CrossRef]
- Brunotte, X.; Meunier, G.; Imhoff, J. Finite Element Modeling of Unbounded Problems Using Transformations: A Rigorous, Powerful and Easy Solution. IEEE Trans. Magn. 1992, 28, 1663–1666. [Google Scholar] [CrossRef]
- Henrotte, F.; Meys, B.; Hedia, H.; Dular, P.; Legros, W. Finite Element Modelling with Transformation Techniques. IEEE Trans. Magn. 1999, 35, 1434–1437. [Google Scholar] [CrossRef]
- Leliaert, J.; Mulkers, J. Tomorrow’s Micromagnetic Simulations. J. Appl. Phys. 2019, 125, 180901. [Google Scholar] [CrossRef]
- Ender, J.; Mohamedou, M.; Fiorentini, S.; de Orio, R.L.; Selberherr, S.; Goes, W.; Sverdlov, V. Efficient Demagnetizing Field Calculation for Disconnected Complex Geometries in STT-MRAM Cells. In Proceedings of the SISPAD Conference, Kobe, Japan, 23 September–6 October 2020; pp. 213–216. [Google Scholar] [CrossRef]
- Fredkin, D.; Koehler, T. Hybrid Method for Computing Demagnetizing Fields. IEEE Trans. Magn. 1990, 26, 415–417. [Google Scholar] [CrossRef]
- Popović, N.; Praetorius, D. -Matrix Techniques for Stray-Field Computations in Computational Micromagnetics. In Proceedings of the Large-Scale Scientific Computing Conference, Sozopol, Bulgaria, 6–10 June 2005; Lirkov, I., Margenov, S., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 102–110. [Google Scholar] [CrossRef]
- H2Lib [Software]. Available online: http://www.h2lib.org (accessed on 19 April 2023).
- Loch, W.J.; Fiorentini, S.; Jørstad, N.P.; Goes, W.; Selberherr, S.; Sverdlov, V. Double Reference Layer STT-MRAM Structures with Improved Performance. Solid-State Electron. 2022, 194, 108335. [Google Scholar] [CrossRef]
- Nishioka, K.; Honjo, H.; Ikeda, S.; Watanabe, T.; Miura, S.; Inoue, H.; Tanigawa, T.; Noguchi, Y.; Yasuhira, M.; Sato, H.; et al. Novel Quad-Interface MTJ Technology and its First Demonstration With High Thermal Stability Factor and Switching Efficiency for STT-MRAM Beyond 2X nm. IEEE Trans. Electron Devices 2020, 67, 995–1000. [Google Scholar] [CrossRef]
- Grimaldi, E.; Krizakova, V.; Sala, G.; Yasin, F.; Couet, S.; Sankar Kar, G.; Garello, K.; Gambardella, P. Single-Shot Dynamics of Spin-Orbit Torque and Spin Transfer Torque Switching in Three-Terminal Magnetic Tunnel Junctions. Nat. Nanotechnol. 2020, 15, 111–117. [Google Scholar] [CrossRef]
- Zhang, W.; Han, W.; Jiang, X.; Yang, S.-H.; Parkin, S.S.P. Role of Transparency of Platinum–Ferromagnet Interfaces in Determining the Intrinsic Magnitude of the Spin Hall Effect. Nat. Phys. 2015, 11, 496–502. [Google Scholar] [CrossRef]
| LLG parameters | Value |
| Saturation magnetization () | A/m |
| Exchange constant () | J/m |
| Interface anisotropy () | J/m |
| Gilbert damping constant () | |
| Drift-diffusion parameters | Value |
| Conductivity polarization, | |
| Diffusion polarization, | |
| FM diffusion coefficient, | m/s |
| NM diffusion coefficient, | m/s |
| HM diffusion coefficient, | m/s |
| TB diffusion coefficient, | m/s |
| FM conductivity | S/m |
| NM conductivity | S/m |
| HM conductivity | S/m |
| FM spin-flip length, | 10 nm |
| NM spin-flip length, | 10 nm |
| HM spin-flip length, | nm |
| Spin exchange length, | nm |
| Spin dephasing length, | nm |
| Spin Hall angle, | 0.19 |
| TB resistance standard and double RL STT-MTJ | Value |
| Resistance parallel () | k |
| Resistance anti-parallel () | k |
| TB resistance ultra-scaled STT-MTJ | Value |
| Resistance parallel () | k |
| Resistance anti-parallel () | k |
| TB resistance SOT-assisted STT-MTJ | Value |
| Resistance parallel () | k |
| Resistance anti-parallel () | k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorentini, S.; Jørstad, N.P.; Ender, J.; de Orio, R.L.; Selberherr, S.; Bendra, M.; Goes, W.; Sverdlov, V. Finite Element Approach for the Simulation of Modern MRAM Devices. Micromachines 2023, 14, 898. https://doi.org/10.3390/mi14050898
Fiorentini S, Jørstad NP, Ender J, de Orio RL, Selberherr S, Bendra M, Goes W, Sverdlov V. Finite Element Approach for the Simulation of Modern MRAM Devices. Micromachines. 2023; 14(5):898. https://doi.org/10.3390/mi14050898
Chicago/Turabian StyleFiorentini, Simone, Nils Petter Jørstad, Johannes Ender, Roberto Lacerda de Orio, Siegfried Selberherr, Mario Bendra, Wolfgang Goes, and Viktor Sverdlov. 2023. "Finite Element Approach for the Simulation of Modern MRAM Devices" Micromachines 14, no. 5: 898. https://doi.org/10.3390/mi14050898
APA StyleFiorentini, S., Jørstad, N. P., Ender, J., de Orio, R. L., Selberherr, S., Bendra, M., Goes, W., & Sverdlov, V. (2023). Finite Element Approach for the Simulation of Modern MRAM Devices. Micromachines, 14(5), 898. https://doi.org/10.3390/mi14050898








