1. Introduction
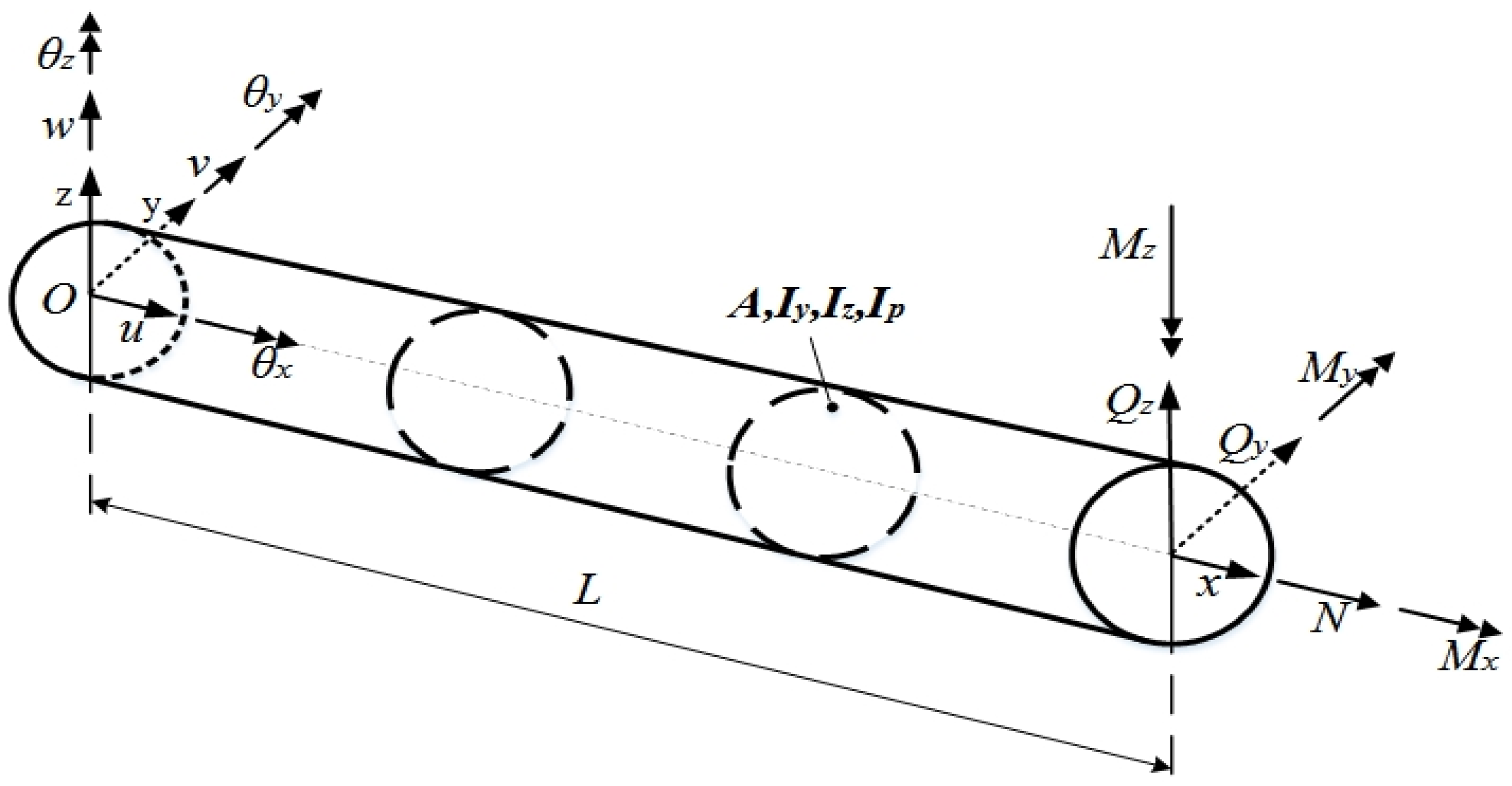
A sub-reflector is an important part of a large-aperture radio telescope, for it has a direct impact on the electrical performance of the system [
1]. Ideally, the position of the sub-reflector relative to the antenna’s main reflector is fixed (
Figure 1). However, as the antenna diameter increases, the dimension of the sub-reflector support frame becomes large, and its rigidity decreases. This causes the support frame to deform easily when put under the influence of environmental loads (such as heat, gravity, etc.). A change in the position of the sub-reflector relative to the main reflector will result in a decrease in the electrical performance of the antenna. In particular, this will have a great impact on the pointing accuracy of the antenna. Therefore, the research on the deformation of the sub-reflector support structure under environmental loads has practical significance for maintaining the electrical performance of a radio telescope.
Adjusting the sub-reflector position by an active surface control system is the main method to improve electrical performance [
2,
3,
4]. In this approach, the position and altitude of a deformed sub-reflector support structure must be accurately obtained first in order to provide an accurate input to the active surface control system. Currently, photogrammetry is generally used in engineering for such measurements. However, this method can only be used offline and at night, which means that it only compensates for the deformation caused by gravity. The Sardinian Radio Telescope (SRT) measurement team developed a non-contact measurement scheme based on a position sensing device (PSD) [
5], which is composed of a laser diode and a complementary metal oxide semiconductor (CMOS) camera. In this scheme, the accuracy of the PSD can reach about 0.1 mm for a 40 mm measurement range. Owing to the laser capturing capability of the CMOS cameras being easily influenced by the incident angle of the sunlight, this measurement scheme is limited to daytime operation. In order to overcome the above limitations, a contact measurement technique was proposed and applied to large structures [
6,
7,
8]. Compared with traditional strain sensors, Fiber Bragg Grating (FBG) has been widely studied and applied in the field of shape perception because of its lightness, high accuracy, anti-electromagnetic interference, and anti-radiation [
9,
10]. Marco Bonopera [
11] presented important advances in the sensing design and principle of FBG-based displacement sensors. Wang et al. discussed the reliability of the traditional temperature compensation method and proposed a novel temperature compensation method specifically for structures under different loading conditions [
12].
The support structure of an antenna sub-reflector is a typical truss structure, which is composed of beam elements. In order to measure the deformation of the beam elements, Ko et al. proposed a load-independent method based on piece-wise continuous polynomials and classical beam theory [
13]. The disadvantage of this method is that it only reconstructs structure deformation in one dimension. In practice, it is necessary to measure the deformation of the support structure for the sub-reflector in three dimensions. Bogert et al. analyzed and verified the effectiveness of the modal conversion method by reconstructing structural deformation [
14]. Although this method has many advantages, it requires an accurate finite element model. In addition, this method requires a substantial amount of eigenvalue analysis and a detailed description of the properties of the elastic and inertial materials.
To address the problem of inadaptability in the Ko and the modal methods when applying to complex topological structures and boundary conditions during reconstruction, Tessler proposed the inverse finite element method (iFEM) based on the variational principle [
15,
16]. From the kinematic assumptions of the iFEM frame and Timoshenko beam theory, Gherlone et al. proposed an inverse finite element method for sensing the deformation of a beam or frame structure [
17,
18]. Bao et al. [
19] developed the single variable iFEM model to reduce the number of strain sensors required in multi-node load. Chen et al. [
20] established a unified reconstruction method for the beam-like structure based on the framework of iFEM, which can reduce the structure identification error by introducing some generalized quantities. Shang et al. [
21] proposed the inverse-plate quadrilateral area coordinates method to replace the Jacobian matrix, such that the error caused by numerical integration can be avoided. Roy et al. [
22] expanded the applicability of the iFEM beam model to include prismatic beams with arbitrary cross-sections. Zhao et al. [
23] combined the Green-Lagrange strain theory to extend the iFEM for nonlinear deformation.
Due to some uncertain factors, including sensor installation position errors and strain measurement errors presented in actual engineering, the accuracy of shape sensing with the iFEM is affected. Pan et al. proposed to use a fuzzy network to approximate the relationship between the measured strains and the inverse solution strains. They established a fuzzy calibration network through 13 sets of working condition data, and the calibrated strain was used to solve the frame deformation displacement [
24]. Fu et al. proposed a fuzzy calibration network with support vectors to generalize the use of the network [
25]. The network is obtained by training with 10 sets of working condition data. Since the above-mentioned approaches use less data for training the calibration network, the resulting network covers less information, which will directly influence the accuracy of the calibration network [
26]. In addition, Li et al. [
27] customize a calibration method using a fuzzy self-framework, which can effectively solve the interference caused by the sensor paste error in iFEM.
However, the reconstruction accuracy of the partial evaluation position was only improved by the above calibration method. In addition, the errors between calibration results and the actual deformation displacement were increased when the faint noise interfered with the working condition data. Considering the reduced influence of external factors on the real-time reconstruction of structural deformation, an online measurement and calibration method for structural deformation based on small samples is proposed in this paper, which can calibrate the reconstruction values of the sub-reflector position and altitude in real-time to improve the reconstruction accuracy. The main original aspects of the proposed method are twofold. Firstly, a reconstruction model between the FBG strain measurements and the deformation displacements of a sub-reflector support structure is established. Secondly, the sample measurement data is extended by the NURBS to provide the training data for the SSFN, which can effectively correct random noise data.
3. The Establishment of Self-Architected Fuzzy Calibration Network
The actual measured displacements at the end of a support leg can be obtained by the measuring device (denoted by
). Hence, the reconstructed end displacement along different axes is
, and their values can be obtained by the inverse finite element method. Hence, the components of the reconstruction errors are
The calibration process is divided into two parts. The first part concerns the construction of a third-order B-spline curve equation based on the measured strain and reconstruction error data. The expansion of the initial data is also performed through Equation (11). The second part involves establishing the self-architected fuzzy calibration network and using the expanded data to realize the real-time calibration of end displacements.
3.1. Expansion of Data Sample
The number of samples used to train the self-architected fuzzy network will directly influence the fineness of the network’s description of the relationship between different variables, which in turn determines the precision of the calibration networks. Therefore, expanding the training data sample capacity is of great significance for improving the precision of network calibration. According to the reconstruction theory discussed in
Section 2, the relationship between strain measurement and reconstruction displacement is nonlinear. Therefore, this paper proposes to use the 3rd B-spline function for data sample expansion.
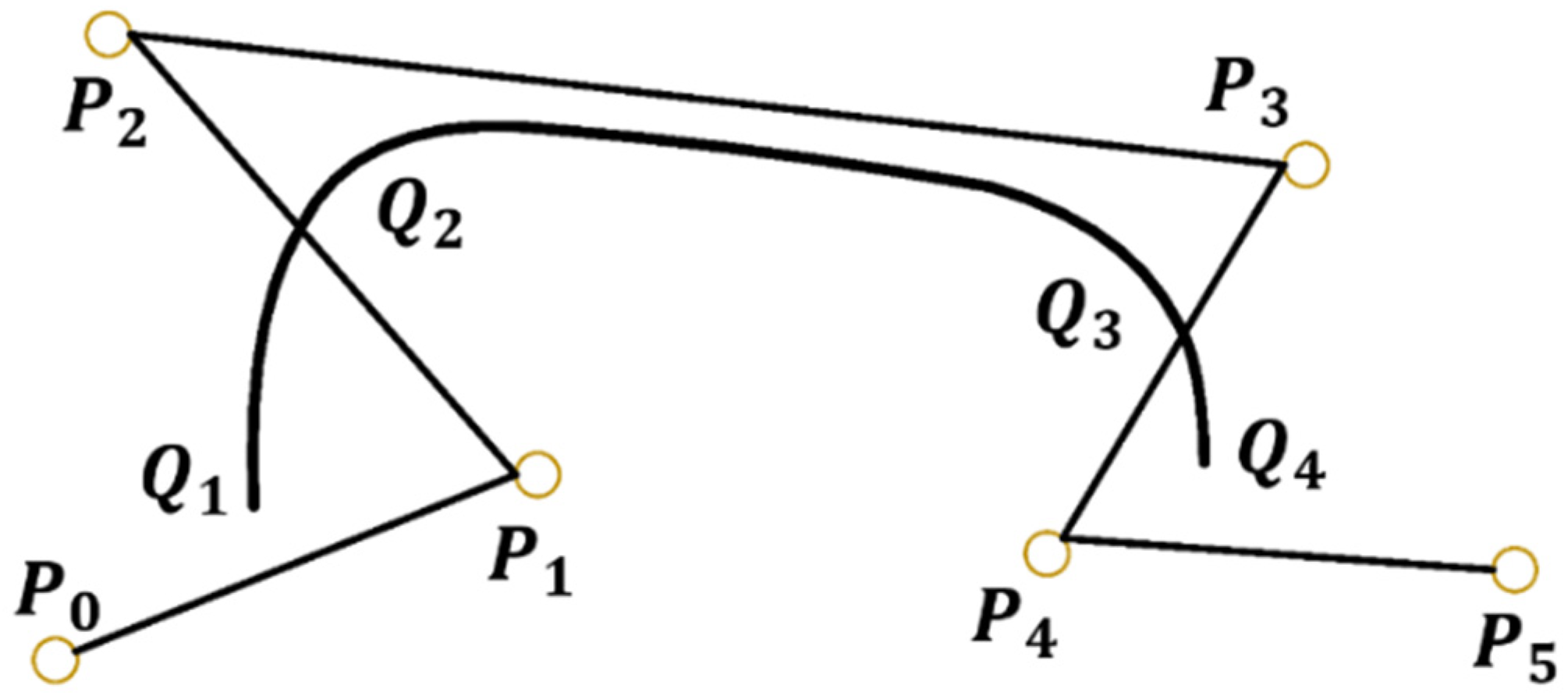
For a given
n + 1 plane or spatial points
, the definition for an
n-th parameter segment on a B-spline curve is given by
Here,
is the
k-th segment on the
n-th degree B-spline curve,
u is the data point parameter;
is the basis function of the
n-th degree B-spline curve, and the polygon formed by its vertex
is called the B-spline curve feature polygon. According to the definition of the B-spline curve, the k segment of an
n-th B-spline curve is only related to
n + 1 control points signified by
. The 3rd B-spline curve is controlled by the 6 control points designated by
is composed of three B-spline curve segments, each is controlled by 4 points in
, as shown in
Figure 5.
The B-spline curve is local. The change of one control point will only influence the adjacent curve segment and will not influence the trend of change on the entire curve. For
n = 3, the 3rd B-spline curve segment
, is given by
where
The basis functions of the cubic B-spline curve are as follows:
It can be written in matrix form as
where
is the basis function matrix of the cubic B-spline,
X and
Y are the coordinate vectors of the control points in each section of the cubic B-spline curve, and
are the coordinates of a point on the cubic B-spline curve. For continuous values of
, a smooth B-spline curve can be determined. For
n control vertices, a complete cubic B-spline curve can be obtained by only moving the control vertices
n−3 times. After successfully fitting the cubic B-spline curve, the data point parameter
u is taken from 0 to 1 in a certain step, such that the corresponding number of points on the curve can be obtained, and the data can be expanded.
3.2. Construction of the Calibration Network
In reality, there are errors in the sensor installation and data collection, which lead to subsequent displacement reconstruction errors. In this paper, the self-architected fuzzy network (SAFN) algorithm is used to calibrate the reconstruction errors. The algorithm uses the triangular membership functions (MF), which independently increases the membership functions and fuzzy rules together with adjusting their distributions, thereby improving the structure of the fuzzy system. Based on the cubic B-splines, large-scale data is obtained, and a further fuzzy network is derived to approximate the measured strain and reconstruction error.
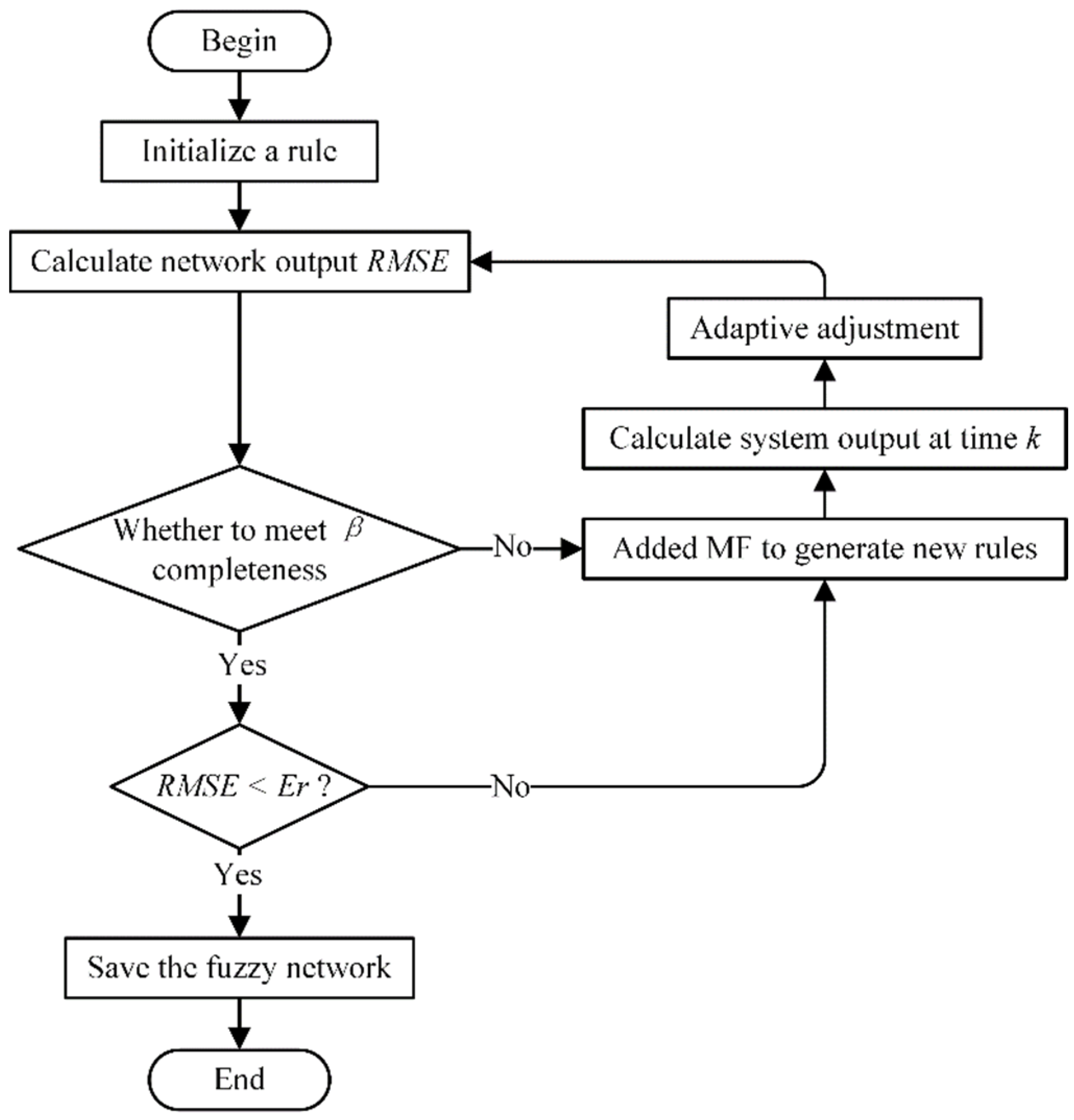
The generation of self-architected fuzzy networks can be divided into three parts: (1) adding MF and generating the rules, (2) establishing self-adapting fuzzy rules and consequent parts, and (3) preserving fuzzy networks [
24]. The algorithm flowchart is shown in
Figure 6.
- 1.
Adding MF and generation rules
The root-mean-square error is used to describe the system error, and its calculation is given by Equation (16). In the equation,
represents the output value from the fuzzy network, and
signifies the reconstruction deformation error. Hence, the system error
can be calculated. The symbol
represents the error threshold in the training phase. If
, the membership function needs to be increased at the input.
-
For any input variable in the working range, the current value can help activate an MF, and the maximum value for of the obtained membership degree is either greater than or equal to the preset β value. If , MF needs to be increased or is otherwise unchanged.
- 2.
The consequence of self-adaptive rules
Based on the current estimated output value and the expected output value from the fuzzy network, the rule consequences are adjusted. At
k moment, the expression for adjusting the consequence of the
j-th rule
is as follows:
where
represents the activation of the
j-th rule at time
,
represents the estimated displacement that is input to the network at the previous time, and
is the calibrated displacement error output from the fuzzy network at the current time. The value of
is artificially adjusted to change the speed of the self-adaptive process of the rule consequence.
- 3.
Fixing the rules and obtaining the fuzzy network
After adding the data, the estimated output error from the network for all training input values becomes very small. For , it means that the autonomous architecture stage of the network is completed. The network training is then stopped, and the fuzzy rules in the current network are saved.
After expanding the samples of strain and reconstruction error through the cubic B-spline theory, the expanded samples are used to train the fuzzy network and generate the fuzzy calibration network. In engineering practice, when the real-time measured strain is input into the fuzzy calibration network, the calibrated displacement error value can be presented in real-time. After that, the accurately reconstructed displacements will be obtained.
4. Experimental Examples
In order to verify the accuracy and effectiveness of the online reconstructed displacement error calibration method presented in this paper, a scaled-down model for a radio telescope test antenna model was constructed, as shown in
Figure 7. Under the elevation motion, the support structure’s deformation measurements and calibration experiment were carried out. The support structure is made of aluminum alloy material. Its Young’s modulus is
, Poisson’s ratio is
, density
, and the entire structure weighs about 43 kg. The support beam is 2000 mm long and has a radius of 20 mm. The total weight of the sub-reflector is 200 kg.
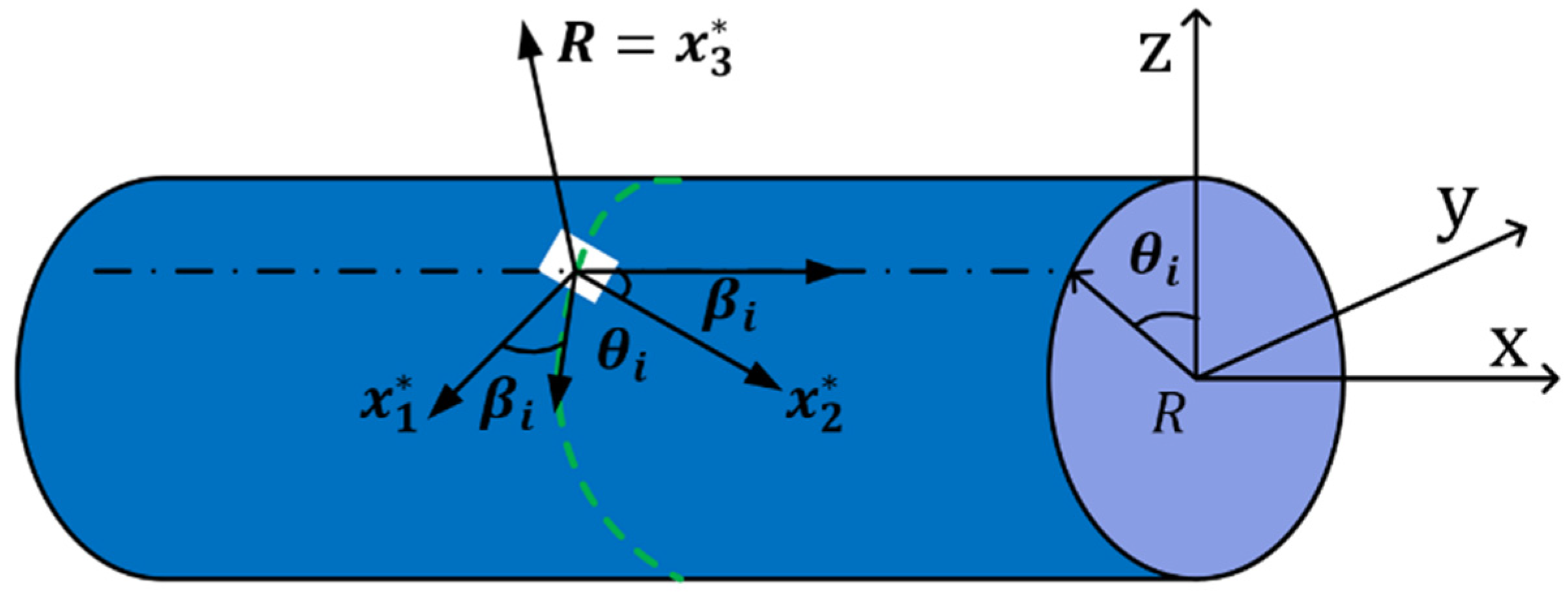
In order to realize the deformation reconstruction for the support legs of the sub-reflector, six fiber grating strain sensors are installed on the surface of each support leg, and three sensors are placed on the same section to capture the surface strain. In the experiments, the strain data is measured by the FBG strain sensor (Fiber Bragg Grating| os1100, Micron Optics, Atlanta, GA, USA) and the FBG demodulator (Optical Sensing Instrument| Si 155, Micron Optics, Atlanta, GA, USA) Strain measurement system. The positions of the six strain sensors are shown in
Table 1. Here,
represents the relative position, and
are the circumferential angle
with angle
between x-axis and the frame, both measured in degrees. The properties of the FBG sensor include 1530–1565 wavelength operating range, 0.23 nm bandwidth, 15 db side-mode rejection ratio, 10 mm grid length, and 1 pm demodulation accuracy.
A high-precision single-point laser tracker (LTS, API Tracker 3, Automated Precision Inc., Rockwell, MD, USA) was used to measure the actual displacement at the end of the support leg and at different elevation angles. The resolution of the LTS is 1 um, and the precision is related to the distance between the LTS and the measured object (the ratio is 5 um/m). During the experiment, the distance between the instrument and the test antenna model was 6 m, and the measurement precision of the laser tracker was 0.03 mm. The entire measurement system is shown in
Figure 8.
In the experiments, the global coordinate system was established on the main reflector. In each local coordinate system, the x-axis was established along the neutral axis of each support beam, the y-axis and z-axis were orthogonal in the beam section, and the four support beams had four different local coordinate systems (
Figure 9).
In order to better validate the effectiveness of the calibration scheme proposed in this paper, the strain and real displacement data at the end of the support leg at each elevation angle were collected at midnight to ensure that the model was in a stable environmental temperature. Assuming the initial position and altitude of 0 degree between the main reflector of the antenna and the horizontal plane, the strain data collected by the fiber demodulator was recorded and returned to zero. The platform was then rotated and stopped every 5 degrees increment to measure the strains and true displacements of the support leg (see
Figure 10).
From 5 to 60 degrees, the strains and displacements at the end of the support legs were collected. As shown in the second section, the reconstruction value of the deformation at the end of the support legs can be calculated by . According to Equation (3), the reconstruction errors can be obtained in the form of . From the 12 working conditions, the data at the elevation angles of , , , and were used to test the precision of the calibration network, and the data of the remaining eight working conditions were used to train the self-architected fuzzy calibration network.
For each support leg, the strain
that shows the greatest reaction to changes of the elevation angle in the model is selected and combined with the reconstruction error to form three control points of deformation direction, designated by
,
and
. Consider
, the eight working conditions form eight vertices. According to
Section 3.1, the cubic B-spline curve can be obtained. The data from the eight groups of working conditions can be expanded based on the value in the parameter u from 0 to 1, in step of 0.002, thereby forming 501 sets of data. Similarly, for
and
, which are also expanded into 501 sets of data. Using the extended data from a single direction of the support leg for training, three sets of fuzzy calibration networks,
,
, and
, can be obtained. This is then followed by inputting the measured strains, obtained at the elevation angles of
,
,
, and
, into each
,
, and
to determine the calibrated displacement error. Finally, the calibration displacement value is obtained by adding the calibration error to the initial reconstruction displacement.
When the fuzzy calibration network is completed, the real-time input strain and output deformation calibration can be realized. In this paper, four elevation angles taken at midnight were used as a case study to validate the calibration network. For the support 1, the displacement and calibration error as shown in
Table 2, and corresponding FBG strains and temperature compensation as shown in
Table 3. Meanwhile, the estimated index of the fuzzy calibration network’s ability defined as
the actual, reconstructed, and calibrated displacements are denoted as
,
and
.
For the support 2, the displacement and calibration error as shown in
Table 4, and corresponding FBG strains and temperature compensation as shown in
Table 5.
For the support 3, the displacement and calibration error as shown in
Table 6, and corresponding FBG strains and temperature compensation as shown in
Table 7.
For the support 4, the displacement and calibration error as shown in
Table 8, and corresponding FBG strains and temperature compensation as shown in
Table 9.
It can be seen from
Table 2,
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8 and
Table 9 that the reconstructed displacements for the end of the support legs can be calibrated well at different elevation angles using the small sample self-architected fuzzy calibration algorithm proposed in this paper. The percentage displacement errors in the x, y, and z directions do not exceed 4% after calibrating the four support legs. In particular, for the elevation angle at 40 degrees, the y-direction displacement percentage error at the end of the No. 1 support leg is 0%. It can be seen from the actual displacements in the x, y, and z directions that the y direction is the main deformation direction. In most cases, the calibration error in the y direction is less than that in the
x and
z directions when the deformation is large. This suggests that the presented calibration scheme in this paper has better calibration ability for the main deformation direction.
In order to further verify the effectiveness of the temperature compensation device designed in this paper, the strain data under the elevation of 55° at noon and from the No. 1 support leg was used. In this case, the strain value
was obtained by Equation (10). It can be seen from
Table 10 that the temperature has a great influence on strain measurement. However, when the measured strains,
are compensated,
becomes stable.
Comparing the displacement reconstruction value , at noon and at midnight with the displacement , the results are as follows.
It can be seen from
Table 11 that the displacement reconstruction value at the end of No. 1 support leg measured at noon has a deviation of 0.67 mm in the
y direction when compared with the measurement taken at night. The deviation decreases to 0.06 mm after temperature compensation for the measured strain. It is clear that the temperature compensation method can greatly reduce the influence of environmental temperature changes on the strain acquisition system. Therefore, the self-structuring fuzzy network and the temperature compensation device proposed in this paper are important for improving the accuracy of traditional inverse finite elements in real-world engineering applications.