A Closed Cavity Ultrasonic Resonator Formed by Graphene/PMMA Membrane for Acoustic Application
Abstract
1. Introduction
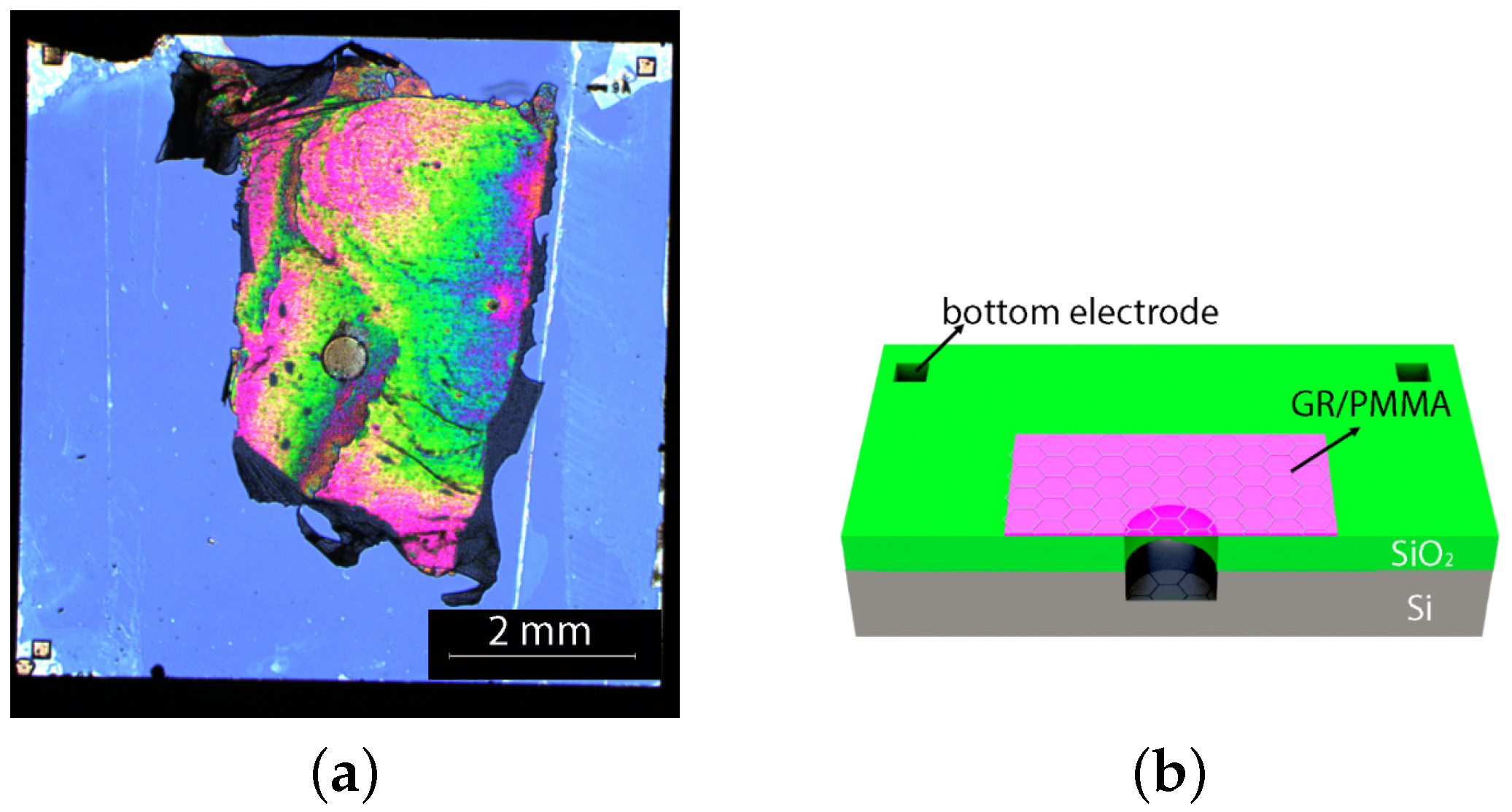
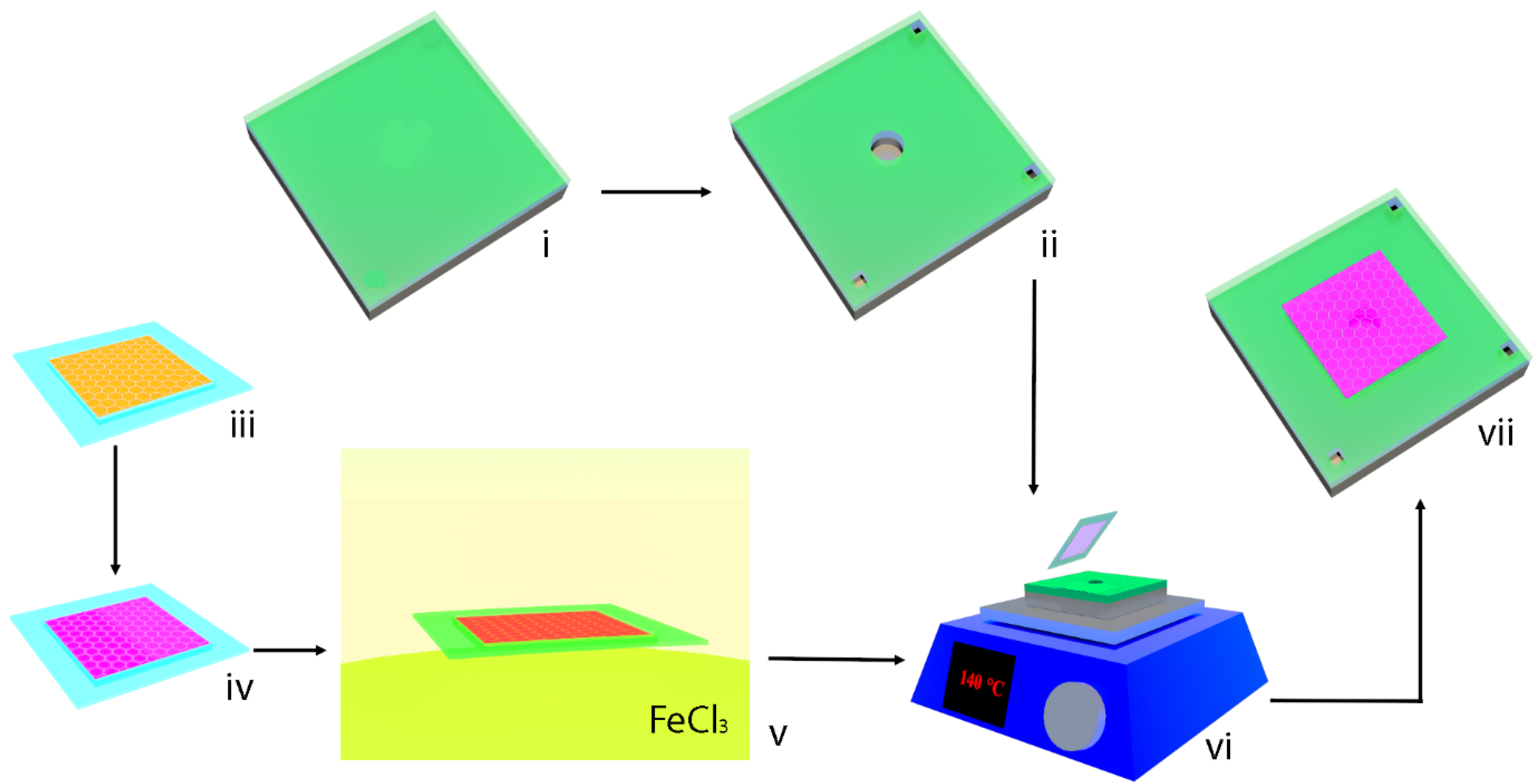
2. Materials and Methods
3. Results and Discussion
3.1. Dynamic Actuation
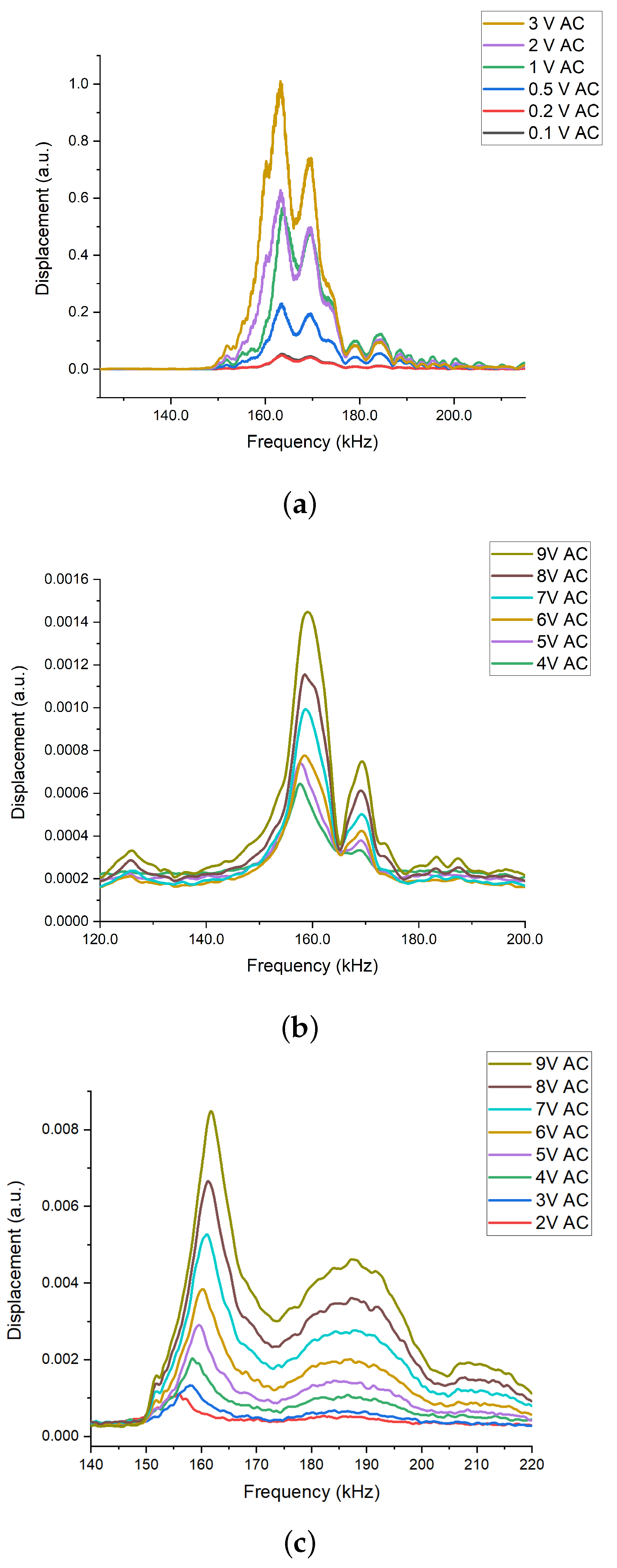
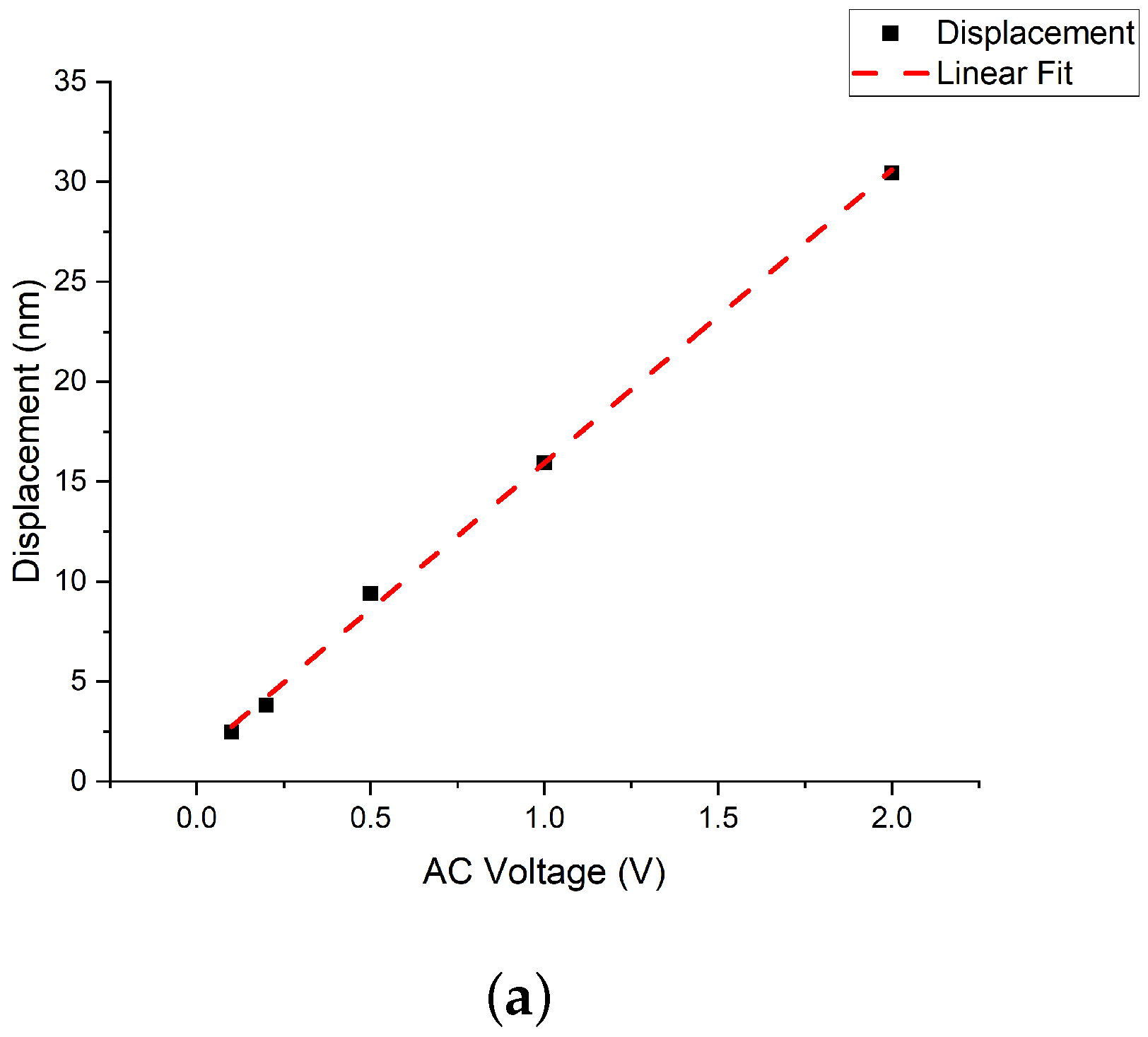
3.1.1. Mechanical Actuation
3.1.2. Electro-Static Actuation
3.1.3. Electro-Thermal Actuation
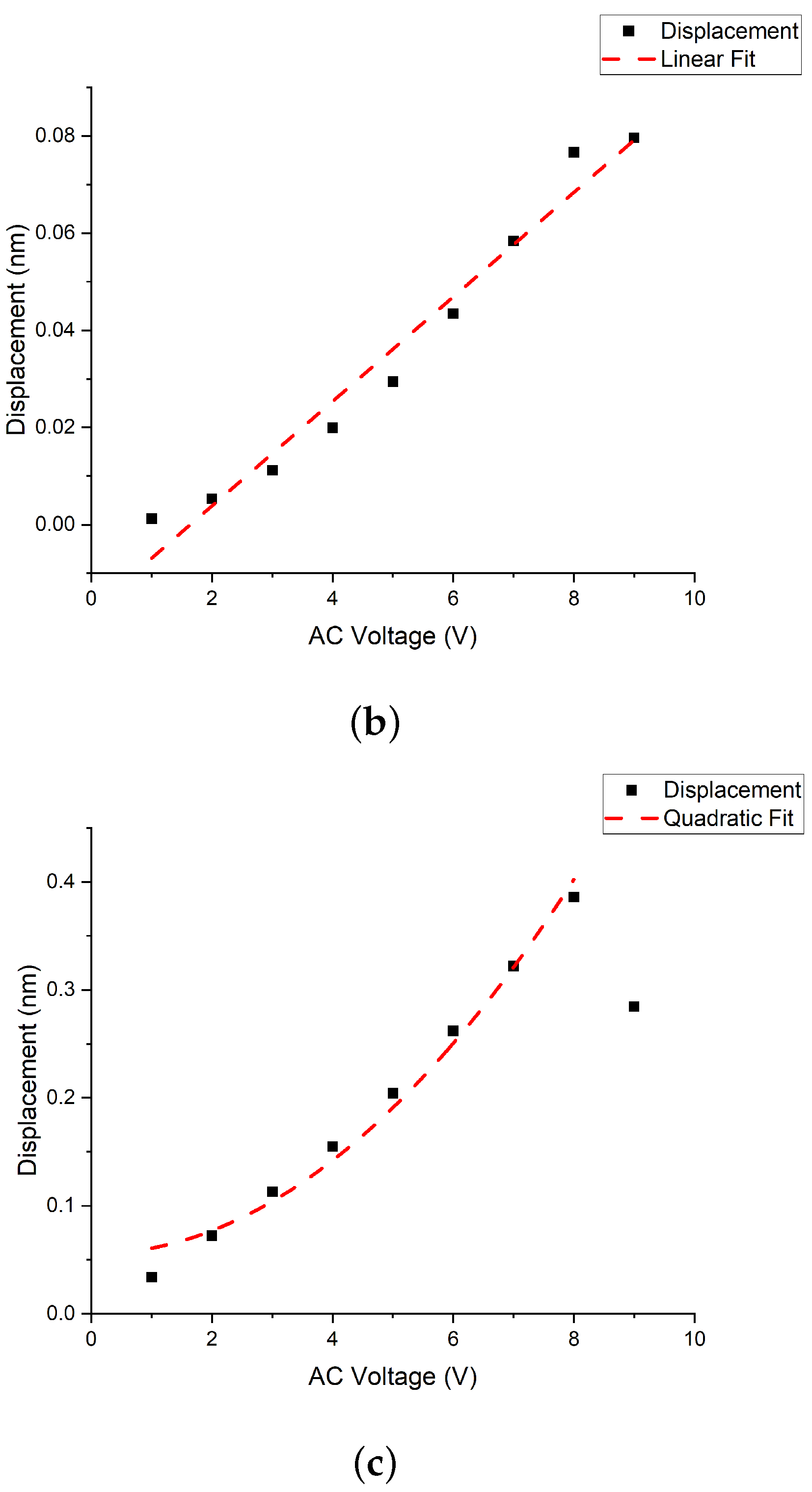
3.2. Sensitivity of Vibration Amplitude
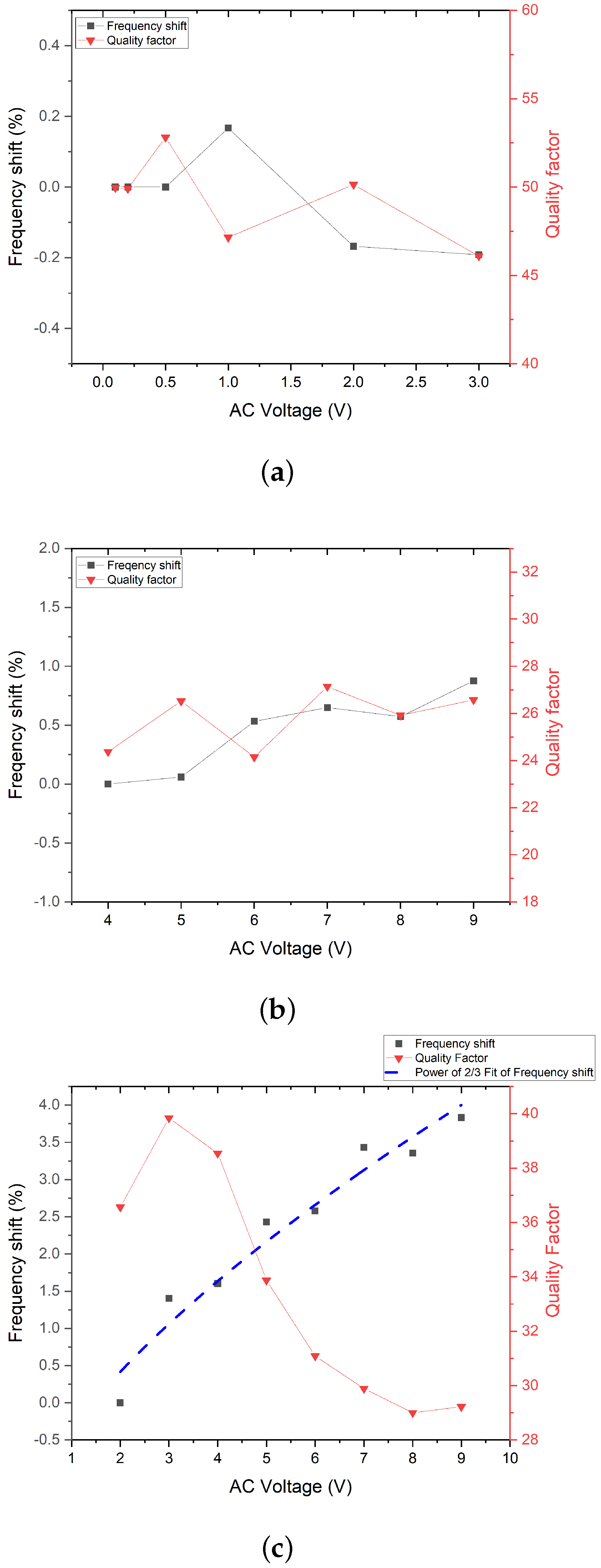
3.3. Frequency Shift and Quality Factor
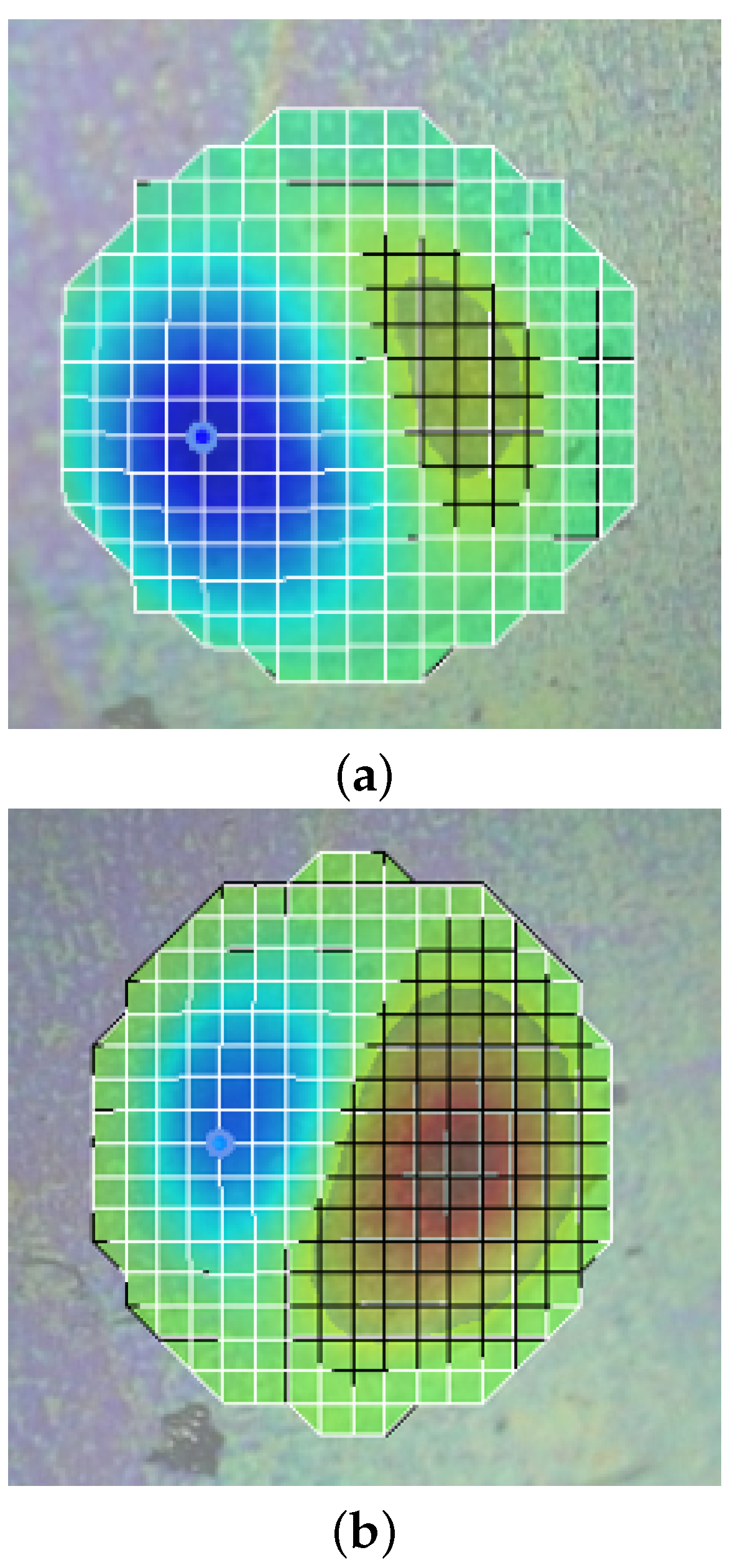
3.4. Mode Shape
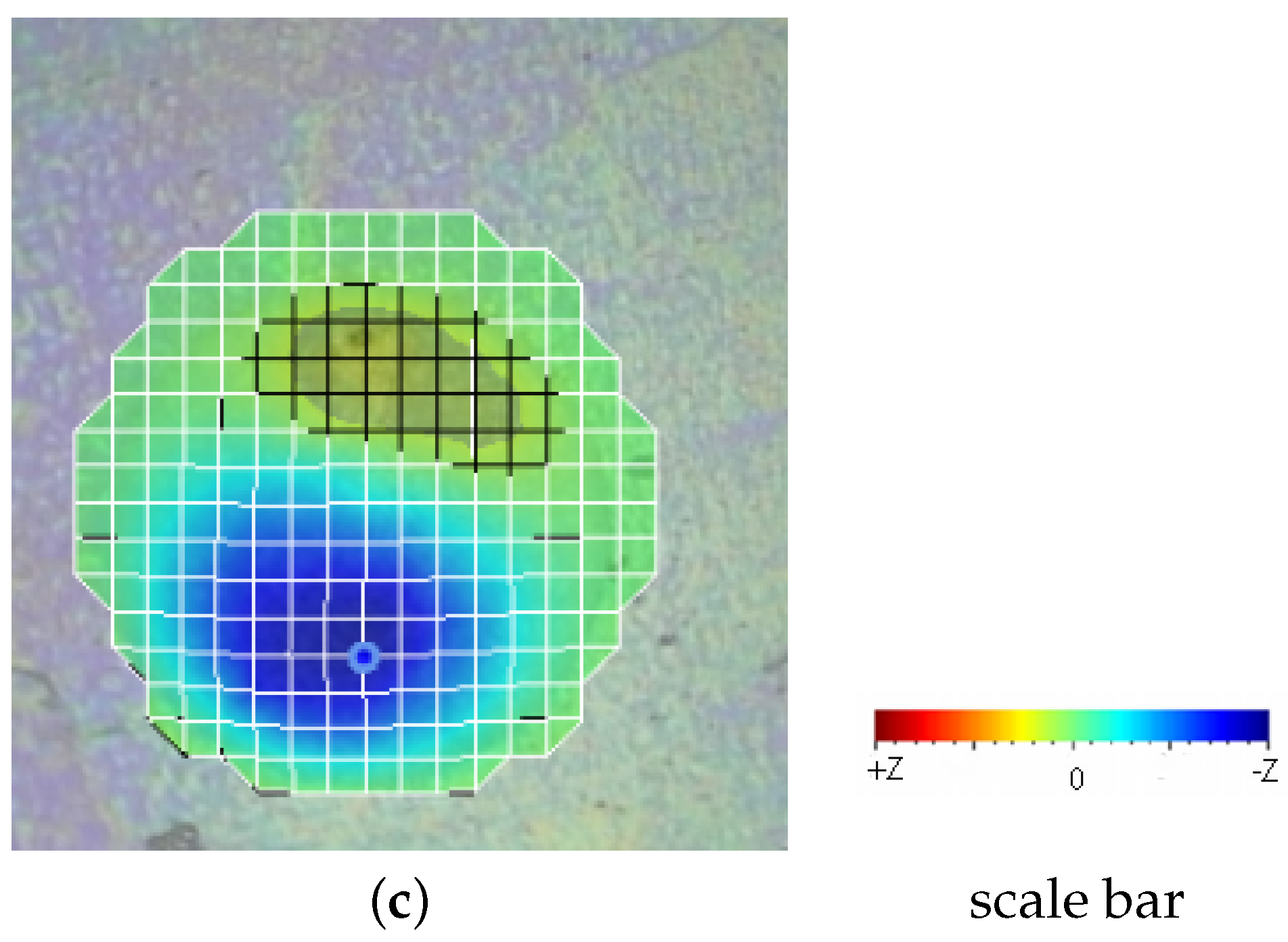
3.5. Strain Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Aguilera-Servin, J.; Miao, T.; Bockrath, M. Nanoscale pressure sensors realized from suspended graphene membrane devices. Appl. Phys. Lett. 2015, 106, 083103. [Google Scholar] [CrossRef]
- Berger, C.; Phillips, R.; Centeno, A.; Zurutuza, A.; Vijayaraghavan, A. Capacitive pressure sensing with suspended graphene-polymer heterostructure membranes. Nanoscale 2017, 9, 17439–17449. [Google Scholar] [CrossRef] [PubMed]
- Dolleman, R.J.; Davidovikj, D.; Cartamil-Bueno, S.J.; van der Zant, H.S.; Steeneken, P.G. Graphene Squeeze-Film Pressure Sensors. Nano Lett. 2016, 16, 568–571. [Google Scholar] [CrossRef]
- Wang, Q.; Hong, W.; Dong, L. Graphene “microdrums” on a freestanding perforated thin membrane for high sensitivity MEMS pressure sensors. Nanoscale 2016, 8, 7663–7671. [Google Scholar] [CrossRef]
- Zhu, S.E.; Shabani, R.; Rho, J.; Kim, Y.; Hong, B.H.; Ahn, J.H.; Cho, H.J. Graphene-based bimorph microactuators. Nano Lett. 2011, 11, 977–981. [Google Scholar] [CrossRef]
- Al-mashaal, A.K.; Wood, G.S.; Torin, A.; Mastropaolo, E.; Newton, M.J.; Cheung, R. Dynamic behavior of ultra large graphene-based membranes using electrothermal transduction. Appl. Phys. Lett. 2017, 111, 243503. [Google Scholar] [CrossRef]
- Al-mashaal, A.K.; Wood, G.S.; Torin, A.; Mastropaolo, E.; Newton, M.J.; Cheung, R. Tunable Graphene-Polymer Resonators for Audio Frequency Sensing Applications. IEEE Sens. J. 2019, 19, 465–473. [Google Scholar] [CrossRef]
- Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef]
- Chen, T.; Mastropaolo, E.; Bunting, A.; Cheung, R. Observation of second flexural mode enhancement in graphene resonators. Electron. Lett. 2015, 51, 1014–1016. [Google Scholar] [CrossRef]
- Lee, S.; Chen, C.; Deshpande, V.V.; Lee, G.H.; Lee, I.; Lekas, M.; Gondarenko, A.; Yu, Y.J.; Shepard, K.; Kim, P.; et al. Electrically integrated SU-8 clamped graphene drum resonators for strain engineering. Appl. Phys. Lett. 2013, 102, 153101. [Google Scholar] [CrossRef]
- Verbiest, G.J.; Kirchhof, J.N.; Sonntag, J.; Goldsche, M.; Khodkov, T.; Stampfer, C. Detecting Ultrasound Vibrations with Graphene Resonators. Nano Lett. 2018, 18, 5132–5137. [Google Scholar] [CrossRef]
- Xu, J.; Wood, G.S.; Al-mashaal, A.K.; Mastropaolo, E.; Newton, M.J.; Cheung, R. Realization of Closed Cavity Resonator Formed by Graphene-PMMA Membrane for Sensing Audio Frequency. IEEE Sens. J. 2020, 20, 4618–4627. [Google Scholar] [CrossRef]
- Ye, F.; Lee, J.; Feng, P.X. Electrothermally Tunable Graphene Resonators Operating at Very High Temperature up to 1200 K. Nano Lett. 2018, 18, 1678–1685. [Google Scholar] [CrossRef]
- Todorović, D.; Matković, A.; Milićević, M.; Jovanović, D.; Gajić, R.; Salom, I.; Spasenović, M. Multilayer graphene condenser microphone. 2D Mater. 2015, 2, 045013. [Google Scholar] [CrossRef]
- Woo, S.; Han, J.H.; Lee, J.H.; Cho, S.; Seong, K.W.; Choi, M.; Cho, J.H. Realization of a High Sensitivity Microphone for a Hearing Aid Using a Graphene-PMMA Laminated Diaphragm. ACS Appl. Mater. Interfaces 2017, 9, 1237–1246. [Google Scholar] [CrossRef]
- Wood, G.S.; Torin, A.; Al-mashaal, A.K.; Smith, L.S.; Mastropaolo, E.; Newton, M.J.; Cheung, R. Design and Characterization of a Micro-Fabricated Graphene-Based MEMS Microphone. IEEE Sens. J. 2019, 19, 7234–7242. [Google Scholar] [CrossRef]
- Zhou, Q.; Zheng, J.; Onishi, S.; Crommie, M.F.; Zettl, A.K. Graphene electrostatic microphone and ultrasonic radio. Proc. Natl. Acad. Sci. USA 2015, 112, 8942–8946. [Google Scholar] [CrossRef]
- Davidovikj, D.; Poot, M.; Cartamil-Bueno, S.J.; Van Der Zant, H.S.J.; Steeneken, P.G. On-chip Heaters for Tension Tuning of Graphene Nanodrums. Nano Lett. 2018, 18, 2852–2858. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.L.; Annamalai, M.; Wang, Z.Q.; Palaniapan, M. Characterization of nanomechanical graphene drum structures. J. Micromech. Microeng. 2010, 20, 115029. [Google Scholar] [CrossRef]
- Pumera, M. Graphene in biosensing. Mater. Today 2011, 14, 308–315. [Google Scholar] [CrossRef]
- Garcia-Sanchez, D.; van der Zande, A.M.; Paulo, A.S.; Lassagne, B.; McEuen, P.L.; Bachtold, A. Imaging mechanical vibrations in suspended graphene sheets. Nano Lett. 2008, 8, 1399–1403. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Nicholl, R.J.T.; Bolotin, K.I.; Ghosh, S. Motion Transduction with Thermo-mechanically Squeezed Graphene Resonator Modes. Nano Lett. 2018, 18, 6719–6724. [Google Scholar] [CrossRef] [PubMed]
- Ophir, J.; Maklad, N.F. Digital scan converters in diagnostic ultrasound imaging. Proc. IEEE 1979, 67, 654–664. [Google Scholar] [CrossRef]
- Green, R.E., Jr. Non-contact ultrasonic techniques. Ultrasonics 2004, 42, 9–16. [Google Scholar] [CrossRef]
- Drinkwater, B.W.; Wilcox, P.D. Ultrasonic arrays for non-destructive evaluation: A review. NDT E Int. 2006, 39, 525–541. [Google Scholar] [CrossRef]
- Hong, H.; Yongtian, W.; Dayuan, Y. A low-cost dynamic range-finding device based on amplitude-modulated continuous ultrasonic wave. IEEE Trans. Instrum. Meas. 2002, 51, 362–367. [Google Scholar] [CrossRef]
- Alexandrov, A.V. Ultrasound identification and lysis of clots. Stroke 2004, 35, 2722–2725. [Google Scholar] [CrossRef]
- Xu, J.; Wood, G.S.; Mastropaolo, E.; Newton, M.J.; Cheung, R. Realization of a graphene/PMMA acoustic capacitive sensor released by silicon dioxide sacrificial layer. ACS Appl. Mater. Interfaces 2021, 13, 38792–38798. [Google Scholar] [CrossRef]
- Fung, W.Y.; Dattoli, E.N.; Lu, W. Radio frequency nanowire resonators and in situ frequency tuning. Appl. Phys. Lett. 2009, 94, 203104. [Google Scholar] [CrossRef]
- Kozinsky, I.; Postma, H.W.C.; Bargatin, I.; Roukes, M.L. Tuning nonlinearity, dynamic range, and frequency of nanomechanical resonators. Appl. Phys. Lett. 2006, 88, 253101. [Google Scholar] [CrossRef]
- Wu, C.C.; Zhong, Z. Capacitive spring softening in single-walled carbon nanotube nanoelectromechanical resonators. Nano Lett. 2011, 11, 1448–1451. [Google Scholar] [CrossRef]
- Chen, K.; Schweizer, K.S. Theory of Yielding, Strain Softening, and Steady Plastic Flow in Polymer Glasses under Constant Strain Rate Deformation. Macromolecules 2011, 44, 3988–4000. [Google Scholar] [CrossRef]
- Lau, C.N.; Bao, W.; Velasco, J. Properties of suspended graphene membranes. Mater. Today 2012, 15, 238–245. [Google Scholar] [CrossRef]
- Schmid, S.; Villanueva, L.G.; Roukes, M.L. Quality Factor. In Fundamentals of Nanomechanical Resonators; Book Section Chapter 2; Springer: Berlin/Heidelberg, Germany, 2016; pp. 57–90. [Google Scholar] [CrossRef]
- Lee, J.; Wang, Z.; He, K.; Shan, J.; Feng, P.X.L. High Frequency MoS2 Nanomechanical Resonators. ACS Nano 2013, 7, 6086–6091. [Google Scholar] [CrossRef]
- Jinling, Y.; Ono, T.; Esashi, M. Energy dissipation in submicrometer thick single-crystal silicon cantilevers. J. Microelectromech. Syst. 2002, 11, 775–783. [Google Scholar] [CrossRef]
- Bunch, J.S.; Verbridge, S.S.; Alden, J.S.; van der Zande, A.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Impermeable atomic membranes from graphene sheets. Nano Lett. 2008, 8, 2458–2462. [Google Scholar] [CrossRef] [PubMed]
| Actuation Methods | Measured Resonant Frequency | Quality Factor | Actuated Sinusoidal Signal Frequency | Varying Input Signal Range of Sinusoidal Signal | Sensitivity of Vibration Amplitude Actuated by Sinusoidal Signal |
|---|---|---|---|---|---|
| Mechanical | 163.150 kHz ± 0.2% | 49.45 ± 6.8% | 163.156 kHz | 0.1 V to 2 V AC | 14 nm/V |
| Electro-static | 158.337 kHz ± 0.4% | 25.64 ± 5.8% | 158.640 kHz | 1 V to 9 V AV | 0.01 nm/V |
| Electro-thermal | 158.965 kHz ± 1.9% | 34.42 ± 15.8% | 156.914 kHz | 1 V to 9 V AV | 0.002 nm/V |
| Actuation Methods | Frequency (kHz) | Tension (N/m) | Strain (%) |
|---|---|---|---|
| Mechanical | 163.150 | 3.00 | 0.0813 |
| Electro-static | 158.384 | 2.83 | 0.0766 |
| Electro-thermal | 158.965 | 2.85 | 0.0772 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Wood, G.S.; Mastropaolo, E.; Lomax, P.; Newton, M.; Cheung, R. A Closed Cavity Ultrasonic Resonator Formed by Graphene/PMMA Membrane for Acoustic Application. Micromachines 2023, 14, 810. https://doi.org/10.3390/mi14040810
Xu J, Wood GS, Mastropaolo E, Lomax P, Newton M, Cheung R. A Closed Cavity Ultrasonic Resonator Formed by Graphene/PMMA Membrane for Acoustic Application. Micromachines. 2023; 14(4):810. https://doi.org/10.3390/mi14040810
Chicago/Turabian StyleXu, Jing, Graham S. Wood, Enrico Mastropaolo, Peter Lomax, Michael Newton, and Rebecca Cheung. 2023. "A Closed Cavity Ultrasonic Resonator Formed by Graphene/PMMA Membrane for Acoustic Application" Micromachines 14, no. 4: 810. https://doi.org/10.3390/mi14040810
APA StyleXu, J., Wood, G. S., Mastropaolo, E., Lomax, P., Newton, M., & Cheung, R. (2023). A Closed Cavity Ultrasonic Resonator Formed by Graphene/PMMA Membrane for Acoustic Application. Micromachines, 14(4), 810. https://doi.org/10.3390/mi14040810







