Simulation and Experimental Study of Laser Processing NdFeB Microarray Structure
Abstract
1. Introduction
2. Numerical Simulation Modeling
- The laser has a Gaussian profile. The ablation process is stable, and the reflection of the laser beam on the surface of the crater is neglected.
- Solid metals are considered very viscous fluids, and molten metals are incompressible non-Newtonian fluids under laminar flow.
- Effects such as the shielding effect of the plasma are ignored.
2.1. Heat Transfer Modeling
2.2. Heat Transfer Boundary Condition
2.3. Solid–Liquid Interface Treatment
2.4. Flow Modelling
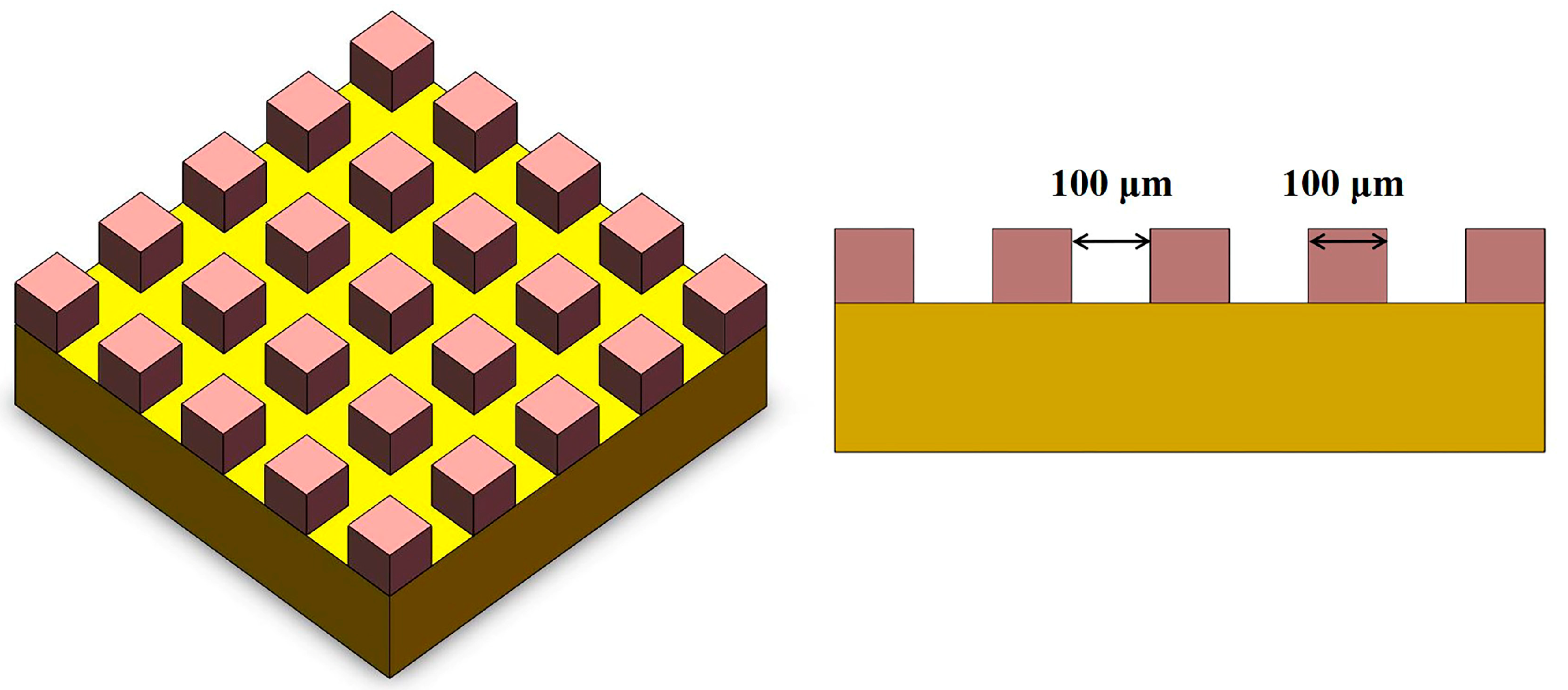
2.5. Ablation Deformation Modelling and Meshing
3. Simulation and Experiment Procedures
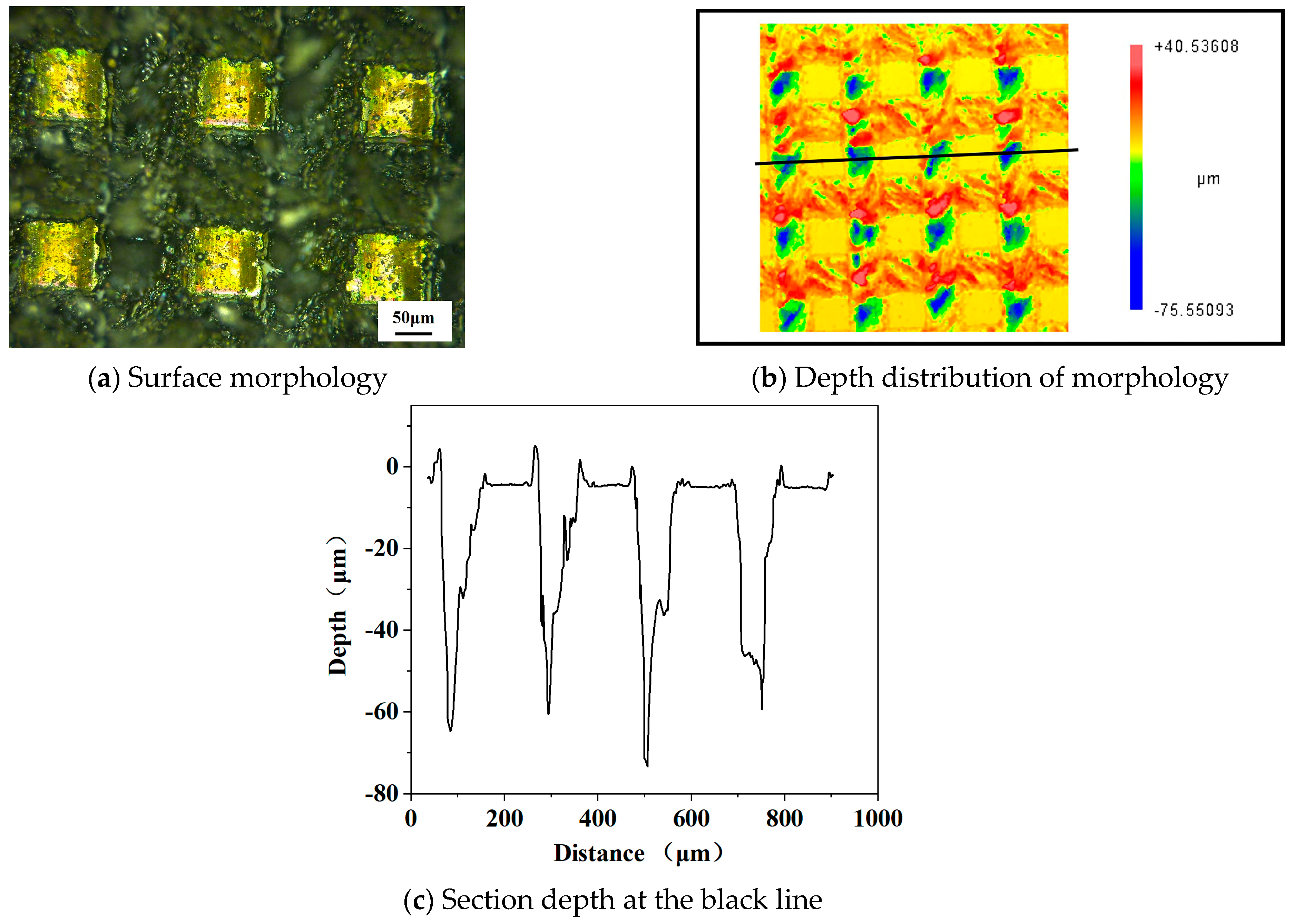
4. Results and Discussion
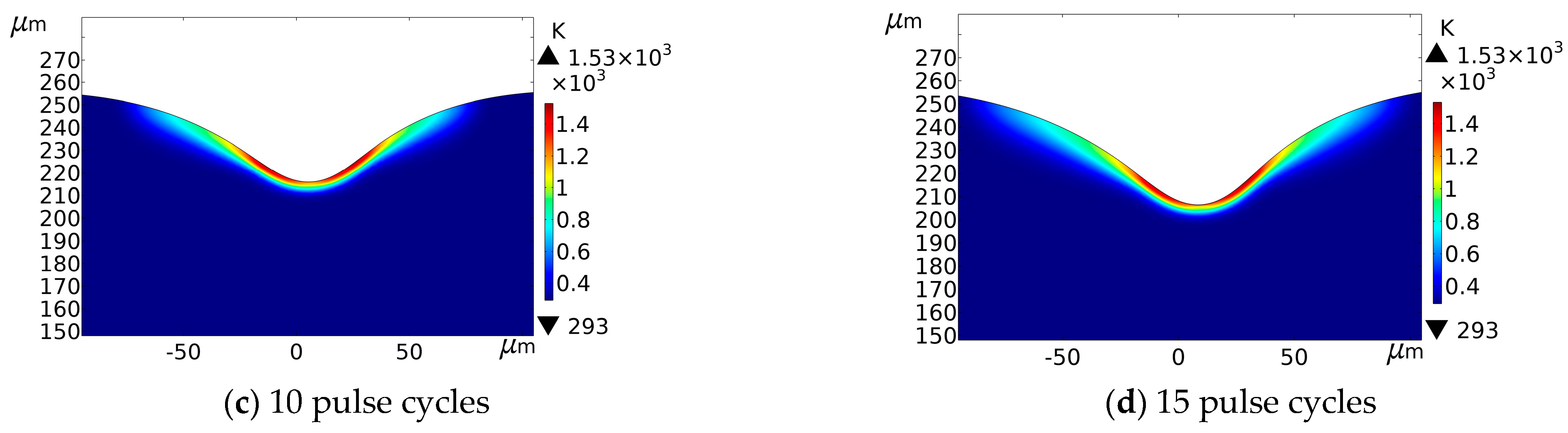
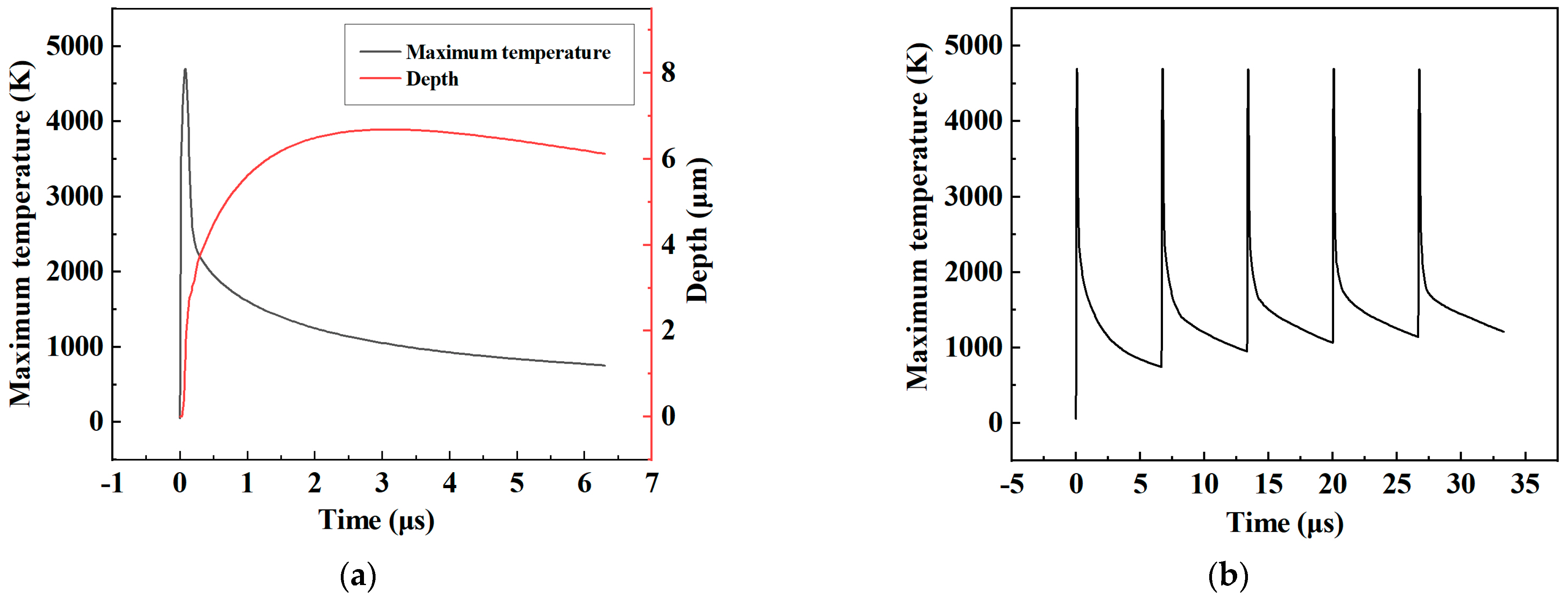
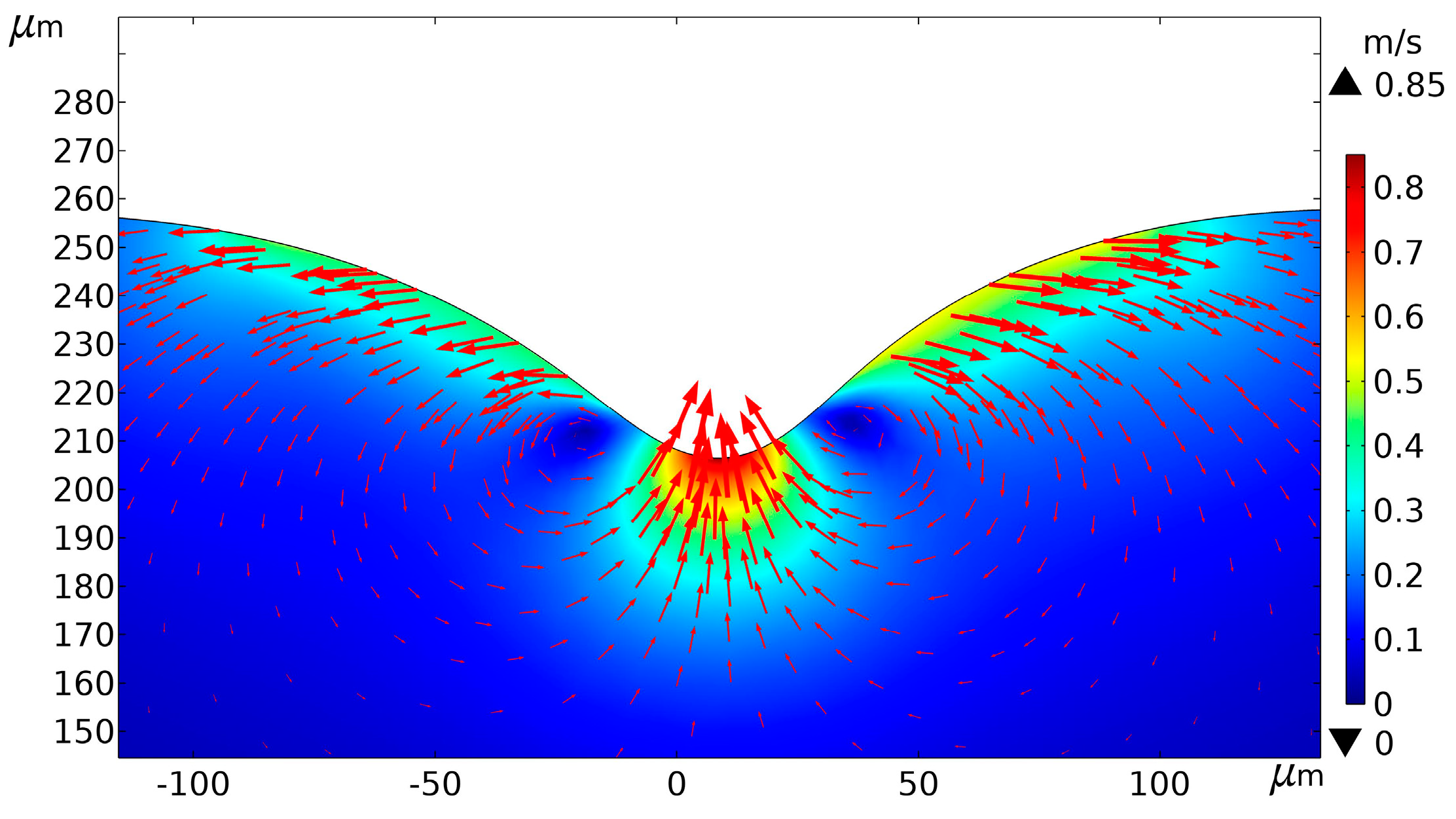
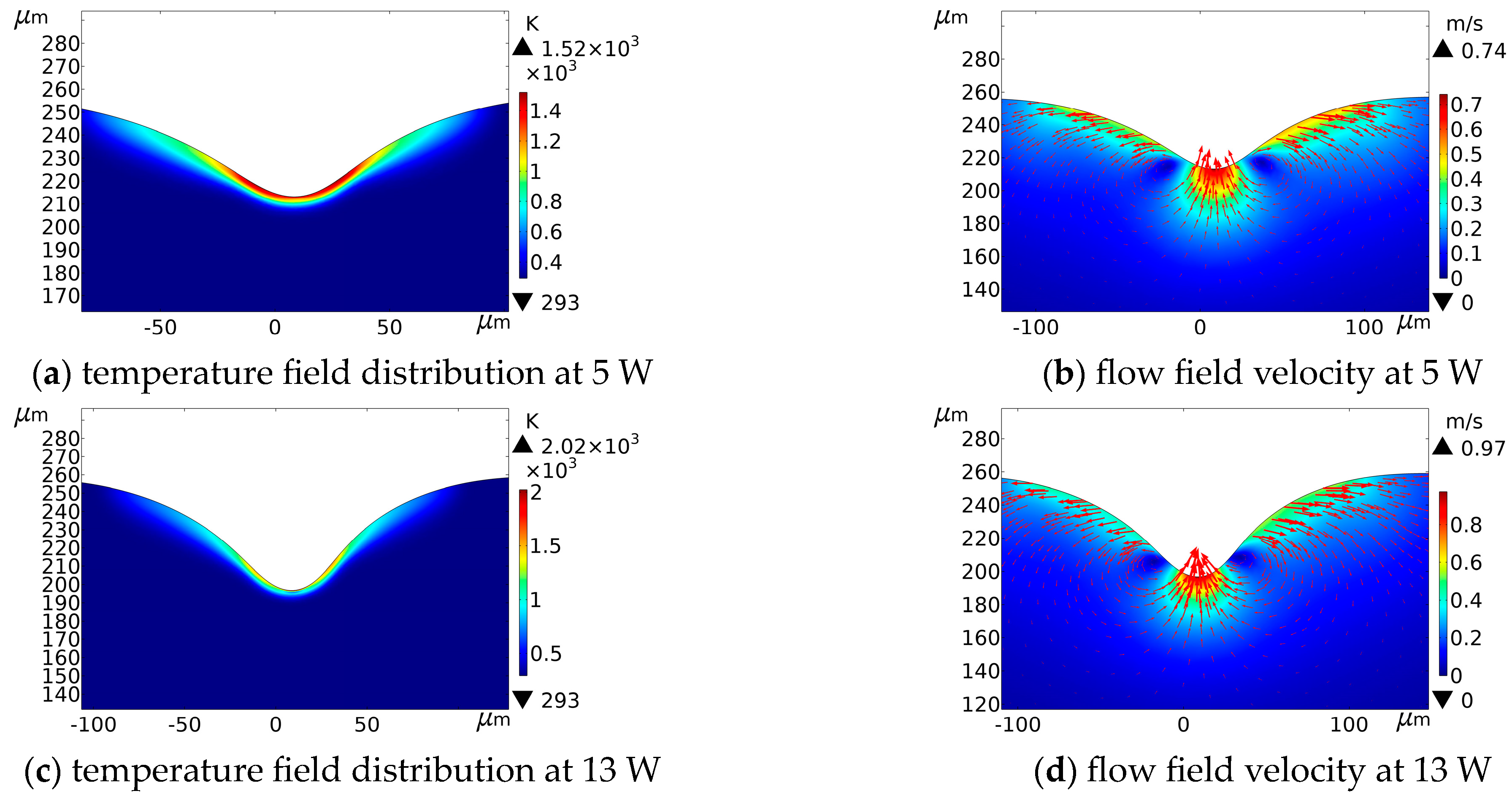
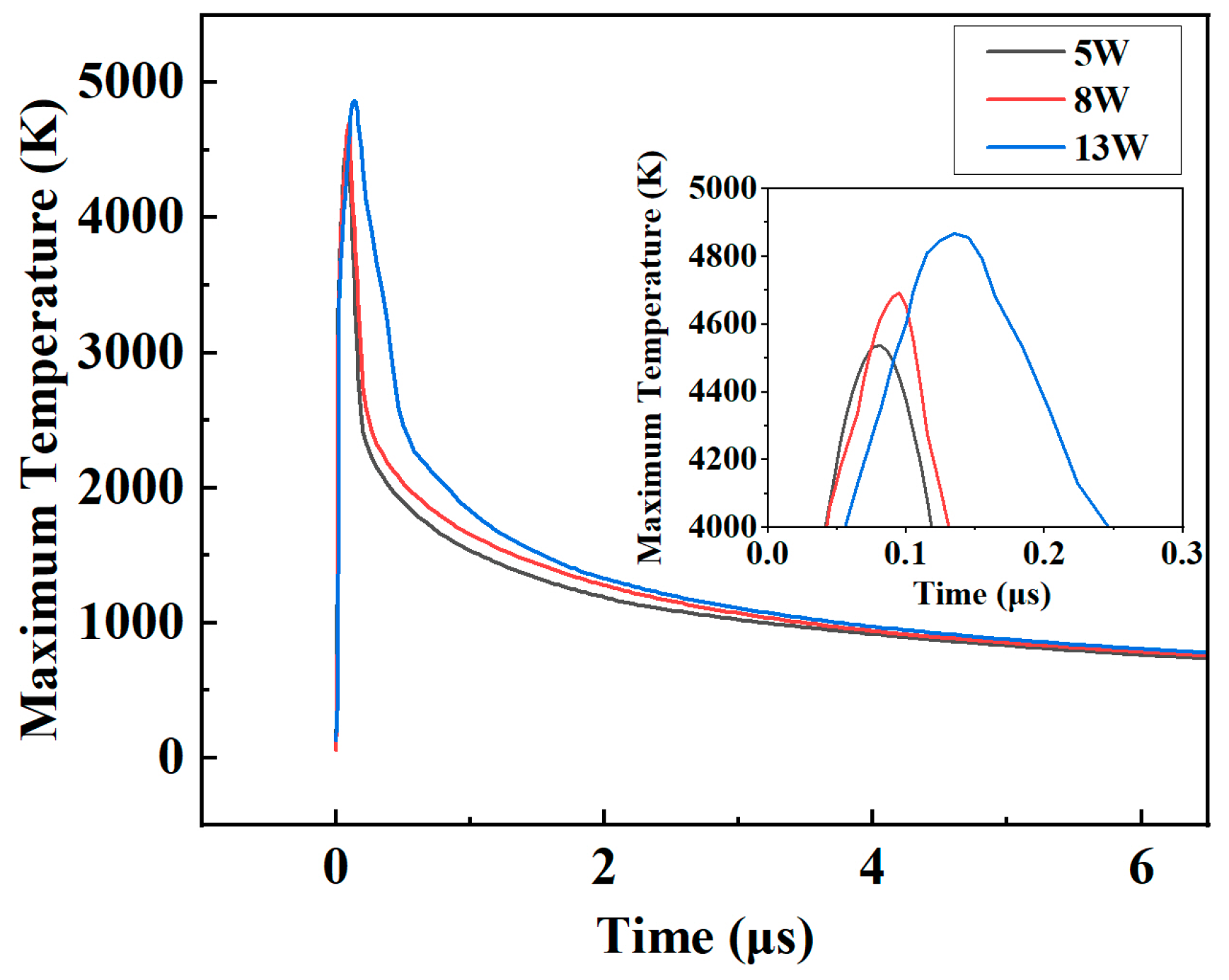
4.1. Temperature Field and Flow Fields Analysis
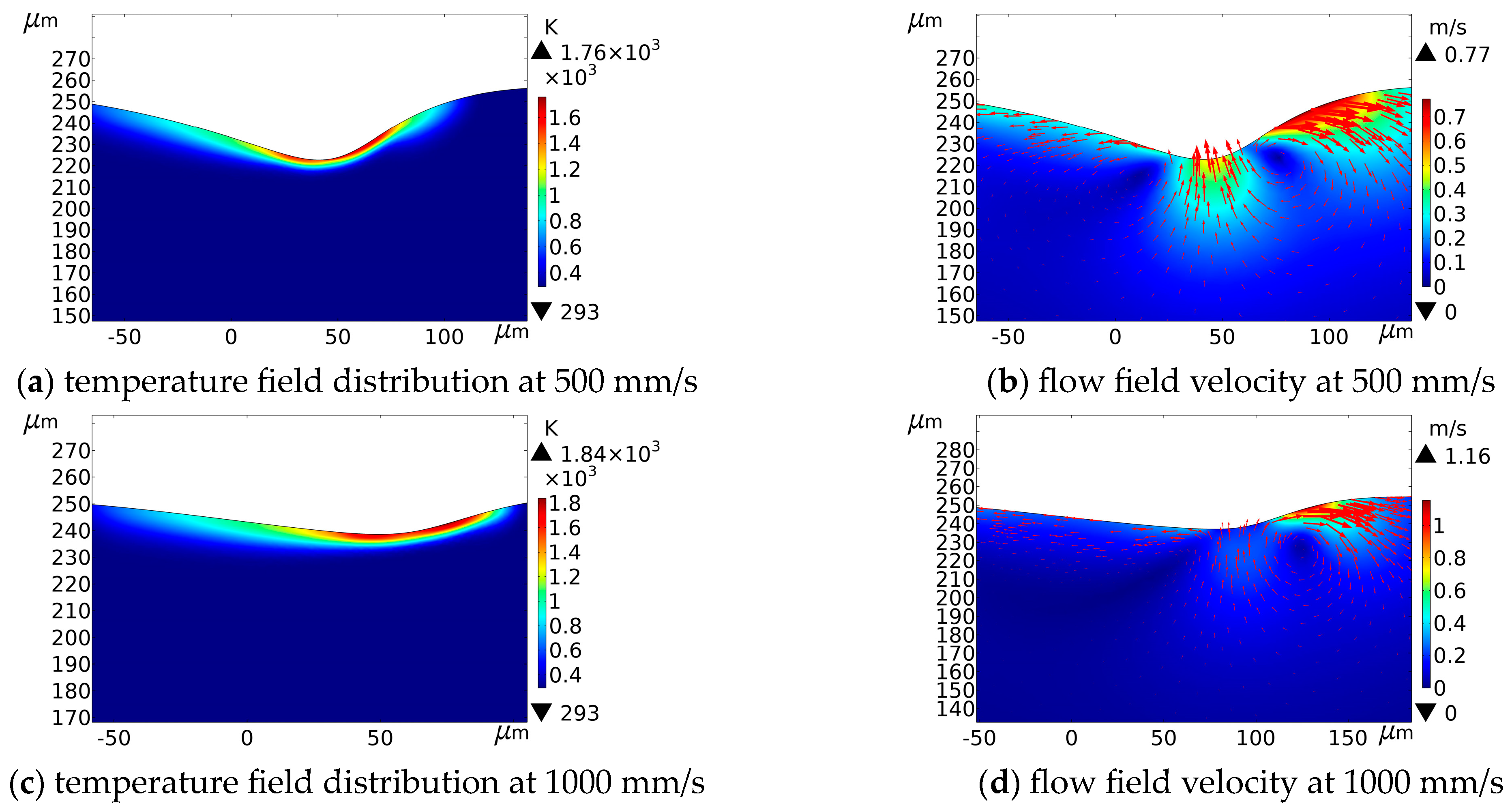
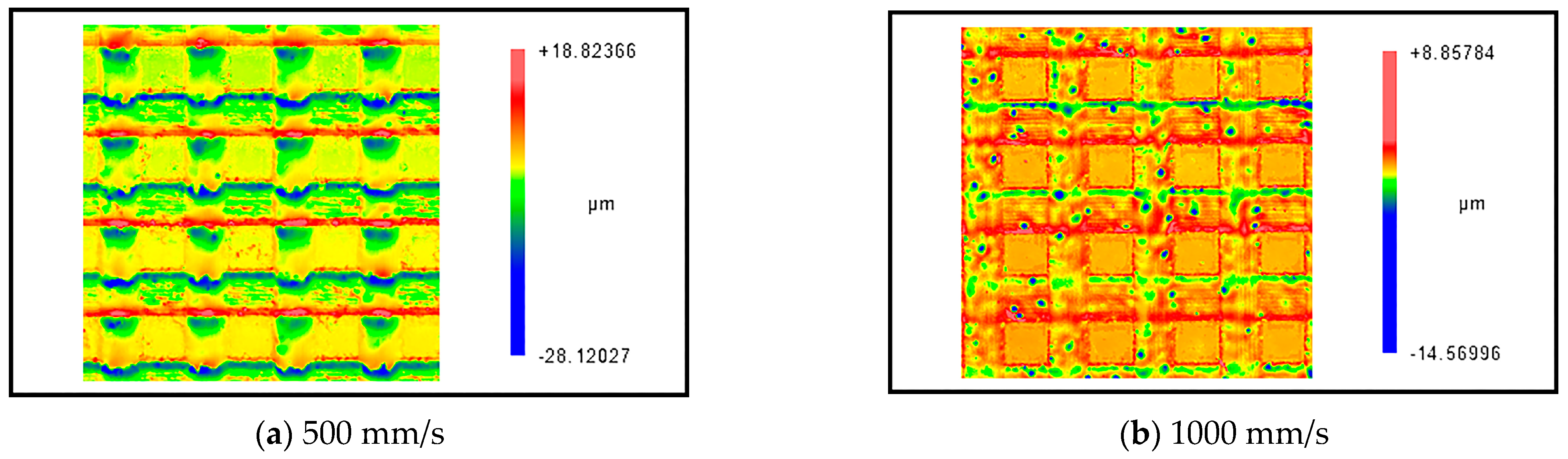
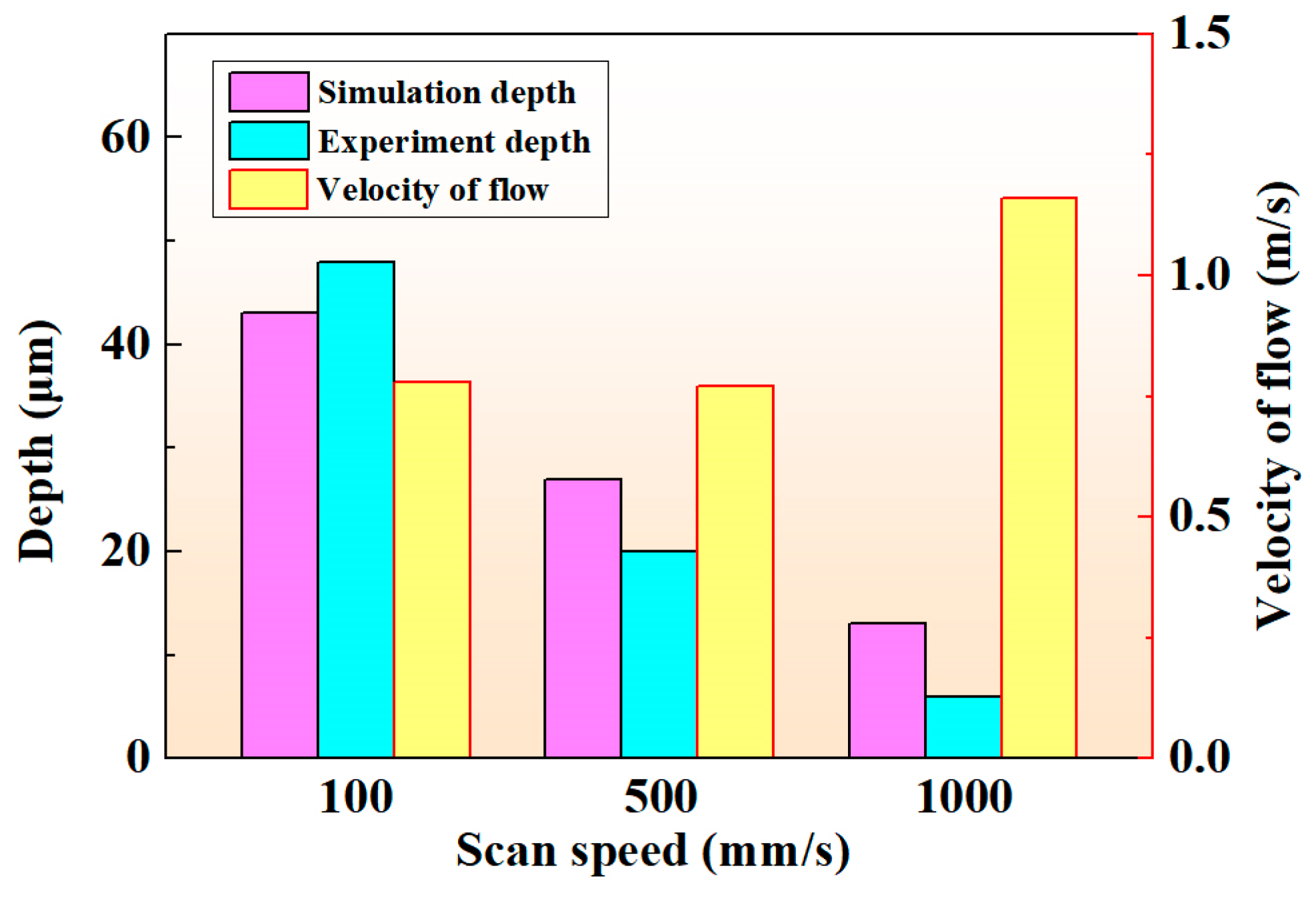
4.2. Effect of Laser Scanning Speed on the Processing Morphology
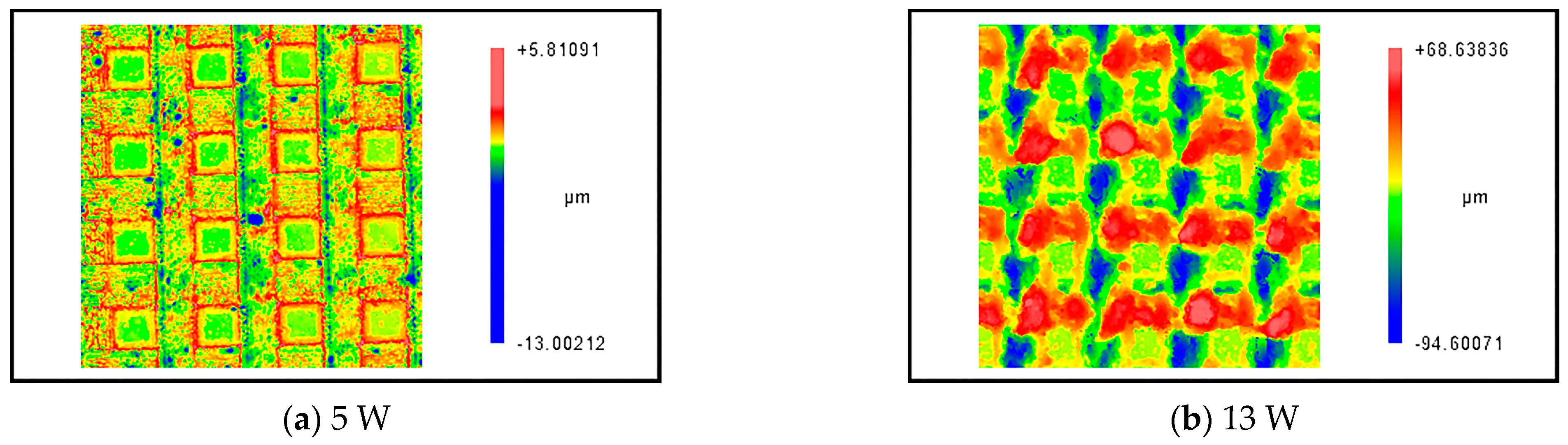
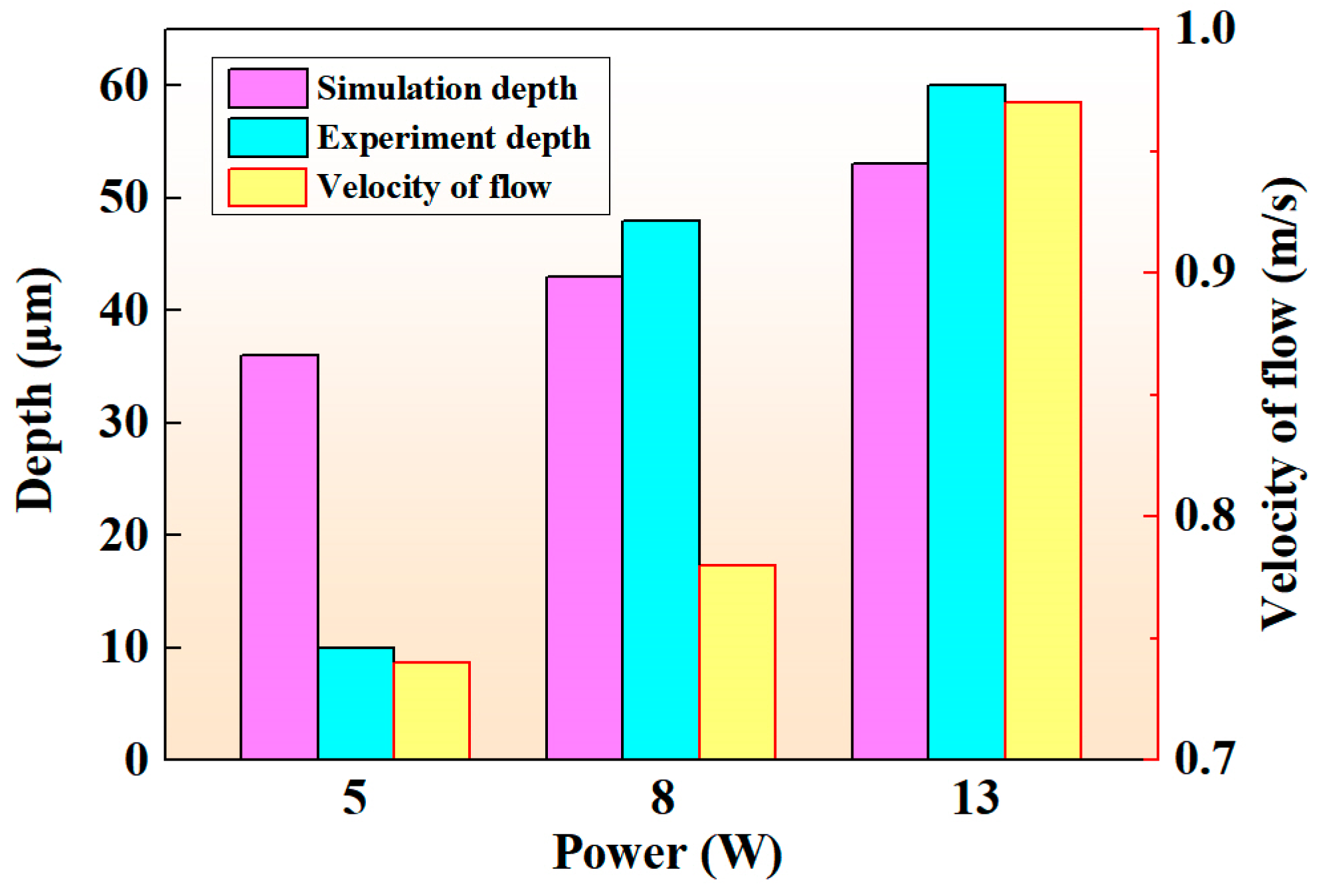
4.3. Effect of Average Power on the Processing Morphology
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhi, C.; Qu, M.; Wang, Y.; Li, Y.; Xie, J.; Feng, W.; Tang, B. Fabrication and characterization of micro electromagnetic linear actuators. J. Micromechan. Microeng. 2020, 30, 125011. [Google Scholar] [CrossRef]
- Wang, Y.; Zhi, C.; Tang, B.; Yang, K.; Xie, J.; Xu, W.; Li, H.; Wang, X. A micro electromagnetic actuator with high force density. Sens. Actuator A Phys. 2021, 331, 112771. [Google Scholar] [CrossRef]
- Feng, Z.; Zhao, H.; Tan, C.; Zhu, B.; Xia, F.; Wang, Q.; Chen, B.; Song, X. Effect of laser texturing on the surface characteristics and bonding property of 30 CrMnSiA steel adhesive joints. J. Manuf. Process. 2019, 47, 219–228. [Google Scholar] [CrossRef]
- Ijaola, A.O.; Bamidele, E.A.; Akisin, C.J.; Bello, I.T.; Oyatobo, A.T.; Abdulkareem, A.; Farayibi, P.K.; Asmatulu, E. Wettability transition for laser textured surfaces: A comprehensive review. Surfaces Interfaces 2020, 21, 100802. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Zhang, J.; Wang, B.; Breisch, M.; Hartmaier, A.; Rostotskyi, I.; Voznyy, V.; Liu, Y. Experimental investigation of laser surface texturing and related biocompatibility of pure titanium. Int. I Adv. Manuf. Technol. 2022, 119, 5993–6005. [Google Scholar] [CrossRef]
- Melo-Fonseca, F.; Guimarães, B.; Gasik, M.; Silva, F.S.; Miranda, G. Experimental analysis and predictive modelling of Ti6Al4V laser surface texturing for biomedical applications. Surf. Interfaces 2022, 35, 102466. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, Y.; Hou, X.; Hong, M. Directional sliding of water: Biomimetic snake scale surfaces. Opto-Electron. 2021, 4, 210008. [Google Scholar] [CrossRef]
- Lim, H.S.; Yoo, J. FEM based simulation of the pulsed laser ablation process in nanosecond fields. J. Mech. Sci. Technol. 2011, 25, 1811–1816. [Google Scholar] [CrossRef]
- Berenyi, R.; Szaffner, D. FEM Based 3D Simulation of Nanosecond UV Laser Ablation; ISSE: Eger, Hungary, 2015; pp. 385–389. [Google Scholar]
- Zhang, J.; Zhao, L.; Rosenkranz, A.; Song, C.; Yan, Y.; Sun, T. Nanosecond pulsed laser ablation of silicon-finite element simulation and experimental validation. J. Micromechanics Microeng. 2019, 29, 75009. [Google Scholar] [CrossRef]
- Ding, X.; Wang, L.; Wang, S. Comparison study of numerical analysis for heat transfer and fluid flow under two different laser scan pattern during selective laser melting. Optik 2016, 127, 10898–10907. [Google Scholar] [CrossRef]
- Yuan, P.; Gu, D. Molten pool behaviour and its physical mechanism during selective laser melting of TiC/AlSi10Mg nanocomposites: Simulation and experiments. J. Phys. D 2015, 48, 35303–35316. [Google Scholar] [CrossRef]
- Cho, W.; Na, S.; Thomy, C.; Vollertsen, F. Numerical simulation of molten pool dynamics in high power disk laser welding. J. Mater. Process. Technol. 2012, 212, 262–275. [Google Scholar] [CrossRef]
- Yuan, W.; Chen, H.; Cheng, T.; Wei, Q. Effects of laser scanning speeds on different states of the molten pool during selective laser melting: Simulation and experiment. Mater. Des. 2020, 189, 108542. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, Z.; Ni, X. Modeling and simulation on long pulse laser drilling processing. Int. J. Heat Mass Transf. 2014, 73, 429–437. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, P.; Tian, Z.; Chen, C.; Hua, X.; Xu, S.; Xie, X. Numerical Study on the Evolution Mechanism of the Crater under a Millisecond Laser. Appl. Sci. 2020, 10, 9054. [Google Scholar] [CrossRef]
- Vasantgadkar, N.A.; Bhandarkar, U.V.; Joshi, S.S. A finite element model to predict the ablation depth in pulsed laser ablation. Thin Solid Films 2010, 519, 1421–1430. [Google Scholar] [CrossRef]
- Vora, H.D.; Santhanakrishnan, S.; Harimkar, S.P.; Boetcher, S.K.S.; Dahotre, N.B. Evolution of surface topography in one-dimensional laser machining of structural alumina. J. Eur. Ceram. Soc. 2012, 32, 4205–4218. [Google Scholar] [CrossRef]
- Courtois, M.; Carin, M.; Masson, P.L.; Gaied, S.; Balabane, M. A new approach to compute multi-reflections of laser beam in a keyhole for heat transfer and fluid flow modelling in laser welding. J. Phys. D 2013, 46, 505305–505314. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.Z.; Ni, X.W. Modeling of dynamic process in the laser-off period during laser drilling. Chin. Opt. Lett. 2015, 13, 62–65. [Google Scholar] [CrossRef]
- Desmaison, O.; Bellet, M.; Guillemot, G. A level set approach for the simulation of the multipass hybrid laser/GMA welding process. Comput. Mater. Sci. 2014, 91, 240–250. [Google Scholar] [CrossRef]
- Sharma, S.; Mandal, V.; Ramakrishna, S.A.; Ramkumar, J. Numerical simulation of melt pool oscillations and protuberance in pulsed laser micro melting of SS304 for surface texturing applications. J. Manuf. Process. 2019, 39, 282–294. [Google Scholar] [CrossRef]
- Sahoo, P.; Debroy, T.; Mcnallan, M.J. Surface tension of binary metal—Surface active solute systems under conditions relevant to welding metallurgy. Met. Mater. Trans. B 1988, 19, 483–491. [Google Scholar] [CrossRef]
- Li, Z.; Li, H.; Yin, J.; Li, Y.; Nie, Z.; Li, X.; You, D.; Guan, K.; Duan, W.; Cao, L.; et al. A review of spatter in laser powder bed fusion additive manufacturing: In situ detection, generation, effects, and countermeasures. Micromachines 2022, 13, 1366. [Google Scholar] [CrossRef] [PubMed]



| Property | Symbol | Value | Unit |
|---|---|---|---|
| Melting temperature | Tm | 1811.2 | K |
| Vaporizing temperature | Tv | 3135.2 | K |
| Ambient temperature | Ta | 293.15 | K |
| Solid phase density | ρs | 7500 | kg/m3 |
| Liquid phase density | ρl | 6500 | kg/m3 |
| Specific heat of solid phase | Cps | 440 | J/(kg∙K) |
| Specific heat of liquid phase | Cpl | 551 | J/(kg∙K) |
| Solid phase thermal conductivity | ks | 9 | W/(m·K) |
| Liquid phase thermal conductivity | kl | 7 | W/(m·K) |
| Latent heat of fusion | Lm | 2.466 × 105 | J/kg |
| Latent heat of vaporization | Lv | 6.071 × 106 | J/kg |
| Coefficient of heat transfer | h1 | 15 | W/(m2·K) |
| Temperature transition interval of melting | ∆T | 50 | K |
| Dynamic viscosity of liquid phase | μl | 8 × 10−3 | Pa·s |
| The surface tension of the pure metal | γ | 1.84 | N/m |
| Surface tension temperature coefficient | Aγ | −5 × 104 | N/(m∙K) |
| Mushy zone constant | Am | 106 | kg/m3∙s |
| Groups | Average Power | Scanning Speed |
|---|---|---|
| 1 | 8 | 100, 500, 1000 |
| 2 | 5, 8, 13 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wang, S.; Yu, W.; Long, P.; Zhang, J.; Tian, W.; Gao, F.; Jin, Z.; Zheng, H.; Wang, C.; et al. Simulation and Experimental Study of Laser Processing NdFeB Microarray Structure. Micromachines 2023, 14, 808. https://doi.org/10.3390/mi14040808
Zhao Y, Wang S, Yu W, Long P, Zhang J, Tian W, Gao F, Jin Z, Zheng H, Wang C, et al. Simulation and Experimental Study of Laser Processing NdFeB Microarray Structure. Micromachines. 2023; 14(4):808. https://doi.org/10.3390/mi14040808
Chicago/Turabian StyleZhao, Yong, Shuo Wang, Wenhui Yu, Pengyu Long, Jinlong Zhang, Wentao Tian, Fei Gao, Zhuji Jin, Hongyu Zheng, Chunjin Wang, and et al. 2023. "Simulation and Experimental Study of Laser Processing NdFeB Microarray Structure" Micromachines 14, no. 4: 808. https://doi.org/10.3390/mi14040808
APA StyleZhao, Y., Wang, S., Yu, W., Long, P., Zhang, J., Tian, W., Gao, F., Jin, Z., Zheng, H., Wang, C., & Guo, J. (2023). Simulation and Experimental Study of Laser Processing NdFeB Microarray Structure. Micromachines, 14(4), 808. https://doi.org/10.3390/mi14040808










