A Numerical Study of an Ellipsoidal Nanoparticles under High Vacuum Using the DSMC Method
Abstract
1. Introduction
2. Theoretical Approach
Drag Force in Slip Regime
3. Numerical Methods
3.1. Direct Simulation Monte Calro
3.2. GPU Computing (CUDA)
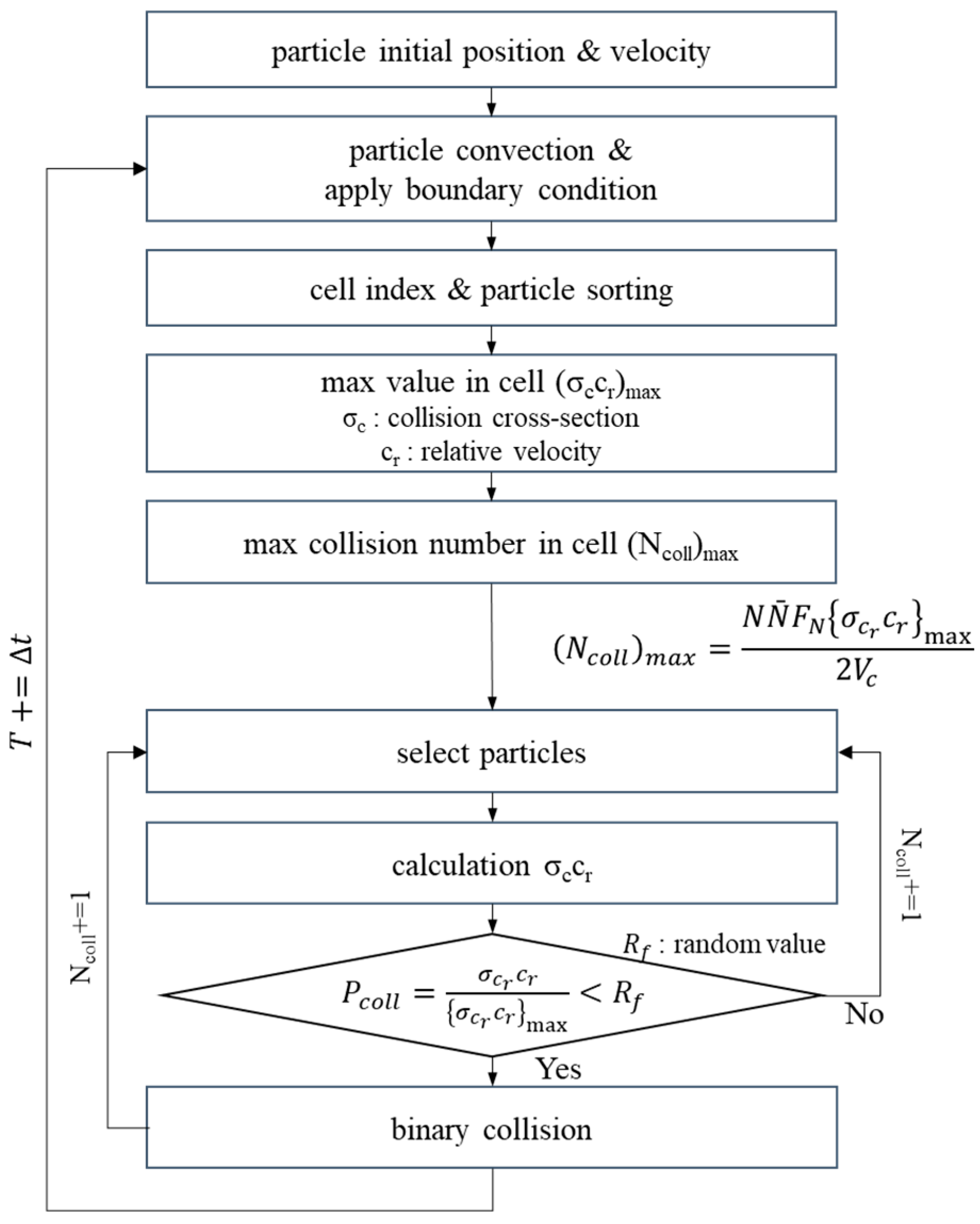
4. Results and Discussion
4.1. Microchannel Flow
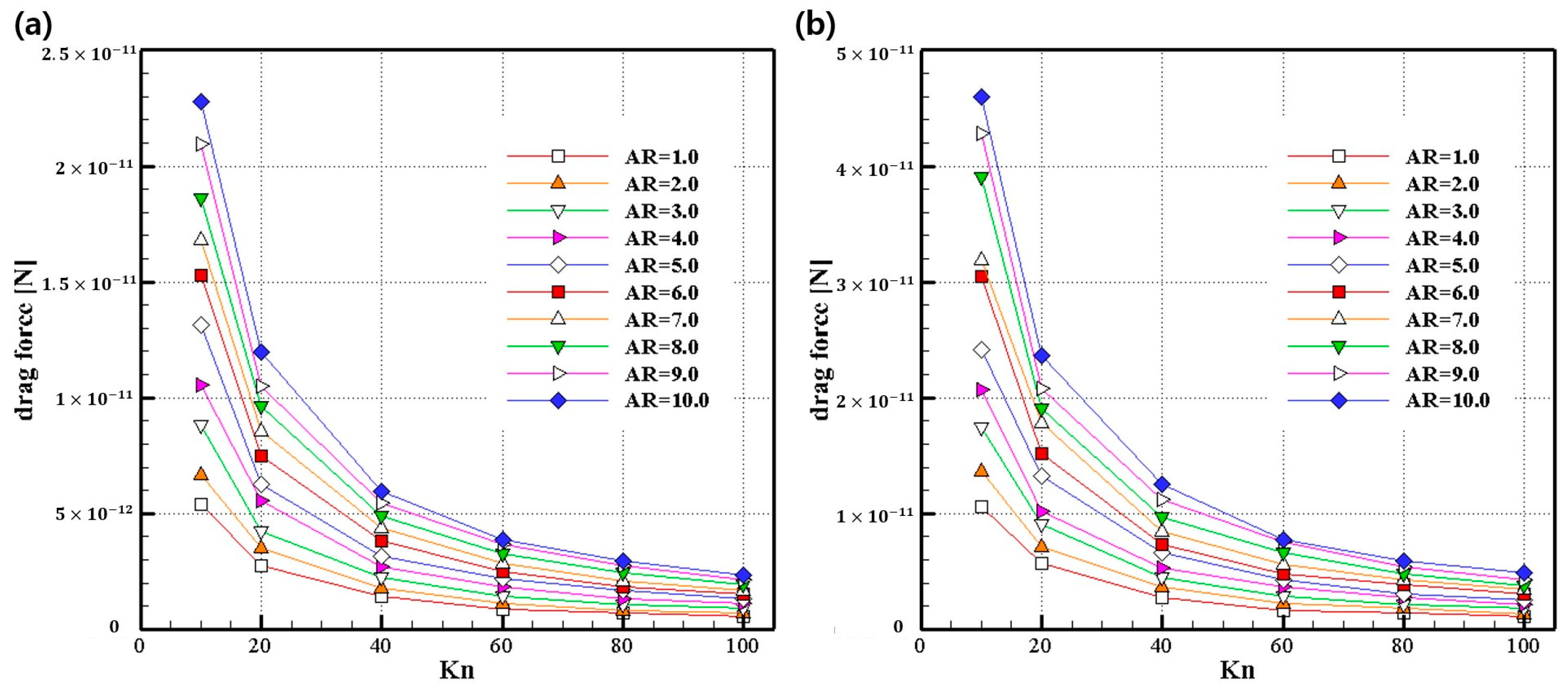
4.2. Nanoparticle Drag Force
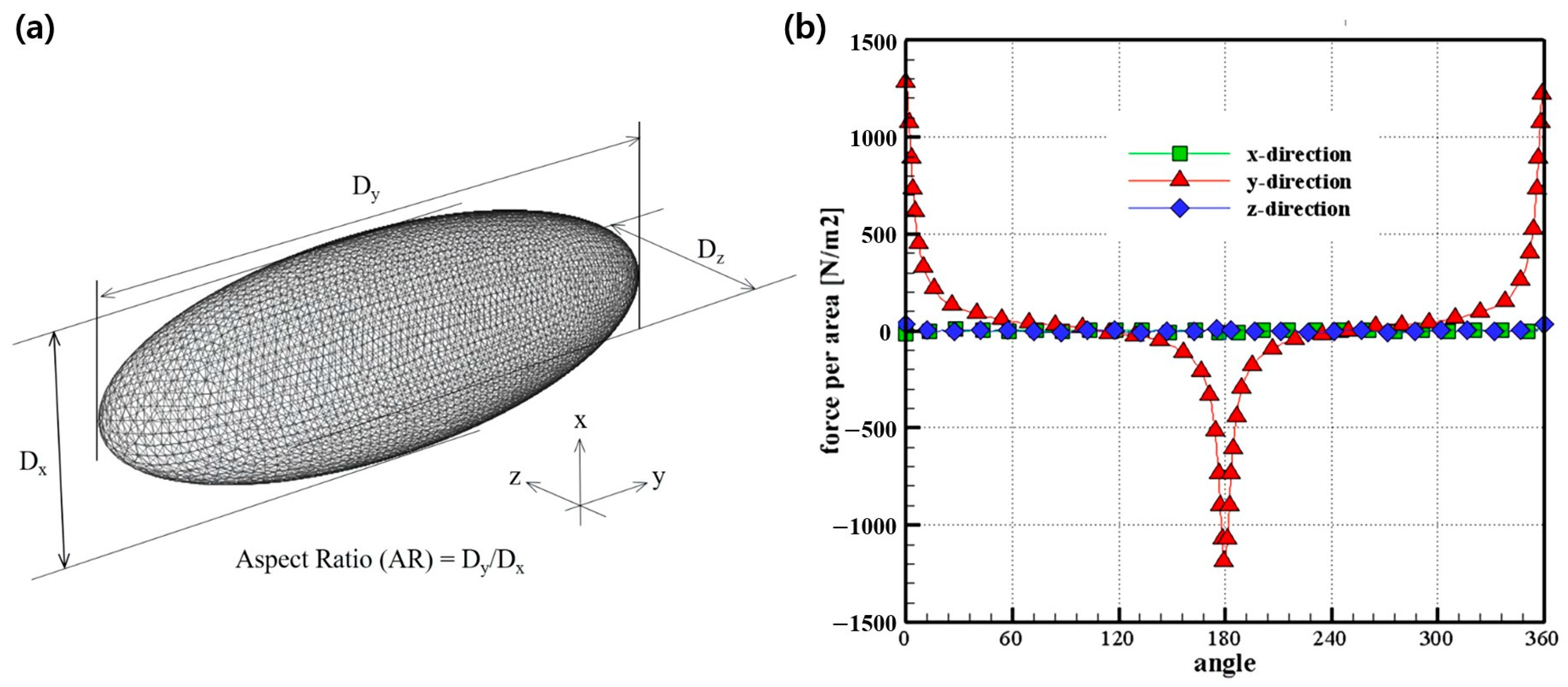
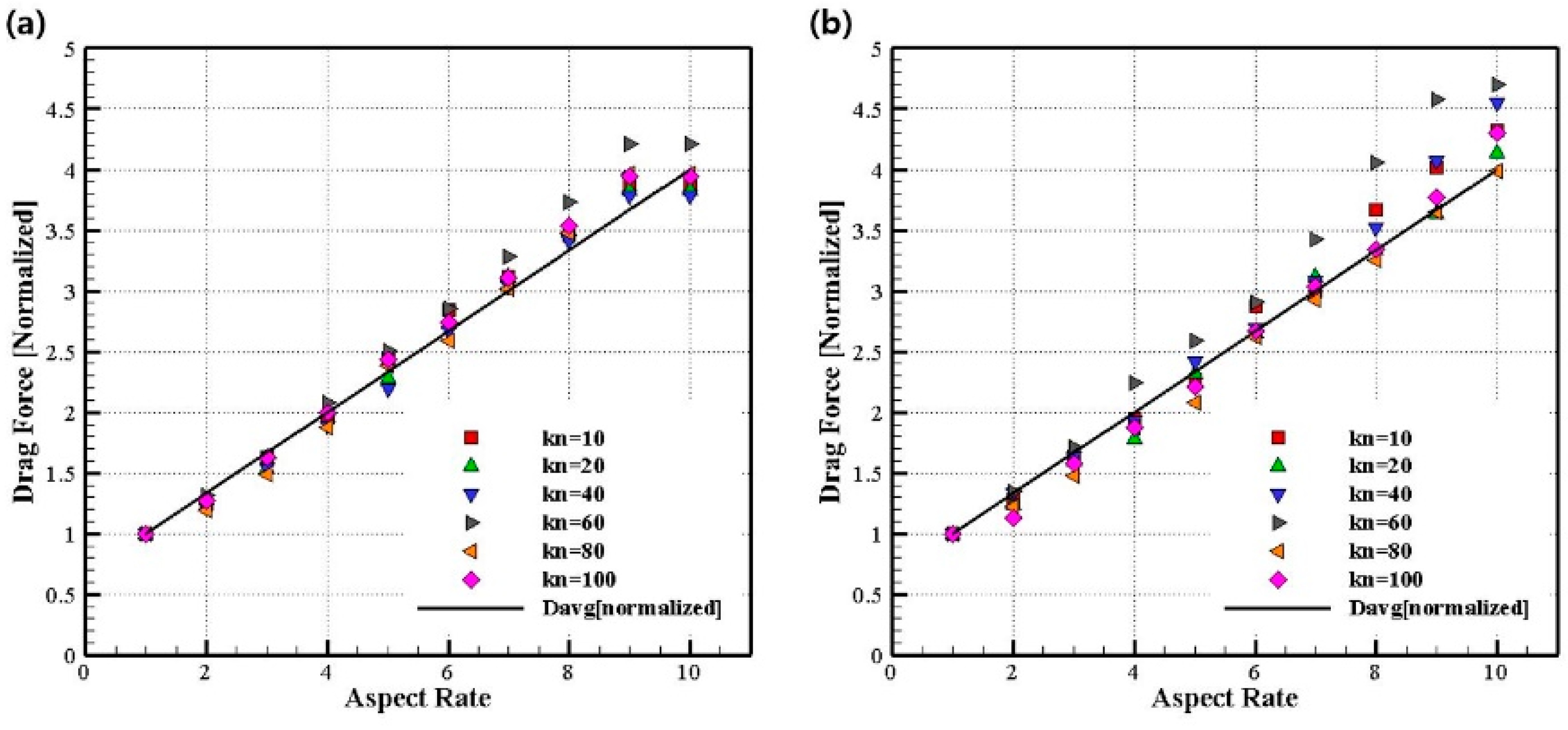
4.3. Drag Force of Ellipsoid Particle
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brenner, H. The Slow Motion of a Sphere through a Viscous Fluid towards a Plane Surface. Chem. Eng. Sci. 1961, 16, 242–251. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1983; Volume 1, ISBN 9024728770. [Google Scholar]
- Loussaief, H.; Pasol, L.; Feuillebois, F. Motion of a Spherical Particle in a Viscous Fluid along a Slip Wall. Q. J. Mech. Appl. Math. 2015, 68, 115–144. [Google Scholar] [CrossRef]
- Maude, A.D. End Effects in a Falling-Sphere Viscometer. Br. J. Appl. Phys. 1961, 12, 293. [Google Scholar] [CrossRef]
- O’Neill, M.E. A Slow Motion of Viscous Liquid Caused by a Slowly Moving Solid Sphere. Mathematika 1964, 11, 67–74. [Google Scholar] [CrossRef]
- Goren, S.L. The Hydrodynamic Force Resisting the Approach of a Sphere to a Plane Wall in Slip Flow. J. Colloid Interface Sci. 1973, 44, 356–360. [Google Scholar] [CrossRef]
- Luo, H.; Pozrikidis, C. Effect of Surface Slip on Stokes Flow Past a Spherical Particle in Infinite Fluid and near a Plane Wall. J. Eng. Math. 2008, 62, 1–21. [Google Scholar] [CrossRef]
- Goswami, P.; Baier, T.; Tiwari, S.; Lv, C.; Hardt, S.; Klar, A. Drag Force on Spherical Particle Moving near a Plane Wall in Highly Rarefied Gas. J. Fluid Mech. 2020, 883, A47. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases; Cambridge University Press: Cambridge, UK, 1990; ISBN 052140844X. [Google Scholar]
- Bird, G.A. Direct Simulation and the Boltzmann Equation. Phys. Fluids 1970, 13, 2676–2681. [Google Scholar] [CrossRef]
- Russo, G.; Pareschi, L.; Trazzi, S.; Shevyrin, A.A.; Bondar, Y.A.; Ivanov, M.S. Plane Couette Flow Computations by TRMC and MFS Methods. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2005; Volume 762, pp. 577–582. [Google Scholar]
- Muntz, E.P.; Weaver, D.P.; Campbell, D.H. Rarefied Gas Dynamics: Theoretical and Computational Techniques; International Symposium, 16th, Pasadena, CA, July 10–16, 1988, Technical Papers; American Institute of Aeronautics and Astronautics, Inc.: Washington, DC, USA, 1989. [Google Scholar]
- Ozawa, T.; Levin, D.A.; Nompelis, I.; Barnhardt, M.; Candler, G.V. Particle and Continuum Method Comparison of a High-Altitude, Extreme-Mach-Number Reentry Flow. J. Thermophys. Heat Trans. 2010, 24, 225–240. [Google Scholar] [CrossRef]
- Sohn, I.; Li, Z.; Levin, D.A.; Modest, M.F. Coupled DSMC-PMC Radiation Simulations of a Hypersonic Reentry. J. Thermophys. Heat Trans. 2012, 26, 22–35. [Google Scholar] [CrossRef]
- Bird, G.A. The Velocity Distribution Function within a Shock Wave. J. Fluid Mech. 1967, 30, 479–487. [Google Scholar] [CrossRef]
- Bird, G.A. The Structure of Normal Shock Waves in a Binary Gas Mixture. J. Fluid Mech. 1968, 31, 657–668. [Google Scholar] [CrossRef]
- Bird, G.A. Aspects of the Structure of Strong Shock Waves. Phys. Fluids 1970, 13, 1172–1177. [Google Scholar] [CrossRef]
- Swaminathan-Gopalan, K.; Stephani, K.A. Recommended Direct Simulation Monte Carlo Collision Model Parameters for Modeling Ionized Air Transport Processes. Phys. Fluids 2016, 28, 027101. [Google Scholar] [CrossRef]
- Stefanov, S.; Roohi, E.; Shoja-Sani, A. A Novel Transient-Adaptive Subcell Algorithm with a Hybrid Application of Different Collision Techniques in Direct Simulation Monte Carlo (DSMC). Phys. Fluids 2022, 34, 092003. [Google Scholar] [CrossRef]
- Bird, G.A. Direct Molecular Simulation of a Dissociating Diatomic Gas. J. Comput. Phys. 1977, 25, 353–365. [Google Scholar] [CrossRef]
- Ozawa, T.; Zhong, J.; Levin, D.A. Development of Kinetic-Based Energy Exchange Models for Noncontinuum, Ionized Hypersonic Flows. Phys. Fluids 2008, 20, 046102. [Google Scholar] [CrossRef]
- Li, Z.; Ozawa, T.; Sohn, I.; Levin, D.A. Modeling of Electronic Excitation and Radiation in Non-Continuum Hypersonic Reentry Flows. Phys. Fluids 2011, 23, 066102. [Google Scholar] [CrossRef]
- Shariati, V.; Roohi, E.; Ebrahimi, A. Numerical Study of Gas Flow in Super Nanoporous Materials Using the Direct Simulation Monte-Carlo Method. Micromachines 2023, 14, 139. [Google Scholar] [CrossRef]
- Schwartzentruber, T.E.; Boyd, I.D. A Hybrid Particle-Continuum Method Applied to Shock Waves. J. Comput. Phys. 2006, 215, 402–416. [Google Scholar] [CrossRef]
- Cunningham, E. On the Velocity of Steady Fall of Spherical Particles through Fluid Medium. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1910, 83, 357–365. [Google Scholar]
- Millikan, R.A. The Isolation of an Ion, a Precision Measurement of Its Charge, and the Correction of Stokes’s Law. Science 1910, 32, 436–448. [Google Scholar] [CrossRef] [PubMed]
- Knudsen, M.; Weber, S. Luftwiderstand Gegen Die Langsame Bewegung Kleiner Kugeln. Ann. Phys. 1911, 341, 981–994. [Google Scholar] [CrossRef]
- Millikan, R.A. The General Law of Fall of a Small Spherical Body through a Gas, and Its Bearing upon the Nature of Molecular Reflection from Surfaces. Phys. Rev. 1923, 22, 1. [Google Scholar] [CrossRef]
- Birge, R.T. The 1944 Values of Certain Atomic Constants with Particular Reference to the Electronic Charge. Am. J. Phys. 1945, 13, 63–73. [Google Scholar] [CrossRef]
- Kim, J.H.; Mulholland, G.W.; Kukuck, S.R.; Pui, D.Y.H. Slip Correction Measurements of Certified PSL Nanoparticles Using a Nanometer Differential Mobility Analyzer (Nano-DMA) for Knudsen Number from 0.5 to 83. J. Res. Natl. Inst. Stand. Technol. 2005, 110, 31. [Google Scholar] [CrossRef]
- Roohi, E.; Stefanov, S. Collision Partner Selection Schemes in DSMC: From Micro/Nano Flows to Hypersonic Flows. Phys. Rep. 2016, 656, 1–38. [Google Scholar] [CrossRef]
- Bird, G.A. Shock-Wave Structure in a Rigid Sphere Gas. In Proceedings of the 4th International Symposium on Rarefied Gas Dynamics, Toronto, ON, Canada, 14–17 July 1964; Academic Press: New York, MY, USA, 1965; Volume 2, pp. 216–222. [Google Scholar]
- Bird, G.A. Perception of Numerical Methods in Rarefied Gasdynamics. Prog. Astronaut. Aeronaut. 1989, 117, 211–226. [Google Scholar]
- Koura, K. Null-collision Technique in the Direct-simulation Monte Carlo Method. Phys. Fluids 1986, 29, 3509–3511. [Google Scholar] [CrossRef]
- Ivanov, M.S.; Rogasinskii, S.V. Theoretical Analysis of Traditional and Modern Schemes of the DSMC Method. In Rarefied Gas Dynamics; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1991; pp. 629–642. [Google Scholar]
- Yanitskiy, V. Operator Approach to Direct Simulation Monte Carlo Theory in Rarefied Gas Dynamics. In Proceedings of the 17th Symposium on Rarefied Gas Dynamics, Aachen, Germany, 8–14 July 1990; VCH New York: New York, NY, USA, 1990; pp. 770–777. [Google Scholar]
- Stefanov, S.K. Particle Monte Carlo Algorithms with Small Number of Particles in Grid Cells. In Proceedings of the Numerical Methods and Applications: 7th International Conference, NMA 2010, Borovets, Bulgaria, 20–24 August 2010; Revised Papers 7. Springer: Berlin/Heidelberg, Germany, 2011; pp. 110–117. [Google Scholar]
- Stefanov, S.K. On DSMC Calculations of Rarefied Gas Flows with Small Number of Particles in Cells. SIAM J. Sci. Comput. 2011, 33, 677–702. [Google Scholar] [CrossRef]
- Piekos, E.S.; Breuer, K.S. Numerical Modeling of Micromechanical Devices Using the Direct Simulation Monte Carlo Method. J. Fluids Eng. Sep. 1996, 118, 464–469. [Google Scholar] [CrossRef]
- Shu, C.; Mao, X.H.; Chew, Y.T. Particle Number per Cell and Scaling Factor Effect on Accuracy of DSMC Simulation of Micro Flows. Int. J. Numer. Methods Heat Fluid Flow 2005, 15, 827–841. [Google Scholar] [CrossRef]
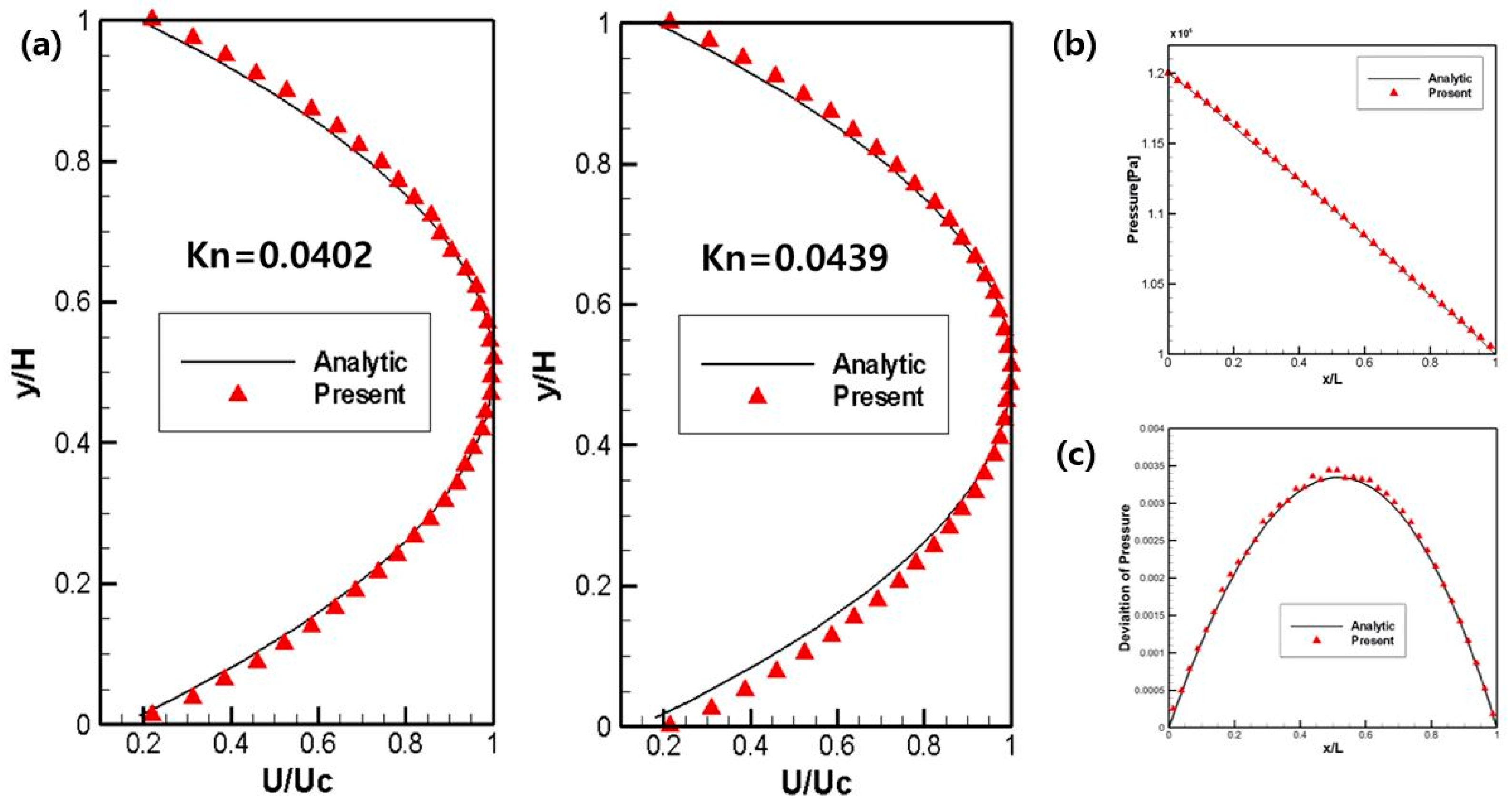

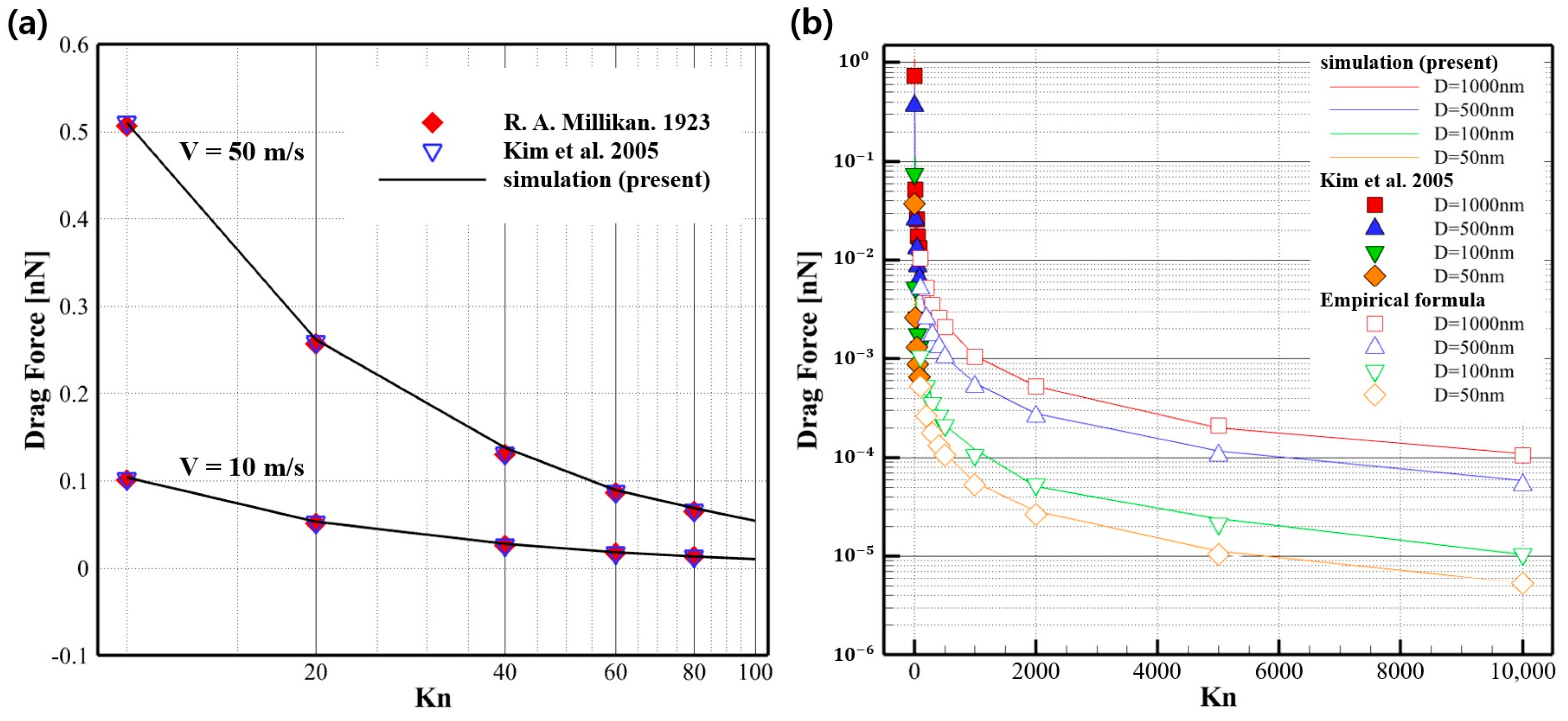
| Case | Inlet Pressure [Pa] | Outlet Pressure [Pa] | |
|---|---|---|---|
| 1 | 0.0402 | ||
| 2 | 0.0439 |
| Knudsen Number | Pressure [Pa] |
|---|---|
| 10 | 13,851 |
| 20 | 6925 |
| 50 | 2770 |
| 100 | 1385 |
| 500 | 277 |
| 1000 | 139 |
| 5000 | 28 |
| 10,000 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, J.; Son, Y.; Lee, S. A Numerical Study of an Ellipsoidal Nanoparticles under High Vacuum Using the DSMC Method. Micromachines 2023, 14, 778. https://doi.org/10.3390/mi14040778
Jang J, Son Y, Lee S. A Numerical Study of an Ellipsoidal Nanoparticles under High Vacuum Using the DSMC Method. Micromachines. 2023; 14(4):778. https://doi.org/10.3390/mi14040778
Chicago/Turabian StyleJang, Jinwoo, Youngwoo Son, and Sanghwan Lee. 2023. "A Numerical Study of an Ellipsoidal Nanoparticles under High Vacuum Using the DSMC Method" Micromachines 14, no. 4: 778. https://doi.org/10.3390/mi14040778
APA StyleJang, J., Son, Y., & Lee, S. (2023). A Numerical Study of an Ellipsoidal Nanoparticles under High Vacuum Using the DSMC Method. Micromachines, 14(4), 778. https://doi.org/10.3390/mi14040778






