MIMU Optimal Redundant Structure and Signal Fusion Algorithm Based on a Non-Orthogonal MEMS Inertial Sensor Array
Abstract
1. Introduction
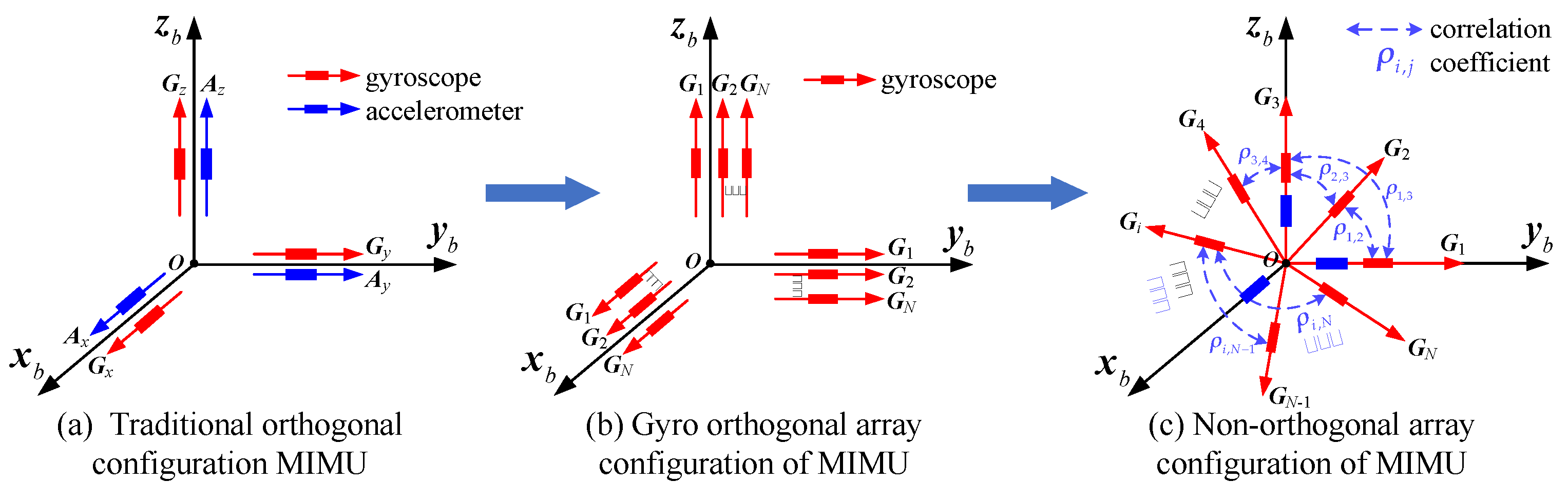
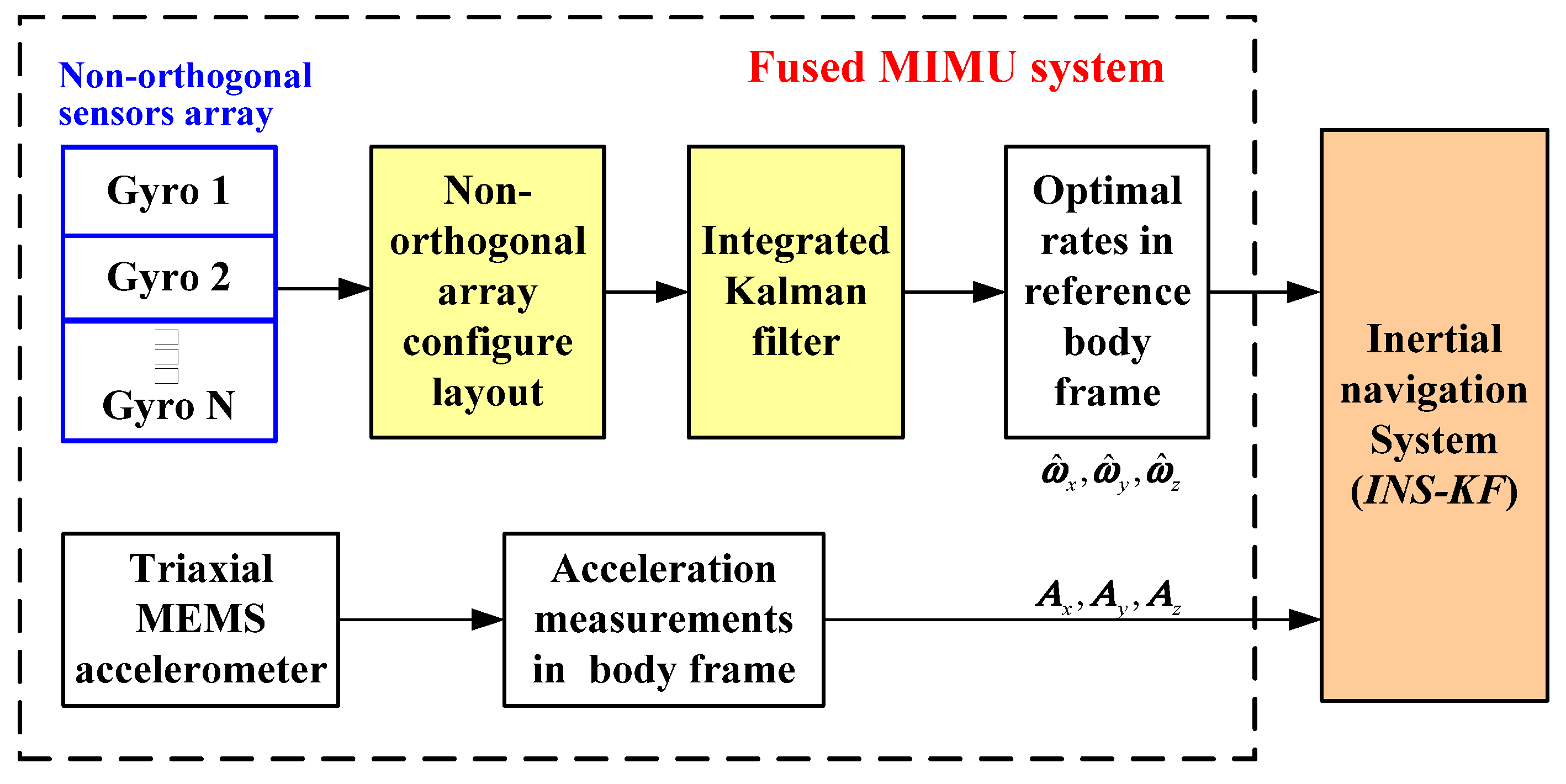
2. Working Principle of a Redundant MIMU System
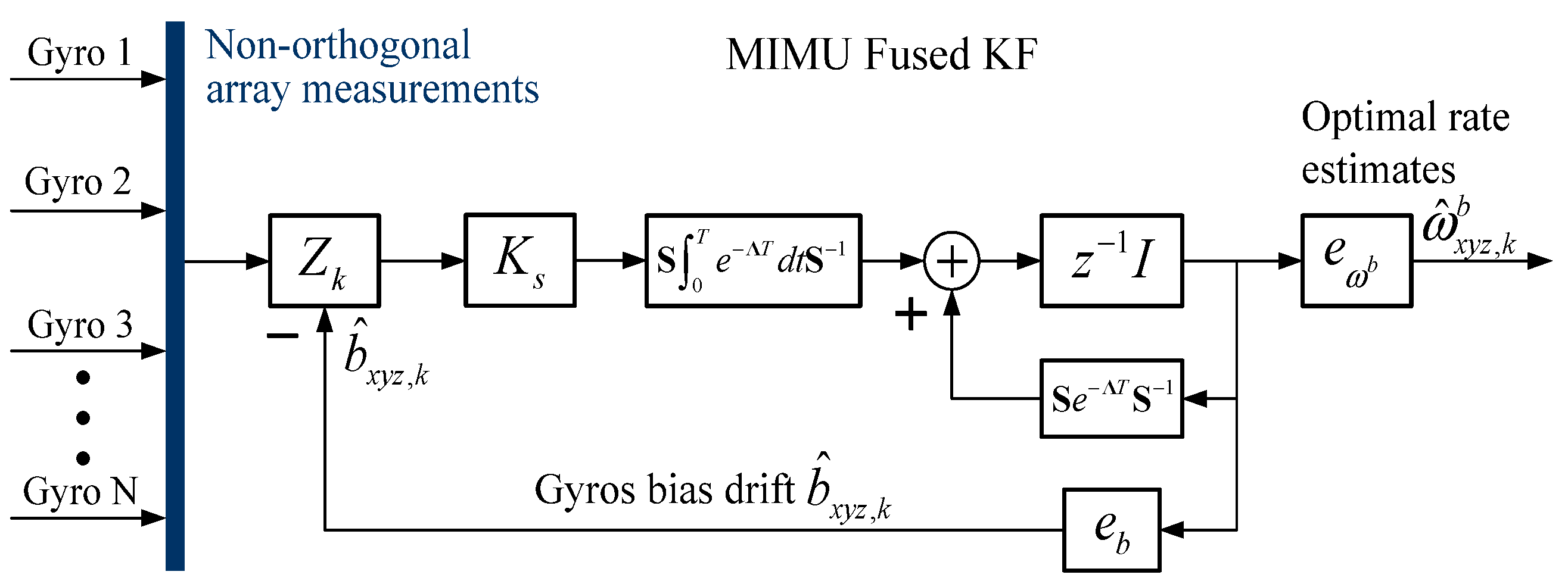
2.1. Modeling of a Fused-Gyro-Array KF Algorithm
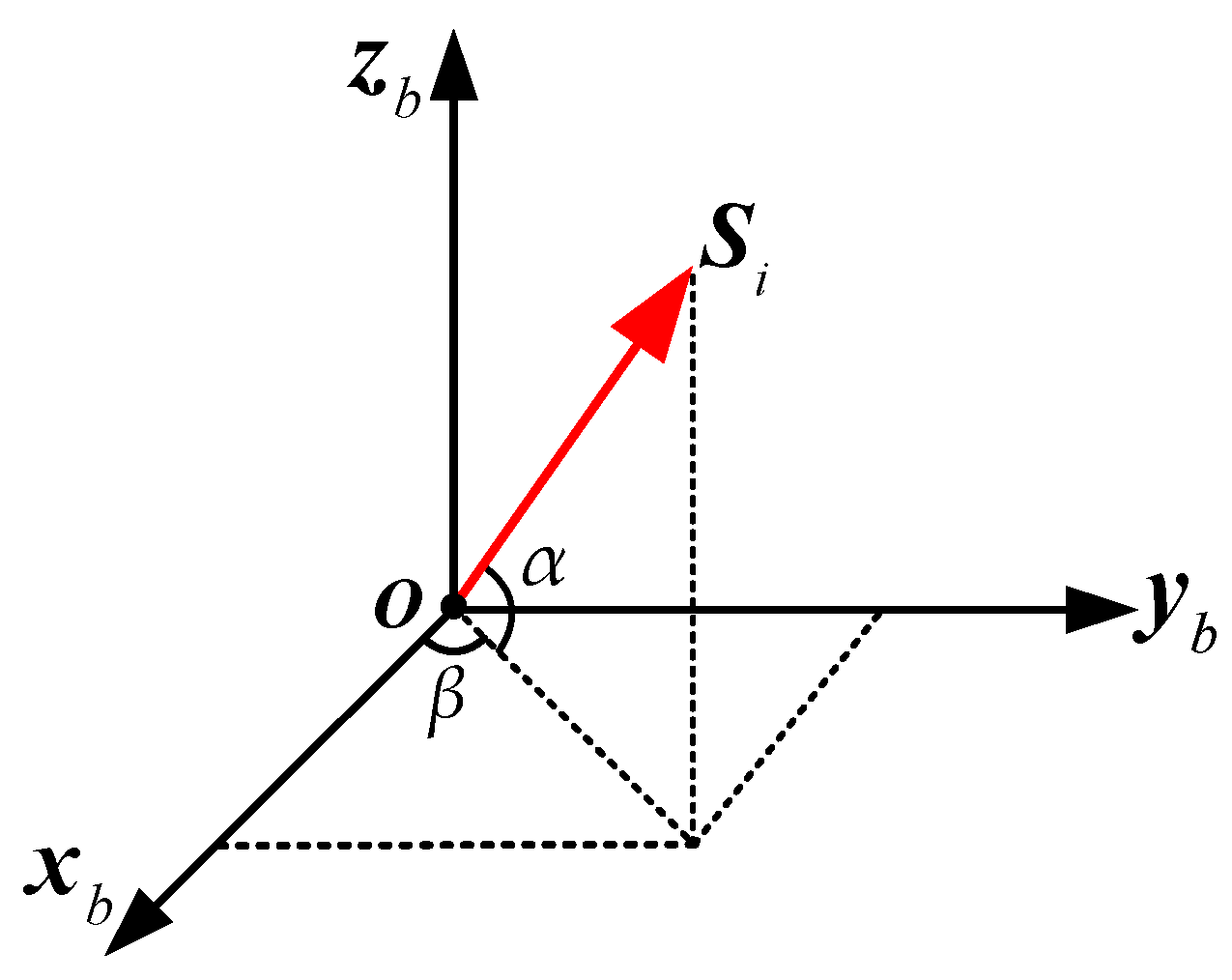
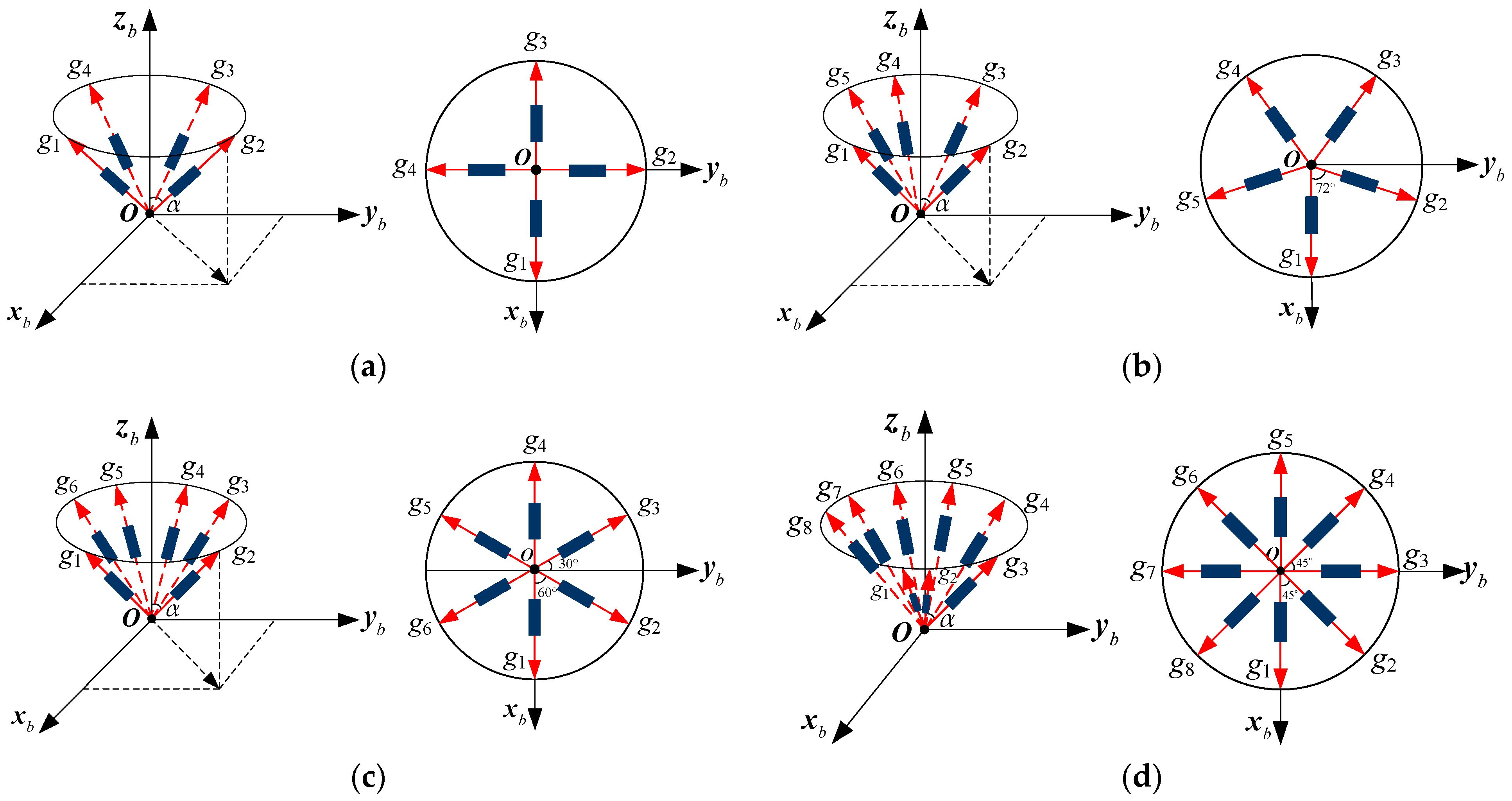
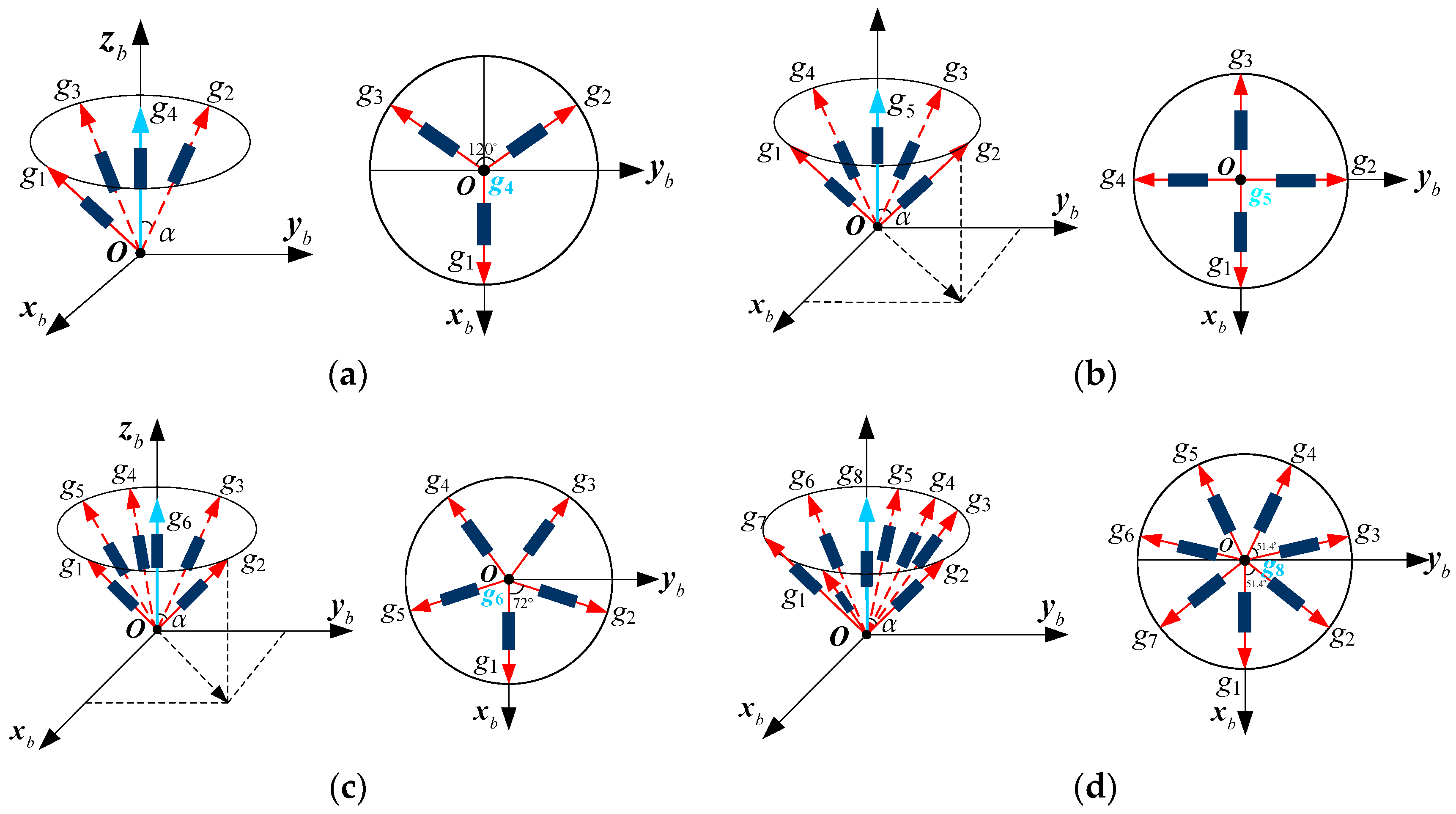
2.2. Structure of a Non-Orthogonal Gyro Array in MIMU
3. Performance of Configuration Structure of Non-Orthogonal Array
4. Simulation Results and Discussion
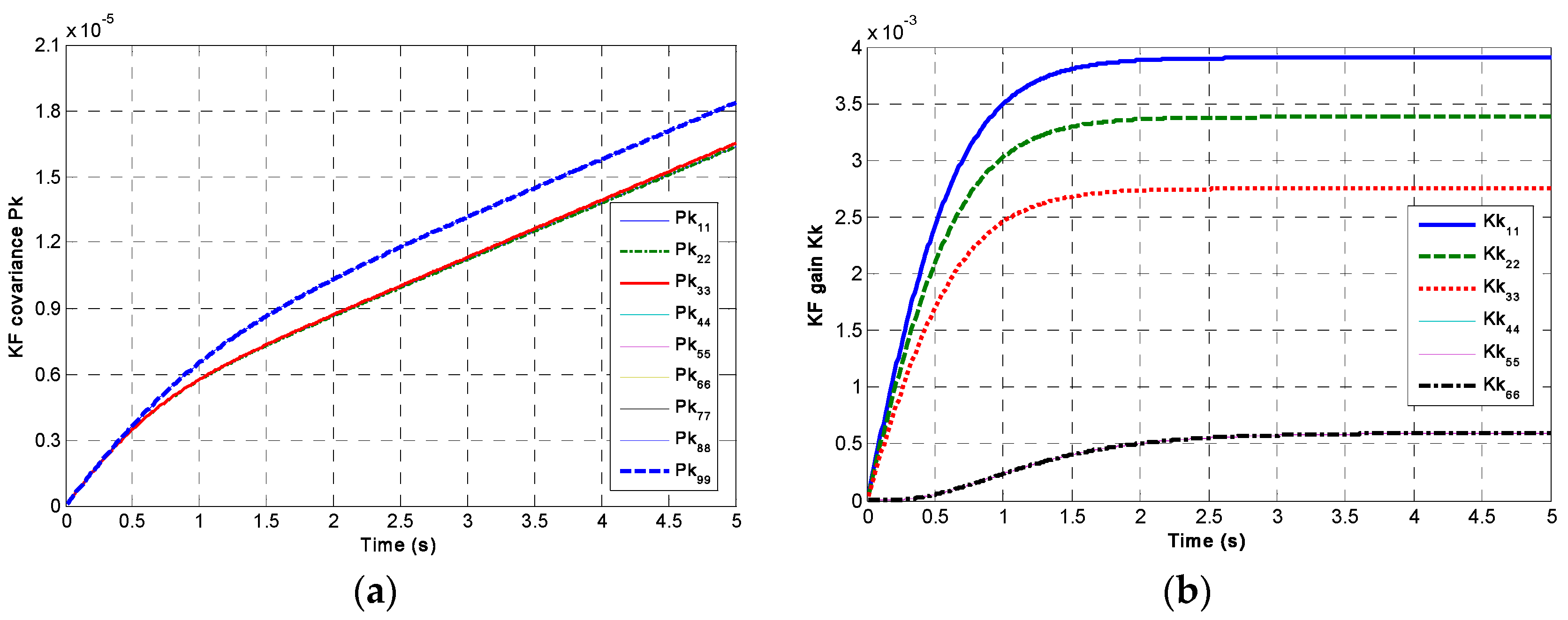
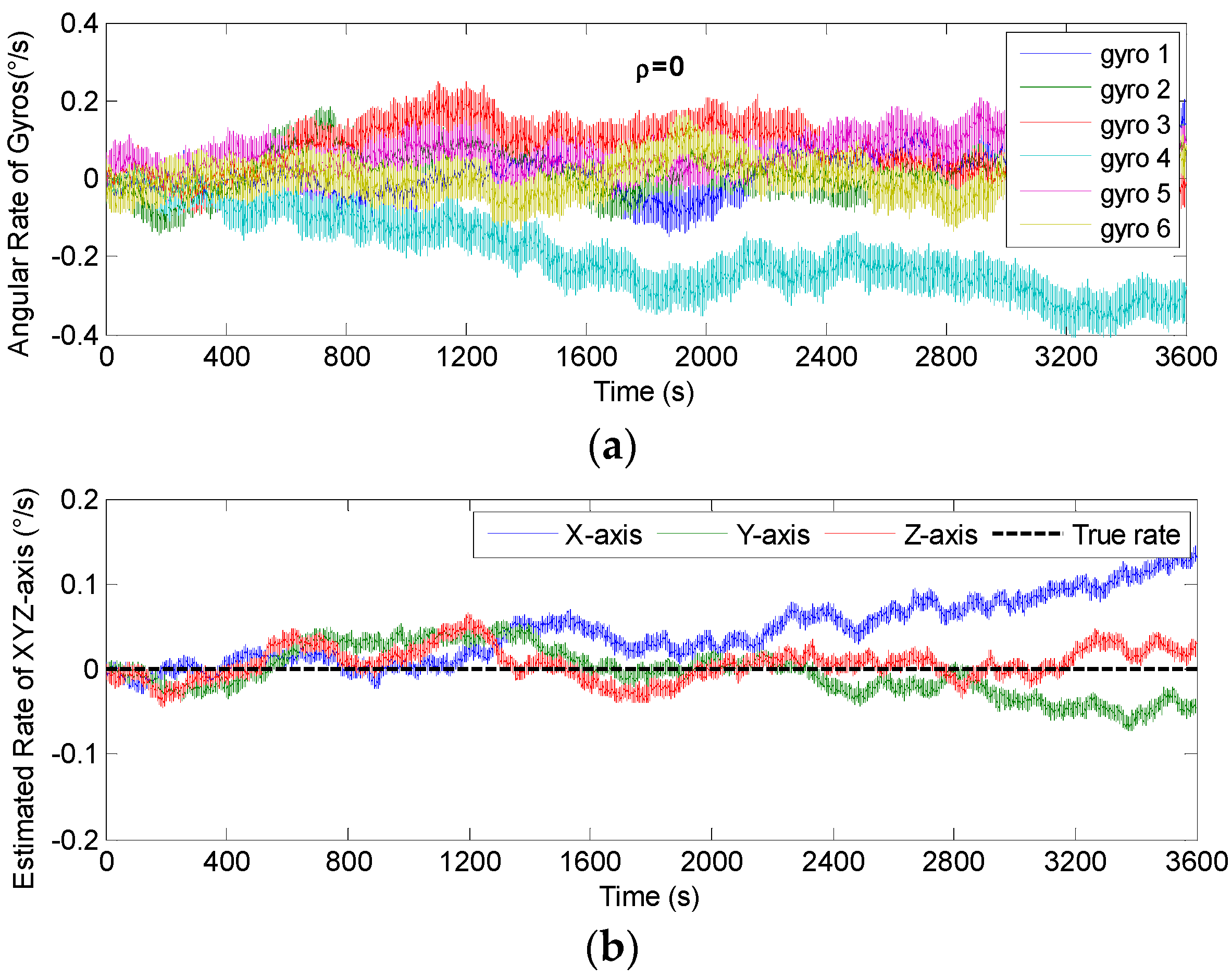
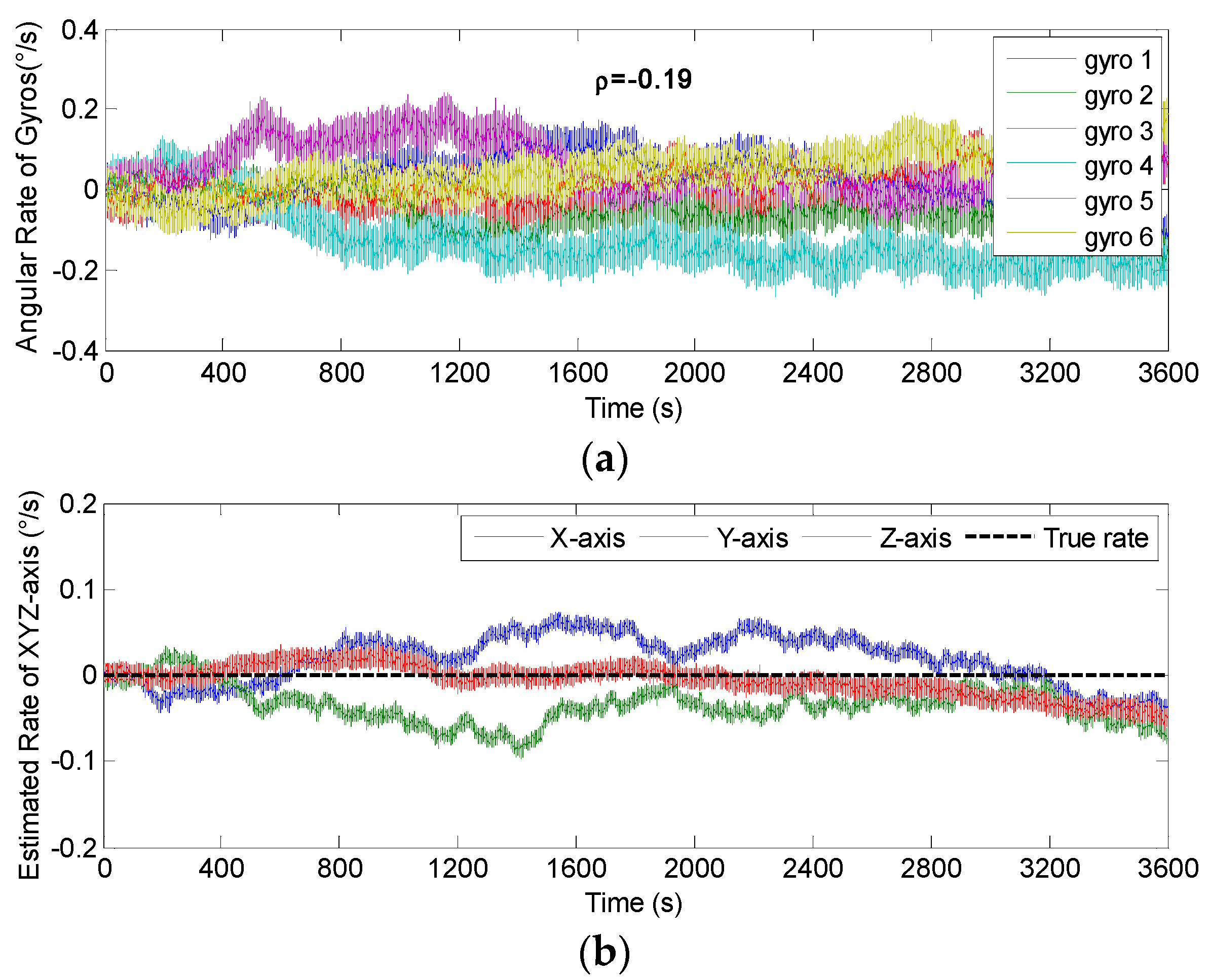
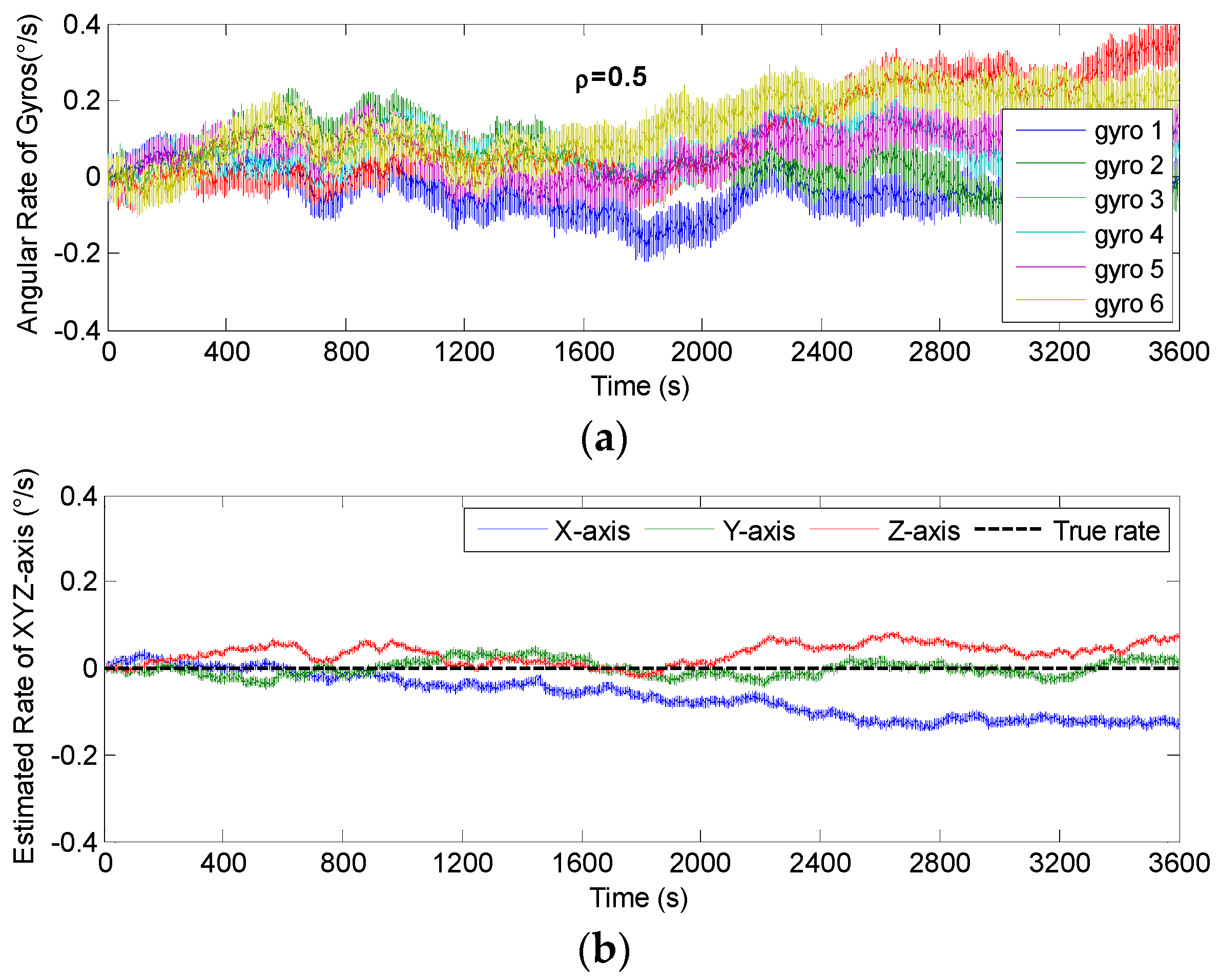
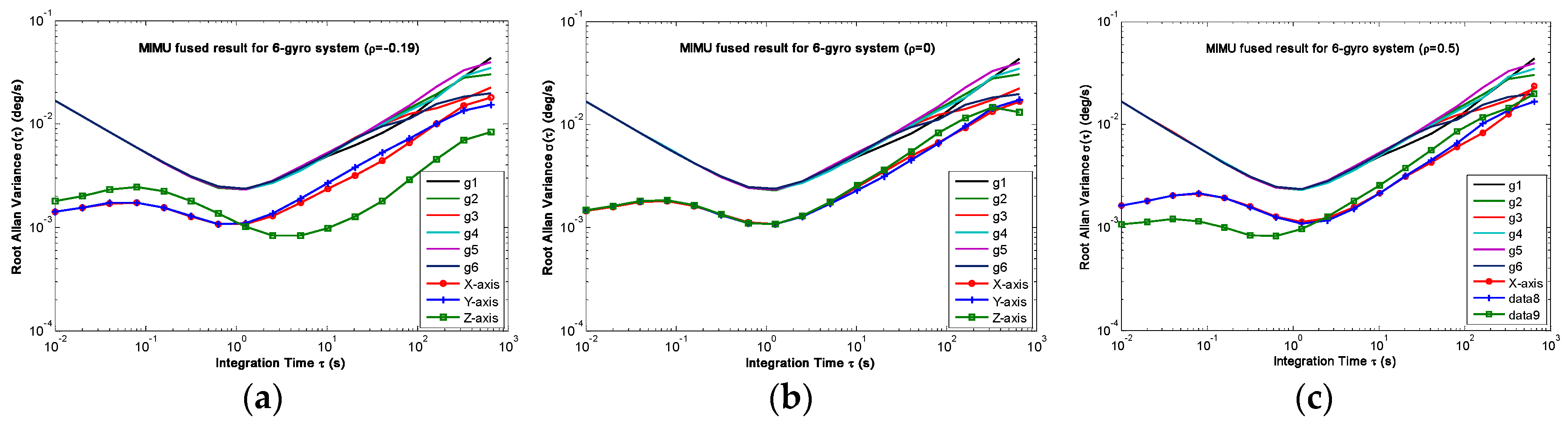
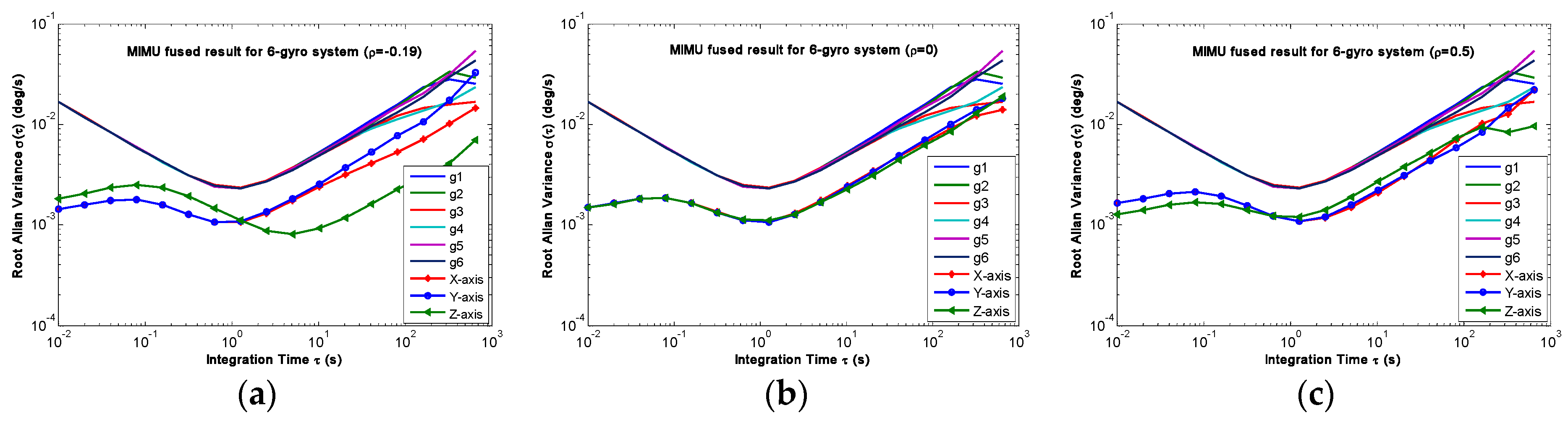
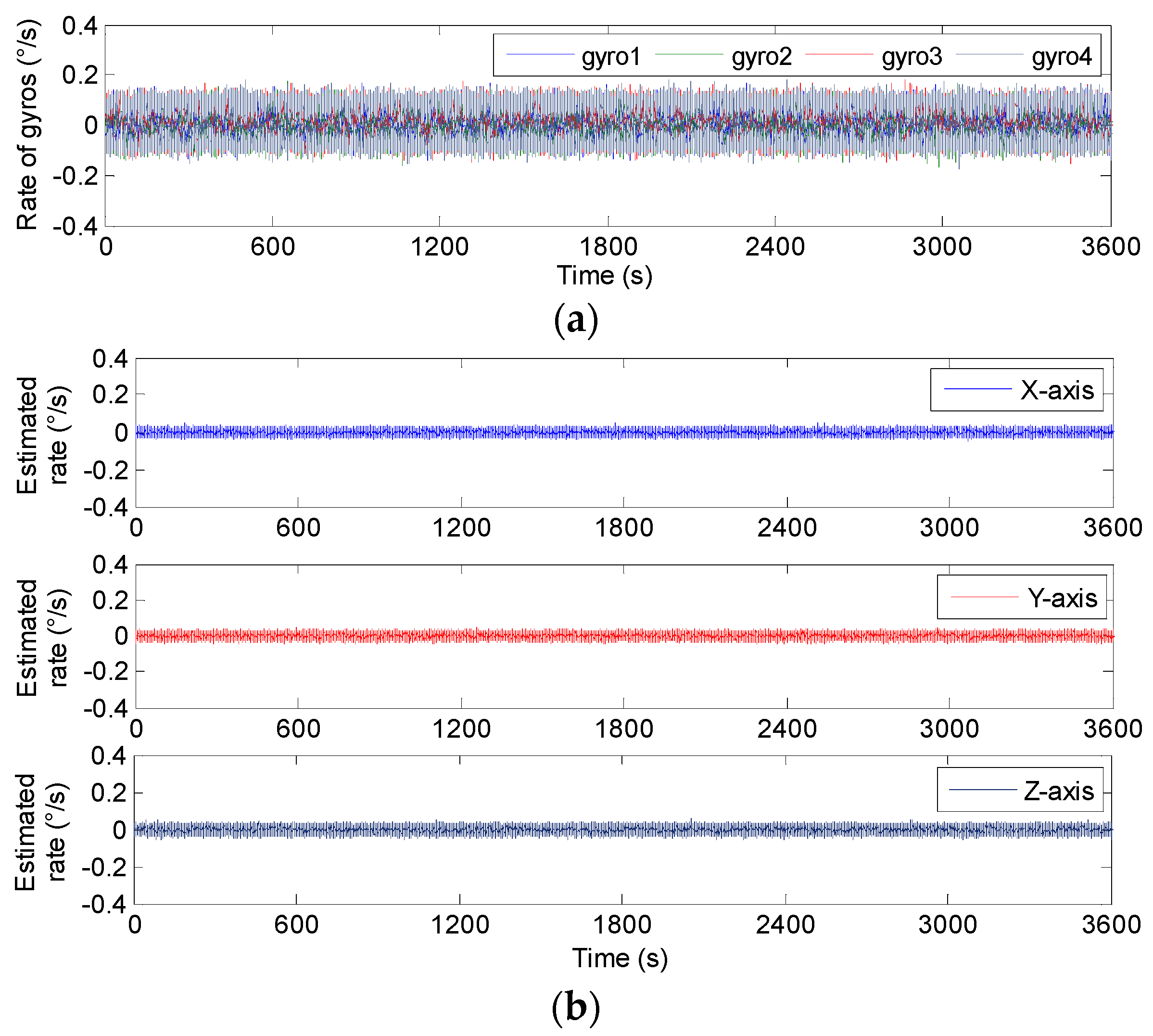
4.1. Results of the Static Simulation
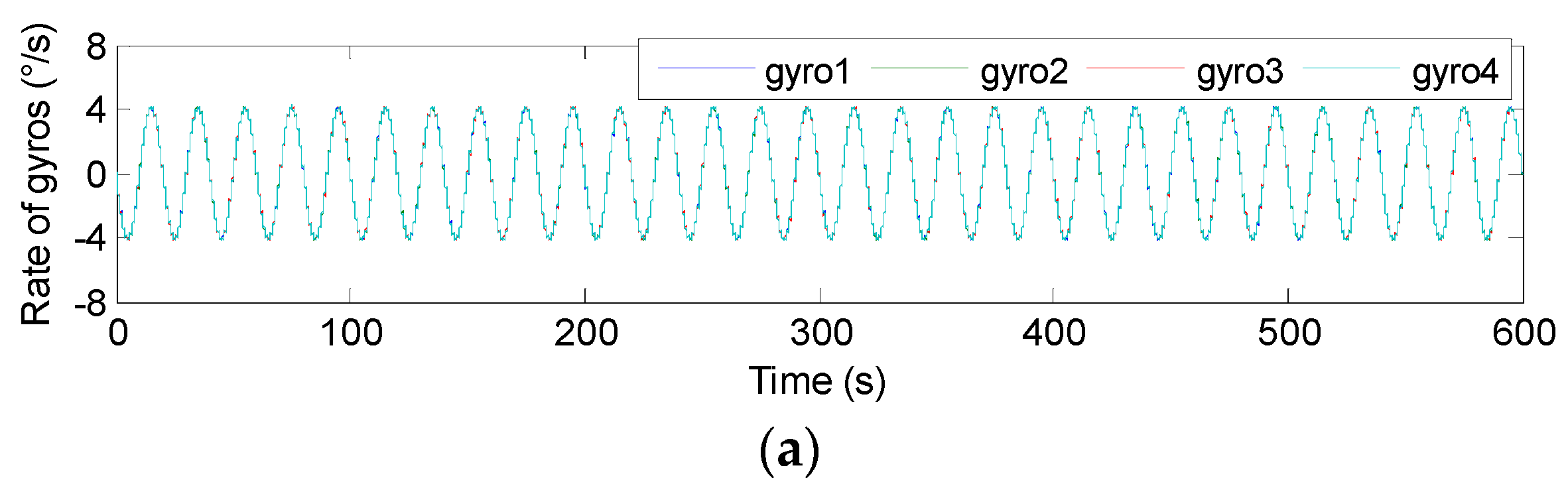
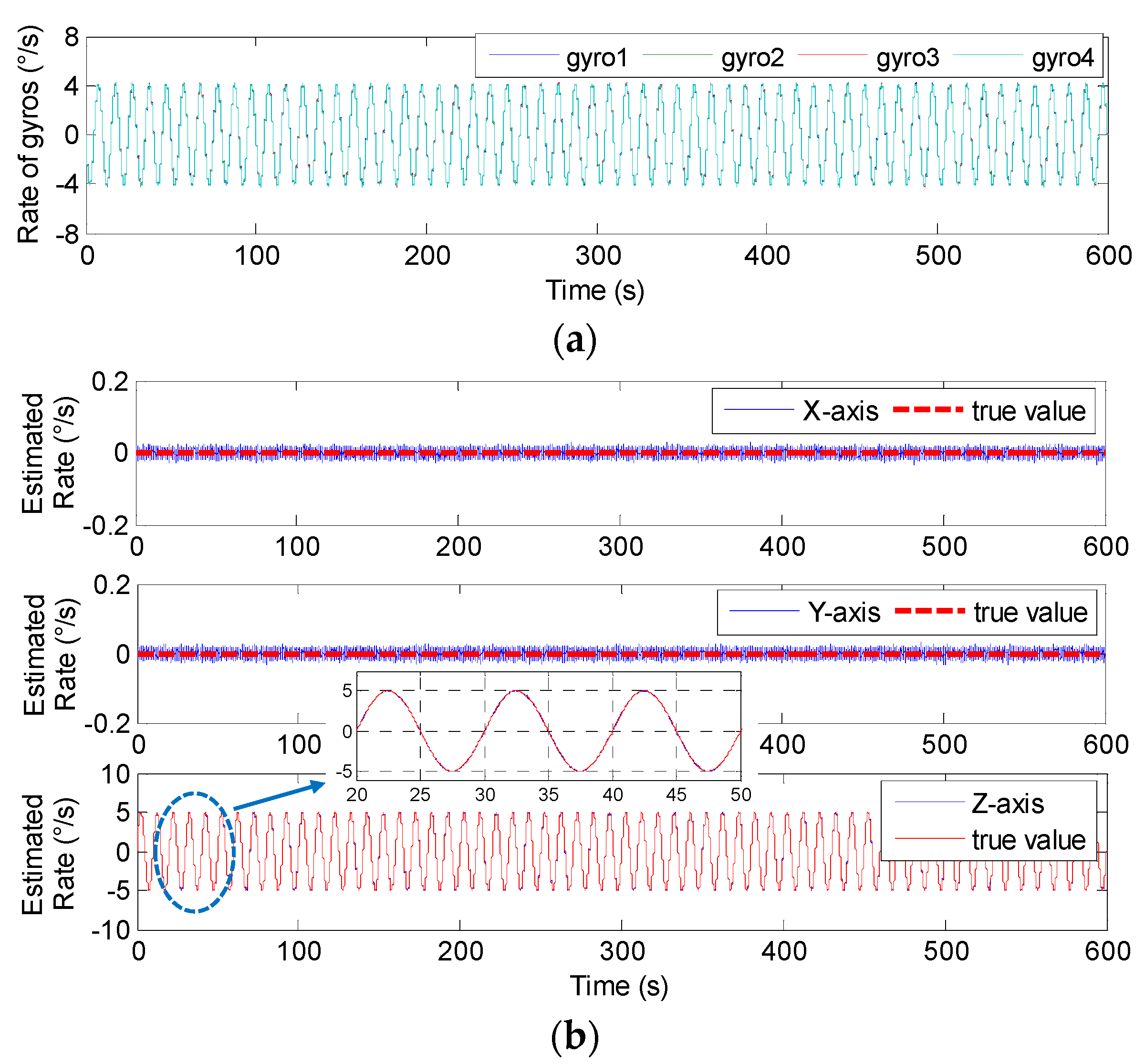
4.2. Results of the Sinusoidal Signal Simulation
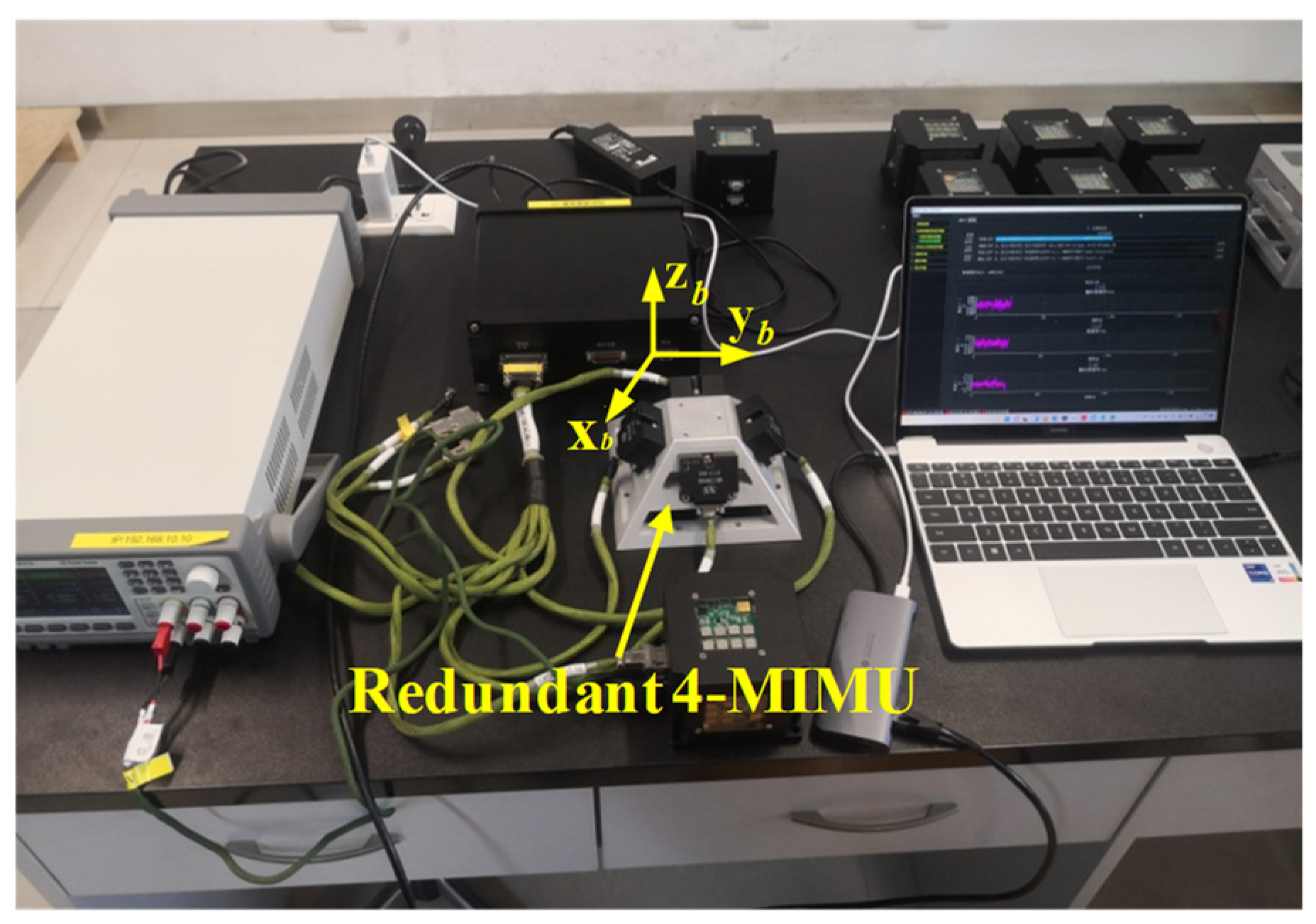
5. Experiment
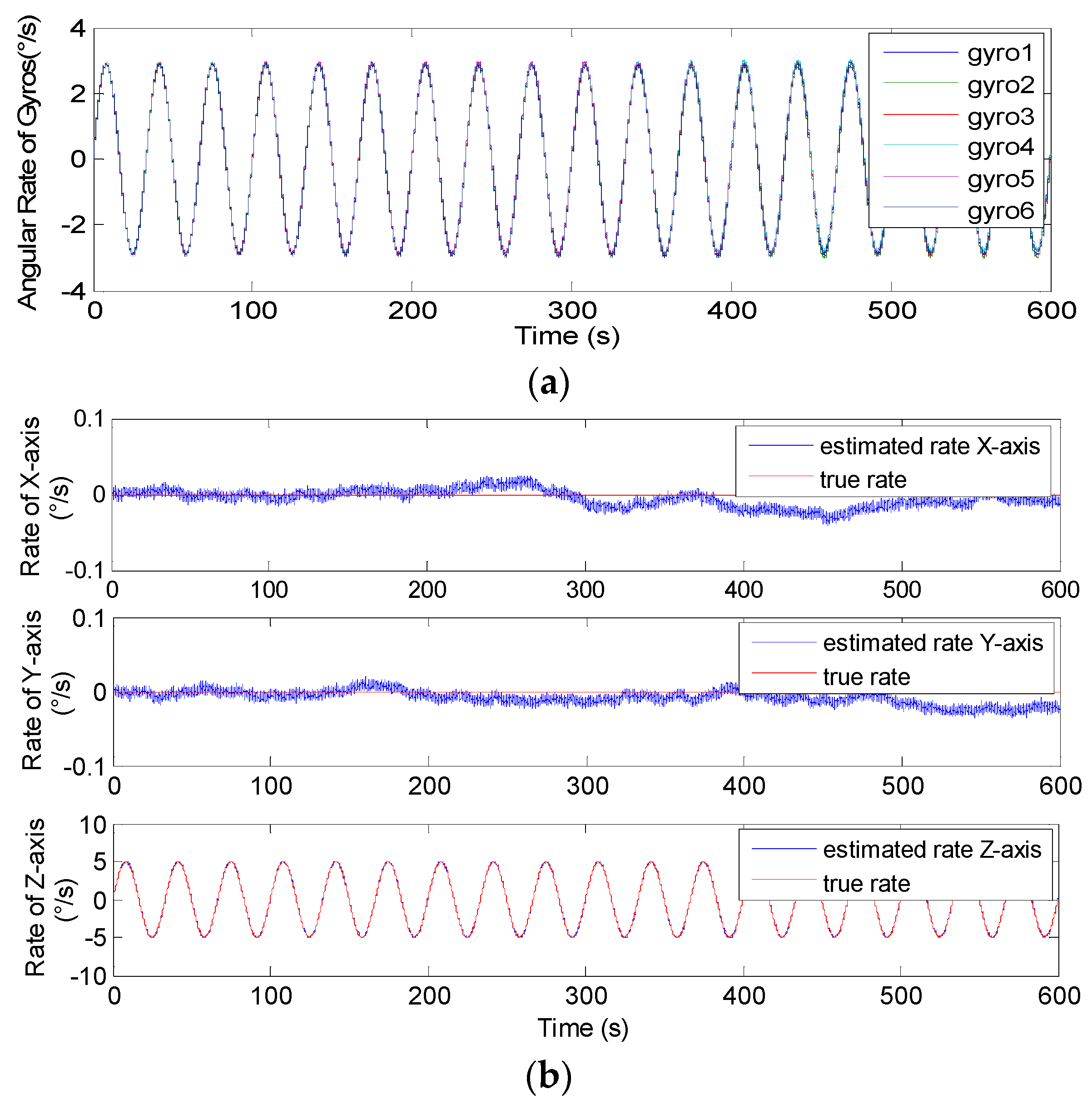
5.1. Static Testing Results
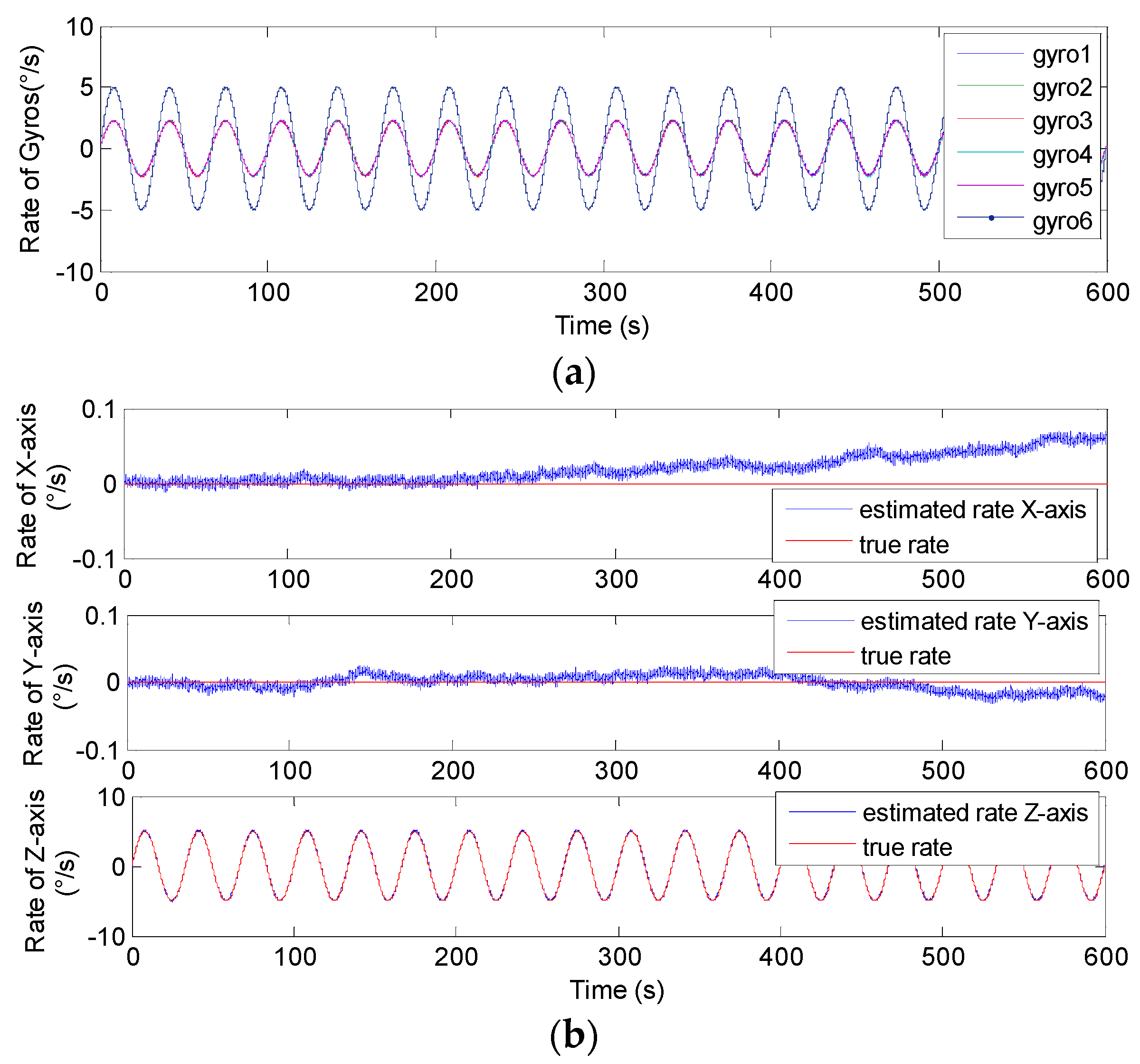
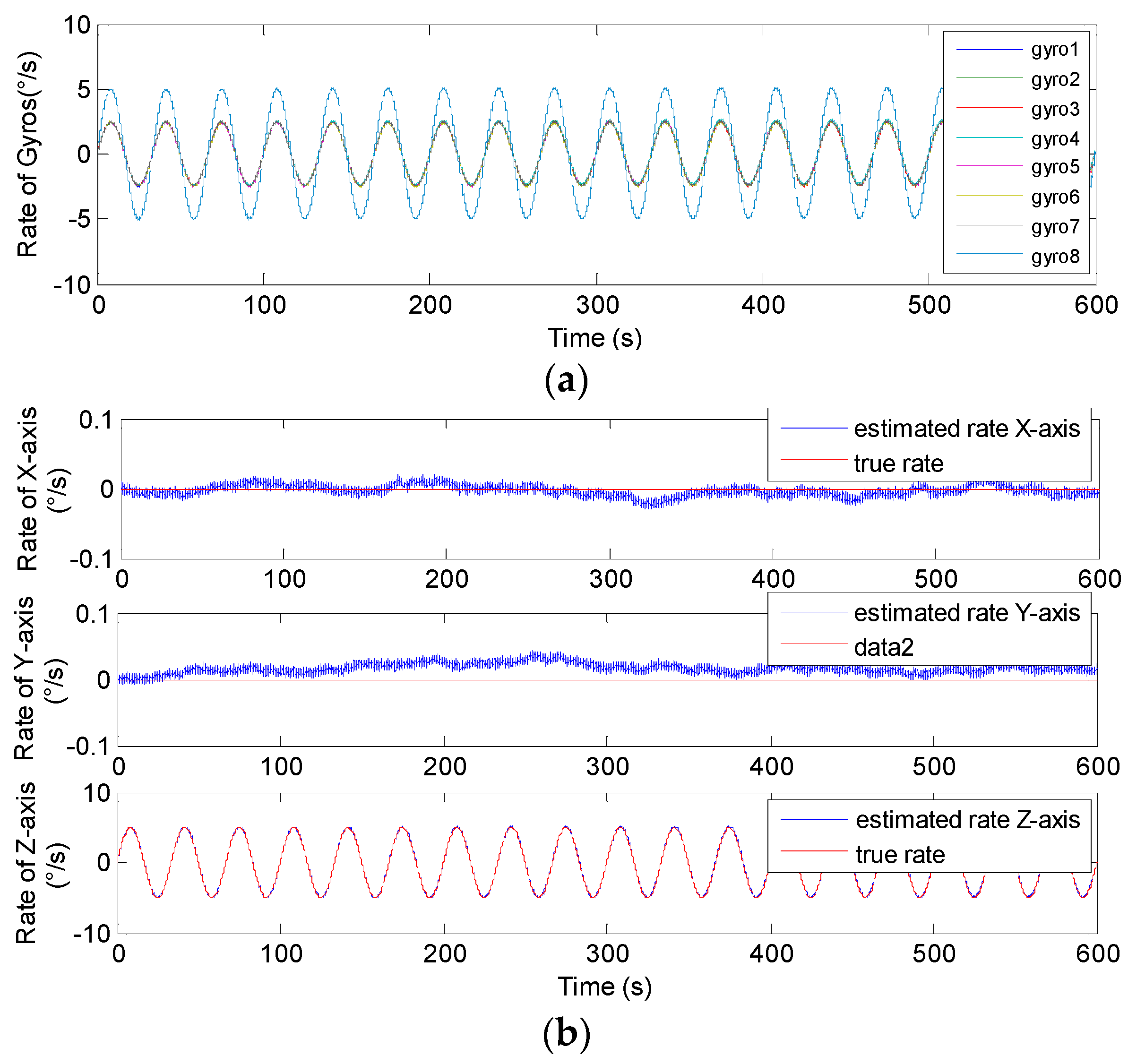
5.2. Swing Signal Testing Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giner, J.; Maeda, D.; Ono, K.; Shkel, A.M.; Sekiguchi, T. MEMS Gyroscope with Concentrated Springs Suspensions Demonstrating Single Digit Frequency Split and Temperature Robustness. J. Microelectromech. Syst. 2019, 28, 25–35. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Yu, S.; Sun, J.K.; Lu, K.; Xu, Y.; Li, Q.S.; Wu, X.Z.; Xiao, D.B. A Rate-Integrating Honeycomb Disk Resonator Gyroscope with 0.038°/h Bias Instability and 7000°/s Measurement Range. IEEE Electron Device Lett. 2021, 42, 581–584. [Google Scholar] [CrossRef]
- Tsukamoto, T.; Tanaka, S.J. Rate Integrating Gyroscope Using Independently Controlled CW and CCW Modes on Single Resonator. J. Microelectromech. Syst. 2021, 30, 15–23. [Google Scholar] [CrossRef]
- Bayard, D.S.; Ploen, S.R. High Accuracy Inertial Sensors from Inexpensive Components. U.S. Patent No. 20030187623A1, 2 October 2003. [Google Scholar]
- Xue, L.; Yang, B.; Yang, X.G.; Yuan, D.; Wang, X.G.; Chang, H.L. A Redundant Fused MIMU Attitude System Algorithm Based on Two-stage Data Fusion of MEMS Gyro Clusters Array. Measurement 2021, 184, 109993. [Google Scholar] [CrossRef]
- Chang, H.L.; Xue, L.; Jiang, C.Y.; Kraft, M.; Yuan, W.Z. Combining Numerous Uncorrelated MEMS Gyroscopes for Accuracy Improvement Based on an Optimal Kalman Filter. IEEE Trans. Instrum. Meas. 2012, 61, 3084–3093. [Google Scholar] [CrossRef]
- Pejsa, A.J. Optimum Skewed Redundant Inertial Navigators. AIAA J. 1974, 12, 899–902. [Google Scholar] [CrossRef]
- Sushchenko, O.A.; Bezkorovainyi, Y.N.; Novytska, N.D. Nonorthogonal Redundant Configurations of Inertial Sensors. In Proceedings of the IEEE 4th International Conference Actual Problems of Unmanned Aerial Vehicles Developments, Kiev, Ukraine, 17–19 October 2017. [Google Scholar]
- Gheorghe, M.V. Study of Virtual Body Frames in Dodecahedron-Based Skew Redundant Inertial Measurement Units. Sens. Transducers 2016, 12, 15–20. [Google Scholar]
- Jafari, M. Optimal Redundant Sensor Configuration for Accuracy Increasing in Space Inertial Navigation System. Aerosp. Sci. Technol. 2015, 47, 467–472. [Google Scholar] [CrossRef]
- Tanenhaus, M.; Carhoun, D.; Geis, T.; Wan, E.; Holland, A. Miniature IMU/INS with Optimally Fused Low Drift MEMS Gyro and Accelerometers for Applications in GPS-denied Environments. In Proceedings of the IEEE Symposium on Position, Location and Navigation, Myrtle Beach, SC, USA, 23–26 April 2012. [Google Scholar]
- Skog, I.; Nilsson, J.O.; Handel, P.; Nehorai, A. Inertial Sensor Arrays, Maximum Likelihood, and Cramér–Rao Bound. IEEE Trans. Signal Process. 2016, 64, 4218–4227. [Google Scholar] [CrossRef]
- Song, J.L.; Shi, Z.Y.; Du, B.H.; Han, L.Y.; Wang, Z.W.; Wang, H.G. The Data Fusion Method of Redundant Gyroscope System Based on Virtual Gyroscope Technology. IEEE Sens. J. 2019, 19, 10736–10743. [Google Scholar] [CrossRef]
- Xue, L.; Yang, B.; Wang, X.G.; Shan, B.; Gao, J.A.; Chang, H.L.; Yao, Y.F. Design of Optimal Estimation Algorithm for Multi-sensor Fusion of a Redundant MEMS Gyro System. IEEE Sens. J. 2023, 23, 4577–4588. [Google Scholar] [CrossRef]
- Skog, I.; Nilsson, J.; Händel, P. Pedestrian Tracking Using an IMU Array. In Proceedings of the IEEE International Conference on Electronics, Computing and Communication Technologies, Bangalore, India, 6–7 January 2014. [Google Scholar]
- Eckenhoff, K.; Geneva, P.; Huang, G.Q. Sensor-Failure-Resilient Multi-IMU Visual-Inertial Navigation. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Zhu, M.H.; Yu, F.; Xiao, S. An Unconventional Multiple Low-Cost IMU and GPS-Integrated Kinematic Positioning and Navigation Method Based on Singer Model. Sensors 2019, 19, 4274. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.Q.; Tang, H.L.; Zhang, T.S.; Chen, Q.J.; Shi, J.W.; Niu, X.J. Improving the Navigation Performance of the MEMS IMU Array by Precise Calibration. IEEE Sens. J. 2021, 21, 26050–26058. [Google Scholar] [CrossRef]
- Xue, L.; Wang, X.G.; Yang, B.; Yuan, W.Z.; Yuan, G.M. Analysis of correlation in MEMS gyroscope array and its influence on accuracy improvement for the combined angular rate signal. Micromachines 2018, 9, 22. [Google Scholar] [CrossRef] [PubMed]






| Scheme | Angle α | N = 4 | N = 5 | N = 6 | N = 8 |
|---|---|---|---|---|---|
| GDOP (Scheme 1) | α = 60° | 1.5327 | 1.3663 | 1.3089 | 1.0801 |
| GDOP (Scheme 2) | α = 60° | 1.5275 | 1.3540 | 1.2293 | 1.0609 |
| GDOP (Scheme 2) | α = 45° | 1.7512 | 1.5275 | 1.3732 | 1.1684 |
| Number | Correlation Factor | Minimum GDOP | Optimal Angle α |
|---|---|---|---|
| ρ = 0.2 | 1.5269 | 49.94° | |
| N = 4 | ρ = −0.1 | 1.4671 | 57.72° |
| ρ = −0.2 | 1.4117 | 61.75° | |
| ρ = 0.2 | 1.4000 | 49.10° | |
| N = 5 | ρ = −0.1 | 1.2845 | 58.71° |
| ρ = −0.2 | 1.1798 | 65.68° | |
| ρ = 0.2 | 1.3076 | 48.36° | |
| N = 6 | ρ = −0.1 | 1.1450 | 59.85° |
| ρ = −0.18 | 1.0160 | 69.11° | |
| ρ = 0.2 | 1.1802 | 47.05° | |
| N = 8 | ρ = −0.1 | 0.9353 | 62.93° |
| ρ = −0.14 | 0.8050 | 75.57° |
| Correlation Factor | MIMU Axis | ARW (°) | RRW (°) | BS (°/h) |
|---|---|---|---|---|
| ρ = −0.19 | Xb | 0.0393 | 279.894 | 3.8459 |
| Yb | 0.0396 | 256.254 | 3.8810 | |
| Zb | 0.0203 | 105.408 | 3.0038 | |
| ρ = 0 | Xb | 0.0420 | 286.842 | 3.8645 |
| Yb | 0.0414 | 281.496 | 3.8893 | |
| Zb | 0.0416 | 265.800 | 3.9016 | |
| ρ = 0.5 | Xb | 0.0484 | 325.752 | 4.0414 |
| Yb | 0.0480 | 313.020 | 3.9326 | |
| Zb | 0.0668 | 312.582 | 2.9394 |
| Correlation Factor | MIMU Axis | ARW (°) | RRW (°) | BS (°/h) |
|---|---|---|---|---|
| ρ = −0.19 | Xb | 0.0398 | 243.432 | 3.8092 |
| Yb | 0.0398 | 307.740 | 3.8684 | |
| Zb | 0.0675 | 95.526 | 2.9332 | |
| ρ = 0 | Xb | 0.0412 | 292.770 | 3.9389 |
| Yb | 0.0414 | 289.590 | 3.8406 | |
| Zb | 0.0418 | 266.388 | 3.9633 | |
| ρ = 0.5 | Xb | 0.0443 | 255.594 | 3.9182 |
| Yb | 0.0494 | 258.210 | 3.8985 | |
| Zb | 0.0476 | 302.604 | 4.3017 |
| Terms | Number | Xb | Yb | Zb | Single Gyro |
|---|---|---|---|---|---|
| Estimated error (1σ, °/s) | N = 6 | 0.0142 | 0.0088 | 0.0224 | 0.0622 |
| N = 8 | 0.0111 | 0.0068 | 0.0203 | 0.0622 | |
| Reduction factor | N = 6 | 4.3803 | 7.0682 | 2.7768 | |
| N = 8 | 5.6036 | 9.1471 | 3.0640 |
| Terms | Number | Xb | Yb | Zb | Single Gyro |
|---|---|---|---|---|---|
| Estimated error (1σ, °/s) | N = 6 | 0.0182 | 0.0107 | 0.0242 | 0.0552 |
| N = 8 | 0.0075 | 0.0075 | 0.0200 | 0.0552 | |
| Reduction factor | N = 6 | 3.0329 | 5.1589 | 2.2810 | |
| N = 8 | 7.3600 | 7.3600 | 2.7600 |
| Gyro Number | g1 | g2 | g3 | g4 |
|---|---|---|---|---|
| g1 | 1 | 0.000309 | 0.001531 | −0.003095 |
| g2 | 0.000309 | 1 | 0.001693 | −0.001061 |
| g3 | 0.001531 | 0.001693 | 1 | −0.000106 |
| g4 | −0.003095 | −0.001061 | −0.000106 | 1 |
| Gyro Number | BS (°/h) | ||
|---|---|---|---|
| gyro1 | 0.1476 | 4.979 | 1.0285 |
| gyro2 | 0.1849 | 2.8545 | 0.9711 |
| gyro3 | 0.1618 | 2.8764 | 0.9399 |
| gyro4 | 0.1519 | 2.6229 | 0.9461 |
| Xb-axis | 0.0429 | 1.1954 | 0.2751 |
| Yb-axis | 0.0459 | 0.6041 | 0.2287 |
| Zb-axis | 0.0525 | 1.3726 | 0.2723 |
| Terms | Frequency f | Xb | Yb | Zb |
|---|---|---|---|---|
| Estimated error (1σ, °/s) | f = 0.05 | 0.0074 | 0.0078 | 0.0125 |
| f = 0.10 | 0.0074 | 0.0079 | 0.0124 | |
| Single gyro | 0.0367 | 0.0367 | 0.0367 | |
| Reduction factor | f = 0.05 | 4.9595 | 4.7051 | 2.9360 |
| f = 0.10 | 4.9595 | 4.6456 | 2.9597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, L.; Yang, B.; Wang, X.; Cai, G.; Shan, B.; Chang, H. MIMU Optimal Redundant Structure and Signal Fusion Algorithm Based on a Non-Orthogonal MEMS Inertial Sensor Array. Micromachines 2023, 14, 759. https://doi.org/10.3390/mi14040759
Xue L, Yang B, Wang X, Cai G, Shan B, Chang H. MIMU Optimal Redundant Structure and Signal Fusion Algorithm Based on a Non-Orthogonal MEMS Inertial Sensor Array. Micromachines. 2023; 14(4):759. https://doi.org/10.3390/mi14040759
Chicago/Turabian StyleXue, Liang, Bo Yang, Xinguo Wang, Guangbin Cai, Bin Shan, and Honglong Chang. 2023. "MIMU Optimal Redundant Structure and Signal Fusion Algorithm Based on a Non-Orthogonal MEMS Inertial Sensor Array" Micromachines 14, no. 4: 759. https://doi.org/10.3390/mi14040759
APA StyleXue, L., Yang, B., Wang, X., Cai, G., Shan, B., & Chang, H. (2023). MIMU Optimal Redundant Structure and Signal Fusion Algorithm Based on a Non-Orthogonal MEMS Inertial Sensor Array. Micromachines, 14(4), 759. https://doi.org/10.3390/mi14040759





