Design and Characterization of an Adjustable Passive Flow Regulator and Application to External CSF Drainage
Abstract
1. Introduction
2. Materials and Methods
2.1. Modeling
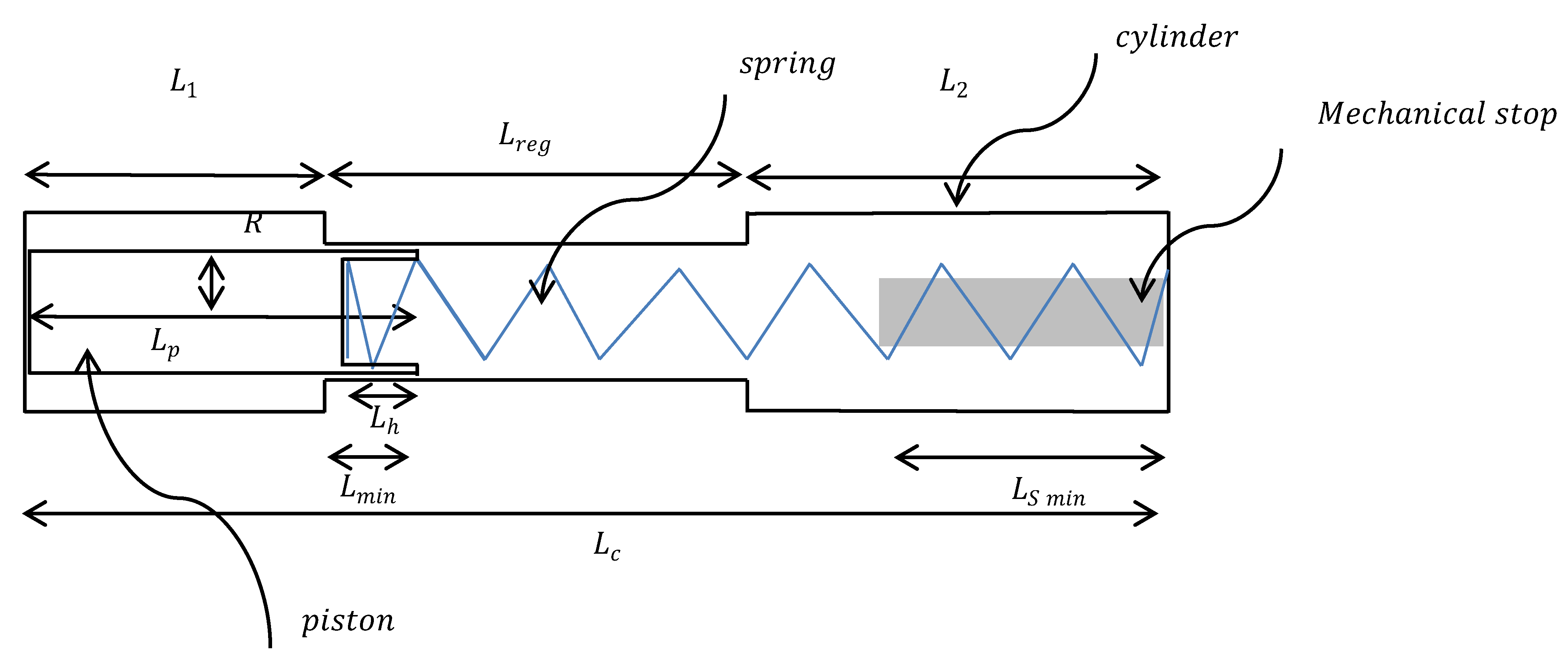
2.1.1. Simplified Model
- Lmin = Lp – L1 > 0 (i.e., there is no free flow at low pressure).
- the channel cross-section is regular.
- the spring stiffness k is constant (i.e., independent from the compression).
- ΔLS0 = Lmin (the condition for a constant flow rate).
- (the effective surface for pressure force calculation is not affected by the channel).
- Lc = Lreg (to simplify the numeral modeling).
- Stage I—low-pressure stage
- Stage II—flow-regulation stage
- Stage III—high pressure

Stage I
Stage II
Stage III
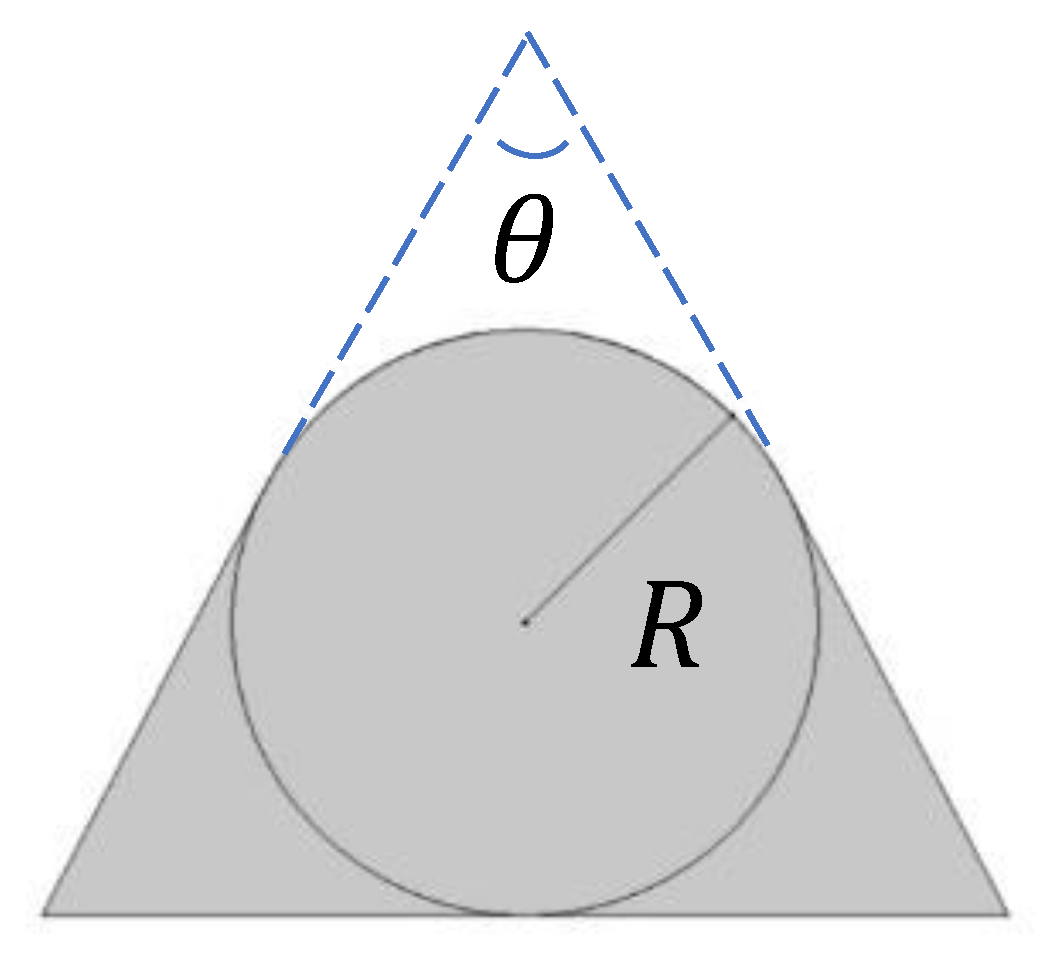
2.1.2. Non-Uniform Channel
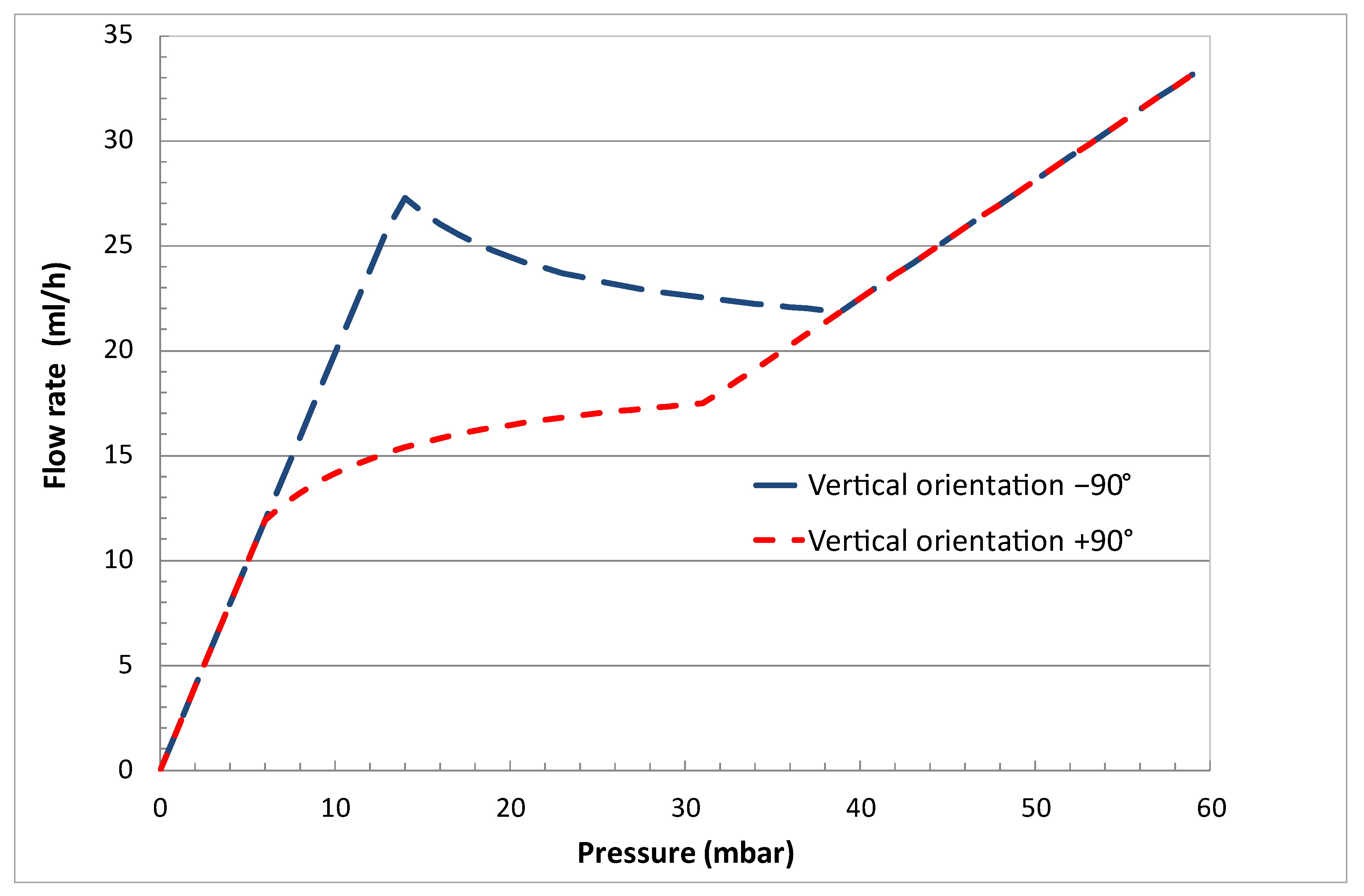
2.1.3. Gravity Effect and Device Orientation
2.1.4. Out-of-Channel Flow
2.1.5. Other Fluid Restrictions
- If , then the flow is simply given by:
- If , both solutions of Equation (33) are possible depending on the initial conditions (see the discussion about hysteresis).
2.2. Simulation
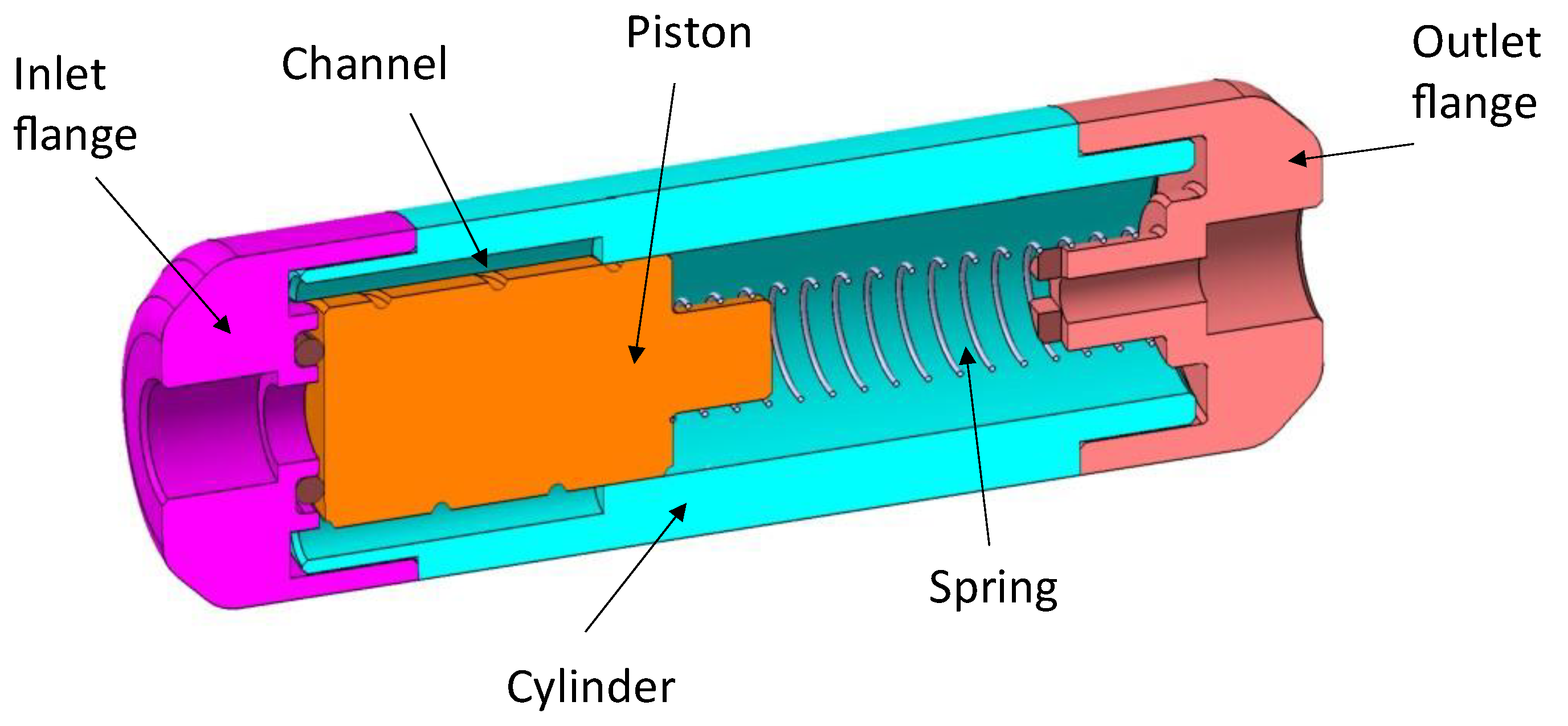
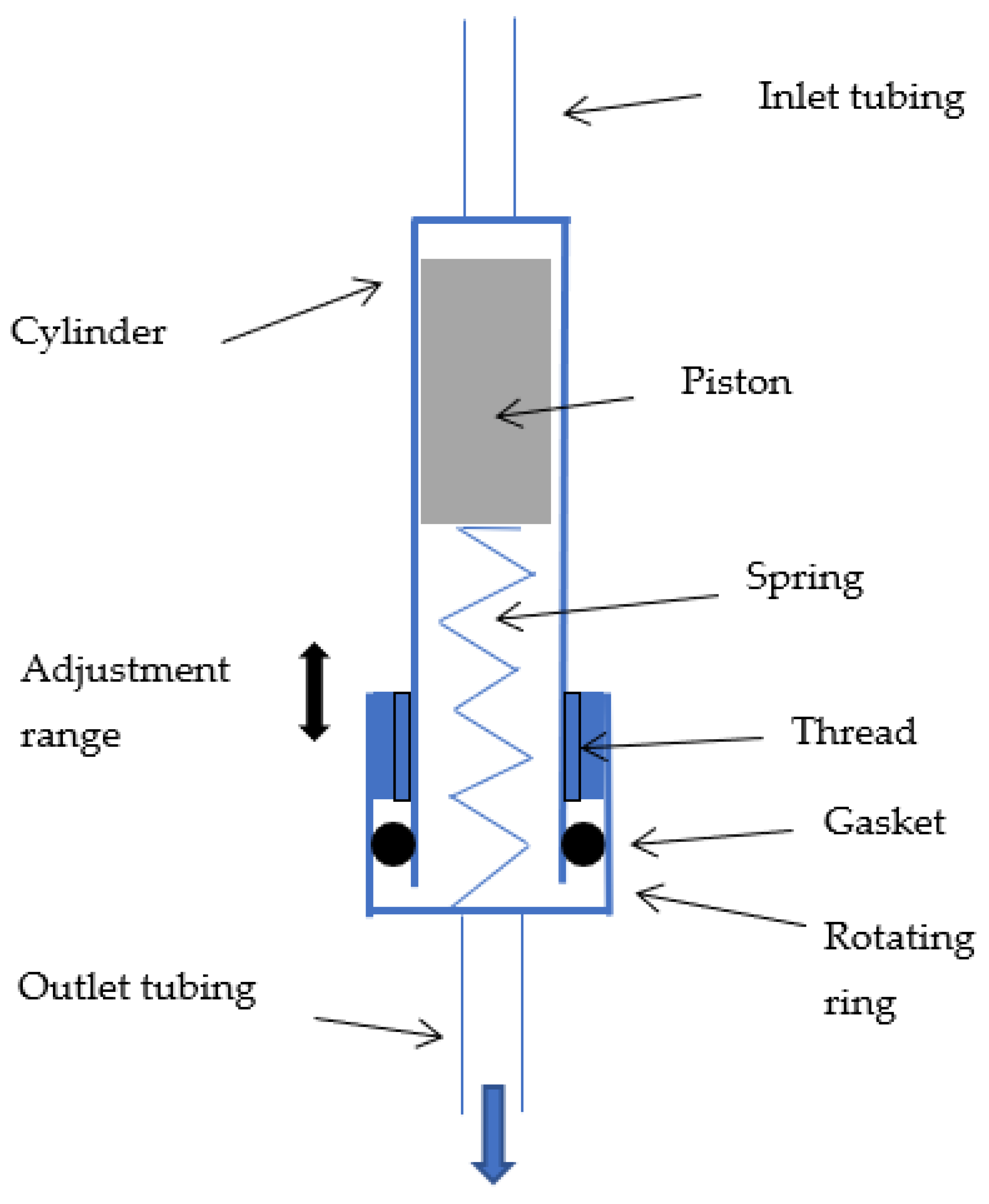
2.3. Prototyping
2.4. Adjusting the Flow Rate
2.5. Adjusting the Pressure-Regulation Range
2.5.1. Regulation Threshold at Low Pressure
2.5.2. Regulation Threshold at High Pressure
2.6. Fluidic Characterization
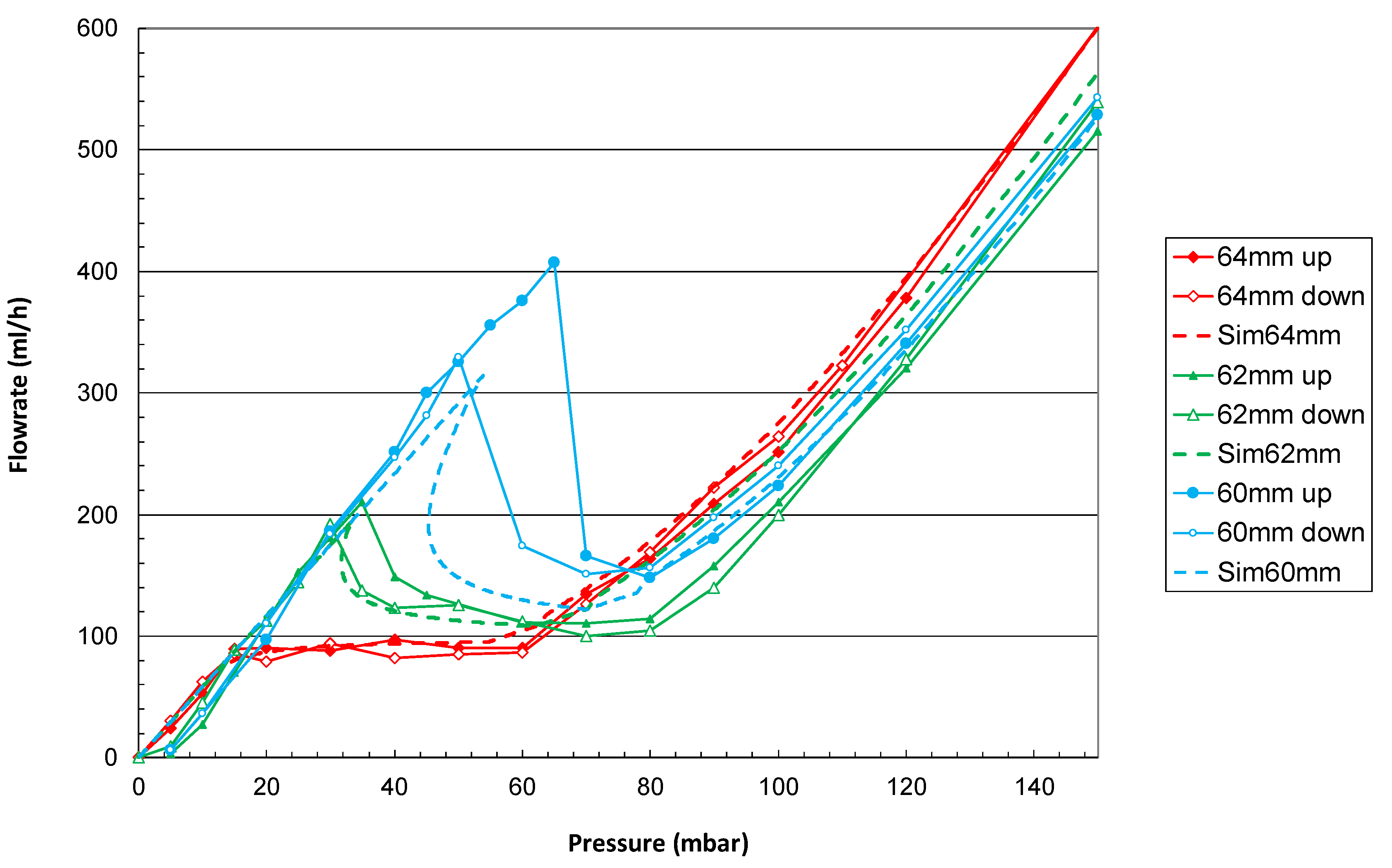
3. Results
Experimental Results
4. Discussion
4.1. Flow Regulation and Variability
4.2. Hysteresis
4.3. Application to CSF Drainage
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Name |
| Cylinder length | |
| Piston length | |
| Inlet groove length | |
| Outlet groove length | |
| Regulation length, with | |
| k | Spring stiffness |
| Hydraulic diameter of the channel | |
| Helix pitch | |
| Length of one loop of the helicoidal channel | |
| Piston radius | |
| Cylinder radius | |
| Channel angle | |
| Dynamic viscosity | |
| Active channel length | |
| P | Applied pressure |
| S | Piston active surface |
| Minimum length of the piston engaged into the narrowest part of the cylinder | |
| Fluidic resistance | |
| Fluidic resistance of the channel | |
| Parasitic fluidic resistance between the cylinder and piston | |
| Fluidic resistance of the fluidic line | |
| Piston displacement | |
| Minimum pressure to move the piston (pretension) | |
| Minimum pressure to reach the piston mechanical stop | |
| Free length of the spring | |
| Minimum spring length | |
| Initial spring compression length | |
| Piston recess | |
| α | Channel length per unit of piston length |
| β | Fluidic resistance of the channel per unit of channel length |
| Device rotation angle | |
| m | Piston effective weight |
| g | Gravitational acceleration |
| Abbreviation | Name |
| CSF | Cerebrospinal fluid |
| EVD | External Ventricular Drain |
| ICP | IntraCranial Pressure |
| MEMS | Microelectromechanical system |
| NPH | Normal-pressure hydrocephalus |
| PDMS | Poly(dimethylsiloxane) |
| PEEK | Polyether ether ketone |
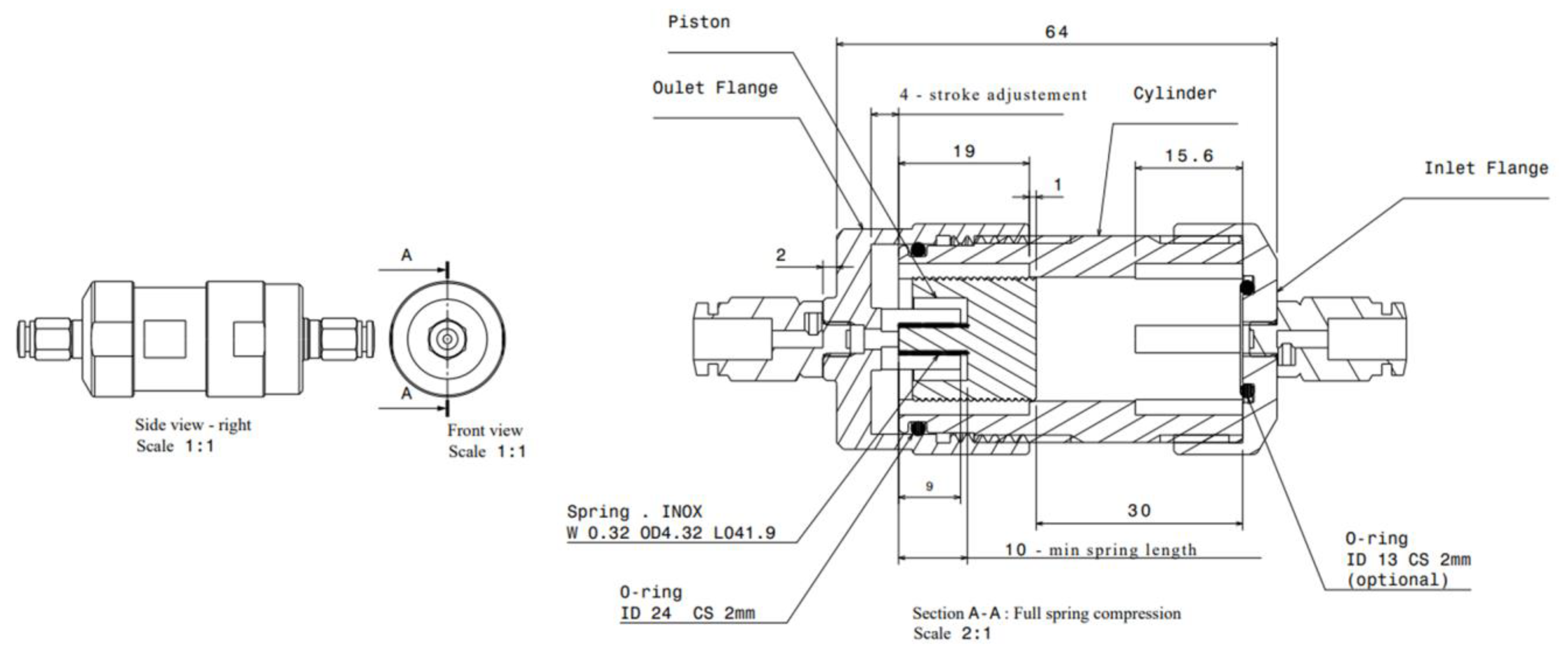
Appendix A. Mechanical Drawings of the Different Parts of the Adjustable Valve
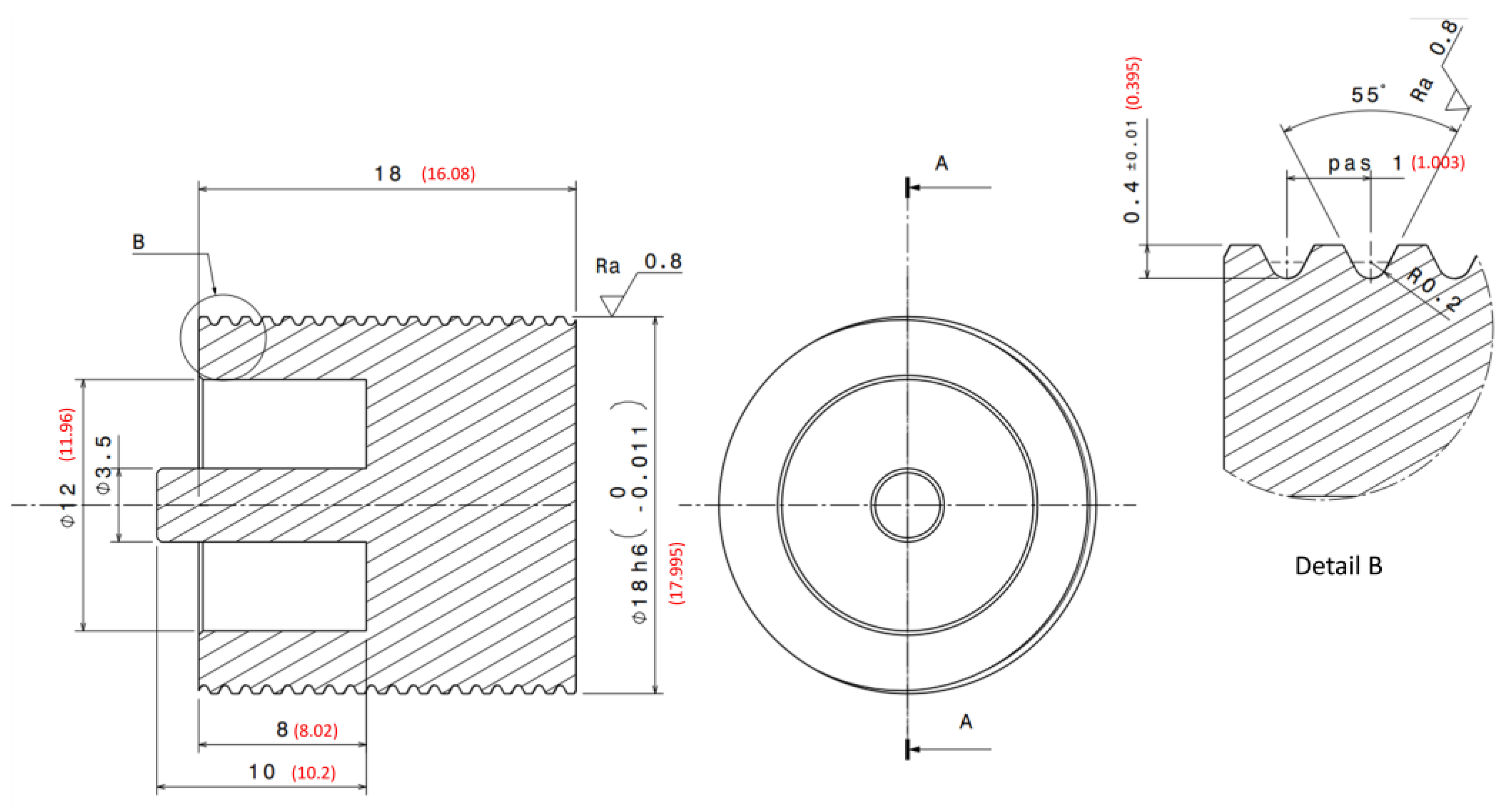
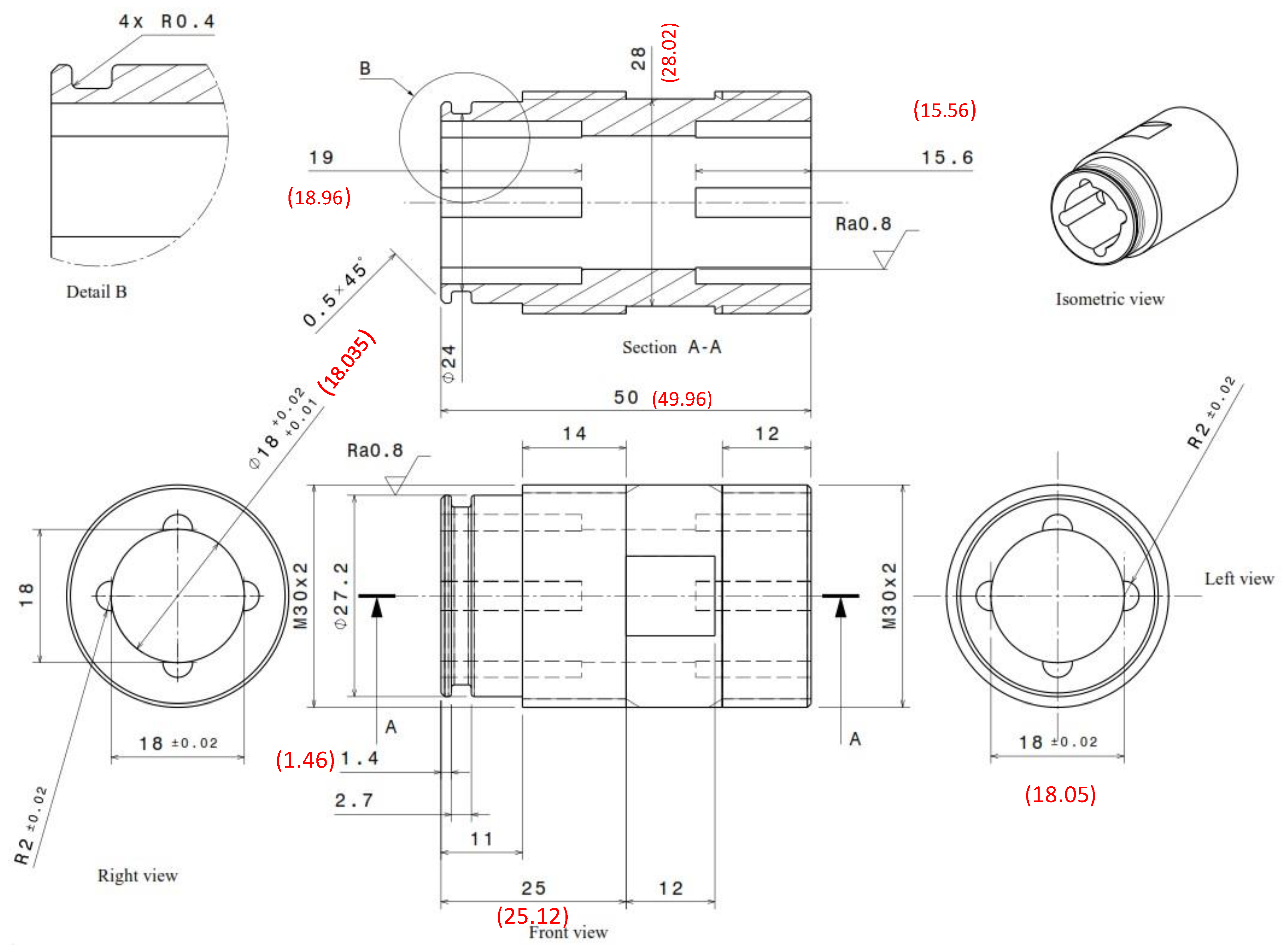
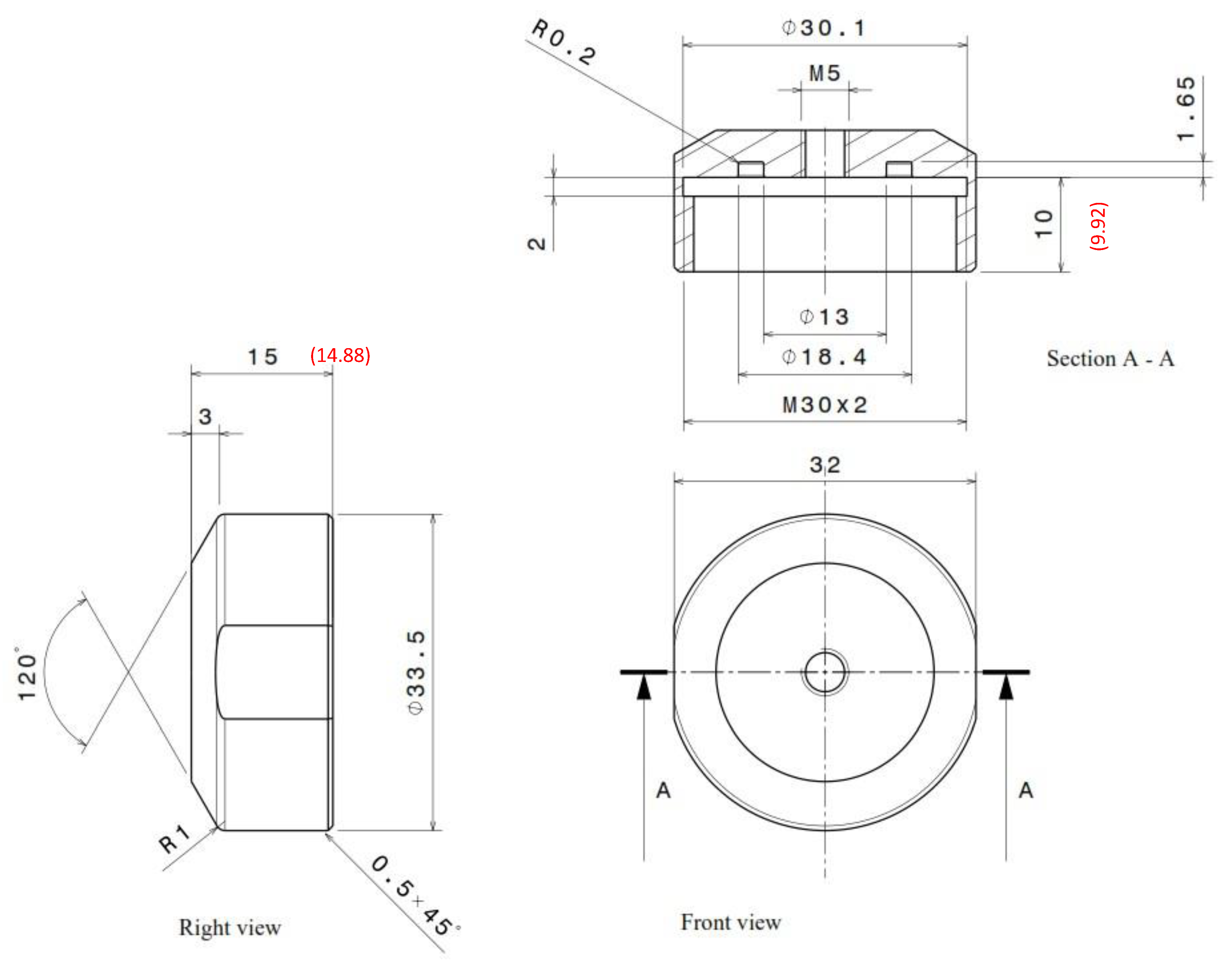
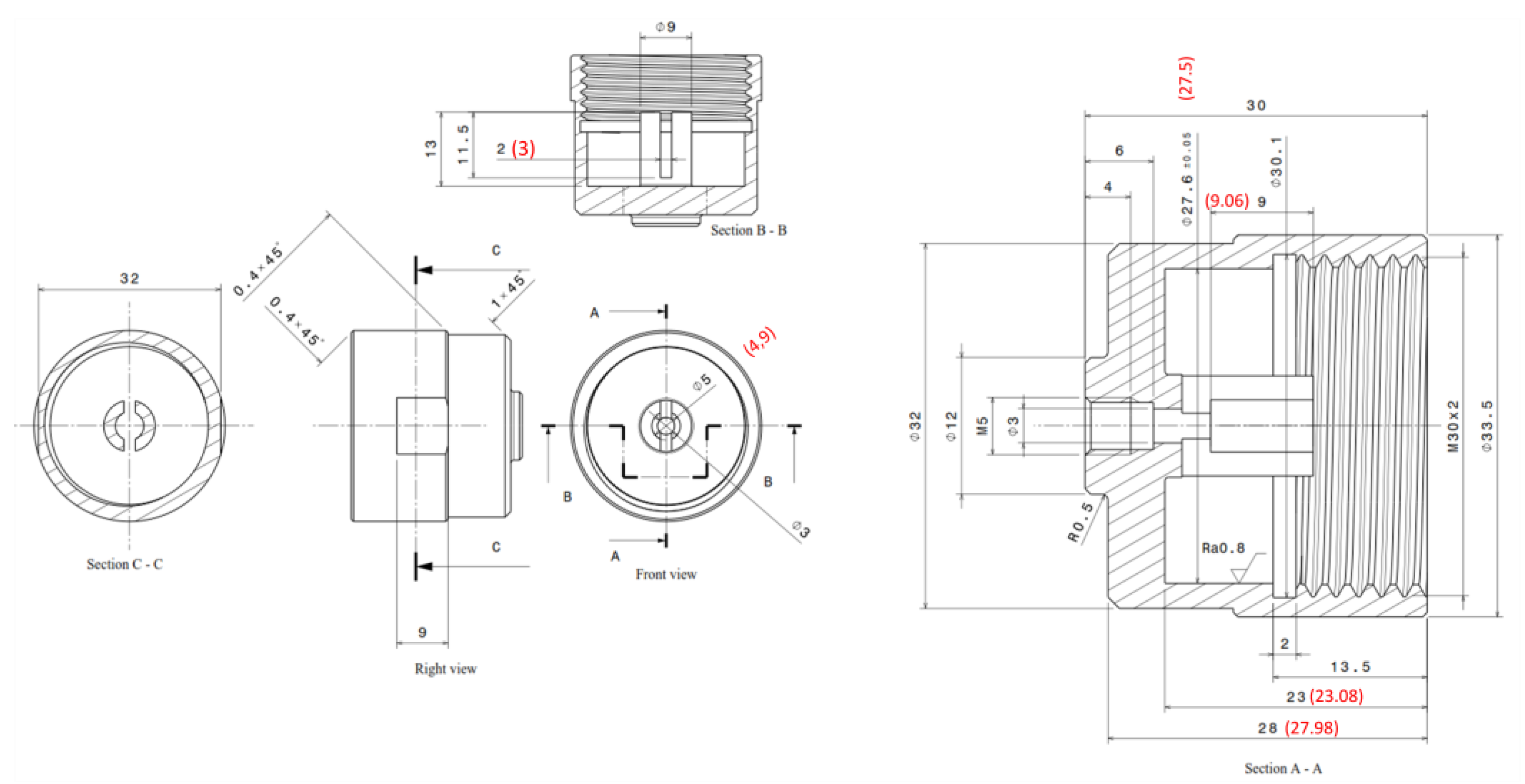
Appendix B. Spring Dimensions and Specifications
| Material | Stainless Steel |
| Wire diameter | 0.32 mm |
| External diameter | 4.32 mm |
| Free length | 41.9 mm |
| Min spring length Lmin | 10 mm |
| Max loaded length | 9.68 mm |
| Solid length | 6.9 mm |
| Spring stiffness k | 0.0776 N/mm |
References
- Chappel, E. A review of Passive Constant Flow Regulators for microfluidic applications. Appl. Sci. 2020, 10, 8858. [Google Scholar] [CrossRef]
- Warring, R.H. Hydraulic Handbook; Gulf Publishing Company: Houston, TX, USA, 1983; pp. 117–119. [Google Scholar]
- Cundiff, J.S. Fluid Power Circuits and Controls: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2001; pp. 140–143. [Google Scholar]
- Park, S.; Ko, W.; Prahl, J. A Constant Flow-Rate Microvalve Actuator Based on Silicon and Micromachining Technology. In Proceedings of the IEEE Technical Digest on Solid-State Sensor and Actuator Workshop, Hilton Head Island, SC, USA, 6–9 June 1988; pp. 136–139. [Google Scholar]
- Amacker, C.; Leung Ki, Y.-S.; Pasquier, V.; Madore, C.; Haller, M.; Renaud, P.; White, N. Passive Micro-Flow Regulator for Drug Delivery System. In Proceedings of the Eurosensors XII conference, Southampton, UK, 13–16 September 1998; pp. 591–594. [Google Scholar]
- Cousseau, P.; Hirschi, R.; Frehner, B.; Gamper, S.; Maillefer, D. Improved micro-flow regulator for drug delivery systems. In Proceedings of the 14th IEEE International Conference on Micro Electro Mechanical Systems MEMS 2001, Interlaken, Switzerland, 21–25 January 2001; pp. 527–530. [Google Scholar]
- Chappel, E.; Dumont-Fillon, D.; Mefti, S. 2014, March. Passive flow regulators for drug delivery and hydrocephalus treatment. In Proceedings of the Microfluidics, BioMEMS, and Medical Microsystems XII Conference, San Francisco, CA, USA, 1–6 February 2014; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 8976, p. 89760S. [Google Scholar]
- Dumont-Fillon, D.; Hannebelle, M.; Van Lintel, H.; Chappel, E. Design of a passive flow regulator using a genetic algorithm. Procedia Eng. 2016, 168, 1016–1019. [Google Scholar] [CrossRef]
- Cornaggia, L.; Conti, L.; Hannebelle, M.; Gamper, S.; Dumont-Fillon, D.; Van Lintel, H.; Renaud, P.; Chappel, E. Passive flow control valve for protein delivery. Cogent Eng. 2017, 4, 1413923. [Google Scholar] [CrossRef]
- Conti, L.; Dumont-Fillon, D.; van Lintel, H.; Chappel, E. Silicon-to-silicon anodic bonding via intermediate borosilicate layer for passive flow control valves. Int. J. Mech. Ind. Aerosp. Sci. 2018, 12, 701–704. [Google Scholar]
- Chappel, E.; Musard, H.; Dumont-fillon, D. Experimental Characterization and Modelling of Microfluidic Radial Diffusers for Passive Self-Regulating Valves. Glob. J. Eng. Technol. Adv. 2019, 1, 10–21. [Google Scholar] [CrossRef]
- Dumont-Fillon, D.; Lamaison, D.; Chappel, E. Design and Characterization of 3-Stack MEMS-Based Passive Flow Regulators for Implantable and Ambulatory Infusion Pumps. J. Microelectromech. Syst. 2020, 29, 170–181. [Google Scholar] [CrossRef]
- Tachatos, N.; Chappel, E.; Dumont-Fillon, D.; Meboldt, M.; Daners, M.S. Posture related in-vitro characterization of a flow regulated MEMS CSF valve. Biomed. Microdevices 2020, 22, 21. [Google Scholar] [CrossRef]
- Kartalov, E.P.; Walker, C.; Taylor, C.R.; Anderson, W.F.; Scherer, A. Microfluidic Vias Enable Nested Bioarrays and Autoregulatory Devices in Newtonian Fluids. Proc. Natl. Acad. Sci. USA 2006, 103, 12280–12284. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, Y.; Taylor, C.R.; Scherer, A.; Kartalov, E.P. Elastomeric Microfluidic Diode and Rectifier Work with Newtonian Fluids. J. Appl. Phys. 2009, 106, 114311. [Google Scholar] [CrossRef]
- Chang, H.-J.; Ye, W.; Kartalov, E.P. Quantitative Modeling of the Behaviour of Microfluidic Autoregulatory Devices. Lab Chip 2012, 12, 1890–1896. [Google Scholar] [CrossRef]
- Doh, I.; Cho, Y.H. Passive flow-rate regulators using pressure-dependent autonomous deflection of parallel membrane valves. Lab Chip 2009, 9, 2070–2075. [Google Scholar] [CrossRef]
- Zhang, X.; Xiang, N.; Tang, W.; Huang, D.; Wang, X.; Yi, H.; Ni, Z. A passive flow regulator with low threshold pressure for high-throughput inertial isolation of microbeads. Lab Chip 2015, 15, 3473–3480. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, X.; Chen, K.; Cheng, J.; Xiang, N.; Ni, Z. Passive Flow Regulator for Precise High-Throughput Flow Rate Control in Microfluidic Environments. RSC Adv. 2016, 6, 31639–31646. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Z.; Ni, Z.; Xiang, N.; Yi, H. Inexpensive, Rapid Fabrication of Polymer-Film Microfluidic Autoregulatory Valve for Disposable Microfluidics. Biomed. Microdevices 2017, 19, 21. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z. Microfluidic Passive Flow Regulatory Device with an Integrated Check Valve for Enhanced Flow Control. Micromachines 2019, 10, 653. [Google Scholar] [CrossRef]
- Chari, A.; Czosnyka, M.; Richards, H.K.; Pickard, J.D.; Czosnyka, Z.H. Hydrocephalus shunt technology: 20 years of experience from the Cambridge Shunt Evaluation Laboratory. J. Neurosurg. 2014, 120, 697–707. [Google Scholar] [CrossRef]
- Codman Specialty Surgical. Flow Regulating Valves; 1100665-1-EN; Integra LifeSciences Corporation: Princeton, NJ, USA, 2018. [Google Scholar]
- Paes, N.A. New Self-Adjusting Flow-Regulating Device for Shunting of CSF. Childs Nerv. Syst. 1996, 12, 619–625. [Google Scholar] [CrossRef]
- Yang, B.; Levis, J.W.; Lin, Q. A PDMS-Based Constant-Flowrate Microfluidic Control Device. In Proceedings of the 17th IEEE International Conference on Micro Electro Mechanical Systems. Maastricht MEMS 2004 Technical Digest, Maastricht, The Netherlands, 25–29 January 2004; pp. 379–382. [Google Scholar]
- Yang, B.; Lin, Q. Planar Micro-Check Valves Exploiting Large Polymer Compliance. Sens. Actuator A Phys. 2007, 134, 186–193. [Google Scholar] [CrossRef]
- Yang, B.; Lin, Q. A Planar Compliance-Based Self-Adaptive Microfluidvariable Resistor. J. Microelectromech. Syst. 2007, 16, 411–419. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, X.; Weng, S.; Zhang, R.; Fang, D.; Zhao, R.; Qi, H.J. Self-Adaptive Flexible Valve as Passive Flow Regulator. Extreme Mech. Lett. 2020, 39, 100824. [Google Scholar] [CrossRef]
- Chappel, E. Design and characterization of a passive flow control valve dedicated to the hydrocephalus treatment. Cogent Eng. 2016, 3, 1247612. [Google Scholar] [CrossRef]
- Su, Q.; Chen, W.; Chen, W.; Jin, Z.; Lin, Z. Flow Regulation Performance Analysis of Microfluidic Passive Valve for High Throughput Liquid Delivery. Micromachines 2022, 13, 687. [Google Scholar] [CrossRef] [PubMed]
- Sainte-Rose, C.; Hooven, M.D.; Hirsch, J.-F. A New Approach in the Treatment of Hydrocephalus. J. Neurosurg. 1987, 66, 213–226. [Google Scholar] [CrossRef] [PubMed]
- Chappel, E.; Hannebelle, M.; Cornaggia, L.; Dumont-Fillon, D.; Momjian, S. Hybrid hydrodynamic characteristic for hydrocephalus valve: A numerical investigation using electrical equivalent networks. Cogent Eng. 2017, 4, 1415103. [Google Scholar] [CrossRef]
- Chappel, E. Method of Adjustment for Hydrocephalus Valve. U.S. Patent N° 2017203083(A1), 20 July 2017. [Google Scholar]
- Czosnyka, M.; Czosnyka, Z.; Whitehouse, H.; Pickard, J.D. Hydrodynamic properties of hydrocephalus shunts: United Kingdom shunt evaluation laboratory. J. Neurol. Neurosurg. Psychiatry 1997, 62, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Chung, D.Y.; Olson, D.M.; John, S.; Mohamed, W.; Kumar, M.A.; Thompson, B.B.; Rordorf, G.A. Evidence-Based Management of External Ventricular Drains. Curr. Neurol. Neurosci. Rep. 2019, 19, 94. [Google Scholar] [CrossRef] [PubMed]
- Chappel, E. Adjustable Passive Flow Regulator. European Patent N° EP2943708B1, 6 September 2017. [Google Scholar]
- Chappel, E. (Ed.) Drug Delivery Devices and Therapeutic Systems; Academic Press: New York, NY, USA, 2020. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]




| Position 0 (64 mm) | Position 1 (62 mm) | Position 2 (60 mm) | ||||
|---|---|---|---|---|---|---|
| Experiment | Simulation | Experiment | Simulation | Experiment | Simulation | |
| Regulation range (mbar) | [+15; +60] | [+15; +60] | [+30; +80] | [+40; +80] | [+60; +80] | [+52; +78] |
| Mean flow rate mL/h | 91 | 92 | 120 | 114 | 160 | 130 |
| St. dev. (%) | 4 | 4 | 14 | 4 | 12 | 5.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chappel, E. Design and Characterization of an Adjustable Passive Flow Regulator and Application to External CSF Drainage. Micromachines 2023, 14, 675. https://doi.org/10.3390/mi14030675
Chappel E. Design and Characterization of an Adjustable Passive Flow Regulator and Application to External CSF Drainage. Micromachines. 2023; 14(3):675. https://doi.org/10.3390/mi14030675
Chicago/Turabian StyleChappel, Eric. 2023. "Design and Characterization of an Adjustable Passive Flow Regulator and Application to External CSF Drainage" Micromachines 14, no. 3: 675. https://doi.org/10.3390/mi14030675
APA StyleChappel, E. (2023). Design and Characterization of an Adjustable Passive Flow Regulator and Application to External CSF Drainage. Micromachines, 14(3), 675. https://doi.org/10.3390/mi14030675






