Compensation Method for the Nonlinear Characteristics with Starting Error of a Piezoelectric Actuator in Open-Loop Controls Based on the DSPI Model
Abstract
1. Introduction
2. Background
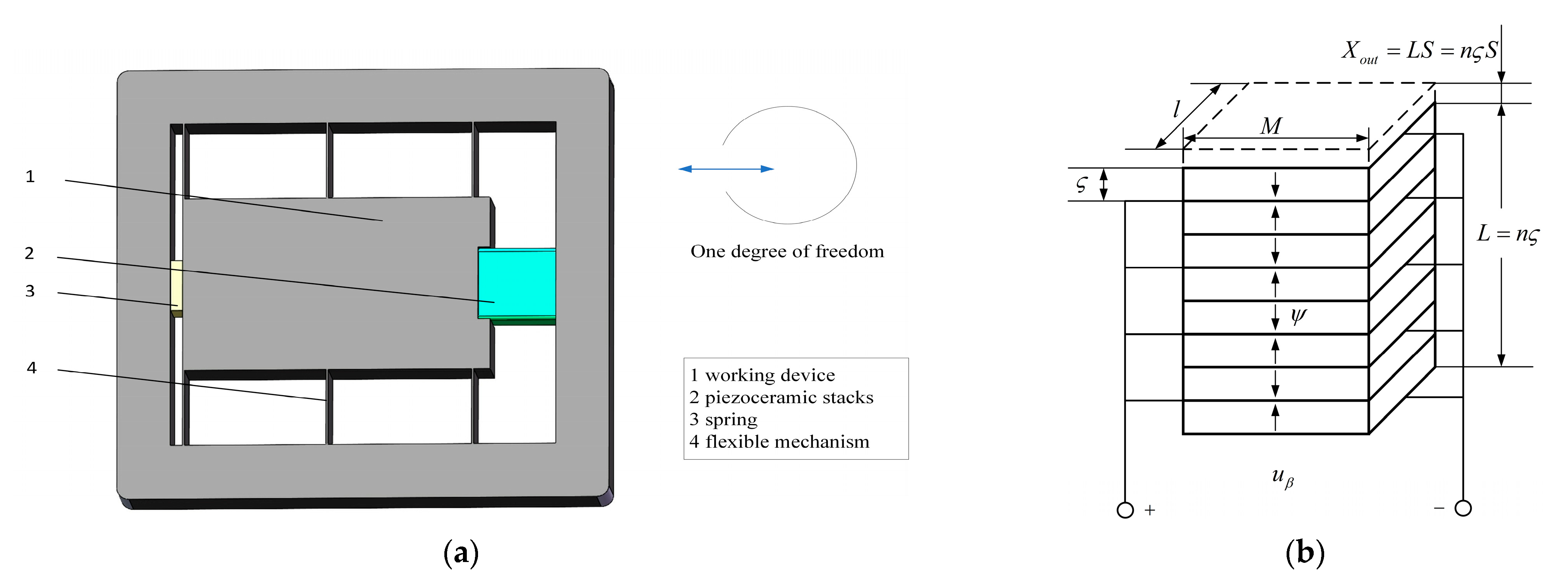
2.1. Mechanical Design
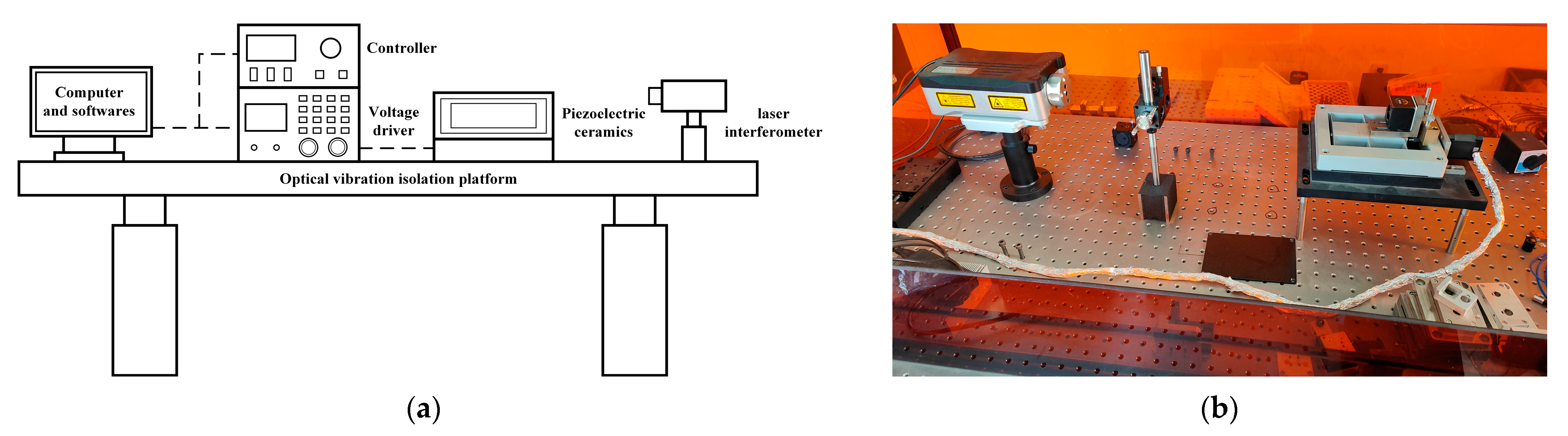
2.2. Experimental Equipment
3. Causes of Starting Error
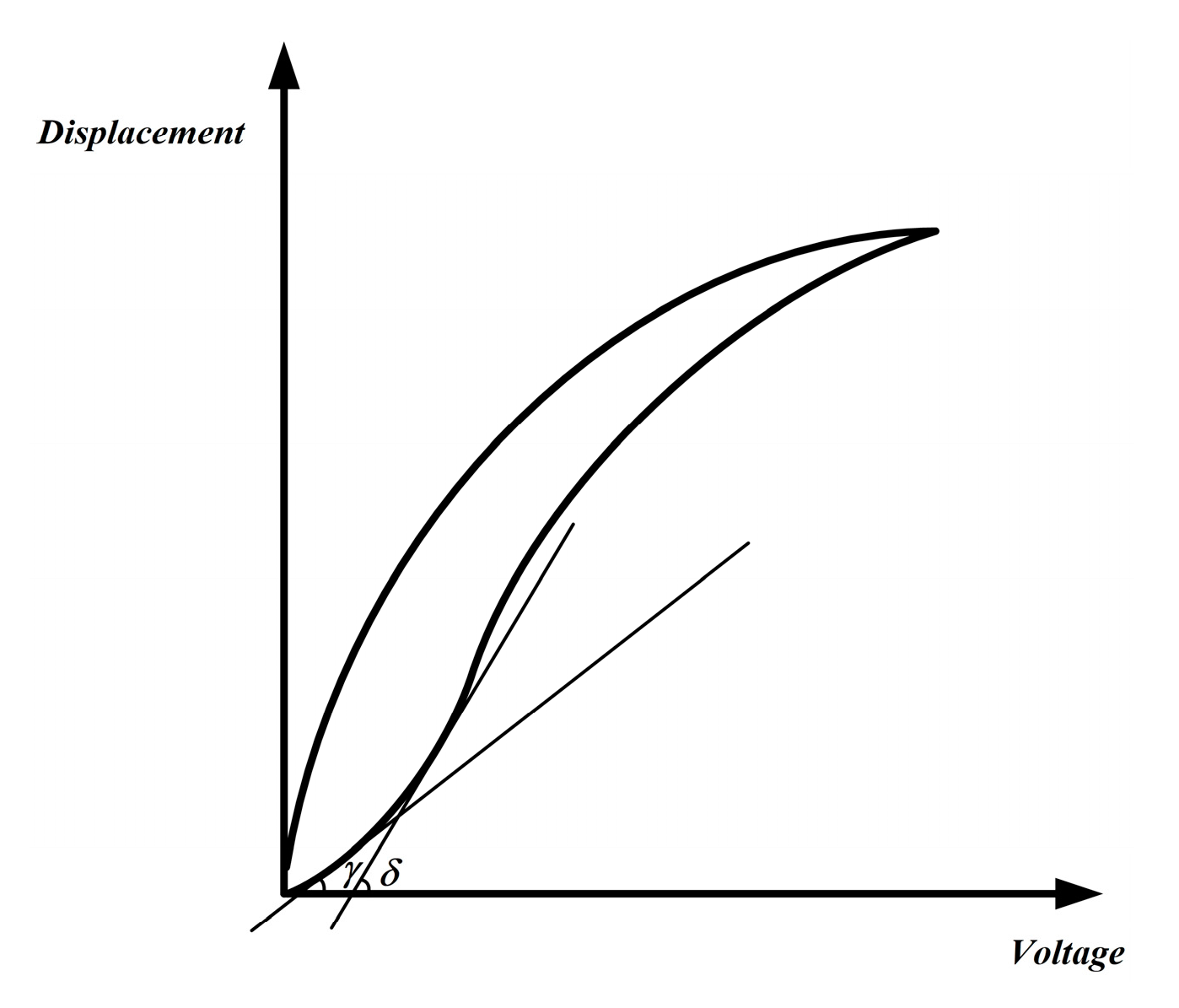
3.1. Start-Up Error Characteristic 1
3.2. Start-Up Error Characteristic 2
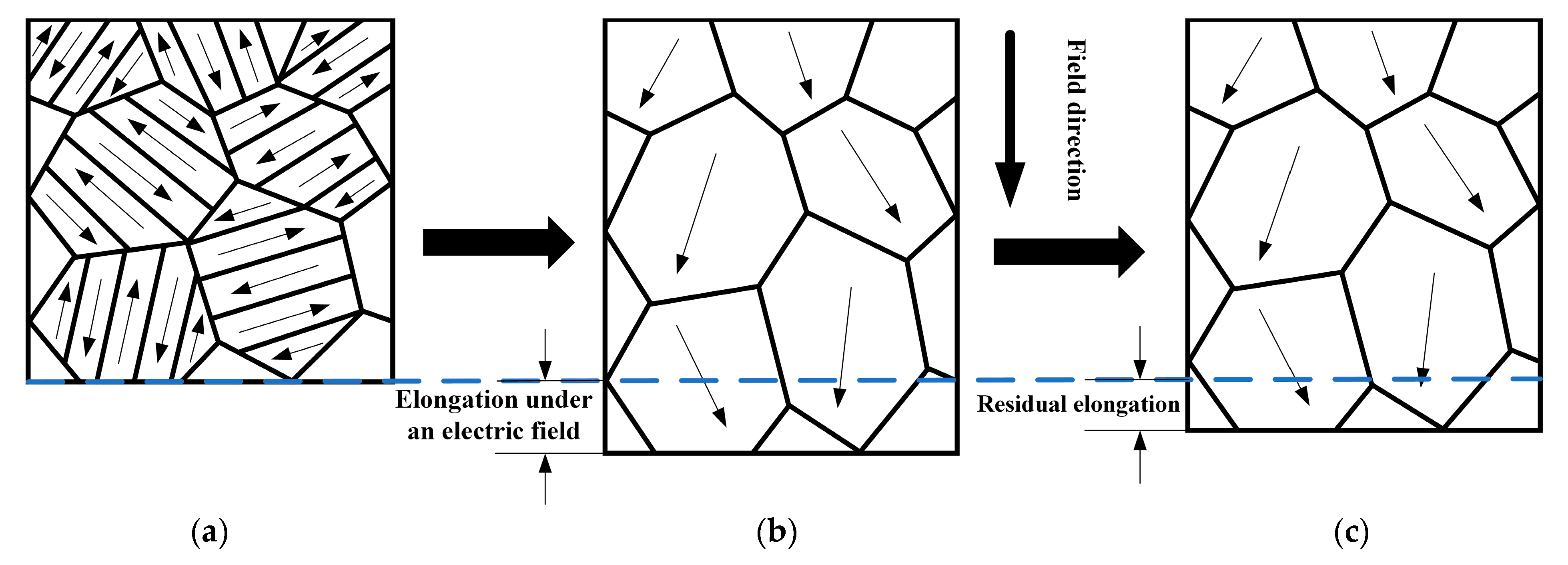
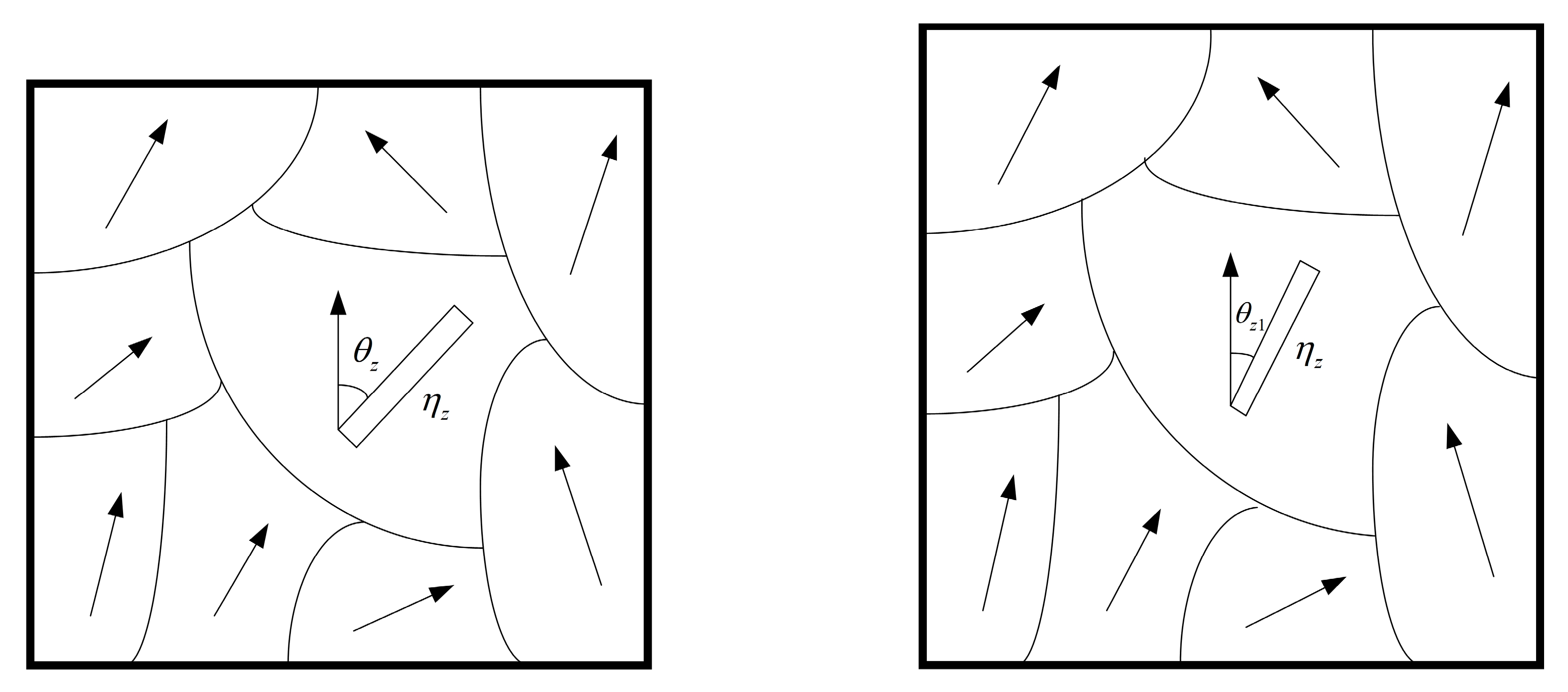
3.2.1. Causes of Voltage-Affected Starting Error
4. Modeling
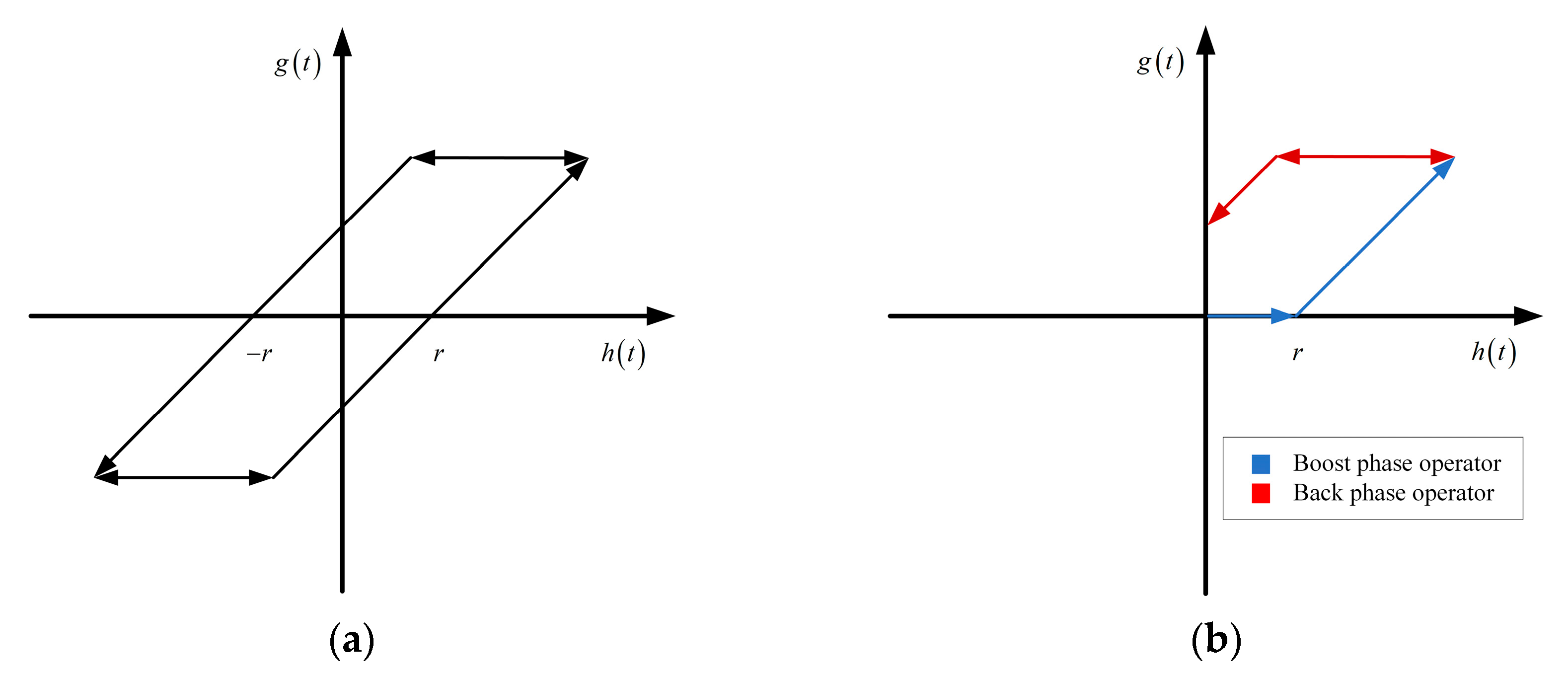
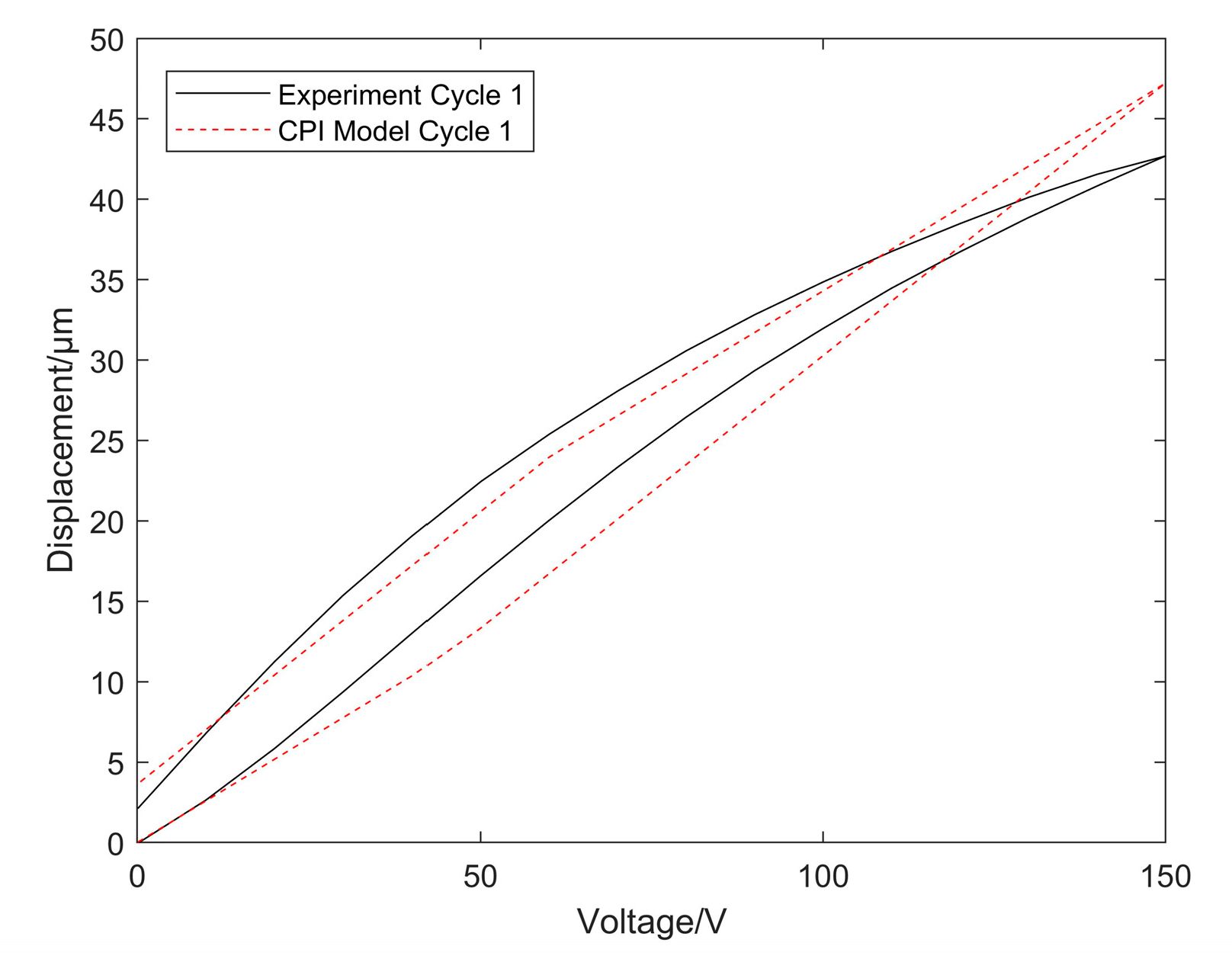
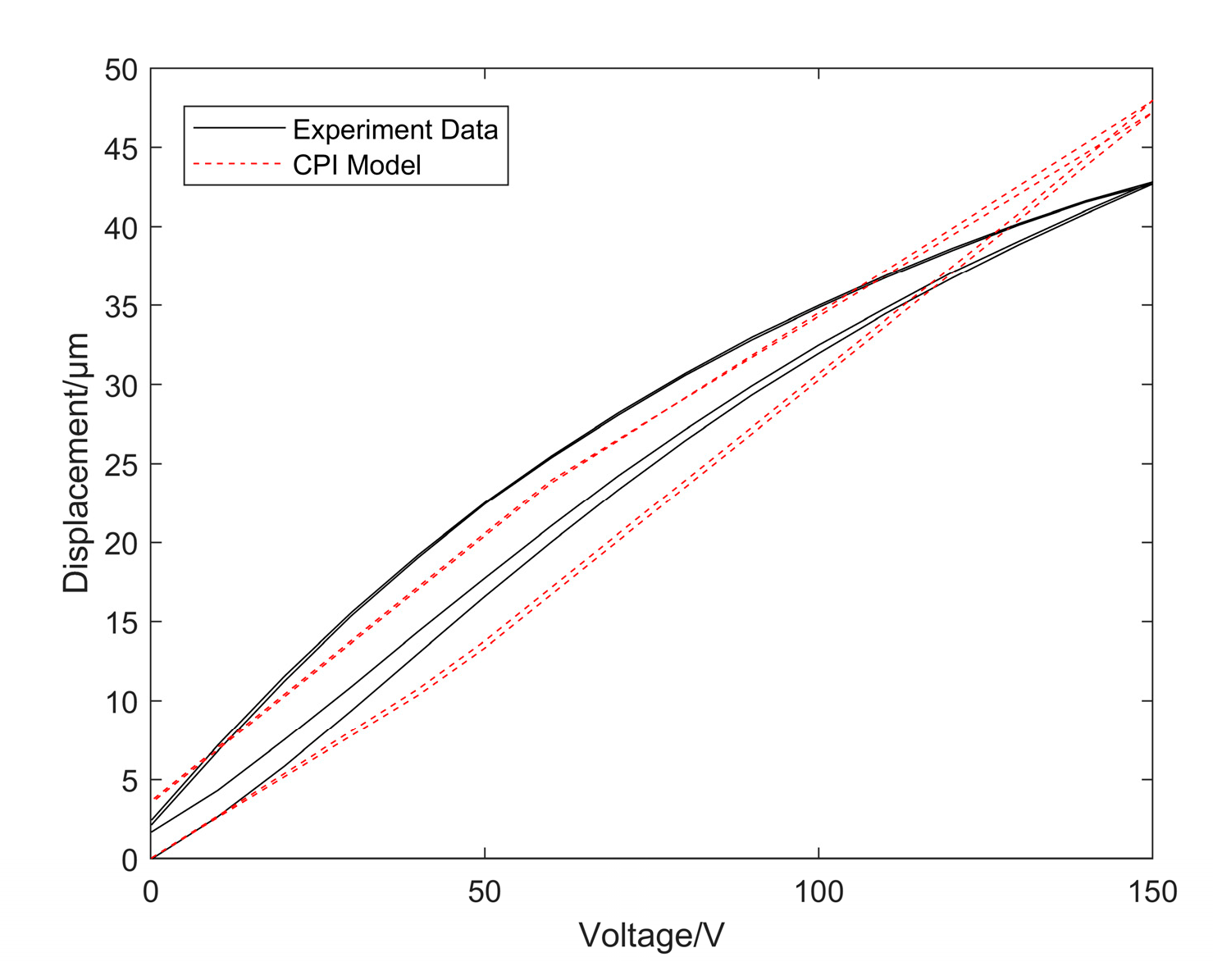
4.1. CPI Model
4.2. Start-Up Error Characteristic 3
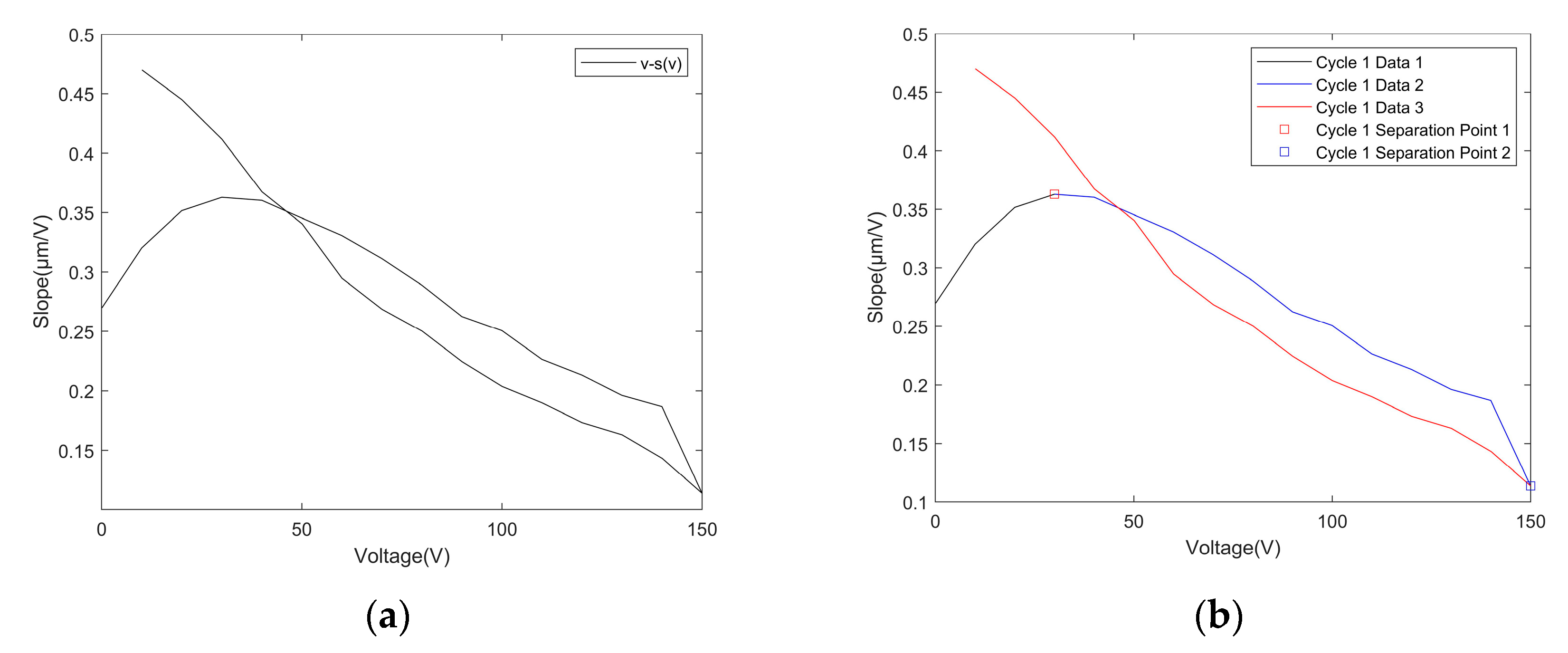
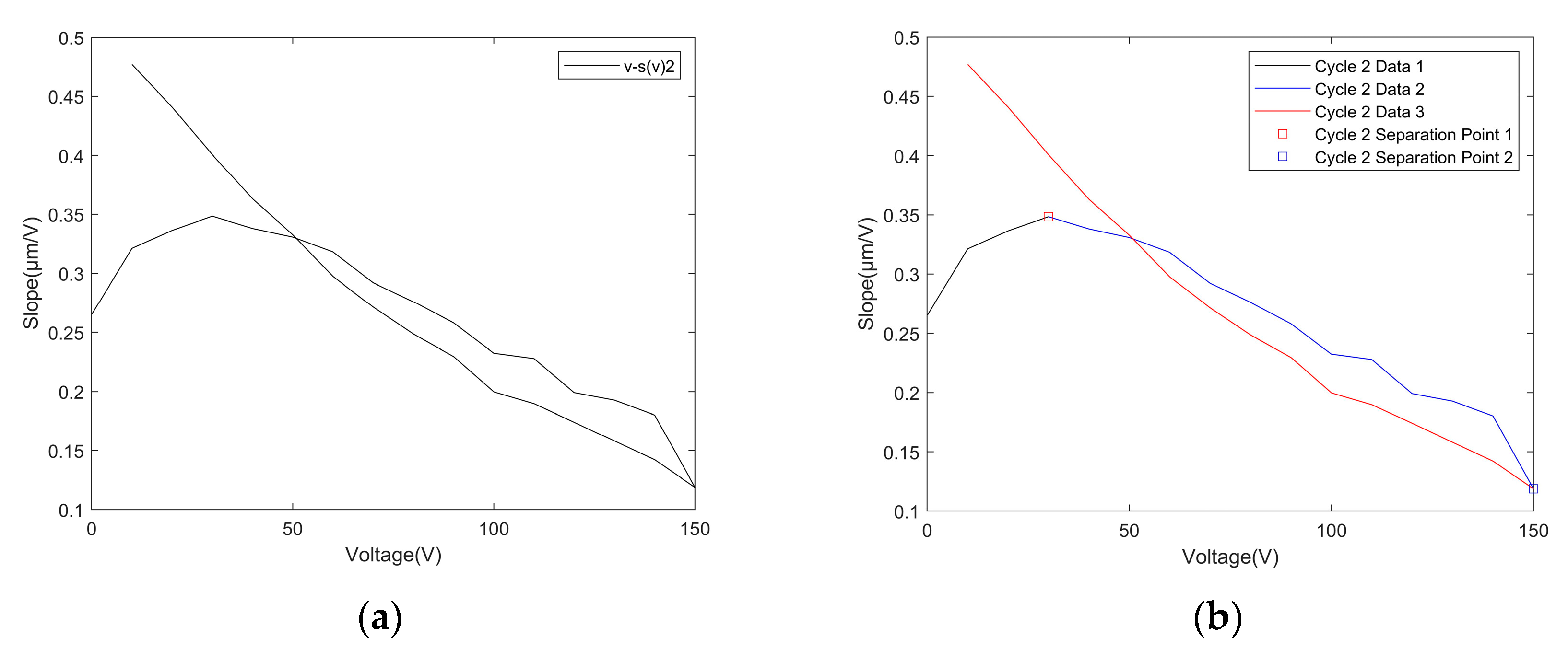
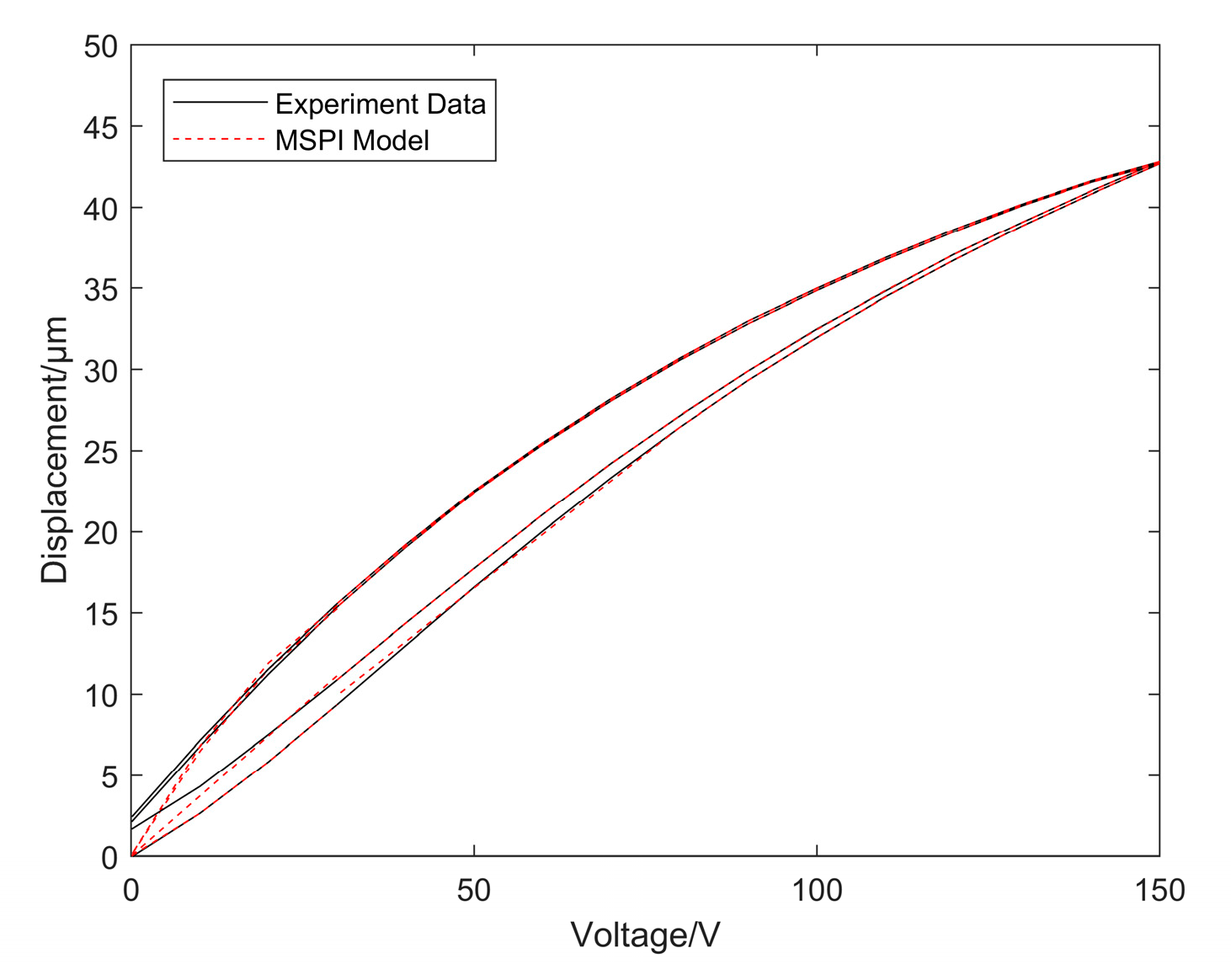
4.3. Data-Separated Prandtl-Ishlinskii Model
4.4. Compensated Control and DSPI Inverse Model
5. Experiments and Discussion
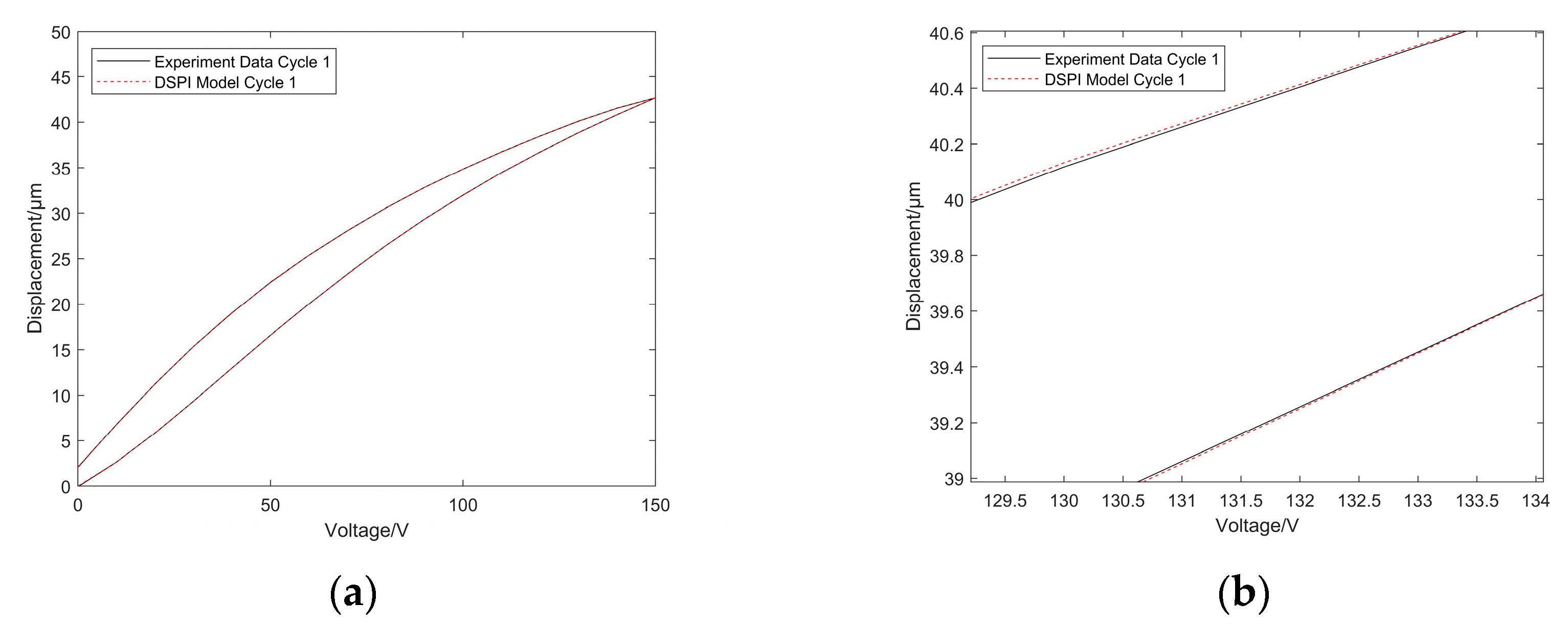
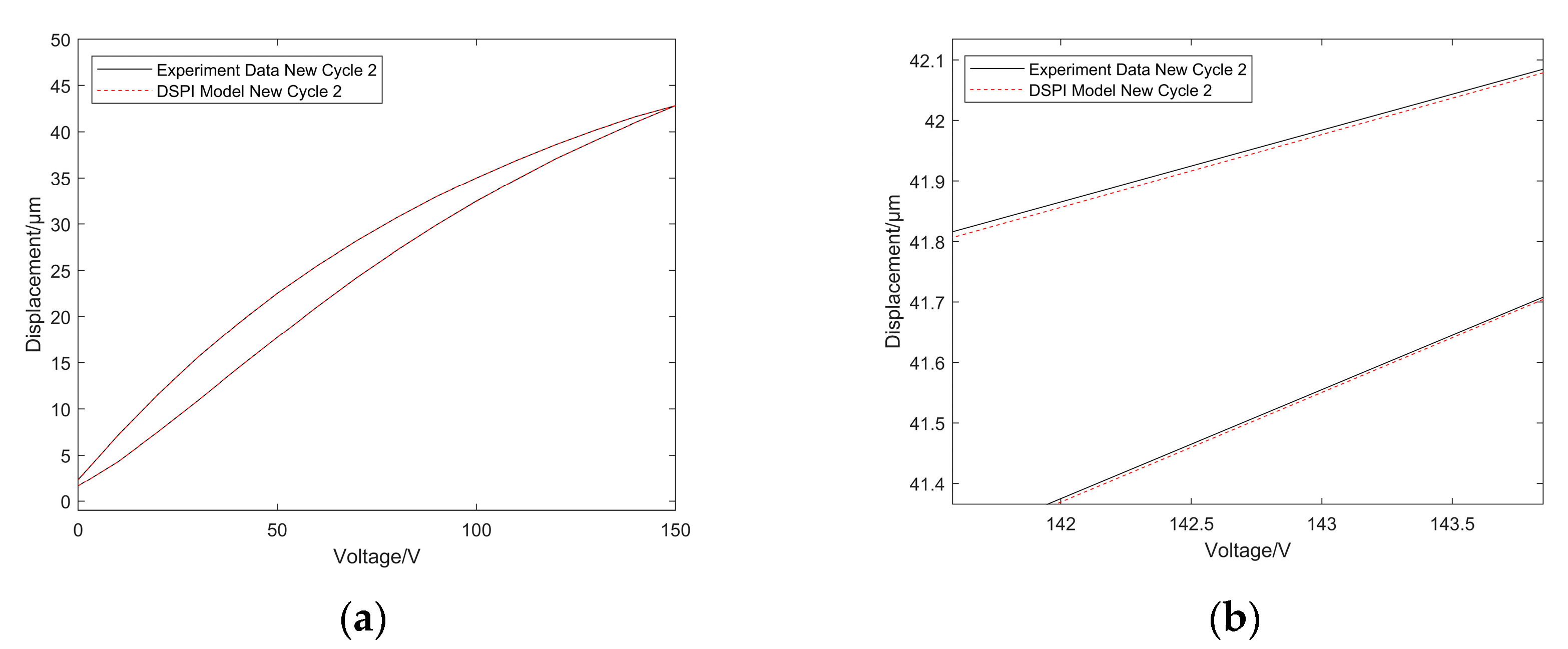
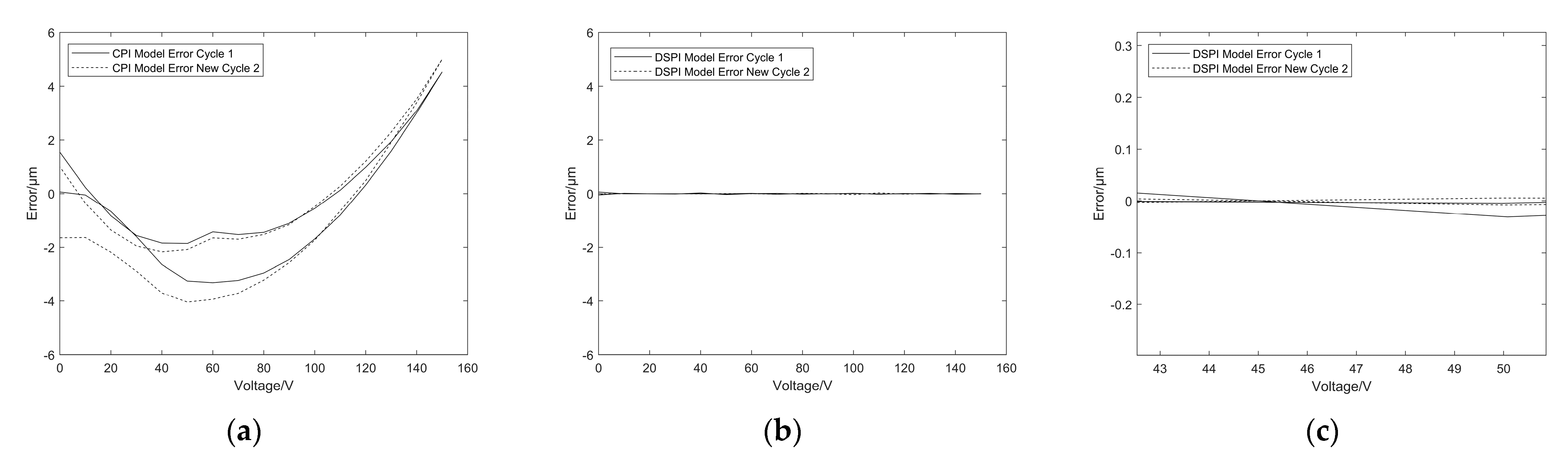
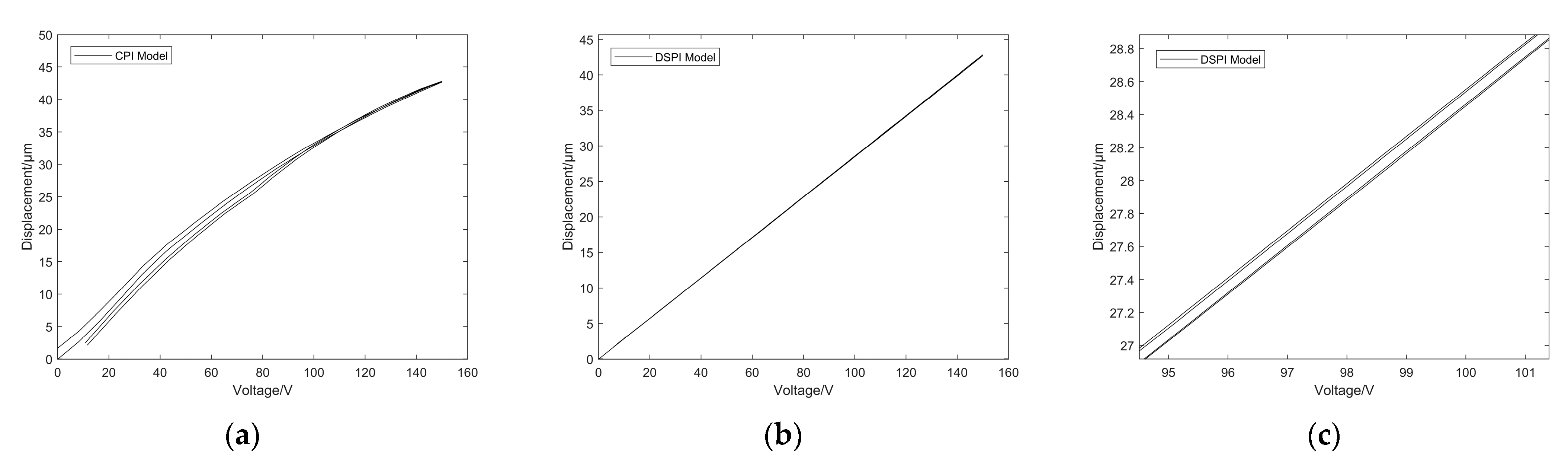
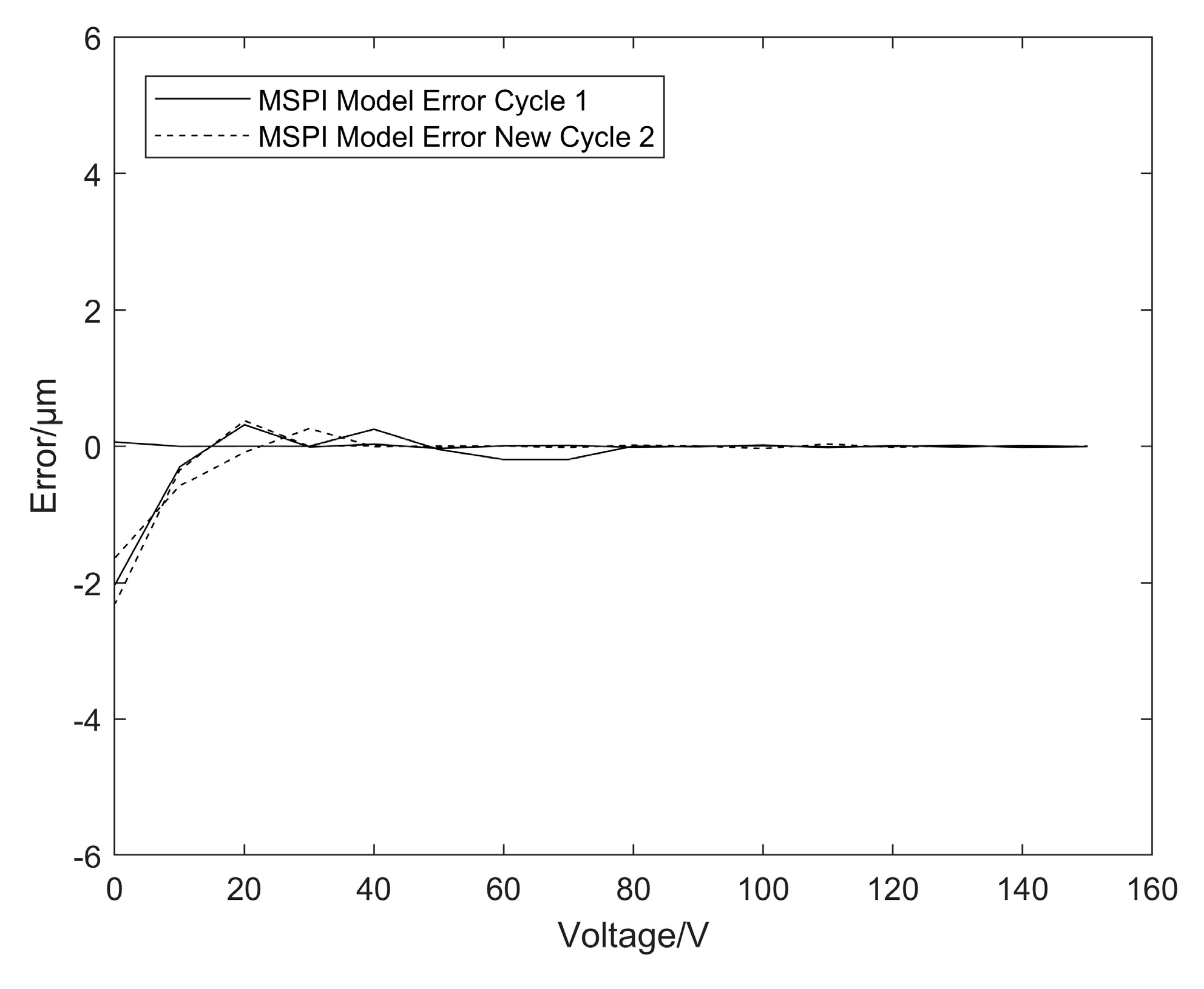
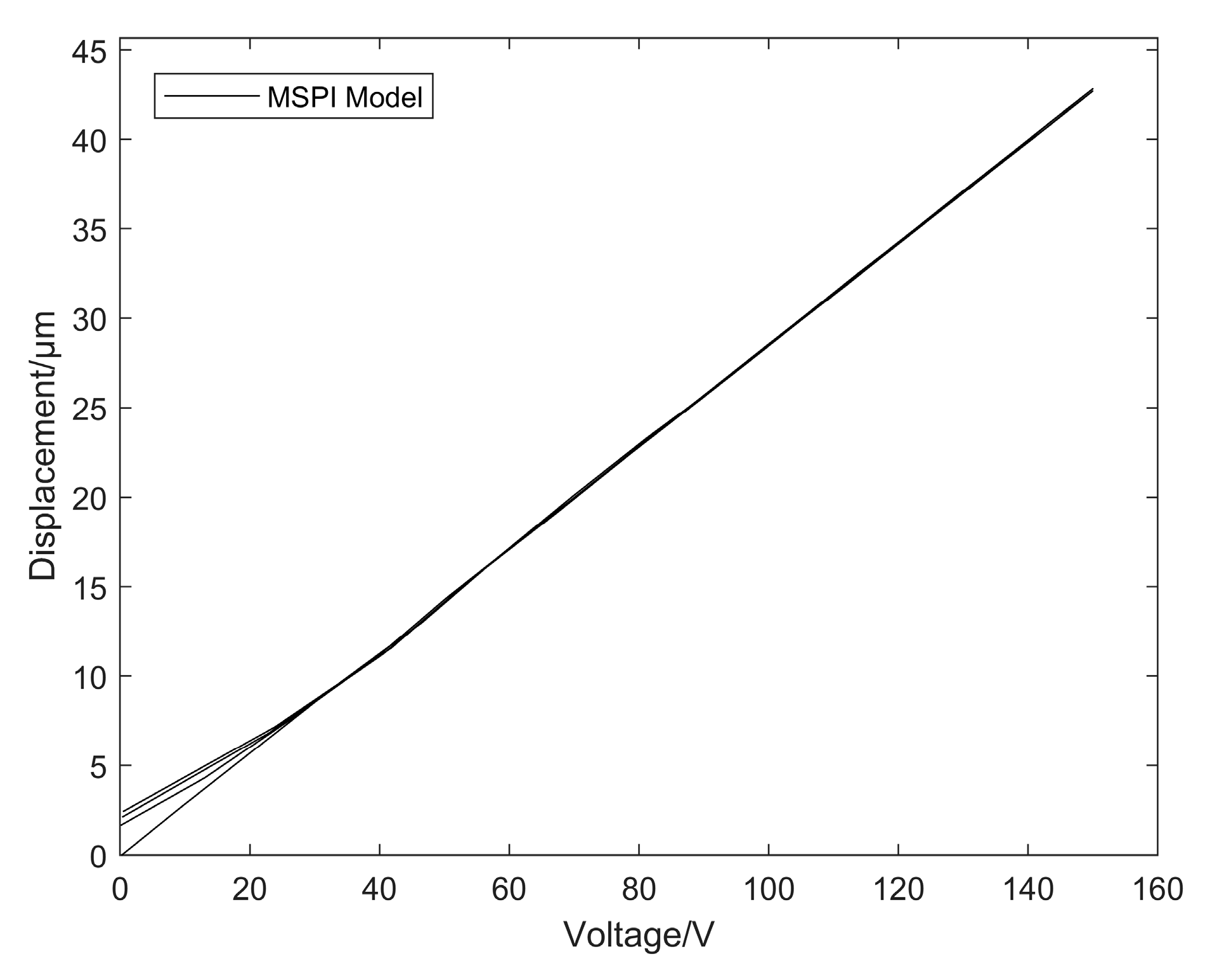
5.1. Results of the DSPI Model
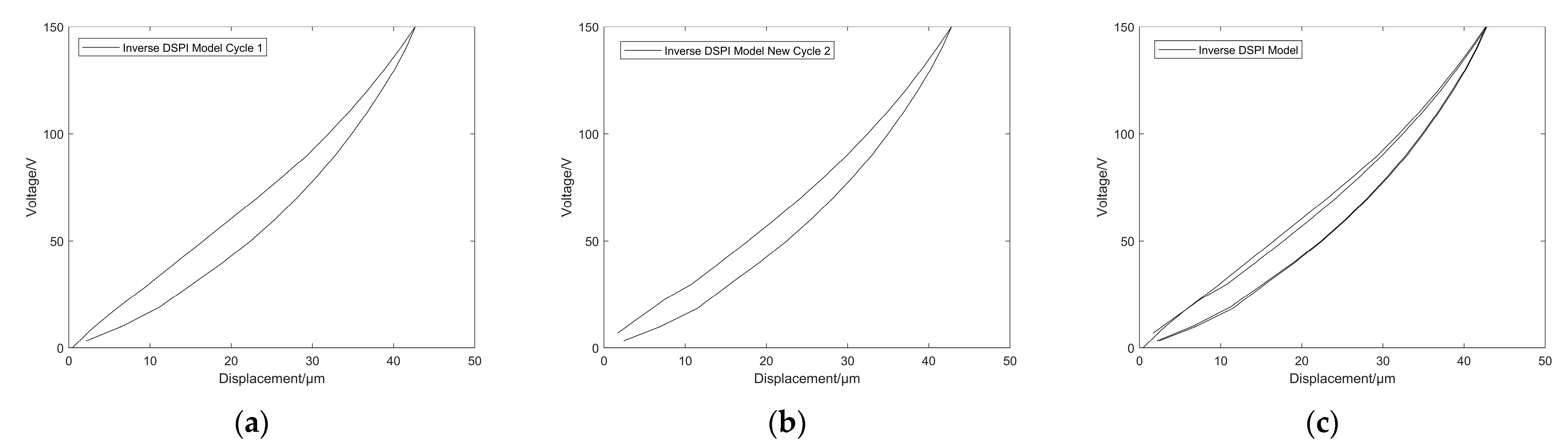
5.2. Results of the DSPI Inverse Model
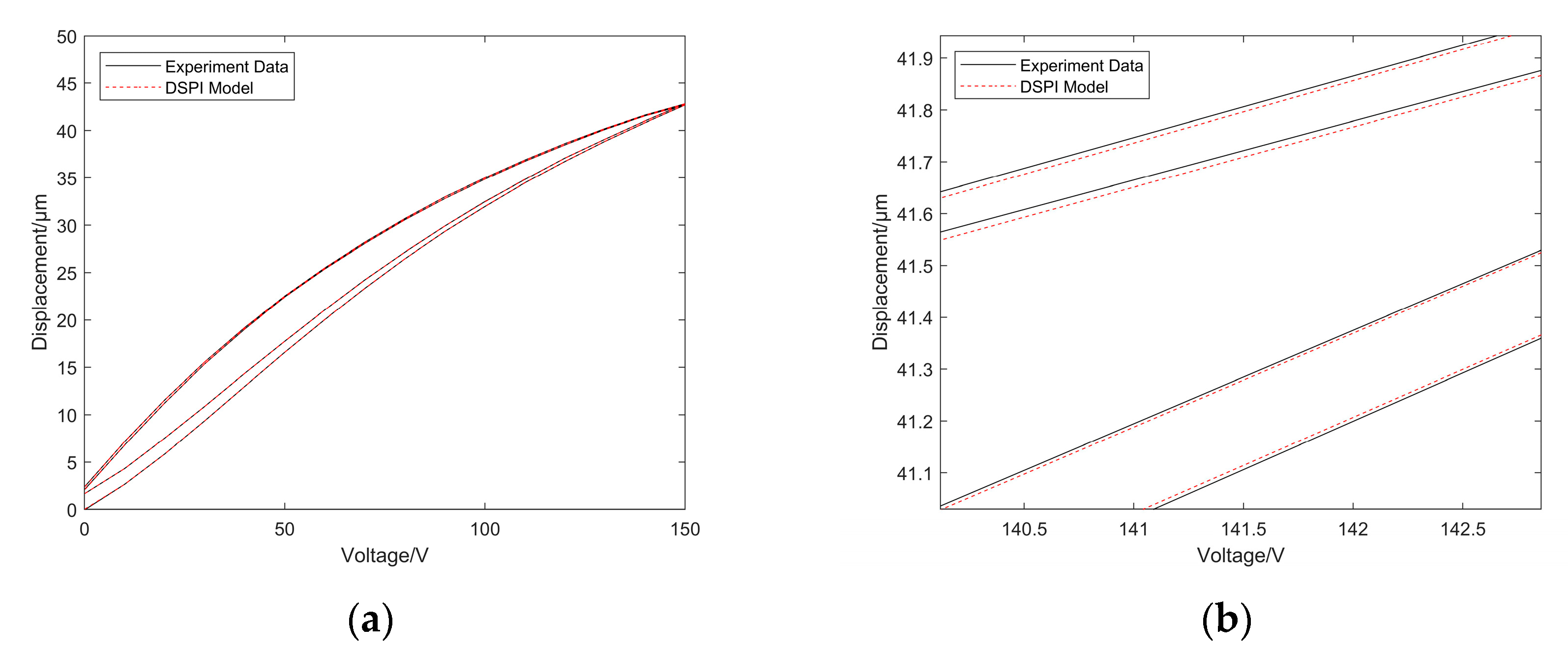
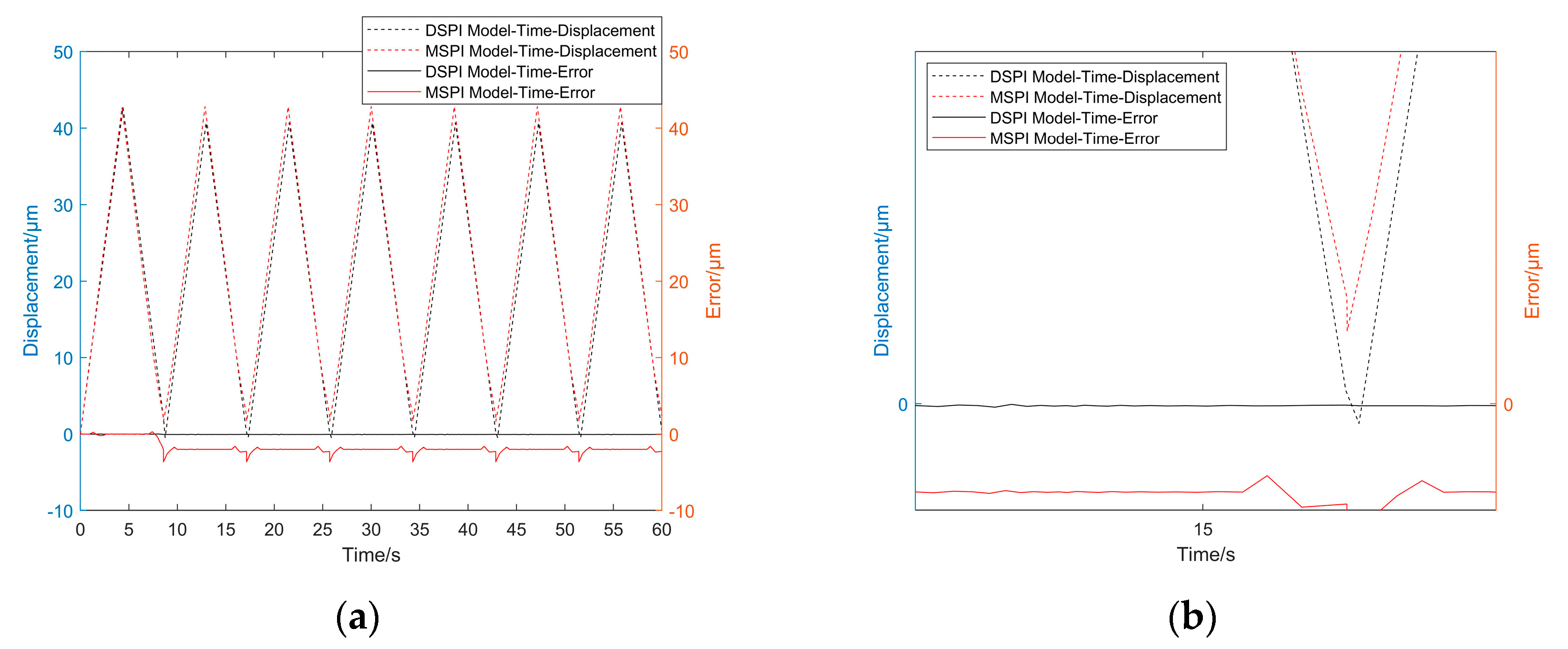
5.3. Model Comparison
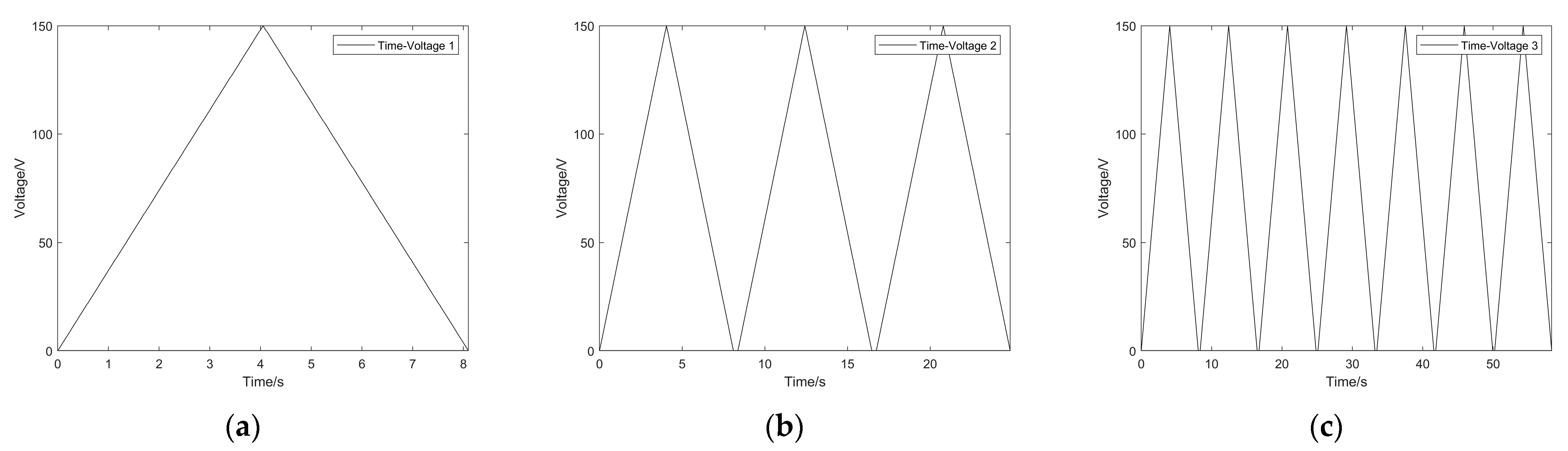
- Adjust the laser interferometer. Connect the computer, laser interferometer, and controller. The relevant software is opened and waiting for a measurement;
- Using the software to make the controller CPI inverse model loaded with the control voltage. The experimental voltage obtained by the CPI inverse model was used for experiment one, and the displacement was measured and recorded at equal time intervals using a laser interferometer. The experimental results are shown in Figure 21;
- Experiment 2 is performed according to the voltage obtained from the DSPI inverse model, and the displacement is measured and recorded at equal time intervals using a laser interferometer. The time interval described in step 3 is kept the same as in 2;
- Change the time interval to complete multiple measurements;
- Check the apparatus and shut it down, and process the final experimental data.
5.4. Another Experimental Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, G.; Bement, M.T.; Hartman, D.A.; Smith, R.E.; Farrar, C.R. The use of active materials for machining processes: A review. Int. J. Mach. Tools Manuf. 2007, 47, 2189–2206. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and development of a new 3-DOF active-type constant-force compliant parallel stage. Mech. Mach. Theory 2019, 140, 654–665. [Google Scholar] [CrossRef]
- Yong, Y.K.; Fleming, A.J.; Moheimani, S.O. A Novel Piezoelectric Strain Sensor for Simultaneous Damping and Tracking Control of a High-Speed Nanopositioner. IEEE/ASME Trans. Mechatron. 2013, 18, 1113–1121. [Google Scholar] [CrossRef]
- Ma, J.; Tian, L.; Li, Y.; Yang, Z.; Cui, Y.; Chu, J. Hysteresis compensation of piezoelectric deformable mirror based on Prandtl–Ishlinskii model. Opt. Commun. 2018, 416, 94–99. [Google Scholar] [CrossRef]
- Woody, S.; Smith, S. Design and performance of a dual drive system for tip-tilt angular control of a 300mm diameter mirror. Mechatronics 2006, 16, 389–397. [Google Scholar] [CrossRef]
- Tao, Y.; Li, H.; Zhu, L. Hysteresis modeling with frequency-separation-based Gaussian process and its application to sinusoidal scanning for fast imaging of atomic force microscope. Sens. Actuators A Phys. 2020, 311, 112070. [Google Scholar] [CrossRef]
- Ling, J.; Rakotondrabe, M.; Feng, Z.; Ming, M.; Xiao, X. A Robust Resonant Controller for High-Speed Scanning of Nanopositioners: Design and Implementation. IEEE Trans. Control Syst. Technol. 2020, 28, 1116–1123. [Google Scholar] [CrossRef]
- Deng, J.; Zhou, H.; Dong, J.; Cohen, P. Three-Dimensional Nanomolds Fabrication for Nanoimprint Lithography. Procedia Manuf. 2019, 34, 228–232. [Google Scholar] [CrossRef]
- Chi, Z.; Xu, Q. Precision control of piezoelectric actuator using fuzzy feedback control with inverse hysteresis compensation. In Proceedings of the 10th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Xi’an, China, 7–11 April 2015; pp. 219–224. [Google Scholar]
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions; Springer: Berlin, Germany, 1996. [Google Scholar]
- Al Janaideh, M.; Rakotondrabe, M.; Al-Darabsah, I.; Aljanaideh, O. Internal model-based feedback control design for inversion-free feedforward rate-dependent hysteresis compensation of piezoelectric cantilever actuator. Control. Eng. Pract. 2018, 72, 29–41. [Google Scholar] [CrossRef]
- Ge, P.; Jouaneh, M. Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators. Precis. Eng. 1997, 20, 99–111. [Google Scholar] [CrossRef]
- Malczyk, R.; Izydorczyk, J. The frequency-dependent Jiles–Atherton hysteresis model. Phys. B Condens. Matter. 2015, 463, 68–75. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Wu, H.; Zou, D. Modelling and compensation of hysteresis in piezoelectric actuators based on Maxwell approach. Electron. Lett. 2016, 52, 188–190. [Google Scholar] [CrossRef]
- Ming, M.; Feng, Z.; Ling, J.; Xiao, X.H. Hysteresis modelling and feedforward compensation of piezoelectric nanopositioning stage with a modified Bouc–Wen model. Micro Nano Lett. 2018, 13, 1170–1174. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, X.; Li, J.; Chen, J. Nonlinear hysteresis identification and compensation based on the discrete Preisach model of an aircraft morphing wing device manipulated by an SMA actuator. Chin. J. Aeronaut. 2019, 32, 1040–1050. [Google Scholar] [CrossRef]
- Delibas, B.; Arockiarajan, A.; Seemann, W. Rate dependent properties of perovskite type tetragonal piezoelectric materials using micromechanical model. Int. J. Solids Struct. 2006, 43, 697–712. [Google Scholar] [CrossRef]
- Song, X.; Duggen, L.; Lassen, B.; Mangeot, C. Modeling and identification of hysteresis with modified Preisach model in piezoelectric actuator. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1538–1543. [Google Scholar]
- Lin, C.; Lin, P. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Comput. Math. Appl. 2012, 64, 766–787. [Google Scholar] [CrossRef]
- Wang, G.; Chen, G.; Bai, F. Modeling and identification of asymmetric Bouc–Wen hysteresis for piezoelectric actuator via a novel differential evolution algorithm. Sens. Actuators A Phys. 2015, 235, 105–118. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, Z.; Zhang, Y.; Li, D. Rate-Dependent Modeling of Piezoelectric Actuators for Nano Manipulation Based on Fractional Hammerstein Model. Micromachines 2022, 13, 42. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Xu, M.; Chen, G. Hysteresis Characteristics and MPI Compensation of Two-Dimensional Piezoelectric Positioning Stage. Micromachines 2022, 13, 321. [Google Scholar] [CrossRef]
- Ko, Y.R.; Hwang, Y.; Chae, M.; Kim, T.H. Direct identification of generalized Prandtl-Ishlinskii model inversion for asymmetric hysteresis compensation. ISA Trans. 2017, 70, 209–218. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakotondrabe, M.; Aljanaideh, O. Further Results on Hysteresis Compensation of Smart Micropositioning Systems With the Inverse Prandtl-Ishlinskii Compensator. IEEE Trans. Control. Syst. Technol. 2016, 24, 428–439. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, F.; Yang, F.; Rui, X. Tracking control of a 3-dimensional piezo-driven micro-positioning system using a dynamic Prandtl–Ishlinskii model. J. Intell. Mater. Syst. Struct. 2022, 33, 1231–1243. [Google Scholar] [CrossRef]
- Kuhnen, K. Modeling, identification and compensation of complex hysteretic nonlinearities: A modified Prandtl-Ishlinskii approach. Eur. J. Control. 2003, 9, 407–417. [Google Scholar] [CrossRef]
- Stefanski, F.; Minorowicz, B.; Persson, J.; Plummer, A.; Bowen, C. Non-linear control of a hydraulic piezo-valve using a generalised Prandtl–Ishlinskii hysteresis model. Mech. Syst. Signal Process. 2017, 82, 412–431. [Google Scholar] [CrossRef]
- Savoie, M.; Shan, J. Temperature-dependent asymmetric Prandtl-Ishlinskii hysteresis model for piezoelectric actuators. Smart Mater. Struct. 2022, 31, 55022. [Google Scholar] [CrossRef]
- Cao, K.; Li, R.; Du, H.; Ma, J. Modeling and compensation of symmetric hysteresis in piezoceramic actuators. Results Phys. 2019, 13, 102095. [Google Scholar] [CrossRef]
- Hii, K.; Vallance, R.R.; Pinar Mengüç, M. Design, operation, and motion characteristics of a precise piezoelectric linear motor. Precis. Eng. 2010, 34, 231–241. [Google Scholar] [CrossRef]
- Yang, S.; Chen, W.; Liu, J.; Chen, W. Design, analysis and testing of a novel decoupled 2-DOF flexure-based micropositioning stage. J. Micromech. Microeng. 2017, 27, 95010. [Google Scholar] [CrossRef]
- Huang, X.; Zeng, J.; Ruan, X.; Zheng, L.; Li, G. Structure, electrical, and thermal expansion properties of PZnTe-PZT ternary system piezoelectric ceramics. J. Am. Ceram. Soc. 2018, 101, 274–282. [Google Scholar] [CrossRef]
- Lancée, C.T.; Souquet, J.; Ohigashi, H.; Bom, N. Transducers in medical ultrasound: Part One. Ferro-electric ceramics versus polymer piezoelectric materials. Ultrasonics 1985, 23, 138. [Google Scholar] [CrossRef]
- Chi, Z.Q.; Xu, Q.S. Recent advances in the control of piezoelectric actuators. Int. J. Adv. Rob. Syst. 2014, 11, 182. [Google Scholar] [CrossRef]
- Sun, Z.; Song, B.; Xi, N.; Yang, R.; Chen, L.; Cheng, Y.; Bi, S.; Li, C.; Hao, L. Systematic Hysteresis compensator design based on Extended Unparallel Prandtl-Ishlinskii model for SPM imaging rectification. IFAC—Pap. Online 2017, 50, 10901–10906. [Google Scholar] [CrossRef]
- An, D.; Yang, Y.; Xu, Y.; Shao, M.; Shi, J.; Yue, G. Compensation of Hysteresis in the Piezoelectric Nanopositioning Stage under Reciprocating Linear Voltage Based on a Mark-Segmented PI Model. Micromachines 2020, 11, 9. [Google Scholar] [CrossRef] [PubMed]
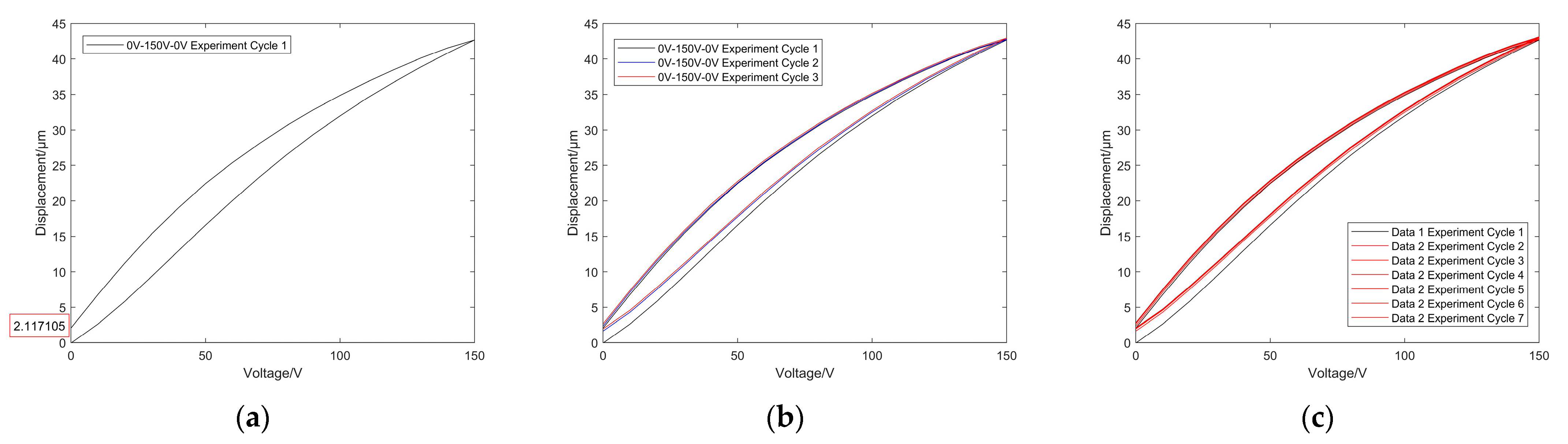
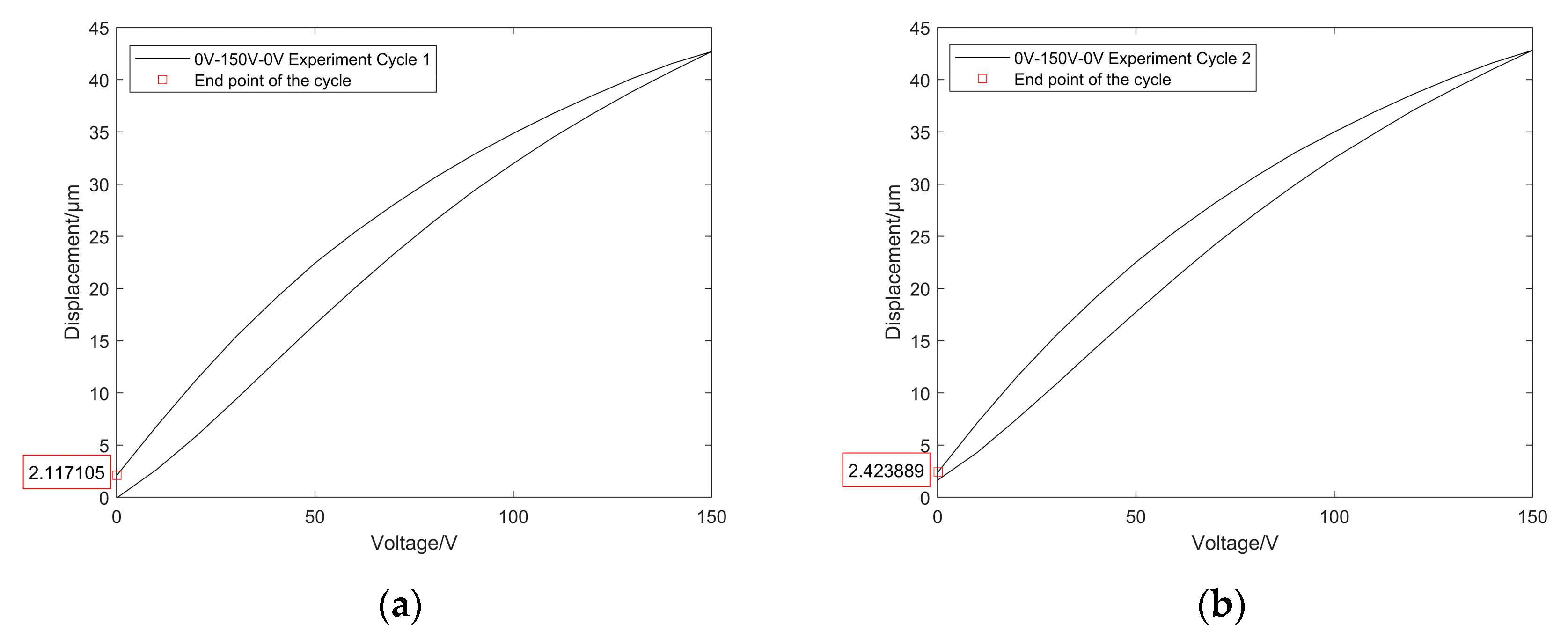


| The Given Voltage | Start-Up Error Value |
|---|---|
| 0–150–0 V | 2.117105 μm |
| 0–100–0 V | 1.411403 μm |
| 0–50–0 V | 0.827996 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, D.; Li, J.; Li, S.; Shao, M.; Wang, W.; Wang, C.; Yang, Y. Compensation Method for the Nonlinear Characteristics with Starting Error of a Piezoelectric Actuator in Open-Loop Controls Based on the DSPI Model. Micromachines 2023, 14, 742. https://doi.org/10.3390/mi14040742
An D, Li J, Li S, Shao M, Wang W, Wang C, Yang Y. Compensation Method for the Nonlinear Characteristics with Starting Error of a Piezoelectric Actuator in Open-Loop Controls Based on the DSPI Model. Micromachines. 2023; 14(4):742. https://doi.org/10.3390/mi14040742
Chicago/Turabian StyleAn, Dong, Ji Li, Songhua Li, Meng Shao, Weinan Wang, Chuan Wang, and Yixiao Yang. 2023. "Compensation Method for the Nonlinear Characteristics with Starting Error of a Piezoelectric Actuator in Open-Loop Controls Based on the DSPI Model" Micromachines 14, no. 4: 742. https://doi.org/10.3390/mi14040742
APA StyleAn, D., Li, J., Li, S., Shao, M., Wang, W., Wang, C., & Yang, Y. (2023). Compensation Method for the Nonlinear Characteristics with Starting Error of a Piezoelectric Actuator in Open-Loop Controls Based on the DSPI Model. Micromachines, 14(4), 742. https://doi.org/10.3390/mi14040742







