Detection of In-Plane Movement in Electrically Actuated Microelectromechanical Systems Using a Scanning Electron Microscope
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
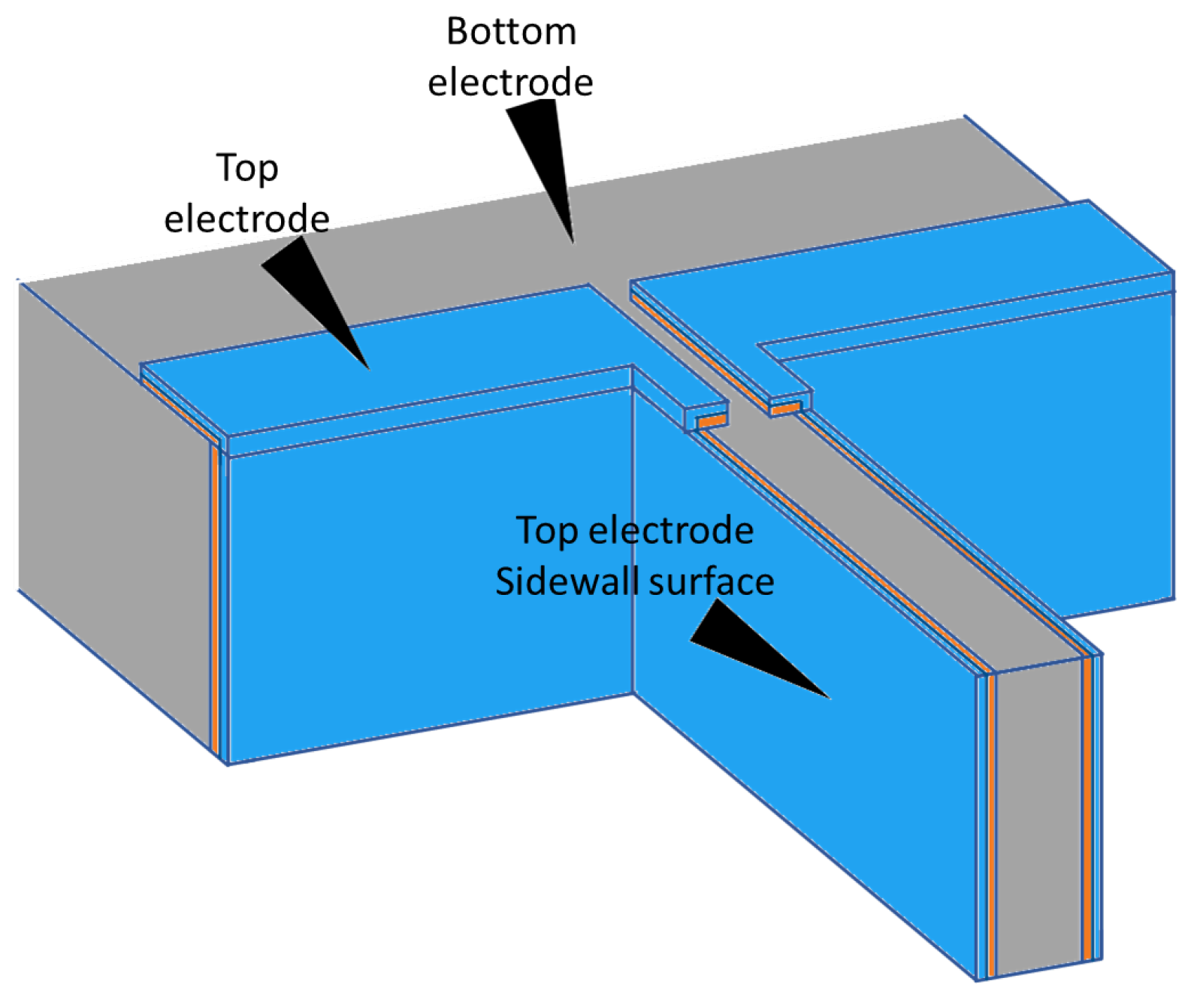
3.1. Capture of SEM images Containing Motion
3.2. Impact of Electrical Actuation
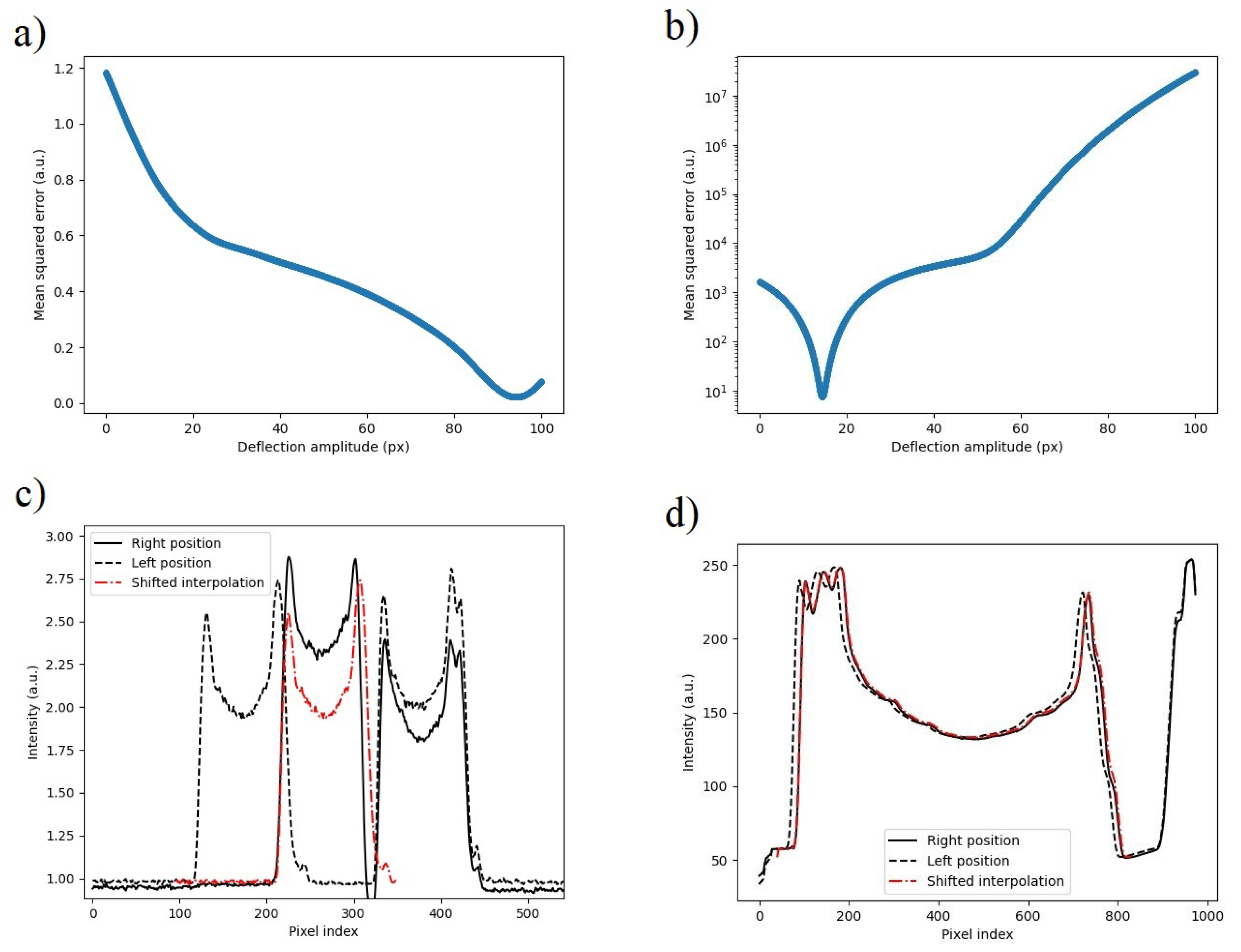
3.3. Calculated Deflection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MEMS | Microelectromechanical systems |
| DHM | Digital holographic microscopy |
| AlN | Aluminum nitride |
| TiN | Titanium nitride |
| MSE | Mean squared error |
References
- Scheeper, P.; van der Donk, A.; Olthuis, W.; Bergveld, P. A review of silicon microphones. Sens. Actuators A Phys. 1994, 44, 1–11. [Google Scholar] [CrossRef]
- He, J.; Zhou, W.; Yu, H.; He, X.; Peng, P. Structural Designing of a MEMS Capacitive Accelerometer for Low Temperature Coefficient and High Linearity. Sensors 2018, 18, 643. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Fedder, G. Fabrication, characterization, and analysis of a DRIE CMOS-MEMS gyroscope. IEEE Sens. J. 2003, 3, 622–631. [Google Scholar] [CrossRef]
- Todaro, M.T.; Guido, F.; Mastronardi, V.; Desmaele, D.; Epifani, G.; Algieri, L.; De Vittorio, M. Piezoelectric MEMS vibrational energy harvesters: Advances and outlook. Microelectron. Eng. 2017, 183–184, 23–36. [Google Scholar] [CrossRef]
- Hu, F.; Yao, J.; Qiu, C.; Ren, H. A MEMS micromirror driven by electrostatic force. J. Electrost. 2010, 68, 237–242. [Google Scholar] [CrossRef]
- Pollock, C.; Javor, J.; Stange, A.; Barrett, L.K.; Bishop, D.J. Extreme angle, tip-tilt MEMS micromirror enabling full hemispheric, quasi-static optical coverage. Opt. Express 2019, 27, 15318–15326. [Google Scholar] [CrossRef]
- Chen, C.J. Electromechanical deflections of piezoelectric tubes with quartered electrodes. Appl. Phys. Lett. 1992, 60, 132–134. [Google Scholar] [CrossRef]
- Huang, Z.; Leighton, G.; Wright, R.; Duval, F.; Chung, H.; Kirby, P.; Whatmore, R. Determination of piezoelectric coefficients and elastic constant of thin films by laser scanning vibrometry techniques. Sens. Actuators A Phys. 2007, 135, 660–665. [Google Scholar] [CrossRef]
- Annovazzi-Lodi, V.; Merlo, S.; Norgia, M. Measurements on a micromachined silicon gyroscope by feedback interferometry. IEEE/ASME Trans. Mechatron. 2001, 6, 1–6. [Google Scholar] [CrossRef]
- Shih, W.C.; Kim, S.G.; Barbastathis, G. High-resolution electrostatic analog tunable grating with a single-mask fabrication process. J. Microelectromech. Syst. 2006, 15, 763–769. [Google Scholar] [CrossRef]
- Schmitt, P.; Hoffmann, M. Engineering a Compliant Mechanical Amplifier for MEMS Sensor Applications. J. Microelectromech. Syst. 2020, 29, 214–227. [Google Scholar] [CrossRef]
- Lawrence, E.M.; Speller, K.E.; Yu, D. MEMS characterization using laser Doppler vibrometry. In Proceedings of the Reliability, Testing, and Characterization of MEMS/MOEMS II; Ramesham, R., Tanner, D.M., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2003; Volume 4980, pp. 51–62. [Google Scholar] [CrossRef]
- Kim, Y.S.; Dagalakis, N.G.; Choi, Y.M. Optical fiber Fabry-Pérot micro-displacement sensor for MEMS in-plane motion stage. Microelectron. Eng. 2018, 187–188, 6–13. [Google Scholar] [CrossRef]
- Conway, J.A.; Osborn, J.V.; Fowler, J.D. Stroboscopic Imaging Interferometer for MEMS Performance Measurement. J. Microelectromech. Syst. 2007, 16, 668–674. [Google Scholar] [CrossRef]
- Hart, M.; Conant, R.; Lau, K.; Muller, R. Stroboscopic interferometer system for dynamic MEMS characterization. J. Microelectromech. Syst. 2000, 9, 409–418. [Google Scholar] [CrossRef]
- Horsley, D.A.; Park, H.; Laut, S.P.; Werner, J.S. Characterization of a bimorph deformable mirror using stroboscopic phase-shifting interferometry. Sens. Actuators A Phys. 2007, 134, 221–230. [Google Scholar] [CrossRef]
- Arabi, M.; Gopanchuk, M.; Abdel-Rahman, E.; Yavuz, M. Measurement of In-Plane Motions in MEMS. Sensors 2020, 20, 3594. [Google Scholar] [CrossRef]
- Gokhale, V.J.; Gorman, J.J. Optical Knife-Edge Displacement Measurement With Sub-Picometer Resolution for RF-MEMS. J. Microelectromech. Syst. 2018, 27, 910–920. [Google Scholar] [CrossRef]
- Novak, E. MEMS metrology techniques. In Proceedings of the Reliability, Packaging, Testing, and Characterization of MEMS/MOEMS IV; Tanner, D.M., Ramesham, R., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2005; Volume 5716, pp. 173–181. [Google Scholar] [CrossRef]
- Emery, Y.; Aspert, N.; Marquet, F. Dynamical topography measurements of MEMS up to 25 MHz, through transparent window, and in liquid by Digital Holographic Microscope (DHM). AIP Conf. Proc. 2012, 1457, 71–77. [Google Scholar] [CrossRef]
- Alexander, R.; Leahy, B.; Manoharan, V.N. Precise measurements in digital holographic microscopy by modeling the optical train. J. Appl. Phys. 2020, 128, 060902. [Google Scholar] [CrossRef]
- Burns, D.; Helbig, H. A system for automatic electrical and optical characterization of microelectromechanical devices. J. Microelectromech. Syst. 1999, 8, 473–482. [Google Scholar] [CrossRef]
- Kokorian, J.; Buja, F.; Spengen, W.M.V. In-Plane Displacement Detection With Picometer Accuracy on a Conventional Microscope. J. Microelectromech. Syst. 2015, 24, 618–625. [Google Scholar] [CrossRef]
- Bschaden, B.; Hubbard, T.; Kujath, M. Measurement of MEMS thermal actuator time constant using image blur. J. Micromech. Microeng. 2011, 21, 045001. [Google Scholar] [CrossRef]
- Schermelleh, L.; Heintzmann, R.; Leonhardt, H. A guide to super-resolution fluorescence microscopy. J. Cell Biol. 2010, 190, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Olivares, J.; Iborra, E.; Clement, M.; Vergara, L.; Sangrador, J.; Sanz-Hervás, A. Piezoelectric actuation of microbridges using AlN. Sen. Actuators A Phys. 2005, 123–124, 590–595. [Google Scholar] [CrossRef]
- Sehr, H.; Tomlin, I.S.; Huang, B.; Beeby, S.P.; Evans, A.G.R.; Brunnschweiler, A.; Ensell, G.J.; Schabmueller, C.G.J.; Niblock, T.E.G. Time constant and lateral resonances of thermal vertical bimorph actuators. J. Micromech. Microeng. 2002, 12, 410–413. [Google Scholar] [CrossRef]
- Bertke, M.; Xu, J.; Fahrbach, M.; Setiono, A.; Wasisto, H.S.; Peiner, E. Strategy toward Miniaturized, Self-out-Readable Resonant Cantilever and Integrated Electrostatic Microchannel Separator for Highly Sensitive Airborne Nanoparticle Detection. Sensors 2019, 19, 901. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieminen, T.; Tiwary, N.; Ross, G.; Paulasto-Kröckel, M. Detection of In-Plane Movement in Electrically Actuated Microelectromechanical Systems Using a Scanning Electron Microscope. Micromachines 2023, 14, 698. https://doi.org/10.3390/mi14030698
Nieminen T, Tiwary N, Ross G, Paulasto-Kröckel M. Detection of In-Plane Movement in Electrically Actuated Microelectromechanical Systems Using a Scanning Electron Microscope. Micromachines. 2023; 14(3):698. https://doi.org/10.3390/mi14030698
Chicago/Turabian StyleNieminen, Tarmo, Nikhilendu Tiwary, Glenn Ross, and Mervi Paulasto-Kröckel. 2023. "Detection of In-Plane Movement in Electrically Actuated Microelectromechanical Systems Using a Scanning Electron Microscope" Micromachines 14, no. 3: 698. https://doi.org/10.3390/mi14030698
APA StyleNieminen, T., Tiwary, N., Ross, G., & Paulasto-Kröckel, M. (2023). Detection of In-Plane Movement in Electrically Actuated Microelectromechanical Systems Using a Scanning Electron Microscope. Micromachines, 14(3), 698. https://doi.org/10.3390/mi14030698







