A Modified Robotic Manipulator Controller Based on Bernstein-Kantorovich-Stancu Operator
Abstract
1. Introduction
- Combining the BKS operator with the perturbation observer in the robotic controller.
- A multi-turbulence simulation based on the new perturbation observer and the pre-researched trajectory tracking controller [26] on the robotic manipulator is performed to verify the effectiveness of the method.
- An experimental platform of the manipulator is built to verify the effectiveness of the proposed controller in the actual manipulator, which reflects the feasibility of the method in practical engineering applications.
2. Model Derivation and Control Objectives
2.1. Manipulator Dynamic Modeling
2.2. Bernstein-Kantorovich-Stancu Operator
3. Controller Design
3.1. Manipulator’s Task Definition
3.2. The Designed Controller
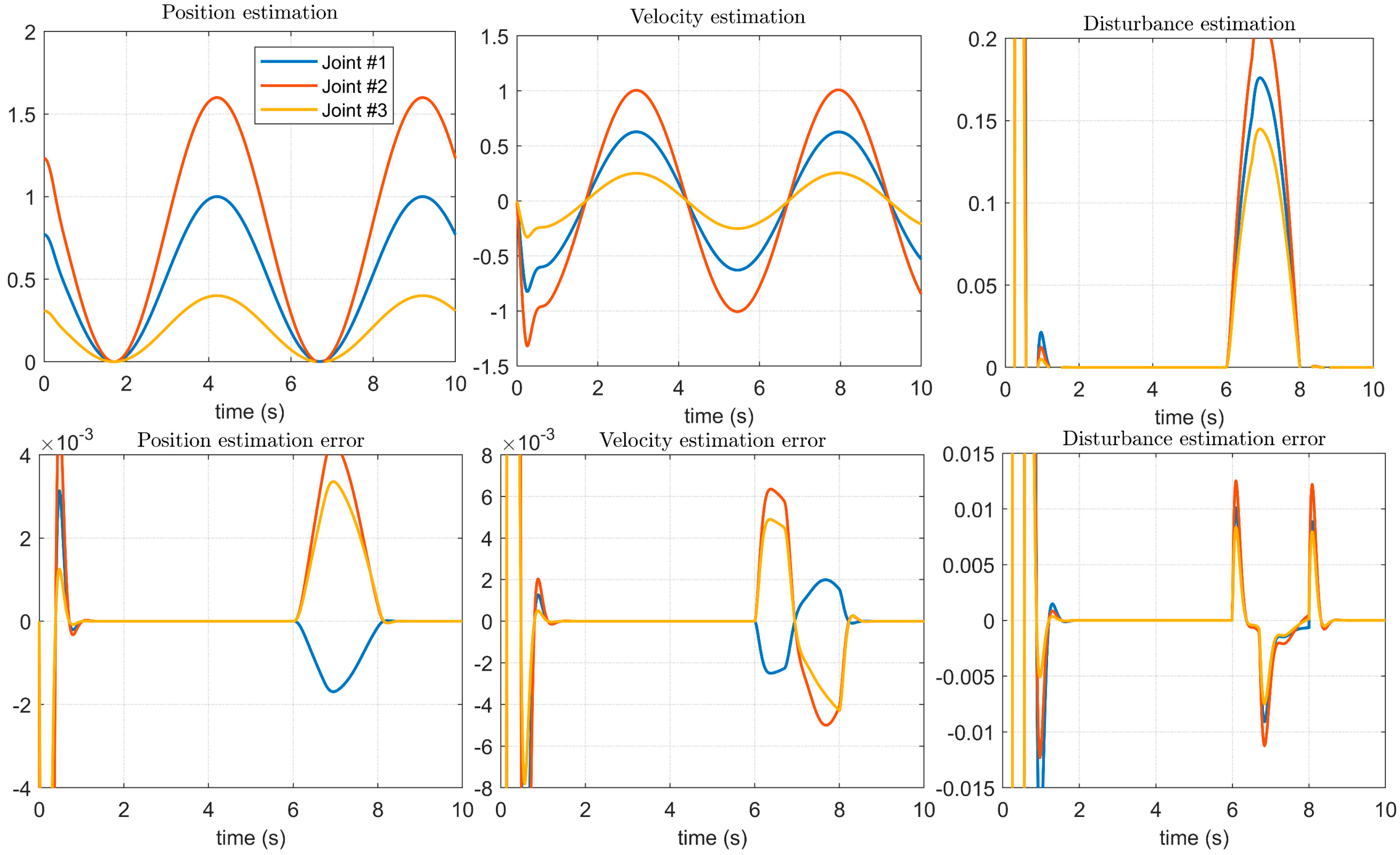
3.3. Design of the Modified Observer
4. Simulation and Discussion
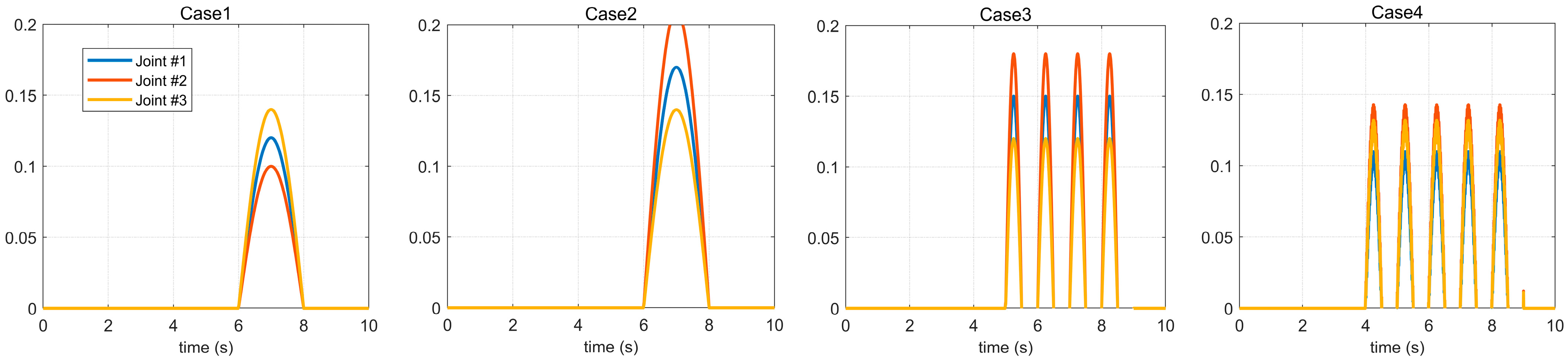
4.1. Disturbance Cases and Control Parameters
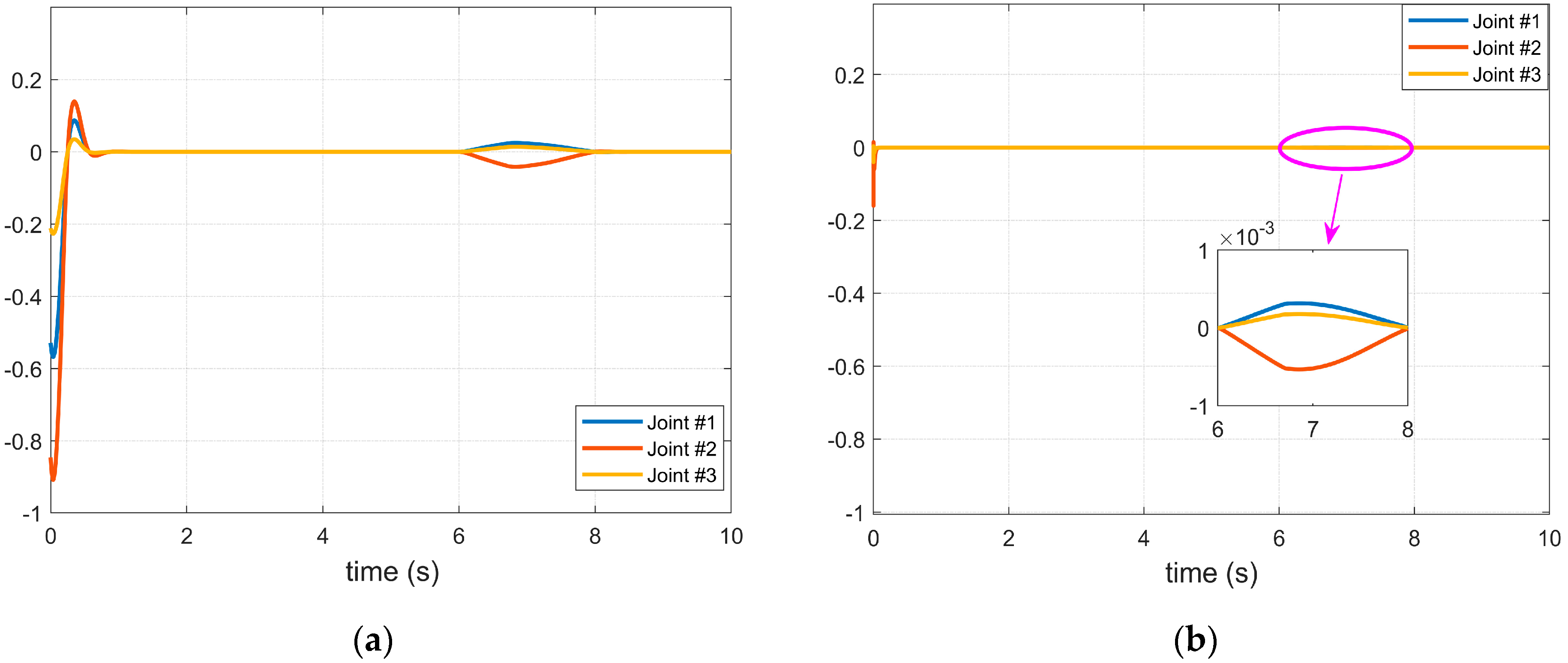
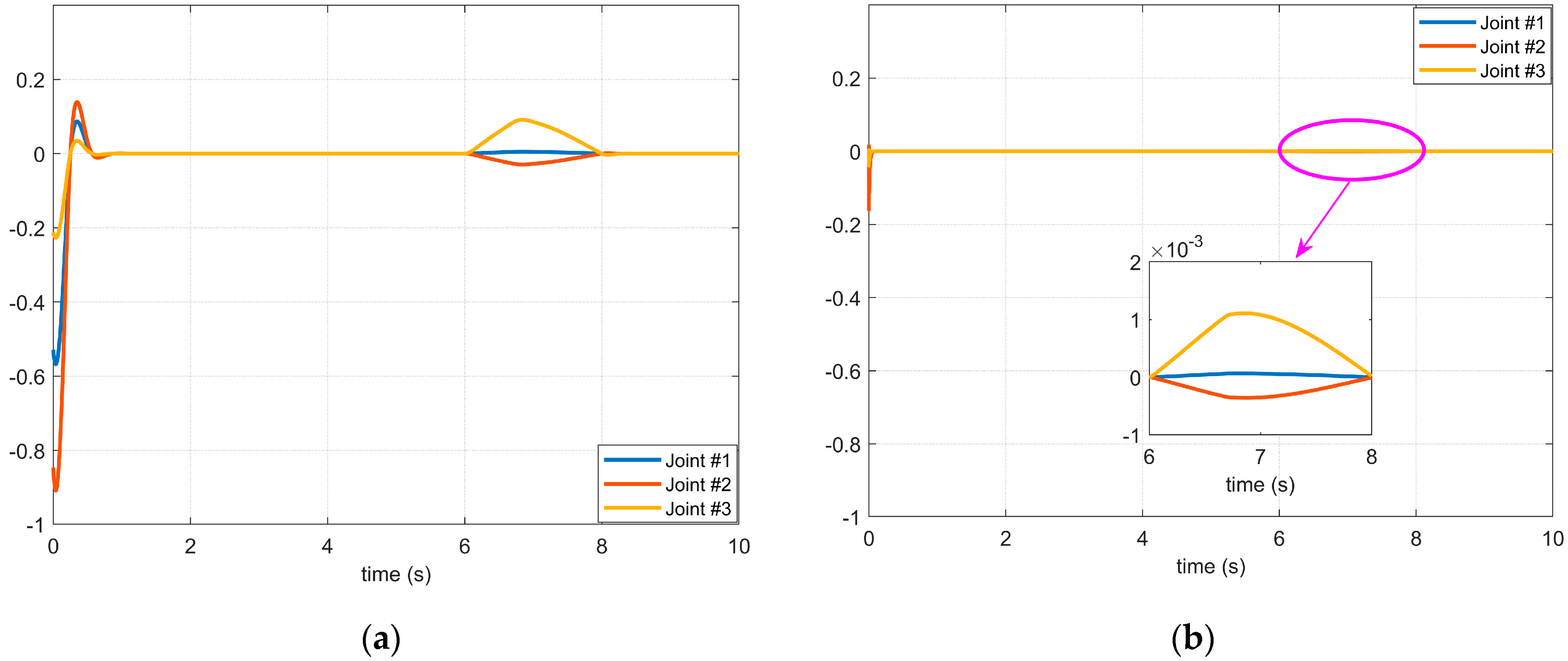
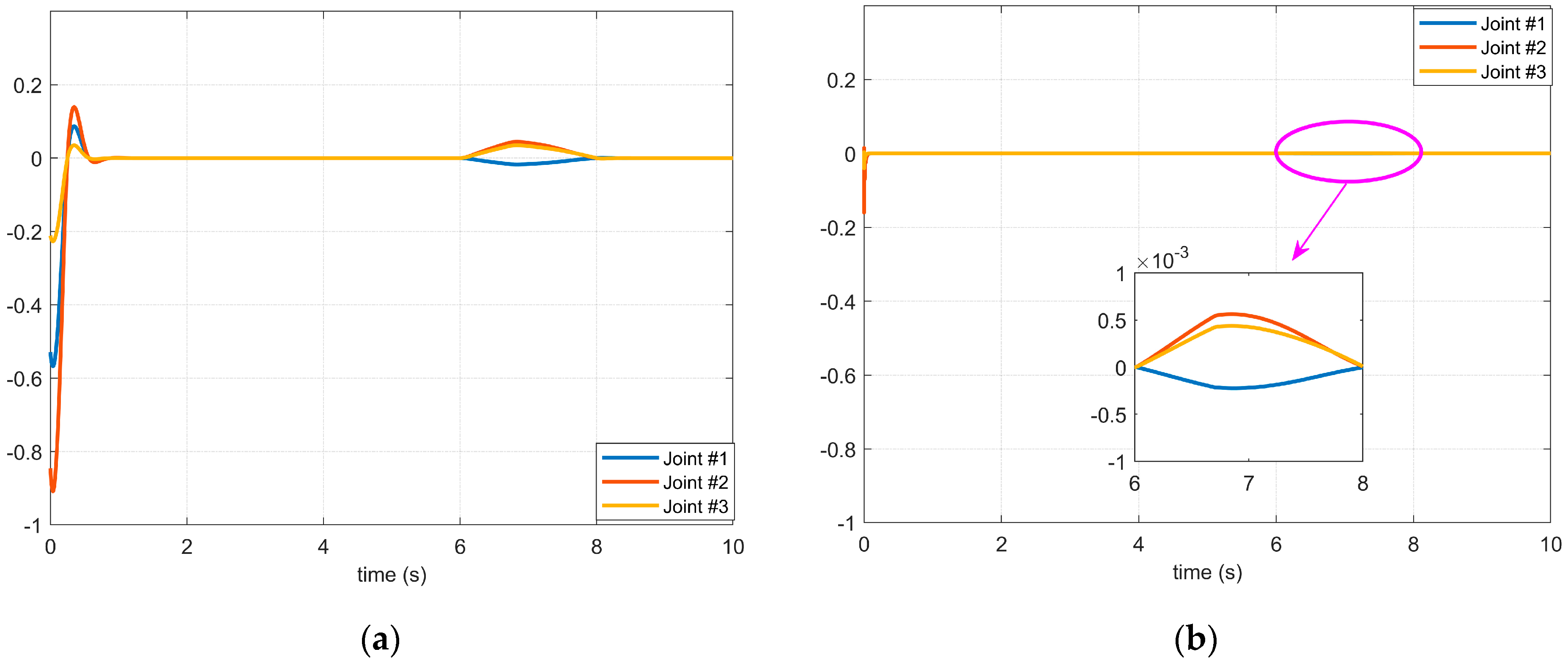
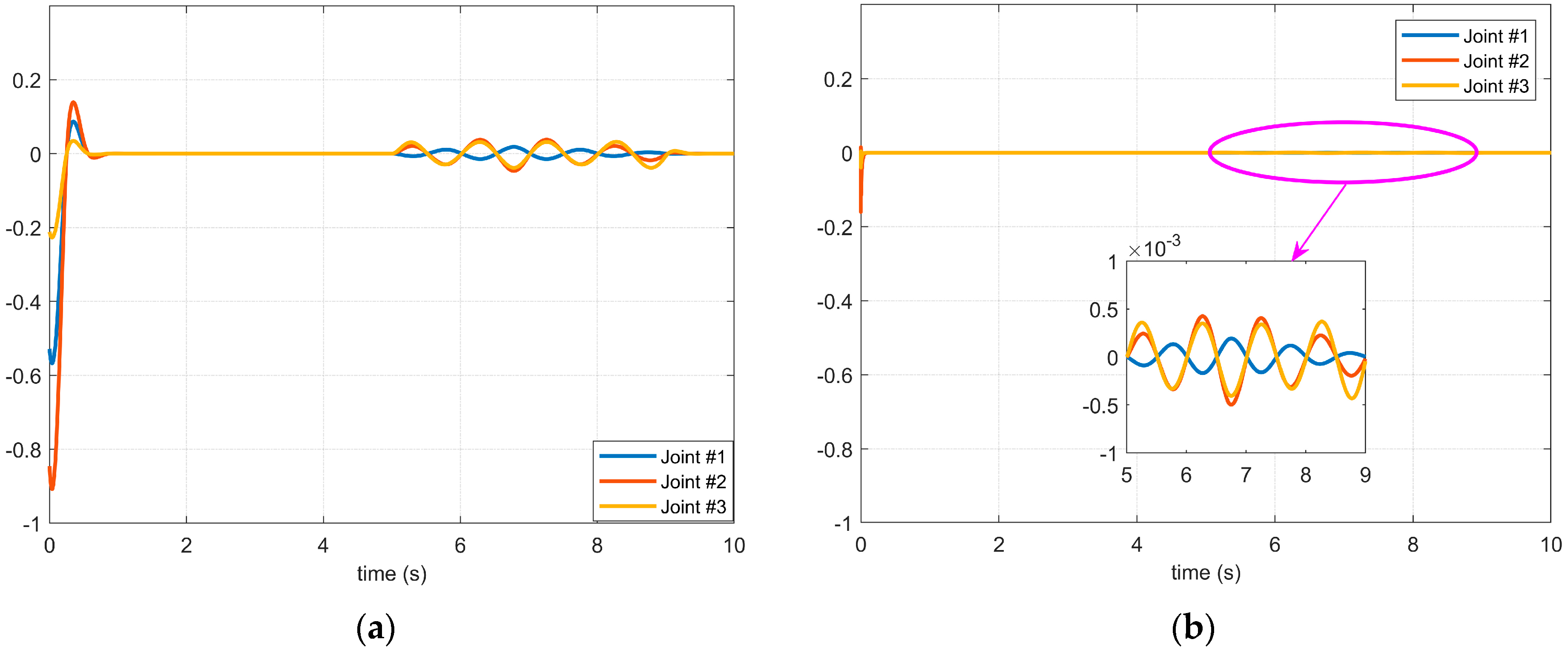
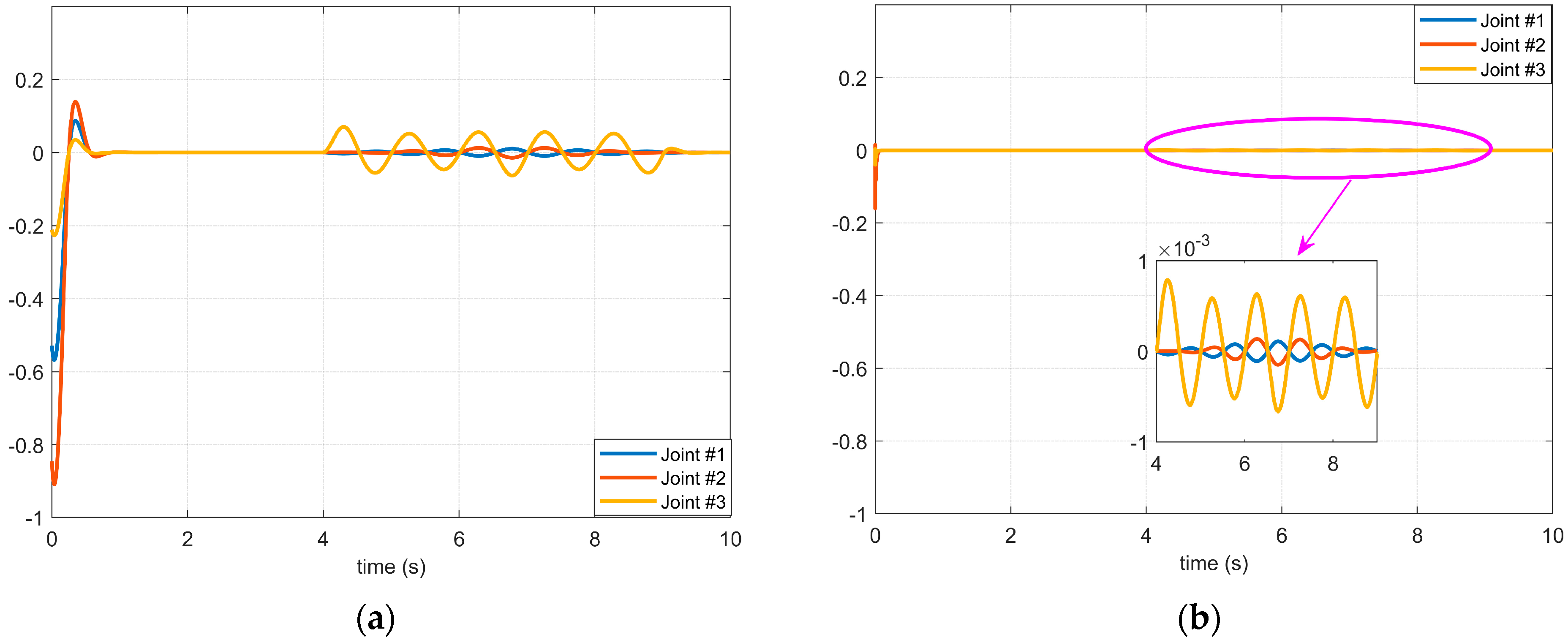
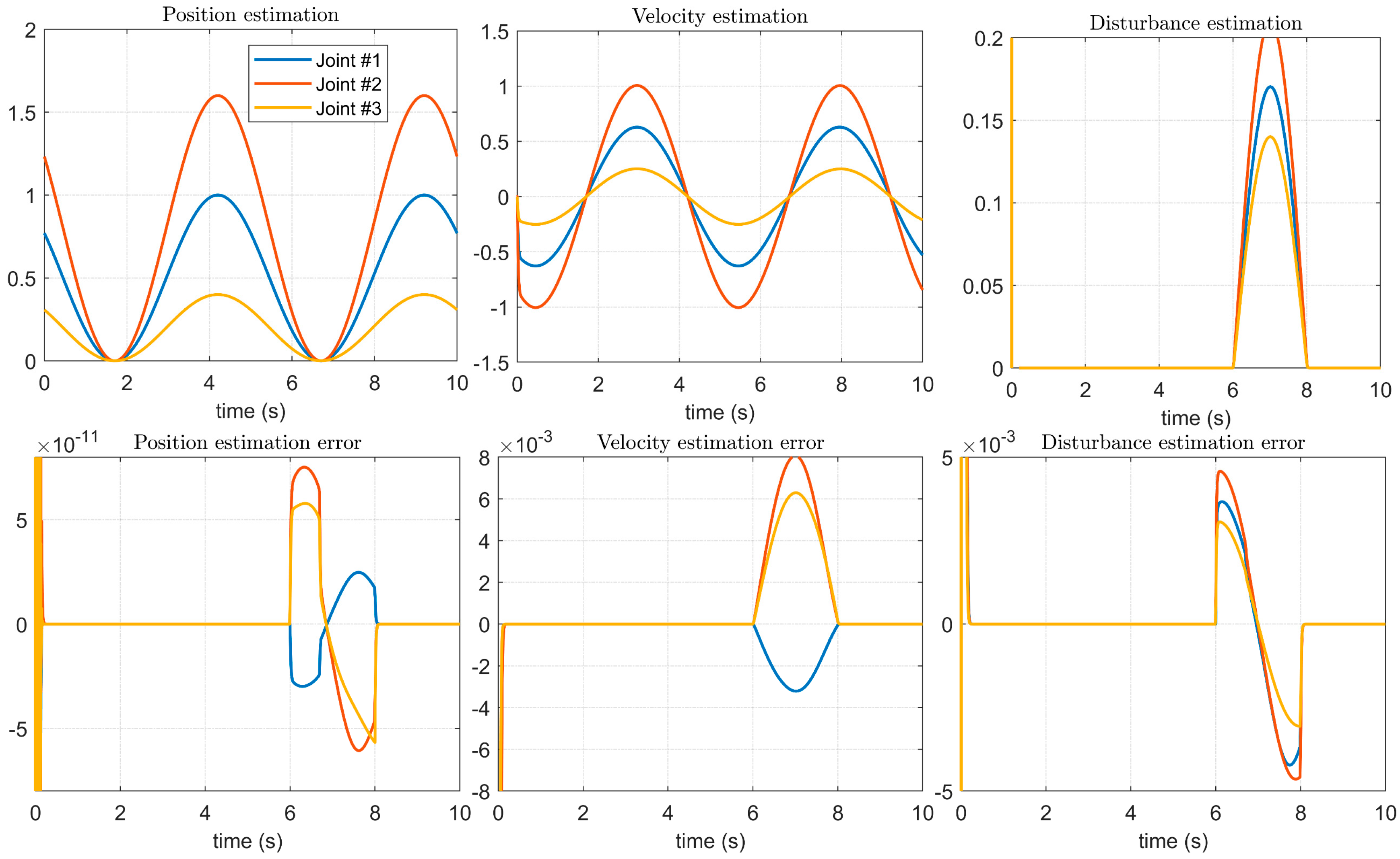
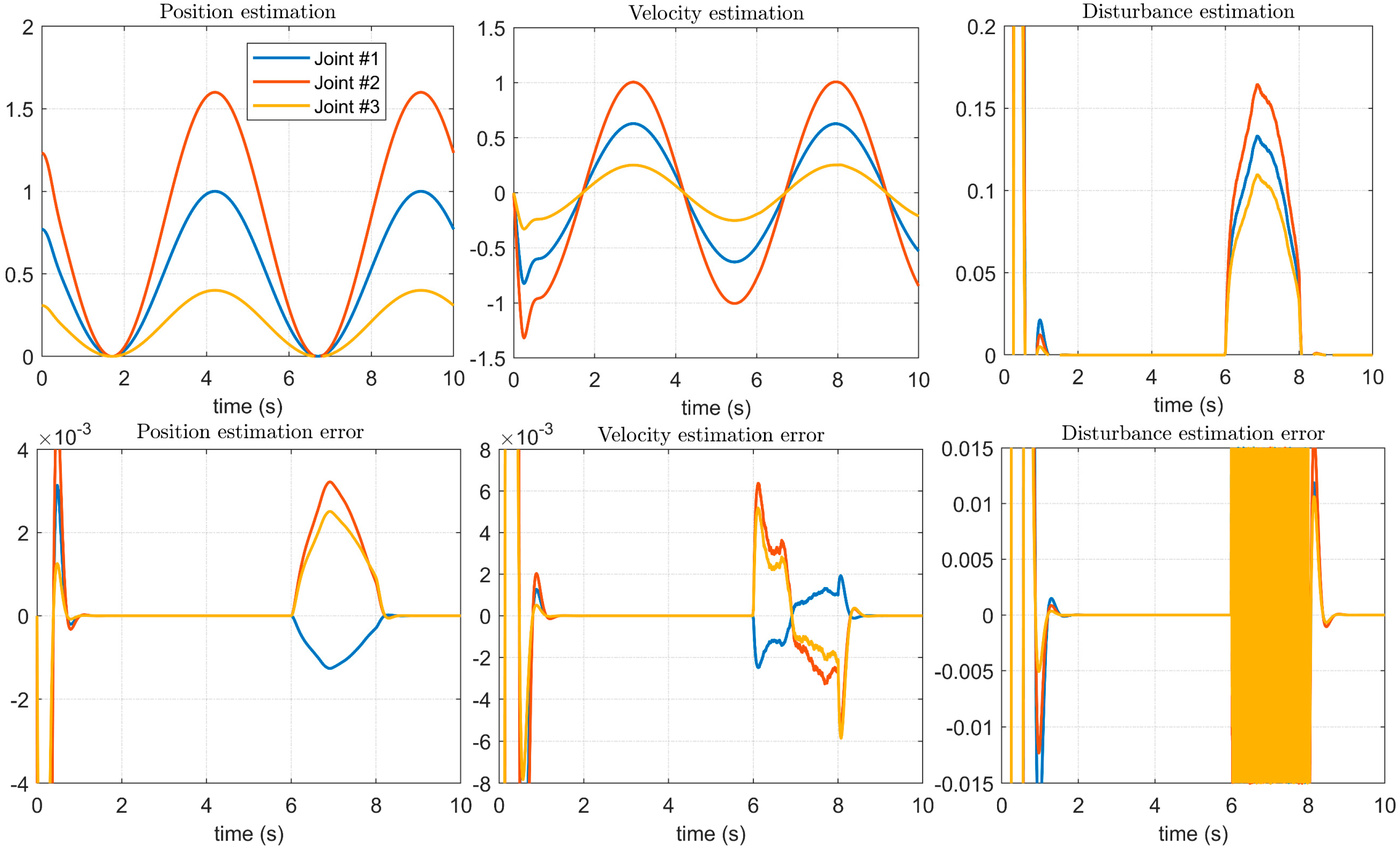
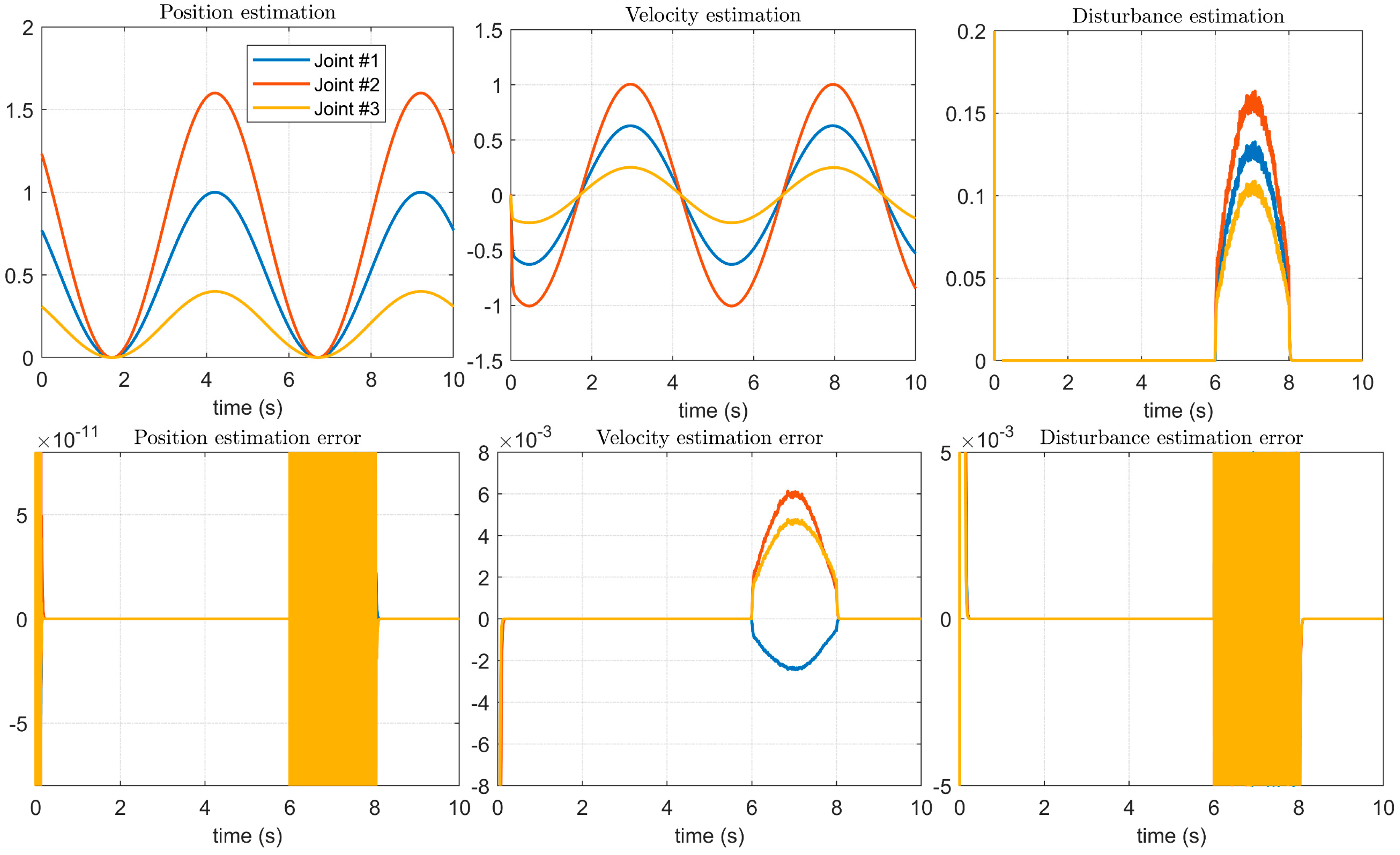
4.2. Simulation Results of the Proposed Controller Using the BKS Operator
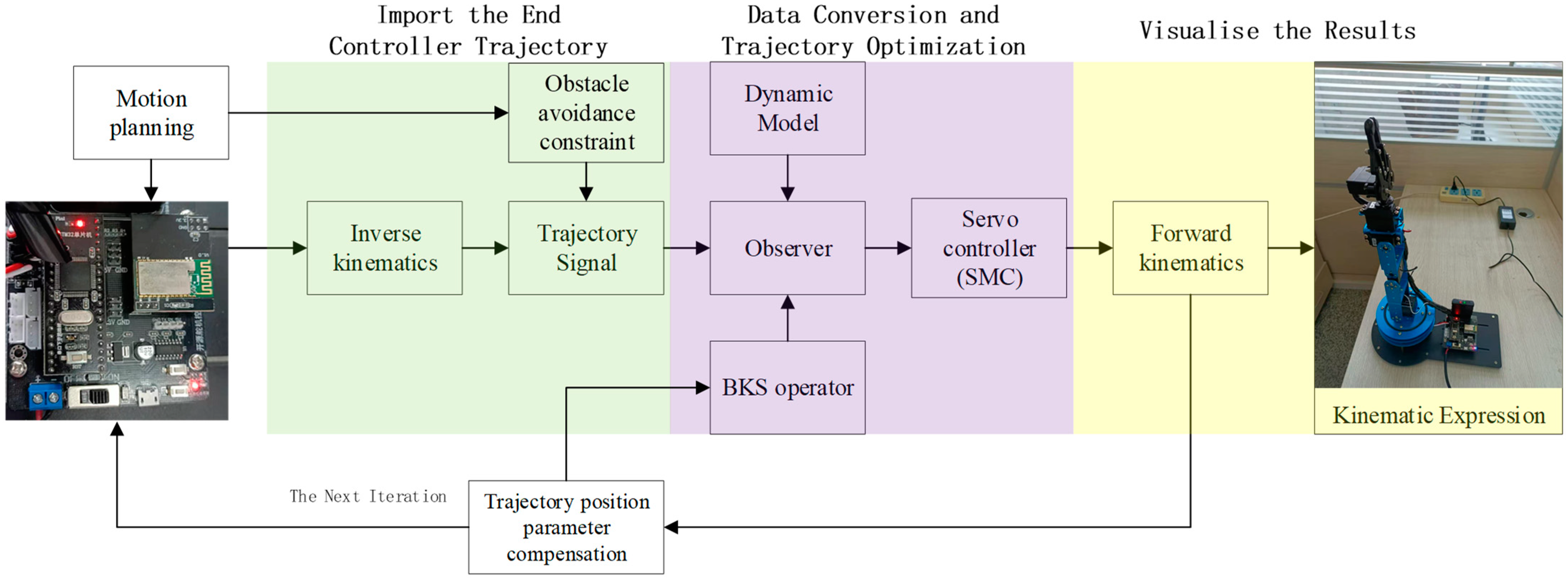
4.3. Experiment Results of the Manipulator Controller in a Complex Environment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, A.; Saha, S.K. Simplified drag modeling for the dynamics of an underwater manipulator. IEEE J. Ocean. Eng. 2019, 46, 40–55. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Q.; Zhang, A. Dexterity Based Viscous Resistance Optimization of a Deep-Sea Manipulator. J. Mar. Sci. Eng. 2022, 10, 876. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, S.; Zhang, L. A path planning method of 6-DOF robot for mirror therapy based on A* algorithm. Technol. Health Care 2022, 30, 105–116. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Chen, X.; Zhang, H.; Shen, C.; Fu, W. Design and Performance Test of a Jujube Pruning Manipulator. Agriculture 2022, 12, 552. [Google Scholar] [CrossRef]
- Shang, D.; Li, X.; Yin, M.; Li, F.; Wen, B. Rotation Angle Control Strategy for Telescopic Flexible Manipulator Based on a Combination of Fuzzy Adjustment and RBF Neural Network. Chin. J. Mech. Eng. 2022, 35, 1–24. [Google Scholar] [CrossRef]
- Yang, G.; Liu, Y.; Ji, J.; Jin, M.; Piao, S. A model-based PID-like motion control method for flexible-joint manipulator with harmonic drives. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 7880–7893. [Google Scholar] [CrossRef]
- Fan, J.; Jin, L.; Xie, Z.; Li, S.; Zheng, Y. Data-driven motion-force control scheme for redundant manipulators: A kinematic perspective. IEEE Trans. Ind. Inform. 2021, 18, 5338–5347. [Google Scholar] [CrossRef]
- Wang, X.; Wang, A.; Wang, D.; Liu, Z.; Qi, Y. A Novel Trajectory Tracking Control with Modified Supertwisting Sliding Mode for Human-Robot Cooperation Manipulator in Assembly Line. J. Sens. 2022, 2022, 1822670. [Google Scholar] [CrossRef]
- Thien, D.; Tai, T.; Ahn, K.K. A consensus sliding mode control for trajectory tracking of multiple manipulators. In Proceedings of the 2021 International Symposium on Electrical and Electronics Engineering (ISEE), Ho Chi Minh City, Vietnam, 15–16 April 2021; IEEE: Manhattan, NY, USA, 2021. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, J.; Sun, Z.; Shen, G.; Xia, Y. Composite trajectory tracking control for robot manipulator with active disturbance rejection. Control Eng. Pract. 2021, 106, 104670. [Google Scholar] [CrossRef]
- Gao, H.; Chen, M. Fixed-time tracking control for two-link rigid manipulator based on disturbance observer. Trans. Inst. Meas. Control 2021, 43, 1924–1935. [Google Scholar] [CrossRef]
- Zhao, Z.; He, X.; Ahn, C.K. Boundary disturbance observer-based control of a vibrating single-link flexible manipulator. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 2382–2390. [Google Scholar] [CrossRef]
- Jung, S.; Lee, J.W. Similarity analysis between a nonmodel-based disturbance observer and a time-delayed controller for robot manipulators in cartesian space. IEEE Access 2021, 9, 122299–122307. [Google Scholar] [CrossRef]
- Razmjooei, H.; Shafiei, M.H.; Palli, G.; Arefi, M.M. Non-linear finite-time tracking control of uncertain robotic manipulators using time-varying disturbance observer-based sliding mode method. J. Intell. Robot. Syst. 2022, 104, 1–13. [Google Scholar] [CrossRef]
- Sun, T.; Cheng, L.; Hou, Z.; Tan, M. Novel sliding-mode disturbance observer-based tracking control with applications to robot manipulators. Sci. China Inf. Sci. 2021, 64, 1–12. [Google Scholar] [CrossRef]
- Gonska, H.H.; Zhou, X.-L. The strong converse inequality for Bernstein-Kantorovich operators. Comput. Math. Appl. 1995, 30, 103–128. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ansari, K.J.; Özger, F.; Özger, Ö.Z. A link between approximation theory and summability methods via four-dimensional infinite matrices. Mathematics 2021, 9, 1895. [Google Scholar] [CrossRef]
- Özger, F.; Aljimi, E.; Ersoy, M.T. Rate of weighted statistical convergence for generalized blending-type Bernstein-Kantorovich operators. Mathematics 2022, 10, 2027. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Özger, F. Approximation of functions by Stancu variant of Bernstein–Kantorovich operators based on shape parameter α. Rev. Real Acad. Cienc. Exactas Físicas Y Naturales. Ser. A. Matemáticas 2020, 114, 1–17. [Google Scholar] [CrossRef]
- Mursaleen, M.; Khan, F.; Khan, A. Approximation properties for King’s type modified q-Bernstein–Kantorovich operators. Math. Methods Appl. Sci. 2015, 38, 5242–5252. [Google Scholar] [CrossRef]
- Cai, Q.-B.; Ansari, K.J.; Ersoy, M.T.; Özger, F. Statistical blending-type approximation by a class of operators that includes shape parameters λ and α. Mathematics 2022, 10, 1149. [Google Scholar] [CrossRef]
- Ansari, K.J.; Özger, F.; Özger, Z.Ö. Numerical and theoretical approximation results for Schurer–Stancu operators with shape parameter λ. Comput. Appl. Math. 2022, 41, 1–18. [Google Scholar] [CrossRef]
- Kanat, K.; Sofyalıoğlu, M. Approximation by (p, q)-Lupaş–Schurer–Kantorovich operators. J. Inequalities Appl. 2018, 2018, 1–17. [Google Scholar] [CrossRef]
- Kanat, K.; Sofyalioğlu, M. On Stancu type generalization of (p, q)-Baskakov-Kantorovich operators. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2019, 68, 1995–2013. [Google Scholar] [CrossRef]
- Kadak, U.; Özlük, M. Extended Bernstein-Kantorovich-Stancu operators with multiple parameters and approximation properties. Numer. Funct. Anal. Optim. 2021, 42, 523–550. [Google Scholar] [CrossRef]
- Wang, X.; Wang, A.; Wang, D.; Song, K.; Ni, Y.; Qi, Y. Multi-task Trajectory Tracking Control of Manipulator Based on Two-Layer Sliding Mode Control. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 25–27 February 2022; IEEE: Manhattan, NY, USA, 2022. [Google Scholar] [CrossRef]
- Kadak, U.; Özger, F. A numerical comparative study of generalized Bernstein-Kantorovich operators. Math. Found. Comput. 2021, 4, 311. [Google Scholar] [CrossRef]
- Huang, K.-L.; Ge, M.-F.; Liang, C.-D.; Dong, J.-W.; Zhao, X.-W. Hierarchical predefined-time control for time-varying formation tracking of multiple heterogeneous Euler–Lagrange agents. Nonlinear Dyn. 2021, 105, 3255–3270. [Google Scholar] [CrossRef]
- Gong, D.; Pei, M.; He, R.; Yu, J. An extended state observer-based full-order sliding mode control for robotic joint actuated by antagonistic pneumatic artificial muscles. Int. J. Adv. Robot. Syst. 2021, 18, 1729881420986036. [Google Scholar] [CrossRef]
- Nasiruzzaman, M.; Srivastava, H.M.; Mohiuddine, S.A. Approximation Process Based on Parametric Generalization of Schurer–Kantorovich Operators and their Bivariate Form. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2022. [Google Scholar] [CrossRef]
- Rahman, S.; Mursaleen, M.; Acu, A.M. Approximation properties of λ-Bernstein-Kantorovich operators with shifted knots. Math. Methods Appl. Sci. 2019, 42, 4042–4053. [Google Scholar] [CrossRef]


| Type of Operator | ||
|---|---|---|
| BK | 0.89441 | 0.31056 |
| -BK | 1.08117 | 1.07137 |
| -BK | 0.80731 | 0.30193 |
| -BK | 0.87743 | 0.30175 |
| BKS | 0.71316 | 0.24901 |
| Parameters | Value |
|---|---|
| 5 | |
| 10 | |
| 2/3 | |
| * | (−2.0, 4, 5.5, 4, −2.0) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Mu, M.; Wang, X. A Modified Robotic Manipulator Controller Based on Bernstein-Kantorovich-Stancu Operator. Micromachines 2023, 14, 44. https://doi.org/10.3390/mi14010044
Zhang Q, Mu M, Wang X. A Modified Robotic Manipulator Controller Based on Bernstein-Kantorovich-Stancu Operator. Micromachines. 2023; 14(1):44. https://doi.org/10.3390/mi14010044
Chicago/Turabian StyleZhang, Qianqian, Mingye Mu, and Xingyu Wang. 2023. "A Modified Robotic Manipulator Controller Based on Bernstein-Kantorovich-Stancu Operator" Micromachines 14, no. 1: 44. https://doi.org/10.3390/mi14010044
APA StyleZhang, Q., Mu, M., & Wang, X. (2023). A Modified Robotic Manipulator Controller Based on Bernstein-Kantorovich-Stancu Operator. Micromachines, 14(1), 44. https://doi.org/10.3390/mi14010044





