Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space
Abstract
1. Introduction
2. Cross-Spectral Density Function
3. Coherent Mode Representation
3.1. Nonparaxial Propagation in Free Space
3.2. Modified Partially Coherent Vortex Bessel–Gauss Beams
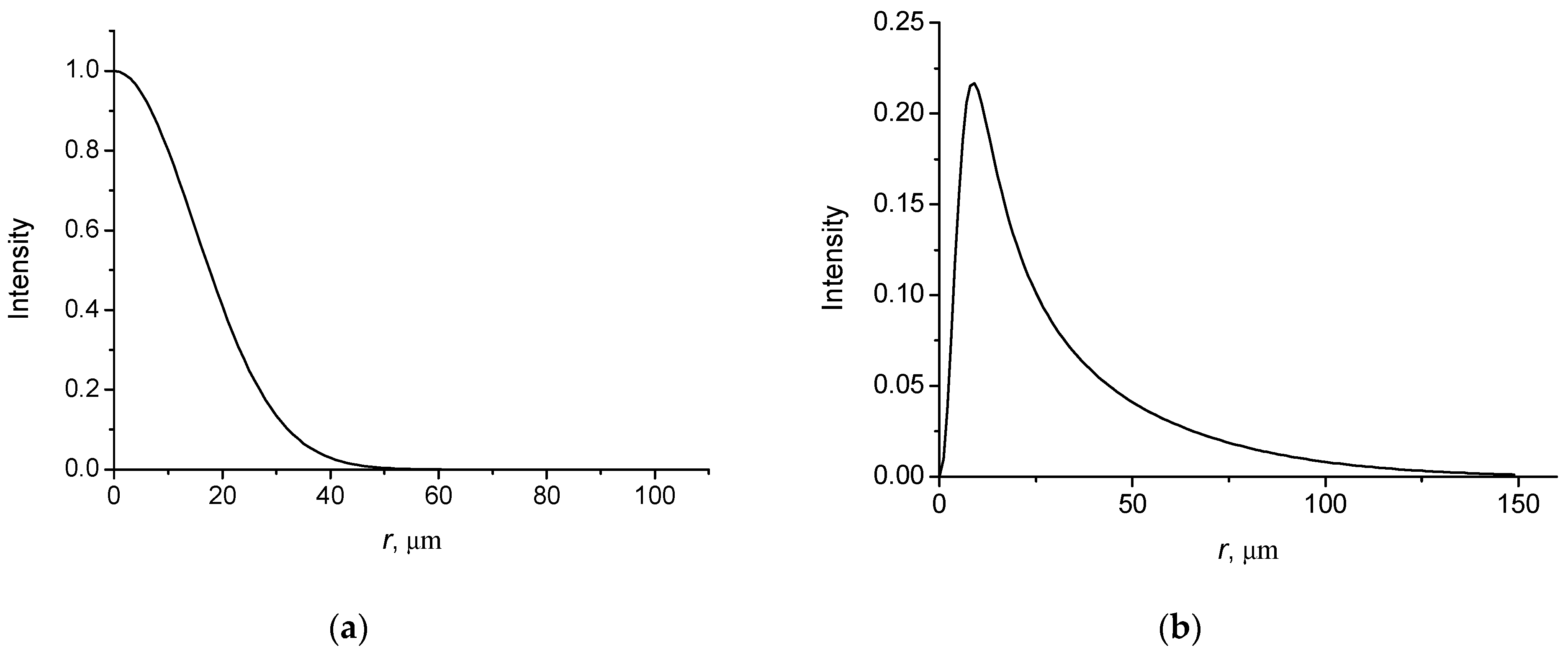
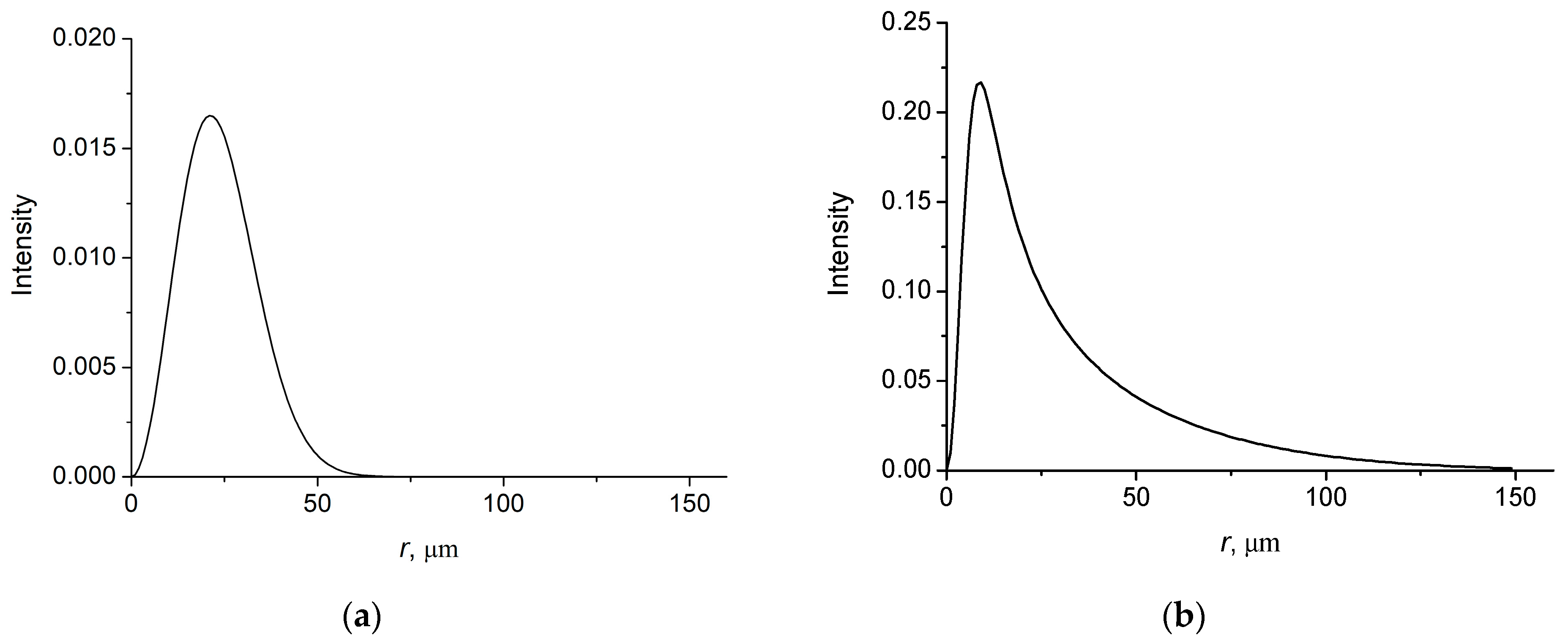
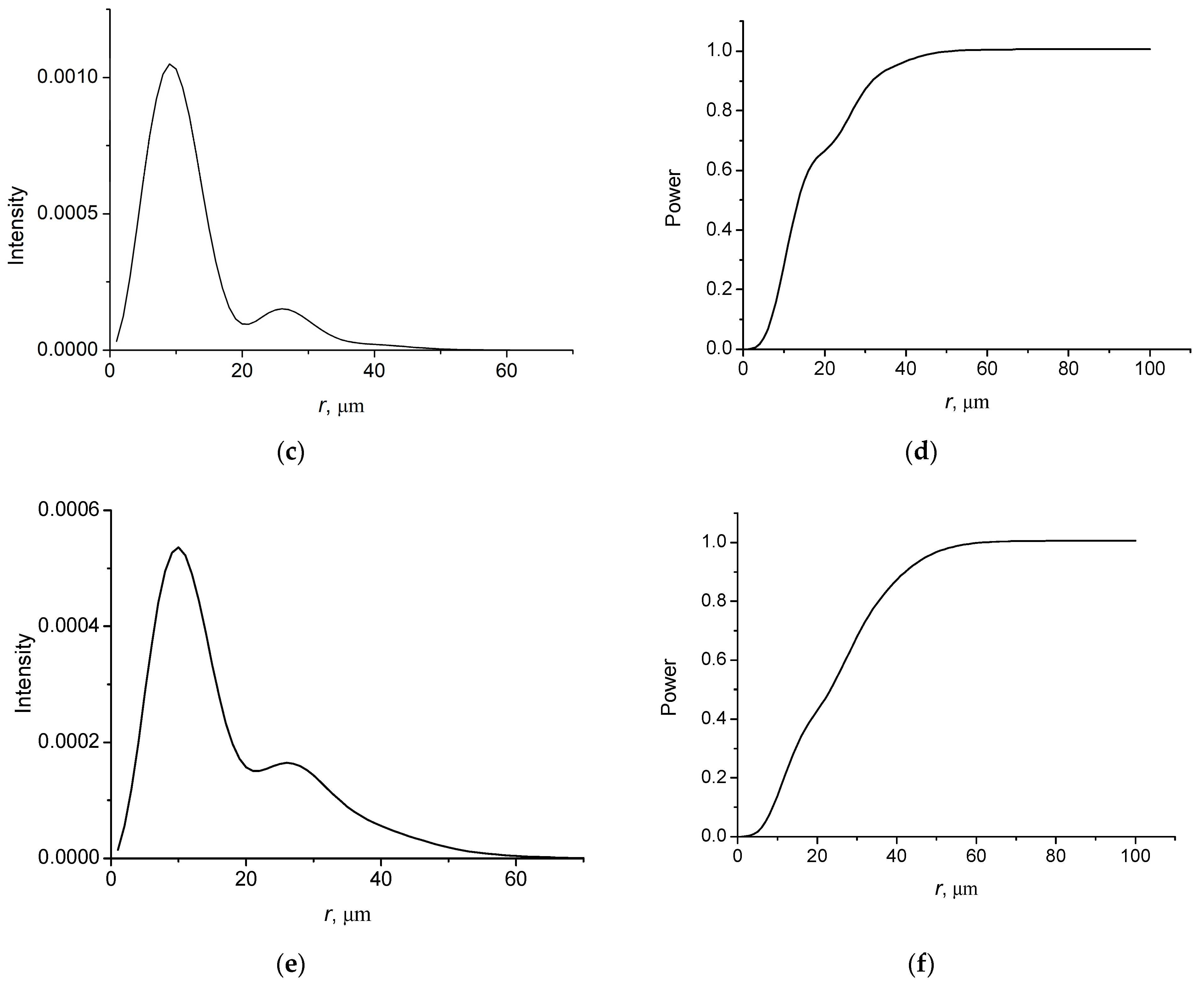
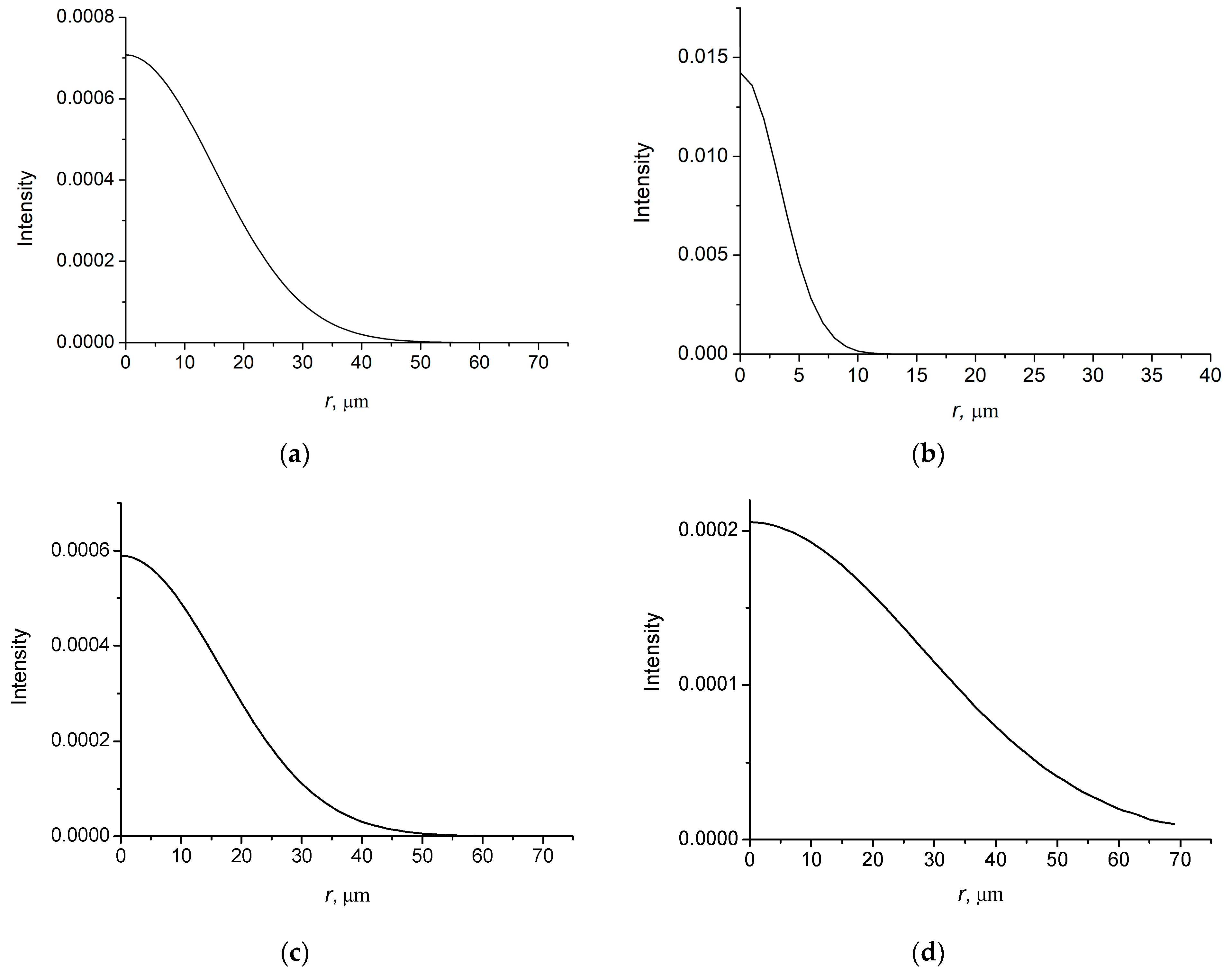
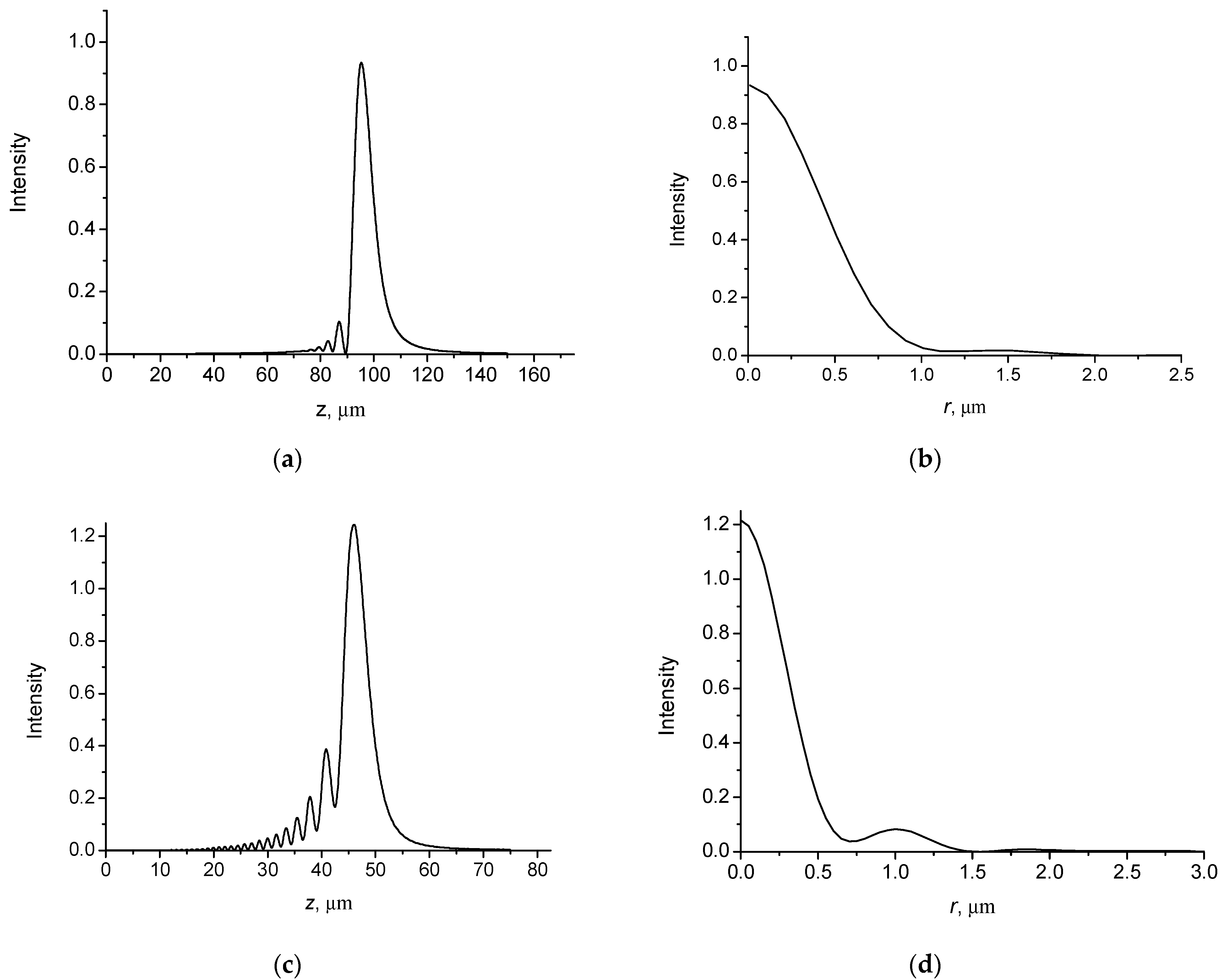
4. Propagation of Coherent Vortex Bessel–Gauss Beams
4.1. Bessel–Gauss Beam with l = 0
4.2. Bessel–Gauss Beam with l = 1
4.3. Nonparaxial Propagation and Focusing of a Gaussian Beam
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
- Tervo, J.; Setala, T.; Friberg, A.T. Theory of partially coherent electromagnetic fields in the space-frequency domain. J. Opt. Soc. Am. A 2004, 21, 2205–2215. [Google Scholar] [CrossRef]
- Wolf, E.; Collett, E. Partially coherent sources which produce the same far-field intensity distribution as a laser. Opt. Commun. 1978, 25, 293–296. [Google Scholar] [CrossRef]
- Foley, J.T.; Zubairy, M. The directionality of gaussian Schell-model beams. Opt. Commun. 1978, 26, 297–300. [Google Scholar] [CrossRef]
- Gori, F.; Palma, C. Partially coherent sources which give rise to highly directional light beams. Opt. Commun. 1978, 27, 185–188. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Van Dijk, T.; Gbur, G.; Visser, T.D. Shaping the focal intensity distribution using spatial coherence. J. Opt. Soc. Am. A 2008, 25, 575–581. [Google Scholar] [CrossRef]
- Palacios, D.M.; Maleev, I.D.; Marathay, A.S.; Swartzlander, G.A. Spatial Correlation Singularity of a Vortex Field. Phys. Rev Lett. 2004, 92, 143905. [Google Scholar] [CrossRef]
- Bogatyryova, G.V.; Fel’de, C.V.; Polyanskii, P.V.; Ponomarenko, S.A.; Soskin, M.S.; Wolf, E. Partially coherent vortex beams with a separable phase. Opt. Lett. 2003, 28, 878–880. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, M.; Mazilu, M.; Mourka, A.; Liu, Y.D.; Dholakia, K. Effect of the radial and azimuthal mode indices of a partially coherent vortex field upon a spatial correlation singularity. N. J. Phys. 2013, 15, 113053. [Google Scholar] [CrossRef][Green Version]
- Yang, Y.; Liu, Y.D. Measuring azimuthal and radial mode indices of a partially coherent vortex field. J. Opt. 2016, 18, 015604. [Google Scholar]
- Alieva, T.; Rodrigo, J.A.; Camara, A.; Abramochkin, E. Partially coherent stable and spiral beams. JOSA A 2013, 30, 2237–2243. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Twisted Gaussian Schell-model beams as series of partially coherent modified Bessel–Gauss beams. Opt. Lett. 2015, 40, 1587–1590. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zeng, J.; Cai, Y. Review on vortex beams with low spatial coherence. Adv. Phys. 2019, 4, 1626766. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, R.; Liu, X.; Zhao, C.; Cai, Y. Review on partially coherent vortex beams. Front. Optoelectron. 2019, 12, 229–248. [Google Scholar] [CrossRef]
- Dong, M.; Zhao, C.; Cai, Y.; Yang, Y. Partially coherent vortex beams: Fundamentals and applications. Sci. China Phys. Mech. Astron. 2021, 64, 1–19. [Google Scholar]
- Martínez-Herrero, R.; Santarsiero, M.; Piquero, G.; González de Sande, J.C. A New Type of Shape-Invariant Beams with Structured Coherence: Laguerre-Christoffel-Darboux Beams. Photonics 2021, 8, 134. [Google Scholar] [CrossRef]
- Santarsiero, M.; Martínez-Herrero, R.; Piquero, G.; de Sande, J.C.G.; Gori, F. Modal Analysis of Pseudo-Schell Model Sources. Photonics 2021, 8, 449. [Google Scholar] [CrossRef]
- Korotkova, O.; Hoover, B.G.; Gamiz, V.L.; Wolf, E. Coherence and polarization properties of far fields generated by quasi-homogeneous planar electromagnetic sources. JOSA A 2005, 22, 2547–2556. [Google Scholar] [CrossRef]
- Dong, Y.; Cai, Y.; Zhao, C.; Yao, M. Statistics properties of a cylindrical vector partially coherent beams. Opt. Exp. 2011, 19, 5979–5992. [Google Scholar] [CrossRef]
- Dong, Y.; Feng, F.; Chen, Y.; Zhao, C.; Cai, Y. Statistical properties of a nonparaxial cylindrical vector partially coherent field in free space. Opt. Exp. 2012, 20, 15908–15927. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, S.A. A class of partially coherent beams carrying optical vortices. J. Opt. Soc. Am. A 2001, 18, 150–156. [Google Scholar] [CrossRef] [PubMed]
- Ostrovsky, A.S.; García-García, J.; Rickenstorff-Parrao, C.; Olvera-Santamaria, M.A. Partially coherent diffraction-free vortex beams with a Bessel-mode structure. Opt. Lett. 2017, 42, 5182–5185. [Google Scholar] [CrossRef] [PubMed]
- Santamaría, M.A.O.; Garciapiña, J.L.R.; García, J.G.; Ostrovsky, A.S. Generation of a partially coherent secondary source with Bessel-mode vortex structure by liquid crystal spatial light modulator. Opt. Commun. 2019, 439, 312–316. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Rafsanjani, S.M.H.; Korotkova, O. Synthesis of Im-Bessel correlated beams via coherent modes. Opt. Lett. 2018, 43, 3590–3593. [Google Scholar] [CrossRef] [PubMed]
- Ferlic, N.A.; van Iersel, M.; Davis, C.C. Simulation of Im-Bessel beam propagation through time-correlated atmospheric turbulence. Proc. SPIE 2021, 11834, 118340L. [Google Scholar]
- Krivoshlykov, S.G.; Petrov, N.I.; Sisakyan, I.N. Spatial coherence of optical fields in longitudinally inhomogeneous media with the square-law index profile. Sov. J. Quantum Electron. 1985, 15, 330–338. [Google Scholar] [CrossRef]
- Krivoshlykov, S.G.; Petrov, N.I.; Sisakyan, I.N. Density-matrix formalism for partially coherent optical fields propagating in slightly inhomogeneous media. Opt. Quant. Electr. 1986, 18, 253–264. [Google Scholar] [CrossRef]
- Krivoshlykov, S.G.; Petrov, N.I.; Sisakyan, I.N. Excitation of modes of the waveguides with the square-law refractive index profile by the partially coherent radiation sources. Zh. Tekhnich. Fiz. 1985, 55, 1763–1772. [Google Scholar]
- Gori, F. Matrix treatment for partially polarized, partially coherent beams. Opt. Lett. 1998, 23, 241–243. [Google Scholar] [CrossRef]
- Soifer, V.A.; Korotkova, O.; Khonina, S.N.; Shchepakina, E.A. Vortex beams in turbulent media: Review. Comput. Opt. 2016, 40, 605–624. [Google Scholar] [CrossRef]
- Petrov, N.I. Holographic diffuser with controlled scattering indicatrix. Comp. Opt. 2017, 41, 831–836. [Google Scholar] [CrossRef]
- Petrov, N.I.; Petrova, G.N. Diffraction of partially coherent light beams by micro-lens arrays. Opt. Express 2017, 25, 22545–22564. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Yin, H.; Wang, Y. Nonparaxial propagation of a partially coherent Lorentz-Gauss beam. Optik 2018, 155, 190–199. [Google Scholar]
- Liu, D.; Zhong, H.; Wang, G.; Yin, H.; Wang, Y. Nonparaxial propagation of a partially coherent four-petal Gaussian vortex beam. Optik 2018, 158, 451–459. [Google Scholar]
- Yuan, Y.; Du, S.; Dong, Y.; Wang, F.; Zhao, C.; Cai, Y. Nonparaxial propagation properties of a vector partially coherent dark hollow beam. JOSA A 2013, 30, 1358–1372. [Google Scholar] [CrossRef]
- Guo, L.; Chen, L.; Lin, R.; Zhang, M.; Dong, Y.; Chen, Y.; Cai, Y. Nonparaxial Propagation Properties of Specially Correlated Radially Polarized Beams in Free Space. Appl. Sci. 2019, 9, 997. [Google Scholar] [CrossRef]
- Fischer, D.G.; Visser, T.D. Spatial correlation properties of focused partially coherent light. J. Opt. Soc. Am. A 2004, 21, 2097–2102. [Google Scholar] [CrossRef]
- Petrov, N.I. Nonparaxial focusing of wave beams in a graded-index medium. Rus. J. Quant. Electron. 1999, 29, 249–255. [Google Scholar] [CrossRef]
- Petrov, N.I. Focusing of beams into subwavelength area in an inhomogeneous medium. Opt. Exp. 2001, 9, 658–673. [Google Scholar] [CrossRef]
- Petrov, N.I. Macroscopic quantum effects for classical light. Phys. Rev. A 2014, 90, 043814. [Google Scholar] [CrossRef]
- Ping, C.; Liang, C.H.; Wang, F.; Cai, Y.J. Radially polarized multi-Gaussian Schell-model beam and its tight focusing properties. Opt. Express 2017, 25, 32475–32490. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, S.; Cai, Y. Experimental study of the focusing properties of a Gaussian Schell-model vortex beam. Opt. Lett. 2011, 36, 3281–3283. [Google Scholar] [CrossRef]
- Zhang, Z.; Pu, J.; Wang, X. Focusing of partially coherent Bessel–Gaussian beams through a high numerical-aperture objective. Opt. Lett. 2008, 33, 49–51. [Google Scholar] [CrossRef]
- Foreman, M.R.; Torok, P. Focusing of spatially inhomogeneous partially coherent, partially polarized electromagnetic fields. J. Opt. Soc. Am. A 2009, 26, 2470–2479. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Z.; Pu, J. Tight focusing of partially coherent and circularly polarized vortex beams. J. Opt. Soc. Am A 2009, 26, 862–869. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, X.; Chen, Z.; Sasaki, O.; Li, Y.; Pu, J. Tight focusing properties of a circular partially coherent Gaussian beam. J. Opt. Soc. Am. A 2018, 35, 1974–1980. [Google Scholar] [CrossRef]
- Petrov, N.I. Evanescent and propagating fields of a strongly focused beam. J. Opt. Soc. Am. A 2003, 20, 2385–2389. [Google Scholar] [CrossRef]
- Petrov, N.I. Reflection and transmission of strongly focused light beams at a dielectric interface. J. Mod. Opt. 2005, 52, 1545–1556. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, F.; Zhao, C.; Cai, Y. Experimental demonstration of a Laguerre-Gaussian correlated Schell-model vortex beam. Opt. Expr. 2014, 22, 5826–5838. [Google Scholar] [CrossRef]
- Petrov, N.I. Speed of structured light pulses in free space. Sci. Rep. 2019, 9, 18332. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. J. Opt. Soc. Am. 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Petrov, N.I.; Sissakian, I.N.; Syssoev, V.S. Computer optics elements in the diagnostics of disperse systems. Comp. Opt. 1988, 3, 97–100. [Google Scholar]
- Valyaev, A.B.; Krivoshlykov, S.G. Mode properties of Bessel beams. Sov. J. Quant. Electr. 1989, 19, 679–680. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Soifer, V.A.; Khonina, S.N. Phase optical components for the generation of free space quasimodes. Quant. Electron. 1991, 21, 1278–1281. [Google Scholar] [CrossRef]
- Bouchal, Z.; Olivik, M. Non-diffractive vector Bessel beams. J. Mod. Opt. 1995, 42, 1555–1566. [Google Scholar] [CrossRef]
- Bouchal, Z.; Perina, J. Non-diffracting beams with controlled spatial coherence. J. Mod. Opt. 2002, 49, 1673–1689. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brichkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon: New York, NY, USA, 1992. [Google Scholar]
- Gori, F.; Guattari, G. Bessel-Gaussian beams. Opt. Commun. 1987, 64, 491–495. [Google Scholar] [CrossRef]
- Stamnes, J.J. Hybrid integration technique for efficient and accurate computation of diffraction integrals. J. Opt. Soc. Am. A 1989, 6, 1330–1342. [Google Scholar] [CrossRef]
- Eide, H.A.; Stamnes, J.J. Exact and approximate solutions for focusing of two-dimensional waves. J. Opt. Soc. Am. A 1998, 15, 1285–1319. [Google Scholar]
- Setälä, T.; Saastamoinen, K.; Friberg, A.T. Coherence Stokes Parameters in the Description of Electromagnetic Coherence. Photonics 2021, 8, 85. [Google Scholar] [CrossRef]
- Korotkova, O.; Visser, T.D.; Wolf, E. Polarization properties of stochastic electromagnetic beams. Opt. Commun. 2008, 281, 515–520. [Google Scholar] [CrossRef]
- Ellis, J.; Dogariu, A.; Ponomarenko, S.; Wolf, E. Degree of polarization of statistically stationary electromagnetic fields. Opt. Commun. 2005, 248, 333–337. [Google Scholar] [CrossRef]
- Salem, M.; Wolf, E. Coherence-induced polarization changes in light beams. Opt. Lett. 2008, 33, 1180–1182. [Google Scholar] [CrossRef]
- Vidal, I.; Fonseca, E.J.S.; Hickmann, J.M. Light polarization control during free-space propagation using coherence. Phys. Rev. A 2011, 84, 033836. [Google Scholar] [CrossRef]
- Wu, G.; Wang, F.; Cai, Y. Coherence and polarization properties of a radially polarized beam with variable spatial coherence. Opt. Exp. 2012, 20, 28301–28318. [Google Scholar] [CrossRef]
- Korotkova, O. Sufficient condition for polarization invariance of beams generated by quasi-homogeneous sources. Opt. Lett. 2011, 36, 3768–3770. [Google Scholar] [CrossRef]
- Wu, G. Propagation properties of a radially polarized partially coherent twisted beam in free space. JOSA A 2016, 33, 345–350. [Google Scholar] [CrossRef]
- Agrawal, G.P.; Wolf, E. Propagation-induced polarization changes in partially coherent optical beams. J. Opt. Soc. Am. A 2000, 17, 2019–2023. [Google Scholar] [CrossRef]
- Zhao, X.; Visser, T.D.; Agrawal, G.P. Controlling the degree of polarization of partially coherent electromagnetic beams with lenses. Opt. Lett. 2018, 43, 2344–2347. [Google Scholar] [CrossRef]
- Joshi, S.; Khan, S.N.; Manisha; Senthilkumaran, P.; Kanseri, B. Coherence-induced polarization effects in vector vortex beams. Opt. Lett. 2020, 45, 4815–4818. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I. Vector and Tensor Polarizations of Light Beams. Las. Phys. 2008, 18, 522–525. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-orbit and tensor interactions of light in inhomogeneous isotropic media. Phys. Rev. A 2013, 88, 023815. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of light in a graded-index isotropic medium. J. Mod. Opt. 1996, 43, 2239–2249. [Google Scholar] [CrossRef]
- Petrov, N.I. Evolution of polarization in an inhomogeneous isotropic medium. JETP 1997, 85, 1085–1093. [Google Scholar] [CrossRef]
- Otte, E.; Nape, I.; Rosales-Guzmán, C.; Valles, A.; Denz, C.; Forbes, A. Recovery of nonseparability in self-healing vector Bessel beams. Phys. Rev. A 2018, 98, 053818. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector Laguerre–Gauss beams with polarization-orbital angular momentum entanglement in a graded-index medium. J. Opt. Soc. Am. A 2016, 33, 1363–1369. [Google Scholar] [CrossRef]
- Petrov, N.I. Splitting of levels in a cylindrical dielectric waveguide. Opt. Lett. 2013, 38, 2020–2022. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of Light in Optical Fibers: Effects of Diffraction and Spin-Orbit Interaction. Fibers 2021, 9, 34. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of vector light beams on propagation in free space. Photonics 2022, 9, 162. [Google Scholar] [CrossRef]
- Dong, M.; Bai, Y.; Yao, J.; Zhao, Q.; Yang, Y. Propagation properties of partially coherent modified Bessel-Gauss beams through the gradient-index medium. Appl. Opt. 2020, 59, 8023–8028. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Large positive and negative Goos-Hänchen shifts near the surface plasmon resonance in subwavelength grating. Opt. Exp. 2020, 28, 7552–7564. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I. Propagation of terahertz surface plasmon polaritons in a dielectric fiber with a metal wire core. Fibers 2022, 10, 89. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, N.I. Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space. Micromachines 2023, 14, 38. https://doi.org/10.3390/mi14010038
Petrov NI. Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space. Micromachines. 2023; 14(1):38. https://doi.org/10.3390/mi14010038
Chicago/Turabian StylePetrov, Nikolai I. 2023. "Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space" Micromachines 14, no. 1: 38. https://doi.org/10.3390/mi14010038
APA StylePetrov, N. I. (2023). Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space. Micromachines, 14(1), 38. https://doi.org/10.3390/mi14010038






