Measurement and Control System for Atomic Force Microscope Based on Quartz Tuning Fork Self-Induction Probe
Abstract
1. Introduction
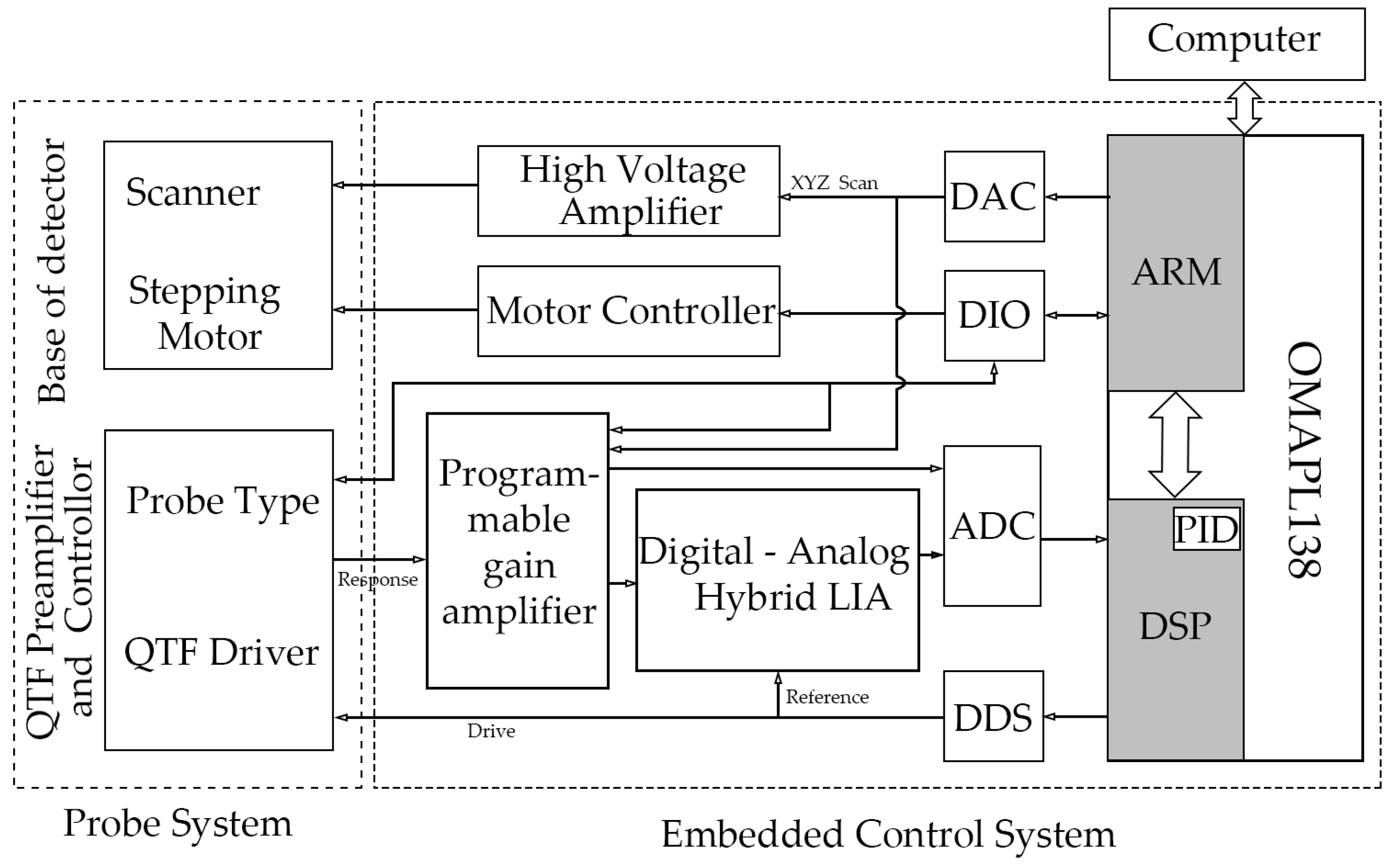
2. Hardware Control System
2.1. Embedded Control System
2.1.1. Microprocessor and Peripherals
2.1.2. Digital–Analog Hybrid Lock-In Amplifier
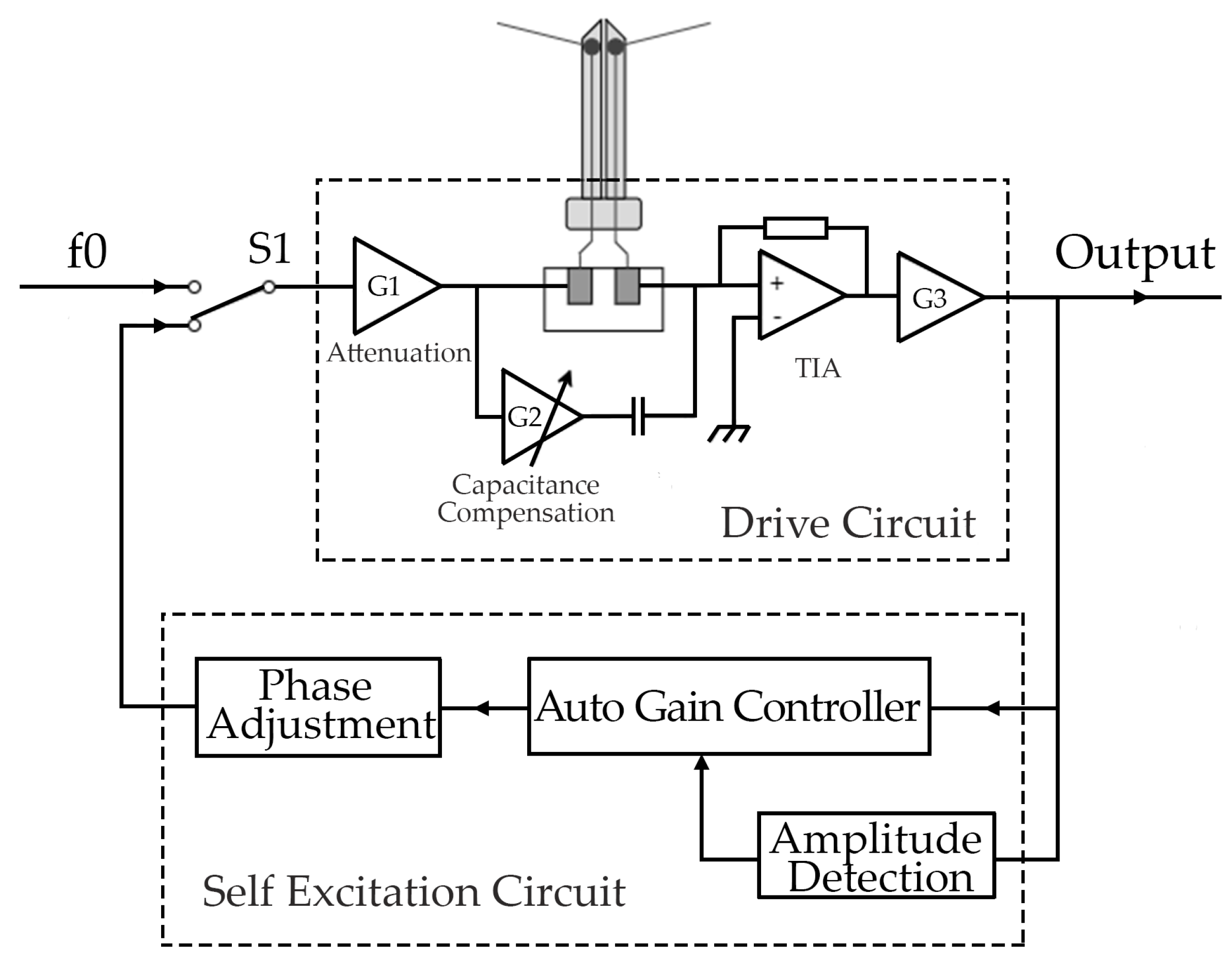
2.2. Probe System
2.2.1. Characteristics of the QTF Probe
2.2.2. Tuning Fork Pre-Circuit and Control
3. Control and Algorithm
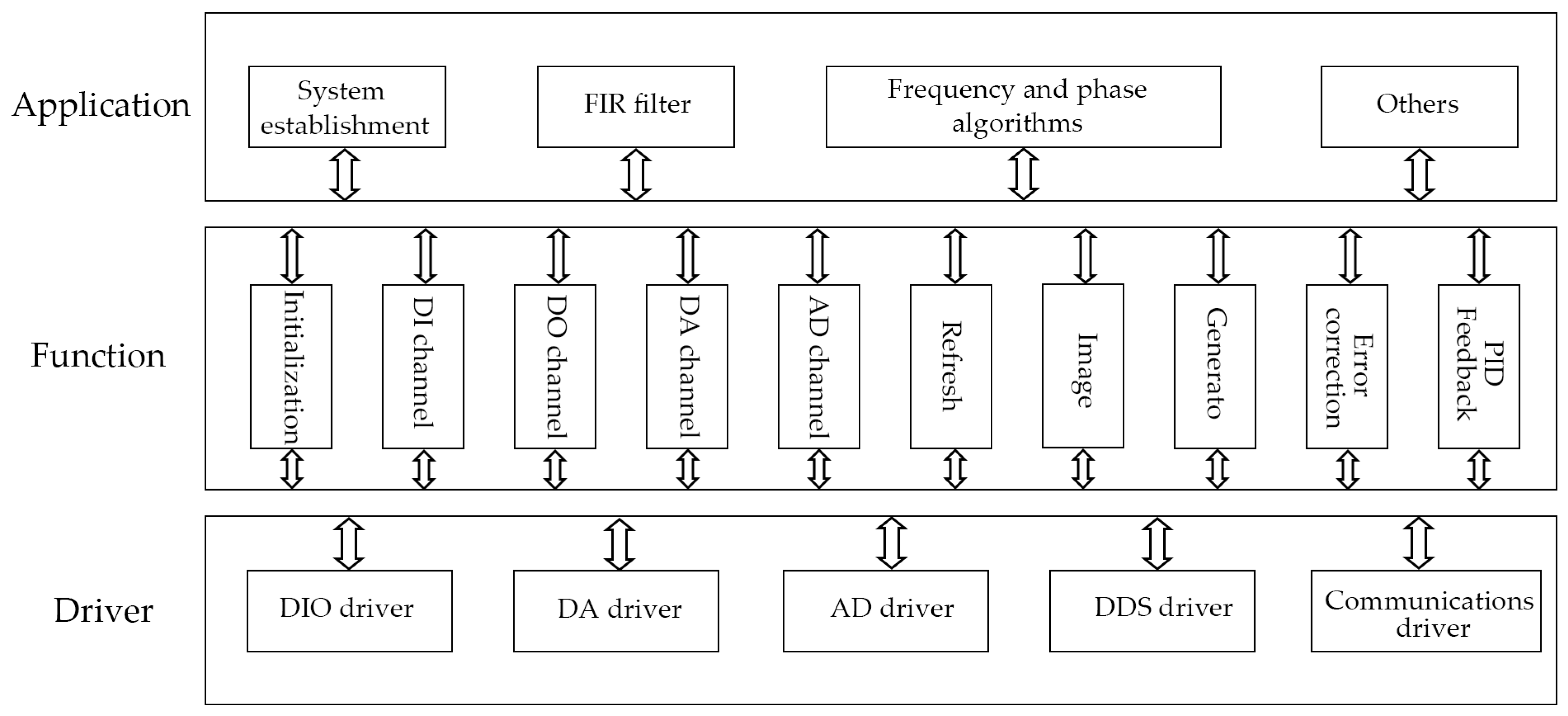
3.1. Software Structure of the Embedded Control System
3.2. Software Frequency Measurement Algorithm
3.3. Relative Error of Frequency Measurement
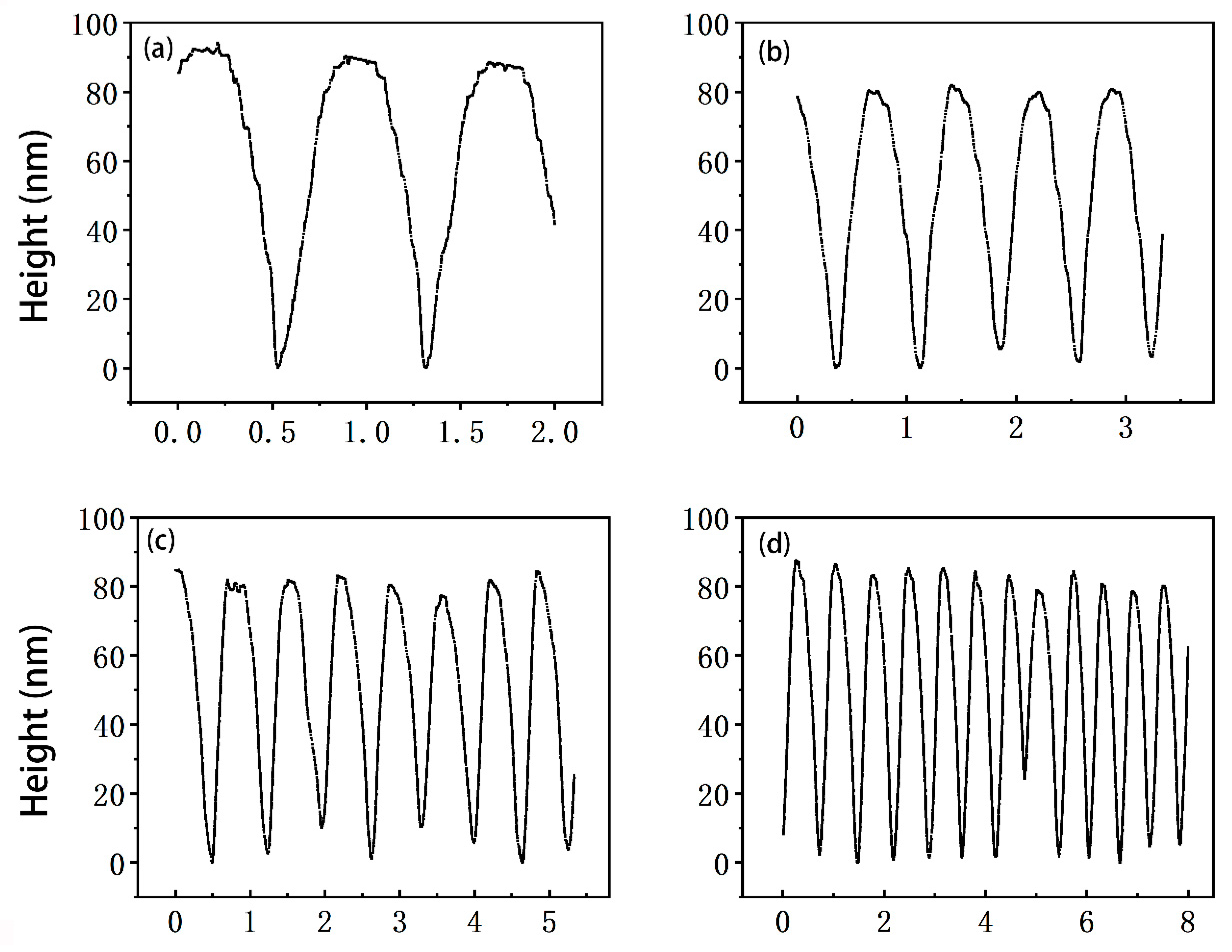
4. Characterization and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Binnig, G.K.; Quate, C.f.; Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Fan, P.; Gao, J.; Mao, H.; Geng, Y.; Yan, Y.; Wang, Y.; Goel, S.; Luo, X. Scanning Probe Lithography: State-of-the-Art and Future Perspectives. Micromachines 2022, 13, 228. [Google Scholar] [CrossRef] [PubMed]
- Porter, T.L. Scanning tunneling microscope data acquisition and control in visual basic. Rev. Sci. Instrum. 1993, 64, 3530–3533. [Google Scholar] [CrossRef]
- Altman, E.I.; Dilella, D.P.; Ibe, J.; Colton, R.J. Data acquisition and control system for molecule and atom-resolved tunneling spectroscopy. Rev. Sci. Instrum. 1993, 64, 1239–1243. [Google Scholar] [CrossRef]
- Hoeven, A.J.; Van Loenen, E.J.; Van Hooft, P.J.G.M.; Oostveen, K. A multiprocessor data acquisition and analysis system for scanning tunneling microscopy. Rev. Sci. Instrum. 1990, 61, 1668–1673. [Google Scholar] [CrossRef]
- Barchesi, C.; Cricenti, A.; Generosi, R.; Giammichele, C.; Luce, M.; Rinaldi, M. A flexible implementation of scanning probe microscopy utilizing a multifunction system linked to a PC-Pentium controller. Rev. Sci. Instrum. 1997, 68, 3799–3802. [Google Scholar] [CrossRef]
- Piner, R.; Reifenberger, R. Computer control of the tunnel barrier width for the scanning tunneling microscope. Rev. Sci. Instrum. 1989, 60, 3123–3127. [Google Scholar] [CrossRef]
- Aloisi, G.; Bacci, F.; Carlà, M.; Dolci, D.; Lanzi, L. Implementation on a desktop computer of the real time feedback control loop of a scanning probe microscope. Rev. Sci. Instrum. 2008, 79, 57. [Google Scholar] [CrossRef]
- Carminati, M.; Scandurra, G. Impact and trends in embedding field programmable gate arrays and microcontrollers in scientific instrumentation. Rev. Sci. Instrum. 2021, 92, 091501. [Google Scholar] [CrossRef]
- Wong, T.M.H.; Welland, M.E. A digital control system for scanning tunnelling microscopy and atomic force microscopy. Meas. Sci. Technol. 1993, 4, 270. [Google Scholar] [CrossRef]
- Davis, S.; Obstbaum, T.; Ari, G.B.; Sivan, U. A constant-frequency feedback loop for non-contact frequency-modulated atomic force microscopy via root locus: Implemented on a single-board field-programmable gate array device. Rev. Sci. Instrum. 2020, 91, 113702. [Google Scholar] [CrossRef] [PubMed]
- Giessibl, F.J. The qPlus sensor, a powerful core for the atomic force microscope. Rev. Sci. Instrum. 2019, 90, 011101. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, T.R.; Grütter, P.; Horne, D.; Rugar, D. Frequency modulation detection using high-Q cantilevers for enhanced force microscope sensitivity. J. Appl. Phys. 1991, 69, 668–673. [Google Scholar] [CrossRef]
- Fukuma, T.; Kimura, M.; Kobayashi, K.; Matsushige, K.; Yamada, H. Development of low noise cantilever deflection sensor for multienvironment frequency-modulation atomic force microscopy. Rev. Sci. Instrum. 2005, 76, 53704. [Google Scholar] [CrossRef]
- Kilpatrick, J.I.; Gannepalli, A.; Cleveland, J.P.; Jarvis, S.P. Frequency modulation atomic force microscopy in ambient environments utilizing robust feedback tuning. Rev. Sci. Instrum. 2009, 80, 23701. [Google Scholar] [CrossRef]
- Dagdeviren, O.E.; Schwarz, U.D. Accuracy of tip-sample interaction measurements using dynamic atomic force microscopy techniques: Dependence on oscillation amplitude, interaction strength, and tip-sample distance. Rev. Sci. Instrum. 2019, 90, 033707. [Google Scholar] [CrossRef]
- Hida, H.; Shikida, M.; Fukuzawa, K.; Murakami, S.; Sato, K.; Asaumi, K.; Iriye, Y.; Sato, K. Fabrication of a quartz tuning-fork probe with a sharp tip for AFM systems. Sens. Actuators A Phys. 2008, 148, 311–318. [Google Scholar] [CrossRef]
- Giessibl, F.J. High-speed force sensor for force microscopy and profilometry utilizing a quartz tuning fork. Appl. Phys. Lett. 1998, 73, 3956–3958. [Google Scholar] [CrossRef]
- Giessibl, F.J.; Bielefeldt, H.; Hembacher, S.; Mannhart, J. Calculation of the optimal imaging parameters for frequency modulation atomic force microscopy. Appl. Surf. Sci. 1999, 140, 352–357. [Google Scholar] [CrossRef]
- Giessibl, F.J.; Hembacher, S.; Herz, M.; Schiller, C.H.; Mannhart, J. Stability considerations and implementation of cantilevers allowing dynamic force microscopy with optimal resolution: The qPlus sensor. Nanotechnology 2004, 15, S79–S86. [Google Scholar] [CrossRef]
- Akiyama, T.; Staufer, U.; de Rooij, N.F. Self-sensing and self-actuating probe based on quartz tuning fork combined with microfabricated cantilever for dynamic mode atomic force microscopy. Appl. Surf. Sci. 2003, 210, 18–21. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Shan, G.; Song, Z.; Yang, R.; Li, H.; Qian, J. A homemade atomic force microscope based on a quartz tuning fork for undergraduate instruction. Am. J. Phys. 2016, 84, 478–482. [Google Scholar] [CrossRef]
- Rust, H.P.; Heyde, M.; Freund, H.J. Signal electronics for an atomic force microscope equipped with a double quartz tuning fork sensor. Rev. Sci. Instrum. 2006, 77, 120. [Google Scholar] [CrossRef]
- Átila, M.B.; José, M.B.; José, R.C.P. Phase-Locked Loop design applied to frequency-modulated atomic force microscope. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3835–3843. [Google Scholar]
- Xu, F.; Guo, X.; Xu, L.; Duan, X.; Zhang, H.; Pang, W.; Fu, X. Mechanical Vibration Measurement of Solidly Mounted Resonator in Fluid by Atomic Force Microscopy. Micromachines 2017, 8, 244. [Google Scholar] [CrossRef]
- Akiyama, T.; de Rooij, N.F.; Staufer, U.; Detterbeck, M.; Braendlin, D.; Waldmeier, S.; Scheidiger, M. Implementation and characterization of a quartz tuning fork based probe consisted of discrete resonators for dynamic mode atomic force microscopy. Rev. Sci. Instrum. 2010, 81, 063706. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Y.; Song, Z.; Lin, R.; Chen, Y.; Qian, J. A High-Q AFM Sensor Using a Balanced Trolling Quartz Tuning Fork in the Liquid. Sensors 2018, 18, 1628. [Google Scholar] [CrossRef]
- Seo, Y.; Choe, H.; Jhe, W. Atomic-resolution noncontact atomic force microscopy in air. Appl. Phys. Lett. 2003, 83, 1860–1862. [Google Scholar] [CrossRef]
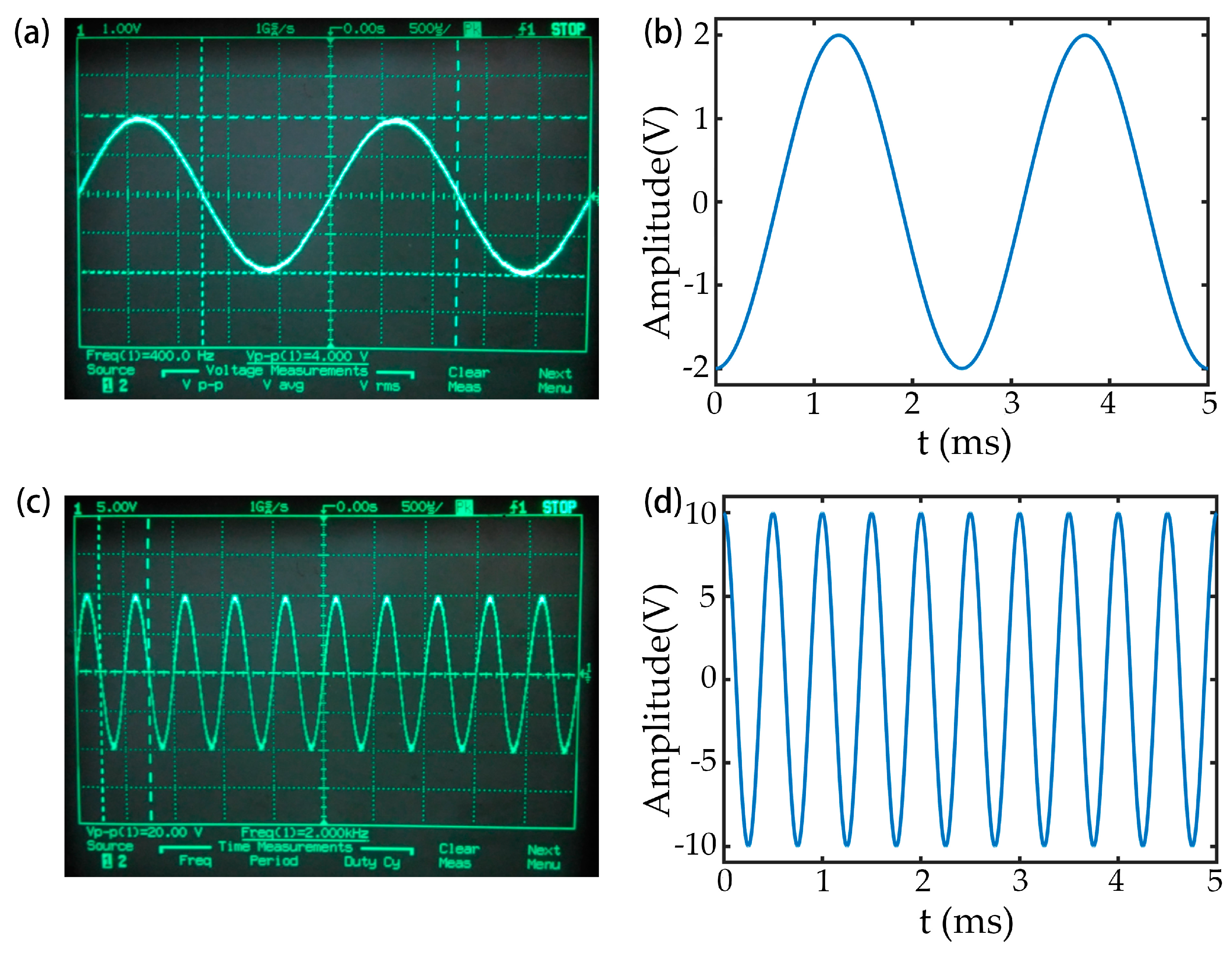
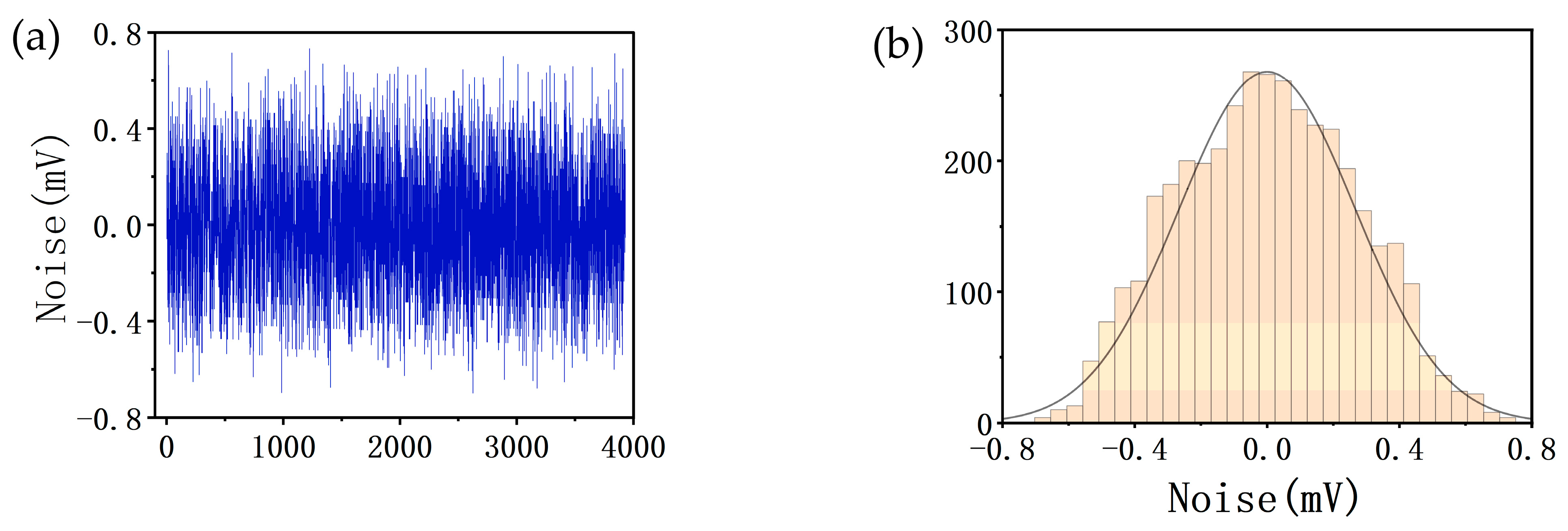


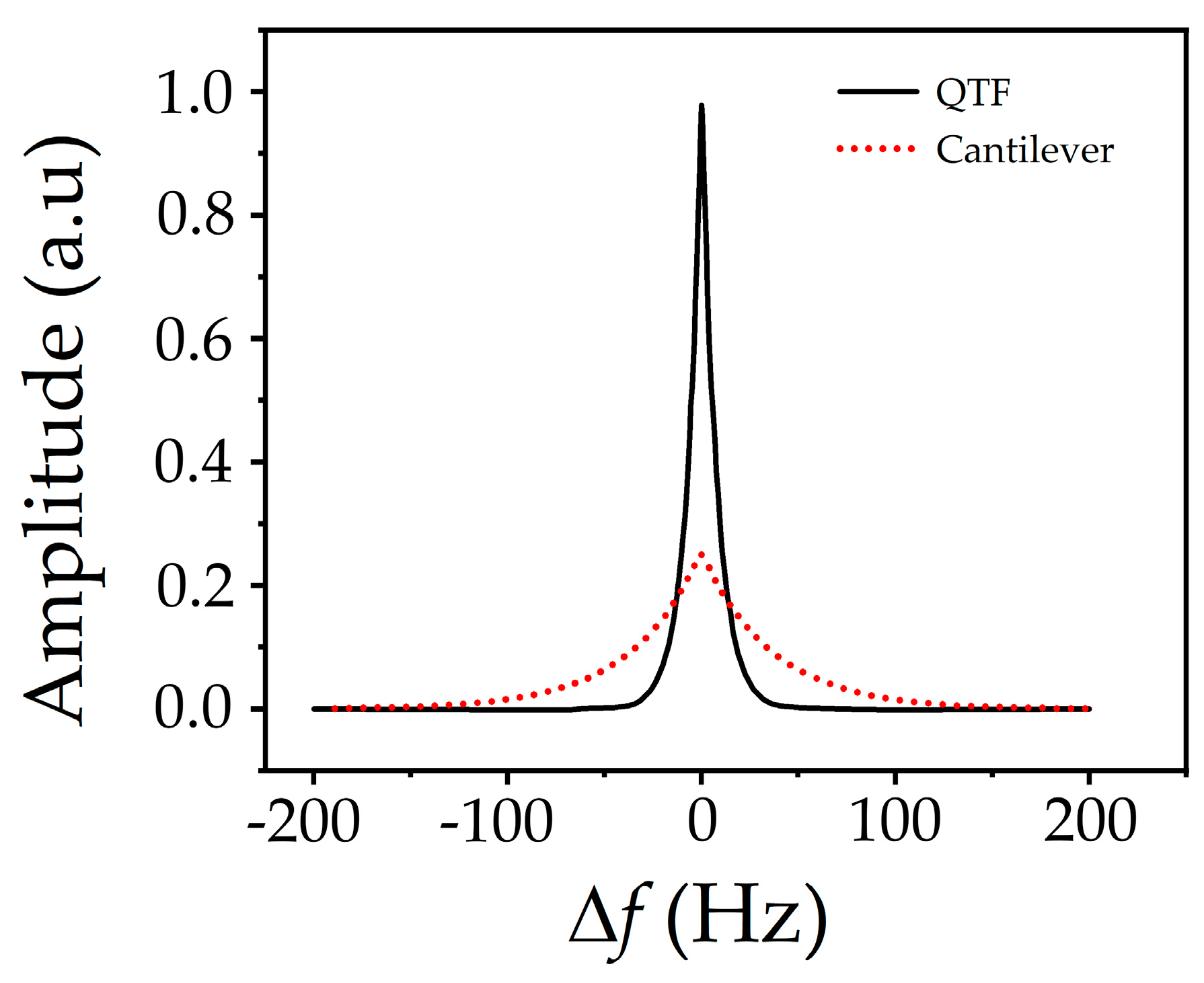



| Channel | AD0 | AD1 | AD2 | AD3 | AD4 | AD5 | AD6 | AD7 |
| Noise (mV) | 0.266 | 0.273 | 0.136 | 0.182 | 0.500 | 0.530 | 0.318 | 0.273 |
| Channel | AD8 | AD9 | AD10 | AD11 | AD12 | AD13 | AD14 | AD15 |
| Noise (mV) | 0.182 | 0.227 | 0.136 | 0.091 | 0.227 | 0.182 | 0.500 | 0.500 |
| Frequency Shift | τ = 40 T | τ = 50 T | ||
|---|---|---|---|---|
| Output Voltage (mV) | Frequency (Hz) | Output Voltage (mV) | Frequency (Hz) | |
| 10 | 190.0 ± 10 | 9.50 ± 0.50 | 192.5 ± 12.5 | 9.63 ± 0.63 |
| 20 | 392.5 ± 17.5 | 19.63 ± 0.88 | 392.5 ± 17.5 | 19.63 ± 0.88 |
| 30 | 585.0 ± 25 | 29.25 ± 1.25 | 592.5 ± 27.5 | 29.63 ± 1.38 |
| 40 | 785.0 ± 35 | 39.25 ± 1.75 | 790 ± 30 | 39.50 ± 1.50 |
| 50 | 980.0 ± 40 | 49.0 ± 2.00 | 990 ± 40 | 49.50 ± 2.00 |
| 60 | 1170.0 ± 40 | 58.50 ± 2.00 | 1185 ± 45 | 59.25 ± 2.25 |
| 70 | 1380.0 ± 50 | 69.00 ± 2.50 | 1385 ± 55 | 69.50 ± 2.75 |
| 80 | 1580.0 ± 60 | 79.00 ± 3.00 | 1580 ± 60 | 79.00 ± 3.00 |
| 90 | 1775.0 ± 65 | 88.75 ± 3.25 | 1780 ± 65 | 89.00 ± 3.25 |
| 100 | 1970.0 ± 70 | 98.50 ± 3.50 | 1980 ± 70 | 99.00 ± 3.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Ding, X.; Chen, T.; Su, T.; Chen, D. Measurement and Control System for Atomic Force Microscope Based on Quartz Tuning Fork Self-Induction Probe. Micromachines 2023, 14, 227. https://doi.org/10.3390/mi14010227
Luo Y, Ding X, Chen T, Su T, Chen D. Measurement and Control System for Atomic Force Microscope Based on Quartz Tuning Fork Self-Induction Probe. Micromachines. 2023; 14(1):227. https://doi.org/10.3390/mi14010227
Chicago/Turabian StyleLuo, Yongzhen, Xidong Ding, Tianci Chen, Tao Su, and Dihu Chen. 2023. "Measurement and Control System for Atomic Force Microscope Based on Quartz Tuning Fork Self-Induction Probe" Micromachines 14, no. 1: 227. https://doi.org/10.3390/mi14010227
APA StyleLuo, Y., Ding, X., Chen, T., Su, T., & Chen, D. (2023). Measurement and Control System for Atomic Force Microscope Based on Quartz Tuning Fork Self-Induction Probe. Micromachines, 14(1), 227. https://doi.org/10.3390/mi14010227








