Efficiency Optimization of the Electroerosive Process in µ-WEDM of Steel MS1 Sintered Using DMLS Technology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Modeling and Optimization of the µ-WEDM Process Efficiency
2.2. Identification of MTP in Relation to MRR and Roughness Parameter Rz in the µ-WEDM Process
2.3. Conditions of the Experiment
3. Results and Discussion
3.1. DoE Statistical Analysis of Experimentally Measured MRR and Rz Data at µ-WEDM
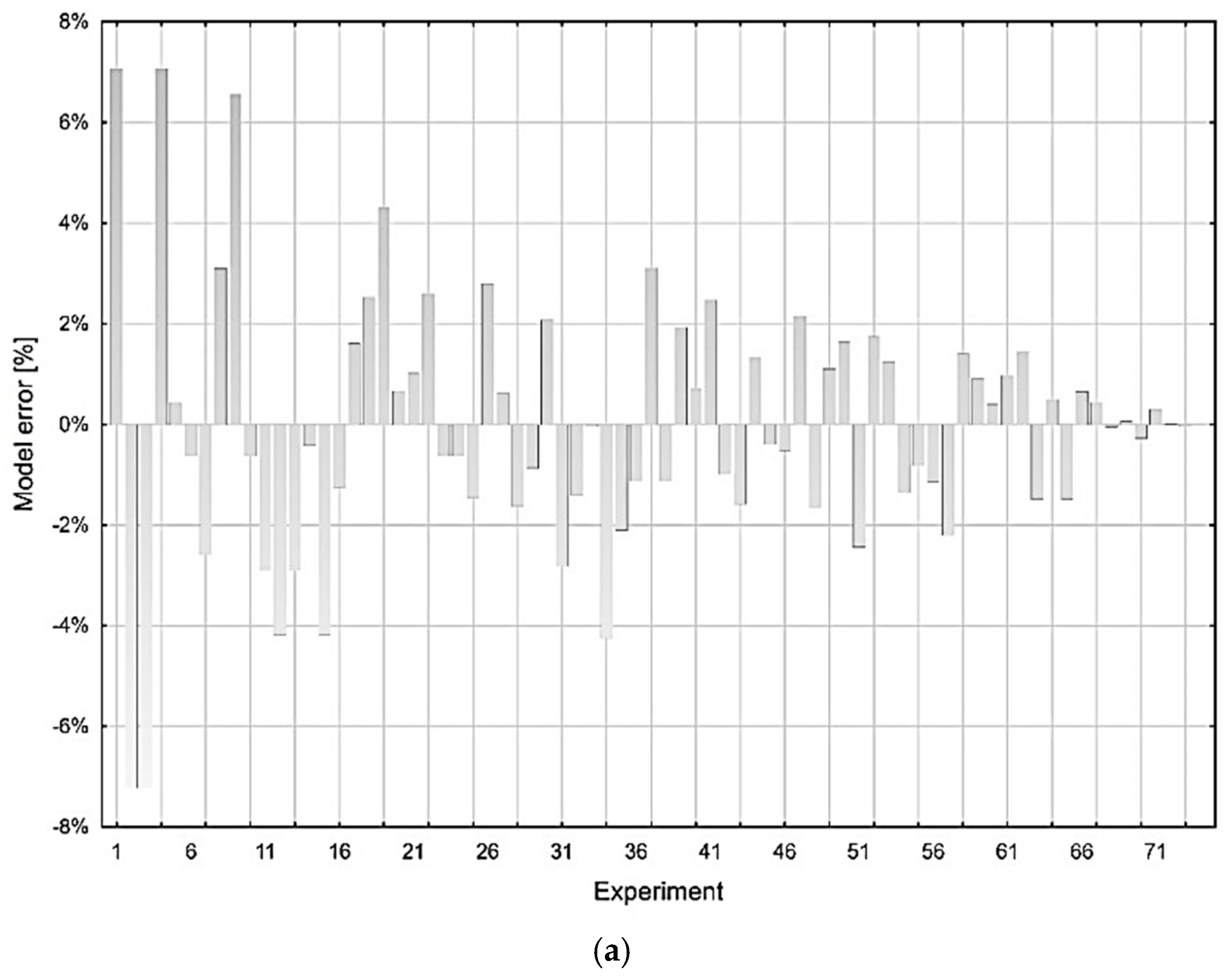
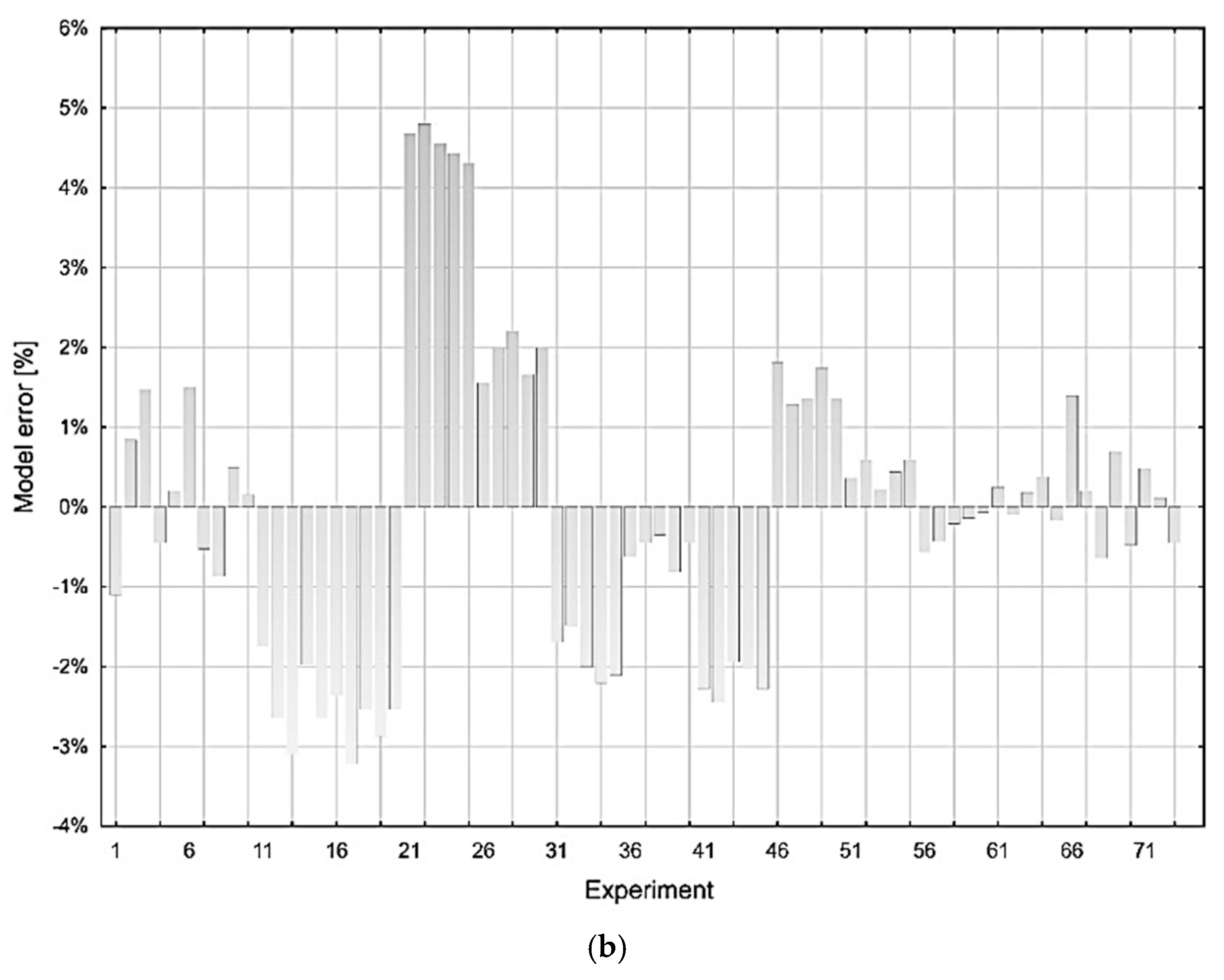
3.2. Design and Validation of the MSC Model for the Prediction of MRR and Rz at µ-WEDM
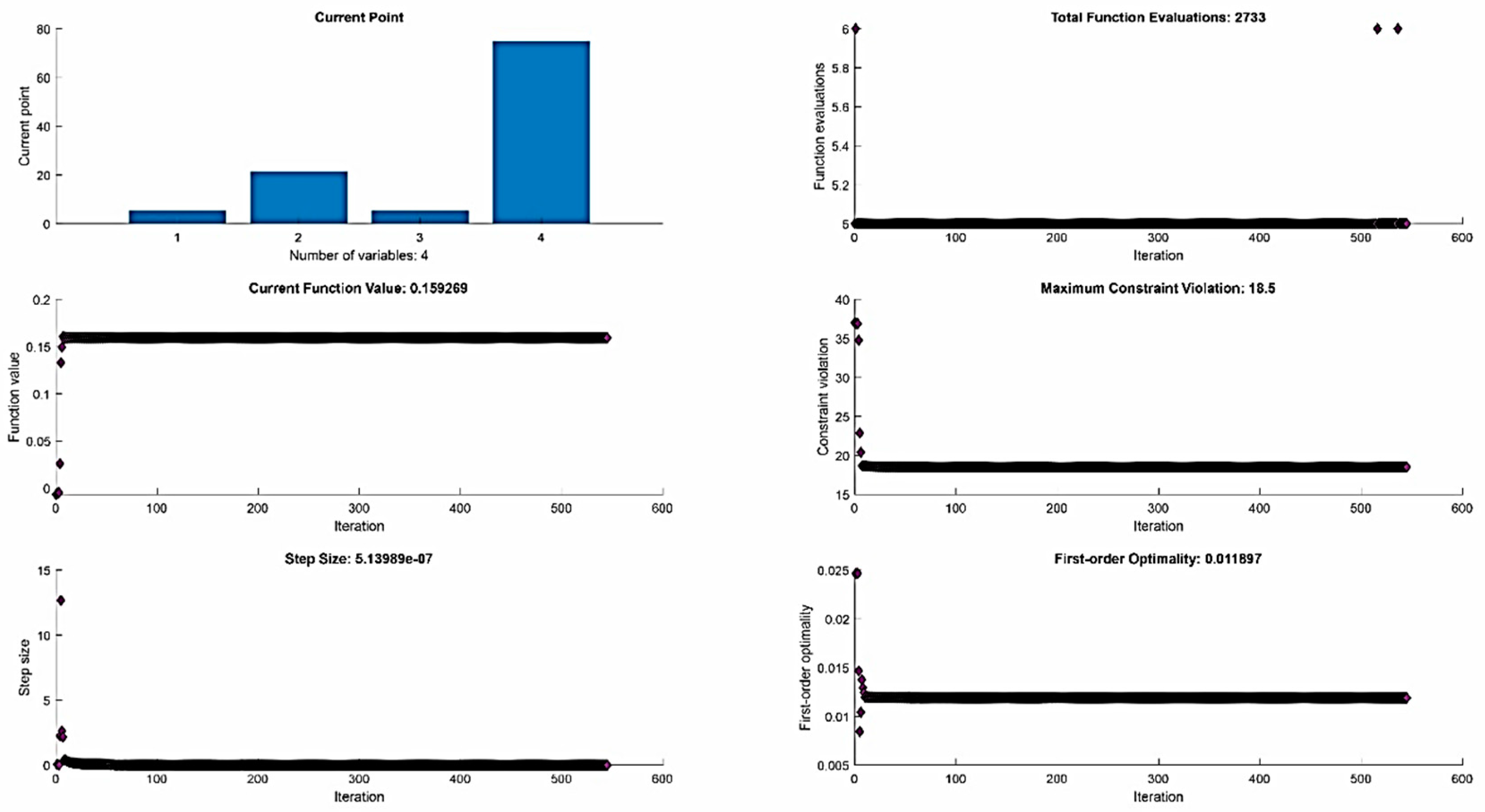
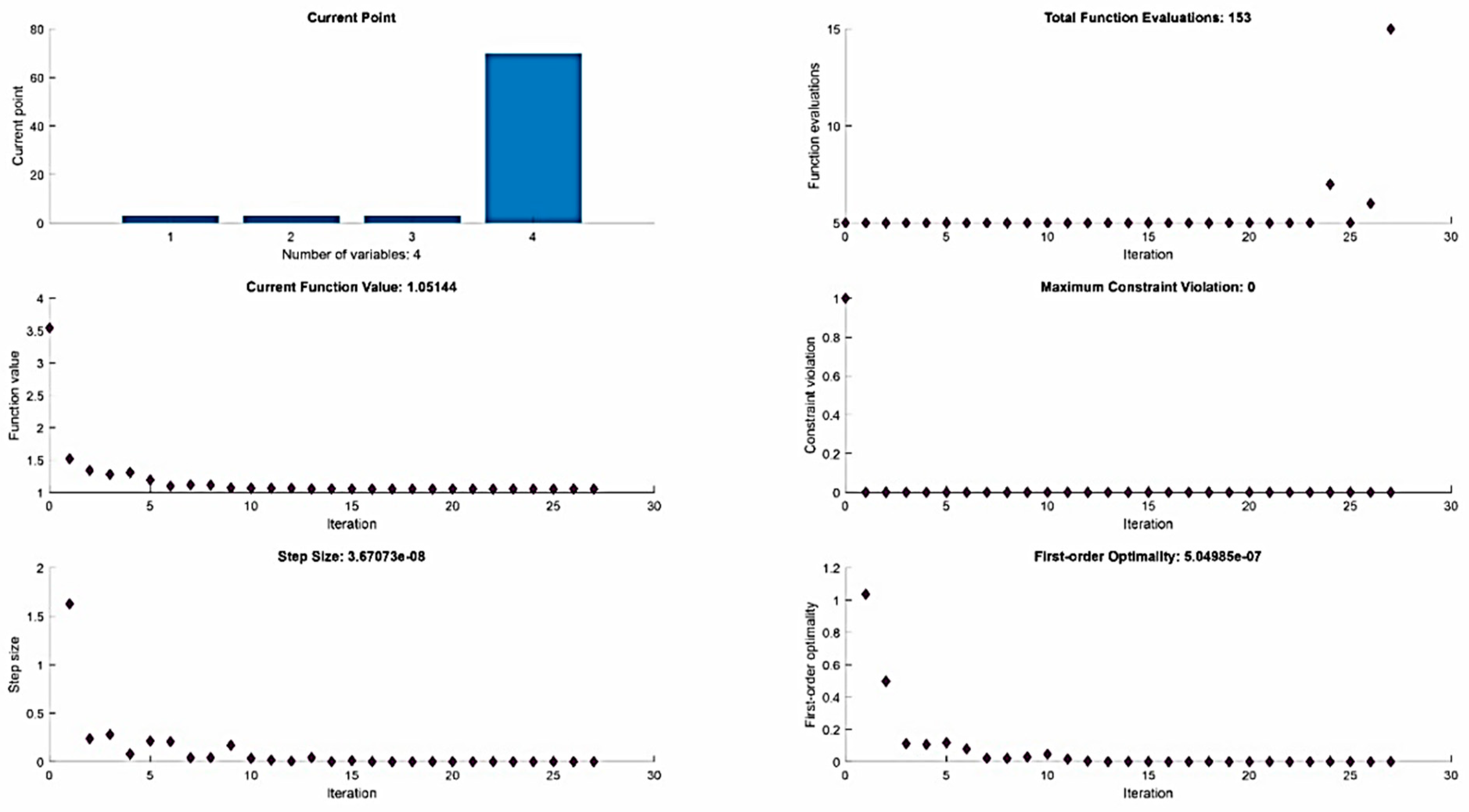
3.3. Optimization of Process Efficiency in µ-WEDM Maraging Steel MS1
5.0 ≤ Pulse-on time duration ton (μs) ≤ 40.0
3.0 ≤ Pulse-off time duration toff (μs) ≤ 15.0
70.0 ≤ Voltage of discharge U (V) ≤ 90.0
4. Conclusions
- ▪
- It was found that in terms of the four considered input factors of the electroerosive process, maximum peak current I with a weight of 37.513%, pulse-on time duration ton with a weight of 11.306%, pulse-off time duration toff with a weight of 9.51%, and voltage of discharge U with a weight of 5.18% have the main influence on MRR;
- ▪
- It was also found that in terms of the four considered input factors of the electroerosive process, maximum peak current I with a weight of 41.466%, pulse-on time duration ton with a weight of 20.814%, pulse-off time duration toff with a weight of 12.76%, and voltage of discharge U with a weight of 7.42% have the main influence on Rz;
- ▪
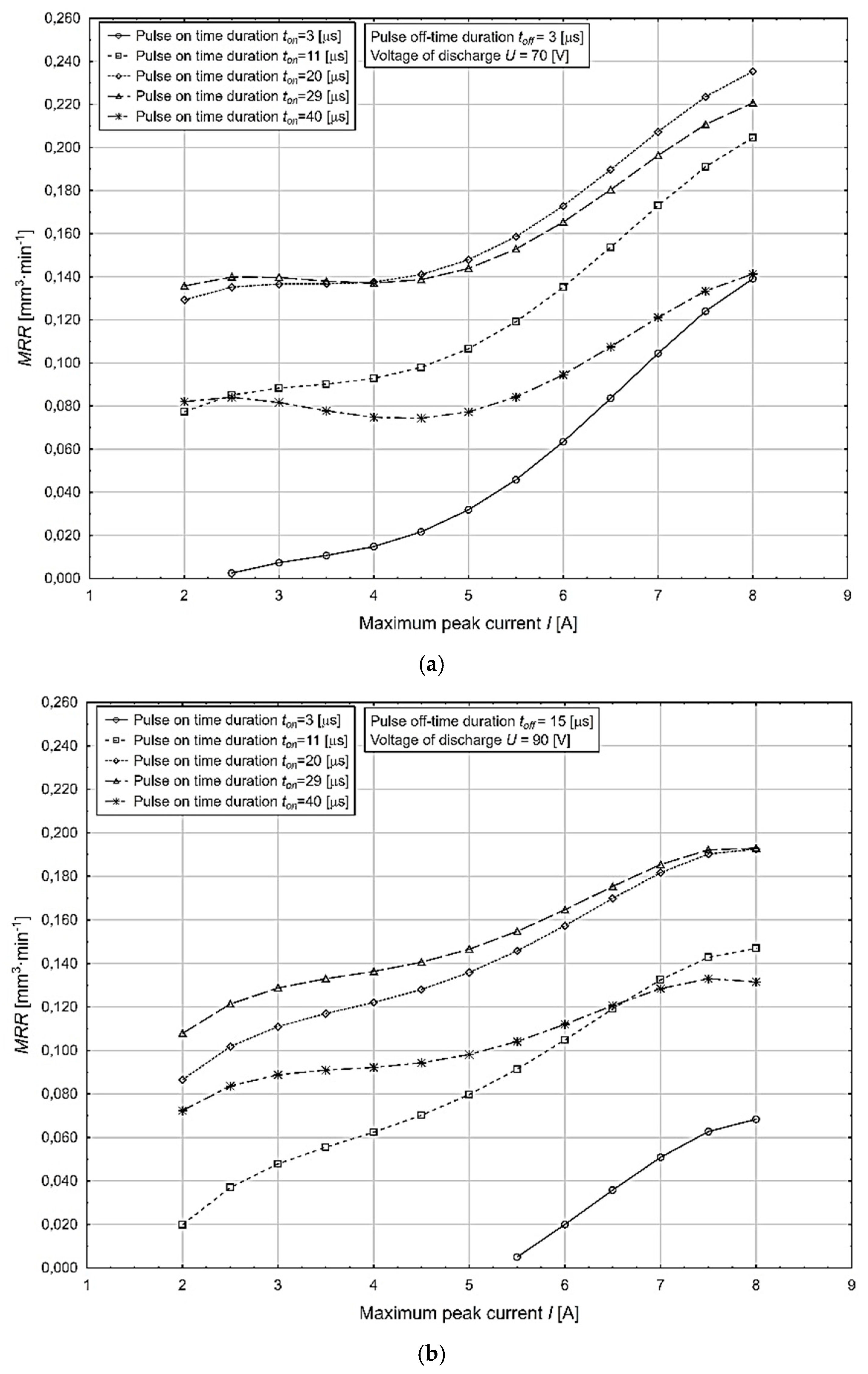
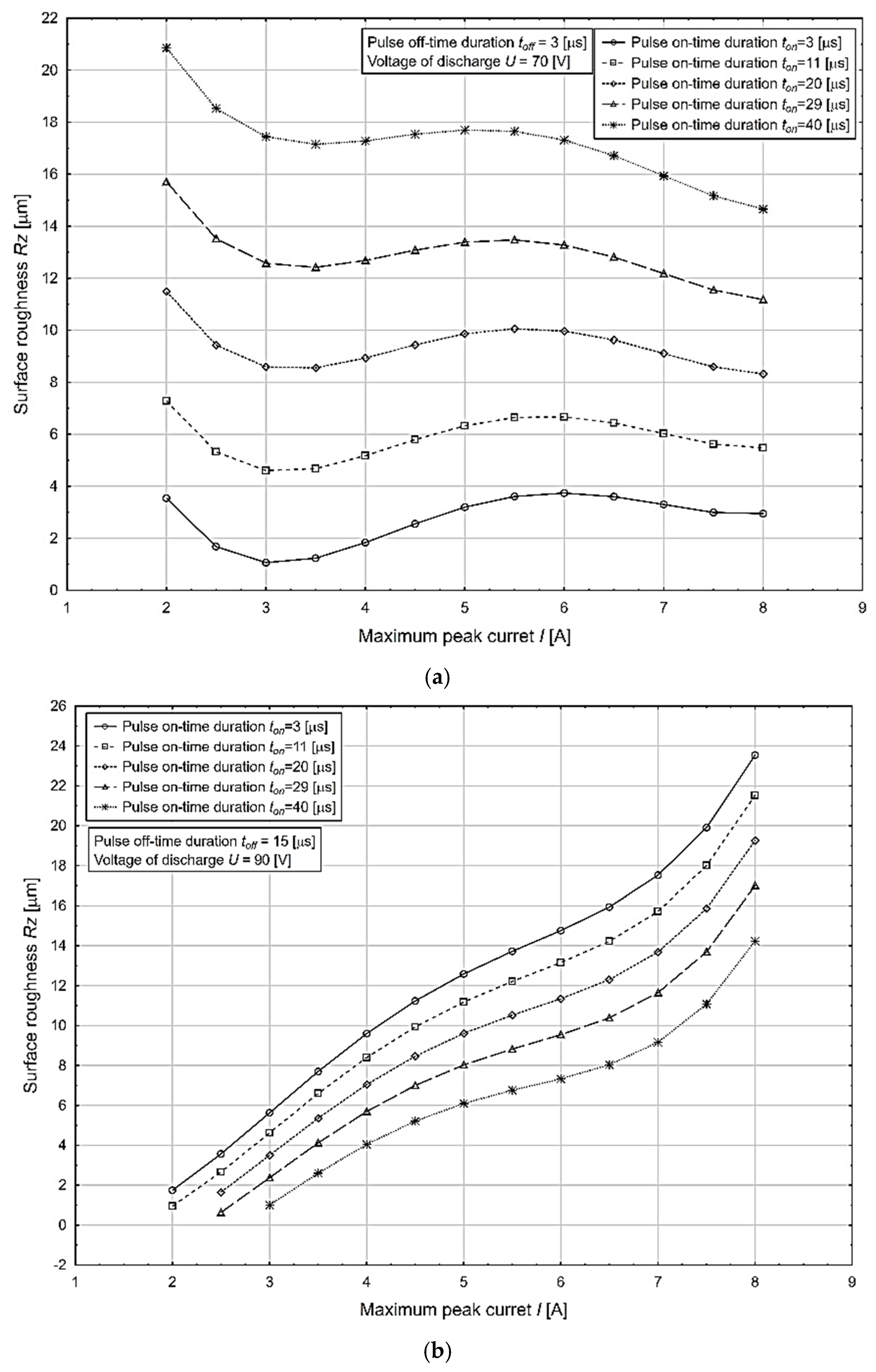
- It was found that with increasing values of the input parameters of the electrical discharge process I and ton, the cutting performance of MRR increases but the quality of the machined surface decreases in terms of the surface roughness parameter Rz. The highest value of the MRR parameter = 0.190 mm3·min−1 was obtained for the combination of MTP: I = 8.0 A, ton = 40 μs, toff = 3 μs, and U = 70 V;
- ▪
- At the same time, it was found that with increasing values of the input parameters of the electrical discharge process toff and U, the cutting performance of the MRR decreases but the quality of the machined surface increases in terms of the surface roughness parameter Rz. The lowest value of the Rz parameter = 0.09 μm was obtained for the combination of MTP: I = 2.5 A, ton = 3 μs, toff = 15 μs, and U = 90 V;
- ▪
- It was found that the aforementioned pairs of MTP input parameters in the electrical discharge process behave oppositely in relation to MRR and Rz;
- ▪
- For the given reasons, it was necessary to search for an appropriate ratio of the MTP input parameters in the electrical discharge process to achieve the optimum value of the process output performance parameter MRR and the quality parameter of the machined surface Rz;
- ▪
- Optimization was performed with respect to maximizing the output parameter of the MRR and minimizing the quality parameter of the machined surface in terms of the surface roughness parameter Rz for µ-WEDM maraging steel MS1. Through the optimization, a local maximum of 0.159 mm3·min−1 of the MRR parameter can be achieved at with MTP settings of I = 5.5 A, ton = 21.5 µs, toff = 5.5 µs, and U = 75 V. Conversely, through optimization a local minimum of 1.051 µm of the Rz parameter can be achieved at MTP settings of I = 3.014 A, ton = 3.0 µs, toff = 3.0 µs, and U = 70 V;
- ▪
- The performed optimization of the electrical discharge process can generally achieve an increase in the overall efficiency of µ-WEDM in the machining of maraging steel MS1.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CDA | Confirmatory Data Analysis |
| DOE | Design of Experiments |
| DMLS | Direct Metal Laser Sintering |
| D | Total required functionality |
| EDA | Exploratory Data Analysis |
| I | Maximum peak current (A) |
| IPM | Interior Point Method |
| MSC | Mathematical-Statistical Computational |
| MTP | Main Technological Parameters |
| MRR | Material Removal Rate |
| NLP | Non-Linear Programming |
| QNM | Quasi-Newton Methods |
| Rz | Ten-point Mean Roughness (µm) |
| SDM | Steepest Descent Method |
| SQP | Sequential Quadratic Programming |
| ton | Pulse-on time duration (µs) |
| toff | Pulse-off time duration (µs) |
| U | Voltage of discharge (V) |
| y | Desired value function |
| ymin/max | Lower/upper response limit values |
| µ-WEDM | micro-Wire Electrical Discharge Machining |
References
- Ali, M.Y.; Banu, A.; Salehan, M.; Adesta, Y.E.T.; Hazza, M.; Shaffiq, M. Dimensional Accuracy in Dry Micro Wire Electrical Discharge Machining. J. Mech. Eng. SCIE 2018, 12, 3321–3329. [Google Scholar]
- Mičietová, A.; Neslušan, M.; Čilliková, M. Influence of surface geometry and structure after non-conventional methods of parting on the following milling operations. Manuf. Technol. 2013, 13, 199–204. [Google Scholar]
- Wang, J.; Sánchez, J.A.; Izquierdo, B.; Ayesta, I. Experimental and numerical study of crater volume in wire electrical discharge machining. Materials 2020, 13, 577. [Google Scholar]
- Daneshjo, N.; Malega, P.; Drabik, P. Techniques for Production Quality Control in the Global Company. Adv. Sci. Technol. Res. J. 2021, 15, 174–183. [Google Scholar]
- Dzionk, S.; Siemiatkowski, M.S. Studying the effect of working conditions on WEDM machining performance of super alloy Inconel 617. Machines 2020, 8, 54. [Google Scholar]
- Firouzabadi, H.A.; Parvizian, J.; Abdullah, A. Improving accuracy of curved corners in wire EDM successive cutting. Int. J. Adv. Manuf. Technol. 2015, 76, 447–459. [Google Scholar]
- Islam, M.N.; Rafai, N.H.; Subramanian, S.S. An Investigation into Dimensional Accuracy Achievable in Wire-cut Electrical Discharge Machining. In Proceedings of the World Congress on Engineering, WCE 2010, London, UK, 30 June–2 July 2010; pp. 1–6. [Google Scholar]
- Trishch, R.; Nechuiviter, O.; Dyadyura, K.; Vasilevskyi, O.; Tsykhanovska, I.; Yakovlev, M. Qualimetric method of assessing risks of low quality products. MM Sci. J. 2021, 10, 4769–4774. [Google Scholar]
- Aggarwal, V.; Khangura, S.S.; Garg, R.K. Parametric modeling and optimization for wire electrical discharge machining of Inconel 718 using response surface methodology. Int. J. Adv. Manuf. Technol. 2015, 79, 31–47. [Google Scholar]
- Evin, E.; Tomáš, M.; Kmec, J. Optimization of electro-discharge texturing parameters for steel sheets’ finishing rollers. Materials 2020, 13, 1223. [Google Scholar]
- Chen, Z.; Huang, Y.; Zhang, Z.; Li, H.; Zhang, G. An analysis and optimization of the geometrical inaccuracy in WEDM rough corner cutting. Int. J. Adv. Manuf. Technol. 2014, 74, 917–929. [Google Scholar]
- Hamed, S.; Al-Juboori, L.A.; Najm, V.N.; Saleh, A.M. Analysis the impact of WEDM parameters on surface microstructure using response surface methodology. In Proceedings of the ASET 2020, Advances in Science and Engineering Technology International Conferences, Dubai, United Arab Emirates, 4–9 February 2020; p. 9118208. [Google Scholar]
- Kiyak, M. Investigation of effects of cutting parameters on surface quality and hardness in the wire-EDM process. Int. J. Adv. Manuf. Tech. 2021, 119, 647–655. [Google Scholar] [CrossRef]
- Mouralova, K.; Zahradnicek, R.; Houska, P. Evaluation of surface quality of X210Cr12 steel for forming tools machined by WEDM. MM Sci. J. 2016, 5, 1366–1369. [Google Scholar] [CrossRef]
- Pi, V.N.; Tam, D.T.; Cuong, N.M.; Tran, T.H. Multi-objective optimization of PMEDM process parameters for processing cylindrical shaped parts using taguchi method and grey relational analysis. Int. J. Mech. Prod. Eng. Res. Develop. 2020, 10, 669–678. [Google Scholar]
- Raksiri, C.; Chatchaikulsiri, P. CNC Wire-Cut Parameter Optimized Determination of the Stair Shape Workpiece. Int. J. Mech. Mechatron. Eng. 2010, 4, 924–929. [Google Scholar]
- Zhu, Z.; Guo, D.; Xu, J.; Lin, J.; Lei, J.; Xu, B.; Wu, X.; Wang, X. Processing Characteristics of Micro Electrical Discharge Machining for Surface Modification of TiNi Shape Memory Alloys Using a TiC Powder Dielectric. Micromachines 2020, 11, 1018. [Google Scholar] [CrossRef]
- Meshram, D.B.; Puri, Y.M. Optimized curved electrical discharge machining-based curvature channel. J. Braz. Soc. Mech. Sci. 2020, 42, 82. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, W.; Zhan, X.; Ding, L.; Zhou, J. Parameter optimisation of laser cladding repair for an Invar alloy mould. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1859–1871. [Google Scholar] [CrossRef]
- Pradhan, B.B.; Masanta, M.; Sarkar, B.R.; Bhattacharyya, B. Investigation of electro-discharge micro-machining of titanium super alloy. Int. J. Adv. Manuf. Technol. 2009, 41, 1094–1106. [Google Scholar] [CrossRef]
- Meena, V.K.; Azad, M.S. Grey relational analysis of micro-EDM machining of Ti-6Al-4V alloy. Mater. Manuf. Process. 2012, 27, 973–977. [Google Scholar] [CrossRef]
- Somashekhar, K.P.; Ramachandran, N.; Mathew, J. Optimization of material removal rate in micro-EDM using artificial neural network and genetic algorithms. Mater. Manuf. Process. 2010, 25, 467–475. [Google Scholar] [CrossRef]
- Jabbaripour, B.; Sadeghi, M.H.; Faridvand, S.; Shabgard, M.R. Investigating the effects of EDM parameters on surface integrity, MRR and TWR in machining of Tie6ALe4V. Mach. Sci. Technol. 2012, 16, 419–444. [Google Scholar] [CrossRef]
- Kuruvila, N.; Ravindra, H.V. Parametric influence and optimization of wire EDM of Hot die steel. Mach. Sci. Technol. 2011, 15, 47–75. [Google Scholar] [CrossRef]
- Mukherjee, R.; Chakraborty, S. Selection of EDM process parameters using biogeography-based optimization algorithm. Mater. Manuf. Process. 2012, 27, 954–962. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, Y.F.; Lin, C.T.; Tzeng, H.J. Electrical discharge machining (EDM) characteristics associated with electrical discharge energy on machining of cemented tungsten carbide. Mater. Manuf. Process. 2008, 23, 391–399. [Google Scholar] [CrossRef]
- Strasky, J.; Janecek, M.; Harcuba, P. Electric Discharge Machining of Tie6Ale4V Alloy for Biomedical Use. In WDS’11. Proceedings of Contributed Papers; Part III; MatfyzPress: Prague, Czechia, 2011; pp. 127–131. [Google Scholar]
- Baron, P.; Kaščák, J. Comparison of selected materials intended for the manufacture of plastic holder for reverse parking sensor with the use of computer simulation tools. MM Sci. J. 2019, 12, 3463–3467. [Google Scholar] [CrossRef]
- Panda, A.N.T.O.N.; Anisimov, V.M.; Anisimov, V.V.; Diadiura, K.O.; Pandova, I.V.E.T.A. Increasing of wear resistance of linear block-polyurethanes by thermal processing methods. MM Sci. J. 2021, 10, 731–4735. [Google Scholar] [CrossRef]
- Simkulet, V.; Mitaľová, Z.; Lehocká, D.; Kočiško, M.; Manduľák, D. Evaluation of Fracture Surface Samples by Impact Energy Test Prepared after DMLS Additive Manufacturing Technology; SAS: Košice, Slovakia, 2017; pp. 82–83. [Google Scholar]
- Pollak, M.; Kocisko, M.; Basistova, A.; Hlavata, S. Production of fiber as an input material for the 3D printing process. MM Sci. J. 2021, 6, 4414–4419. [Google Scholar] [CrossRef]
- Mascenik, J.; Pavlenko, S. Determination of stress and deformation during laser welding of aluminium alloys with the PC support. MM Sci. J. 2020, 2020, 4104–4107. [Google Scholar] [CrossRef]
- Simkulet, V.; Duplakova, D.; Kovalcikova, A.; Hatala, M.; Botko, F.; Mitalova, Z.; Vandzura, R. Evaluation of tribological characteristics of material prepared by DMLS technology. MM Sci. J. 2021, 10, 4941–4945. [Google Scholar] [CrossRef]
- Rimár, M.; Abraham, M.; Fedák, M.; Kulikov, A.; Oravec, P.; Váhovský, J. Methods of increasing the efficiency of cogeneration based energy equipment. MM Sci. J. 2019, 6, 2935–2938. [Google Scholar] [CrossRef]
- Sarafan, S.; Wanjara, P.; Gholipour, J.; Bernier, F.; Osman, M.; Sikan, F.; Molavi-Zarandi, M.; Soost, J.; Brochu, M. Evaluation of Maraging Steel Produced Using Hybrid Additive/Subtractive Manufacturing. J. Manuf. Mater. Process. 2021, 5, 107. [Google Scholar] [CrossRef]
- Yan, M.T.; Wang, P.W.; Lai, J.C. Improvement of part straightness accuracy in rough cutting of wire EDM through a mechatronic system design. Int. J. Adv. Manuf. Technol. 2016, 84, 2623–2635. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X. Simulation of the inventory cost for rotable spare with fleet size impact. Acad. J. Manu. Eng. 2017, 15, 124–132. [Google Scholar]
- Grigoriev, S.N.; Pivkin, P.M.; Kozochkin, M.P.; Volosova, M.A.; Okunkova, A.A.; Porvatov, A.N.; Zelensky, A.A.; Nadykto, A.B. Physicomechanical nature of acoustic emission preceding wire breakage during wire electrical discharge machining (WEDM) of advanced cutting tool materials. Metals 2021, 11, 1865. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of electric impact drills using thermal imaging. Measurement 2021, 171, 108815. [Google Scholar] [CrossRef]
- Yaman, S.; Cakir, O. Investigation of the effects of EDM parameters on surface roughness. J. Adv. Manu. Eng. 2020, 1, 46–55. [Google Scholar]
- Ivanov, V.; Dehtiarov, I.; Evtuhov, A.; Pavlenko, I.; Ruban, A. Multiaxis machining of fork-type parts: Fixture design and numerical simulation. Int. Conf. New Technol. Dev. Appl. 2021, 233, 42–152. [Google Scholar]
- Kascak, J.; Gaspar, S.; Pasko, J.; Husar, J.; Knapcikova, L. Polylactic acid and its cellulose based composite as a significant tool for the production of optimized models modified for additive manufacturing. Sustainability 2021, 13, 1256. [Google Scholar] [CrossRef]
- Mascenik, J.; Pavlenko, S. Controlled testing of belt transmissions at different loads. MM Sci. J. 2021, 12, 5497–5501. [Google Scholar] [CrossRef]
- Van, D.N.; Van, B.P.; Huu, P.N. Application of Deng’s similarity-based analytic hierarchy process approach in parametric optimization of the electrical discharge machining process of SDK11 die steel. Trans. Can. Soc. Mech. Eng. 2020, 44, 294–310. [Google Scholar] [CrossRef]
- Mouralova, K.; Benes, L.; Zahradnicek, R.; Bednar, J.; Zadera, A.; Fries, J.; Kana, V. WEDM Used for machining high entropy alloys. Materials 2020, 13, 4823. [Google Scholar] [CrossRef]
- Rani, S.S.; Sundari, V.K.; Jose, P.S.H.; Sivaranjani, S.; Stalin, B.; Pritima, D. Enrichment of material subtraction rate on Eglin steel using electrical discharge machining process through modification of electrical circuits. Mater. Today 2020, 33, 4428–4430. [Google Scholar] [CrossRef]
- Mižáková, J.; Piteľ, J. An analytical dynamic model of heat transfer from the heating body to the heated room. MATEC Web Conf. 2017, 125, 02047. [Google Scholar] [CrossRef]
- Świercz, R.; Oniszczuk-Świercz, D. Experimental Investigation of Surface Layer Properties of High Thermal Conductivity Tool Steel after Electrical Discharge Machining. Metals 2017, 7, 550. [Google Scholar] [CrossRef]
- Sanchez, J.A.; Rodil, J.L.; Herrero, A.; De Lacalle, L.N.L.; Lamikiz, A. On the influence of cutting speed limitation on the accuracy of wire-EDM corner-cutting. J. Mater. Process. Technol. 2007, 182, 574–579. [Google Scholar] [CrossRef]
- Ranjan, J.; Patra, K.; Szalay, T.; Mia, M.; Gupta, M.K.; Song, Q.; Krolczyk, G.; Chudy, R.; Pashnyov, V.A.; Pimenov, D.Y. artificial intelligence-based hole quality prediction in micro-drilling using multiple sensors. Sensors 2020, 20, 885. [Google Scholar] [CrossRef]
- Oniszczuk-Swiercz, D.; Swiercz, R.; Chmielewski, T.; Salacinski, T. Experimental investigation of influence WEDM parameters on surface roughness and flatness deviation. METAL 2020, 29, 611–617. [Google Scholar]
- Maraging Steel MS1 Properties. Available online: https://www.scribd.com/document/48576364/z3T-Maraging-Steel-1-2709-EOS-MS1 (accessed on 20 July 2022).
- Sambaran, M.; Devesh, R. EDM of titanium foam: Electrode wear rate, oversize, and MRR. Mater. Manuf. Process. 2021, 37, 825–837. [Google Scholar]
- Rashedul, I.M.; Zhang, Y.; Zhou, K.; Wang, G.; Xi, T.; Ji, L. Influence of different tool electrode materials on electrochemical discharge machining performances. Micromachines 2021, 12, 1077. [Google Scholar] [CrossRef]
- Ťavodová, M. Research state heat affected zone of the material after wire EDM. Acta Fac. Tech. 2014, 19, 145–152. [Google Scholar]
- Židek, K.; Piteľ, J.; Adámek, M.; Lazorík, P.; Hošovský, A. Digital Twin of Experimental Smart Manufacturing Assembly System for Industry 4.0 Concept. Sustainability 2020, 12, 3658. [Google Scholar] [CrossRef]
- Sun, S.; Przystupa, K.; Wei, M.; Yu, H.; Ye, Z.; Kochan, O. Fast bearing fault diagnosis of rolling element using Levy Moth-Flame optimization algorithm and Naive Bayes. Eksploat. Niezawodn.—Maint. Reliab. 2020, 22, 730–740. [Google Scholar] [CrossRef]
- Iyyappan, S.; Sudhakarapandian, G.R.; Sakthivel, M. Influence of silicon carbide mixed used engine oil dielectric fluid on EDM characteristics of AA7075/SiCp/B4Cp hybrid composites. Mater. Res. Express 2021, 8, 086514. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Kozochkin, M.P.; Porvatov, A.N.; Volosova, M.A.; Okunkova, A.A. Electrical discharge machining of ceramic nanocomposites: Sublimation phenomena and adaptive control. Heliyon 2019, 5, e02629. [Google Scholar] [CrossRef] [PubMed]
- Hašová, S.; Straka, Ľ. Design and verification of software for simulation of selected quality indicators of machined surface after WEDM. Acad. J. Manu. Eng. 2016, 14, 13–20. [Google Scholar]
- Rouniyar, A.K.; Shandilya, P. Fabrication and experimental investigation of magnetic field assisted powder mixed electrical discharge machining on machining of aluminum 6061 alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 2283–2291. [Google Scholar] [CrossRef]


| MTP | µ-WEDM Operation | Setting Range | Influence of MTP on Rz | Influence of MTP on MRR |
|---|---|---|---|---|
| Maximum peak current I (A) | roughing | 6.0–8.0 | As the value of parameter I increases, the surface roughness deteriorates [13]. | As the value of parameter I increases, the MRR increases [22]. |
| semifinishing | 4.0–6.0 | |||
| finishing | 2.0–4.0 | |||
| Pulse-on time duration ton (μs) | roughing | 20.0–40.0 | As the value of the parameter ton increases, the surface roughness deteriorates [14]. | As the value of the parameter ton increases, the MRR increases [22]. |
| semifinishing | 10.0–20.0 | |||
| finishing | 5.0–10.0 | |||
| Pulse-off time duration toff (μs) | roughing | 9.0–15.0 | As the value of the parameter toff increases, the surface roughness improves [23]. | As the value of the parameter toff increases, the MRR decreases [23]. |
| semifinishing | 6.0–9.0 | |||
| finishing | 3.0–6.0 | |||
| Voltage of discharge U (V) | roughing | 85–90 | As the value of parameter U increases, the surface roughness improves [40]. | As the value of the parameter U increases, the MRR decreases [51]. |
| semifinishing | 75–80 | |||
| finishing | 70–75 |
| Fe | Ni | Co | Mo | Ti | Al | Cr | C | Mn, Si | P, S |
|---|---|---|---|---|---|---|---|---|---|
| Zb. | 17–19% | 8.5–9.5% | 4.5–5.2% | 0.6–0.8% | 0.05–0.15% | ≤0.5 | ≤0.03 | each ≤ 0.1% | each ≤ 0.01% |
| Mechanical properties of maraging steel MS1 | ||
| Parameter | As built | After age hardening |
| Tensile strength (MPa) | 1200 ± 100 | 1950 ± 100 |
| Yield strength Rp 0.2% (MPa) | 1100 ± 100 | 1900 ± 100 |
| Elongation at break (%) | 8 ± 3 | 2 ± 1 |
| Hardness (HRC) | 33–37 | 50–54 |
| Ductility (J) | 45 ± 10 | 11 ± 4 |
| Modulus of elasticity (GPa) | 150 ± 25 | |
| Physical properties of maraging steel MS1 | ||
| Density (g·cm−3) | 8.0–8.1 | |
| Electrical conductivity (Siemens·m·mm−2) | 2.25 | |
| Thermal conductivity (W·m−1·°C) | 15 ± 0.8 | |
| Specific heat capacity (J·kg−1·°C) | 450 ± 20 | |
| Melting temperature (°C) | 1370–1400 | |
| Source | DF | Sum of Squares | Mean Square | F Ratio | Prob > F |
|---|---|---|---|---|---|
| Model | DFModel = a − 1 | SModel | MSModel = SModel/DFModel | F = MSModel/MSError | pM |
| Error | DFError = N − a | SError | MSError = SError/DFError | ||
| C.Total | DFC.Total = N − 1 | SC.Total | MSC.Total = SC.Total/DFC.Total |
| Term for MRR | Estimate | Std Error | t-Ratio | Prob > |t| |
| Intercept (x0) | −0.010813 | 0.020121 | −0.54 | 0.5929 |
| x1 | 0.0165482 | 0.000279 | 59.26 | 0.0001 * |
| x2 | 0.0012834 | 7.19 × 10−5 | 17.86 | 0.0001 * |
| x3 | −0.001947 | 0.00014 | −13.94 | 0.0001 * |
| x4 | 0.0008016 | 0.000237 | 3.38 | 0.0013 * |
| (x1 − 5)⋯(x1 − 5) | 0.0128791 | 0.003127 | 4.12 | 0.0001 * |
| (x1 − 5)⋯(x2 − 22.8767) | −0.000387 | 0.000016 | −24.17 | 0.0001 * |
| (x2 − 22.8767)⋯(x2 − 22.8767) | −0.000275 | 8.03 × 10−5 | −3.42 | 0.0011 * |
| (x2 − 22.8767)⋯(x3 − 9) | 0.0000673 | 0.000008 | 8.40 | 0.0001 * |
| (x2 − 22.8767)⋯(x4 − 80) | 0.0000419 | 4.70 × 10−6 | 8.93 | 0.0001 * |
| (x1 − 5)⋯(x1 − 5)⋯(x4 − 80) | −0.000165 | 2.62 × 10−5 | −6.32 | 0.0001 * |
| (x1 − 5)⋯(x1 − 5)⋯(x1 − 5)⋯(x1 − 5) | −0.000438 | 5.73 × 10−5 | −7.63 | 0.0001 * |
| Term for Rz | Estimate | Std Error | t-Ratio | Prob > |t| |
| Intercept (x0) | 4.312305 | 0.462060 | 9.33 | <0.0001 * |
| x1 | 1.263985 | 0.017863 | 70.76 | <0.0001 * |
| x2 | 0.108301 | 0.003054 | 35.46 | <0.0001 * |
| x3 | −0.115140 | 0.009508 | −12.11 | <0.0001 * |
| x4 | −0.025370 | 0.005077 | −5.00 | <0.0001 * |
| (x1 − 5)⋯(x1 − 5) | −0.459620 | 0.148820 | −3.09 | 0.0030 * |
| (x1 − 5)⋯(x2 − 22.8767) | −0.025260 | 0.001029 | −24.55 | <0.0001 * |
| (x1 − 5)⋯(x3 − 9) | 0.113915 | 0.035306 | 3.23 | 0.0020 * |
| (x2 − 22,8767)⋯(x3 − 9) | −0.031130 | 0.011999 | −2.59 | 0.0119 * |
| (x2 − 22,8767)⋯(x4 − 80) | −0.009710 | 0.003622 | −2.68 | 0.0094 * |
| (x1 − 5)⋯(x1 − 5)⋯(x1 − 5)⋯(x1 − 5) | 0.051696 | 0.016525 | 3.13 | 0.0027 * |
| (x1 − 5)⋯(x1 − 5)⋯(x1 − 5)⋯(x4 − 80) | 0.013128 | 0.004660 | 2.82 | 0.0065 * |
| Parameter for MRR | Value |
| RSquare | 0.998175 |
| RSquare Adj | 0.997846 |
| Root Mean Square Error | 0.002675 |
| Mean of Response | 0.136644 |
| Observations (or Sum Wgts) | 73 |
| Parameter for Rz | Value |
| RSquare | 0.998773 |
| RSquare Adj | 0.998528 |
| Root Mean Square Error | 0.164369 |
| Mean of Response | 9.332192 |
| Observations (or Sum Wgts) | 73 |
| SourceforMRR | DF | Sum of Squares | Mean Square | F-Ratio | Prob > F |
| Model | 11 | 0.2387703 | 0.021706 | 3033.879 | 0.0001 * |
| Error | 61 | 0.0004364 | 7.16 × 10−6 | ||
| C. Total | 72 | 0.2392067 | |||
| Source for Rz | DF | Sum of Squares | Mean Square | F-Ratio | Prob > F |
| Model | 12 | 1319.781 | 109.982 | 4070.833 | 0.0001 * |
| Error | 60 | 1.621 | 0.027 | ||
| C. Total | 72 | 1321.402 |
| Source | DF | Sum of Squares | Mean Square | F Ratio | Prob > F |
| Lack of Fit | 7 | 0.0001104 | 0.000016 | 2.6133 | 0.0513 |
| Pure Error | 54 | 0.000326 | 6.04 × 10−6 | ||
| Total Error | 61 | 0.0004364 | |||
| Source | DF | Sum of Squares | Mean Square | F Ratio | Prob > F |
| Lack of Fit | 6 | 1.588221 | 0.264703 | 435.7923 | 0.0677 |
| Pure Error | 54 | 0.0328 | 0.000607 | ||
| Total Error | 60 | 1.621021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straka, Ľ.; Gombár, M.; Vagaská, A.; Kuchta, P. Efficiency Optimization of the Electroerosive Process in µ-WEDM of Steel MS1 Sintered Using DMLS Technology. Micromachines 2022, 13, 1446. https://doi.org/10.3390/mi13091446
Straka Ľ, Gombár M, Vagaská A, Kuchta P. Efficiency Optimization of the Electroerosive Process in µ-WEDM of Steel MS1 Sintered Using DMLS Technology. Micromachines. 2022; 13(9):1446. https://doi.org/10.3390/mi13091446
Chicago/Turabian StyleStraka, Ľuboslav, Miroslav Gombár, Alena Vagaská, and Patrik Kuchta. 2022. "Efficiency Optimization of the Electroerosive Process in µ-WEDM of Steel MS1 Sintered Using DMLS Technology" Micromachines 13, no. 9: 1446. https://doi.org/10.3390/mi13091446
APA StyleStraka, Ľ., Gombár, M., Vagaská, A., & Kuchta, P. (2022). Efficiency Optimization of the Electroerosive Process in µ-WEDM of Steel MS1 Sintered Using DMLS Technology. Micromachines, 13(9), 1446. https://doi.org/10.3390/mi13091446






