State of Charge Estimation of Lithium-Ion Batteries Using Stacked Encoder–Decoder Bi-Directional LSTM for EV and HEV Applications
Abstract
:1. Introduction
1.1. Related Work
- (1)
- A novel hybrid architecture using a stacked Bi-LSTM and encoder–decoder Bi-LSTM is used to estimate SOC at varying temperatures. The network can take advantage of the bi-directional functionality of Bi-LSTMs and capture sequential tendencies more accurately and provide a more accurate SOC sequence. By providing a SOC sequence estimate as opposed to single value SOC estimates, the trend in battery capacity and battery state in real-world scenarios can be more effectively monitored.
- (2)
- The stacked Bi-LSTM was built with deep structures to take advantage of deep neural network architectures, and the use of Bi-LSTM units aid in capturing the temporal dependencies from the forward and backwards directions. Since the encoder and decoder blocks are trained simultaneously, the training time of the network is also reduced.
- (3)
- The model is tested on a standard open-source lithium-ion battery dataset. The proposed network performs better than similar pre-existing architectures. Experimental testing proves that the SED network can accurately estimate SOC sequence at varying temperatures provided current, voltage and temperature measurement sequences. A mean absolute error (MAE) of 0.62% was observed for HWFET conditions at varying ambient temperatures, which shows the proper functionality of the proposed network.
1.2. Battery Management Systems
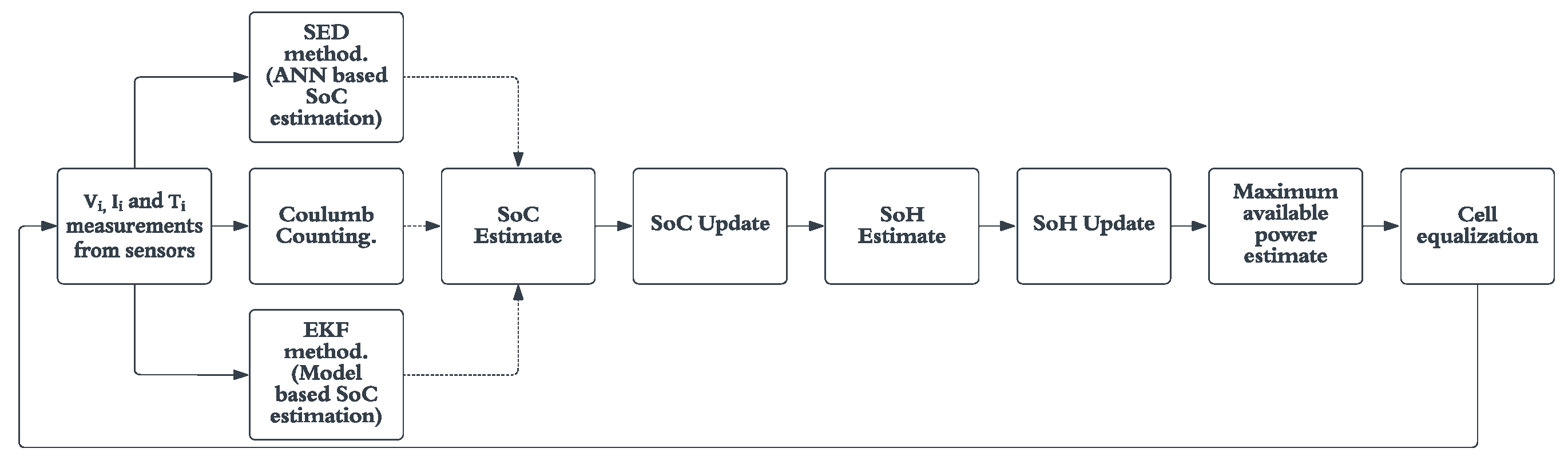
1.3. State of Charge Estimation Techniques
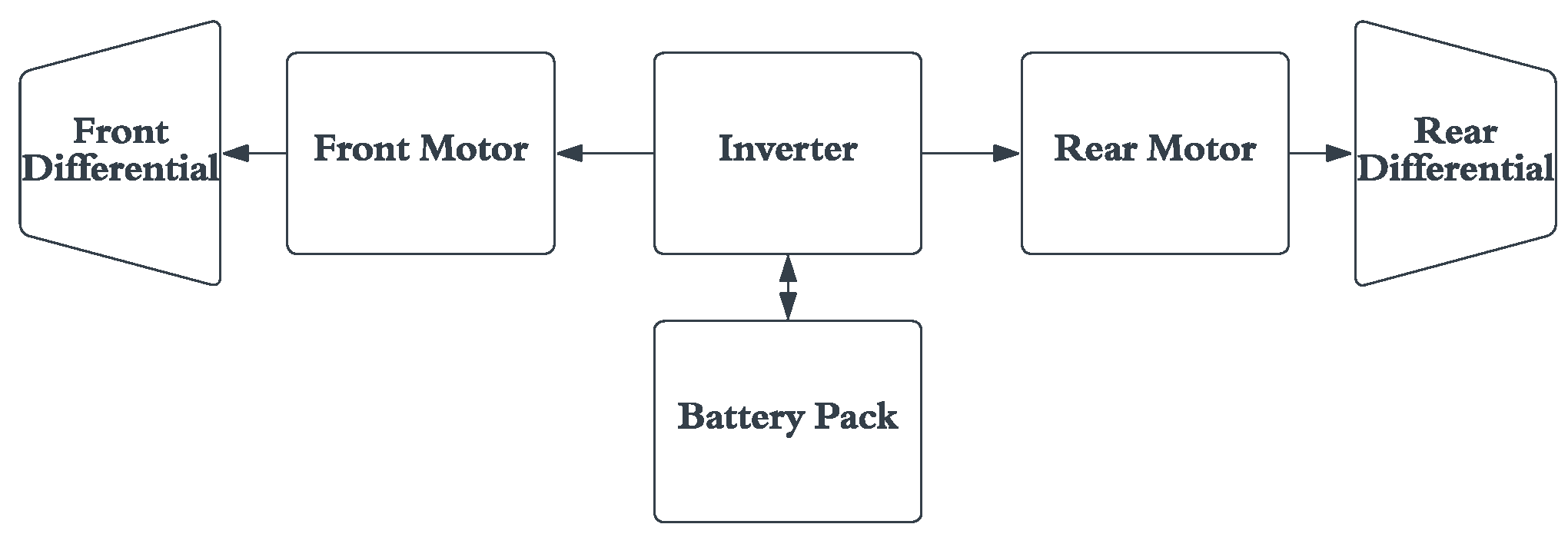
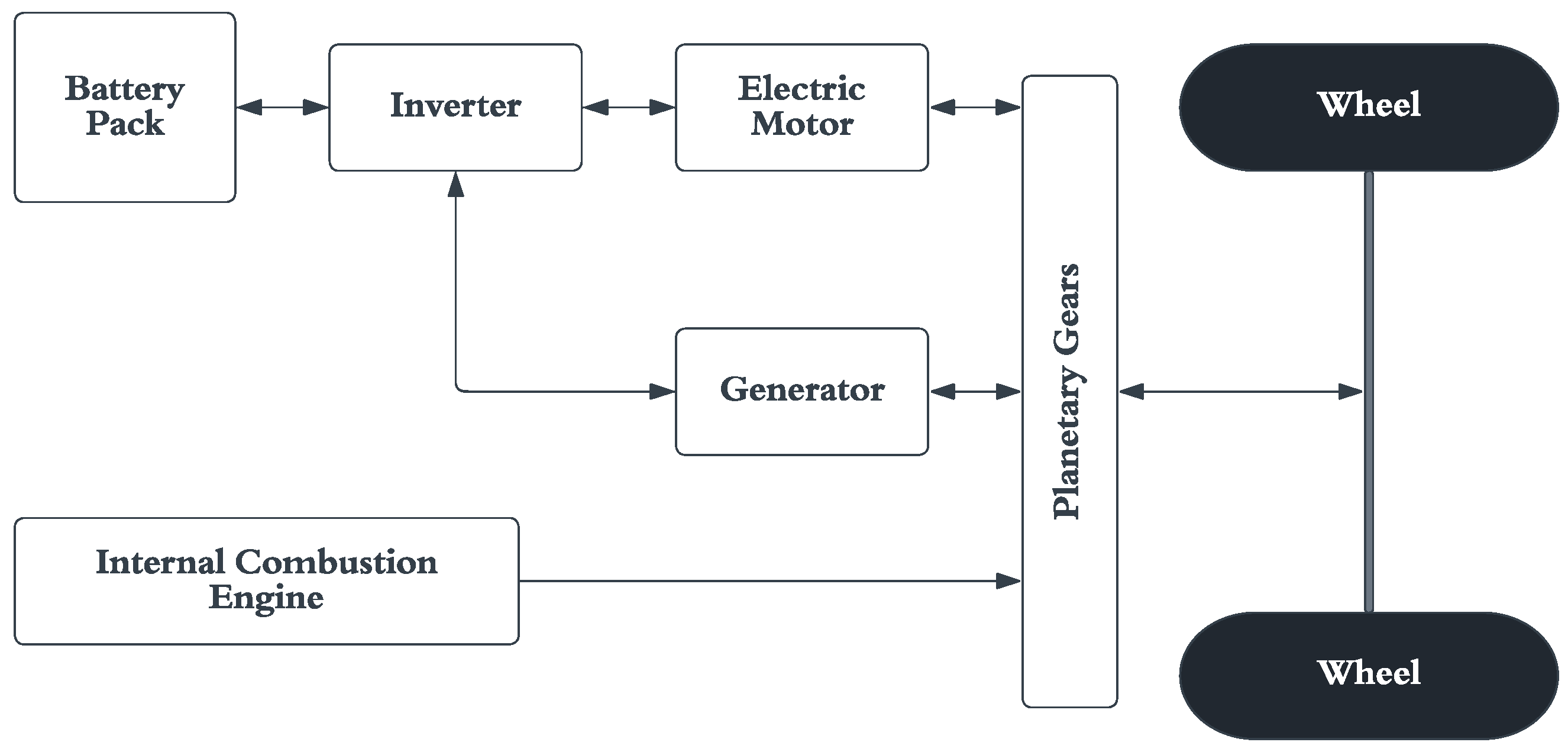
SOC Estimation Requirements in HEV Applications
- During acceleration at the start, most of the workload is carried by the electric system because of the incredible torque provided by the electric motor. The power draw from the battery is the maximum during this phase. In most HEVs, the ICE is entirely shut down while starting from a complete stop.
- During normal conditions, the power draw from the battery is reduced massively, and power coming from the ICE is split to drive the generator and the wheels. The generator is in turn used to power the electric motors.
- During sudden changes to the vehicle’s momentum, i.e., sudden acceleration or deceleration, power from the battery is either drawn to support the ICE output or the electric motors are used as generators and the battery pack is charged while regenerative braking is performed.
- During charge condition, the battery pack can be charged using the ICE output to drive the generator. The battery charge levels are monitored to maintain a minimum level of charge.
2. Materials and Methods
2.1. Performance Metrics
2.1.1. Mean Absolute Error
2.1.2. Root Mean Square Error
3. Proposed Network Architecture
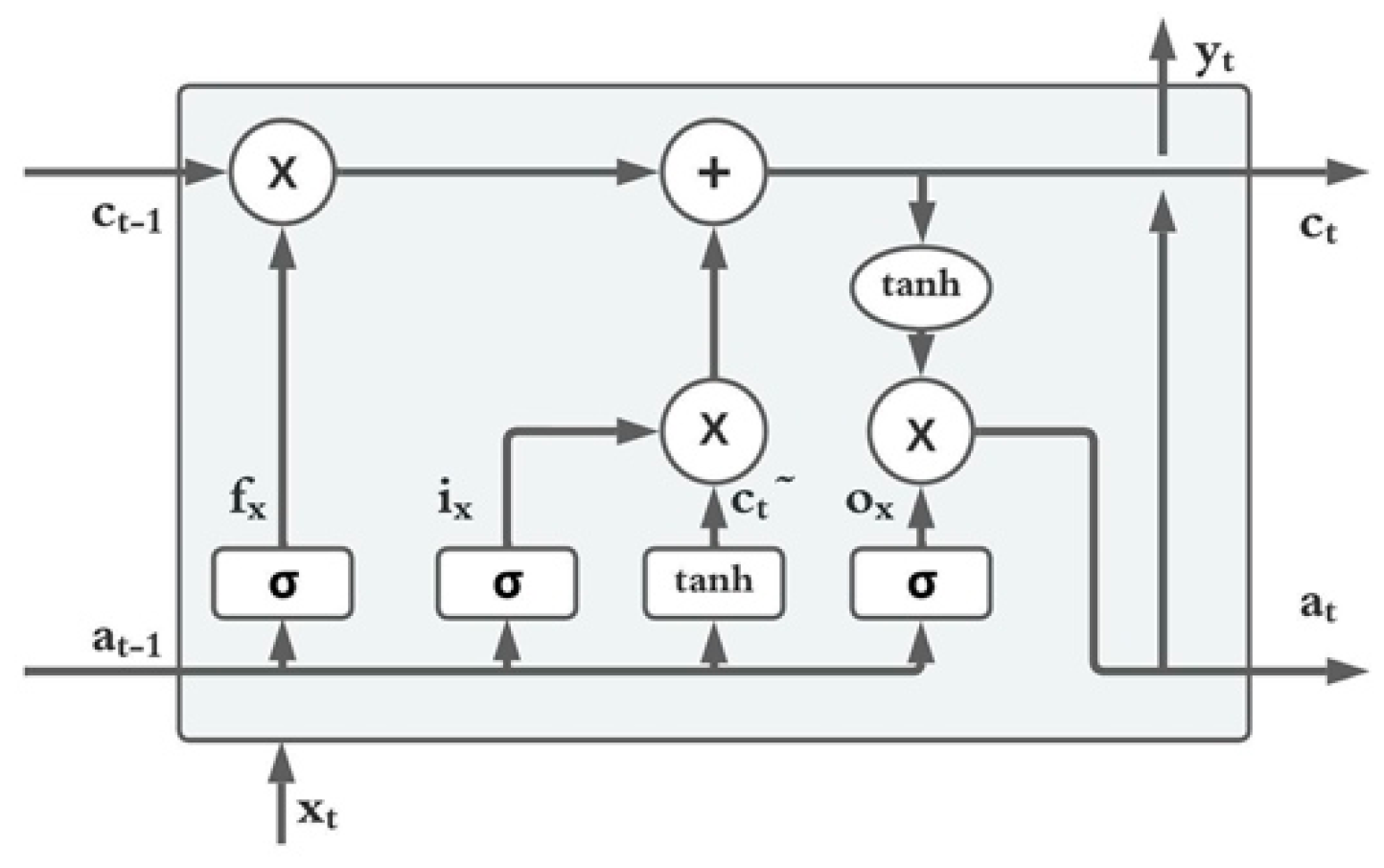
3.1. Long Short-Term Memory
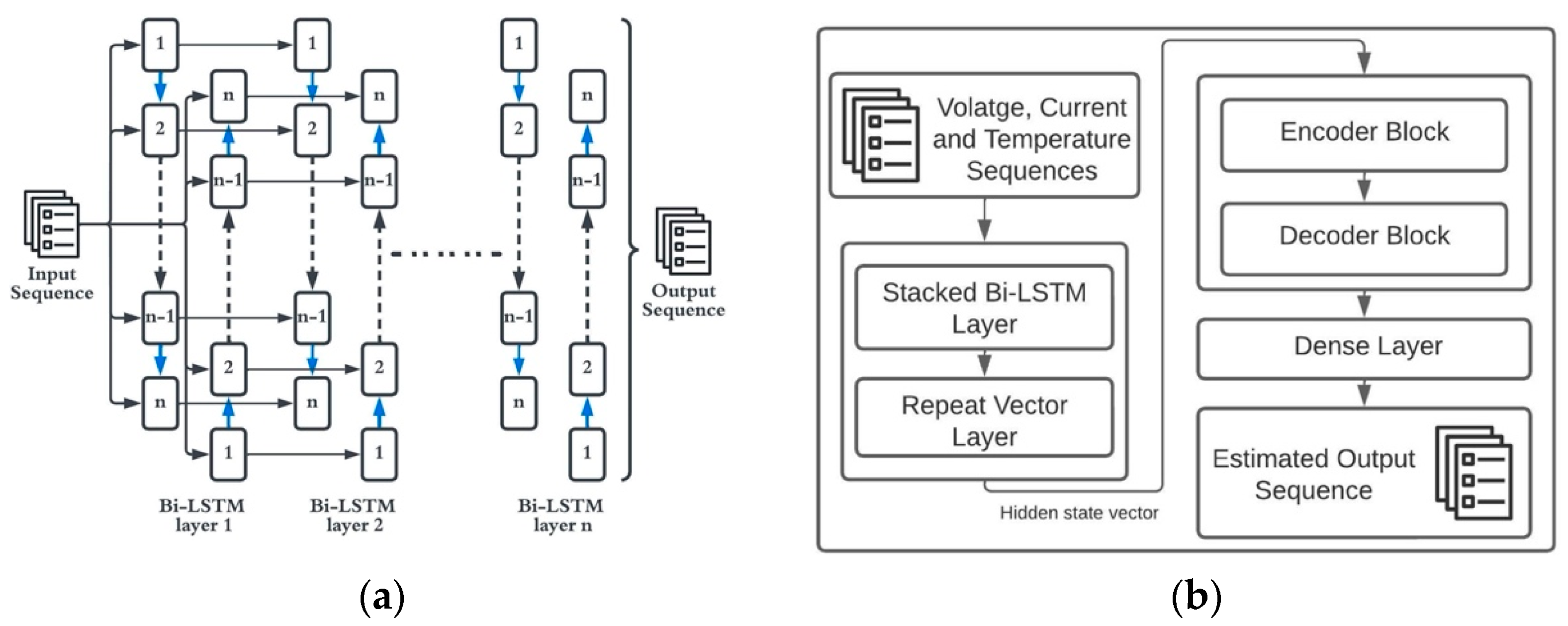
Bi-Directional LSTM
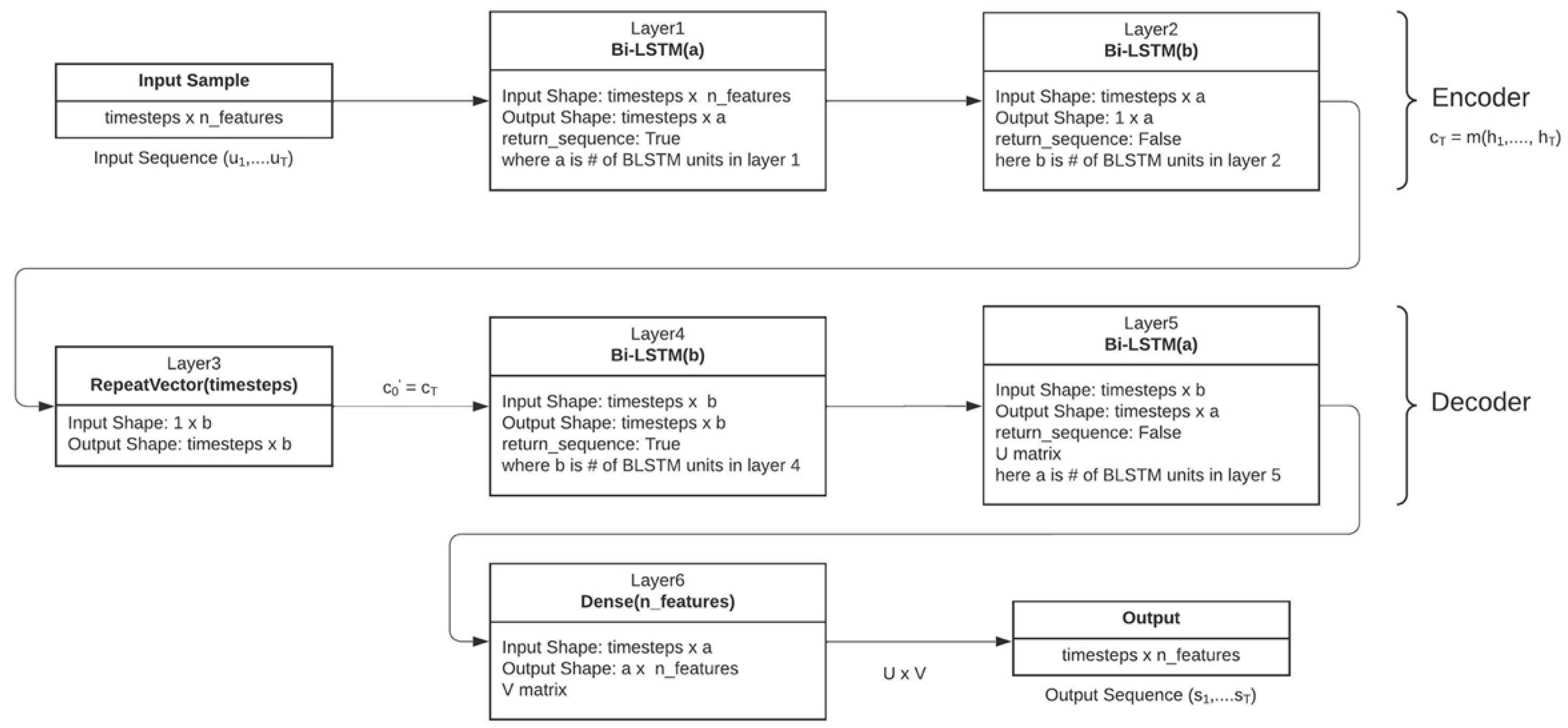
3.2. Proposed Stacked Encoder–Decoder Bi-LSTM
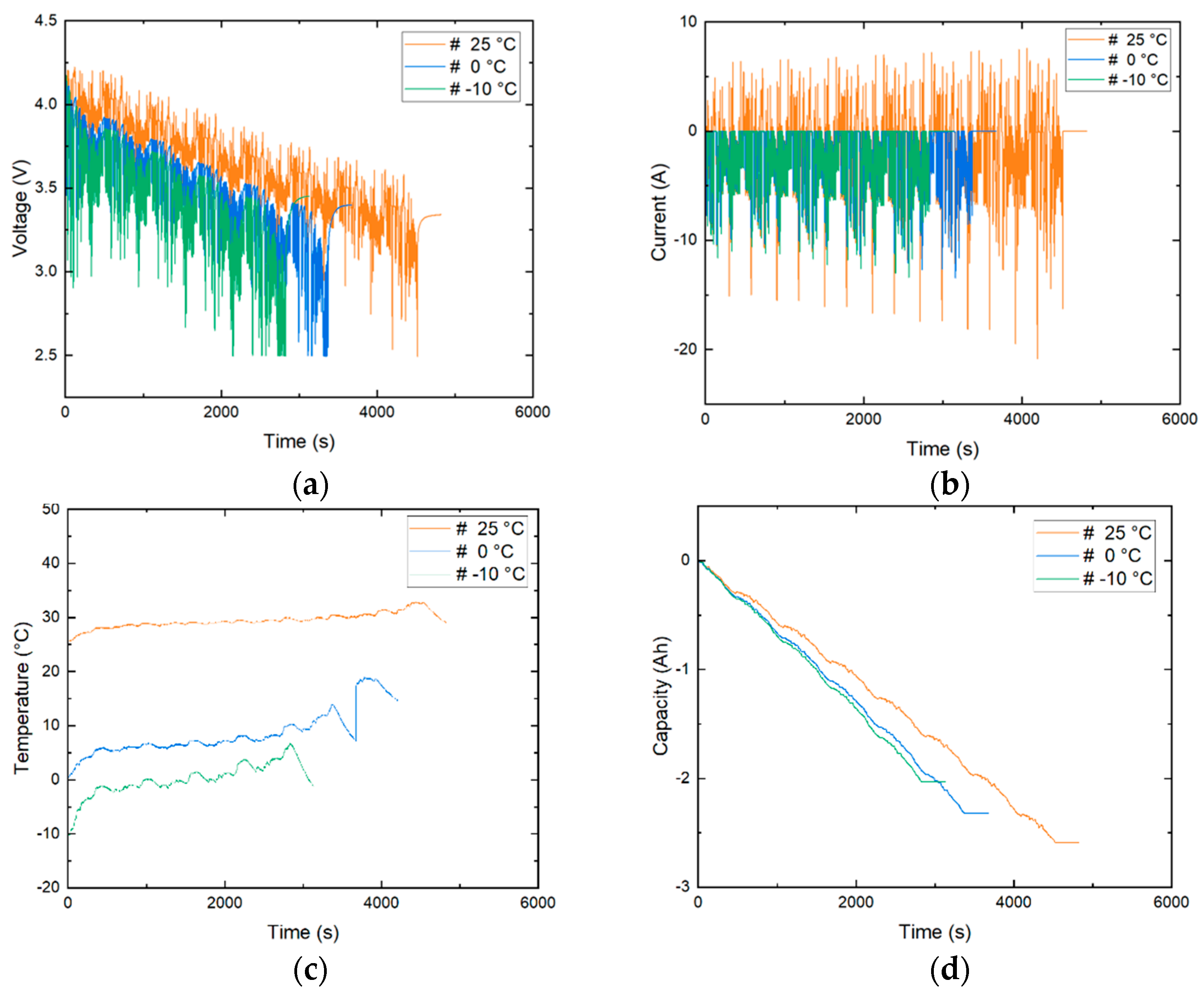
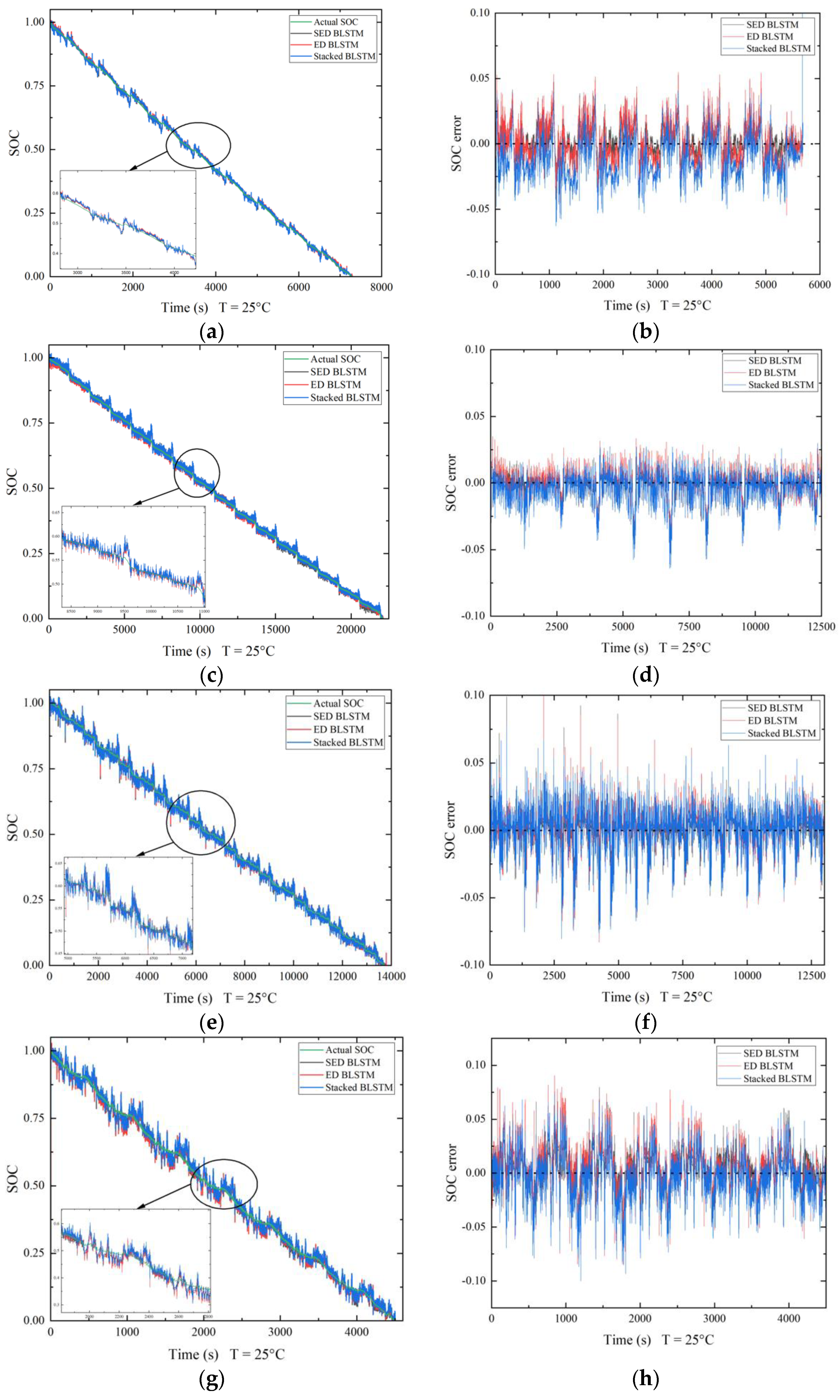
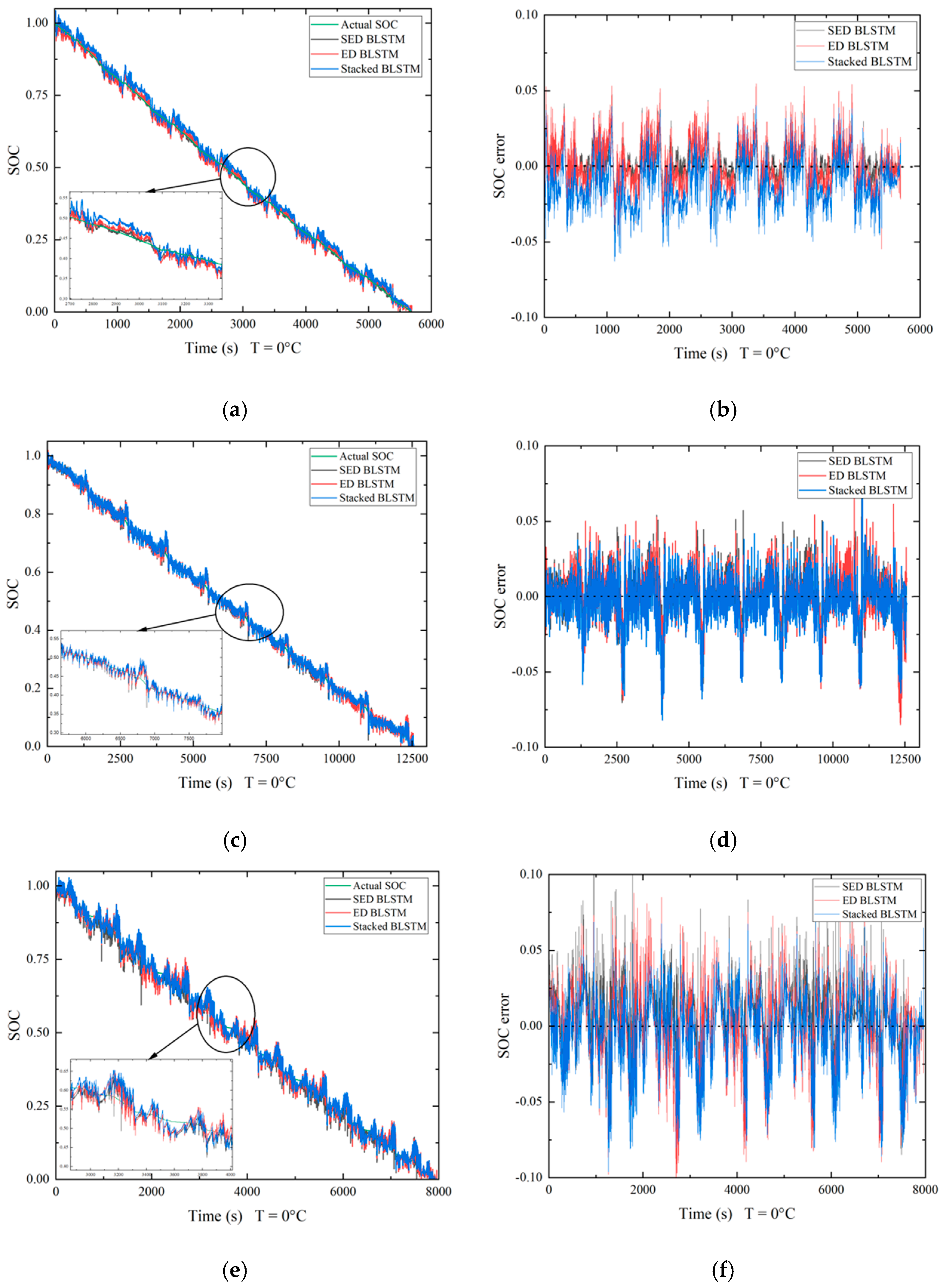
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Agency, I.E. Global EV Outlook. 2021. Available online: https://www.iea.org/reports/global-ev-outlook-2021 (accessed on 23 June 2022).
- IEA. Tracking Transport 2021, IEA, Paris. 2021. Available online: https://www.iea.org/reports/tracking-transport-2021 (accessed on 23 June 2022).
- Kang, L.; Zhao, X.; Ma, J. A new neural network model for the state-of-charge estimation in the battery degradation process. Appl. Energy 2014, 121, 20–27. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Shen, Y. Adaptive online state-of-charge determination based on neuro-controller and neural network. Energy Convers. Manag. 2010, 51, 1093–1098. [Google Scholar] [CrossRef]
- Dong, C.; Wang, G. Estimation of power battery SOC based on improved BP neural network. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014. [Google Scholar]
- Sun, B.; Wang, L. The SOC estimation of NIMH battery pack for HEV based on BP neural network. In Proceedings of the 2009 International Workshop on Intelligent Systems and Applications, Wuhan, China, 23–24 May 2009. [Google Scholar]
- Bialer, O.; Garnett, N.; Tirer, T. Performance Advantages of Deep Neural Networks for Angle of Arrival Estimation. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3907–3911. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A.; Kollmeyer, P. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2017, 65, 6730–6739. [Google Scholar] [CrossRef]
- Abbas, G.; Nawaz, M.; Kamran, F. Performance comparison of NARX & RNN-LSTM neural networks for LiFePO4 battery state of charge estimation. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 18–20 January 2019; pp. 463–468. [Google Scholar] [CrossRef]
- Zhao, R.; Kollmeyer, P.J.; Lorenz, R.D.; Jahns, T.M. A compact methodology via a recurrent neural network for accurate equivalent circuit type modeling of lithiumion batteries. IEEE Trans. Ind. Appl. 2019, 55, 1922–1931. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Li, C.; Xiao, F.; Fan, Y. An Approach to State of Charge Estimation of Lithium-Ion Batteries Based on Recurrent Neural Networks with Gated Recurrent Unit. Energies 2019, 12, 1592. [Google Scholar] [CrossRef]
- Chen, J.; Lu, C.; Chen, C.; Cheng, H.; Xuan, D. An Improved Gated Recurrent Unit Neural Network for State-of-Charge Estimation of Lithium-Ion Battery. Appl. Sci. 2022, 12, 2305. [Google Scholar] [CrossRef]
- Cui, Z.; Ke, R.; Wang, Y. Deep Bidirectional and Unidirectional LSTM Recurrent Neural Network for Network-wide Traffic Speed Prediction. arXiv 2018, arXiv:1801.02143. [Google Scholar]
- Bian, C.; He, H.; Yang, S. Stacked bidirectional long short-term memory networks for state-of-charge estimation of lithium-ion batteries. Energy 2020, 191, 116538. [Google Scholar] [CrossRef]
- Bian, C.; He, H.; Yang, S.; Huang, T. State-of-charge sequence estimation of lithium-ion battery based on bidirectional long short-term memory encoder-decoder architecture. J. Power Sources 2020, 449, 227558. [Google Scholar] [CrossRef]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.-I.; Stroe, A.-I.; Teodorescu, R. An Overview and Comparison of Online Implementable SOC Estimation Methods for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [Google Scholar] [CrossRef]
- Cui, S.; Han, S.; Chan, C.C. Overview of multi-machine drive systems for electric and hybrid electric vehicles. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Baccouche, I.; Mlayah, A.; Jemmali, S.; Manai, B.; Ben Amara, N.E. $Implementation of a Coulomb counting algorithm for SOC estimation of Li-Ion battery for multimedia applications. In Proceedings of the 2015 IEEE 12th International Multi-Conference on Systems, Signals & Devices (SSD15), Mahdia, Tunisia, 16–19 March 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, P.; Vinjamuri, R.; Wang, X.; Reisner, D. Design and implementation of a fuzzy logic-based state-of-charge meter for Li-ion batteries used in portable defibrillators. J. Power Sources 2006, 162, 829–836. [Google Scholar] [CrossRef]
- Hametner, C.; Jakubek, S. State of charge estimation for Lithium Ion cells: Design of experiments, nonlinear identification and fuzzy observer design. J. Power Sources 2013, 238, 413–421. [Google Scholar] [CrossRef]
- Singh, P.; Fennie, C.; Reisner, D. Fuzzy logic modelling of state-of-charge and available capacity of nickel/metal hydride batteries. J. Power Sources 2004, 136, 322–333. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Moura, S.J.; Krstic, M.; Chaturvedi, N.A. Adaptive PDE Observer for Battery SOC/SOH Estimation. In Proceedings of the Dynamic Systems and Control Conference (DSCC12), Fort Lauderdale, FL, USA, 17–19 October 2012; pp. 101–110. [Google Scholar] [CrossRef]
- Babaeiyazdi, I.; Rezaei-Zare, A.; Shokrzadeh, S. State of charge prediction of EV Li-ion batteries using EIS: A machine learning approach. Energy 2021, 223, 120116. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Sources 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Viejo, C.B.; Vilan, J.A.V. Support Vector Machines Used to Estimate the Battery State of Charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Antón, J.C.Á.; Nieto, P.J.G.; de Cos Juez, F.J.; Lasheras, F.S.; Vega, M.G.; Gutiérrez, M.N.R. Battery state-of-charge estimator using the SVM technique. Appl. Math. Model. 2013, 37, 6244–6253. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Chaibi, R.; Ben Amara, N.E. Hardware implementation of an algorithm based on kalman filtrer for monitoring low capacity Li-ion batteries. In Proceedings of the 2016 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22 March 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.; Hu, Z.; Zhang, Y.; Zhang, J. A Battery SOC Estimation Method Based on AFFRLS-EKF. Sensors 2021, 21, 5698. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 3. State and parameter estimation. J. Power Sour. 2004, 34, 277–292. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs, Part 2, Modeling and identifica- tion. J. Power Sour. 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs, Part 1, Background. J. Power Sour. 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Gabbar, H.; Othman, A.; Abdussami, M. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- James, P.E.; Mun, H.K.; Vaithilingam, C.A. A Hybrid Spoken Language Processing System for Smart Device Troubleshooting. Electronics 2019, 8, 681. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Shao, Y.; Ding, B. LSTM-convolutional-BLSTM encoder-decoder network for minimum mean-square error approach to speech enhancement. Appl. Acoust. 2021, 172, 107647. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, B.; Kang, C.M.; Chung, C.C.; Choi, J.W. Sequence-to-sequence prediction of vehicle trajectory via LSTM encoder-decoder architecture. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1672–1678. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]

| Rated Capacity | 2700 mAh | 2615 mAh | |
| Capacity | Minimum | 2750 mAh | 2665 mAh |
| Typical | 2900 mAh | 2810 mAh | |
| Nominal Voltage | 3.6 V | ||
| Charging | Voltage | 4.20 V | 4.15 V |
| Current | 0.5 C | ||
| Energy Density | Volumetric | 577 Wh/L | 559 Wh/L |
| Gravimetric | 207 Wh/kg | 200 Wh/kg |
| Bi-LSTM Layers | Metrics (%) | Temp (°C) | |||
|---|---|---|---|---|---|
| 25 | 10 | 0 | −10 | ||
| 1 layer | MAE | 0.7226 | 1.0292 | 1.2268 | 1.4880 |
| RMSE | 1.0019 | 1.2988 | 1.5101 | 1.9876 | |
| 2 layers | MAE | 0.6229 | 0.9957 | 1.1066 | 1.2021 |
| RMSE | 0.8615 | 1.2832 | 1.3884 | 1.7240 | |
| 3 layers | MAE | 0.8268 | 2.3668 | 1.3155 | 1.5877 |
| RMSE | 1.0365 | 2.9332 | 1.6815 | 2.0852 |
| Network Model | Temperature (°C) | UDDS MAE (%) | RMSE (%) | HWFET MAE (%) | RMSE (%) | US06 MAE (%) | RMSE (%) | LA92 MAE (%) | RMSE (%) |
|---|---|---|---|---|---|---|---|---|---|
| SED | −10 | 0.7768 | 1.2233 | 1.2021 | 1.7240 | 1.2289 | 1.8075 | 0.6843 | 1.3100 |
| 0 | 1.0502 | 1.4381 | 1.1066 | 1.3884 | 1.9743 | 2.7022 | 1.6693 | 2.0993 | |
| 10 | 0.8829 | 1.2134 | 0.9957 | 1.2832 | 1.9457 | 2.5715 | 1.1107 | 1.6442 | |
| 25 | 0.6478 | 0.9278 | 0.6229 | 0.8615 | 1.3780 | 1.8510 | 0.9508 | 1.3381 | |
| ED | −10 | 1.4543 | 2.0943 | 1.5284 | 1.9751 | 2.5922 | 3.5435 | 2.5011 | 3.3832 |
| 0 | 1.0195 | 1.4330 | 1.1760 | 1.4570 | 2.4400 | 3.2085 | 1.9554 | 2.5138 | |
| 10 | 0.9843 | 1.3669 | 1.0656 | 1.3695 | 2.5067 | 3.2818 | 1.6248 | 2.1145 | |
| 25 | 0.6819 | 0.9543 | 0.7375 | 0.9531 | 1.6231 | 2.1357 | 1.0169 | 1.3792 | |
| Stacked | −10 | 1.5341 | 2.2080 | 1.7923 | 2.2359 | 2.9908 | 4.0846 | 2.7319 | 3.5576 |
| 0 | 1.0294 | 1.4654 | 1.5315 | 1.8561 | 2.5751 | 3.3895 | 1.7562 | 2.3026 | |
| 10 | 0.9640 | 1.3942 | 1.0493 | 1.3720 | 2.5767 | 3.3570 | 1.4743 | 2.0378 | |
| 25 | 0.6827 | 1.0098 | 1.7187 | 1.0461 | 1.6089 | 2.1293 | 1.0363 | 1.4184 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terala, P.K.; Ogundana, A.S.; Foo, S.Y.; Amarasinghe, M.Y.; Zang, H. State of Charge Estimation of Lithium-Ion Batteries Using Stacked Encoder–Decoder Bi-Directional LSTM for EV and HEV Applications. Micromachines 2022, 13, 1397. https://doi.org/10.3390/mi13091397
Terala PK, Ogundana AS, Foo SY, Amarasinghe MY, Zang H. State of Charge Estimation of Lithium-Ion Batteries Using Stacked Encoder–Decoder Bi-Directional LSTM for EV and HEV Applications. Micromachines. 2022; 13(9):1397. https://doi.org/10.3390/mi13091397
Chicago/Turabian StyleTerala, Pranaya K., Ayodeji S. Ogundana, Simon Y. Foo, Migara Y. Amarasinghe, and Huanyu Zang. 2022. "State of Charge Estimation of Lithium-Ion Batteries Using Stacked Encoder–Decoder Bi-Directional LSTM for EV and HEV Applications" Micromachines 13, no. 9: 1397. https://doi.org/10.3390/mi13091397
APA StyleTerala, P. K., Ogundana, A. S., Foo, S. Y., Amarasinghe, M. Y., & Zang, H. (2022). State of Charge Estimation of Lithium-Ion Batteries Using Stacked Encoder–Decoder Bi-Directional LSTM for EV and HEV Applications. Micromachines, 13(9), 1397. https://doi.org/10.3390/mi13091397






