Experimental Investigation on Ablation of 4H-SiC by Infrared Femtosecond Laser
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
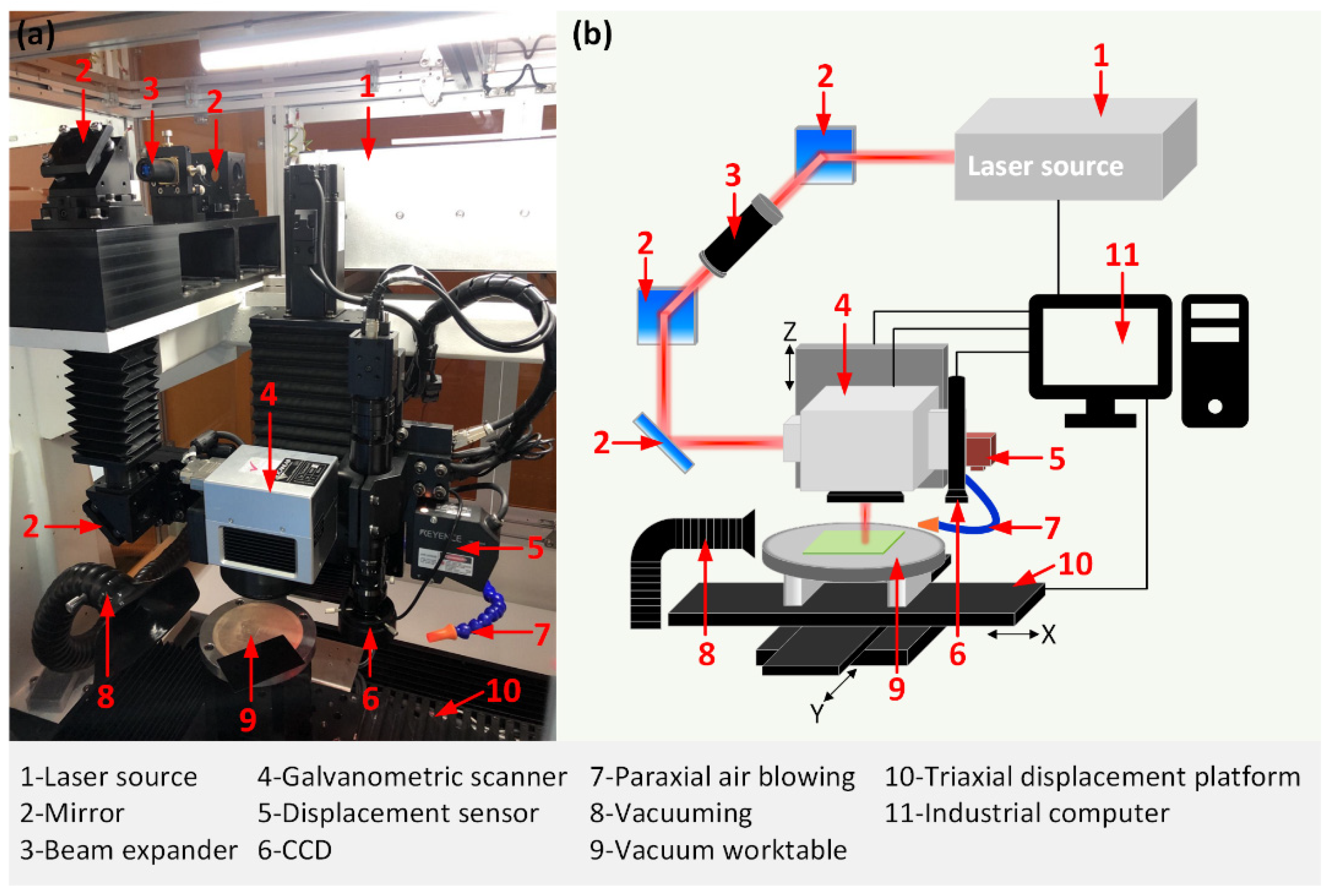
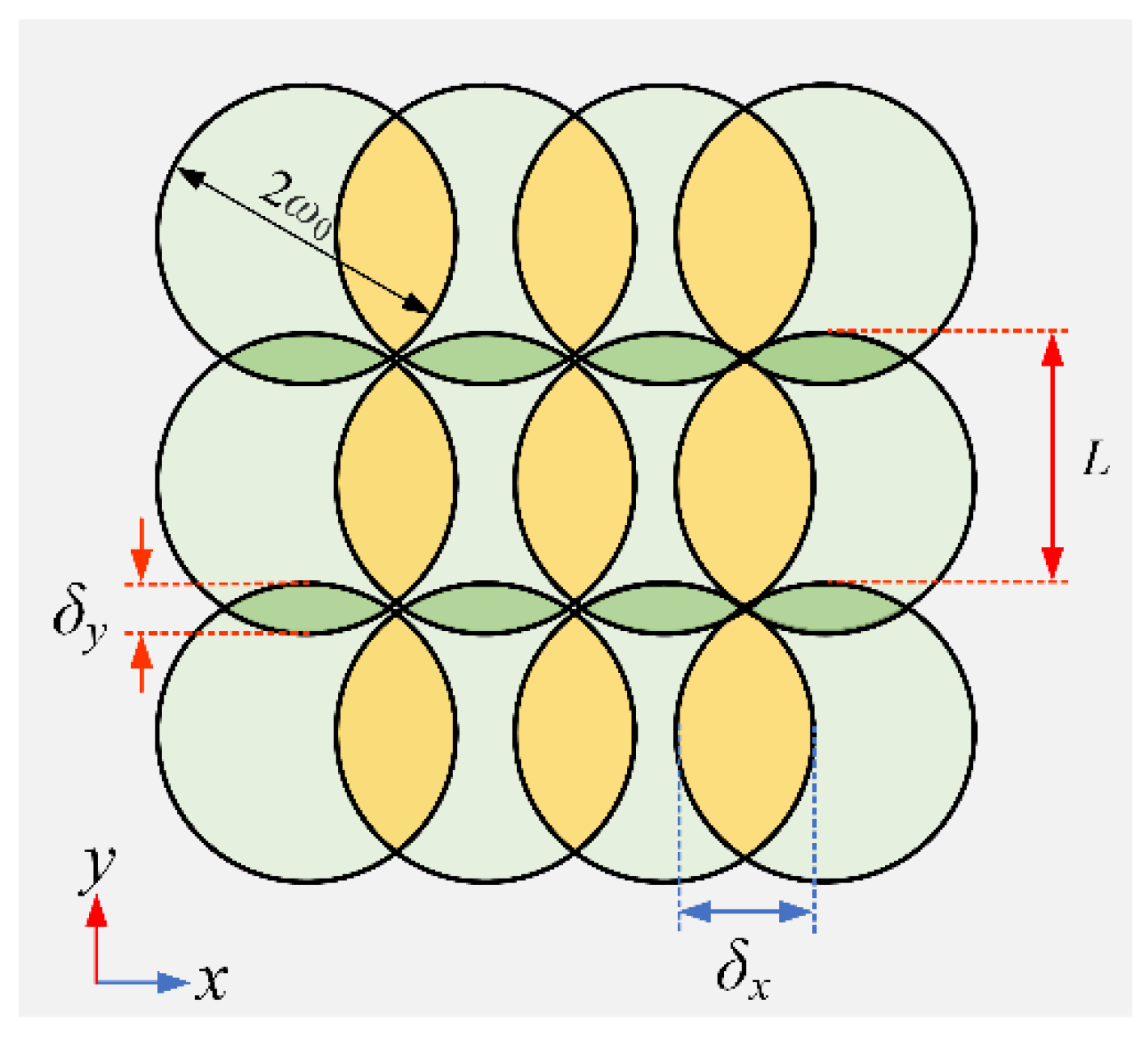
2.2. Laser Processing
3. Results and Discussion
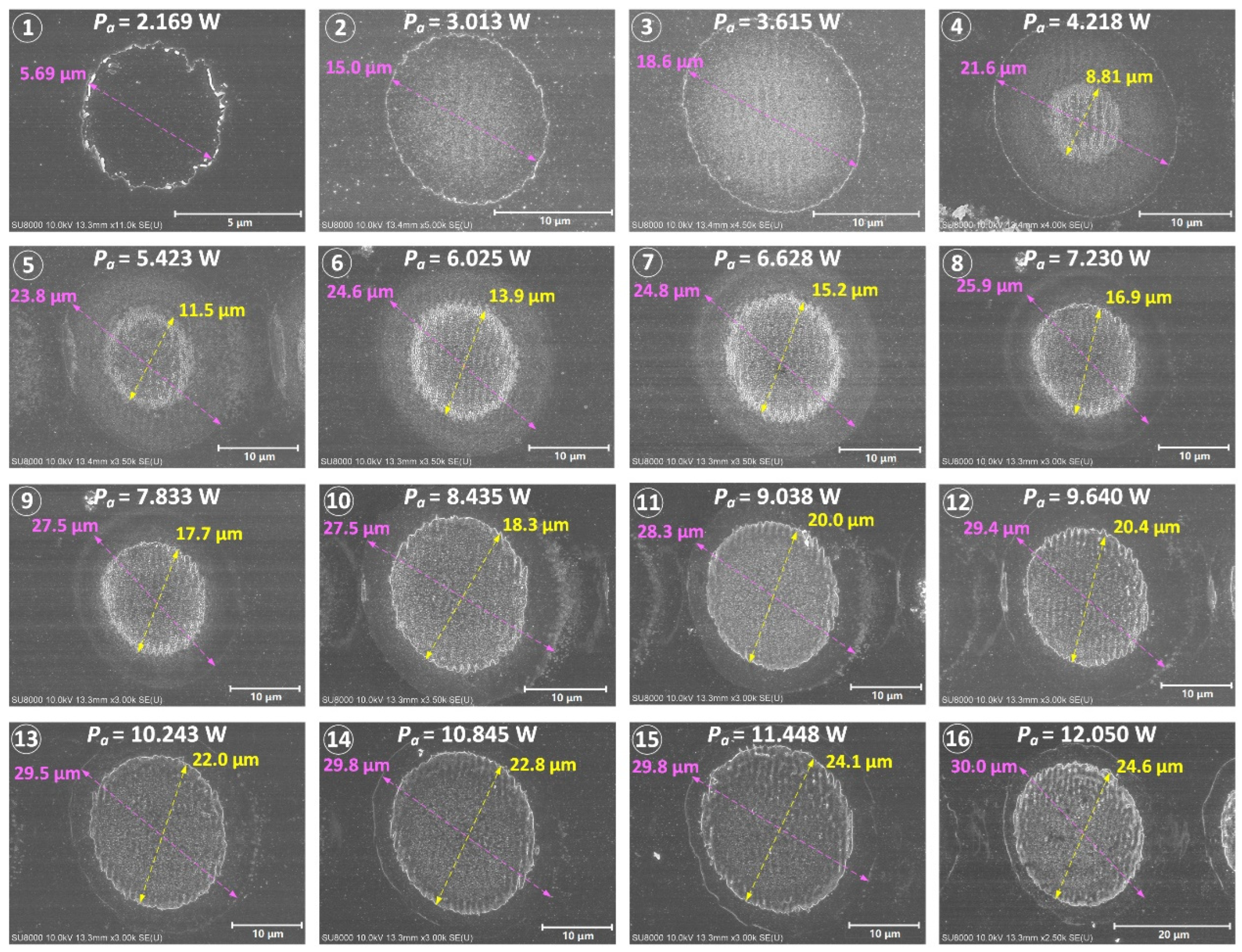
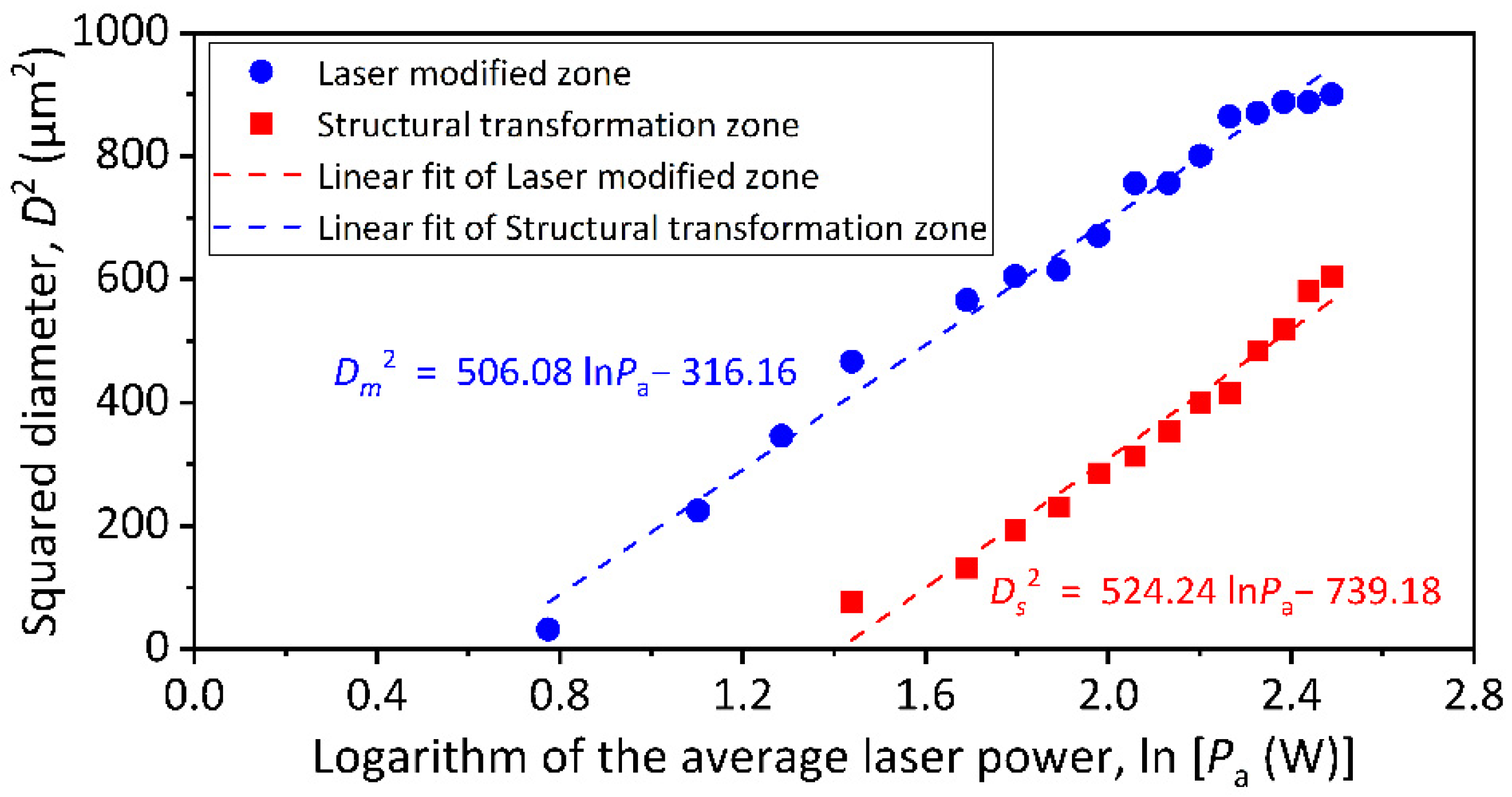
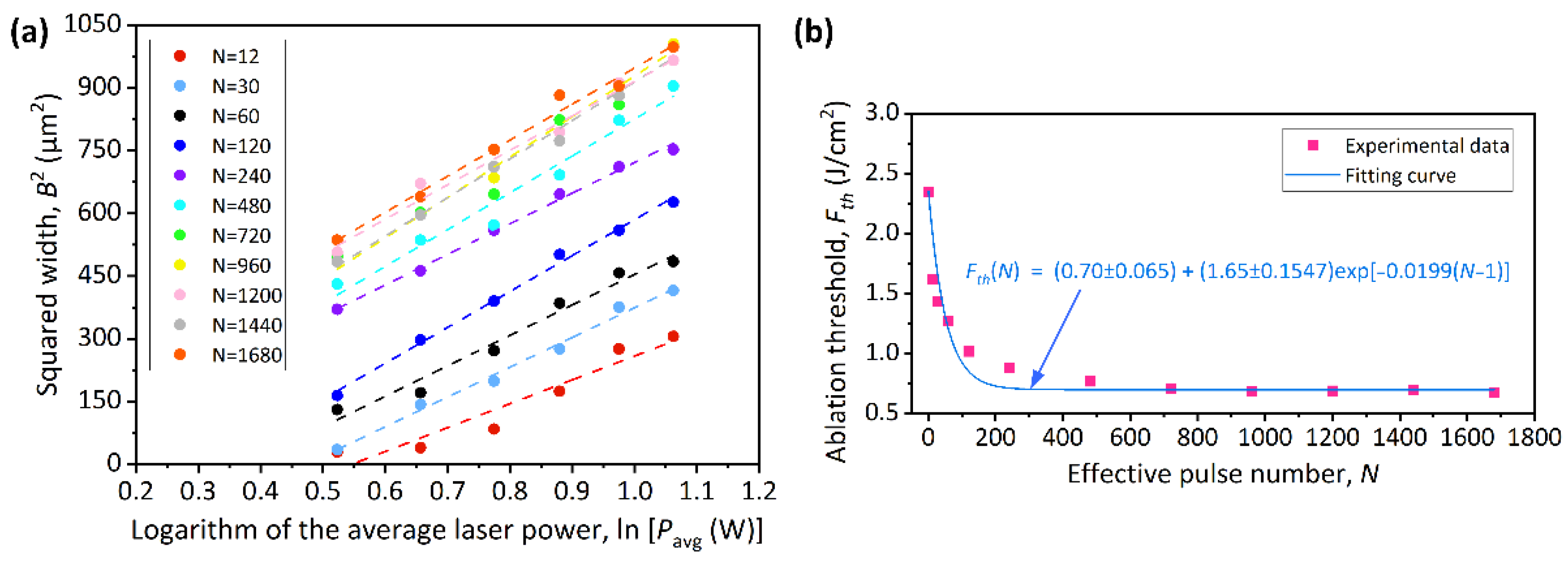
3.1. Measurement of Single-Pulse Ablation Threshold
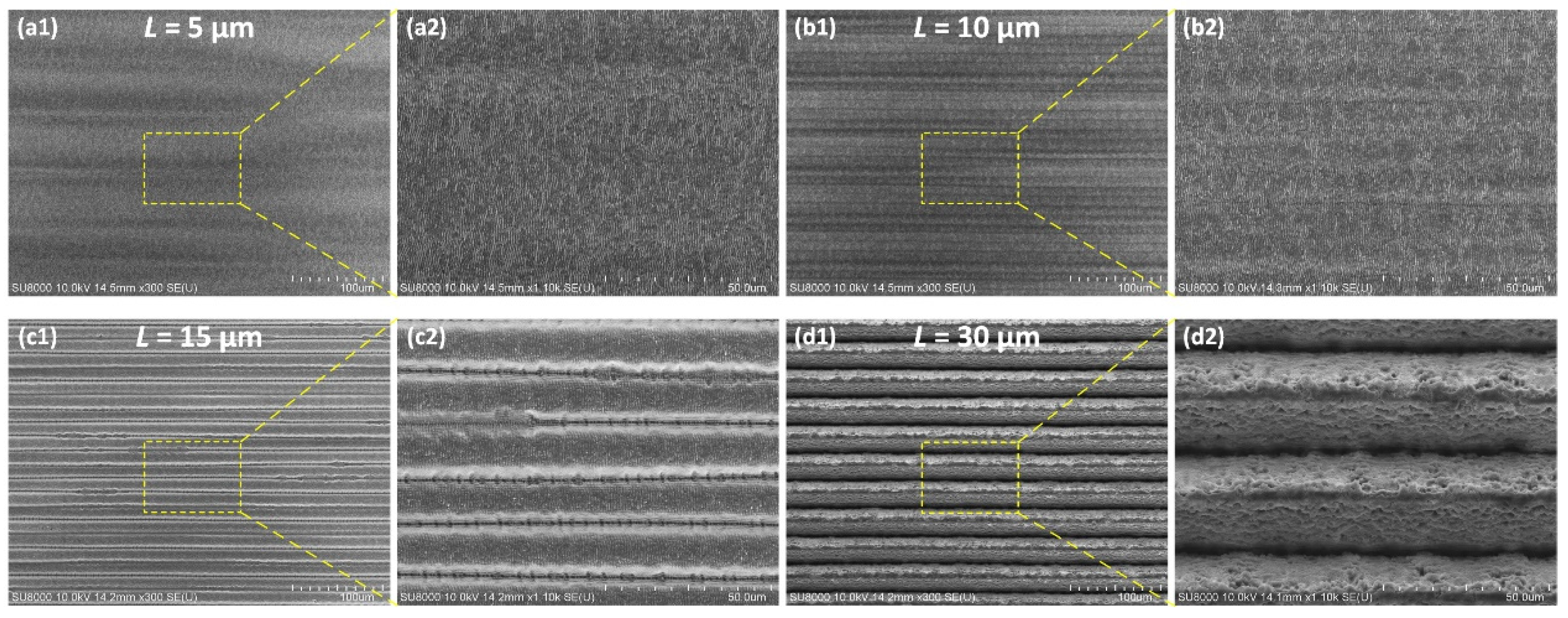
3.2. Multiple-Pulse Scribing Ablation for Microgrooves
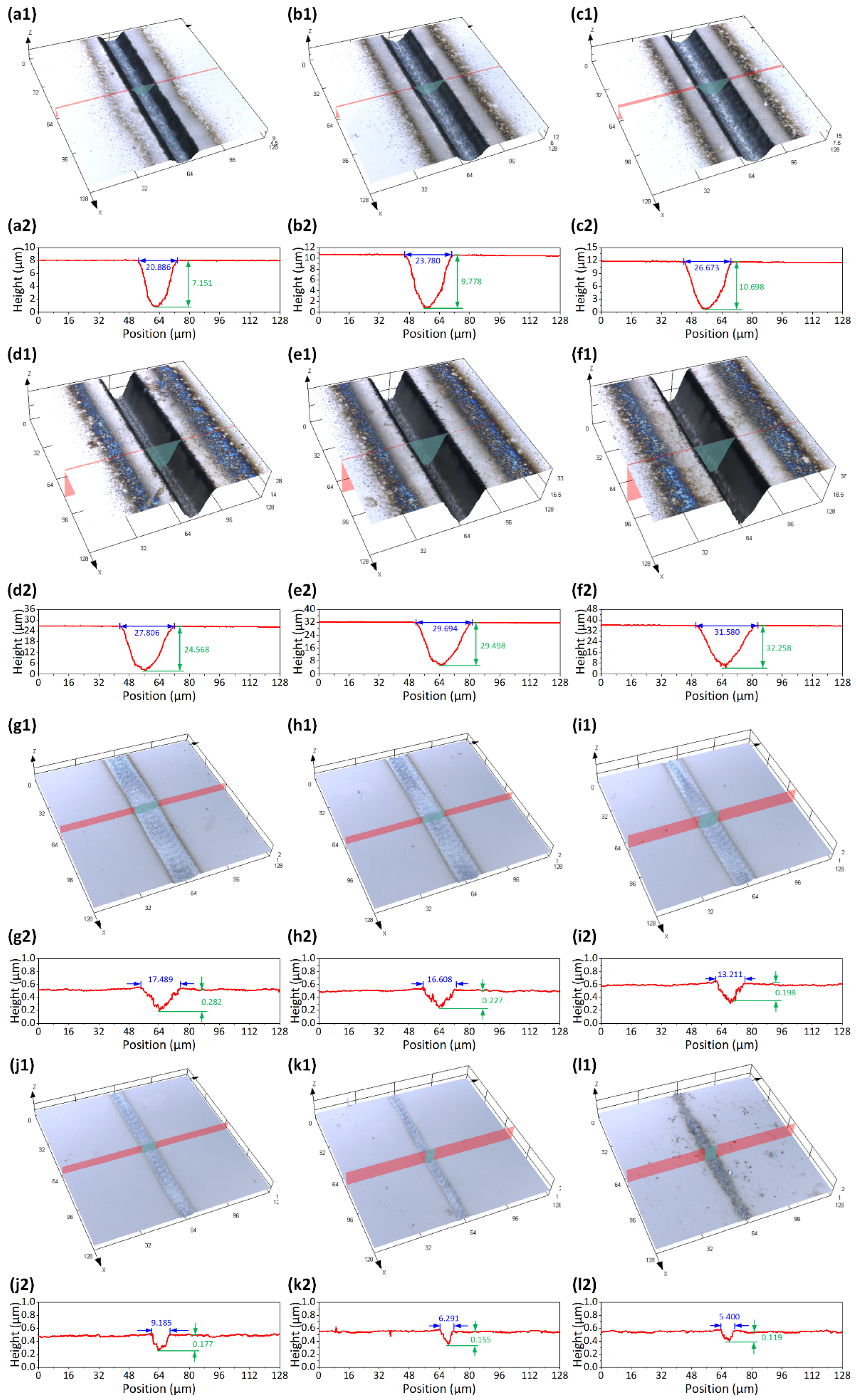
3.3. Large-Area and Bulk Ablation
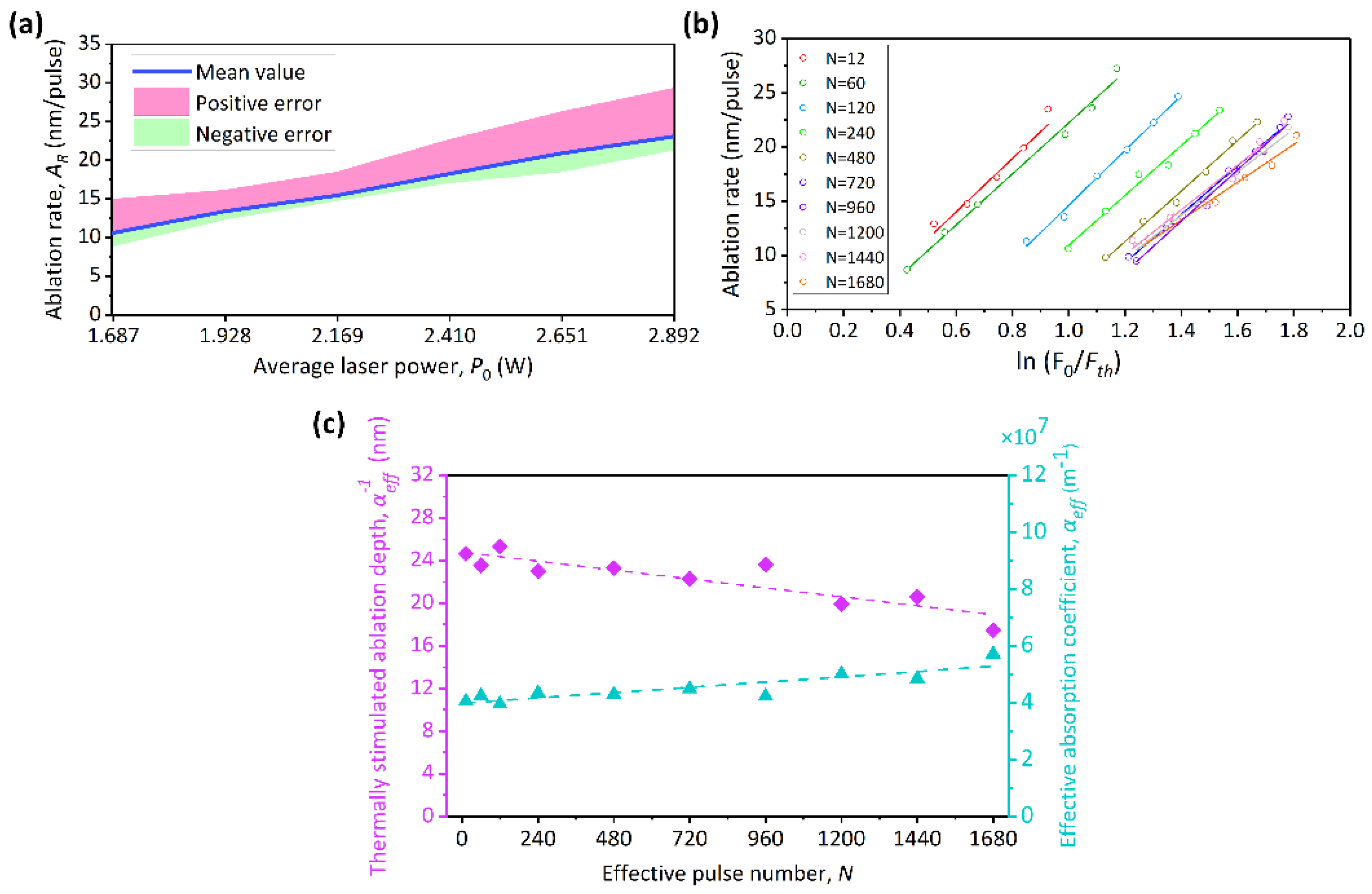
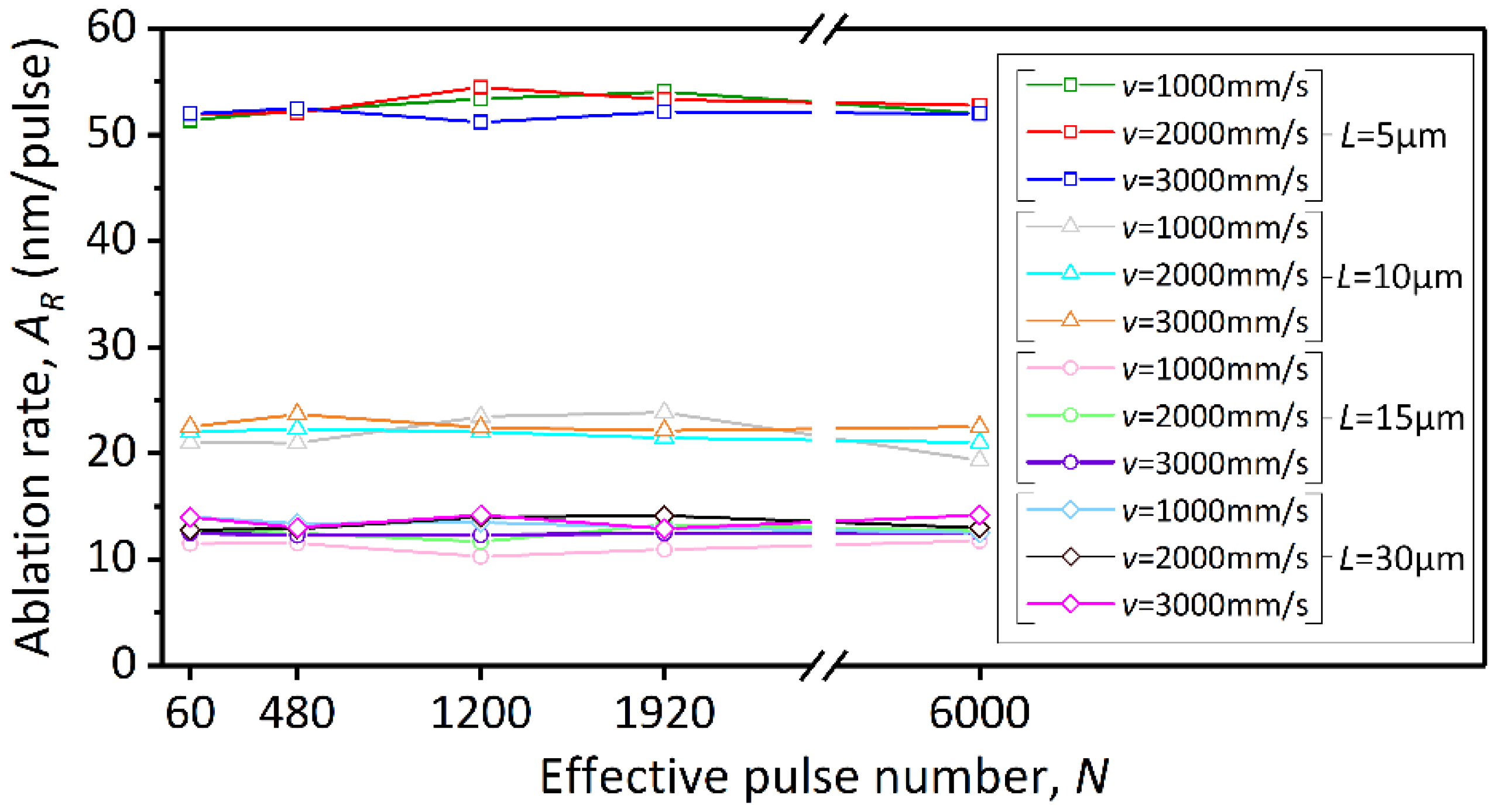
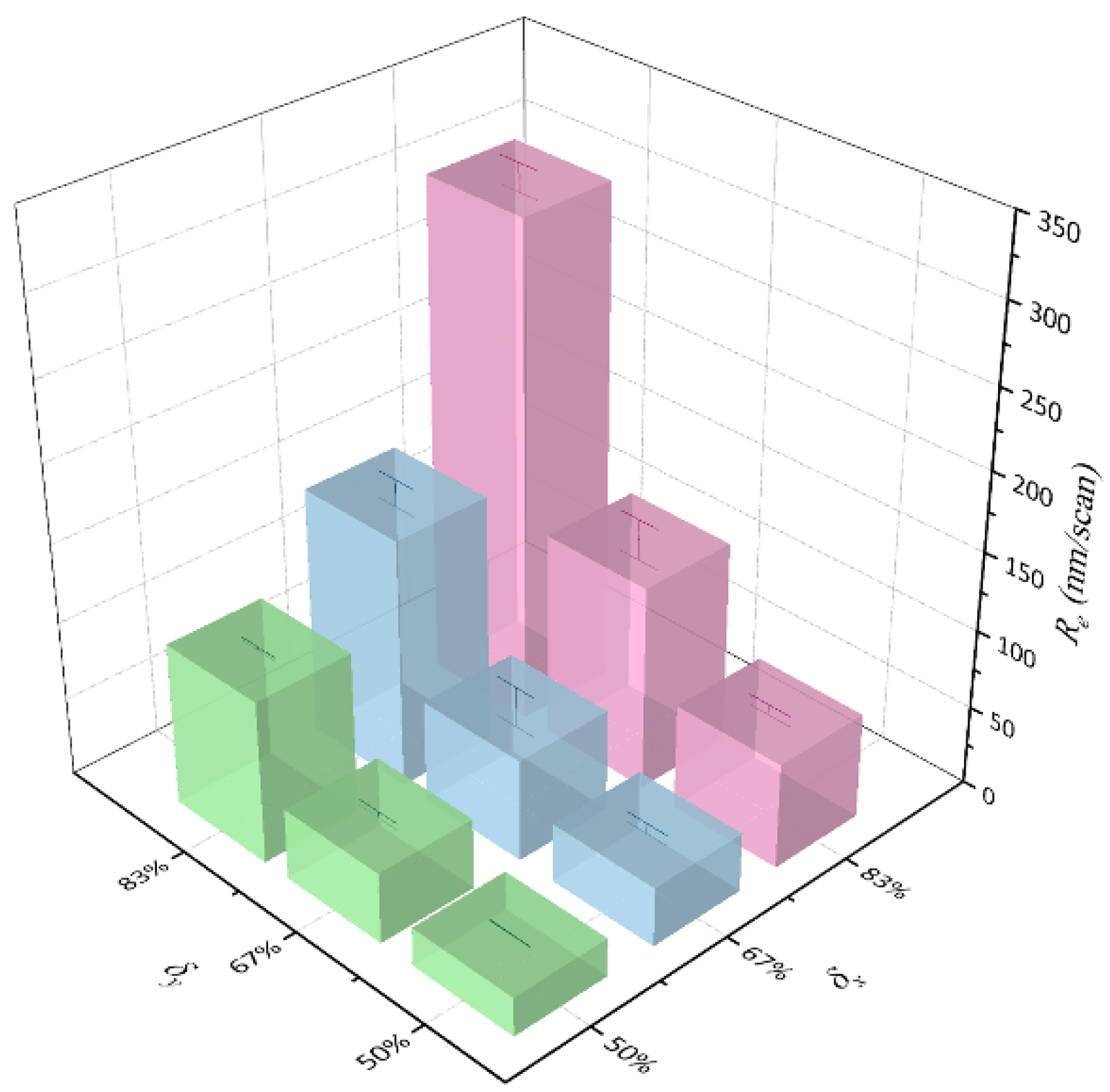
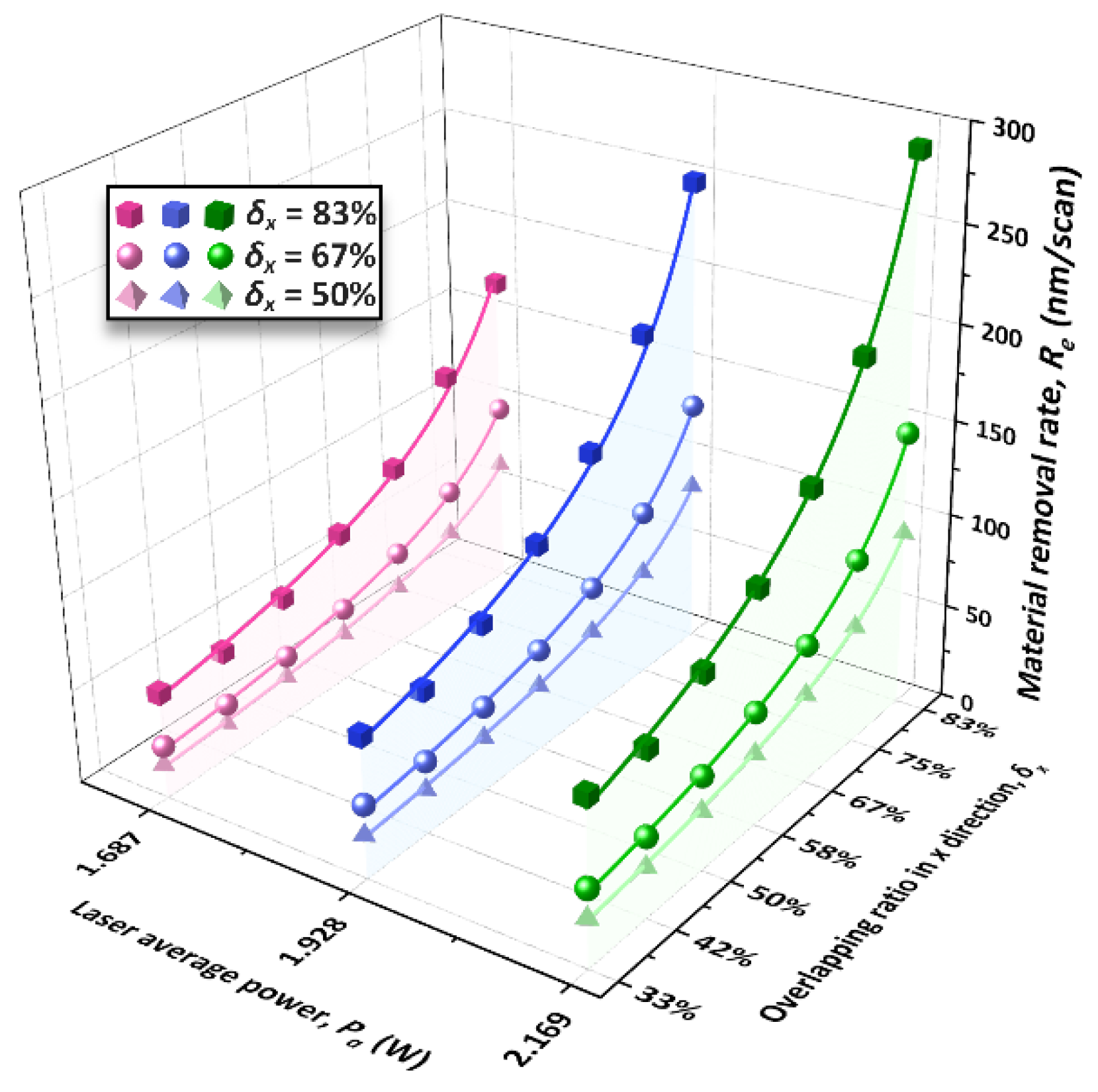
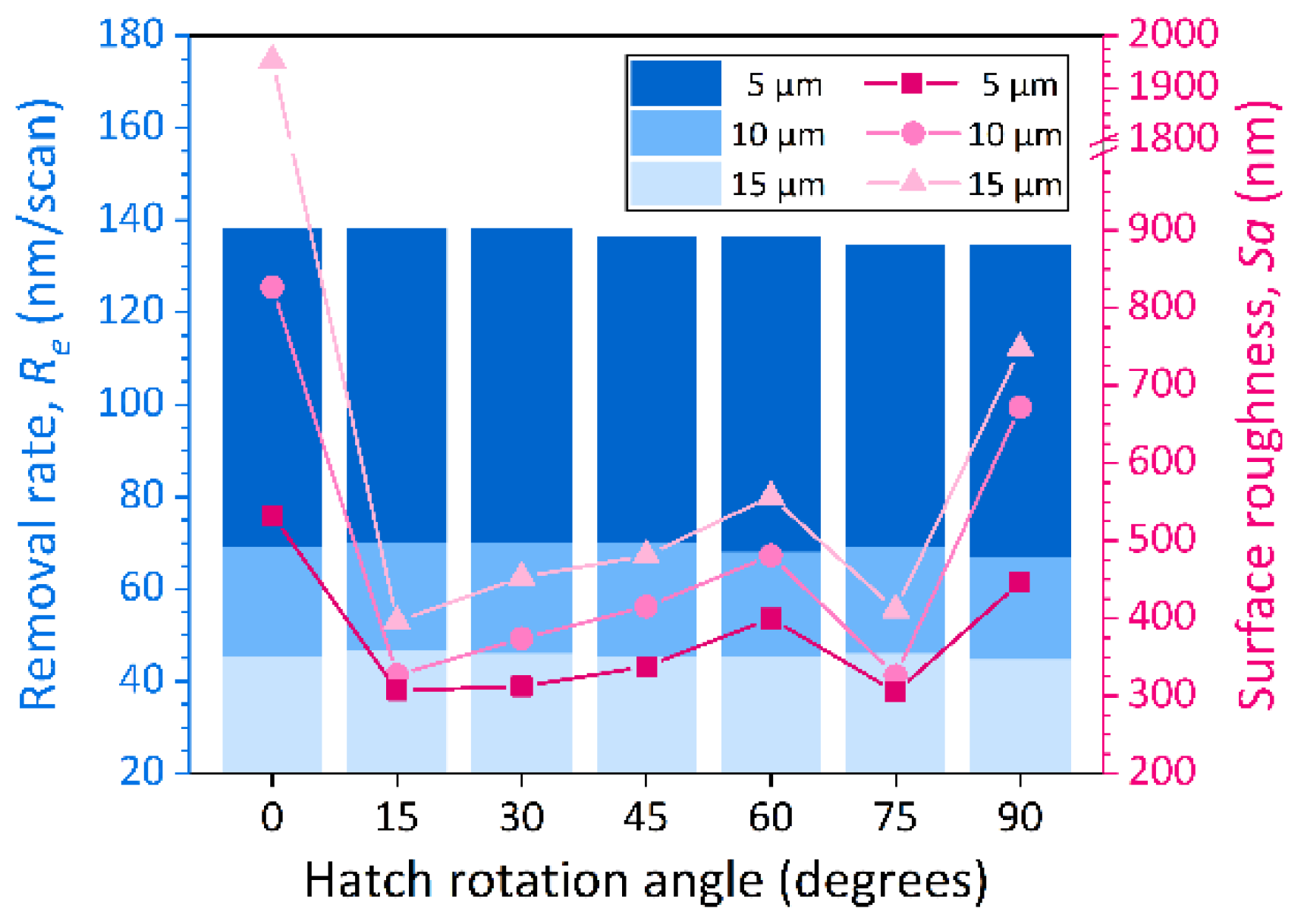
3.3.1. Analysis of Process Parameters Effect on the Material Removal Rate
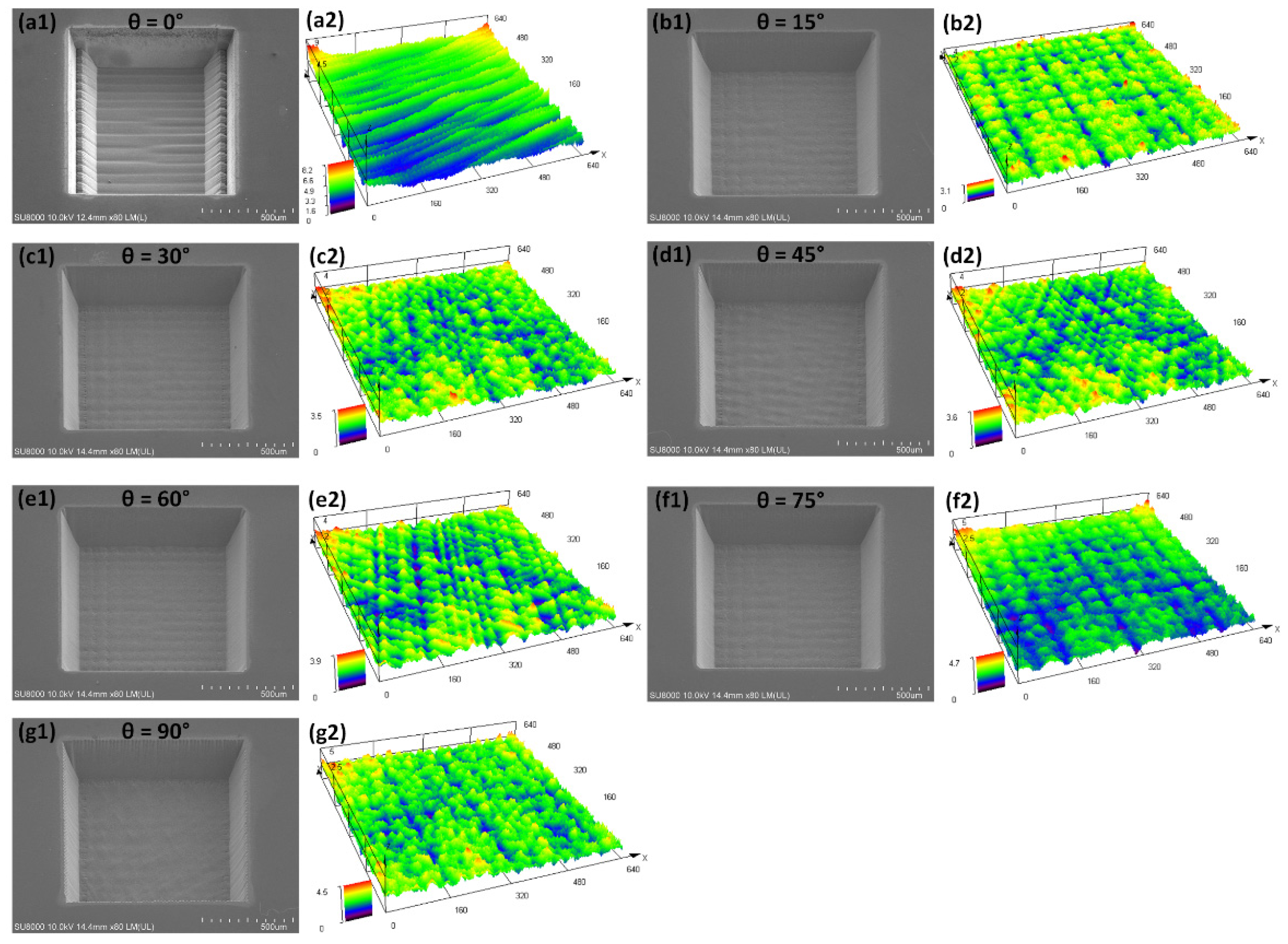
3.3.2. Planarization Processing Surface
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mehregany, M.; Zorman, C.A.; Rajan, N.; Wu, C.H. Silicon carbide MEMS for harsh environments. Proc. IEEE 1998, 86, 1594–1609. [Google Scholar] [CrossRef]
- Senesky, D.G.; Jamshidi, B.; Cheng, K.B.; Pisano, A.P. Harsh Environment Silicon Carbide Sensors for Health and Performance Monitoring of Aerospace Systems: A Review. IEEE Sens. J. 2009, 9, 1472–1478. [Google Scholar] [CrossRef]
- Erbacher, K.; Mackowiak, P.; Schiffer, M.; Lang, K.D.; Ngo, H.D. Investigation of Deep Dry Etching of 4H SIC Material for MEMS Applications Using DOE Modelling. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Virtual Conference, 25–29 January 2021. [Google Scholar]
- Zhuang, D.; Edgar, J.H. Wet etching of GaN, AlN, and SiC: A review. Mater. Sci. Eng. R 2005, 48, 1–46. [Google Scholar] [CrossRef]
- Akiyama, T.; Briand, D.; Rooij, N.D. Piezoresistive n-type 4H-SiC pressure sensor with membrane formed by mechanical milling. Proc. IEEE Sens. 2011, 1, 222–225. [Google Scholar]
- Wieczorek, G.; Schellin, B.; Obermeier, E.; Fa Gnani, G.; Drera, L. SiC Based Pressure Sensor for High-Temperature Environments. In Proceedings of the IEEE, Atlanta, GA, USA, 28–31 October 2007; pp. 748–751. [Google Scholar]
- Wang, L.; Zhao, Y.; Zhao, Y.; Yang, Y.; Ren, W. Design and Fabrication of Bulk Micromachined 4H-SiC Piezoresistive Pressure Chips Based on Femtosecond Laser Technology. Micromachines 2021, 12, 56. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhao, Y.; Yang, Y.; Zhao, Y. Two-step femtosecond laser etching for bulk micromachining of 4H–SiC membrane applied in pressure sensing—ScienceDirect. Ceram. Int. 2022, 48, 12359–12367. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Y.-L.; Wang, L.-K. Application of femtosecond laser micromachining in silicon carbide deep etching for fabricating sensitive diaphragm of high temperature pressure sensor. Sens. Actuators A Phys. 2020, 309, 112017. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, Y.; Wang, L.; Zhao, Y. Application of femtosecond laser etching in the fabrication of bulk SiC accelerometer. J. Mater. Res. Technol. 2022, 17, 2577–2586. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, Y.; Liu, J.; Tang, J.; Li, J.; Ma, Z.; Cao, H.; Zhao, R.; Kou, Z.; Huang, K. UV nanosecond laser machining and characterization for SiC MEMS sensor application. Sens. Actuators A Phys. 2018, 276, 196–204. [Google Scholar] [CrossRef]
- Huang, Y.; Tang, F.; Ma, D.; Liu, Z.; Wang, X. Design, fabrication, characterization, and application of an ultra-high temperature 6H-SiC sapphire fiber optic vibration sensor. IEEE Photonics J. 2019, 11, 6802512. [Google Scholar] [CrossRef]
- Vendan, M.; Molian, P. Femtosecond pulsed laser microfabrication of SiC MEMS microgripper. J. Laser Appl. 2007, 19, 149–154. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Q.; Wu, R.; Sha, J.; Lu, Y.; Xuan, F. Laser direct writing of ultrahigh sensitive SiC-based strain sensor arrays on elastomer toward electronic skins. Adv. Funct. Mater. 2019, 29, 1806786. [Google Scholar] [CrossRef]
- Rupp, R.; Kern, R.; Gerlach, R. Laser backside contact annealing of SiC Power devices: A Prerequisite for SiC thin wafer technology. In Proceedings of the 2013 25th International Symposium on Power Semiconductor Devices & IC’s (ISPSD), Kanazawa, Japan, 26–30 May 2013; pp. 51–54. [Google Scholar]
- Wang, L.; Zhao, Y.; Yang, Y.; Pang, X.; Hao, L.; Zhao, Y. Piezoresistive 4H-SiC Pressure Sensor with Diaphragm Realized by Femtosecond Laser. IEEE Sens. J. 2022, 22, 11535–11542. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Zhao, Y.; Yang, Y.; Li, B.; Gong, T. Mass fabrication of 4H-SiC high temperature pressure sensors by femtosecond laser etching. In Proceedings of the 2021 IEEE 16th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Xiamen, China, 25–29 April 2021; pp. 1478–1481. [Google Scholar]
- Wang, L.; Zhao, Y.; Yang, Y.; Pang, X.; Hao, L.; Zhao, Y.; Liu, J. Development of Laser-Micromachined 4H-SiC MEMS Piezoresistive Pressure Sensors for Corrosive Environments. IEEE Trans. Electron Devices 2022, 69, 2009–2014. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, R.; Huang, C.; Wang, J.; Jia, Z.; Wang, J. An investigation of recast behavior in laser ablation of 4H-silicon carbide wafer. Mater. Sci. Semicond. Processing 2020, 105, 104701. [Google Scholar] [CrossRef]
- Duc, D.H.; Naoki, I.; Kazuyoshi, F. A study of near-infrared nanosecond laser ablation of silicon carbide. Int. J. Heat Mass Transf. 2013, 65, 713–718. [Google Scholar] [CrossRef]
- Molian, P.; Pecholt, B.; Gupta, S. Picosecond pulsed laser ablation and micromachining of 4H-SiC wafers. Appl. Surf. Sci. 2009, 255, 4515–4520. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, C.; Wang, J.; Zhu, H.; Yao, P.; Feng, S. Micromachining of 4H-SiC using femtosecond laser. Ceram. Int. 2018, 44, 17775–17783. [Google Scholar] [CrossRef]
- Wang, C.; Kurokawa, S.; Doi, T.; Yuan, J.; Fan, L.; Mitsuhara, M.; Lu, H.; Yao, W.; Zhang, Y.; Zhang, K. SEM, AFM and TEM studies for repeated irradiation effect of femtosecond laser on 4H-SiC surface morphology at near threshold fluence. ECS J. Solid State Sci. Technol. 2018, 7, P29. [Google Scholar] [CrossRef]
- Iwatani, N.; Doan, H.D.; Fushinobu, K. Optimization of near-infrared laser drilling of silicon carbide under water. Int. J. Heat Mass Transf. 2014, 71, 515–520. [Google Scholar] [CrossRef]
- Wu, C.; Fang, X.; Kang, Q.; Sun, H.; Zhao, L.; Tian, B.; Fang, Z.; Pan, M.; Maeda, R.; Jiang, Z. Crystal cleavage, periodic nanostructure and surface modification of SiC ablated by femtosecond laser in different media. Surf. Coat. Technol. 2021, 424, 127652. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Wang, B.; Guan, Y. Machine learning methods for prediction analyses of 4H-SiC microfabrication via femtosecond laser processing. J. Mater. Res. Technol. 2022, 18, 2152–2165. [Google Scholar] [CrossRef]
- Liu, J. Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196–198. [Google Scholar] [CrossRef]
- Shi, H.; Song, Q.; Hou, Y.; Yue, S.; Li, Y.; Zhang, Z.; Li, M.; Zhang, K.; Zhang, Z. Investigation of structural transformation and residual stress under single femtosecond laser pulse irradiation of 4H–SiC. Ceram. Int. 2022, 48, 24276–24282. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Yu, Z.; Chen, J.; Yang, J. A processing technology of grooves by picosecond ultrashort pulse laser in Ni alloy: Enhancing efficiency and quality. Opt. Laser Technol. 2019, 111, 214–221. [Google Scholar] [CrossRef]
- Ashkenasi, D.; Lorenz, M.; Stoian, R.; Rosenfeld, A. Surface damage threshold and structuring of dielectrics using femtosecond laser pulses: The role of incubation. Appl. Surf. Sci. 1999, 150, 101–106. [Google Scholar] [CrossRef]
- Kitriotis, D.; Merkle, L.D. Multiple pulse laser-induced damage phenomena in silicates. Appl. Opt. 1989, 28, 949–958. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; Von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Gemini, L.; Hashida, M.; Shimizu, M.; Miyasaka, Y.; Inoue, S.; Tokita, S.; Limpouch, J.; Mocek, T.; Sakabe, S. Periodic nanostructures self-formed on silicon and silicon carbide by femtosecond laser irradiation. Appl. Phys. A 2014, 117, 49–54. [Google Scholar] [CrossRef]
- Jia, X.; Zhao, X. Thermal accumulation at kilohertz repetition rates inside fused silica under ultrafast laser irradiation. Opt. Lett. 2020, 45, 3390–3393. [Google Scholar] [CrossRef]
- Kim, B.; Iida, R.; Kiyokawa, S.; Fushinobu, K. Effect of beam profile on nanosecond laser drilling of 4H-SIC. J. Laser Appl. 2018, 30, 032207. [Google Scholar] [CrossRef]
- Thorstensen, J.; Erik Foss, S. Temperature dependent ablation threshold in silicon using ultrashort laser pulses. J. Appl. Phys. 2012, 112, 103514. [Google Scholar] [CrossRef]
- Kononenko, T.V.; Sovyk, D.N.; Kononenko, V.V.; Konov, V.I. Optimization strategy for high-quality laser milling of silicon. Opt. Laser Technol. 2022, 150, 107921. [Google Scholar] [CrossRef]
| Model | Value |
|---|---|
| Central wavelength | 1035 nm |
| Pulse width | 300 fs |
| Maximum output power | 40 W |
| Repetition rate | 25 kHz–5 MHz |
| Power stability | <2% |
| Pulse energy | 80 μJ |
| Beam quality | M2 < 1.3 |
| Beam divergence | <2 mrad |
| Number | Scanning Speed (mm/s) | Number of Scans | Effective Pulse Number | Hatch Spacing (μm) |
|---|---|---|---|---|
| 1 | 1000 | 10 | 60 | 5, 10, 15, 30 |
| 2 | 2000 | 20 | ||
| 3 | 3000 | 30 | ||
| 4 | 1000 | 80 | 480 | 5, 10, 15, 30 |
| 5 | 2000 | 160 | ||
| 6 | 3000 | 240 | ||
| 7 | 1000 | 200 | 1200 | 5, 10, 15, 30 |
| 8 | 2000 | 400 | ||
| 9 | 3000 | 600 | ||
| 10 | 1000 | 320 | 1920 | 5, 10, 15, 30 |
| 11 | 2000 | 640 | ||
| 12 | 3000 | 960 | ||
| 13 | 1000 | 1000 | 6000 | 5, 10, 15, 30 |
| 14 | 2000 | 2000 | ||
| 15 | 3000 | 3000 |
| v (mm/s) | Δx | L (μm) | δy |
|---|---|---|---|
| 1000 | 83% | 5 | 83% |
| 2000 | 67% | 10 | 67% |
| 3000 | 50% | 15 | 50% |
| 6000 | 0% | 30 | 0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhao, Y.; Yang, Y.; Zhang, M.; Zhao, Y. Experimental Investigation on Ablation of 4H-SiC by Infrared Femtosecond Laser. Micromachines 2022, 13, 1291. https://doi.org/10.3390/mi13081291
Wang L, Zhao Y, Yang Y, Zhang M, Zhao Y. Experimental Investigation on Ablation of 4H-SiC by Infrared Femtosecond Laser. Micromachines. 2022; 13(8):1291. https://doi.org/10.3390/mi13081291
Chicago/Turabian StyleWang, Lukang, You Zhao, Yu Yang, Manman Zhang, and Yulong Zhao. 2022. "Experimental Investigation on Ablation of 4H-SiC by Infrared Femtosecond Laser" Micromachines 13, no. 8: 1291. https://doi.org/10.3390/mi13081291
APA StyleWang, L., Zhao, Y., Yang, Y., Zhang, M., & Zhao, Y. (2022). Experimental Investigation on Ablation of 4H-SiC by Infrared Femtosecond Laser. Micromachines, 13(8), 1291. https://doi.org/10.3390/mi13081291







