Miniature Mobile Robot Using Only One Tilted Vibration Motor
Abstract
:1. Introduction
2. Robot Design
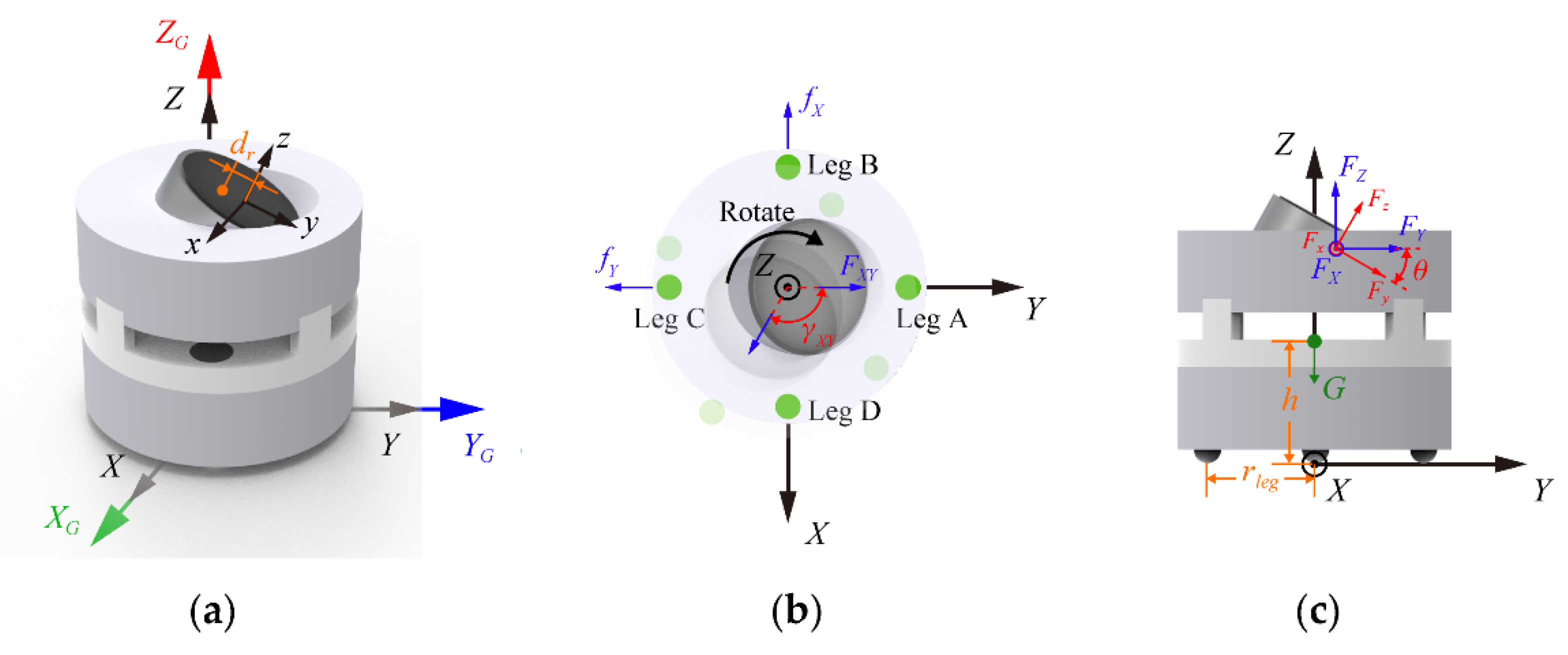
2.1. Mechanical Design
2.2. Locomotion
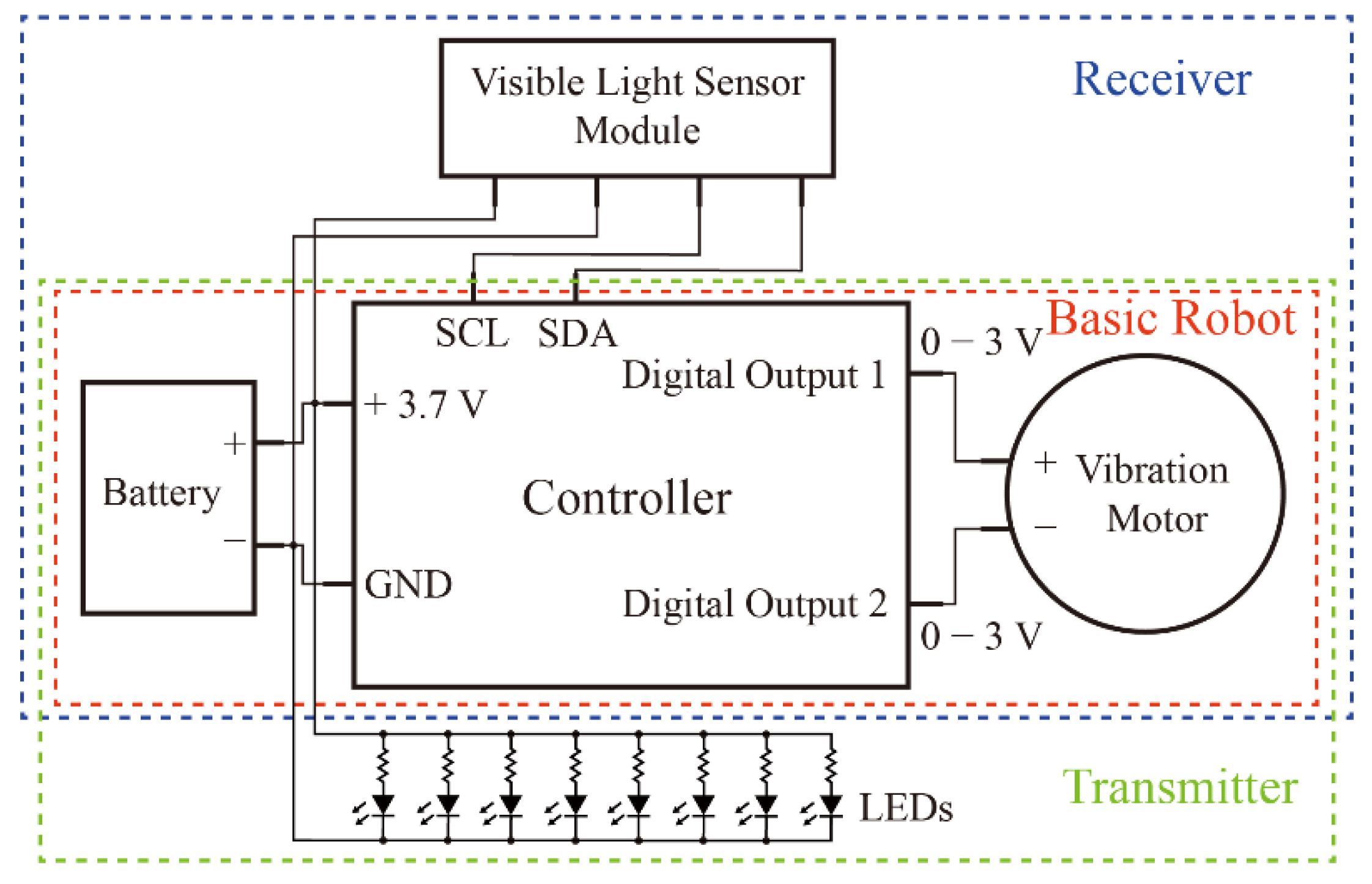
2.3. Communication and Sensing
2.4. Electrical Circuit
2.5. Cost
3. Modeling
3.1. Kinematics and Dynamics Analysis
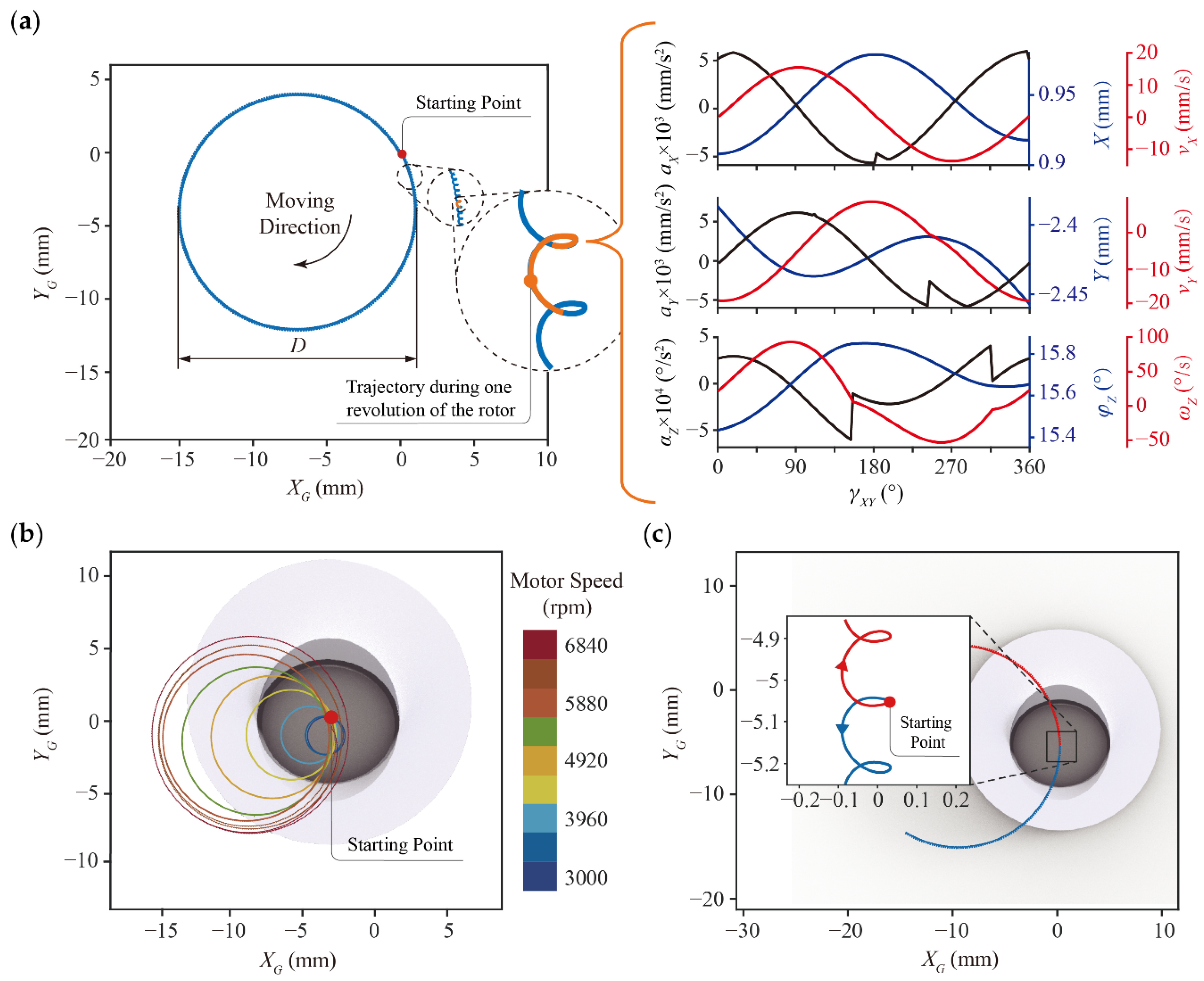
3.2. Trajectory Modeling
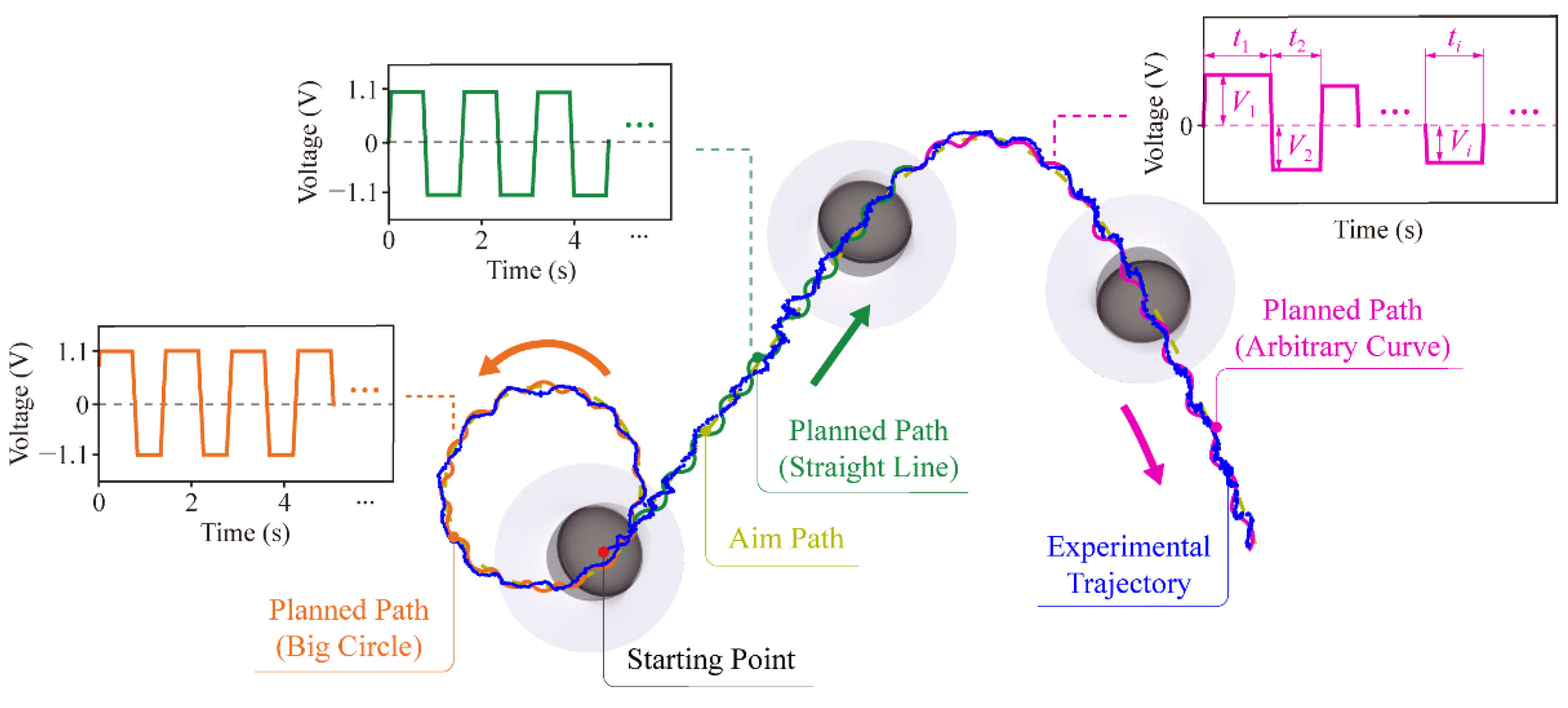
4. Motion Strategy
5. Experiments
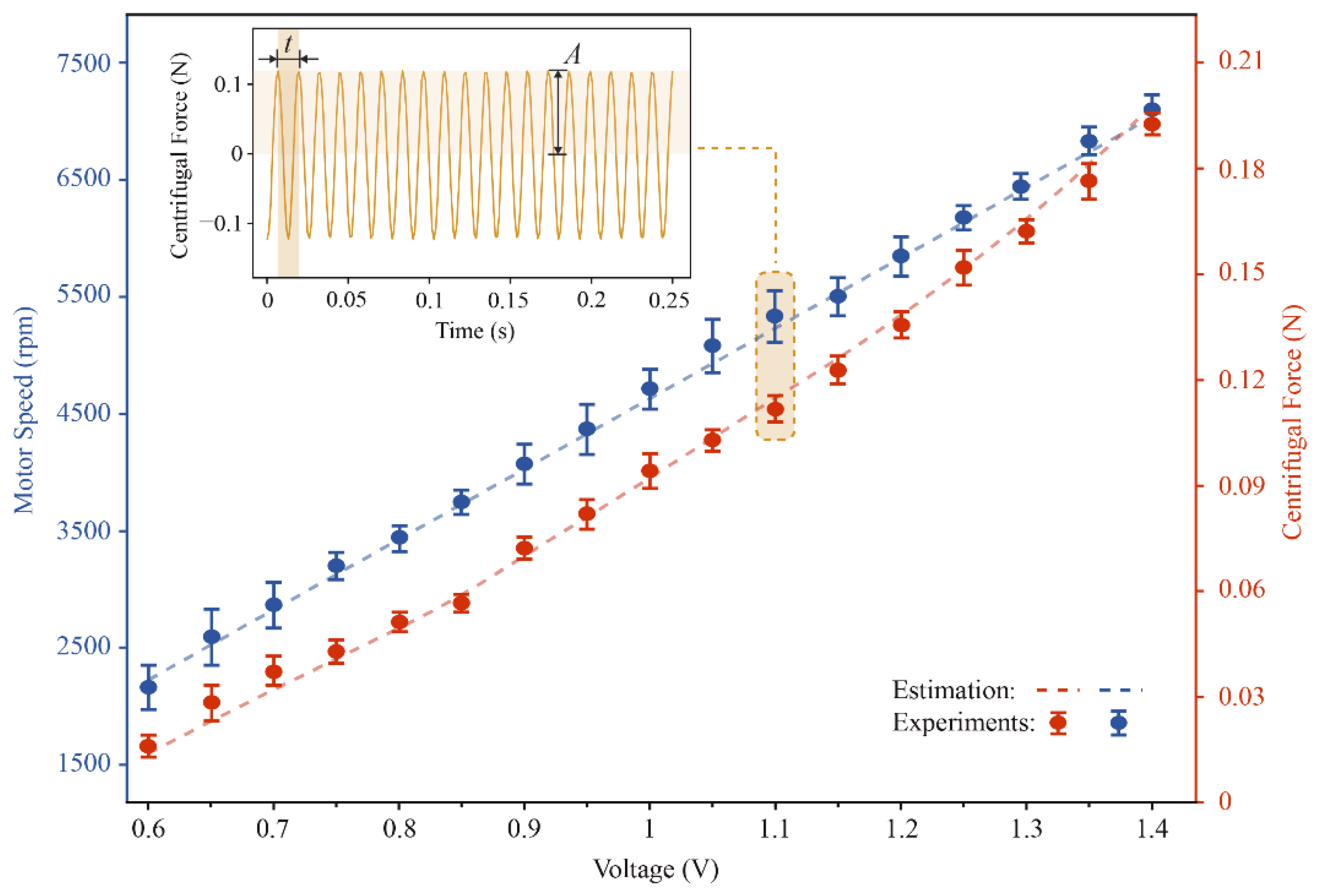
5.1. Performance of the Motor
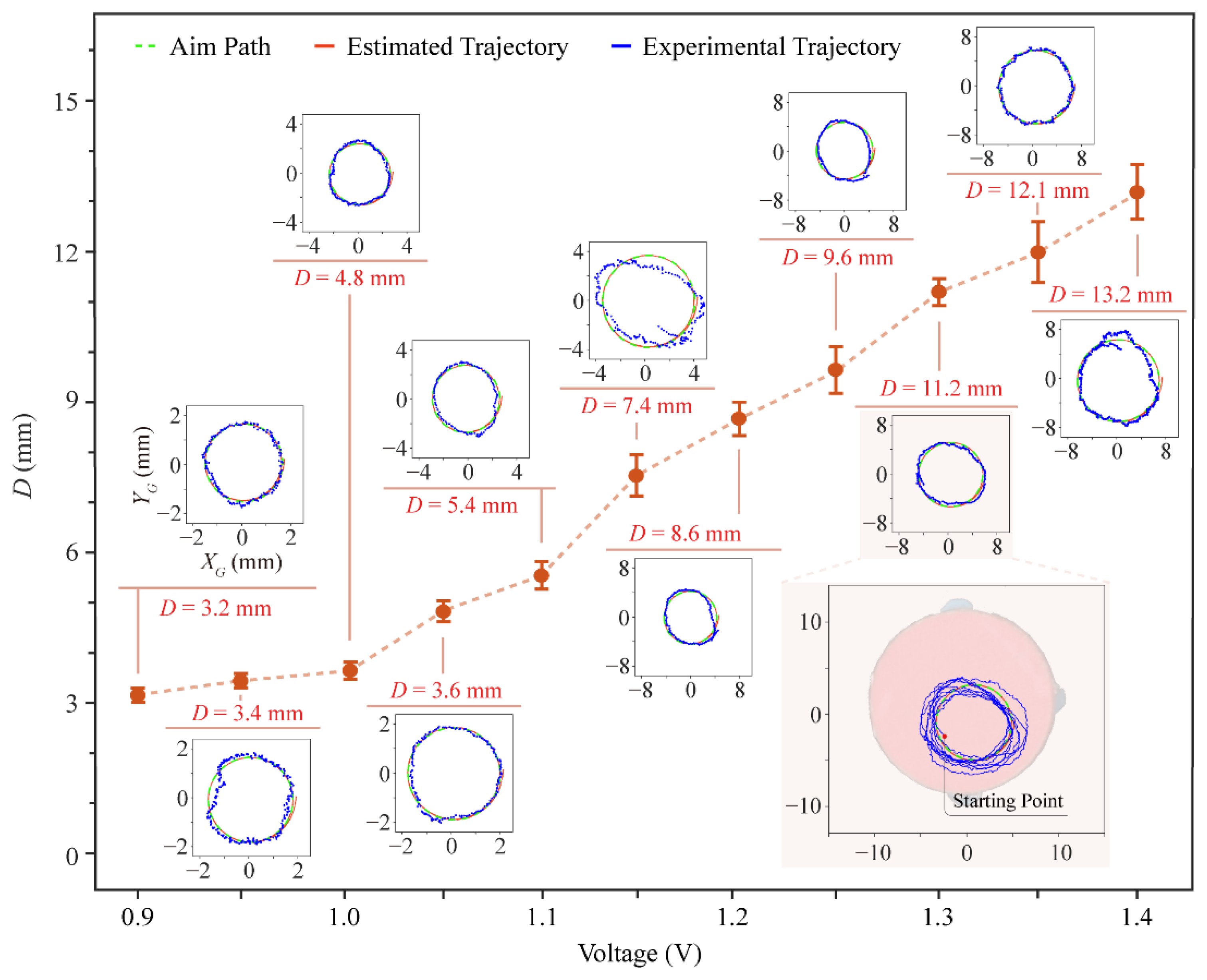
5.2. Following Circular Trajectories
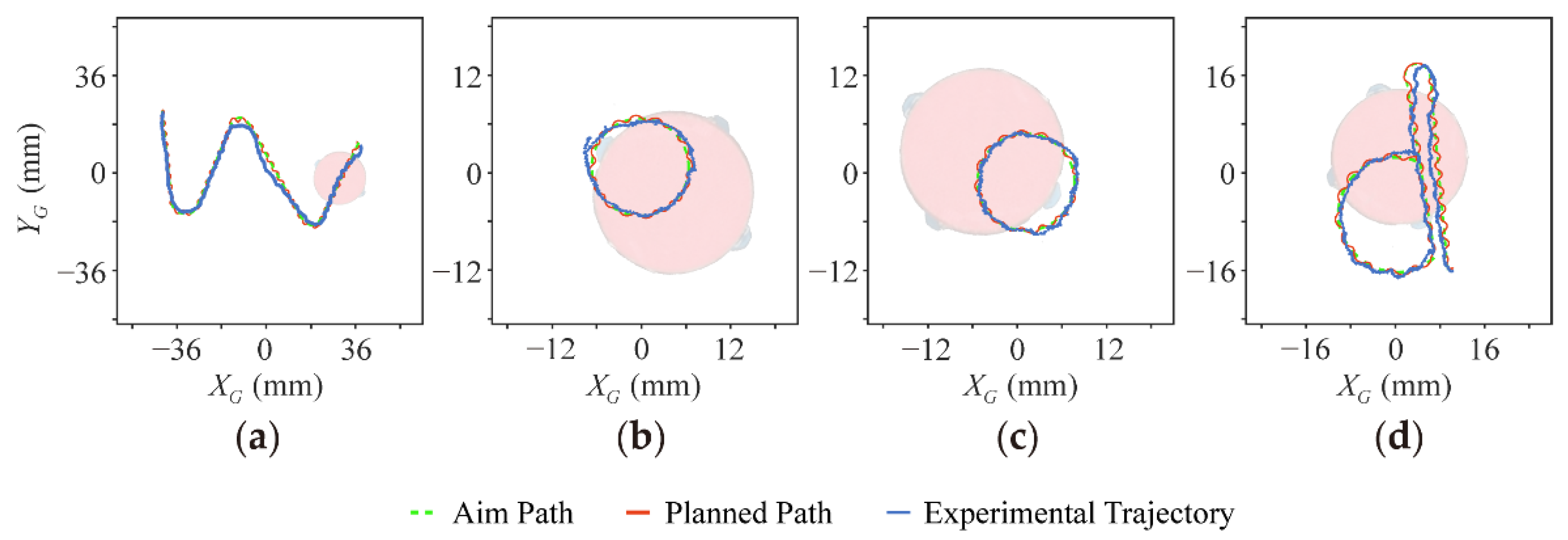
5.3. Following Arbitrary Trajectories
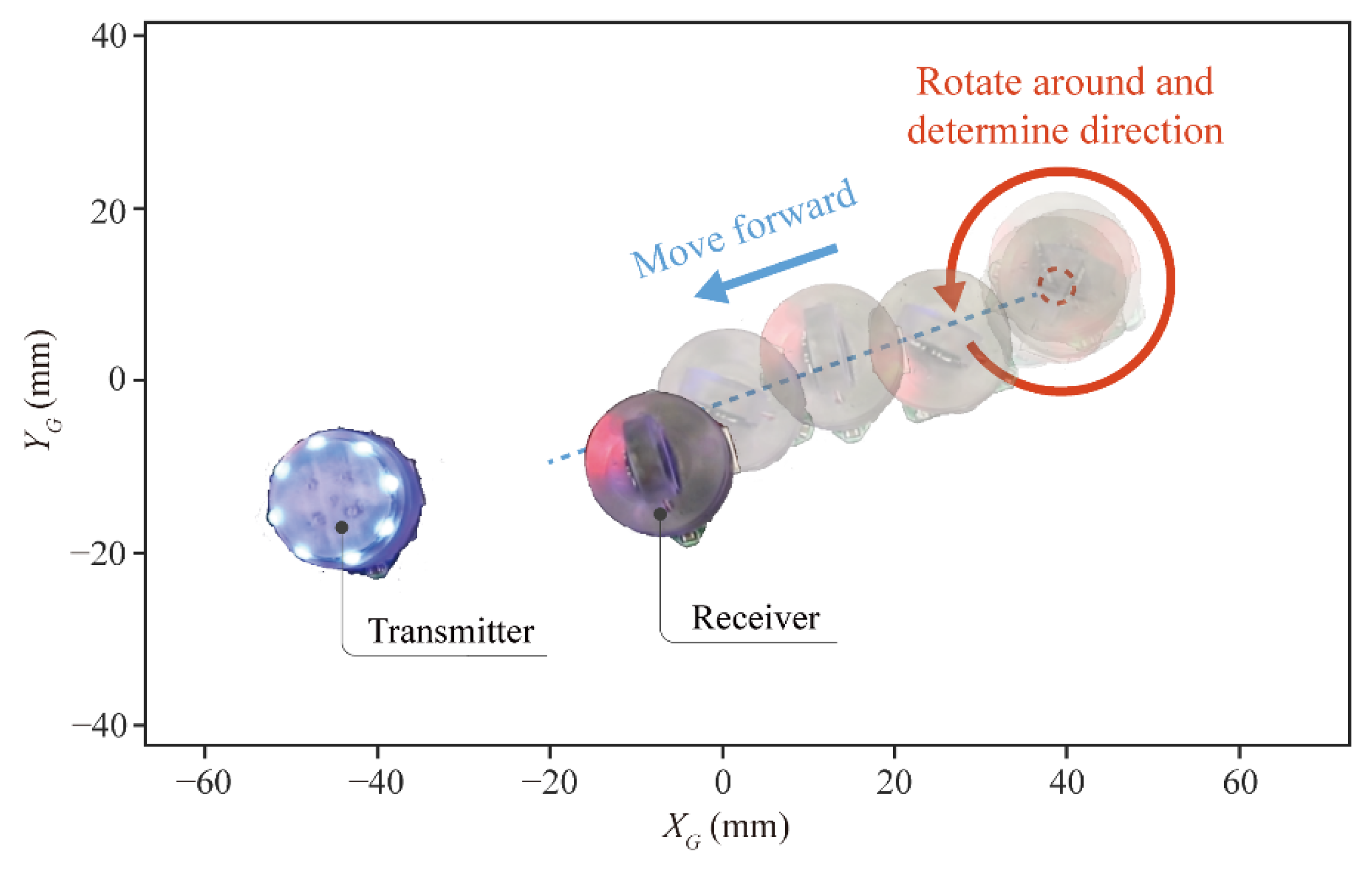
5.4. Commuication and Sensing
6. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbols | Description |
|---|---|
| Coordinate system 1 (on the vibration motor) | |
| Coordinate system 2 (on the robot body) | |
| Coordinate system 3 (the global coordinate system) | |
| The mass of the rotor and eccentric mass | |
| The angular speed of the vibration motor | |
| axis | |
| The centrifugal force generated by the rotor | |
| The tilt angle of the motor | |
| directions | |
| directions | |
| plane | |
| plane | |
| axis | |
| The coefficient of friction between the robot legs and the ground | |
| The mass of the robot | |
| Gravitational acceleration | |
| The distance between the origins of coordinate system 1 and 2 | |
| The distance between the robot gravity center and the origin of coordinate system 2 | |
| directions | |
| directions | |
| axis | |
| axis | |
| axis at the initial status | |
| The time step for each iteration | |
| directions | |
| axis | |
| directions | |
| axis during each iteration | |
| The position of the robot in the global coordinate system |
| Parameters | Value |
| kg | |
| m | |
| 3600 rpm | |
| 30° | |
| 0.3 | |
| . | kg |
| m | |
| 0.01 m | |
| s |
References
- Suri, S.; Jain, A.; Verma, N.; Prasertpoj, N. SCARA Industrial Automation Robot. In Proceedings of the International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018. [Google Scholar]
- Al Khawli, T.; Anwar, M.; Alzaabi, A.; Sunda-Meya, A.; Islam, S. Machine learning for robot-assisted industrial automation of aerospace applications. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018. [Google Scholar]
- Mohammadi Amin, F.; Rezayati, M.; van de Venn, H.W.; Karimpour, H. A Mixed-Perception Approach for Safe Human-Robot Collaboration in Industrial Automation. Sensors 2020, 20, 6347. [Google Scholar] [CrossRef] [PubMed]
- Freschi, C.; Ferrari, V.; Melfi, F.; Ferrari, M.; Mosca, F.; Cuschieri, A. Technical review of the da Vinci surgical telemanipulator. Int. J. Med. Robot. 2013, 9, 396–406. [Google Scholar] [CrossRef]
- Yang, C.; Guo, S.; Bao, X. An Isomorphic Interactive Device for the Interventional Surgical Robot after In Vivo Study. Micromachines 2022, 13, 111. [Google Scholar] [CrossRef]
- Wang, W.; Li, J.; Wang, S.; Su, H.; Jiang, X. System design and animal experiment study of a novel minimally invasive surgical robot. Int. J. Med. Robot. 2016, 12, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Petereit, J.; Beyerer, J.; Asfour, T.; Gentes, S.; Hein, B.; Hanebeck, U.D.; Kirchner, F.; Dillmann, R.; Götting, H.H.; Weiser, M. ROBDEKON: Robotic systems for decontamination in hazardous environments. In Proceedings of the IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Würzburg, Germany, 2 September 2019. [Google Scholar]
- Lee, C.H.; Kim, S.H.; Kang, S.C.; Kim, M.S.; Kwak, Y.K. Double-track mobile robot for hazardous environment applications. Adv. Robot. 2003, 17, 447–459. [Google Scholar] [CrossRef] [Green Version]
- Luk, B.L.; Cooke, D.S.; Galt, S.; Collie, A.A.; Chen, S. Intelligent legged climbing service robot for remote maintenance applications in hazardous environments. Rob. Auton. Syst. 2005, 53, 142–152. [Google Scholar] [CrossRef] [Green Version]
- Seward, D.; Pace, C.; Agate, R. Safe and effective navigation of autonomous robots in hazardous environments. Auton. Robot. 2007, 22, 223–242. [Google Scholar] [CrossRef]
- Mondada, F.; Bonani, M.; Raemy, X.; Pugh, J.; Cianci, C.; Klaptocz, A.; Magnenat, S.; Zufferey, J.C.; Floreano, D.; Martinoli, A. The e-puck, a robot designed for education in engineering. In Proceedings of the 9th Conference on Autonomous Robot Systems and Competitions, Castelo Branco, Portugal, 7 May 2009. [Google Scholar]
- Li, S.; Batra, R.; Brown, D.; Chang, H.D.; Ranganathan, N.; Hoberman, C.; Rus, D.; Lipson, H. Particle robotics based on statistical mechanics of loosely coupled components. Nature 2019, 567, 361–365. [Google Scholar] [CrossRef]
- Erdem, E.Y.; Chen, Y.M.; Mohebbi, M.; Suh, J.W.; Kovacs, G.T.A.; Darling, R.B.; Bohringer, K.F. Thermally Actuated Omnidirectional Walking Microrobot. J. Microelectromech. Syst. 2010, 19, 433–442. [Google Scholar] [CrossRef]
- Kim, S.; Clark, J.E.; Cutkosky, M.R. iSprawl: Design and Tuning for High-speed Autonomous Open-loop Running. Int. J. Rob. Res. 2016, 25, 903–912. [Google Scholar] [CrossRef]
- Baisch, A.T.; Ozcan, O.; Goldberg, B.; Ithier, D.; Wood, R.J. High speed locomotion for a quadrupedal microrobot. Int. J. Rob. Res. 2014, 33, 1063–1082. [Google Scholar] [CrossRef]
- Arvin, F.; Samsudin, K.; Ramli, A.R. Development of a miniature robot for swarm robotic application. Int. J. Electr. Comput. Eng. 2009, 1, 436–442. [Google Scholar] [CrossRef]
- Goldberg, B.; Zufferey, R.; Doshi, N.; Helbling, E.F.; Whittredge, G.; Kovac, M.; Wood, R.J. Power and Control Autonomy for High-Speed Locomotion With an Insect-Scale Legged Robot. IEEE Rob. Autom. Lett. 2018, 3, 987–993. [Google Scholar] [CrossRef]
- Nemitz, M.P.; Sayed, M.E.; Mamish, J.; Ferrer, G.; Teng, L.J.; McKenzie, R.M.; Hero, A.O.; Olson, E.; Stokes, A.A. HoverBots: Precise Locomotion Using Robots That Are Designed for Manufacturability. Front. Robot. AI 2017, 4, 55. [Google Scholar] [CrossRef] [Green Version]
- Birkmeyer, P.; Peterson, K.; Fearing, R.S. DASH: A dynamic 16g hexapedal robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), St. Louis, MO, USA, 11–15 October 2009. [Google Scholar]
- Hoover, A.M.; Steltz, E.; Fearing, R.S. RoACH: An autonomous 2. In 4 g crawling hexapod robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Nice, France, 26 September 2008. [Google Scholar]
- Zhu, P.; Peng, H.; Lu, X.; Guo, M.; Zhao, G.; Liu, W. A steerable miniature legged robot based on piezoelectric bending actuators. Smart Mater. Struct. 2020, 29, 045009. [Google Scholar] [CrossRef]
- Ng, C.S.X.; Tan, M.W.M.; Xu, C.; Yang, Z.; Lee, P.S.; Lum, G.Z. Locomotion of Miniature Soft Robots. Adv. Mater. 2021, 33, e2003558. [Google Scholar] [CrossRef]
- Fan, X.; Dong, X.; Karacakol, A.C.; Xie, H.; Sitti, M. Reconfigurable multifunctional ferrofluid droplet robots. Proc. Natl. Acad. Sci. USA 2020, 117, 27916–27926. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Xiao, J.; Xi, N. Minimal power control of a miniature climbing robot. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kobe, Japan, 20–24 July 2003. [Google Scholar]
- Kossett, A.; D’Sa, R.; Purvey, J.; Papanikolopoulos, N. Design of an improved land/air miniature robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010. [Google Scholar]
- Seok, S.; Onal, C.D.; Cho, K.-J.; Wood, R.J.; Rus, D.; Kim, S. Meshworm: A peristaltic soft robot with antagonistic nickel titanium coil actuators. IEEE/ASME Trans. Mechatron. 2012, 18, 1485–1497. [Google Scholar] [CrossRef]
- Kohut, N.J.; Hoover, A.M.; Ma, K.Y.; Baek, S.S.; Fearing, R.S. MEDIC: A legged millirobot utilizing novel obstacle traversal. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Pickem, D.; Lee, M.; Egerstedt, M. The GRITSBot in its natural habitat-a multi-robot testbed. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Pullin, A.O.; Kohut, N.J.; Zarrouk, D.; Fearing, R.S. Dynamic turning of 13 cm robot comparing tail and differential drive. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012. [Google Scholar]
- Rios, S.A.; Fleming, A.J.; Yong, Y.K. Miniature resonant ambulatory robot. IEEE Rob. Autom. Lett. 2016, 2, 337–343. [Google Scholar] [CrossRef]
- Rubenstein, M.; Ahler, C.; Nagpal, R. Kilobot: A Low Cost Scalable Robot System for Collective Behaviors. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012. [Google Scholar]
- Klingner, J.; Kanakia, A.; Farrow, N.; Reishus, D.; Correll, N. A stick-slip omnidirectional powertrain for low-cost swarm robotics: Mechanism, calibration, and control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Zarrouk, D.; Fearing, R.S. Controlled In-Plane Locomotion of a Hexapod Using a Single Actuator. IEEE Trans. Rob. 2015, 31, 157–167. [Google Scholar] [CrossRef]
- Zarrouk, D.; Fearing, R.S. Compliance-based dynamic steering for hexapods. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012. [Google Scholar]
- Dharmawan, A.G.; Hariri, H.H.; Foong, S.; Soh, G.S.; Wood, K.L. Steerable miniature legged robot driven by a single piezoelectric bending unimorph actuator. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Wang, G.; Li, C.; Yuan, T. Design and experiment of a small-scale walking robot employing stick-slip motion principle. Rev. Sci. Instrum. 2017, 88, 115001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhu, R.; Wu, J.; Wang, H. SimoBot: An Underactuated Miniature Robot Driven by a Single Motor. IEEE/ASME Trans. Mechatron. 2022, 26, 2616–2628. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Zhang, Y.; Wang, H. Miniature Mobile Robot Using Only One Tilted Vibration Motor. Micromachines 2022, 13, 1184. https://doi.org/10.3390/mi13081184
Zhu R, Zhang Y, Wang H. Miniature Mobile Robot Using Only One Tilted Vibration Motor. Micromachines. 2022; 13(8):1184. https://doi.org/10.3390/mi13081184
Chicago/Turabian StyleZhu, Renjie, Yifan Zhang, and Hongqiang Wang. 2022. "Miniature Mobile Robot Using Only One Tilted Vibration Motor" Micromachines 13, no. 8: 1184. https://doi.org/10.3390/mi13081184
APA StyleZhu, R., Zhang, Y., & Wang, H. (2022). Miniature Mobile Robot Using Only One Tilted Vibration Motor. Micromachines, 13(8), 1184. https://doi.org/10.3390/mi13081184






