Electronic Processes at the Carbon-Covered (100) Collector Tungsten Surface
Abstract
:1. Introduction
2. Method
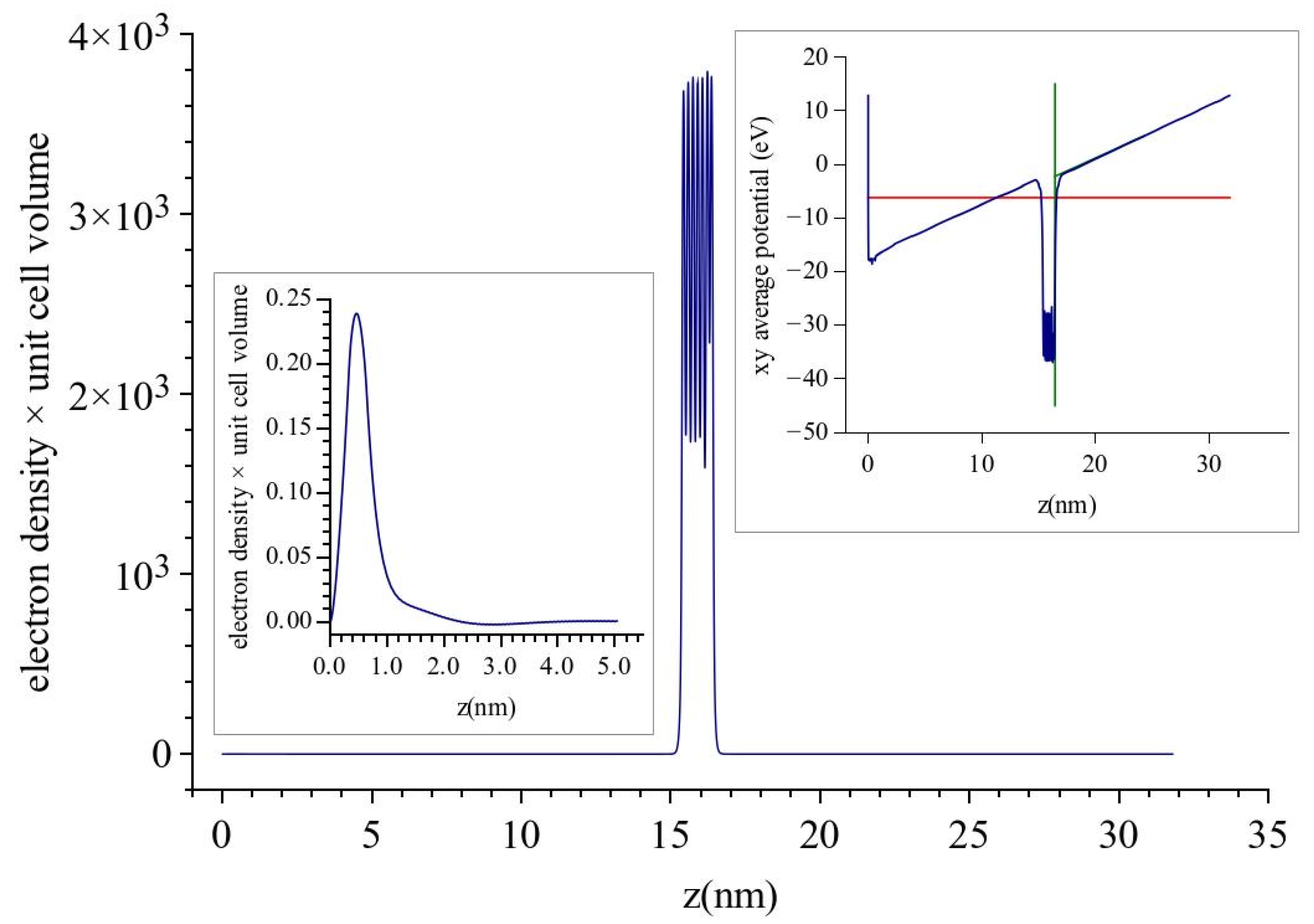
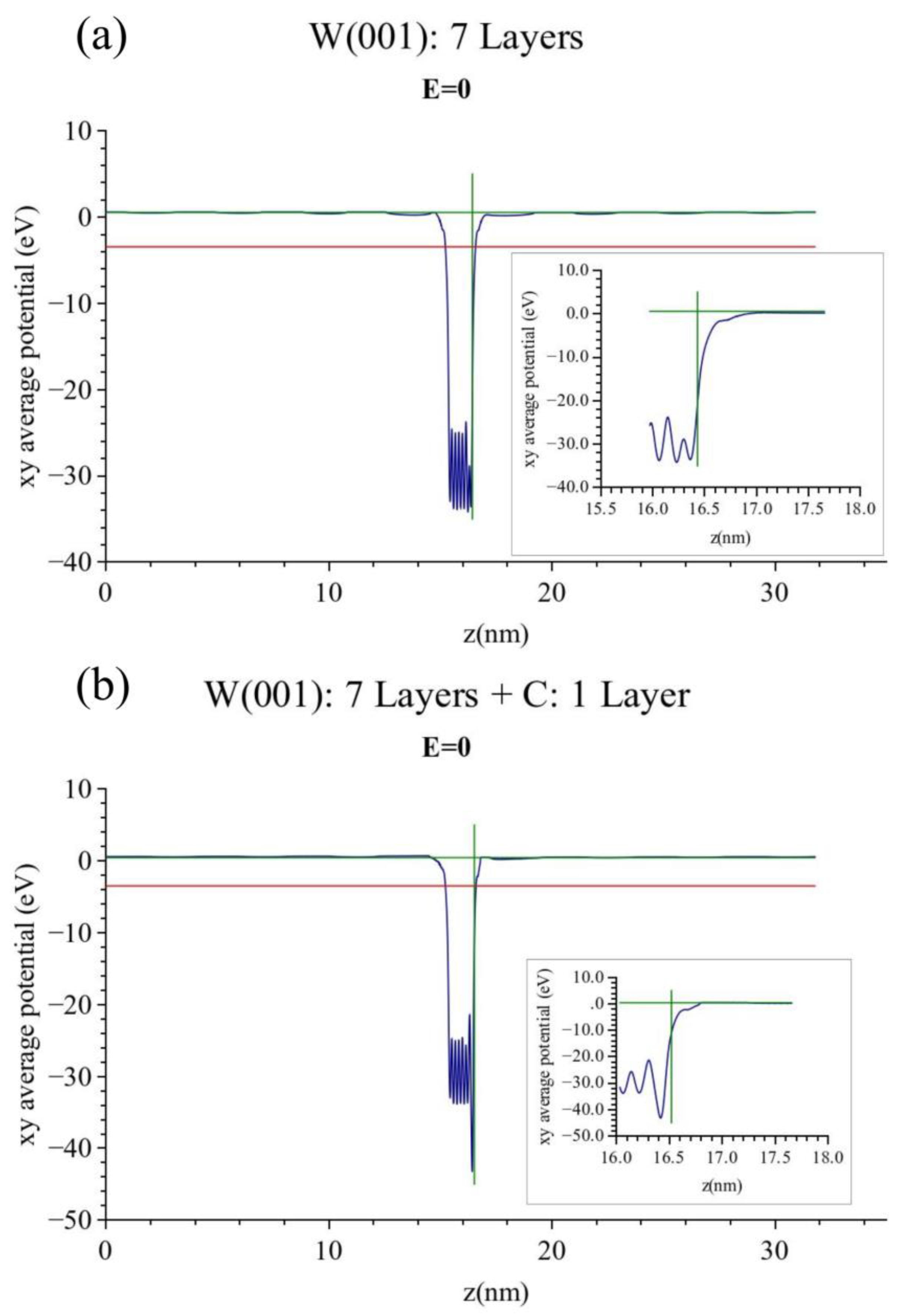
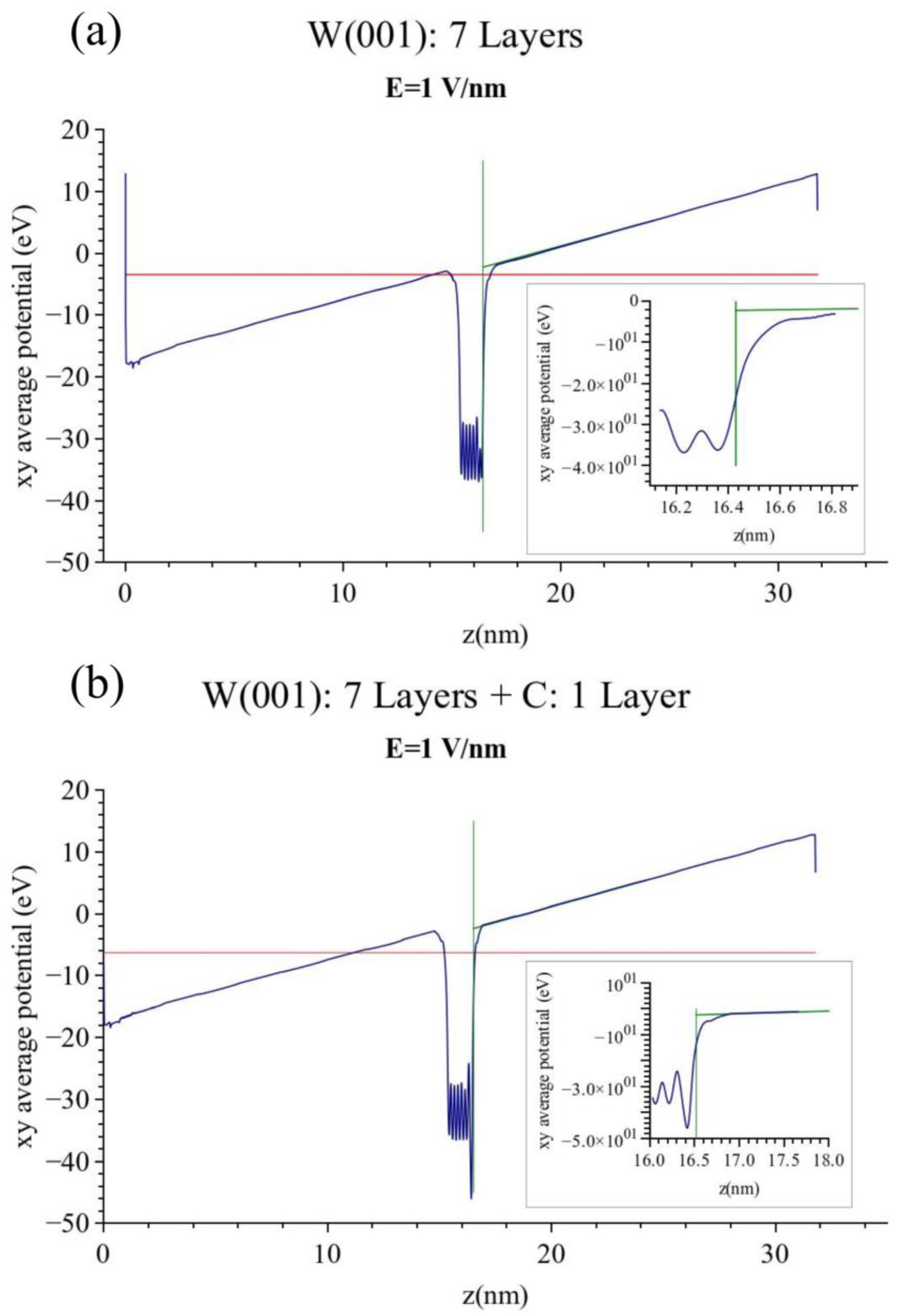
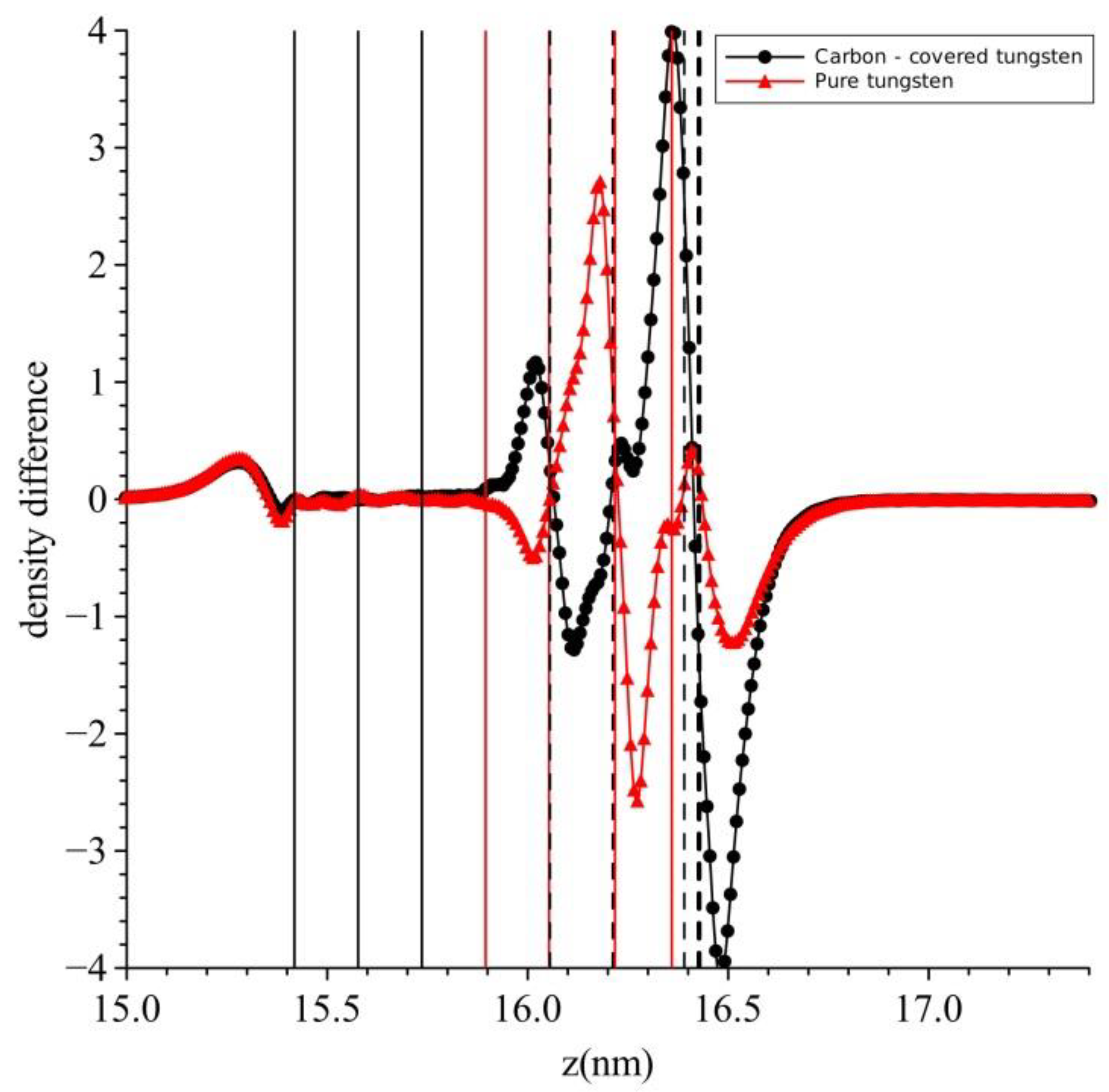
3. Results-Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bertolini, G.; Gurlu, O.; Proebsting, R.; Westholm, D.; Wei, J.; Ramsperger, U.; Zanin, D.A.; Cabrera, H.; Pescia, D.; Xanthakis, J.P.; et al. Non-topographic current contrast in scanning field emission microscopy. R. Soc. Open Sci. 2021, 8, 5009064. [Google Scholar] [CrossRef] [PubMed]
- Fowler, R.H.; Nordheim, L.W. Electron emission in intense electric fields. Proc. R. Soc. Lond. A 1928, 119, 173. [Google Scholar]
- Nordheim, L.W. The effect of the image force on the emission and reflexion of electrons by metals. Proc. R. Soc. Lond. A 1928, 121, 626. [Google Scholar]
- Murphy, E.L.; Good, R.H. Thermionic Emission, Field Emission, and the Transition Region. Phys. Rev. 1956, 102, 1464. [Google Scholar] [CrossRef]
- Simmons, J.G. Electric tunnel effect between dissimilar electrodes separated by a thin insulating film. J. Appl. Phys. 1963, 34, 2581. [Google Scholar] [CrossRef]
- Simmons, J.G. Intrinsic Fields in thin Insulating films between dissimilar Electrodes. Phys. Rev. Lett. 1963, 10, 10. [Google Scholar] [CrossRef]
- Forbes, R.G. Use of energy-space diagrams in free-electron models of field electron emission. Surf. Interface Anal. 2004, 36, 395. [Google Scholar] [CrossRef]
- Jensen, K.L. General formulation of thermal, field, and photoinduced electron emission. J. Appl. Phys. 2007, 102, 024911. [Google Scholar] [CrossRef]
- Jensen, K.L. A Reformulated General Thermal-Field Emission equation. J. Appl. Phys. 2019, 126, 065302. [Google Scholar] [CrossRef]
- Kyritsakis, A.; Xanthakis, J.P. Derivation of a generalized Fowler–Nordheim equation for nanoscopic field-emitters. Proc. R. Soc. A 2015, 471, 20140811. [Google Scholar] [CrossRef]
- Jensen, K.L. Semianalytical model of electron source potential barriers. J. Vac. Sci. Technol. B 1999, 17, 515. [Google Scholar] [CrossRef]
- Gundlach, K.H. Zur Berechnung des tunnelstroms durch eine trapezformige potentialstufe. Solid State Electron. 1966, 9, 949. [Google Scholar] [CrossRef]
- Durrani, Z.; Jones, M.; Abualnaga, F.; Wang, C.; Kaestner, M.; Lenk, S.; Lenk, C.; Rangelow, I.W.; Andreev, A. Room-temperature single dopant atom quantum dot transistors in silicon, formed by field-emission scanning probe lithography. J. Appl. Phys. 2018, 124, 144502. [Google Scholar] [CrossRef]
- Zhu, Z.-Z.; Hou, Z.-F.; Huang, M.-C.; Huang, R.-B.; Zheng, L.-S. Change of Work Function of Pd, Ag, K on Al(001) as a function of External Electric Field. Chin. Phys. Lett. 2001, 18, 1111. [Google Scholar]
- Marquez-Mijares, M.; Lepetit, B. A three dimensional numerical quantum mechanical model of field electron emission from metallic surfaces covered with carbon adsorbates. J. Appl. Phys. 2019, 126, 065107. [Google Scholar] [CrossRef] [Green Version]
- Neugebauer, J.; Scheffer, M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Phys. Rev. B 1992, 46, 16067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lepetit, B. A three dimensional numerical quantum mechanical model of electronic field emission from metallic surfaces with nanoscale corrugation. J. Appl. Phys. 2019, 125, 025107. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Xu, L.; Hsu, H.-Y.; Leung, T.-C.; Lin, M.-C. First-principles study of clean tungsten surface work function under electric field. J. Vac. Sci. Technol. B 2020, 38, 022209. [Google Scholar] [CrossRef]
- Lang, N.D.; Kohn, W. Theory of Metal Surfaces: Induced Surface Charge and Image potential. Phys. Rev. B 1973, 7, 3541. [Google Scholar] [CrossRef]
- Forbes, R.G. The electrical surface as centroid of the surface-induced charge. Ultramicroscopy 1999, 79, 25. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gotsis, H.J.; Bacalis, N.C.; Xanthakis, J.P. Electronic Processes at the Carbon-Covered (100) Collector Tungsten Surface. Micromachines 2022, 13, 888. https://doi.org/10.3390/mi13060888
Gotsis HJ, Bacalis NC, Xanthakis JP. Electronic Processes at the Carbon-Covered (100) Collector Tungsten Surface. Micromachines. 2022; 13(6):888. https://doi.org/10.3390/mi13060888
Chicago/Turabian StyleGotsis, Harilaos J., Naoum C. Bacalis, and John P. Xanthakis. 2022. "Electronic Processes at the Carbon-Covered (100) Collector Tungsten Surface" Micromachines 13, no. 6: 888. https://doi.org/10.3390/mi13060888
APA StyleGotsis, H. J., Bacalis, N. C., & Xanthakis, J. P. (2022). Electronic Processes at the Carbon-Covered (100) Collector Tungsten Surface. Micromachines, 13(6), 888. https://doi.org/10.3390/mi13060888




