Calculation of Effective Thermal Conductivity for Human Skin Using the Fractal Monte Carlo Method
Abstract
1. Introduction
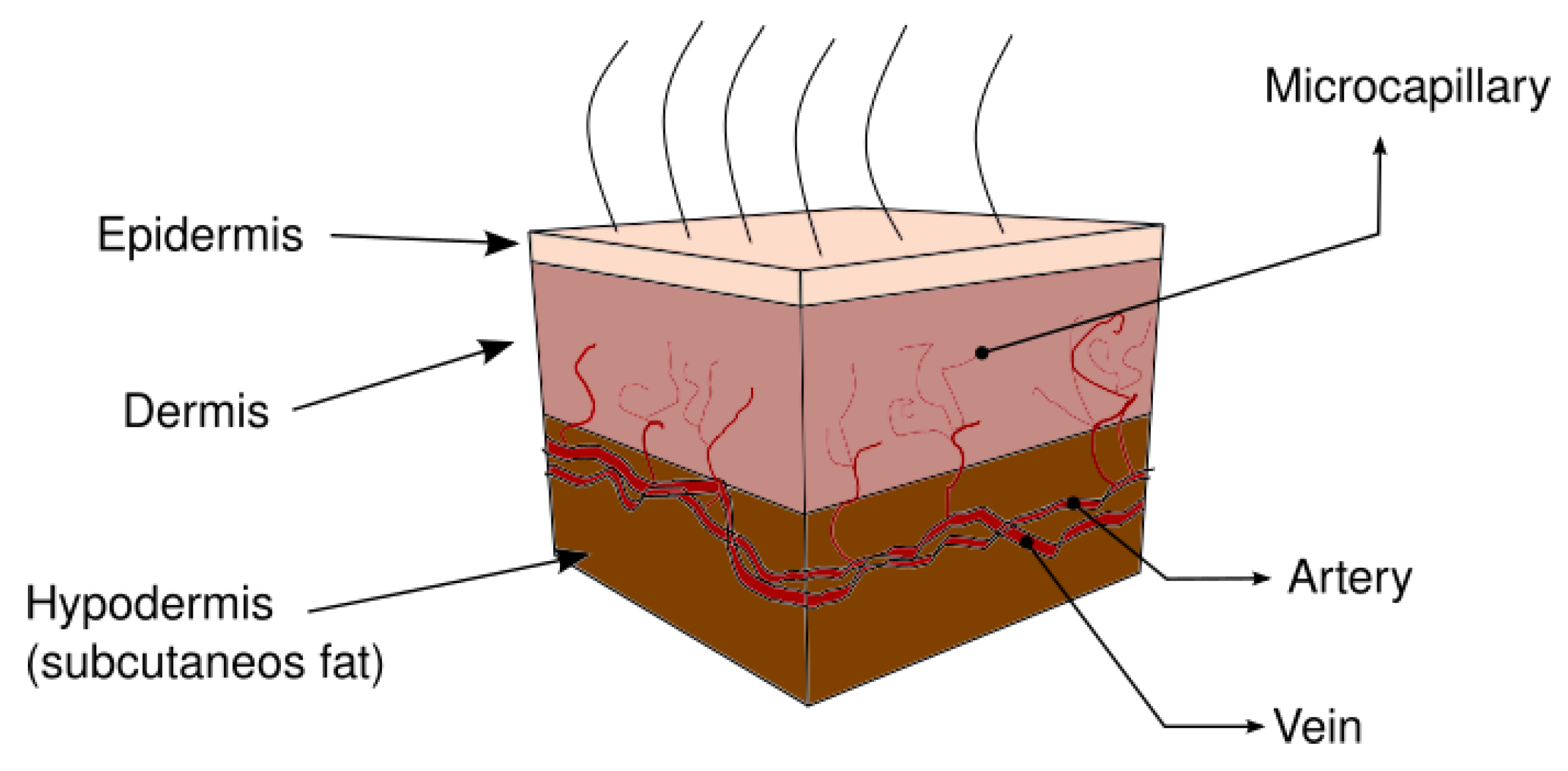
2. Heat Transfer in Human Skin
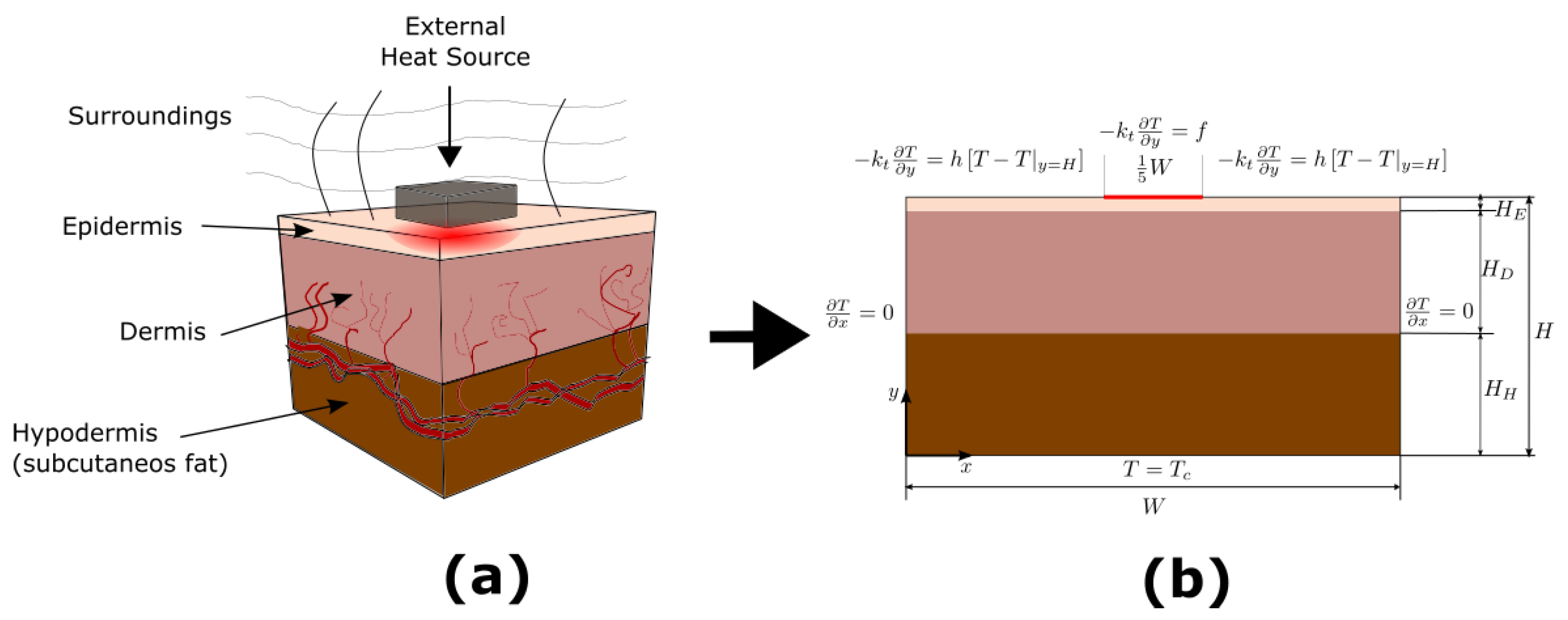
3. Mathematical Modeling
3.1. Fractal Scaling Method
3.2. The Fractal ETC of the REV
3.3. Fractal Dimensions, and
3.4. Non-Newtonian Fractal Velocity
3.5. Monte Carlo Method
3.6. Dimensionless Governing Equation
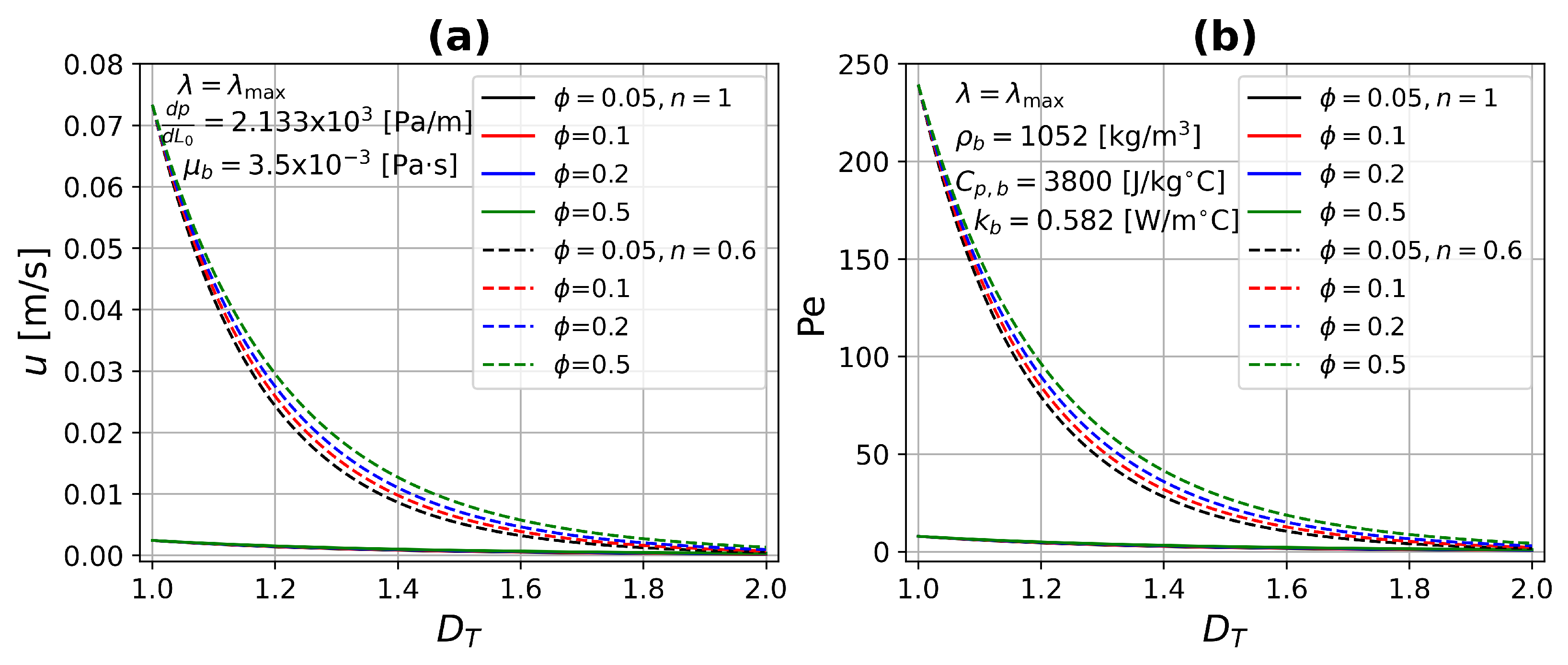
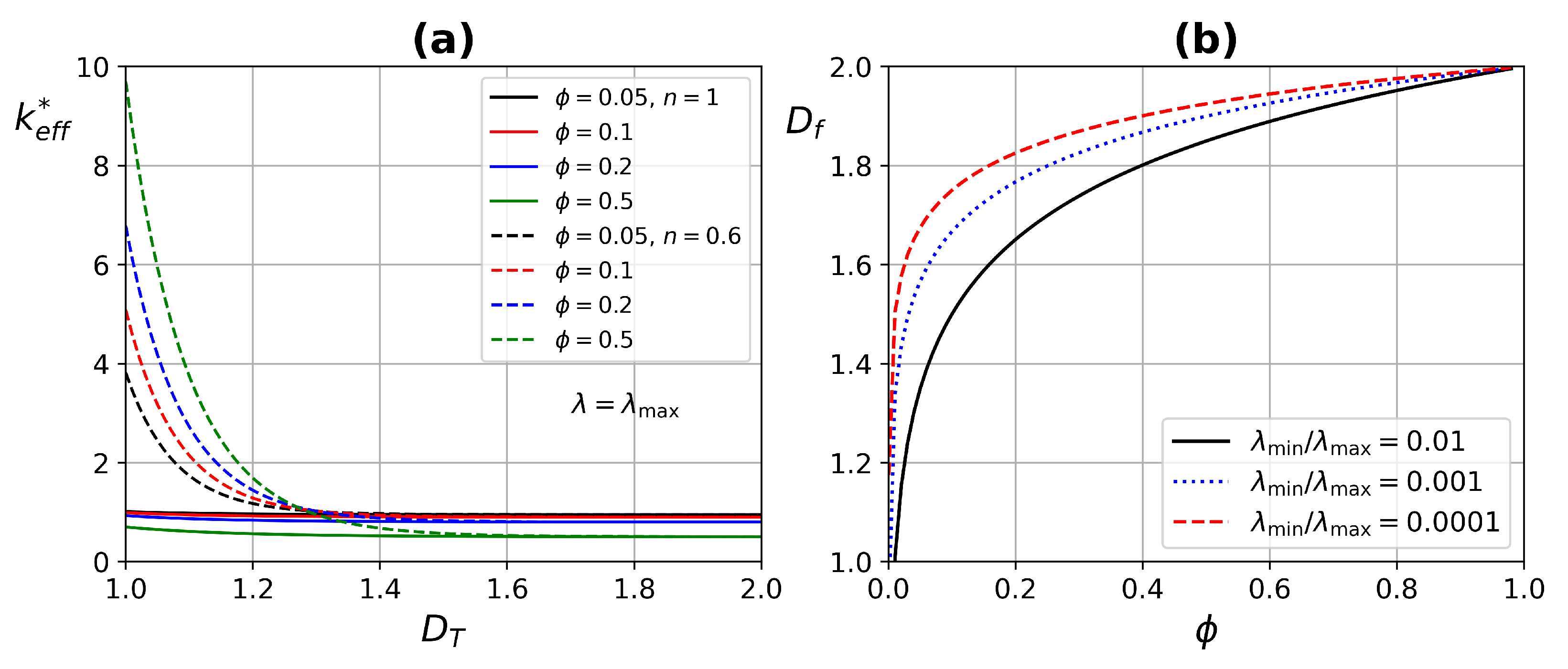
4. Results
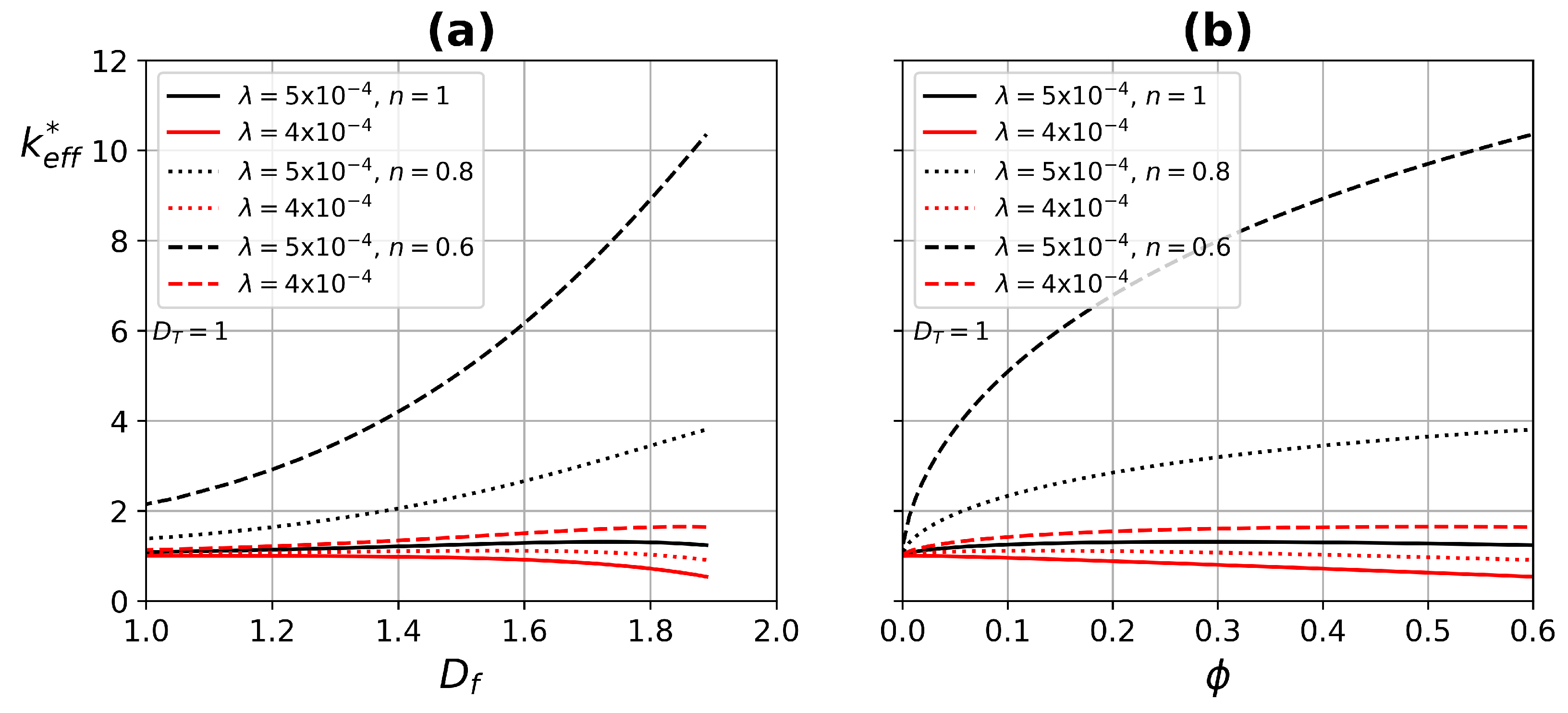
4.1. ETC Analysis
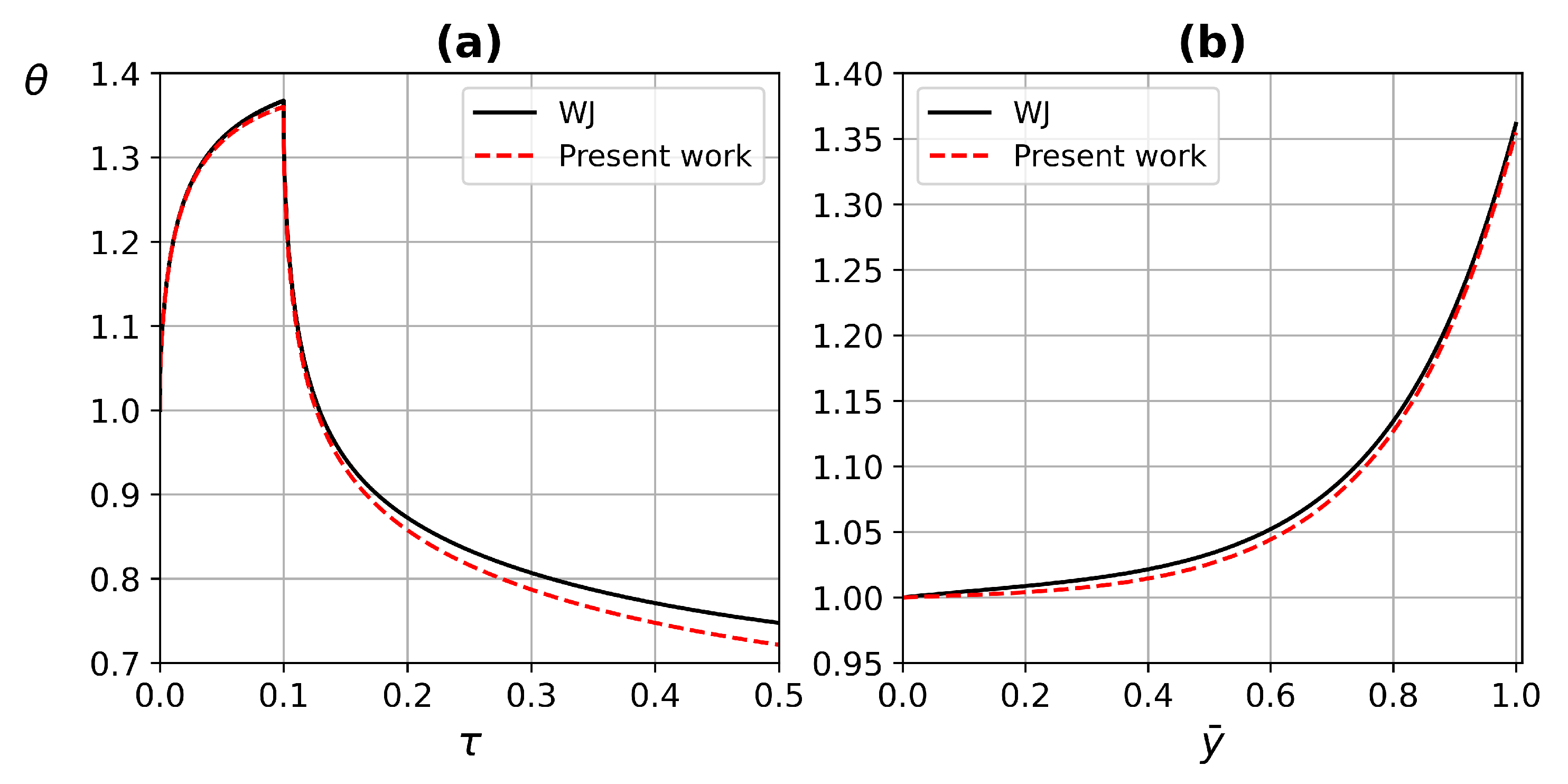
4.2. Code Validation
4.3. Dynamical Test Simulations
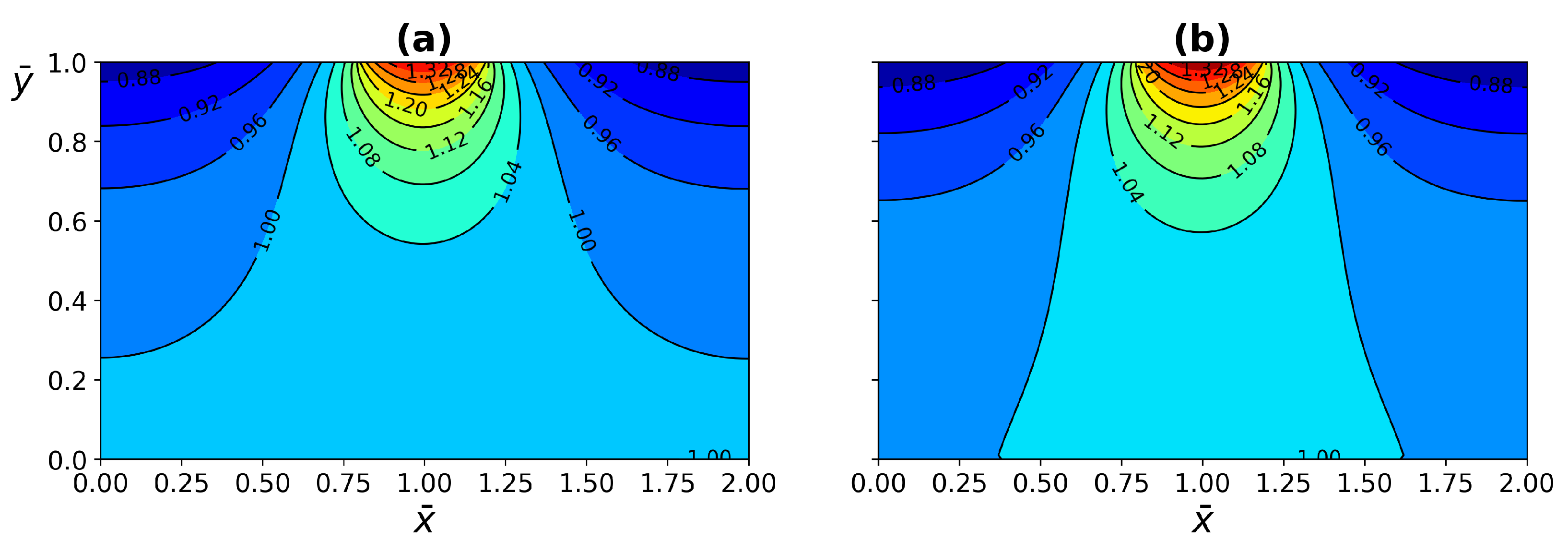
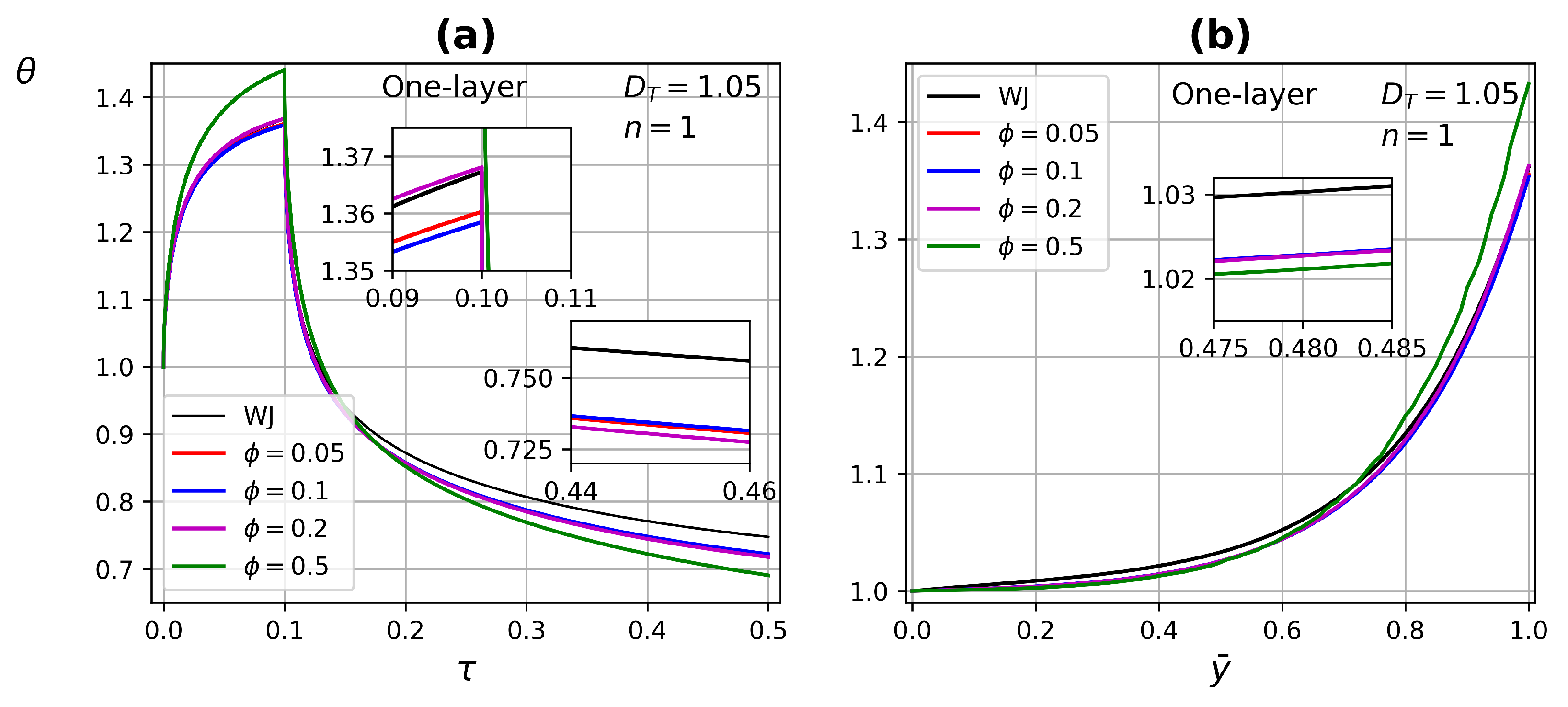
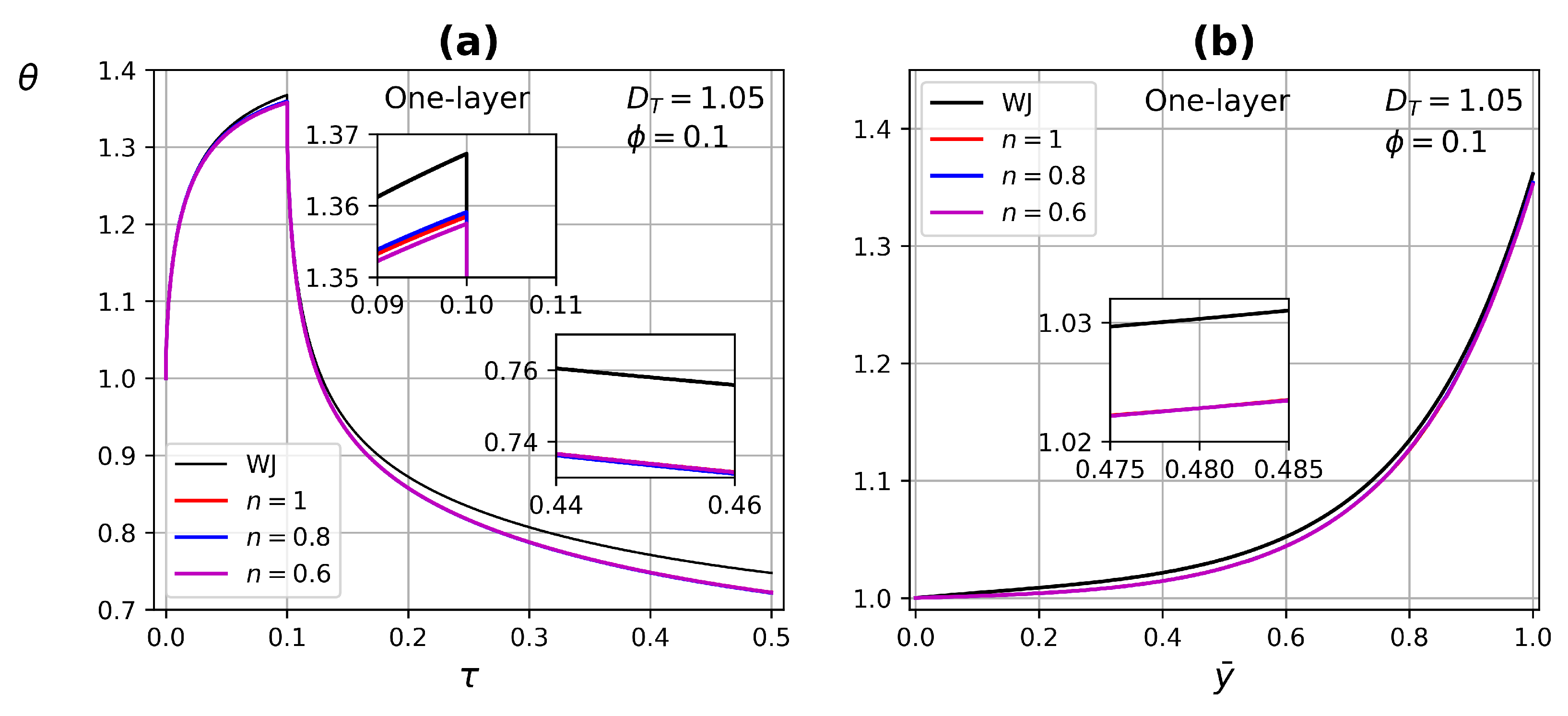
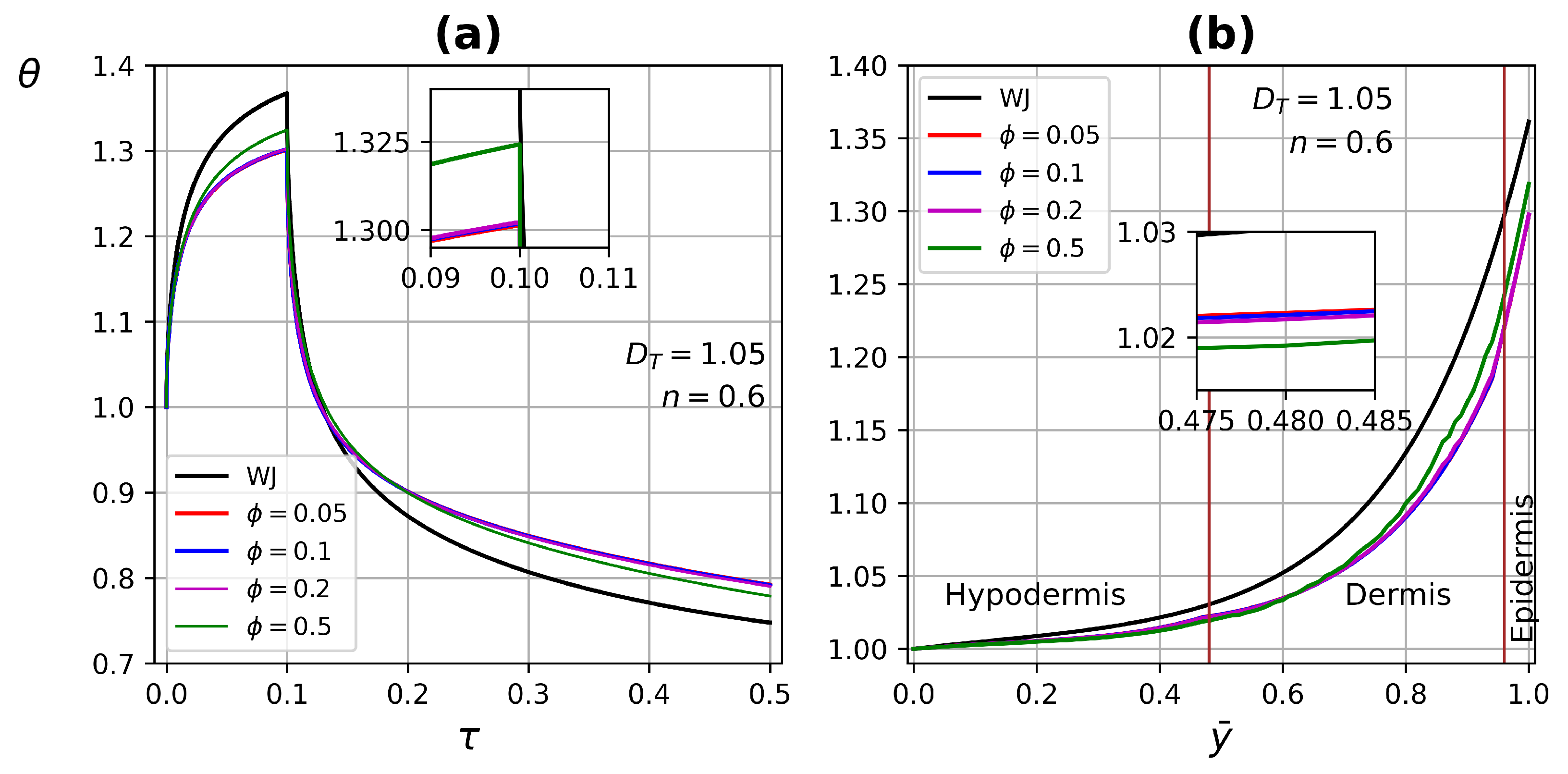
4.3.1. One-Layer Tissue Analysis
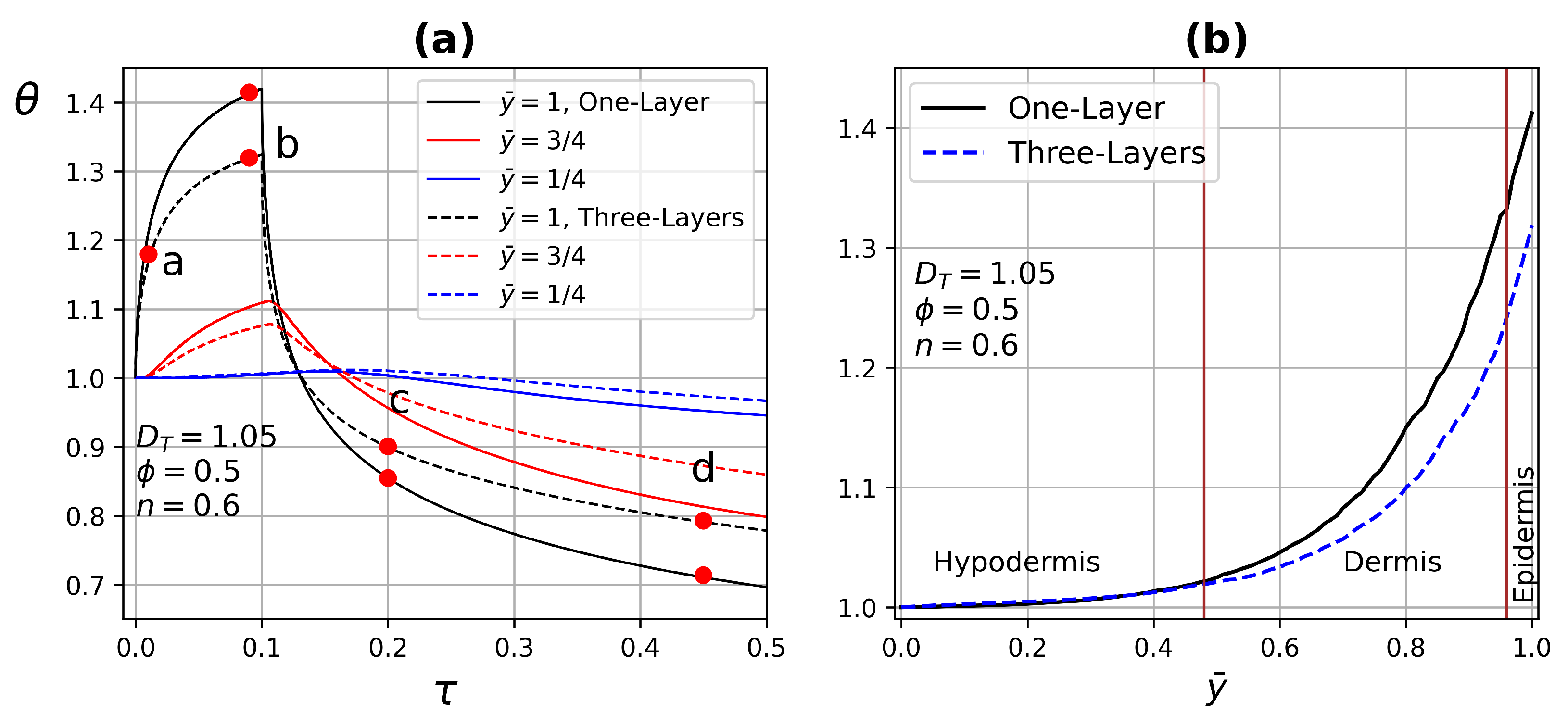
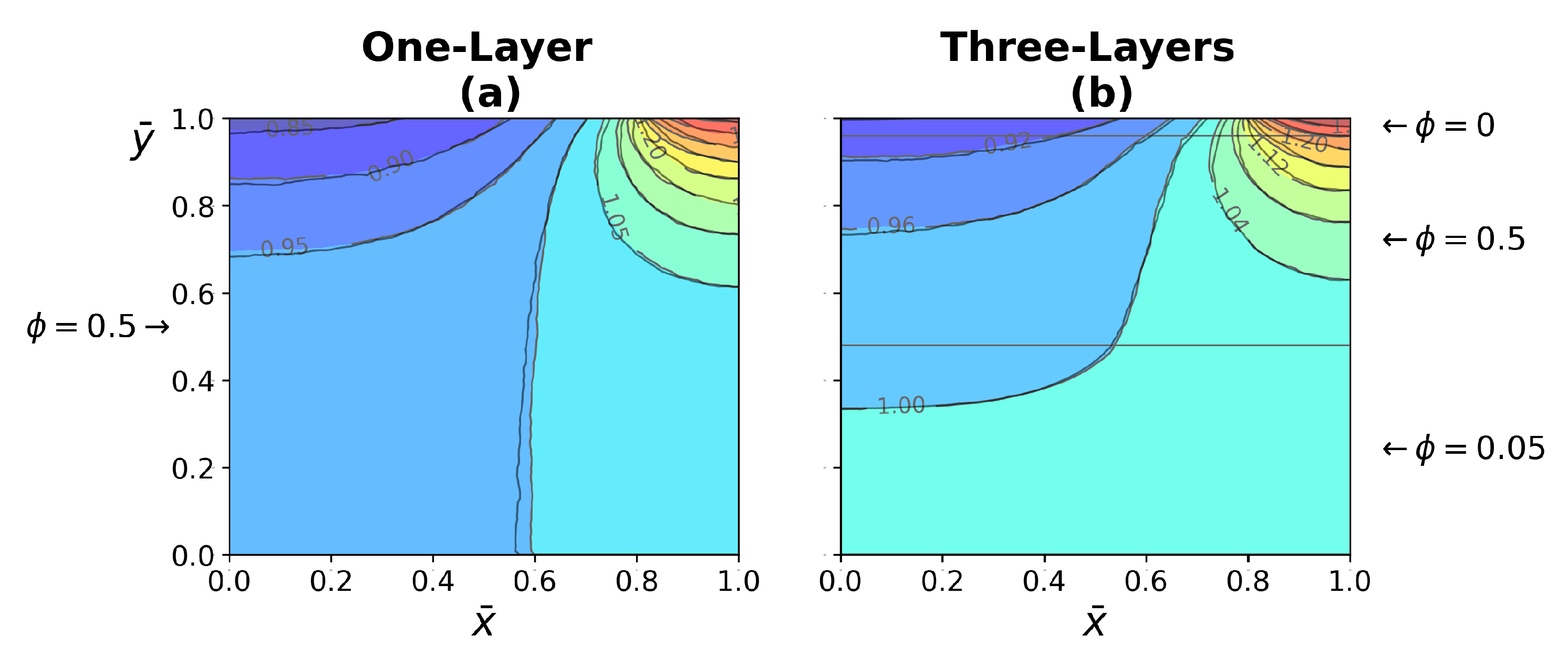
4.3.2. Three-Layer Tissue Analysis
5. Conclusions
- The effect of fractal dimension on the ETC was mainly in the range of 1–.
- Higher porosity improves ETC, due to increased blood flow through the tissue, having a higher thermal conductivity.
- In one-layer tissues of low porosity, no significant changes in ETC were found. Increasing porosity, the effect of the power-law index is reflected in both heating and relaxation processes.
- The Peclet number increases substantially due to the combination of large pore diameters and shear thinning fluids.
- In three-layer tissues with different porosities, perfusion with a shear-thinning fluid contributes to the understanding of the heat transfer process in some parts of the human body.
- The ETC involves the main variables of the heat transfer process in human skin; moreover, it is easy to implement for other case studies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| ETC | effective thermal conductivity |
| WJ | Weinbaum and Jiji |
| REV | representative elementary volume |
References
- Xu, F.; Lu, T.J.; Seffen, K.A. Skin thermal pain modeling—A holistic method. J. Therm. Biol. 2008, 33, 223–237. [Google Scholar] [CrossRef]
- Xu, F.; Seffen, K.; Lu, T. Non-Fourier analysis of skin biothermomechanics. Int. J. Heat Mass Transf. 2008, 51, 2237–2259. [Google Scholar] [CrossRef]
- Hristov, J. Bio-heat models revisited: Concepts, derivations, nondimensalization and fractionalization approaches. Front. Phys. 2019, 7, 1–36. [Google Scholar] [CrossRef]
- Dai, T.; Pikkula, B.M.; Wang, L.V.; Anvari, B. Comparison of human skin opto-thermal response to near-infrared and visible laser irradiations: A theoretical investigation. Phys. Med. Biol. 2004, 49, 4861–4877. [Google Scholar] [CrossRef] [PubMed]
- Dai, W.; Wang, H.; Jordan, P.M.; Mickens, R.E.; Bejan, A. A mathematical model for skin burn injury induced by radiation heating. Int. J. Heat Mass Transf. 2008, 51, 5497–5510. [Google Scholar] [CrossRef]
- Xu, F.; Wen, T.; Seffen, K.; Lu, T. Modeling of skin thermal pain: A preliminary study. Appl. Math. Comput. 2008, 205, 37–46. [Google Scholar] [CrossRef]
- Xu, F.; Lu, T.J.; Seffen, K.A.; Ng, E.Y.K. Mathematical modeling of skin bioheat transfer. Appl. Mech. Rev. 2009, 62, 1–35. [Google Scholar] [CrossRef]
- Xu, F.; Lu, T. Introduction to Skin Biothermomechanics and Thermal Pain, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zolfaghari, A.; Maerefat, M. Bioheat transfer. Dev. Heat Transf. 2011, 153–170. [Google Scholar] [CrossRef]
- Liu, K.C.; Wang, Y.N.; Chen, Y.S. Investigation on the bio-heat transfer with the Dual-Phase-Lag effect. Int. J. Therm. Sci. 2012, 58, 29–35. [Google Scholar] [CrossRef]
- Weinbaum, S.; Jiji, L.M. A new simplified bioheat equation for the effect of blood flow on local average tissue temperature. J. Biomech. Eng. 1985, 107, 131–139. [Google Scholar] [CrossRef]
- Nakayama, A.; Sano, Y.; Yoshikawa, K. A rigorous derivation of the bioheat equation for local tissue heat transfer based on a volume averaging theory. Heat Mass Transf. 2010, 46, 739–746. [Google Scholar] [CrossRef]
- Charny, C.K. Mathematical models of bioheat transfer. Adv. Heat Transf. 1992, 22, 19–155. [Google Scholar]
- Jiji, L.M. Heat Conduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Wulff, W. The energy conservation equation for living tissues. IEEE Trans. Biomed. Eng. 1974, 21, 494–495. [Google Scholar] [CrossRef]
- Klinger, H.G. Heat transfer in perfused biological tissue I: General theory. Bull. Math. Biol. 1974, 36, 403–415. [Google Scholar] [PubMed]
- Chen, M.M.; Holmes, K.R. Microvascular contributions in tissue heat transfer. Ann. N. Y. Acad. Sci. 1980, 335, 137–150. [Google Scholar] [CrossRef]
- Weinbaum, S.; Jiji, L.M.; Lemons, D.E. Theory and experiment for the effect of vascular microstructure on surface tissue heat transfer: Part I: Anatomical foundation and model conceptualization. J. Biomech. Eng. 1984, 106, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Weinbaum, S.; Jiji, L.M.; Lemons, D.E. Theory and experiment for the effect of vascular microstructure on surface tissue heat transfer: Part II: Anatomical foundation and model conceptualization. J. Biomech. Eng. 1984, 106, 331–341. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.H. Thermal (heat) shock biothermomechanical viewpoint. J. Biomech. Eng. 1993, 115, 617–621. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, X.; Xu, L.X. New thermal wave aspects on burn evaluation of skin subjected to instantaneous heating. IEEE Trans. Biomed. Eng. 1999, 46, 420–428. [Google Scholar]
- Tzou, D.Y. Macro- to Microscale Heat Transfer: The Lagging Behaviour, 1st ed., Taylor and Francis: Abingdon, UK, 1997.
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Analytical estimations of temperature in a living tissue generated by laser irradiation using experimental data. J. Therm. Biol. 2019, 85, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Hobiny, A.; Abbas, I. Thermal response of cylindrical tissue induced by laser irradiation with experimental study. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 4013–4023. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I. Analytical estimation of temperature in living tissues using the tpl bioheat model with experimental verification. Mathematics 2020, 8, 1188. [Google Scholar] [CrossRef]
- Kumari, T.; Singh, S.K. A numerical study of space-fractional three-phase-lag bioheat transfer model during thermal therapy. Heat Transf. 2022, 51, 470–489. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Liu, D. Generalized bio-heat transfer model combining with the relaxation mechanism and nonequilibrium heat transfer. J. Heat Transf. 2021, 144, 031209. [Google Scholar] [CrossRef]
- Arkin, H.; Xu, L.X.; Holmes, K.R. Recent developments in modeling heat transfer in blood perfused tissues. IEEE Trans. Biomed. Eng. 1994, 41, 97–107. [Google Scholar] [CrossRef]
- Khaled, A.R.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar] [CrossRef]
- Goldstein, R.; Ibele, W.; Patankar, S.; Simon, T.; Kuehn, T.; Strykowski, P.; Tamma, K.; Heberlein, J.; Davidson, J.; Bischof, J.; et al. Heat transfer—A review of 2003 literature. Int. J. Heat Mass Transf. 2006, 49, 451–534. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Ibele, W.E.; Patankar, S.V.; Simon, T.W.; Kuehn, T.H.; Strykowski, P.J.; Tamma, K.K.; Heberlein, J.V.R.; Davidson, J.H.; Bischof, J.; et al. Heat transfer—A review of 2005 literature. Int. J. Heat Mass Transf. 2010, 53, 4397–4447. [Google Scholar] [CrossRef]
- Yang, X.; Liang, Y.; Chen, W. A spatial fractional seepage model for the flow of non-Newtonian fluid in fractal porous medium. Commun. Nonlinear Sci. Numer. Simul. 2018, 65, 70–78. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. Synthesis of mathematical models representing bioheat transport. Adv. Numer. Heat Transf. 2009, 3, 1–28. [Google Scholar]
- Roetzel, W.; Xuan, Y. Bioheat equation of the human thermal system. Chem. Eng. Technol. 1997, 20, 268–276. [Google Scholar]
- Nakayama, A.; Kuwahara, F. A general bioheat transfer model based on the theory of porous media. Int. J. Heat Mass Transf. 2008, 51, 3190–3199. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, P.; Qiu, S.; Rao, B.; Yu, B. A generalized thermal conductivity model for unsaturated porous media with fractal geometry. Int. J. Heat Mass Transf. 2020, 152, 119540. [Google Scholar] [CrossRef]
- Zhao, C. Review on thermal transport in high porosity cellular metal foams with open cells. Int. J. Heat Mass Transf. 2012, 55, 3618–3632. [Google Scholar] [CrossRef]
- Belova, I.V.; Murch, G.E. Monte Carlo simulation of the effective thermal conductivity in two-phase material. J. Mater. Process. Technol. 2004, 153, 741–745. [Google Scholar] [CrossRef]
- Song, Y.; Youn, J. Evaluation of effective thermal conductivity for carbon nanotube/polymer composites using control volume finite element method. J. Carbon 2006, 44, 710–717. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1982. [Google Scholar]
- Yu, B. Analysis of flow in fractal porous media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Xu, P.; Mujumdar, A.S.; Sasmito, A.P.; Yu, B.M. Multiscale Modeling of Porous Media, 1st ed.; Taylor and Francis: Abingdon, UK, 2019. [Google Scholar]
- Kou, J.; Liu, Y.; Wu, F.; Fan, J.; Lu, H.; Xu, Y. Fractal analysis of effective thermal conductivity for three-Phase (unsaturated) porous media. J. Appl. Phys. 2009, 106, 054905. [Google Scholar] [CrossRef]
- Xu, P. A discussion on fractal models for transport physics of porous media. Fractals 2015, 23, 1530001. [Google Scholar] [CrossRef]
- Yu, B.; Zou, M.; Feng, Y. Permeability of fractal porous media by Monte Carlo simulations. Int. J. Heat Mass Transf. 2005, 48, 2787–2794. [Google Scholar] [CrossRef]
- Zou, M.; Yu, B.; Feng, Y.; Xu, P. A Monte Carlo method for simulating fractal surfaces. Physica A 2007, 386, 176–186. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, B.; Feng, K.; Xu, P.; Zou, M. Thermal conductivity of nanofluids and size distribution of nanoparticles by Monte Carlo simulations. J. Nanopart. Res. 2008, 10, 1319–1328. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.; Qiao, X.; Qiu, S.; Jiang, Z. Radial permeability of fractured porous media by Monte Carlo simulations. Int. J. Heat Mass Transf. 2013, 57, 369–374. [Google Scholar] [CrossRef]
- Vadapalli, U.; Srivastava, R.P.; Vedanti, N.; Dimri, V.P. Estimation of permeability of a sandstone reservoir by a fractal and Monte Carlo simulation approach: A case study. Nonlinear Process. Geophys. 2014, 21, 9–18. [Google Scholar] [CrossRef]
- Xu, Y.; Zheng, Y.; Kou, J. Prediction of effective thermal conductivity of porous media with fractal-Monte Carlo simulations. Fractals 2014, 22, 1440004. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, X.; Jiang, G.; Long, G.; Wang, W.; Zhang, Y.; Liu, G. Kozeny–Carman constant for gas flow through fibrous porous media by fractal-Monte Carlo simulations. Fractals 2019, 27, 1950062. [Google Scholar] [CrossRef]
- Yang, J.; Wang, M.; Wu, L.; Liu, Y.; Qiu, S.; Xu, P. A novel Monte Carlo simulation on gas flow in fractal shale reservoir. Energy 2021, 236, 121513. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Wu, J.; Yu, B. A fractal resistance model for flow through porous media. Int. J. Heat Mass Transf. 2007, 50, 3925–3932. [Google Scholar] [CrossRef]
- Shen, H.; Ye, Q.; Meng, G. Anisotropic fractal model for the effective thermal conductivity of random metal fiber porous media with high porosity. Phys. Lett. A 2017, 381, 3193–3196. [Google Scholar] [CrossRef]
- Qin, X.; Cai, J.; Xu, P.; Dai, S.; Gan, Q. A fractal model of effective thermal conductivity for porous media with various liquid saturation. Int. J. Heat Mass Transf. 2019, 128, 1149–1156. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, B.; Zou, M.; Zhang, D. A generalized model for the effective thermal conductivity of porous media based on self-similarity. J. Phys. D Appl. Phys. 2004, 37, 3030–3040. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, B.; Wang, H.; Yun, M. A fractal analysis of permeability for power-law fluids in porous media. Fractals 2006, 14, 171–177. [Google Scholar] [CrossRef]
- Xu, F.; Wen, T.; Lu, T.; Seffen, K.A. Skin biothermomechanics for medical treatments. J. Mech. Behav. Biomed. Mater. 2008, 1, 172–187. [Google Scholar] [CrossRef]
- Kumar, S.; Damor, R.S.; Shukla, A.K. Numerical study on thermal therapy of triple layer skin tissue using fractional bioheat model. Int. J. Biomath. 2018, 11, 1850052. [Google Scholar] [CrossRef]
- Johnston, B.M.; Johnston, P.R.; Corney, S.; Kilpatrick, D. Non–Newtonian blood flow in human right coronary arteries: Steady state simulations. J. Biomech. 2004, 37, 709–720. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Cai, J.; Zou, M. On the physical properties of apparent two-phase fractal porous media. Vadose Zone J. Fractals 2009, 8, 177–186. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojas-Altamirano, G.; Vargas, R.O.; Escandón, J.P.; Mil-Martínez, R.; Rojas-Montero, A. Calculation of Effective Thermal Conductivity for Human Skin Using the Fractal Monte Carlo Method. Micromachines 2022, 13, 424. https://doi.org/10.3390/mi13030424
Rojas-Altamirano G, Vargas RO, Escandón JP, Mil-Martínez R, Rojas-Montero A. Calculation of Effective Thermal Conductivity for Human Skin Using the Fractal Monte Carlo Method. Micromachines. 2022; 13(3):424. https://doi.org/10.3390/mi13030424
Chicago/Turabian StyleRojas-Altamirano, Guillermo, René O. Vargas, Juan P. Escandón, Rubén Mil-Martínez, and Alan Rojas-Montero. 2022. "Calculation of Effective Thermal Conductivity for Human Skin Using the Fractal Monte Carlo Method" Micromachines 13, no. 3: 424. https://doi.org/10.3390/mi13030424
APA StyleRojas-Altamirano, G., Vargas, R. O., Escandón, J. P., Mil-Martínez, R., & Rojas-Montero, A. (2022). Calculation of Effective Thermal Conductivity for Human Skin Using the Fractal Monte Carlo Method. Micromachines, 13(3), 424. https://doi.org/10.3390/mi13030424







