Thermal and Flow Analysis of Fully Developed Electroosmotic Flow in Parallel-Plate Micro- and Nanochannels with Surface Charge-Dependent Slip
Abstract
1. Introduction
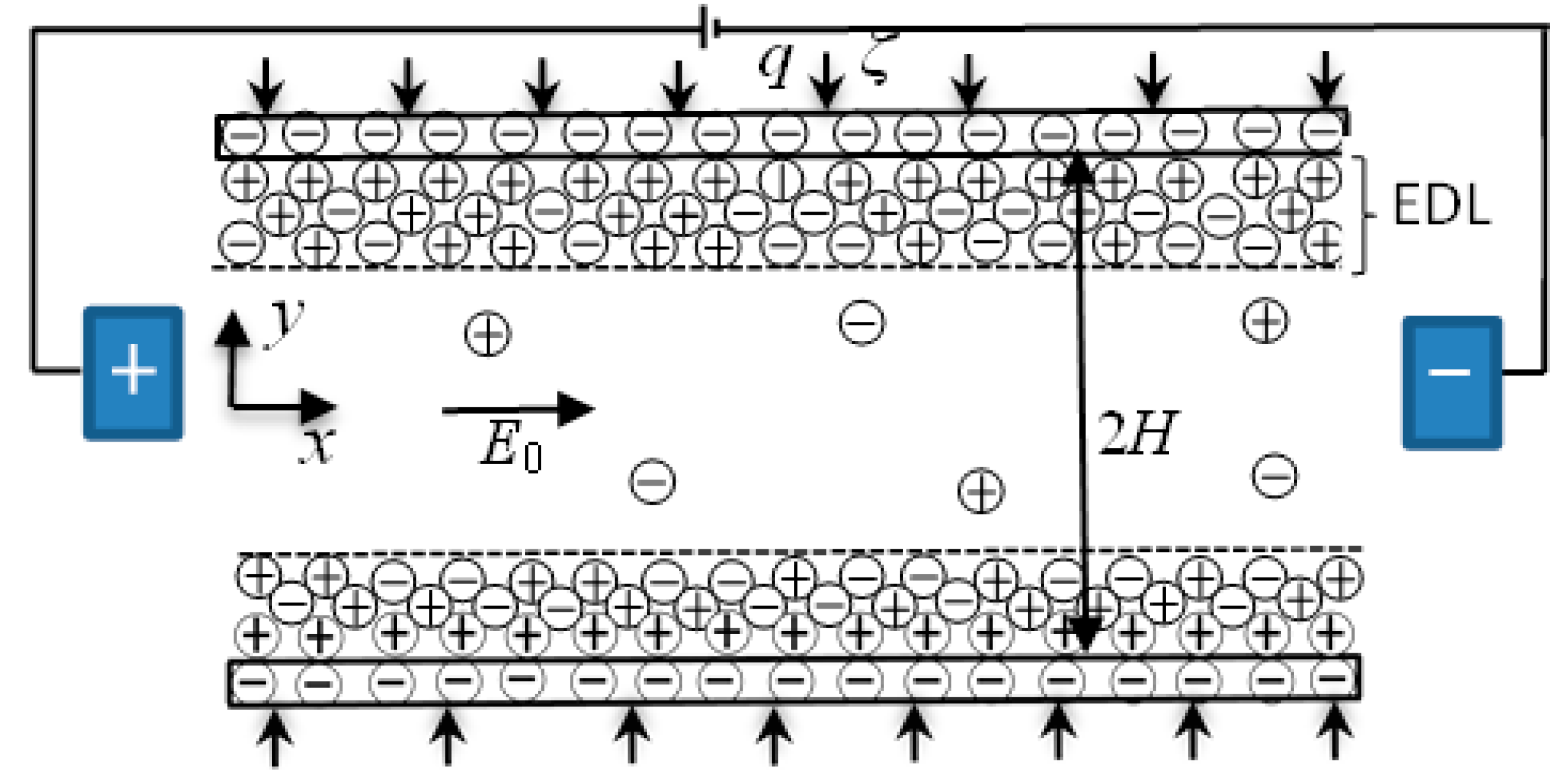
2. Mathematical Modeling
2.1. Electric Potential Distribution
2.2. Velocity Distribution
2.3. Temperature Distribution
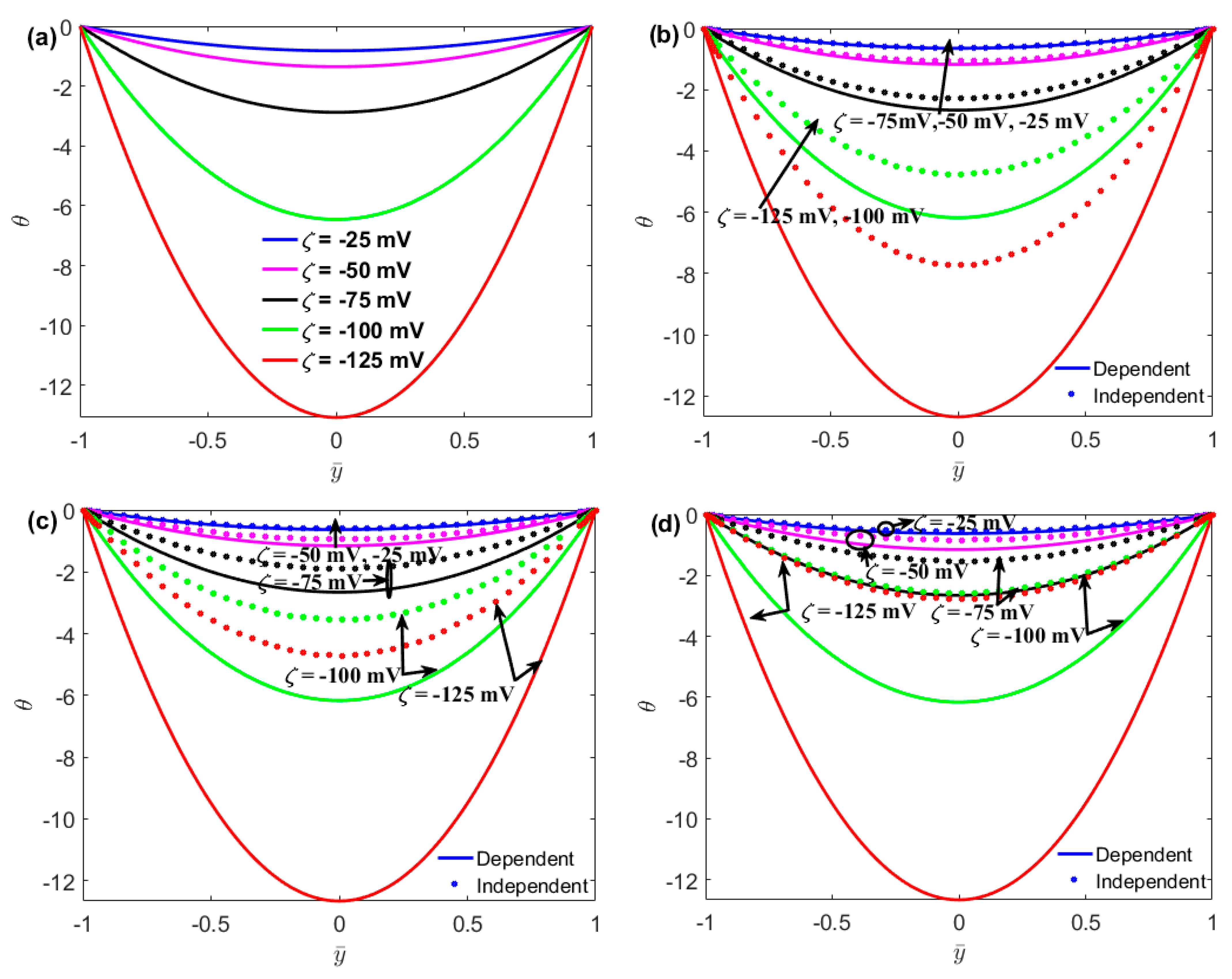
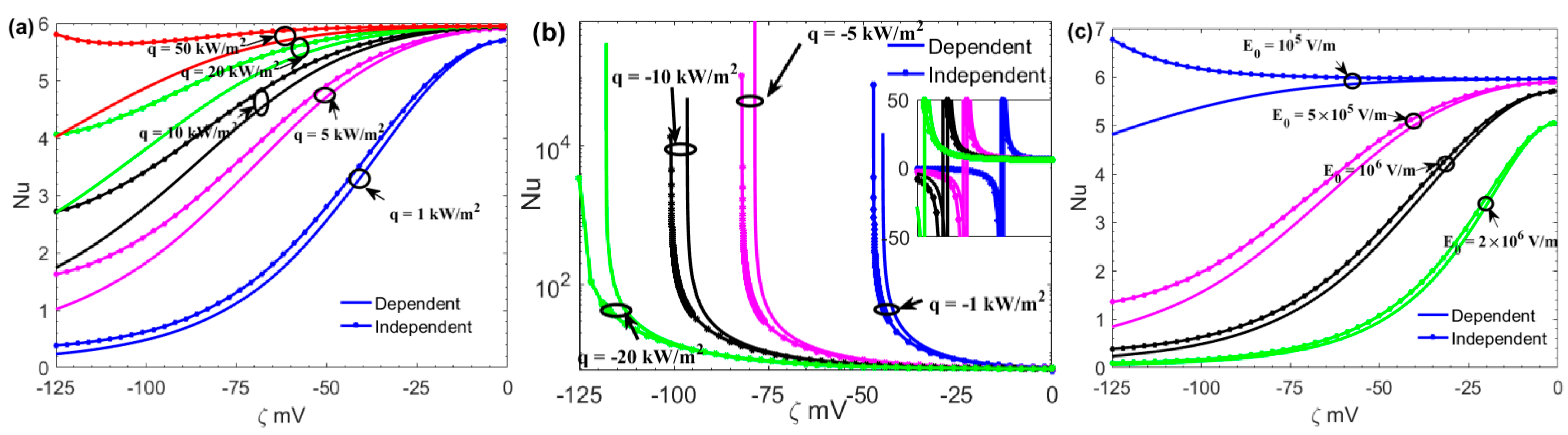
3. Results and Discussion
4. Conclusions
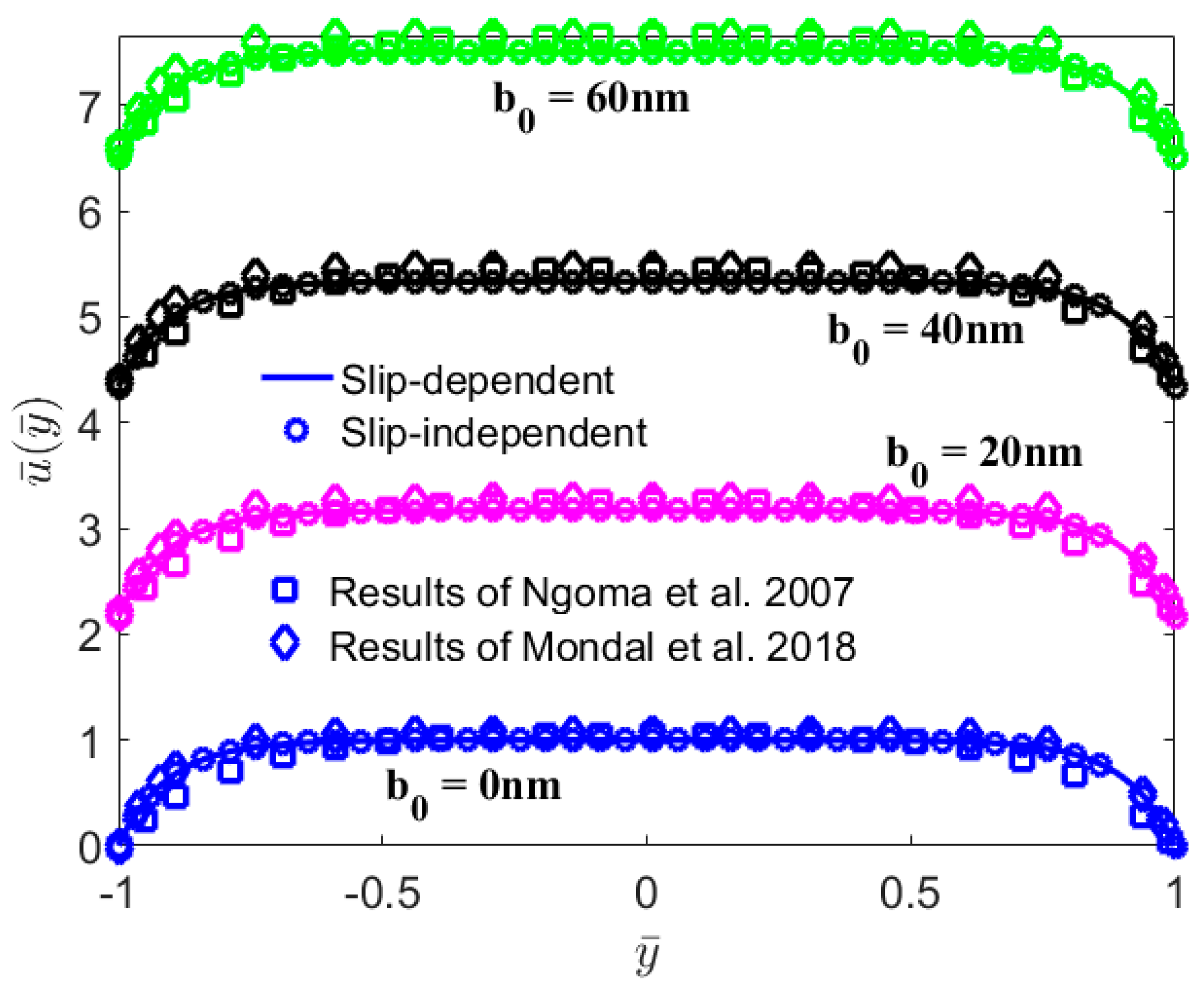
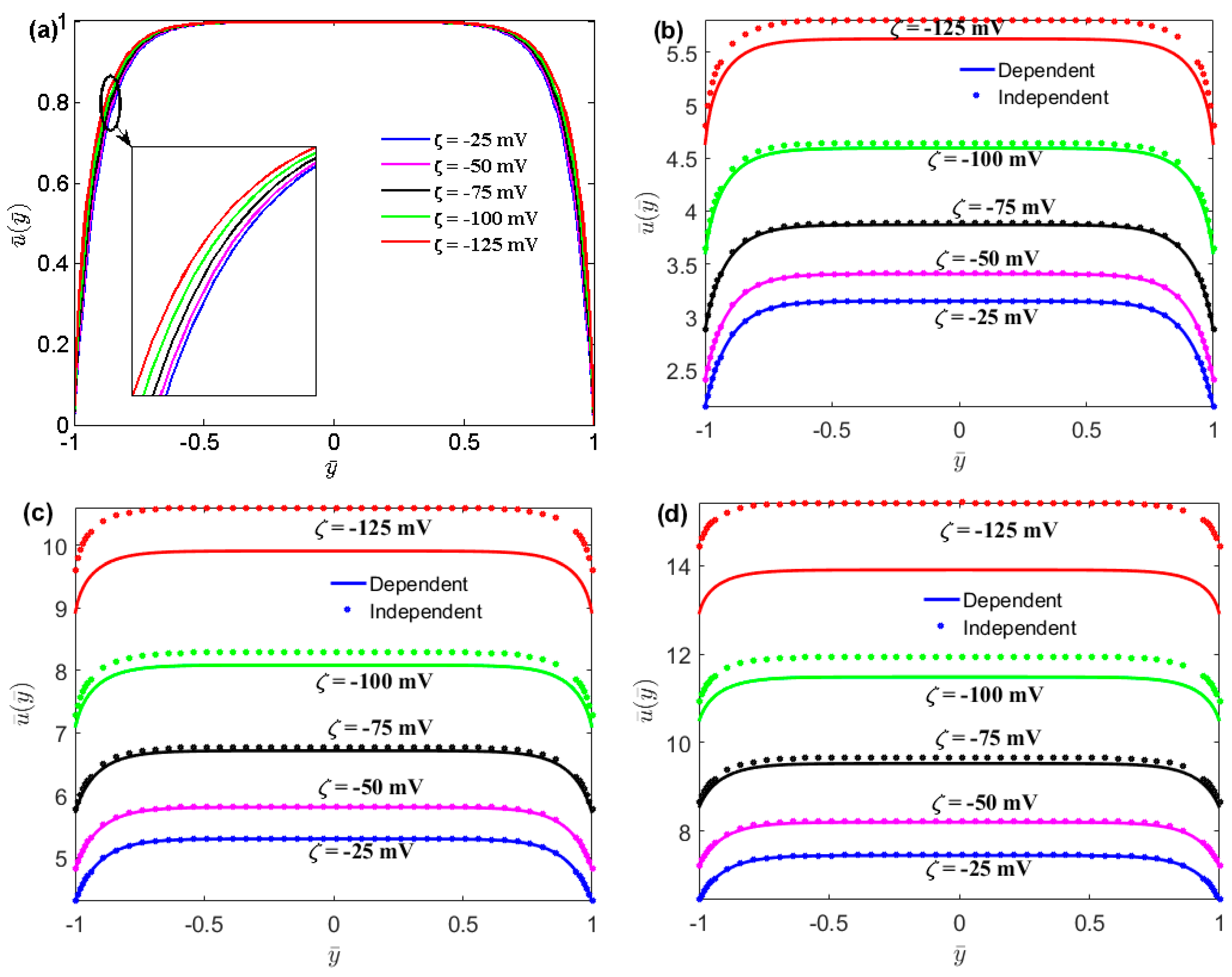
- For a given large zeta potential, the EDL velocity variation is limited to the thin layer that clings to both solid walls.
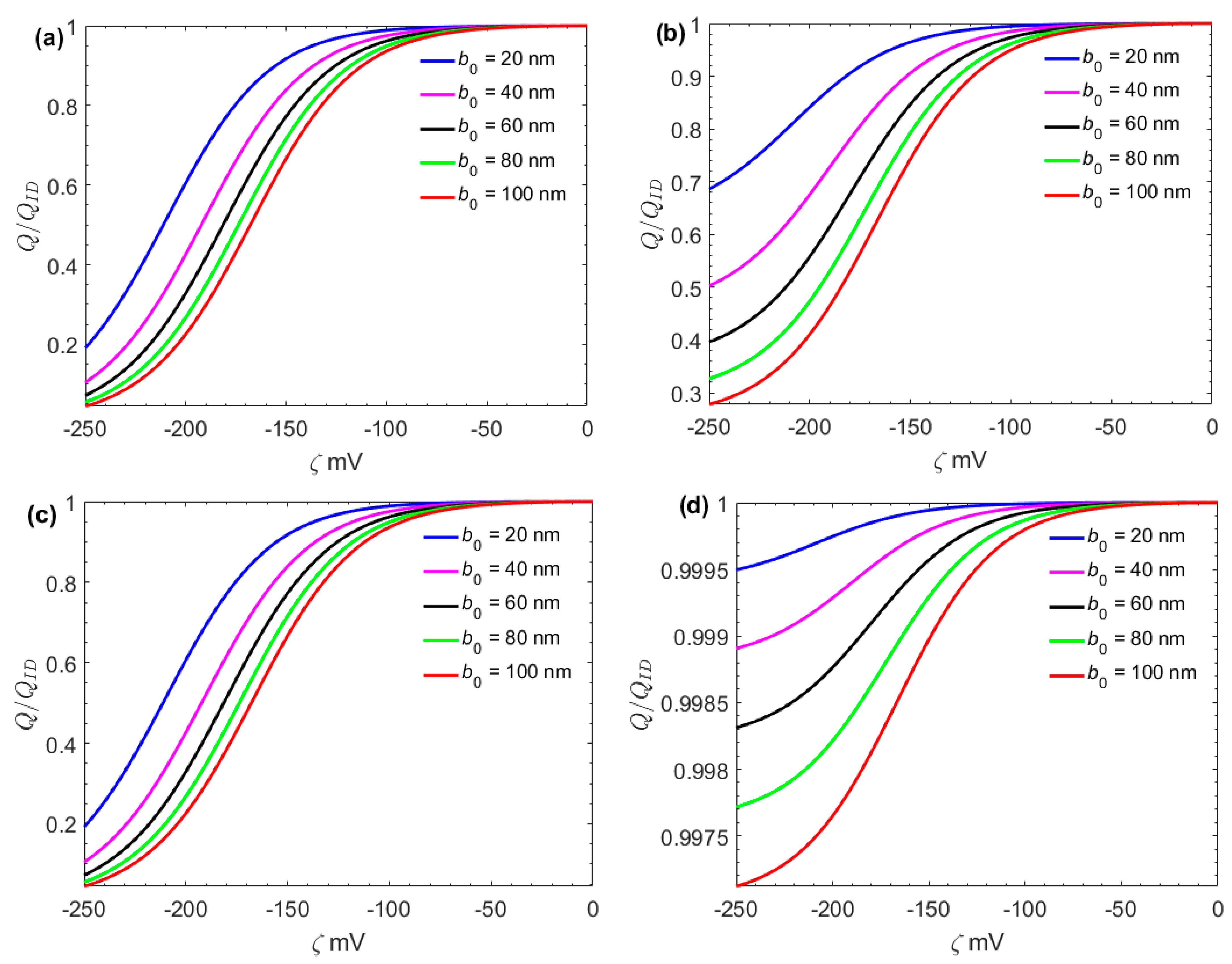
- Compared with the velocity of the surface charge-independent slip flow, that of the surface charge-dependent slip flow showed a significant reduction.
- The increase in zeta potential causes an increase in the dimensionless temperature in the nanochannel.
- The dimensionless temperature of the surface charge-dependent slip flow is larger than that of the surface charge-independent slip flow.
- For a given zeta potential, the effective Joule heating Ee decreases as the channel height increases; for a given channel height, as the zeta potential ζ increases, the effective Joule heating Ee is increased, especially in the nanochannel.
- Ion density n0 can inhibit the increase of Joule heat.
- The Nu decreases with Joule heating S and increases with positive heat transfer coefficient q.
- The Nu is large when the applied electric field E0 and zeta potential ζ are small.
- The Nu in the surface charge-dependent slip flow is smaller than that in the surface charge-independent slip flow.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| (x, y, z) | Cartesian orthonormal coordinate system |
| W | channel width |
| H | half channel height |
| L | channel length |
| b | slip length |
| b0 | original slip length without considering the surface charge effect |
| e | elementary charge |
| d | equilibrium distance of Lennard-Jones potential |
| Tav | average absolute temperature |
| kB | Boltzmann constant |
| n0 | ion density of bulk liquid |
| zv | valence of ion |
| K | dimensionless electrokinetic width = κH |
| dimensionless Cartesian coordinate system | |
| E0 | electric field strength |
| Z | dimensionless zeta potential |
| u | axial velocity |
| P | pressure |
| Ueo | Helmholtz−Smoluchowski electroosmotic velocity = –εζE0/μ |
| dimensionless axial velocity | |
| dimensionless slip length | |
| ur | ratio of the velocity of pressure-driven flow and that of EOF between two parallel plates = umax/Ueo |
| umax | velocity of pressure-driven flow = −H2 (2μ)−1 dp/dx |
| Q* | volumetric flow rate |
| Q | dimensional volumetric flow rate |
| QID | flow rate without considering the effect of the surface charge on the slip length |
| s | rate of volumetric heat generation due to Joule heating = ie2σρ |
| D | the diffusivity of ions in the electrolyte |
| cp | specific heat at constant pressure |
| k | thermal conductivity |
| T | temperature |
| ie | current density |
| Tb | bulk temperature |
| Tw | wall temperature |
| um | axial mean velocity |
| dimensionless axial mean velocity = um/Ueo | |
| Br | Brinkman number = μUeo2/qH |
| S | dimensionless volumetric heat generation due to Joule heating = E02H/σρq |
| Nu | Nusselt number |
| EJH | total Joule heating per unit length |
| Ee | dimensionless total Joule heating |
| h | heat transfer coefficient |
| Greek symbols | |
| ρ | density |
| σ | electric conductivity |
| σs | surface charge density |
| α | a numerical factor |
| ε | dielectric constant |
| ψ | electric potential |
| ζ | zeta potential |
| κ−1 | Debye length |
| ρe | net volumetric charge density |
| dimensionless electric potential | |
| μ | dynamic viscosity |
| σρ | liquid electrical resistivity |
| θ | dimensionless temperature |
| β | integral parameter |
| γ | integral parameter |
| Subscripts | |
| av | average |
| b | bulk |
| w | wall |
| m | mean |
| JH | Joule heating |
| s | surface |
| r | ratio |
References
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices: Microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Li, D. Encyclopedia of Microfluidics and Nanofluidics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Cetin, B.; Li, D. Effect of Joule heating on electrokinetic transport. Electrophoresis 2008, 29, 994–1005. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.H.; Zhang, X.D.; Lou, S.T.; Zhang, Z.X.; Sun, J.L.; Hu, J. Degassing and temperature effects on the formation of nanobubbles at the mica/water interface. Langmuir 2004, 20, 3813–3815. [Google Scholar] [CrossRef] [PubMed]
- Bayraktar, T.; Pidugu, S.B. Characterization of liquid flows in micro-fluidic systems. Int. J. Heat Mass Tran. 2006, 49, 815–824. [Google Scholar] [CrossRef]
- Keimanesh, M.; Rashidi, M.M.; Chamkha, A.J.; Jafari, R. Study of a third grade non-Newtonian fluid flow between two parallel plates using the multi-step differential transform method. Comput. Math. Appl. 2011, 62, 2871–2891. [Google Scholar] [CrossRef]
- Chamkha, A.J. On laminar hydromagnetic mixed convection flow in a vertical channel with symmetric and asymmetric wall heating conditions. Int. J. Heat Mass Tran. 2002, 45, 2509–2525. [Google Scholar] [CrossRef]
- VeeraKrishna, M.; Subba Reddy, G.; Chamkha, A.J. Hall effects on unsteady MHD oscillatory free convective flow of second grade fluid through porous medium between two vertical plates. Phys. Fluid. 2018, 30, 023106. [Google Scholar] [CrossRef]
- Raza, J.; Mebarek-Oudina, F.; Chamkha, A.J. Magnetohydrodynamic flow of molybdenum disulfide nanofluid in a channel with shape effects. Multidiscip. Model. Mater. Struct. 2019, 15, 737–757. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F.; Chamkha, A.J. Role of magnetic field on forced convection of nanofluid in a branching channel. Int. J. Numer. Method. Heat Fluid Flow 2020, 30, 1755–1772. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Chang, L.; Jian, Y.; Buren, M.; Liu, Q.; Sun, Y. Electroosmotic flow through a microtube with sinusoidal roughness. J. Mol. Liq. 2016, 220, 258–264. [Google Scholar] [CrossRef]
- Chang, L.; Jian, Y.; Buren, M.; Sun, Y. Electroosmotic flow through a microparallel channel with 3D wall roughness. Electrophoresis 2016, 37, 482–492. [Google Scholar] [CrossRef]
- Jian, Y.; Yang, L.; Liu, Q. Time periodic electro-osmotic flow through a microannulus. Phys. Fluid. 2010, 22, 042001. [Google Scholar] [CrossRef]
- Wang, C.Y.; Liu, Y.H.; Chang, C.C. Analytical solution of electro-osmotic flow in a semicircular microchannel. Phys. Fluid. 2008, 20, 063105. [Google Scholar] [CrossRef]
- Kang, Y.; Yang, C.; Huang, X. Electroosmotic flow in a capillary annulus with high zeta potentials. J. Colloid Interf. Sci. 2002, 253, 285–294. [Google Scholar] [CrossRef]
- Wang, X.; Chen, B.; Wu, J. A semianalytical solution of periodical electro-osmosis in a rectangular microchannel. Phys. Fluid. 2007, 19, 127101. [Google Scholar] [CrossRef]
- Rojas, G.; Arcos, J.; Peralta, M.; Méndez, F.; Bautista, O. Pulsatile electroosmotic flow in a microcapillary with the slip boundary condition. Colloid Surf. A 2017, 513, 57–65. [Google Scholar] [CrossRef]
- Ng, C.O.; Zhou, Q. Dispersion due to electroosmotic flow in a circular microchannel with slowly varying wall potential and hydrodynamic slippage. Phys. Fluid. 2012, 24, 112002. [Google Scholar] [CrossRef]
- Bian, X.; Li, F.; Jian, Y. The Streaming Potential of Fluid through a Microchannel with Modulated Charged Surfaces. Micromachines 2022, 13, 66. [Google Scholar] [CrossRef] [PubMed]
- Kadet, V.V.; Koryuzlov, P.S. Experimental study of electroosmotic flow in thin slit channels. J. Appl. Mech. Tech. Physic. 2009, 50, 805–808. [Google Scholar] [CrossRef]
- Monteferrante, M.; Melchionna, S.; Marconi, U.M.B.; Cretich, M.; Chiari, M.; Sola, L. Electroosmotic flow in polymer-coated slits: A joint experimental/simulation study. Microfluid. Nanofluid. 2015, 18, 475–482. [Google Scholar] [CrossRef]
- Kundu, B.; Saha, S. Review and Analysis of Electro-Magnetohydrodynamic Flow and Heat Transport in Microchannels. Energies 2022, 15, 7017. [Google Scholar] [CrossRef]
- Sabzpoushan, S.; Jafari Mosleh, H.; Kavian, S.; Saffari Pour, M.; Mohammadi, O.; Aghanajafi, C.; Ahmadi, M.H. Nonisothermal two-phase modeling of the effect of linear nonuniform catalyst layer on polymer electrolyte membrane fuel cell performance. Energy Sci. Eng. 2020, 8, 3575–3587. [Google Scholar] [CrossRef]
- Wang, Z.; Jian, Y. Heat Transport of Electrokinetic Flow in Slit Soft Nanochannels. Micromachines 2019, 10, 34. [Google Scholar] [CrossRef]
- Deng, S.; Xiao, T. Transient Two-Layer Electroosmotic Flow and Heat Transfer of Power-Law Nanofluids in a Microchannel. Micromachines 2022, 13, 405. [Google Scholar] [CrossRef]
- Jian, Y. Transient MHD heat transfer and entropy generation in a microparallel channel combined with pressure and electroosmotic effects. Int. J. Heat Mass Tran. 2015, 89, 193–205. [Google Scholar] [CrossRef]
- Su, J.; Jian, Y.; Chang, L. Thermally fully developed electroosmotic flow through a rectangular microchannel. Int. J. Heat Mass Tran. 2012, 55, 6285–6290. [Google Scholar] [CrossRef]
- Xie, Z.Y.; Jian, Y.J. Entropy generation of two-layer magnetohydrody-namic electroosmotic flow through microparallel channels. Energy 2017, 139, 1080–1093. [Google Scholar] [CrossRef]
- Maynes, D.; Webb, B.W. Fully-developed thermal transport in combined pressure and electro-osmotically driven flow in microchannels. J. Heat Tran. 2003, 125, 889–895. [Google Scholar] [CrossRef]
- Maynes, D.; Webb, B.W. The effect of viscous dissipation in thermally fully-developed electro-osmotic heat transfer in microchannels. Int. J. Heat Mass Tran. 2004, 47, 987–999. [Google Scholar] [CrossRef]
- Liechty, B.C.; Webb, B.W.; Maynes, R.D. Convective heat transfer characteristics of electro-osmotically generated flow in microtubes at high wall potential. Int. J. Heat Mass Tran. 2005, 48, 2360–2371. [Google Scholar] [CrossRef]
- Tang, G.Y.; Yang, C.; Chai, C.K.; Gong, H.Q. Numerical analysis of the thermal effect on electroosmotic flow and electrokinetic mass transport in microchannels. Anal. Chim. Acta 2004, 507, 27–37. [Google Scholar] [CrossRef]
- Chakraborty, S. Analytical solutions of Nusselt number for thermally fully developed flow in microtubes under a combined action of electroosmotic forces and imposed pressure gradients. Int. J. Heat Mass Tran. 2006, 49, 810–813. [Google Scholar] [CrossRef]
- Sadeghi, A.; Saidi, M.H. Viscous dissipation effects on thermal transport characteristics of combined pressure and electroosmotically driven flow in microchannels. Int. J. Heat Mass Tran. 2010, 53, 3782–3791. [Google Scholar] [CrossRef]
- Mondal, A.; Shit, G.C. Electro-osmotic flow and heat transfer in a slowly varying asymmetric micro-channel with Joule heating effects. Fluid Dyn. Res. 2018, 50, 065502. [Google Scholar] [CrossRef]
- Ngoma, G.D.; Erchiqui, F. Heat flux and slip effects on liquid flow in a microchannel. Int. J. Therm. Sci. 2007, 46, 1076–1083. [Google Scholar] [CrossRef]
- Vinogradova, O.I.; Belyaev, A.V. Wetting, roughness and flow boundary conditions. J. Phys. Condens. Mat. 2011, 23, 184104. [Google Scholar] [CrossRef]
- Pan, Y.; Bhushan, B.; Zhao, X. The study of surface wetting, nanobubbles and boundary slip with an applied voltage: A review. Beilstein J. Nanotechnol. 2014, 5, 1042–1065. [Google Scholar] [CrossRef]
- Jing, D.; Bhushan, B. The coupling of surface charge and boundary slip at the solid–liquid interface and their combined effect on fluid drag: A review. J. Colloid Interf. Sci. 2015, 454, 152–179. [Google Scholar] [CrossRef]
- Maduar, S.R.; Belyaev, A.V.; Lobaskin, V.; Vinogradova, O.I. Electrohydrodynamics near hydrophobic surfaces. Phys. Rev. Lett. 2015, 114, 118301. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Huang, X.; Chuan, T.K. MEMS-micropumps: A review. J. Fluids Eng. 2002, 124, 384–392. [Google Scholar] [CrossRef]
- Laohalertdecha, S.; Naphon, P.; Wongwises, S. A review of electrohydrodynamic enhancement of heat transfer. Renew. Sustain. Energy Rev. 2007, 11, 858–876. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35. [Google Scholar] [CrossRef]
- Park, H.M.; Kim, T.W. Extension of the Helmholtz-Smoluchowski velocity to the hydrophobic microchannels with velocity slip. Lab Chip 2009, 9, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Liu, Z.; Qiao, N.; Feng, Z.; Tian, Z.Q. The electroviscous effect in nanochannels with overlapping electric double layers considering the height size effect on surface charge. Electrochim. Acta 2022, 419, 140421. [Google Scholar] [CrossRef]
- Buren, M.; Jian, Y.; Zhao, Y.; Chang, L. Electroviscous effect and electrokinetic energy conversion in time periodic pressure-driven flow through a parallel-plate nanochannel with surface charge-dependent slip. J. Phys. D Appl. Phys. 2018, 51, 205601. [Google Scholar] [CrossRef]
- Buren, M.; Jian, Y.; Zhao, Y.; Chang, L.; Liu, Q. Effects of surface charge and boundary slip on time-periodic pressure-driven flow and electrokinetic energy conversion in a nanotube. Beilstein J. Nanotech. 2019, 10, 1628–1635. [Google Scholar] [CrossRef]
- Joly, L.; Ybert, C.; Trizac, E.; Bocquet, L. Liquid friction on charged surfaces: From hydrodynamic slippage to electrokinetics. J. Chem. Phys. 2006, 125, 204716. [Google Scholar] [CrossRef]
- Jing, D.; Bhushan, B. Electroviscous effect on fluid drag in a microchannel with large zeta potential. Beilstein J. Nanotech. 2015, 6, 2207–2216. [Google Scholar] [CrossRef]
- Jing, D.; Pan, Y. Electroviscous effect and convective heat transfer of pressure-driven flow through microtubes with surface charge-dependent slip. Int. J. Heat Mass Tran. 2016, 101, 648–655. [Google Scholar] [CrossRef]
- Jing, D.; Bhushan, B. Effect of boundary slip and surface charge on the pressure-driven flow. J. Colloid Interf. Sci. 2013, 392, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Jing, D.; Bhushan, B. Quantification of surface charge density and its effect on boundary slip. Langmuir 2013, 29, 6953–6963. [Google Scholar] [CrossRef]
- Banerjee, D.; Mehta, S.K.; Pati, S.; Biswas, P. Analytical solution to heat transfer for mixed electroosmotic and pressure-driven flow through a microchannel with slip-dependent zeta potential. Int. J. Heat Mass Tran. 2021, 181, 121989. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Liu, X.; Feng, Z.; Mo, X. Combined effect of surface charge and boundary slip on pressure-driven flow and convective heat transfer in nanochannels with overlapping electric double layer. Int. J. Heat Mass Tran. 2021, 176, 121353. [Google Scholar] [CrossRef]
- Jing, D.; Pan, Y.; Wang, X. Joule heating, viscous dissipation and convective heat transfer of pressure-driven flow in a microchannel with surface charge-dependent slip. Int. J. Heat Mass Tran. 2017, 108, 1305–1313. [Google Scholar] [CrossRef]
- Jing, D.; Pan, Y.; Wang, X. The non-monotonic overlapping EDL-induced electroviscous effect with surface charge—Dependent slip and its size dependence. Int. J. Heat Mass Tran. 2017, 113, 32–39. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, L.; Sun, Y.; Buren, M.; Jian, Y. Thermal and Flow Analysis of Fully Developed Electroosmotic Flow in Parallel-Plate Micro- and Nanochannels with Surface Charge-Dependent Slip. Micromachines 2022, 13, 2166. https://doi.org/10.3390/mi13122166
Chang L, Sun Y, Buren M, Jian Y. Thermal and Flow Analysis of Fully Developed Electroosmotic Flow in Parallel-Plate Micro- and Nanochannels with Surface Charge-Dependent Slip. Micromachines. 2022; 13(12):2166. https://doi.org/10.3390/mi13122166
Chicago/Turabian StyleChang, Long, Yanjun Sun, Mandula Buren, and Yongjun Jian. 2022. "Thermal and Flow Analysis of Fully Developed Electroosmotic Flow in Parallel-Plate Micro- and Nanochannels with Surface Charge-Dependent Slip" Micromachines 13, no. 12: 2166. https://doi.org/10.3390/mi13122166
APA StyleChang, L., Sun, Y., Buren, M., & Jian, Y. (2022). Thermal and Flow Analysis of Fully Developed Electroosmotic Flow in Parallel-Plate Micro- and Nanochannels with Surface Charge-Dependent Slip. Micromachines, 13(12), 2166. https://doi.org/10.3390/mi13122166






