Design of GHz Mechanical Nanoresonator with High Q-Factor Based on Optomechanical System
Abstract
1. Introduction
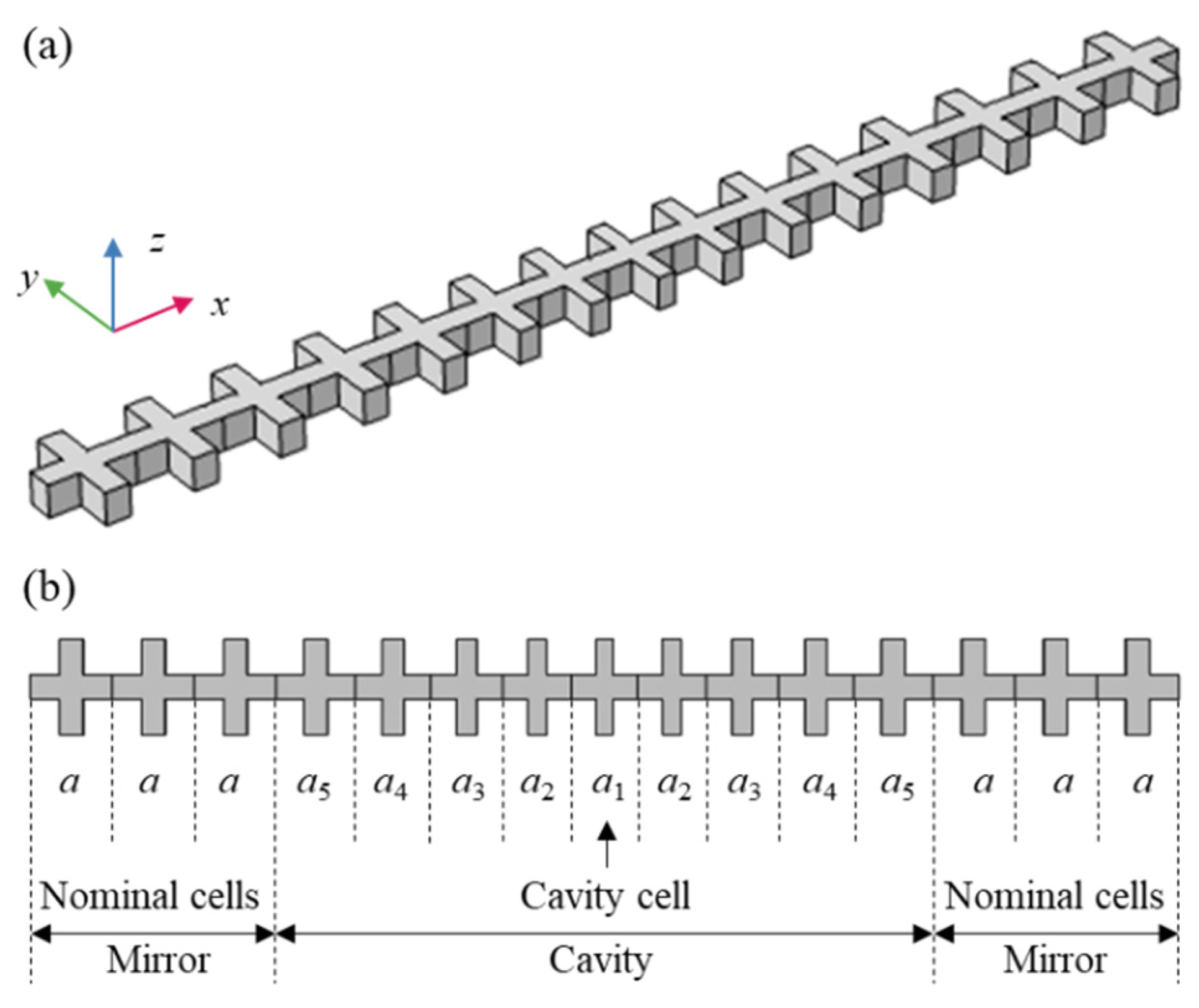
2. The Mechanical Nanoresonator Model
3. Results and Discussions
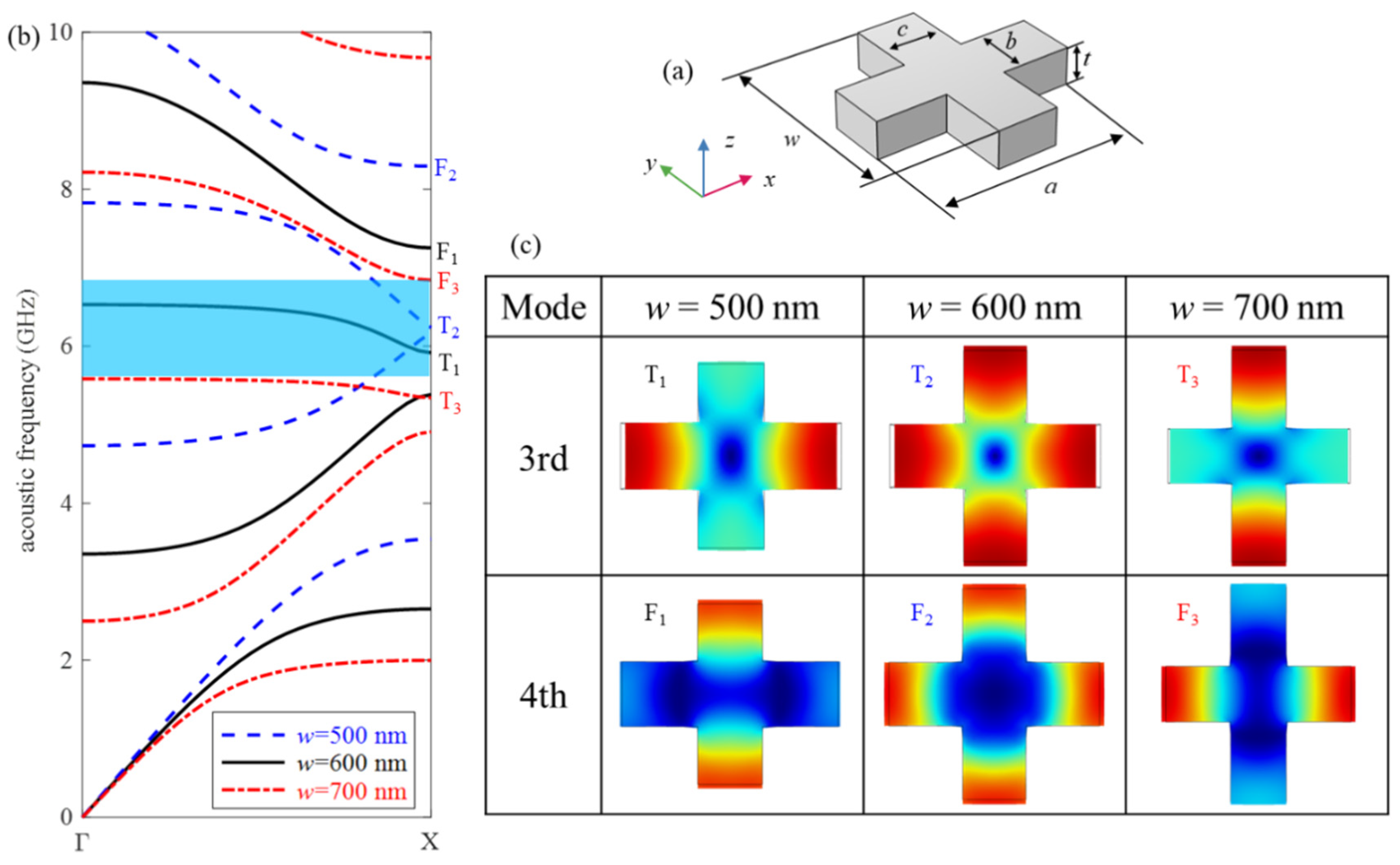
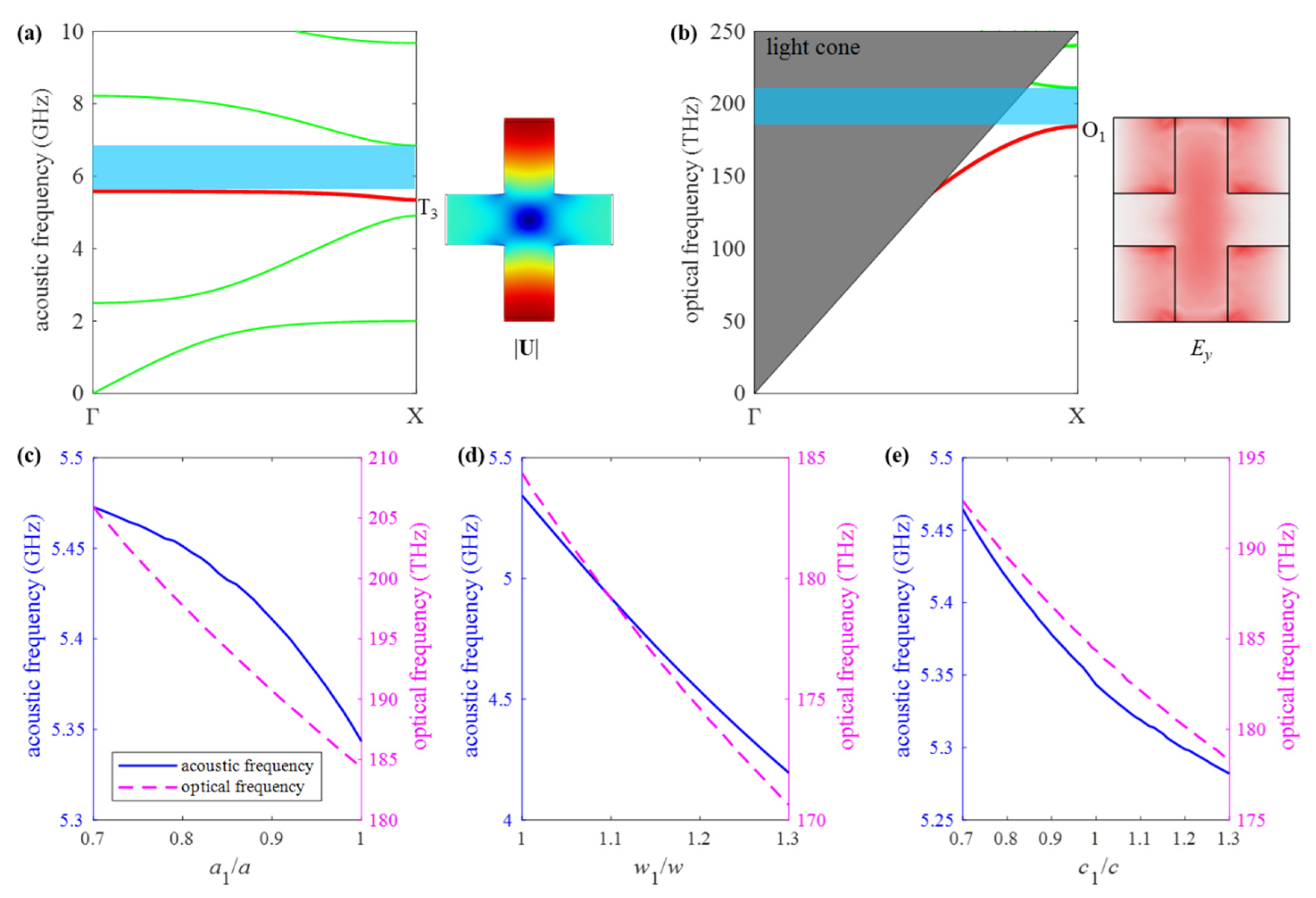
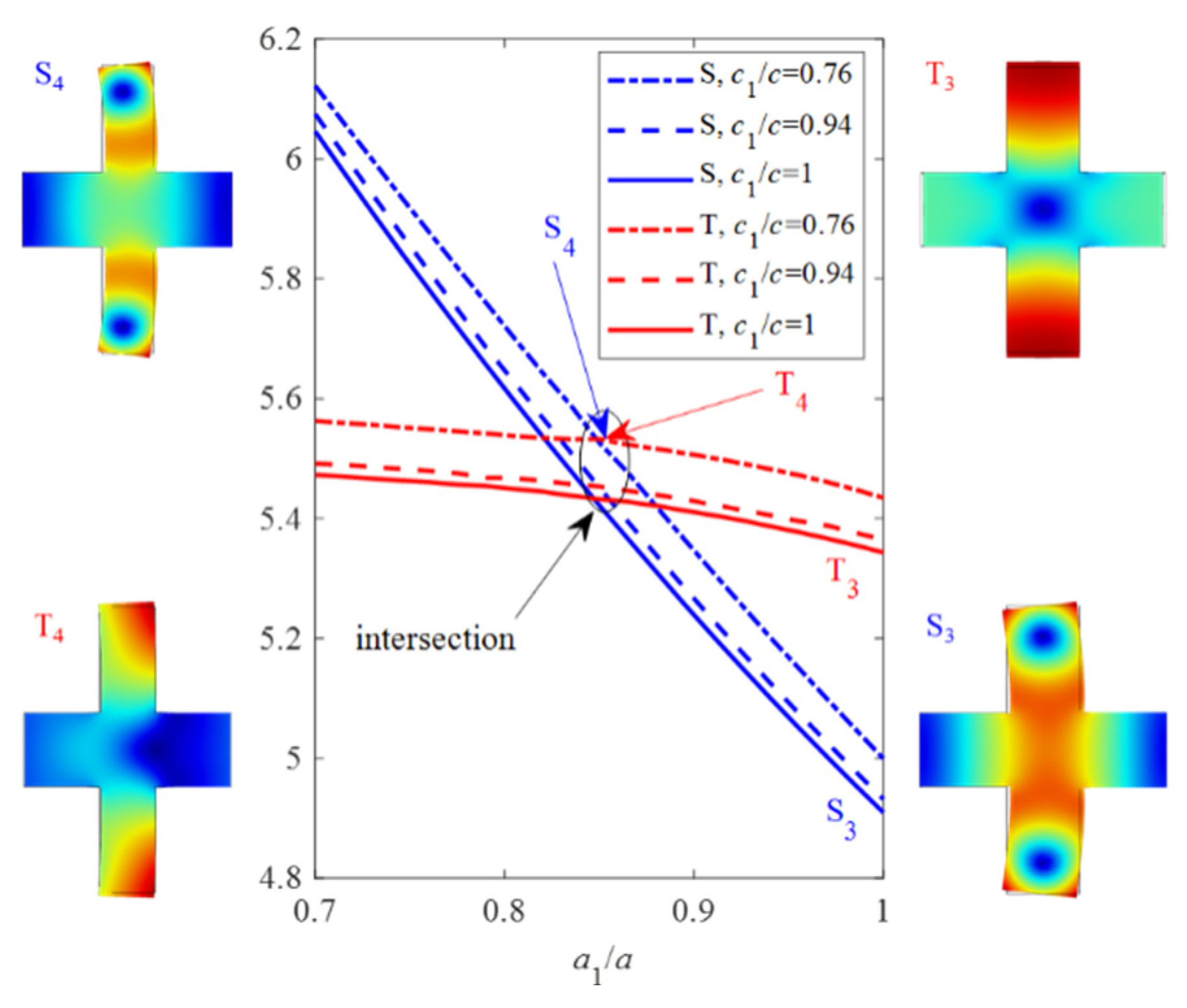
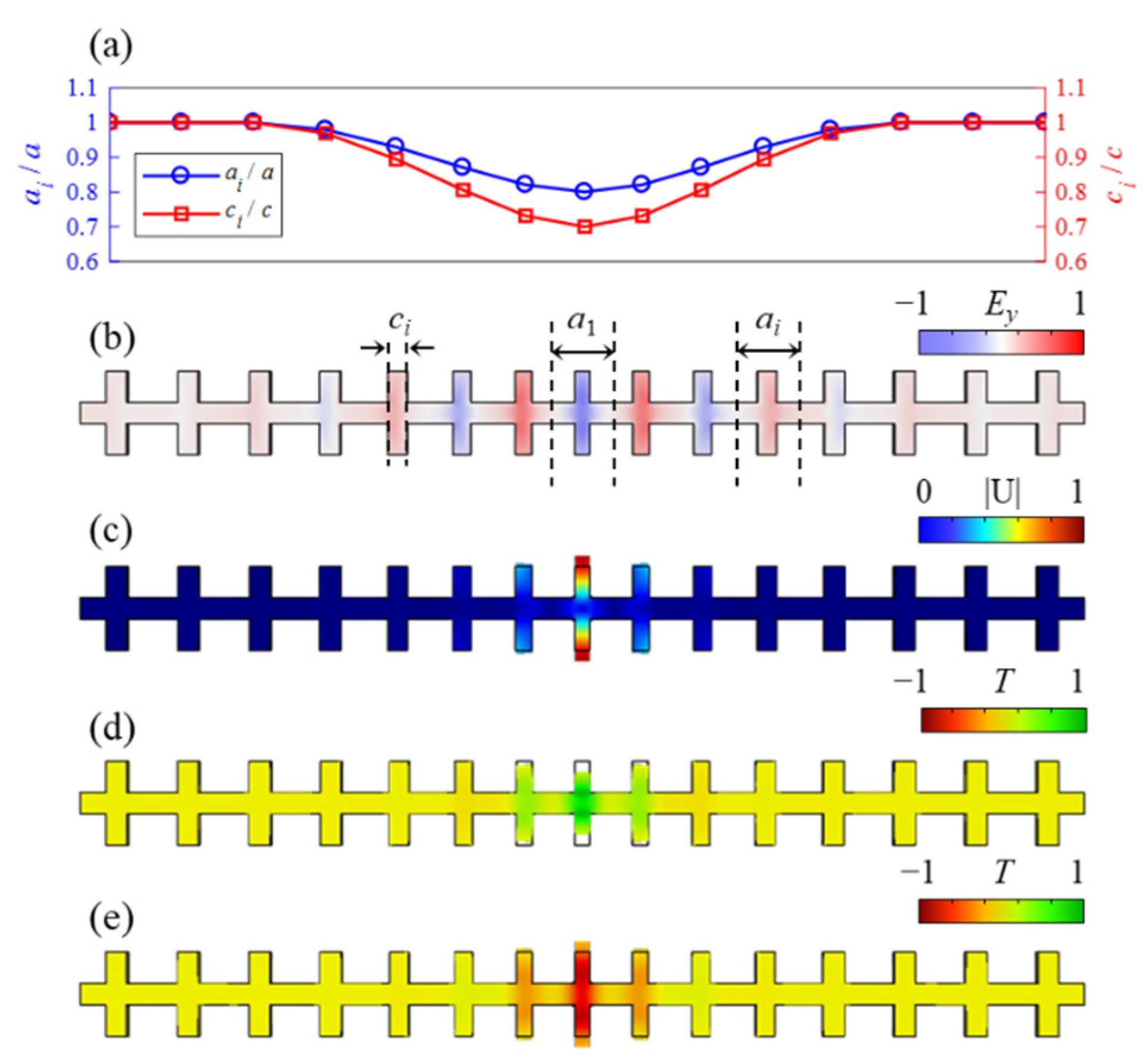
3.1. Design and Optimization
3.2. Mechanical Losses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, J.; Zhang, Y.; Huang, D.; Huang, X.; Hu, H. The optimization of AT-cut quartz resonator with circular electrode. In Proceedings of the 2019 13th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Harbin, China, 11–14 January 2019; pp. 1–4. [Google Scholar]
- Jin, J.; Huang, D.; Zhang, X.; Hu, H. Geometry optimization on mesa-type quartz resonator. In Proceedings of the 2019 14th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019; pp. 1–4. [Google Scholar]
- Duan, Q.; Jin, J.; Yang, F.; Hu, H. Research on inverted-mesa-type quartz resonator. In Proceedings of the 2020 15th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Zhengzhou, China, 16–19 April 2021; pp. 71–75. [Google Scholar]
- Liu, J.; Du, J.; Wang, J.; Yang, J. Effects of surface impedance on current density in a piezoelectric resonator for impedance distribution sensing. Appl. Math. Mech. 2021, 42, 677–688. [Google Scholar] [CrossRef]
- Mazalan, M.B.; Noor, A.M.; Wahab, Y.; Yahud, S.; Zaman, W.S.W.K. Current development in interdigital transducer (IDT) surface acoustic wave devices for live cell in vitro studies: A Review. Micromachines 2021, 13, 30. [Google Scholar] [CrossRef] [PubMed]
- Lamanna, L.; Rizzi, F.; Bhethanabotla, V.R.; De Vittorio, M. GHz AlN-based multiple mode SAW temperature sensor fabricated on PEN substrate. Sens. Actuators A Phys. 2020, 315, 112268. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Z.; Fang, Z.; Liu, Z.; Zhu, Y.; Du, L. High-performance FBAR humidity sensor based on the PI film as the multifunctional layer. Sens. Actuators B Chem. 2020, 308, 127694. [Google Scholar] [CrossRef]
- Huang, H.; Li, N.; Wang, B.; Qian, Z.; Huang, B.; Ma, T.; Kuznetsova, I. Two-dimensional coupling vibration analysis of laterally acoustically coupled two-port thin-film bulk acoustic resonators. Acta Mech. Solida Sin. 2020, 33, 464–478. [Google Scholar] [CrossRef]
- Madiot, G.; Ng, R.C.; Arregui, G.; Florez, O.; Albrechtsen, M.; Stobbe, S.; Garcia, P.D.; Sotomayor-Torres, C.M. Optomechanical generation of coherent GHz vibrations in a phononic waveguide. arXiv 2022, arXiv:2206.06913. [Google Scholar]
- Chan, J.; Alegre, T.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef]
- Cui, K.Y.; Huang, Z.L.; Wu, N.; Xu, Q.C.; Pan, F.; Xiong, J.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y.D. Phonon lasing in a hetero optomechanical crystal cavity. Photonics Res. 2021, 9, 937–943. [Google Scholar] [CrossRef]
- Mercadé, L.; Pelka, K.; Burgwal, R.; Xuereb, A.; Martínez, A.; Verhagen, E. Floquet phonon lasing in multimode optomechanical systems. Phys. Rev. Lett. 2021, 127, 073601. [Google Scholar] [CrossRef]
- Yang, C.; Wei, X.; Sheng, J.; Wu, H. Phonon heat transport in cavity-mediated optomechanical nanoresonators. Nat. Commun. 2020, 11, 4656. [Google Scholar] [CrossRef]
- Patel, R.N.; Sarabalis, C.J.; Jiang, W.; Hill, J.T.; Safavi-Naeini, A.H. Engineering phonon leakage in nanomechanical resonators. Phys. Rev. Appl. 2017, 8, 041001. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Alegre, T.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.-H.; Shen, Z.; Zou, C.-L.; Zhang, Y.-L.; Fu, W.; Guo, G.-C. Brillouin-scattering-induced transparency and non-reciprocal light storage. Nat. Commun. 2015, 6, 6193. [Google Scholar] [CrossRef] [PubMed]
- Weis, S.; Rivière, R.; Deléglise, S.; Gavartin, E.; Arcizet, O.; Schliesser, A.; Kippenberg, T.J. Optomechanically induced transparency. Science 2010, 330, 1520–1523. [Google Scholar] [CrossRef] [PubMed]
- Kini, R.N.; Kent, A.J.; Stanton, N.M.; Henini, M. Generation and detection of terahertz coherent transverse-polarized acoustic phonons by ultrafast optical excitation of GaAs/AlAs superlattices. Appl. Phys. Lett. 2006, 88, 134112. [Google Scholar] [CrossRef]
- Pascual Winter, M.F.; Fainstein, A.; Jusserand, B.; Perrin, B.; Lemaître, A. Optimized optical generation and detection of superlattice acoustic phonons. Appl. Phys. Lett. 2009, 94, 103103. [Google Scholar] [CrossRef]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Perrin, B.; Jusserand, B. Theory of coherent generation and detection of THz acoustic phonons using optical microcavities. Phys. Rev. B 2011, 84, 064307. [Google Scholar] [CrossRef]
- Pascual-Winter, M.F.; Fainstein, A.; Jusserand, B.; Perrin, B.; Lemaître, A. Spectral responses of phonon optical generation and detection in superlattices. Phys. Rev. B 2012, 85, 235443. [Google Scholar] [CrossRef]
- Patel, R.N.; McKenna, T.P.; Wang, Z.; Witmer, J.D.; Jiang, W.; Van Laer, R.; Sarabalis, C.J.; Safavi-Naeini, A.H. Room-temperature mechanical resonator with a single added or subtracted phonon. Phys. Rev. Lett. 2021, 127, 133602. [Google Scholar] [CrossRef]
- Anguiano, S.; Bruchhausen, A.E.; Jusserand, B.; Favero, I.; Lamberti, F.R.; Lanco, L.; Sagnes, I.; Lemaitre, A.; Lanzillotti-Kimura, N.D.; Senellart, P.; et al. Micropillar Resonators for Optomechanics in the Extremely High 19-95-GHz Frequency Range. Phys. Rev. Lett. 2017, 118, 263901. [Google Scholar] [CrossRef]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Wang, X.; Zhan, L.; Hu, H. Strong quadratic acousto-optic coupling in 1D multilayer phoxonic crystal cavity. Nanotechnol. Rev. 2021, 10, 443–452. [Google Scholar] [CrossRef]
- Jin, J.; Jiang, S.; Hu, H.; Zhan, L.; Wang, X.; Laude, V. Acousto-optic cavity coupling in 2D phoxonic crystal with combined convex and concave holes. J. Appl. Phys. 2021, 130, 123104. [Google Scholar] [CrossRef]
- Biegelsen, D.K. Photoelastic tensor of silicon and the volume dependence of the average gap. Phys. Rev. Lett. 1974, 32, 1196. [Google Scholar] [CrossRef]
- Johnson, S.G.; Ibanescu, M.; Skorobogatiy, M.A.; Weisberg, O.; Joannopoulos, J.D.; Fink, Y. Perturbation theory for Maxwell’s equations with shifting material boundaries. Phys. Rev. E 2002, 65, 066611. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Jusserand, B. Towards GHz-THz cavity optomechanics in DBR-based semiconductor resonators. Ultrasonics 2015, 56, 80–89. [Google Scholar] [CrossRef]
- Chan, J.; Safavi-Naeini, A.H.; Hill, J.T.; Meenehan, S.; Painter, O. Optimized optomechanical crystal cavity with acoustic radiation shield. Appl. Phys. Lett. 2012, 101, 081115. [Google Scholar] [CrossRef]
- Amir, H.; Safavi-Naeini, O.P. Design of optomechanical cavities and waveguides on a simultaneous bandgap phononic-photonic crystal slab. Opt. Express 2010, 18, 14926–14943. [Google Scholar]
- Akahane, Y.; Asano, T.; Song, B.-S.; Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003, 425, 944–947. [Google Scholar] [CrossRef]
- Bereyhi, M.J.; Beccari, A.; Groth, R.; Fedorov, S.A.; Arabmoheghi, A.; Kippenberg, T.J.; Engelsen, N.J. Hierarchical tensile structures with ultralow mechanical dissipation. Nat. Commun. 2022, 13, 3097. [Google Scholar] [CrossRef] [PubMed]
- de Jong, M.H.; Wolde, M.A.t.; Cupertino, A.; Steeneken, P.G.; Norte, R.A. Mechanical dissipation by substrate-mode coupling in SiN resonators. arXiv 2022, arXiv:2206.00990. [Google Scholar] [CrossRef]
- Wollack, E.A.; Cleland, A.Y.; Arrangoiz-Arriola, P.; McKenna, T.P.; Gruenke, R.G.; Patel, R.N.; Jiang, W.; Sarabalis, C.J.; Safavi-Naeini, A.H. Loss channels affecting lithium niobate phononic crystal resonators at cryogenic temperature. Appl. Phys. Lett. 2021, 118, 123501. [Google Scholar] [CrossRef]
- MacCabe, G.S.; Ren, H.; Luo, J.; Cohen, J.D.; Zhou, H.; Sipahigil, A.; Mirhosseini, M.; Painter, O. Nano-acoustic resonator with ultralong phonon lifetime. Science 2020, 370, 840–843. [Google Scholar] [CrossRef] [PubMed]
- Wilson-Rae, I.; Barton, R.; Verbridge, S.; Southworth, D.; Ilic, B.; Craighead, H.G.; Parpia, J. High-Q nanomechanics via destructive interference of elastic waves. Phys. Rev. Lett. 2011, 106, 047205. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wang, T.; Jia, Q.; Yang, J.; Yuan, Q.; Zhu, Y.; Yang, F. A novel Lamé mode RF-MEMS resonator with high quality factor. Int. J. Mech. Sci. 2021, 204, 106484. [Google Scholar] [CrossRef]
- Akhieser, A. On the absorption of sound in solids. J. Phys. 1939, 1, 277. [Google Scholar]
- Lifshitz, R.; Roukes, M.L. Thermoelastic damping in micro-and nanomechanical systems. Phys. Rev. B 2000, 61, 5600. [Google Scholar] [CrossRef]
- Unterreithmeier, Q.P.; Faust, T.; Kotthaus, J.P. Damping of nanomechanical resonators. Phys. Rev. Lett. 2010, 105, 027205. [Google Scholar] [CrossRef]
- Chan, J. Laser Cooling of an Optomechanical Crystal Resonator to Its Quantum Ground State of Motion; California Institute of Technology: Pasadena, CA, USA, 2012. [Google Scholar]
- Tabrizian, R.; Rais-Zadeh, M.; Ayazi, F. Effect of phonon interactions on limiting the f.Q product of micromechanical resonators. In Proceedings of the TRANSDUCERS 2009-2009 International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 13 October 2009; pp. 2131–2134. [Google Scholar]
- Philip, J.; Breazeale, M. Third-order elastic constants and Grüneisen parameters of silicon and germanium between 3 and 300° K. J. Appl. Phys. 1983, 54, 752–757. [Google Scholar] [CrossRef]
- Glassbrenner, C.J.; Slack, G.A. Thermal conductivity of silicon and germanium from 3 K to the melting point. Phys.Rev. 1964, 134, A1058. [Google Scholar] [CrossRef]
- Lambade, S.; Sahasrabudhe, G.; Rajagopalan, S. Temperature dependence of acoustic attenuation in silicon. Phys. Rev. B 1995, 51, 15861. [Google Scholar] [CrossRef] [PubMed]
- Sheikhlou, M.; Sadeghi, F.; Najafi, S.; Azimloo, H. Surface and Nonlocal Effects on the Thermoelastic Damping in Axisymmetric Vibration of Circular Graphene Nanoresonators. Acta Mech. Solida Sin. 2022, 35, 527–540. [Google Scholar] [CrossRef]
- Dong, J.; Li, Q.; Xie, Y.; Cao, Z.; Li, X. A 2.5-GHz FBAR-based push-pull class-C oscillator with low phase noise. In Proceedings of the 2020 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Hangzhou, China, 7–9 December 2020; pp. 1–3. [Google Scholar]


| Cell Number i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| ai (nm) | 480 | 492 | 522 | 558 | 588 |
| ci (nm) | 126 | 132 | 145 | 161 | 174 |
| Resonator Type | Material | Resonant Frequency (GHz) | Q-Factor | f.Qm |
|---|---|---|---|---|
| SAW [6] | AlN | 1.325 | 109 | 1.4 × 1011 |
| FBAR [7] | PI | 1.055 | 210 | 2.2 × 1011 |
| FBAR [49] | AlN | 2.5 | 850 | 2.5 × 1012 |
| OMC Resonator [37] | Si | 5 | 4.9 × 1010 | 2.6 × 1020 |
| This work | Si | 5.69 | 1.17 × 104 | 8.5 × 1013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, J.; Hu, N.; Zhan, L.; Wang, X.; Zhang, Z.; Hu, H. Design of GHz Mechanical Nanoresonator with High Q-Factor Based on Optomechanical System. Micromachines 2022, 13, 1862. https://doi.org/10.3390/mi13111862
Jin J, Hu N, Zhan L, Wang X, Zhang Z, Hu H. Design of GHz Mechanical Nanoresonator with High Q-Factor Based on Optomechanical System. Micromachines. 2022; 13(11):1862. https://doi.org/10.3390/mi13111862
Chicago/Turabian StyleJin, Jun, Ningdong Hu, Lamin Zhan, Xiaohong Wang, Zenglei Zhang, and Hongping Hu. 2022. "Design of GHz Mechanical Nanoresonator with High Q-Factor Based on Optomechanical System" Micromachines 13, no. 11: 1862. https://doi.org/10.3390/mi13111862
APA StyleJin, J., Hu, N., Zhan, L., Wang, X., Zhang, Z., & Hu, H. (2022). Design of GHz Mechanical Nanoresonator with High Q-Factor Based on Optomechanical System. Micromachines, 13(11), 1862. https://doi.org/10.3390/mi13111862







