An Energy Efficient Thermally Regulated Optical Spectroscopy Cell for Lab-on-Chip Devices: Applied to Nitrate Detection
Abstract
1. Introduction
2. Materials and Methods
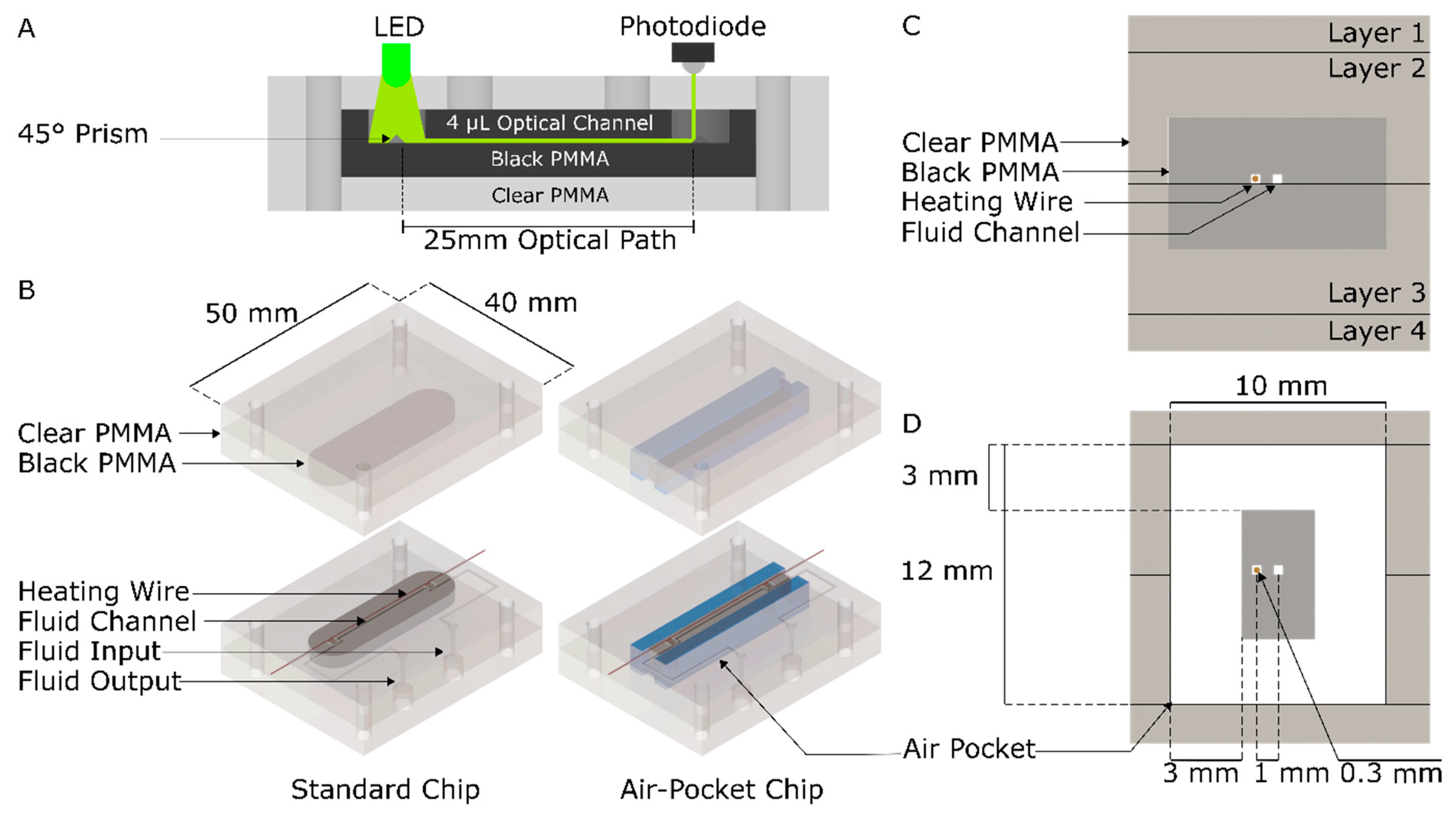
2.1. Chip Fabrication
2.2. Reagent Preparation
2.3. Characterization Procedure
2.4. Data Analysis
3. Results and Discussion
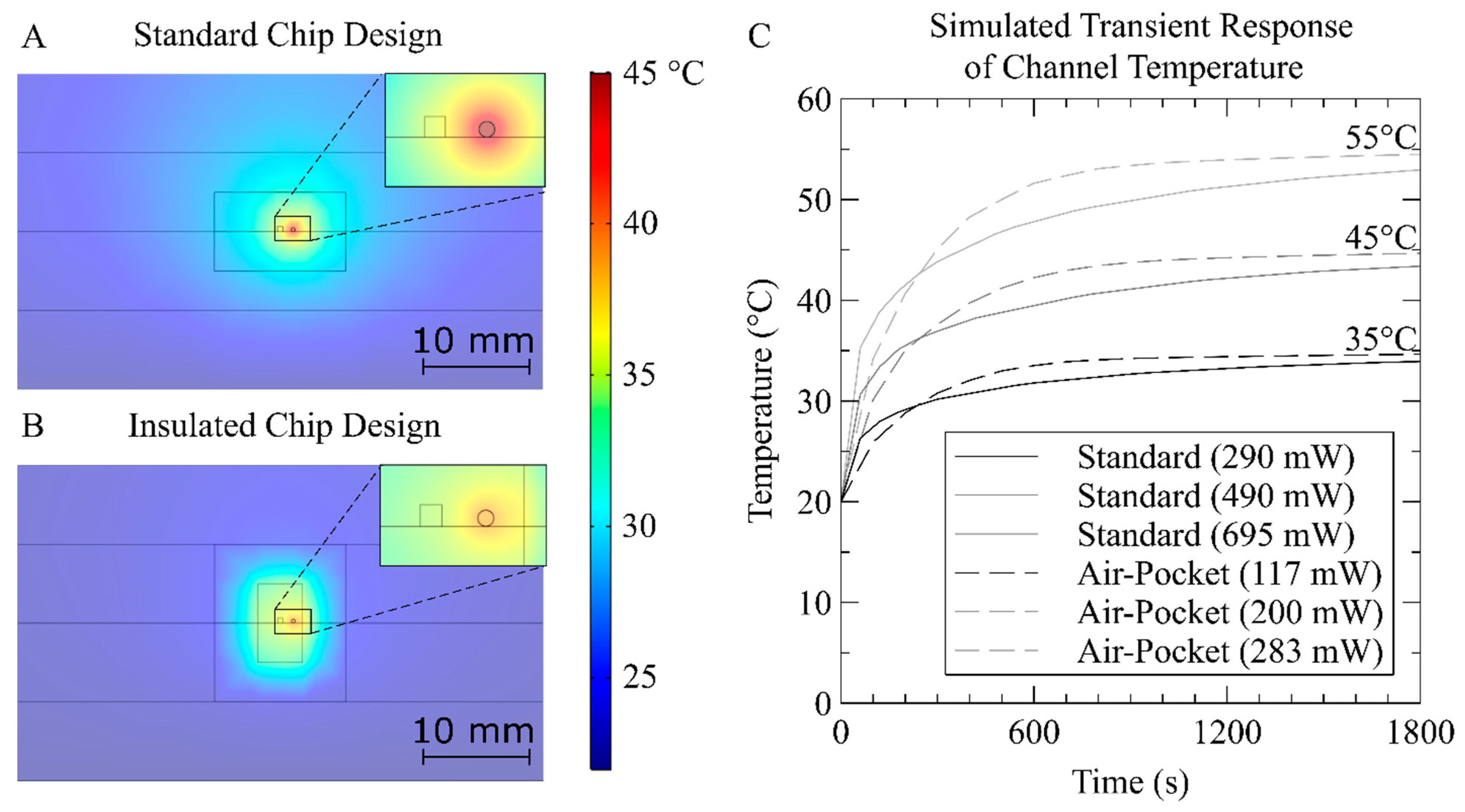
3.1. Heater Simulation
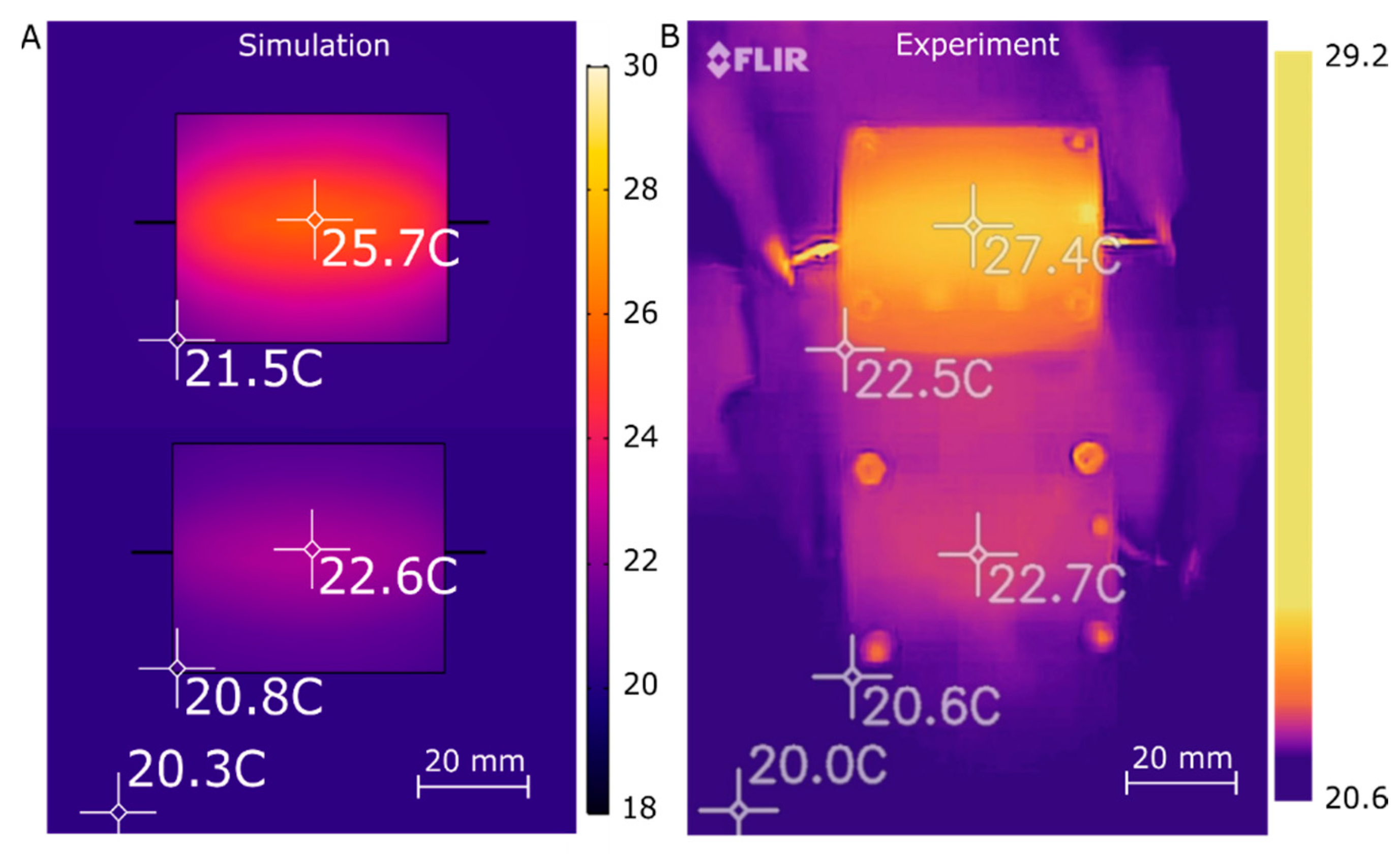
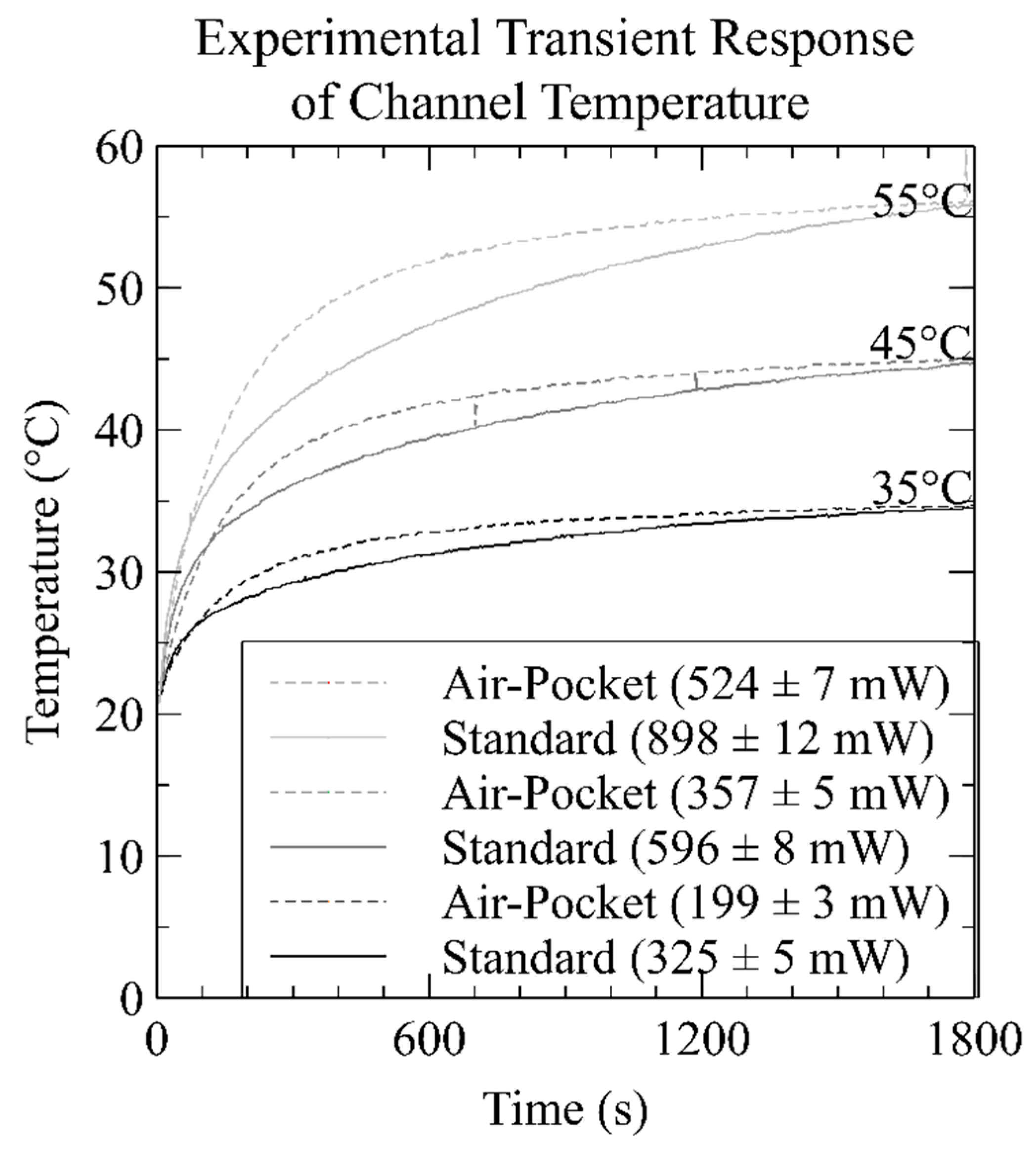
3.2. Heater Experimental Characterization
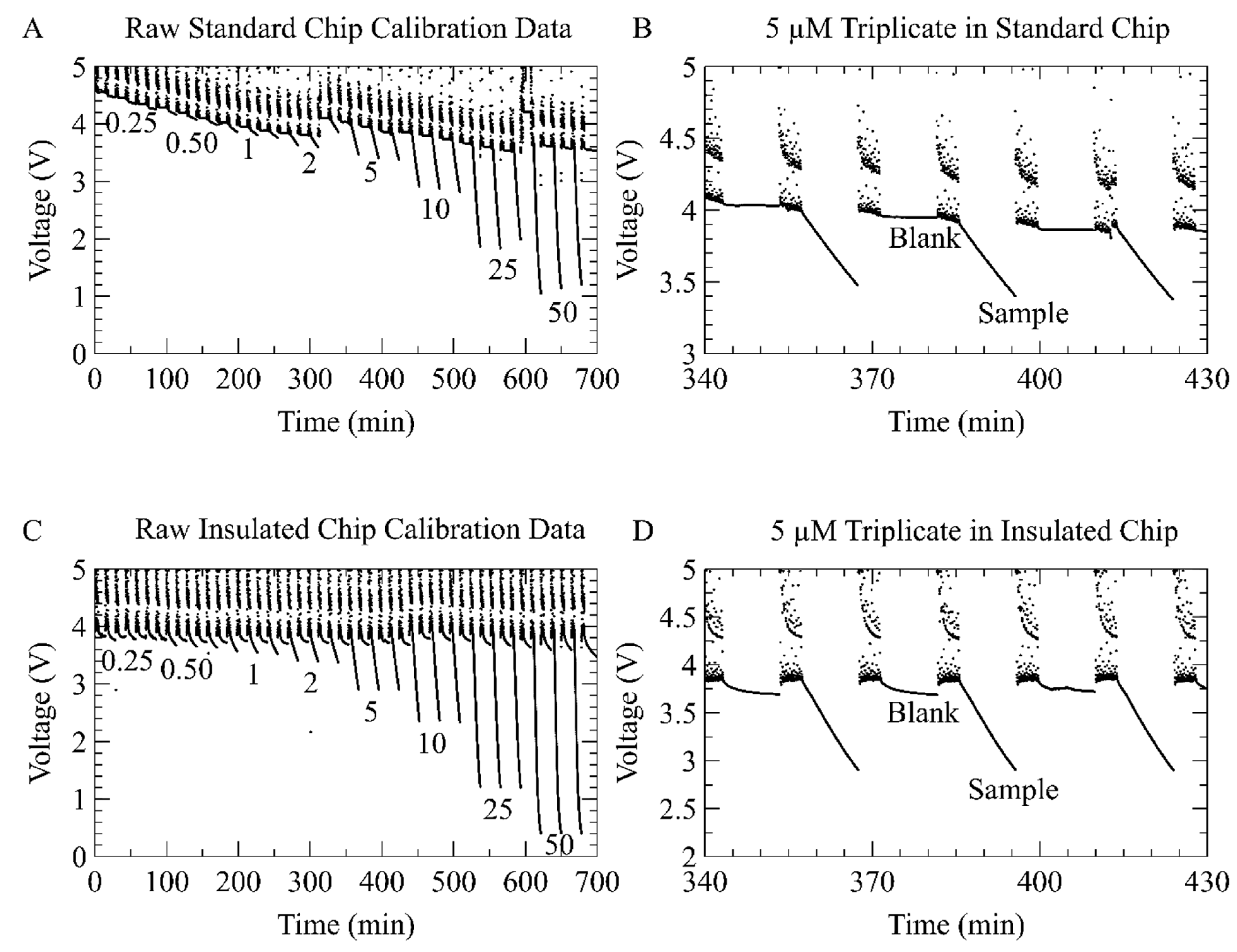
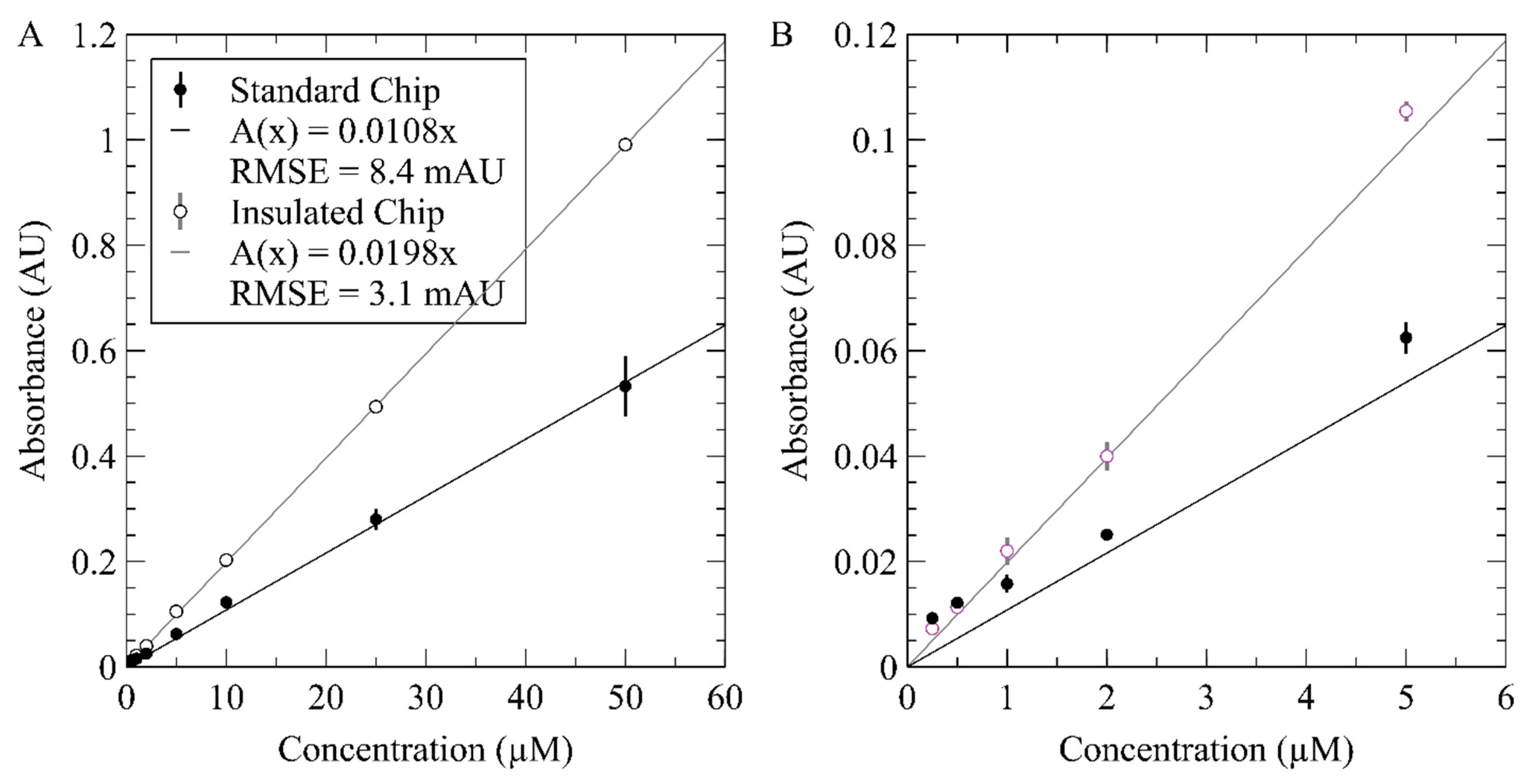
3.3. On-Chip Measurement of Nitrate Using the Inlaid Optical Cell
3.4. Nitrate Detection Using Integral Heater with Inlaid Optical Cell
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nightingale, A.M.; Beaton, A.D.; Mowlem, M.C. Trends in microfluidic systems for in situ chemical analysis of natural waters. Sens. Actuators B Chem. 2015, 221, 1398–1405. [Google Scholar] [CrossRef]
- Schnetger, B.; Lehners, C. Determination of nitrate plus nitrite in small volume marine water samples using vanadium(III)chloride as a reduction agent. Mar. Chem. 2014, 160, 91–98. [Google Scholar] [CrossRef]
- Tovar, A.; Moreno, C.; Mánuel-Vez, M.P.; García-Vargas, M. A simple automated method for the speciation of dissolved inorganic nitrogen in seawater. Anal. Chim. Acta 2002, 469, 235–242. [Google Scholar] [CrossRef]
- Justic, D.; Turner, R.E.; Rabalais, N.N. Climatic influences on riverine nitrate flux: Implications for coastal marine eutrophication and hypoxia. Estuaries 2003, 26, 1–11. [Google Scholar] [CrossRef]
- Diego-McGlone, M.L.S.; Azanza, R.V.; Villanoy, C.L.; Jacinto, G.S. Eutrophic waters, algal bloom and fish kill in fish farming areas in Bolinao, Pangasinan, Philippines. Mar. Pollut. Bull. 2008, 57, 295–301. [Google Scholar] [CrossRef]
- Galalgorchev, H. Who Guidelines for Drinking-Water Quality. In Iwsa Specialized Conference on Quality Aspects of Water Supply; Fiessinger, F., Ed.; Blackwell Scientific Publ.: Oxford, UK, 1992; Volume 11, pp. 1–16. [Google Scholar]
- Nightingale, A.M.; Hassan, S.; Warren, B.M.; Makris, K.; Evans, G.W.H.; Papadopoulou, E.; Coleman, S.; Niu, X. A Droplet Microfluidic-Based Sensor for Simultaneous in situ Monitoring of Nitrate and Nitrite in Natural Waters. Environ. Sci. Technol. 2019, 53, 9677–9685. [Google Scholar] [CrossRef] [PubMed]
- Beaton, A.D.; Sieben, V.J.; Floquet, C.F.A.; Waugh, E.M.; Bey, S.A.K.; Ogilvie, I.R.G.; Mowlem, M.C.; Morgan, H. An automated microfluidic colourimetric sensor applied in situ to determine nitrite concentration. Sens. Actuators B Chem. 2011, 156, 1009–1014. [Google Scholar] [CrossRef]
- MacIntyre, G.; Plache, B.; Lewis, M.R.; Andrea, J.; Feener, S.; McLean, S.D.; Johnson, K.S.; Coletti, L.J.; Jannasch, H.W. ISUS/SUNA Nitrate Measurements in Networked Ocean Observing Systems. In Oceans 2009, Vols 1–3; IEEE: New York, NY, USA, 2009; p. 2125. ISBN 978-1-4244-4960-6. [Google Scholar]
- Beaton, A.D.; Cardwell, C.L.; Thomas, R.S.; Sieben, V.J.; Legiret, F.-E.; Waugh, E.M.; Statham, P.J.; Mowlem, M.C.; Morgan, H. Lab-on-Chip Measurement of Nitrate and Nitrite for in situ Analysis of Natural Waters. Environ. Sci. Technol. 2012, 46, 9548–9556. [Google Scholar] [CrossRef]
- Wang, Q.-H.; Yu, L.-J.; Liu, Y.; Lin, L.; Lu, R.; Zhu, J.; He, L.; Lu, Z.-L. Methods for the detection and determination of nitrite and nitrate: A review. Talanta 2017, 165, 709–720. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, Y.; Linthicum, W.; Liu, F.; Beringhs, A.O.; Dang, Y.; Xu, Z.; Chang, S.-Y.; Ling, J.; Huey, B.D.; et al. Toward Long-Term Accurate and Continuous Monitoring of Nitrate in Wastewater Using Poly(tetrafluoroethylene) (PTFE)–Solid-State Ion-Selective Electrodes (S-ISEs). ACS Sens. 2020. [Google Scholar] [CrossRef]
- Murray, E.; Roche, P.; Briet, M.; Moore, B.; Morrin, A.; Diamond, D.; Paull, B. Fully automated, low-cost ion chromatography system for in-situ analysis of nitrite and nitrate in natural waters. Talanta 2020, 216, 120955. [Google Scholar] [CrossRef]
- Edwards, A.C.; Hooda, P.S.; Cook, Y. Determination of nitrate in water containing dissolved organic carbon by ultraviolet spectroscopy. Int. J. Environ. Anal. Chem. 2001, 80, 49–59. [Google Scholar] [CrossRef]
- Jian, Z.; Xu, J.; Huang, X.; Yang, W.; Hu, Q. Optical Absorption Characteristics, Spatial Distribution, and Source Analysis of Colored Dissolved Organic Matter in Wetland Water around Poyang Lake. Water 2021, 13, 274. [Google Scholar] [CrossRef]
- Mahmud, M.A.P.; Ejeian, F.; Azadi, S.; Myers, M.; Pejcic, B.; Abbassi, R.; Razmjou, A.; Asadnia, M. Recent progress in sensing nitrate, nitrite, phosphate, and ammonium in aquatic environment. Chemosphere 2020, 259, 127492. [Google Scholar] [CrossRef]
- Hassan, S.; Galal Eldin, A.; Amr, A.E.-G.; Al-Omar, M.; Kamel, A.; Khalifa, N.M. Improved Solid-Contact Nitrate Ion Selective Electrodes Based on Multi-Walled Carbon Nanotubes (MWCNTs) as an Ion-to-Electron Transducer. Sensors 2019, 19, 3891. [Google Scholar] [CrossRef]
- Moorcroft, M.J.; Davis, J.; Compton, R.G. Detection and determination of nitrate and nitrite: A review. Talanta 2001, 54, 785–803. [Google Scholar] [CrossRef]
- Yaqoob, M.; Biot, B.F.; Nabi, A.; Worsfold, P.J. Determination of nitrate and nitrite in freshwaters using flow-injection with luminol chemiluminescence detection. Luminescence 2012, 27, 419–425. [Google Scholar] [CrossRef]
- Johnson, K.S.; Petty, R.L. Determination of Nitrate and Nitrite in Seawater by Flow Injection Analysis. Limnol. Oceanogr. 1983, 28, 1260–1266. [Google Scholar] [CrossRef]
- Wang, S.; Lin, K.; Chen, N.; Yuan, D.; Ma, J. Automated determination of nitrate plus nitrite in aqueous samples with flow injection analysis using vanadium (III) chloride as reductant. Talanta 2016, 146, 744–748. [Google Scholar] [CrossRef] [PubMed]
- Luy, E.A.; Morgan, S.C.; Creelman, J.J.; Murphy, B.J.; Sieben, V.J. Inlaid microfluidic optics: Absorbance cells in clear devices applied to nitrite and phosphate detection. J. Micromech. Microeng. 2020, 30, 095001. [Google Scholar] [CrossRef]
- Petsul, P.; Greenway, G.; Haswell, S. The development of an on-chip micro-flow injection analysis of nitrate with a cadmium reductor. Anal. Chim. Acta 2001, 428, 155–161. [Google Scholar] [CrossRef]
- Miralles, V.; Huerre, A.; Malloggi, F.; Jullien, M.-C. A Review of Heating and Temperature Control in Microfluidic Systems: Techniques and Applications. Diagnostics 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Guijt, R.M.; Dodge, A.; van Dedem, G.W.K.; de Rooij, N.F.; Verpoorte, E. Chemical and physical processes for integrated temperature control in microfluidic devices. Lab Chip 2003, 3, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Issadore, D.; Humphry, K.J.; Brown, K.A.; Sandberg, L.; Weitz, D.A.; Westervelt, R.M. Microwave dielectric heating of drops in microfluidic devices. Lab Chip 2009, 9, 1701–1706. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Baker-Fales, M.; Vlachos, D.G. Operation and Optimization of Microwave-Heated Continuous-Flow Microfluidics. Ind. Eng. Chem. Res. 2020, 59, 10408–10417. [Google Scholar] [CrossRef]
- Spruit, R.G.; van Omme, J.T.; Ghatkesar, M.K.; Garza, H.H.P. A Review on Development and Optimization of Microheaters for High-Temperature in situ Studies. J. Microelectromech. Syst. 2017, 26, 1165–1182. [Google Scholar] [CrossRef]
- Hoang, V.N. Thermal Management Strategies for Microfluidic Devices. Masters Thesis, University of Alberta, Edminton, AB, Canada, 2008. [Google Scholar]
- Zhao, Y.; Veltkamp, H.-W.; Schut, T.V.P.; Sanders, R.G.P.; Breazu, B.; Groenesteijn, J.; de Boer, M.J.; Wiegerink, R.J.; Lötters, J.C. Heavily-Doped Bulk Silicon Sidewall Electrodes Embedded between Free-Hanging Microfluidic Channels by Modified Surface Channel Technology. Micromachines 2020, 11, 561. [Google Scholar] [CrossRef]
- Dijkstra, M.; de Boer, M.J.; Berenschot, J.W.; Lammerink, T.S.J.; Wiegerink, R.J.; Elwenspoek, M. Miniaturized thermal flow sensor with planar-integrated sensor structures on semicircular surface channels. Sens. Actuators Phys. 2008, 143, 1–6. [Google Scholar] [CrossRef]
- Schut, T.V.P.; Wiegerink, R.J.; Lotters, J.C. mu-Coriolis Mass Flow Sensor With Differential Capacitive Readout. IEEE Sens. J. 2021, 21, 5886–5894. [Google Scholar] [CrossRef]
- Ali, U.; Karim, K.J.B.A.; Buang, N.A. A Review of the Properties and Applications of Poly (Methyl Methacrylate) (PMMA). Polym. Rev. 2015, 55, 678–705. [Google Scholar] [CrossRef]
- Shin, J.Y.; Park, J.Y.; Liu, C.; He, J.; Kim, S.C. Chemical structure and physical properties of cyclic olefin copolymers (IUPAC Technical Report). Pure Appl. Chem. 2005, 77, 801–814. [Google Scholar] [CrossRef]
- He, Y.; Wu, Y.; Fu, J.; Gao, Q.; Qiu, J. Developments of 3D Printing Microfluidics and Applications in Chemistry and Biology: A Review. Electroanalysis 2016, 28, 1658–1678. [Google Scholar] [CrossRef]
- Rafiee, M.; Farahani, R.D.; Therriault, D. Multi-Material 3D and 4D Printing: A Survey. Adv. Sci. 2020, 7, 1902307. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Robledo, E.; Corzo, A.; Papaspyrou, S. A fast and direct spectrophotometric method for the sequential determination of nitrate and nitrite at low concentrations in small volumes. Mar. Chem. 2014, 162, 30–36. [Google Scholar] [CrossRef]
- Curran, A.; Klein, M.; Hepokoski, M.; Packard, C. Improving the accuracy of infrared measurements of skin temperature. Extreme Physiol. Med. 2015, 4, A140. [Google Scholar] [CrossRef][Green Version]
- Martinez-Quijada, J.; Caverhill-Godkewitsch, S.; Reynolds, M.; Sloan, D.; Backhouse, C.J.; Elliott, D.G.; Sameoto, D. Deterministic Design of Thin-Film Heaters for Precise Spatial Temperature Control in Lab-on-Chip Systems. J. Microelectromech. Syst. 2016, 25, 508–516. [Google Scholar] [CrossRef]
- He, X.; Wang, B.; Meng, J.; Zhang, S.; Wang, S. How to Prevent Bubbles in Microfluidic Channels. Langmuir 2021, 37, 2187–2194. [Google Scholar] [CrossRef]
- Hoang, V.N.; Kaigala, G.V.; Backhouse, C.J. Dynamic temperature measurement in microfluidic devices using thermochromic liquid crystals. Lab Chip 2008, 8, 484–487. [Google Scholar] [CrossRef]
- Saffari, P.; Basaligheh, A.; Sieben, V.J.; Moez, K. An RF-Powered Wireless Temperature Sensor for Harsh Environment Monitoring With Non-Intermittent Operation. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 65, 1529–1542. [Google Scholar] [CrossRef]
- Kaigala, G.V.; Hoang, V.N.; Stickel, A.; Lauzon, J.; Manage, D.; Pilarski, L.M.; Backhouse, C.J. An inexpensive and portable microchip-based platform for integrated RT–PCR and capillary electrophoresis. Analyst 2008, 133, 331–338. [Google Scholar] [CrossRef]
- Sieben, V.J.; Floquet, C.F.A.; Ogilvie, I.R.G.; Mowlem, M.C.; Morgan, H. Microfluidic colourimetric chemical analysis system: Application to nitrite detection. Anal. Methods 2010, 2, 484–491. [Google Scholar] [CrossRef]
- Shrivastava, A. Methods for the determination of limit of detection and limit of quantitation of the analytical methods. Chron. Young Sci. 2011, 2, 21–25. [Google Scholar] [CrossRef]

| Temperature (°C) | Simulation (mW) | Simulation with Thermocouple (mW) | Experiment (mW) | |||
|---|---|---|---|---|---|---|
| Standard | Insulated | Standard | Insulated | Standard | Insulated | |
| 35 | 290 | 117 | 350 | 177 | 325 | 199 |
| 45 | 490 | 200 | 596 | 301 | 596 | 357 |
| 55 | 695 | 283 | 838 | 428 | 898 | 524 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murphy, B.J.; Luy, E.A.; Panzica, K.L.; Johnson, G.; Sieben, V.J. An Energy Efficient Thermally Regulated Optical Spectroscopy Cell for Lab-on-Chip Devices: Applied to Nitrate Detection. Micromachines 2021, 12, 861. https://doi.org/10.3390/mi12080861
Murphy BJ, Luy EA, Panzica KL, Johnson G, Sieben VJ. An Energy Efficient Thermally Regulated Optical Spectroscopy Cell for Lab-on-Chip Devices: Applied to Nitrate Detection. Micromachines. 2021; 12(8):861. https://doi.org/10.3390/mi12080861
Chicago/Turabian StyleMurphy, Benjamin J., Edward A. Luy, Katerina L. Panzica, Gregory Johnson, and Vincent J. Sieben. 2021. "An Energy Efficient Thermally Regulated Optical Spectroscopy Cell for Lab-on-Chip Devices: Applied to Nitrate Detection" Micromachines 12, no. 8: 861. https://doi.org/10.3390/mi12080861
APA StyleMurphy, B. J., Luy, E. A., Panzica, K. L., Johnson, G., & Sieben, V. J. (2021). An Energy Efficient Thermally Regulated Optical Spectroscopy Cell for Lab-on-Chip Devices: Applied to Nitrate Detection. Micromachines, 12(8), 861. https://doi.org/10.3390/mi12080861






