A Three-Dimensional Micromixer Using Oblique Embedded Ridges
Abstract
:1. Introduction
2. Materials and Methods
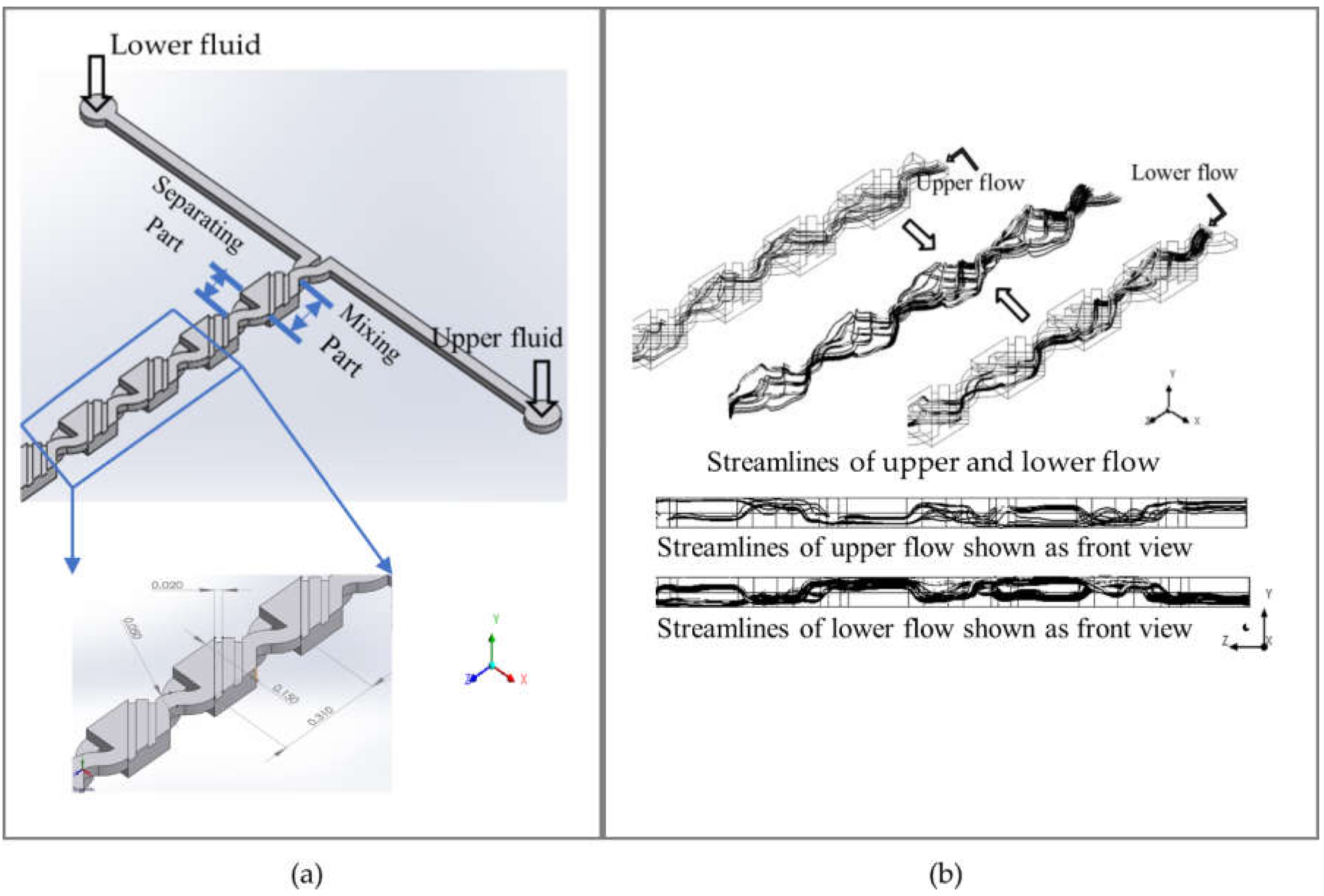
2.1. Micromixer Design
2.2. Numerical Modeling
2.3. Micromixer Fabrication and Experiment Setup
3. Results
3.1. Results and Discussion of Numerical Simulation
3.2. Experimental Results and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chia, M.C.; Sweeney, C.M.; Odom, T.W. Chemistry in microfluidic channels. J. Chem. Educ. 2015, 88, 461–464. [Google Scholar] [CrossRef]
- Abou-Hassan, A.; Sandre, O.; Cabuil, V. Microfluidics in inorganic chemistry. Angew. Chem. Int. Ed. 2010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, W.Y.; Wang, Y.; Wang, S.; Tseng, H.R. Integrated microfluidic reactors. Nano Today 2009, 4, 470–481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, H.; Xuan, W.; Li, D. Microfluidic whole-blood immunoassays. Microfluid. Nanofluid. 2011, 10, 941–964. [Google Scholar] [CrossRef]
- Goddard, J.M.; Erickson, D. Bioconjugation techniques for microfluidic biosensors. Anal. Bioanal. Chem. 2009, 394, 469–479. [Google Scholar] [CrossRef] [Green Version]
- Kastrup, C.J.; Runyon, M.K.; Lu Cc Hetta, E.M.; Price, J.M.; Ismagilov, R.F. Using chemistry and microfluidics to understand the spatial dynamics of complex biological networks. Acc. Chem. Res. 2008, 41, 549–558. [Google Scholar] [CrossRef] [Green Version]
- Yi, S.; Liu, Y.; Qu, W.; Jiang, X. Combining nanosurface chemistry and microfluidics for molecular analysis and cell biology. Anal. Chim. Acta 2009, 650, 98–105. [Google Scholar] [CrossRef]
- Dexter, J.P.; Parker, W. Parallel combinatorial chemical synthesis using single-layer poly(dimethylsiloxane) microfluidic devices. Biomicrofluidics 2009, 3, 034106. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Modrow, H.; Henry, L.L.; Cheng, K.S.; Kumar, C. Microfluidic synthesis of cobalt nanoparticles. Chem. Mater. 2006, 18, 2817–2827. [Google Scholar] [CrossRef]
- Schulte, T.H.; Bardell, R.L.; Weigl, B.H. Microfluidic technologies in clinical diagnostics. Clinica Chimica Acta 2002, 321, 1–10. [Google Scholar] [CrossRef]
- Dua, N.Z.; Colls, K.H.; Cheng, M.W.; Vaughn, L. Microfluidic-based diagnostics for cervical cancer cells. Biosens. Bioelectron. 2006, 21, 1991–1995. [Google Scholar] [CrossRef]
- Bessette, P.H.; Hu, X.; Soh, H.T.; Daugherty, P.S. Microfluidic library screening for mapping antibody epitopes. Anal. Chem. 2007, 79, 2174–2178. [Google Scholar] [CrossRef] [PubMed]
- Bange, A.; Halsall, H.B.; Heineman, W.R. Microfluidic immunosensor systems. Biosens. Bioelectron. 2005, 20, 2488–250320. [Google Scholar] [CrossRef] [PubMed]
- Movahed, S.; Li, D. Microfluidics cell electroporation. Microfluid. Nanofluid. 2011, 10, 703–734. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Chang, H.C.; Chan, P.; Friend, J.R. Microfluidic devices for bioapplications. Small 2011, 7, 12–48. [Google Scholar] [CrossRef]
- Kee, S.P.; Gavriilidis, A. Design and characterisation of the staggered herringbone mixer. Chem. Eng. J. 2008, 142, 109–121. [Google Scholar] [CrossRef]
- Wong, S.H.; Ward, M.C.L.; Wharton, C.W. Micro t-mixer as a rapid mixing micromixer. Sens. Actuators B Chem. 2004, 359–379. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesidesl, G.M. Chaotic Mixer for Microchannets. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Jiang, Z.; Chung, B.; Dutta, P. A rapid magnetic particle driven micromixer. Microfluid. Nanofluid. 2008, 4, 375–389. [Google Scholar] [CrossRef]
- Himstedt, H.H.; Yang, Q.; Dasi, P.; Qian, X.; Wickramasinghe, R.; Ulbricht, M. Magnetically activated micromixers for separation membranes. Langmuir 2011, 27, 5574–5581. [Google Scholar] [CrossRef]
- Jannig, O.; Nguyen, N.T. A polymeric high-throughput pressure-driven micromixer using a nanoporous membrane. Microfluid. Nanofluid. 2011, 10, 513–519. [Google Scholar] [CrossRef] [Green Version]
- Mouheb, N.A.; Montillet, A.; Solliec, C.; Havlica, J.; Legentilhomme, P.; Comiti, J.; Tihon, J. Flow characterization in t-shaped and cross-shaped micromixers. Microfluid. Nanofluid. 2011, 10, 1185–1197. [Google Scholar] [CrossRef]
- Zhang, C.; Da, X.; Li, Y. Micropumps, microvalves, and micromixers within pcr microfluidic chips: Advances and trends. Biotechnol. Adv. 2007, 25, 483–514. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Kang, H.J.; Choi, B. A study on the novel micromixer with chaotic flows. Microsyst. Technol. 2009, 15, 269–277. [Google Scholar] [CrossRef]
- Fan, Y.; Hassan, I. Numerical Investigation and Geometric Parameterization of Lamination Inlet of Passive Micromixer. In Proceedings of the ASME 2010 8th International Conference on Nanochannels, Microchannels, and Minichannels, Montreal, QC, Canada, 1–5 August 2010; ASME: New York, NY, USA, 2010; Volume 54501, pp. 1213–1219. [Google Scholar]
- De Moura, A.P.S.; Grebogi, C. Three-dimensional effects in active chaotic flows. AIP Conf. Proc. 2004, 742, 161–164. [Google Scholar]
- Chung, C.K.; Shih, T.R.; Wu, B.H.; Chang, C.K. Design and mixing efficiency of rhombic micromixer with flat angles. Microsyst. Technol. 2010, 16, 1595–1600. [Google Scholar] [CrossRef]
- Tsai, R.T.; Wu, C.Y. An efficient micromixer based on multidirectional vortices due to baffles and channel curvature. Biomicrofluidics 2011, 5, 014103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, J.M.; Seo, K.D.; Kwon, T.H. A chaotic micromixer using obstruction-pairs. J. Micromech. Microeng. 2010, 20, 15023. [Google Scholar] [CrossRef]
- Sayah, A.; Thivolle, P.; Parashar, V.K.; Gijs, M. Three-dimensional mixers with non-planar microchannels in a monolithic glass substrate using oblique powder blasting. J. Micromech. Microeng. 2010, 20, 85028–85035. [Google Scholar] [CrossRef]
- Kang, T.G.; Singh, M.K.; Anderson, P.D.; Han, E. A chaotic serpentine mixer efficient in the creeping flow regime: From design concept to optimization. Microfluid. Nanofluid. 2009, 7, 783–794. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.; Kim, M.C.; Park, J.S.; Lee, N.E. An effective passive microfluidic mixer utilizing chaotic advection. Sens. Actuators B Chem. 2008, 132, 172–181. [Google Scholar] [CrossRef]
- Yang, J.T.; Huang, K.J.; Tung, K.Y.; Hu, I.C.; Lyu, P.C. A chaotic micromixer modulated by constructive vortex agitation. J. Micromech. Microeng. 2007, 17, 2084–2092. [Google Scholar] [CrossRef]
- Hao, C.; Meiners, J.C. Topologic mixing on a microfluidic chip. Appl. Phys. Lett. 2004, 84, 2193–2195. [Google Scholar] [CrossRef]
- Wang, L.; Yang, J.T. An overlapping crisscross micromixer using chaotic mixing principles. J. Micromech. Microeng. 2006, 16, 2684–2691. [Google Scholar] [CrossRef]
- Adeosun, J.T.; Lawal, A. Mass transfer enhancement in microchannel reactors by reorientation of fluid interfaces and stretching. Sens. Actuators B 2005, 110, 101–111. [Google Scholar] [CrossRef]
- Xia, H.M.; Wan, S.Y.; Shu, C.; Chew, Y.T. Chaotic micromixers using two-layer crossing channels to exhibit fast mixing at low Reynolds numbers. Lab Chip 2005, 5, 748–755. [Google Scholar] [CrossRef]
- Jing, W.; Zhao, W.; Liu, S.; Li, L.; Tsai, C.T.; Fan, X.; Wu, W.; Li, J.; Yang, X.; Sui, G. Microfluidic device for efficient airborne bacteria capture and enrichment. Anal. Chem. 2013, 85, 5255–5562. [Google Scholar] [CrossRef]







| Normal Fluid | Hard-to-Mix Fluid |
|---|---|
| Re | |
| 0.007 | 0.0007 |
| 0.07 | 0.007 |
| 0.7 | 0.07 |
| 4.7 | 0.7 |
| 6.7 | |
| 13.3 | |
| 66.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Chen, Q.; Sui, G.; Qian, J.; Tsai, C.-T.; Cheng, X.; Jing, W. A Three-Dimensional Micromixer Using Oblique Embedded Ridges. Micromachines 2021, 12, 806. https://doi.org/10.3390/mi12070806
Li L, Chen Q, Sui G, Qian J, Tsai C-T, Cheng X, Jing W. A Three-Dimensional Micromixer Using Oblique Embedded Ridges. Micromachines. 2021; 12(7):806. https://doi.org/10.3390/mi12070806
Chicago/Turabian StyleLi, Lin, Qingde Chen, Guodong Sui, Jing Qian, Chi-Tay Tsai, Xunjia Cheng, and Wenwen Jing. 2021. "A Three-Dimensional Micromixer Using Oblique Embedded Ridges" Micromachines 12, no. 7: 806. https://doi.org/10.3390/mi12070806
APA StyleLi, L., Chen, Q., Sui, G., Qian, J., Tsai, C.-T., Cheng, X., & Jing, W. (2021). A Three-Dimensional Micromixer Using Oblique Embedded Ridges. Micromachines, 12(7), 806. https://doi.org/10.3390/mi12070806






