Heterogeneously-Integrated Optical Phase Shifters for Next-Generation Modulators and Switches on a Silicon Photonics Platform: A Review
Abstract
1. Introduction
2. Optical Phase Shifters
2.1. Optical Modulators
2.2. Optical Switches
3. Discussion
3.1. Optical Modulators
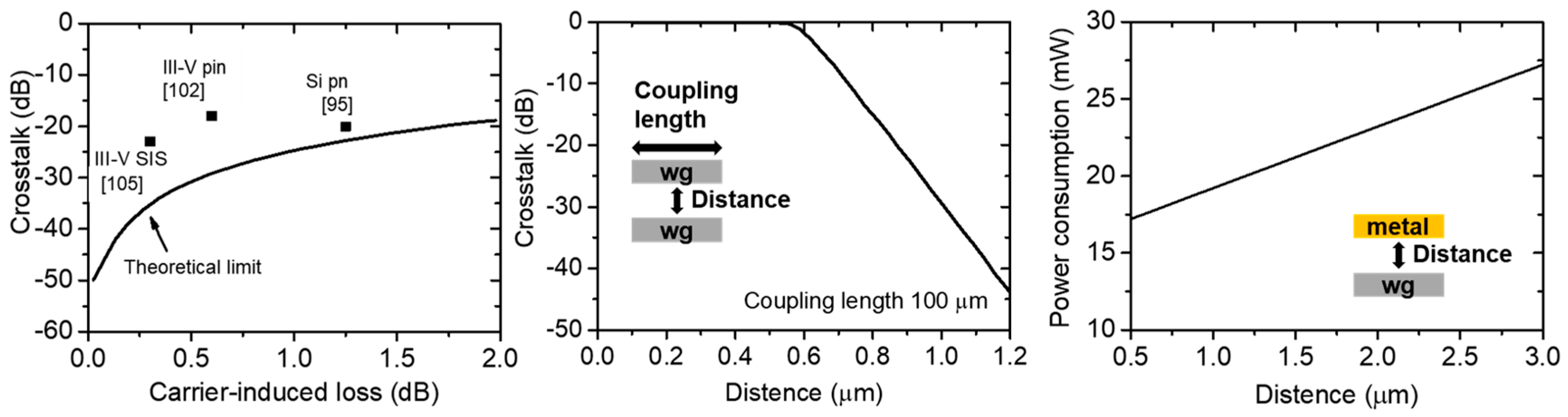
3.2. Optical Switches
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- BEREC. Reports on the Status of Internet Capacity during Coronavirus Confinement Measures. Available online: https://ec.europa.eu/digital-single-market/en/news/reports-status-internet-capacity-during-coronavirus-confinement-measures (accessed on 27 April 2021).
- E Hochberg, M.; Baehr-Jones, T. Towards fabless silicon photonics. Nat. Photonics 2010, 4, 492–494. [Google Scholar] [CrossRef]
- Van Campenhout, J.; Ban, Y.; De Heyn, P.; Srinivasan, A.; De Coster, J.; Lardenois, S.; Snyder, B.; Balakrishnan, S.; Lepage, G.; Golshani, N.; et al. Silicon Photonics for 56G NRZ Optical Interconnects. In Proceedings of the Optical Fiber Communication Conference Postdeadline Papers, San Diego, CA, USA, 11–15 March 2018. [Google Scholar]
- Wang, J.; Long, Y. On-chip silicon photonic signaling and processing: A review. Sci. Bull. 2018, 63, 1267–1310. [Google Scholar] [CrossRef]
- Boeuf, F.; Cremer, S.; Temporiti, E.; Fere, M.; Shaw, M.; Baudot, C.; Vulliet, N.; Pinguet, T.; Mekis, A.; Masini, G.; et al. Silicon Photonics R&D and Manufacturing on 300-mm Wafer Platform. J. Light. Technol. 2016, 34, 286–295. [Google Scholar] [CrossRef]
- Thomson, D.; Zilkie, A.; E Bowers, J.; Komljenovic, T.; Reed, G.T.; Vivien, L.; Marris-Morini, D.; Cassan, E.; Virot, L.; Fédéli, J.-M.; et al. Roadmap on silicon photonics. J. Opt. 2016, 18, 073003. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Yamada, K.; Tsuchizawa, T.; Nishi, H.; Kou, R.; Hiraki, T.; Takeda, K.; Fukuda, H.; Ishikawa, Y.; Wada, K.; Yamamoto, T. High-performance silicon photonics technology for telecommunications applications. Sci. Technol. Adv. Mater. 2014, 15, 24603. [Google Scholar] [CrossRef]
- Heck, M.J.R. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, L.; Zhang, Q.; Zhang, W. Si Photonics for Practical LiDAR Solutions. Appl. Sci. 2019, 9, 4225. [Google Scholar] [CrossRef]
- Vandoorne, K.; Mechet, P.; Van Vaerenbergh, T.; Fiers, M.; Morthier, G.; Verstraeten, D.; Schrauwen, B.; Dambre, J.; Bienstman, P. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun. 2014, 5, 3541. [Google Scholar] [CrossRef] [PubMed]
- Tait, A.N.; Nahmias, M.A.; Shastri, B.; Prucnal, P.R. Broadcast and Weight: An Integrated Network For Scalable Photonic Spike Processing. J. Light. Technol. 2014, 32, 4029–4041. [Google Scholar] [CrossRef]
- Tait, A.N.; De Lima, T.F.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Cheng, Q.; Kwon, J.; Glick, M.; Bahadori, M.; Carloni, L.P.; Bergman, K. Silicon Photonics Codesign for Deep Learning; IEEE: Piscataway, NJ, USA, 2020; Volume 108, pp. 1261–1282. [Google Scholar]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; LaRochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Soref, R.; Bennett, B. Electrooptical effects in silicon. IEEE J. Quantum Electron. 1987, 23, 123–129. [Google Scholar] [CrossRef]
- Nedeljkovic, M.; A Soref, R.; Mashanovich, G.Z. Free-Carrier Electrorefraction and Electroabsorption Modulation Predictions for Silicon Over the 1–14-μm Infrared Wavelength Range. IEEE Photonics J. 2011, 3, 1171–1180. [Google Scholar] [CrossRef]
- Akiyama, S.; Tatsuya, U. High-Speed and Efficient Silicon Modulator Based on Forward-Biased Pin Diodes. Front. Phys. 2014, 2, 1–7. [Google Scholar] [CrossRef]
- Liu, A.; Liao, L.; Rubin, D.; Nguyen, H.; Ciftcioglu, B.; Chetrit, Y.; Izhaky, N.; Paniccia, M. High-speed optical modulation based on carrier depletion in a silicon waveguide. Opt. Express 2007, 15, 660–668. [Google Scholar] [CrossRef]
- Tu, X.; Liow, T.-Y.; Song, J.; Luo, X.; Fang, Q.; Yu, M.; Lo, G.-Q. 50-Gb/s silicon optical modulator with traveling-wave electrodes. Opt. Express 2013, 21, 12776–12782. [Google Scholar] [CrossRef] [PubMed]
- Dong, P.; Liao, S.; Feng, D.; Liang, H.; Zheng, D.; Shafiiha, R.; Kung, C.-C.; Qian, W.; Li, G.; Zheng, X.; et al. Low V_pp, ultralow-energy, compact, high-speed silicon electro-optic modulator. Opt. Express 2009, 17, 22484–22490. [Google Scholar] [CrossRef] [PubMed]
- Thomson, D.J.; Gardes, F.Y.; Fedeli, J.-M.; Zlatanovic, S.; Hu, Y.; Kuo, B.P.P.; Myslivets, E.; Alic, N.; Radic, S.; Mashanovich, G.Z.; et al. 50-Gb/s Silicon Optical Modulator. IEEE Photonics Technol. Lett. 2012, 24, 234–236. [Google Scholar] [CrossRef]
- Dong, P.; Chen, L.; Chen, Y.-K. High-speed low-voltage single-drive push-pull silicon Mach-Zehnder modulators. Opt. Express 2012, 20, 6163–6169. [Google Scholar] [CrossRef]
- Reed, G.T.; Mashanovich, G.Z.; Gardes, F.Y.; Nedeljkovic, M.; Hu, Y.; Thomson, D.J.; Li, K.; Wilson, P.R.; Chen, S.-W.; Hsu, S.S. Recent breakthroughs in carrier depletion based silicon optical modulators. Nanophotonics 2014, 3, 229–245. [Google Scholar] [CrossRef]
- Liu, A.; Jones, R.N.; Liao, L.; Samara-Rubio, D.; Rubin, D.; Cohen, O.; Nicolaescu, R.; Paniccia, M.J. A high-speed silicon optical modulator based on a metal–oxide–semiconductor capacitor. Nat. Cell Biol. 2004, 427, 615–618. [Google Scholar] [CrossRef]
- Liao, L.; Samara-Rubio, D.; Morse, M.; Liu, A.; Hodge, D.; Rubin, D.; Keil, U.D.; Franck, T. High speed silicon Mach-Zehnder modulator. Opt. Express 2005, 13, 3129–3135. [Google Scholar] [CrossRef]
- Fujikata, J.; Takahashi, M.; Takahashi, S.; Horikawa, T.; Nakamura, T. High-speed and high-efficiency Si optical modulator with MOS junction, using solid-phase crystallization of polycrystalline silicon. Jpn. J. Appl. Phys. 2016, 55, 042202. [Google Scholar] [CrossRef]
- Xiong, C.; Gill, D.M.; Proesel, J.E.; Orcutt, J.S.; Haensch, W.; Green, W.M.J. Monolithic 56 Gb/s silicon photonic pulse-amplitude modulation transmitter. Optica 2016, 3, 1060–1065. [Google Scholar] [CrossRef]
- Dong, P.; Liu, X.; Chandrasekhar, S.; Buhl, L.L.; Aroca, R.; Chen, Y.-K. Monolithic Silicon Photonic Integrated Circuits for Compact 100 +Gb/s Coherent Optical Receivers and Transmitters. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 150–157. [Google Scholar] [CrossRef]
- Ding, R.; Liu, Y.; Li, Q.; Yang, Y.; Ma, Y.; Padmaraju, K.; Lim, A.E.-J.; Lo, G.-Q.; Bergman, K.; Baehr-Jones, T.; et al. Design and characterization of a 30-GHz bandwidth low-power silicon traveling-wave modulator. Opt. Commun. 2014, 321, 124–133. [Google Scholar] [CrossRef]
- Streshinsky, M.; Ding, R.; Liu, Y.; Novack, A.; Yang, Y.; Ma, Y.; Tu, X.; Chee, E.K.S.; Lim, A.E.-J.; Lo, P.G.-Q.; et al. Low power 50 Gb/s silicon traveling wave Mach-Zehnder modulator near 1300 nm. Opt. Express 2013, 21, 30350–30357. [Google Scholar] [CrossRef]
- Ogawa, K.; Ishihara, H.; Goi, K.; Mashiko, Y.; Lim, S.T.; Sun, M.J.; Seah, S.; Png, C.E.; Liow, T.-Y.; Tu, X.; et al. Fundamental characteristics and high-speed applications of carrier-depletion silicon Mach-Zehnder modulators. IEICE Electron. Express 2014, 11, 20142010. [Google Scholar] [CrossRef]
- Ding, R.; Liu, Y.; Ma, Y.; Yang, Y.; Li, Q.; Lim, A.E.-J.; Lo, G.-Q.; Bergman, K.; Baehr-Jones, T.; Hochberg, M. High-Speed Silicon Modulator With Slow-Wave Electrodes and Fully Independent Differential Drive. J. Light. Technol. 2014, 32, 2240–2247. [Google Scholar] [CrossRef]
- Younghyun, K.; Taewon, J.; Youngjoo, B. A comparative simulation study on lateral and L shape pn-junction phase shifters for single-drive 50 Gbps lumped Mach-Zehnder modulators. Jpn. J. Appl. Phys. 2021, 60, 052002. [Google Scholar]
- Manipatruni, S.; Preston, K.; Chen, L.; Lipson, M. Ultra-low voltage, ultra-small mode volume silicon microring modulator. Opt. Express 2010, 18, 18235–18242. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Chang, E.; Amberg, P.; Shubin, I.; Lexau, J.; Liu, F.; Thacker, H.; Djordjevic, S.S.; Lin, S.; Luo, Y.; et al. A high-speed, tunable silicon photonic ring modulator integrated with ultra-efficient active wavelength control. Opt. Express 2014, 22, 12628–12633. [Google Scholar] [CrossRef]
- Xiao, X.; Li, X.; Xu, H.; Hu, Y.; Xiong, K.; Li, Z.; Chu, T.; Yu, J.; Yu, Y. 44-Gb/s Silicon Microring Modulators Based on Zigzag PN Junctions. IEEE Photonics Technol. Lett. 2012, 24, 1712–1714. [Google Scholar] [CrossRef]
- Kim, Y.; Jo, Y.; Kim, M.; Yu, B.-M.; Mai, C.; Lischke, S.; Zimmermann, L.; Choi, W.-Y.; Lars, Z. Parametric optimization of depletion-type Si micro-ring modulator performances. Jpn. J. Appl. Phys. 2019, 58, 062006. [Google Scholar] [CrossRef]
- Terada, Y.; Kondo, K.; Abe, R.; Baba, T. Full C-band Si photonic crystal waveguide modulator. Opt. Lett. 2017, 42, 5110–5112. [Google Scholar] [CrossRef]
- Hinakura, Y.; Akiyama, D.; Ito, H.; Baba, T. Silicon Photonic Crystal Modulators for High-Speed Transmission and Wavelength Division Multiplexing. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–8. [Google Scholar] [CrossRef]
- Melikyan, A.; Alloatti, L.; Muslija, A.; Hillerkuss, D.; Schindler, P.C.; Li, J.; A Palmer, R.; Korn, D.; Muehlbrandt, S.; Van Thourhout, D.; et al. High-speed plasmonic phase modulators. Nat. Photonics 2014, 8, 229–233. [Google Scholar] [CrossRef]
- Reed, G.T.; Mashanovich, G.; Gardes, F.Y.; Thomson, D.J. Silicon optical modulators. Nat. Photonics 2010, 4, 518–526. [Google Scholar] [CrossRef]
- Komma, J.; E Schwarz, C.; O Hofmann, G.; Heinert, D.; Nawrodt, R. Thermo-optic coefficient of silicon at 1550 nm and cryogenic temperatures. Appl. Phys. Lett. 2012, 101, 041905. [Google Scholar] [CrossRef]
- Errando-Herranz, C.; Takabayashi, A.Y.; Edinger, P.; Sattari, H.; Gylfason, K.B.; Quack, N. MEMS for Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–16. [Google Scholar] [CrossRef]
- Cheng, Q.; Bahadori, M.; Glick, M.; Rumley, S.; Bergman, K. Recent advances in optical technologies for data centers: A review. Optica 2018, 5, 1354–1370. [Google Scholar] [CrossRef]
- Quack, N.; Sattari, H.; Takabayashi, A.Y.; Zhang, Y.; Verheyen, P.; Bogaerts, W.; Edinger, P.; Errando-Herranz, C.; Gylfason, K.B. MEMS-Enabled Silicon Photonic Integrated Devices and Circuits. IEEE J. Quantum Electron. 2019, 56, 1–10. [Google Scholar] [CrossRef]
- Zhang, Z.; You, Z.; Chu, D. Fundamentals of phase-only liquid crystal on silicon (LCOS) devices. Light. Sci. Appl. 2014, 3, e213. [Google Scholar] [CrossRef]
- Soref, R. Tutorial: Integrated-photonic switching structures. APL Photonics 2018, 3, 021101. [Google Scholar] [CrossRef]
- Yong, Z.; Sacher, W.D.; Huang, Y.; Mikkelsen, J.C.; Yang, Y.; Luo, X.; Dumais, P.; Goodwill, D.; Bahrami, H.; Lo, P.G.-Q.; et al. U-shaped PN junctions for efficient silicon Mach-Zehnder and microring modulators in the O-band. Opt. Express 2017, 25, 8425–8439. [Google Scholar] [CrossRef]
- Azadeh, S.S.; Merget, F.; Romero-García, S.; Moscoso-Mártir, A.; von den Driesch, N.; Müller, J.; Mantl, S.; Buca, D.; Witzens, J. Low Vπ Silicon photonics modulators with highly linear epitaxially grown phase shifters. Opt. Express 2015, 23, 23526–23550. [Google Scholar] [CrossRef] [PubMed]
- Walton, A.K.; Metcalfe, S.F. Free-carrier absorption at low temperatures in uniaxially stressed n-type Ge, Si and GaAs. J. Phys. C Solid State Phys. 1976, 9, 3605–3625. [Google Scholar] [CrossRef]
- Belyaev, A.; Gorodnichii, O.; Pidlisny, E.; Demidenko, Z.; Tomchuk, P. Free carrier absorption in uniaxially stressed n-Si. Solid State Commun. 1982, 42, 441–445. [Google Scholar] [CrossRef]
- Kim, Y.; Takenaka, M.; Osada, T.; Hata, M.; Takagi, S. Strain-induced enhancement of plasma dispersion effect and free-carrier absorption in SiGe optical modulators. Sci. Rep. 2014, 4, 1–6. [Google Scholar] [CrossRef]
- Takenaka, M.; Takagi, S. Strain Engineering of Plasma Dispersion Effect for SiGe Optical Modulators. IEEE J. Quantum Electron. 2011, 48, 8–16. [Google Scholar] [CrossRef]
- Kim, Y.; Fujikata, J.; Takahashi, S.; Takenaka, M.; Takagi, S. Demonstration of record-low injection-current variable optical attenuator based on strained SiGe with optimized lateral pin junction. Opt. Express 2015, 23, 12354–12361. [Google Scholar] [CrossRef]
- Kim, Y.; Takenaka, M.; Takagi, S. Numerical Analysis of Carrier-Depletion Strained SiGe Optical Modulators with Vertical p-n Junction. IEEE J. Quantum Electron. 2015, 51, 1–7. [Google Scholar] [CrossRef]
- Fujikata, J.; Noguchi, M.; Kim, Y.; Han, J.; Takahashi, S.; Nakamura, T.; Takenaka, M. High-speed and highly efficient Si optical modulator with strained SiGe layer. Appl. Phys. Express 2018, 11, 32201. [Google Scholar] [CrossRef]
- Douix, M.; Perez-Galacho, I.D.; Charlet, C.; Baudot, P.; Acosta-Alba, S.; Kerdiles, C.; Euvrard, P.; Grosse, J.; Planchot, R.; Blanc, R.; et al. Sige-Enhanced Si Capacitive Modulator Integration in a 300 Mm Silicon Photonics Platform for Low Power Consumption. Opt. Express 2019, 27, 17701–17707. [Google Scholar]
- Charlet, I.; Desieres, Y.; Marris-Morini, D.; Boeuf, F. Capacitive Modulator Design Optimization Using Si and Strained-SiGe for Datacom Applications. IEEE J. Sel. Top. Quant. Electron. 2021, 27, 3400508. [Google Scholar] [CrossRef]
- Bennett, B.; Soref, R.A.; Del Alamo, J.A. Carrier-induced change in refractive index of InP, GaAs and InGaAsP. IEEE J. Quantum Electron. 1990, 26, 113–122. [Google Scholar] [CrossRef]
- Han, J.-H.; Boeuf, F.; Fujikata, J.; Takahashi, S.; Takagi, S.; Takenaka, M. Efficient low-loss InGaAsP/Si hybrid MOS optical modulator. Nat. Photonics 2017, 11, 486–490. [Google Scholar] [CrossRef]
- Hiraki, T.; Aihara, T.; Hasebe, K.; Takeda, K.; Fujii, T.; Kakitsuka, T.; Tsuchizawa, T.; Fukuda, H.; Matsuo, S. Heterogeneously Integrated Iii-V/Si Mos Capacitor Mach-Zehnder Modulator. Nat. Photonics 2017, 11, 482–486. [Google Scholar] [CrossRef]
- Hiraki, T.; Aihara, T.; Hasebe, K.; Takeda, K.; Fujii, T.; Kakitsuka, T.; Tsuchizawa, T.; Fukuda, H.; Matsuo, S. Integration of a High-Efficiency Mach-Zehnder Modulator with a Dfb Laser Using Membrane Inp-Based Devices on a Si Photonics Platform. Opt. Express 2021, 29, 2431–2441. [Google Scholar] [CrossRef] [PubMed]
- Thiessen, T.; Grosse, P.; Da Fonseca, J.; Billondeau, P.; Szelag, B.; Jany, C.; Poon, J.k.S.; Menezo, S. 30 GHz heterogeneously integrated capacitive InP-on-Si Mach–Zehnder modulators. Opt. Express 2019, 27, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Tian, B.; Pantouvaki, M.; Guo, W.; Absil, P.; Van Campenhout, J.; Merckling, C.; Van Thourhout, D. Room-temperature InP distributed feedback laser array directly grown on silicon. Nat. Photonics 2015, 9, 837–842. [Google Scholar] [CrossRef]
- Waldron, N.; Merckling, C.; Teugels, L.; Ong, P.; Ibrahim, S.A.U.; Sebaai, F.; Pourghaderi, A.; Barla, K.; Collaert, N.; Thean, A.V.-Y. InGaAs Gate-All-Around Nanowire Devices on 300mm Si Substrates. IEEE Electron Device Lett. 2014, 35, 1097–1099. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, S.; Ban, Y.; Lardenois, S.; Yudistira, D.; Pantouvaki, M.; Van Campenhout, J. Proposal and Simulation of a Low Loss, Highly Efficient Monolithic III-V/Si Optical Phase Shifter. In Proceedings of the 2019 IEEE 16th International Conference on Group IV Photonics (GFP), Singapore, 28–30 August 2019; pp. 1–2. [Google Scholar]
- Kim, S.; Kim, Y.; Ban, Y.; Pantouvaki, M.; Van Campenhout, J. Simulation Study of a Monolithic III-V/Si V-Groove Carrier Depletion Optical Phase Shifter. IEEE J. Quantum Electron. 2020, 56, 1–8. [Google Scholar] [CrossRef]
- Wooten, E.; Kissa, K.; Yi-Yan, A.; Murphy, E.; Lafaw, D.; Hallemeier, P.; Maack, D.; Attanasio, D.; Fritz, D.; McBrien, G.; et al. A review of lithium niobate modulators for fiber-optic communications systems. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 69–82. [Google Scholar] [CrossRef]
- Poberaj, G.; Hu, H.; Sohler, W.; Gunter, P. Lithium niobate on insulator (LNOI) for micro-photonic devices. Laser Photonics Rev. 2012, 6, 488–503. [Google Scholar] [CrossRef]
- Krasnokutska, I.; Tambasco, J.-L.; Li, X.; Peruzzo, A. Ultra-low loss photonic circuits in lithium niobate on insulator. Opt. Express 2018, 26, 897–904. [Google Scholar] [CrossRef]
- Takigawa, R.; Asano, T. Thin-film lithium niobate-on-insulator waveguides fabricated on silicon wafer by room-temperature bonding method with silicon nanoadhesive layer. Opt. Express 2018, 26, 24413–24421. [Google Scholar] [CrossRef]
- He, M.; Xu, M.; Ren, Y.; Jian, J.; Ruan, Z.; Xu, Y.; Gao, S.; Sun, S.; Wen, X.; Zhou, L.; et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
- Abel, S.; Eltes, F.; Ortmann, J.E.; Messner, A.; Castera, P.; Wagner, T.; Urbonas, D.; Rosa, A.; Gutierrez, A.M.; Tulli, D.; et al. Large Pockels effect in micro- and nanostructured barium titanate integrated on silicon. Nat. Mater. 2019, 18, 42–47. [Google Scholar] [CrossRef]
- Eltes, F.; Mai, C.; Caimi, D.; Kroh, M.; Popoff, Y.; Winzer, G.; Petousi, D.; Lischke, S.; Ortmann, J.E.; Czornomaz, L.; et al. A BaTiO3-Based Electro-Optic Pockels Modulator Monolithically Integrated on an Advanced Silicon Photonics Platform. J. Light. Technol. 2019, 37, 1456–1462. [Google Scholar] [CrossRef]
- Eltes, F.; Villarreal-Garcia, G.E.; Caimi, D.; Siegwart, H.; Gentile, A.A.; Hart, A.; Stark, P.; Marshall, G.D.; Thompson, M.G.; Barreto, J.; et al. An integrated optical modulator operating at cryogenic temperatures. Nat. Mater. 2020, 19, 1164–1168. [Google Scholar] [CrossRef] [PubMed]
- Messner, A.; Eltes, F.; Ma, P.; Abel, S.; Baeuerle, B.; Josten, A.; Heni, W.; Caimi, D.; Fompeyrine, J.; Leuthold, J. Plasmonic Ferroelectric Modulators. J. Light. Technol. 2018, 37, 281–290. [Google Scholar] [CrossRef]
- Cheng, Q.; Rumley, S.; Bahadori, M.; Bergman, K. Photonic switching in high performance datacenters [Invited]. Opt. Express 2018, 26, 16022–16043. [Google Scholar] [CrossRef]
- Tu, X.; Song, C.; Huang, T.; Chen, Z.; Fu, H. State of the Art and Perspectives on Silicon Photonic Switches. Micromachines 2019, 10, 51. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, K.; Suzuki, K.; Konoike, R.; Namiki, S.; Kawashima, H. Large-scale silicon photonics switch based on 45-nm CMOS technology. Opt. Commun. 2020, 466, 125677. [Google Scholar] [CrossRef]
- Tanizawa, K.; Suzuki, K.; Toyama, M.; Ohtsuka, M.; Yokoyama, N.; Matsumaro, K.; Seki, M.; Koshino, K.; Sugaya, T.; Suda, S.; et al. Ultra-compact 32 × 32 strictly-non-blocking Si-wire optical switch with fan-out LGA interposer. Opt. Express 2015, 23, 17599–17606. [Google Scholar] [CrossRef]
- Suzuki, K.; Konoike, R.; Hasegawa, J.; Suda, S.; Matsuura, H.; Ikeda, K.; Namiki, S.; Kawashima, H. Low-Insertion-Loss and Power-Efficient 32 × 32 Silicon Photonics Switch With Extremely High-Δ Silica PLC Connector. J. Lightwave Technol. 2019, 37, 116–122. [Google Scholar] [CrossRef]
- Dumais, P.; Goodwill, D.J.; Celo, D.; Jiang, J.; Zhang, C.; Zhao, F.; Tu, X.; Yan, S.; He, J.; Li, M.; et al. Silicon Photonic Switch Subsystem With 900 Monolithically Integrated Calibration Photodiodes and 64-Fiber Package. J. Lightwave Technol. 2017, 36, 233–238. [Google Scholar] [CrossRef]
- Nikolova, D.; Calhoun, D.M.; Liu, Y.; Rumley, S.; Novack, A.; Baehr-Jones, T.; Hochberg, M.; Bergman, K. Modular architecture for fully non-blocking silicon photonic switch fabric. Microsys. Nanoeng. 2017, 3, 16071. [Google Scholar] [CrossRef]
- Seok, T.J.; Quack, N.; Han, S.; Muller, R.S.; Wu, M.C. Large-scale broadband digital silicon photonic switches with vertical adiabatic couplers. Optica 2016, 3, 64–70. [Google Scholar] [CrossRef]
- Han, S.; Seok, T.J.; Yu, K.; Quack, N.; Muller, R.S.; Wu, M.C. Large-Scale Polarization-Insensitive Silicon Photonic MEMS Switches. J. Light. Technol. 2018, 36, 1824–1830. [Google Scholar] [CrossRef]
- Seok, T.J.; Kwon, K.; Henriksson, J.; Luo, J.; Wu, M.C. 240 × 240 wafer-scale silicon photonic switches. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 3–7 March 2019; pp. 1–5. [Google Scholar]
- Han, S.; Beguelin, J.; Ochikubo, L.; Jacobs, J.; Seok, T.J.; Yu, K.; Quack, N.; Kim, C.-K.; Muller, R.S.; Wu, M.C. 32 × 32 silicon photonic MEMS switch with gap-adjustable directional couplers fabricated in commercial CMOS foundry. J. Opt. Microsyst. 2021, 1, 024003. [Google Scholar] [CrossRef]
- Wu, M.C.; Seok, T.J.; Kwon, K.; Henriksson, J.; Luo, J. Large Scale Silicon Photonics Switches Based on MEMS Technology. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Jacques, M.; Samani, A.; El-Fiky, E.; Patel, D.; Xing, Z.; Plant, D.V. Optimization of thermo-optic phase-shifter design and mitigation of thermal crosstalk on the SOI platform. Opt. Express 2019, 27, 10456–10471. [Google Scholar] [CrossRef]
- Kang, J.; Nishiyama, N.; Atsumi, Y.; Amemiya, T.; Arai, S. Multi-stacked silicon wire waveguides and couplers toward 3D optical interconnects. In Proceedings of the SPIE. Photonics west: Optoelectronic Interconnects XIII, San Francisco, CA, USA, 3–6 February 2013. [Google Scholar]
- Han, S. Highly Scalable Silicon Photonic Switches Based on Waveguide Crossbar with Movable Waveguide Couplers. Ph.D. Thesis, UC Berkeley, Berkeley, CA, USA, 2016. [Google Scholar]
- Lee, B.G.; Rylyakov, A.V.; Green, W.M.J.; Assefa, S.; Baks, C.W.; Rimolo-Donadio, R.; Kuchta, D.M.; Khater, M.H.; Barwicz, T.; Reinholm, C.; et al. Monolithic Silicon Integration of Scaled Photonic Switch Fabrics, CMOS Logic, and Device Driver Circuits. J. Light. Technol. 2014, 32, 743–751. [Google Scholar] [CrossRef]
- Jiang, J.; Goodwill, D.J.; Dumais, P.; Celo, D.; Zhang, C.; Mehrvar, H.; Rad, M.; Bernier, E.; Li, M.; Zhao, F.; et al. 16 × 16 silicon photonic switch with nanosecond switch time and low-crosstalk architecture. In Proceedings of the European Conference on Optical Communications (ECOC 2019), Dublin, Ireland, 22–26 September 2019; p. M.2.A.4. [Google Scholar]
- Zanzi, A.; Vagionas, C.; Griol, A.; Rosa, A.; Lechago, S.; Moralis-Pegios, M.; Vyrsokinos, K.; Pleros, N.; Kraft, J.; Sidorov, V.; et al. Alignment tolerant, low voltage, 0.23 Vcm, push-pull silicon photonic switches based on a vertical pn junction. Opt. Express 2019, 27, 32409–32426. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Wonfor, A.; Wei, J.L.; Penty, R.V.; White, I.H. Low-Energy, High-Performance Lossless 8 × 8 SOA Switch. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22–26 March 2015; pp. 4–6. [Google Scholar]
- Wang, H.; Wonfor, A.; Williams, K.A.; Penty, R.V.; White, I.H. Demonstration of a lossless monolithic 16 × 16 QW SOA switch. In Proceedings of the 2009 35th European Conference on Optical Communication, Vienna, Austria, 20–24 September 2009; pp. 1–2. [Google Scholar]
- Stabile, R.P.; Albores-Mejía, A.A.; Williams, K.K. Monolithic active-passive 16 × 16 optoelectronic switch. Opt. Lett. 2012, 37, 4666–4668. [Google Scholar] [CrossRef]
- Kwack, M.-J.; Tanemura, T.; Higo, A.; Nakano, Y. Monolithic InP strictly non-blocking 8 × 8 switch for high-speed WDM optical interconnection. Opt. Express 2012, 20, 28734–28741. [Google Scholar] [CrossRef]
- Takenaka, M.; Kim, Y.; Han, J.; Kang, J.; Ikku, Y.; Cheng, Y.; Park, J.; Yoshida, M.; Takashima, S.; Takagi, S. Heterogeneous CMOS Photonics based on SiGe/Ge and III-V Semiconductors Integrated on Si Platform. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1. [Google Scholar] [CrossRef]
- Ikku, Y.; Yokoyama, M.; Ichikawa, O.; Hata, M.; Takenaka, M.; Takagi, S. Low-driving-current InGaAsP Photonic-wire Optical Switches using III-V CMOS Photonics Platform. Opt. Express 2012, 20, B357–B364. [Google Scholar] [CrossRef] [PubMed]
- Liang, D.; Labs, H.P.E.H.P.; Bowers, J.E. Recent Progress in Heterogeneous III-V-on-Silicon Photonic Integration. Light. Adv. Manuf. 2021, 2, 1–25. [Google Scholar] [CrossRef]
- Cheung, S.; Kawakita, Y.; Shang, K.; Ben Yoo, S.J. Highly efficient chip-scale III-V/silicon hybrid optical amplifiers. Opt. Express 2015, 23, 22431–22443. [Google Scholar] [CrossRef] [PubMed]
- Van Gasse, K.; Wang, R.; Roelkens, G. 27 dB gain III–V-on-silicon semiconductor optical amplifier with >17 dBm output power. Opt. Express 2019, 27, 293–302. [Google Scholar] [CrossRef]
- Li, Q.; Han, J.-H.; Ho, C.P.; Takagi, S.; Takenaka, M. Ultra-power-efficient 2 × 2 Si Mach-Zehnder interferometer optical switch based on III-V/Si hybrid MOS phase shifter. Opt. Express 2018, 26, 35003–35012. [Google Scholar] [CrossRef]
- Bogaerts, W.; Pérez, D.; Capmany, J.; Miller, D.A.B.; Poon, J.; Englund, D.; Morichetti, F.; Melloni, A. Programmable photonic circuits. Nat. Cell Biol. 2020, 586, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Khanolkar, A.; Xu, P.; Colburn, S.; Deshmukh, S.; Myers, J.; Frantz, J.; Pop, E.; Hendrickson, J.; Doylend, J.; et al. GST-on-silicon hybrid nanophotonic integrated circuits: A non-volatile quasi-continuously reprogrammable platform. Opt. Mater. Express 2018, 8, 1551–1561. [Google Scholar] [CrossRef]
- Stark, P.; Geler-Kremer, J.; Eltes, F.; Caimi, D.; Fompeyrine, J.; Offrein, B.J.; Abel, S. Novel Electro-optic Components for Integrated Photonic Neural Networks. In Proceedings of the Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 8–12 March 2020; p. M2I.4. [Google Scholar]
- Sattari, H.; Toros, A.; Graziosi, T.; Quack, N. Bistable silicon photonic MEMS switches. In Proceedings of the MOEMS and Miniaturized Systems XVIII, San Francisco, CA, USA, 2–7 February 2019. [Google Scholar]
- Bidenko, P.; Han, J.-H.; Song, J.; Kim, S.H. Study on Charge-Enhanced Ferroelectric SIS Optical Phase Shifters Utilizing Negative Capacitance Effect. IEEE J. Quantum Electron. 2020, 56, 1–10. [Google Scholar] [CrossRef]
- Han, S.-M.; Rho, D.-W.; Ahn, D.-H.; Song, J.-D.; Choi, W.-Y.; Han, J.-H. Non-Volatile Operation of a Si PN Ring Resonator with a Ferroelectric Capacitor. In Proceedings of the Optical Fiber Communication Conference (OFC), Washington, DC, USA, 6–11 June 2021. W6A.29. [Google Scholar]
- Boeuf, F.; Han, J.H.; Takagi, S.; Takenaka, M. Benchmarking Si, SiGe, and III-V/Si Hybrid SIS Optical Modulators for Datacenter Applications. J. Light. Technol. 2017, 35, 4047–4055. [Google Scholar] [CrossRef]
- Lee, B.G.; Dupuis, N. Silicon Photonic Switch Fabrics: Technology and Architecture. J. Light. Technol. 2019, 37, 6–20. [Google Scholar] [CrossRef]
- Fujigaki, T.; Takagi, S.; Takenaka, M. High-efficiency Ge thermo-optic phase shifter on Ge-on-insulator platform. Opt. Express 2019, 27, 6451–6458. [Google Scholar] [CrossRef]
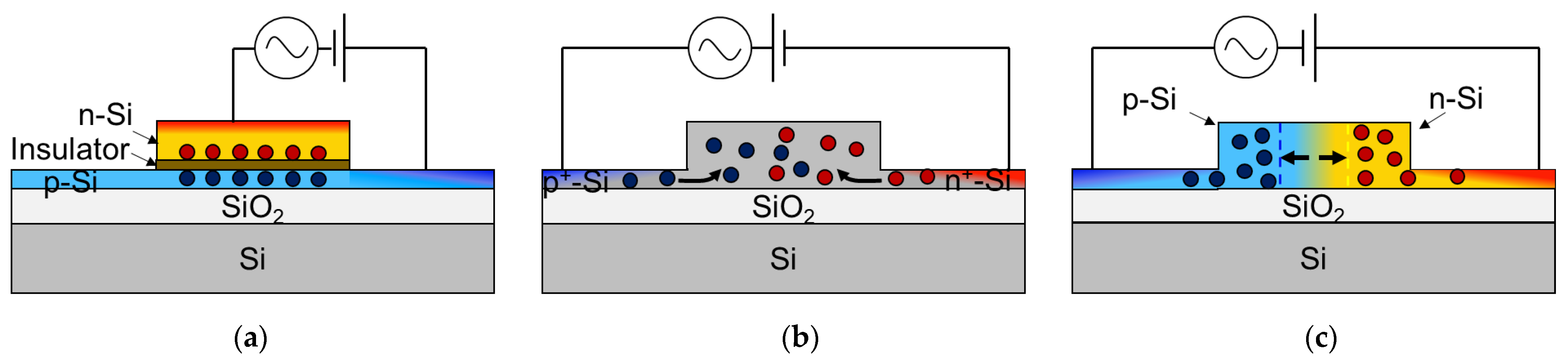
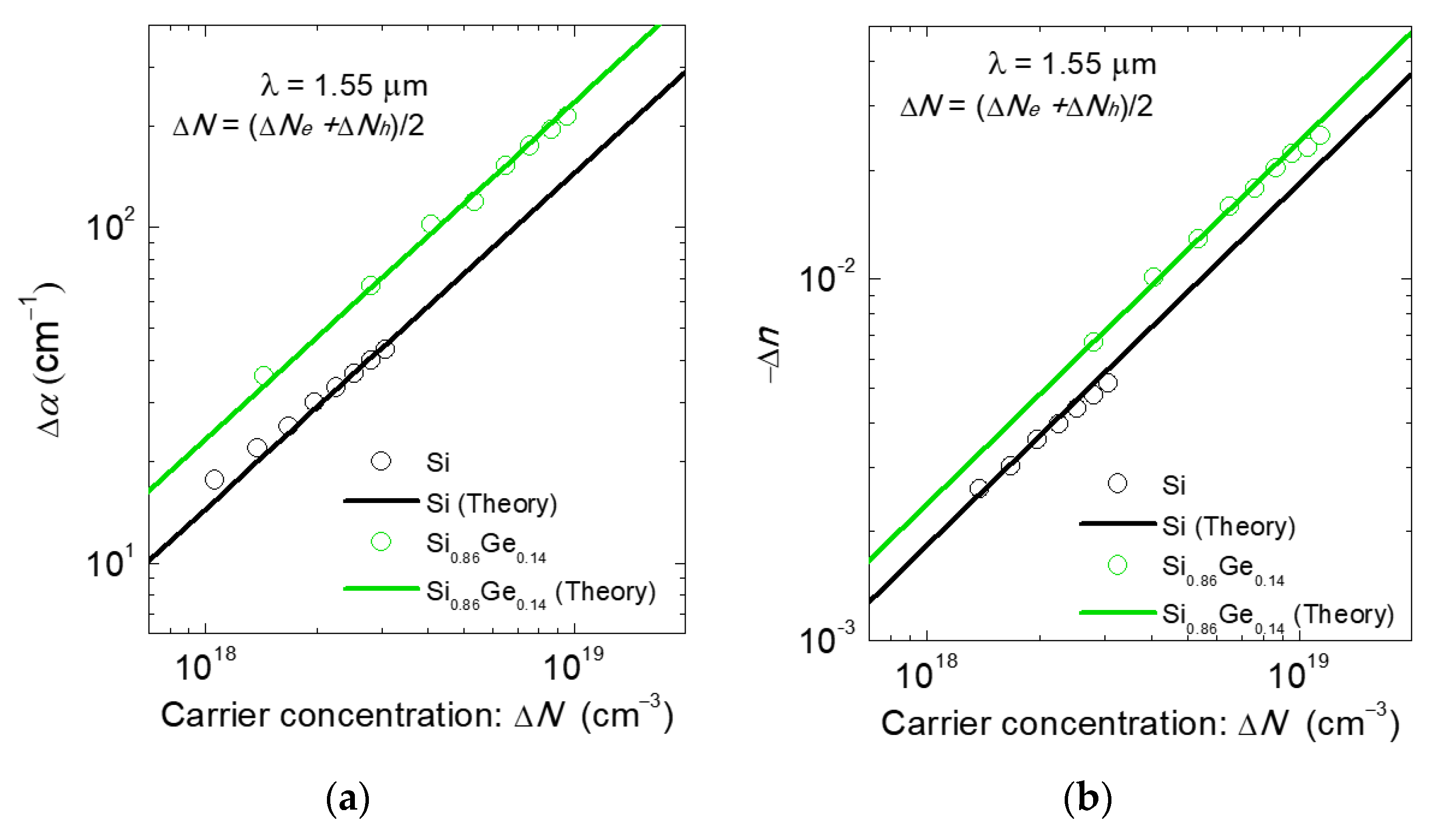
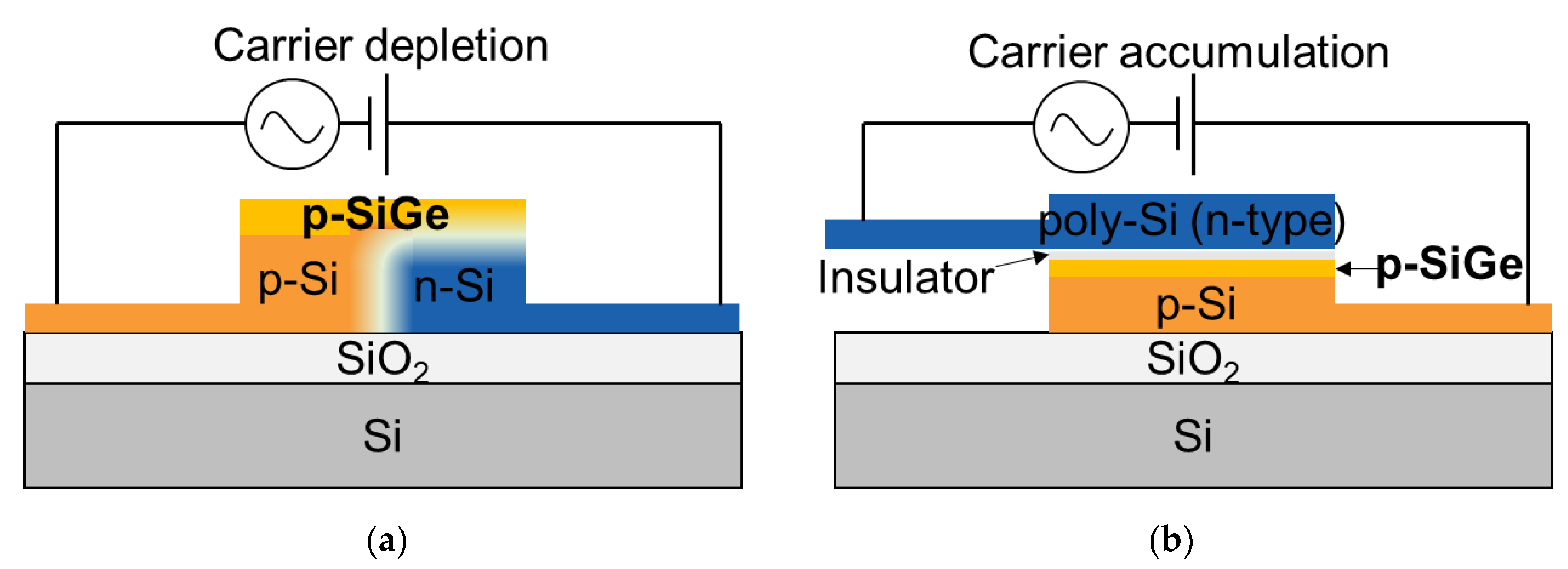
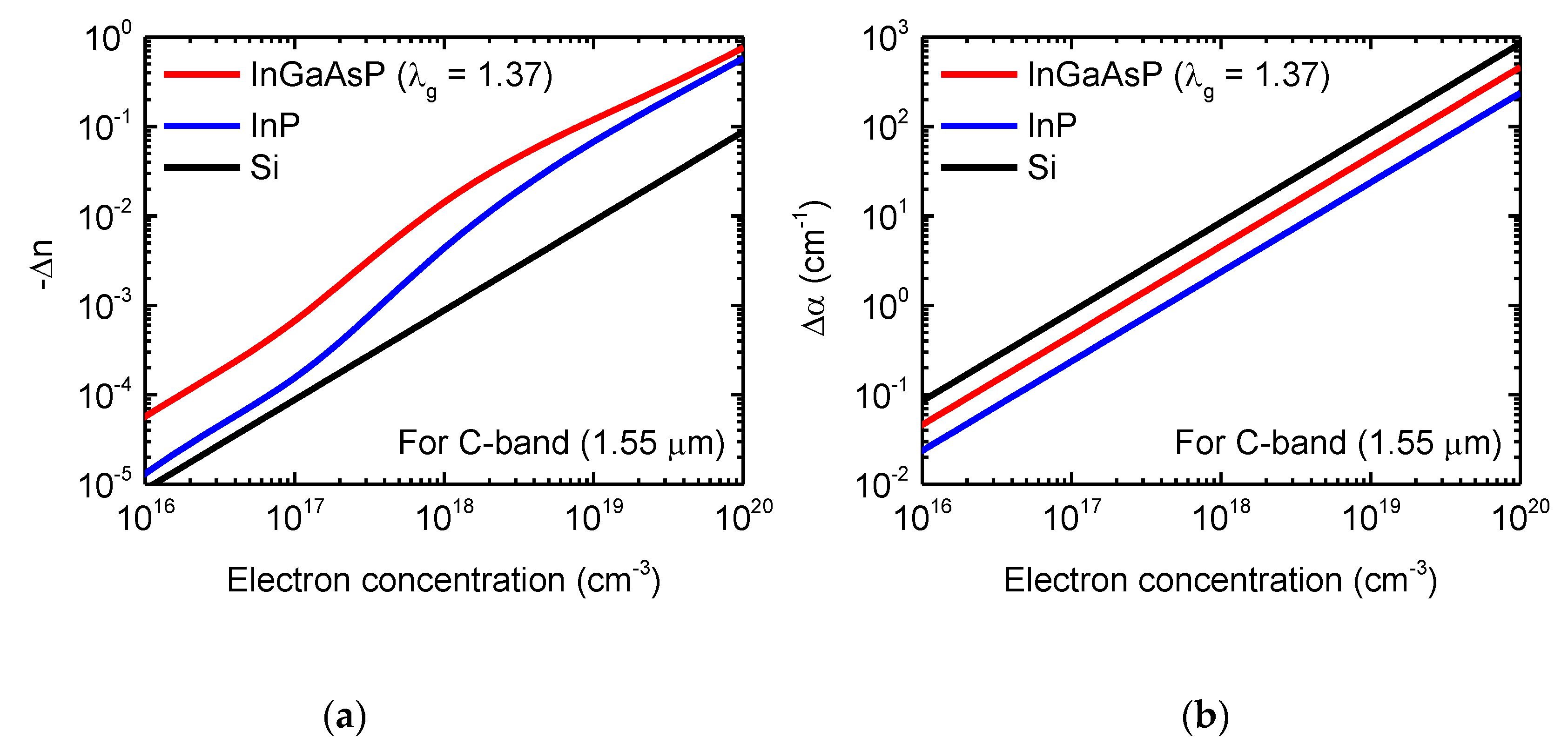
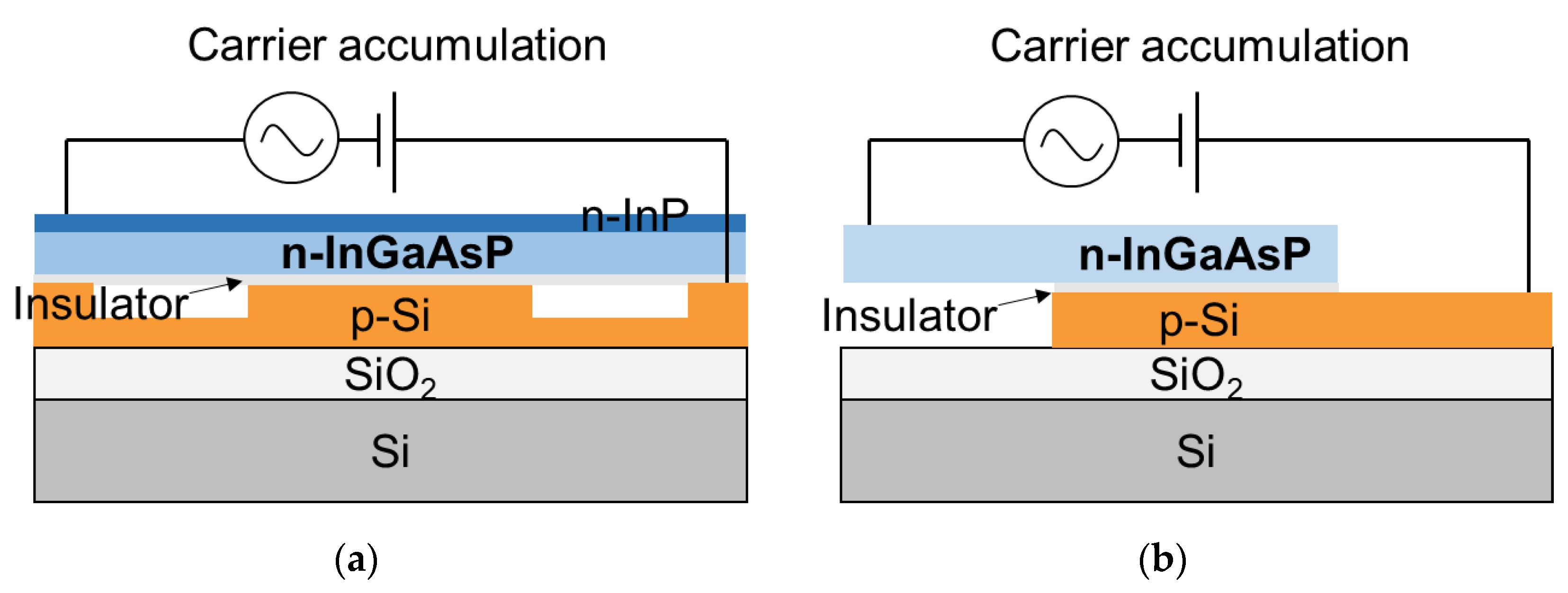
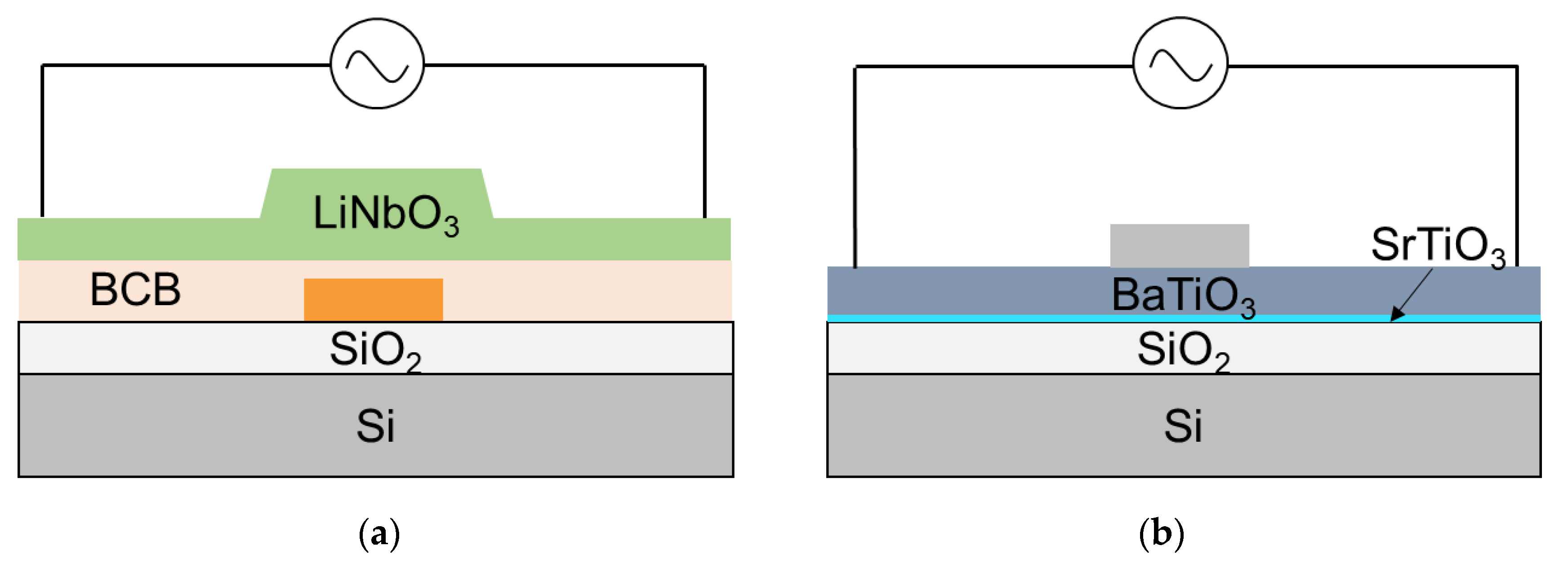
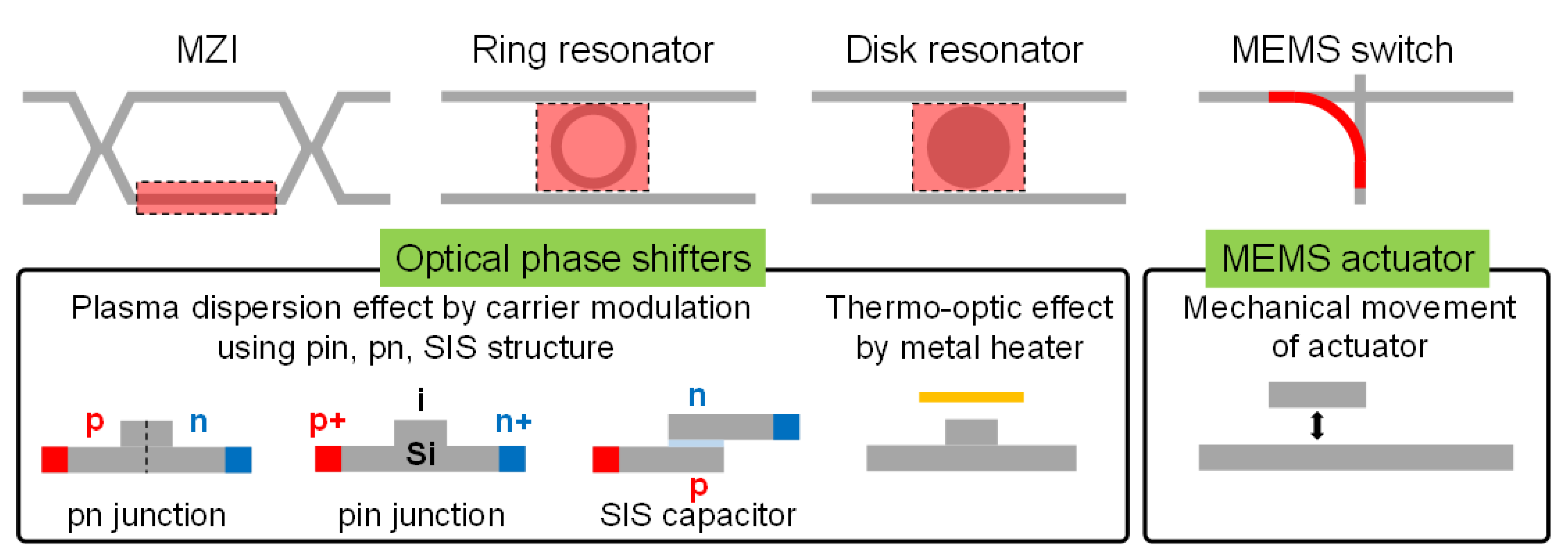
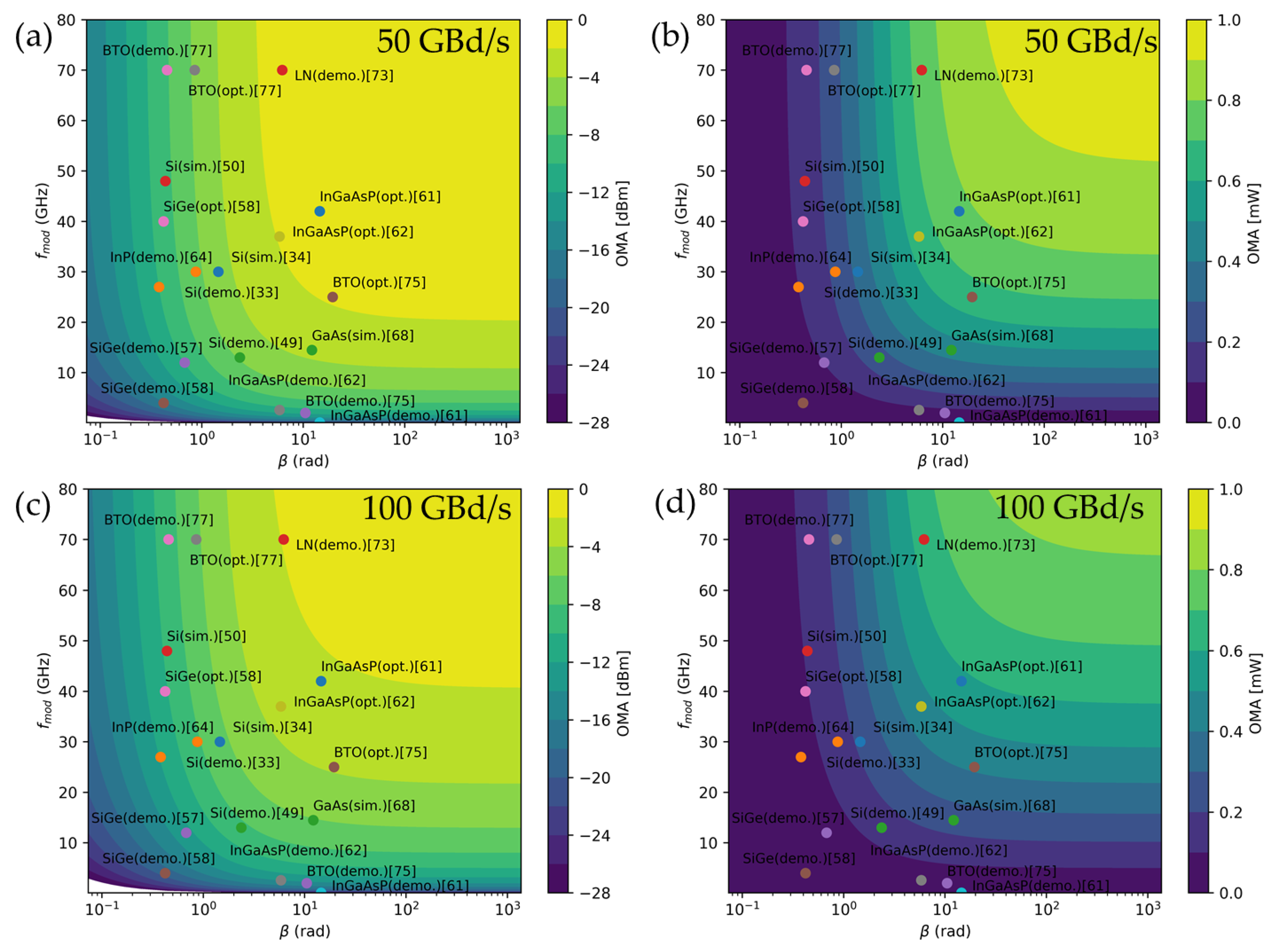
| Ref. | Material/Structure | Sim./Demo./Opt. a | α (dB/mm) | VπL (Vcm) | αVπL (VdB) | fmod (GHz) | |||
|---|---|---|---|---|---|---|---|---|---|
| [34] | Si/pn | sim. | 1.05 | (at 0 V) | 0.89 | (0 to −2 V) | 9.35 | 30.00 | (at 0 V, Intrinsic) |
| [33] | Si/pn | demo. | 1.20 | (N/A) | 3.00 | (0 to −4 V) | 36.00 | 36.0 | (at 0 V, Intrinsic) |
| [49] | Si/pn | demo. | 1.25 | (at 0 V) | 0.46 | (at −0.5 V) | 5.75 | 13.00 | (at −2 V, EO S21) |
| [50] | Si/SIS | sim. | 4.20 | (at −1 V) | 0.74 | (0 to −2 V) | 31.08 | 48.00 | (at −1 V, Intrinsic) |
| [57] | SiGe/pn | demo. | 3.00 | (IL = 1.5 dB, de Vice 0.5 mm) | 0.67 | (at −0.5 V) | 20.10 | 12.00 | (at −1 V, EO S21) |
| [58] | SiGe/SIS | demo. | 3.00 | (at 1.8 V) | 1.08 | (0.9 V to 1.8 V) | 32.40 | 4.00 | (at 0.9 V, EO S21) |
| [58] | SiGe/SIS | opt. | 3.00 | (at 1.8 V) | 1.08 | (0.9 V to 1.8 V) | 32.40 | 40.00 | (expected by sim., EO S21) |
| [62] | InGaAsP/ SIS | demo. | 2.60 | (at −1.5 V) | 0.09 | (in accumulation mode) | 2.34 | 2.60 | (at 1.5 V, EO S21) |
| [62] | InGaAsP/ SIS | opt. | 2.60 | (at −1.5 V) | 0.09 | (in accumulation mode) | 2.34 | 37.00 | (at 1.5 V, intrinsic) |
| [61] | InGaAsP/ SIS | demo. | 2.00 | (at 0 V) | 0.05 | 0.94 | 0.10 | (EO S21) | |
| [61] | InGaAsP/ SIS | opt. | 2.00 | (at 0 V) | 0.05 | 0.94 | 42.00 | (Intrinsic) | |
| [64] | InP/SIS | demo. | 1.20 | (at 0 V) | 1.30 | (0 to 4 V) | 15.60 | 30.00 | (at 0 V, 250 um, EO S21) |
| [67] | GaAs/pn | sim. | 1.60 | (at 0 V) | 0.07 | (0 to −0.3 V) | 1.12 | 14.47 | (0 V, Intrinsic) |
| [73] | LN | demo. | 0.10 | 2.20 | 2.20 | 70.00 | (EO S21) | ||
| [75] | BTO | demo. | 0.57 | 0.23 | 1.30 | 2.00 | (EO S21) | ||
| [75] | BTO | opt. | 0.30 | 0.23 | 0.70 | 25.00 | (EO S21, measured value using micro-ring modulator) | ||
| [77] | BTO | demo. | 1500.00 | 0.002 | 30.00 | 70.00 | (EO S21) | ||
| [77] | BTO | opt. | 800.00 | 0.002 | 16.00 | 70.00 | (EO S21) | ||
| Ref | Switching Principle | Structure | Reported Largest Scalability | Speed | Crosstalk (dB) | Insertion Loss (dB) | Power Consumption |
|---|---|---|---|---|---|---|---|
| [82,83,84,85] | Thermo-optic | Metal heater | 32 × 32 | ~30 μs | >35 | 8.4 | 1.9 W |
| [86,87,88,89] | MEMS | MEMS actuator | 240 × 240 | Sub-μs | >60 | <6.5 | (20–40 V) a |
| [83,94,95] | Electro-optic | Si pin | 32 × 32 | <10 ns | >10 | <5 | 1.2 W |
| [95] | Si pn | 2 × 2 | Sub-ns | >10 | <11.5 | 4.7 mW | |
| [97,98,99] | III-V SOA | 16 × 16 | <3.3 ns | >51.6 | - | 1.26 W | |
| [100,102] | III-V pin | 8 × 8 | <5 ns | >18 | <6.3 (sim.) | - | |
| [105] | III-V/Si hybrid SIS | 2 × 2 | <20 ns | >23 | >0.07 (sim.) | 0.18 W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Han, J.-H.; Ahn, D.; Kim, S. Heterogeneously-Integrated Optical Phase Shifters for Next-Generation Modulators and Switches on a Silicon Photonics Platform: A Review. Micromachines 2021, 12, 625. https://doi.org/10.3390/mi12060625
Kim Y, Han J-H, Ahn D, Kim S. Heterogeneously-Integrated Optical Phase Shifters for Next-Generation Modulators and Switches on a Silicon Photonics Platform: A Review. Micromachines. 2021; 12(6):625. https://doi.org/10.3390/mi12060625
Chicago/Turabian StyleKim, Younghyun, Jae-Hoon Han, Daehwan Ahn, and Sanghyeon Kim. 2021. "Heterogeneously-Integrated Optical Phase Shifters for Next-Generation Modulators and Switches on a Silicon Photonics Platform: A Review" Micromachines 12, no. 6: 625. https://doi.org/10.3390/mi12060625
APA StyleKim, Y., Han, J.-H., Ahn, D., & Kim, S. (2021). Heterogeneously-Integrated Optical Phase Shifters for Next-Generation Modulators and Switches on a Silicon Photonics Platform: A Review. Micromachines, 12(6), 625. https://doi.org/10.3390/mi12060625








