Study on Material Removal Model by Reciprocating Magnetorheological Polishing
Abstract
1. Introduction
2. MRR Model of the RMRP
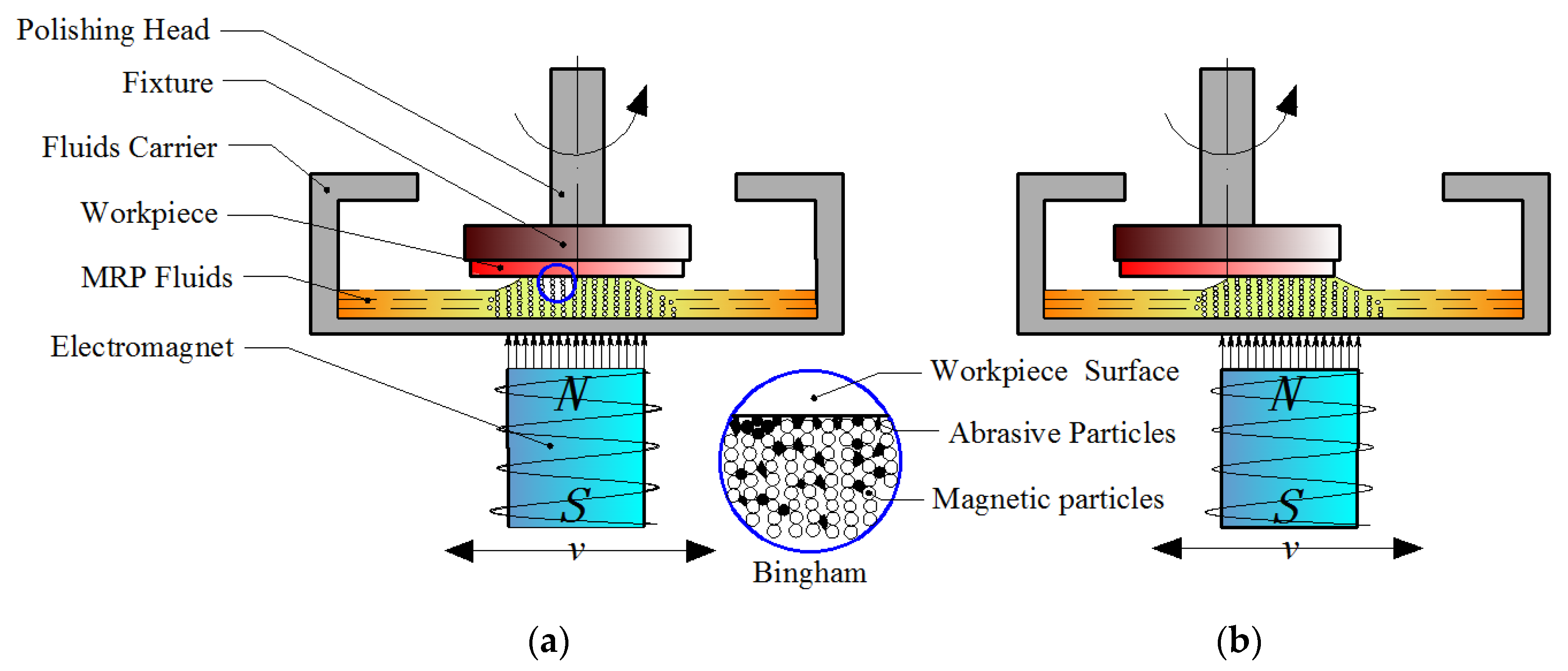
2.1. Material Removal Principle of the RMRP
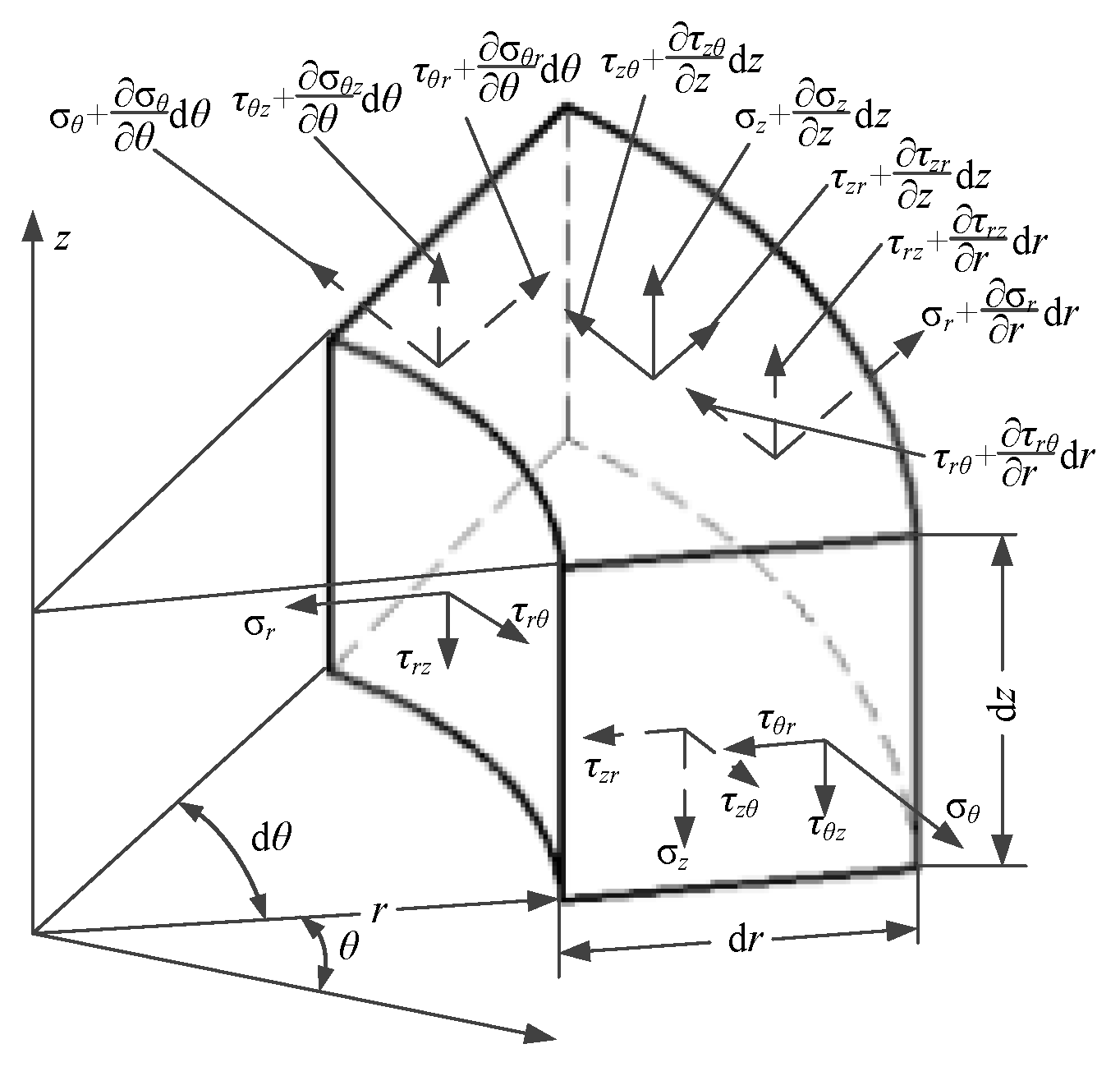
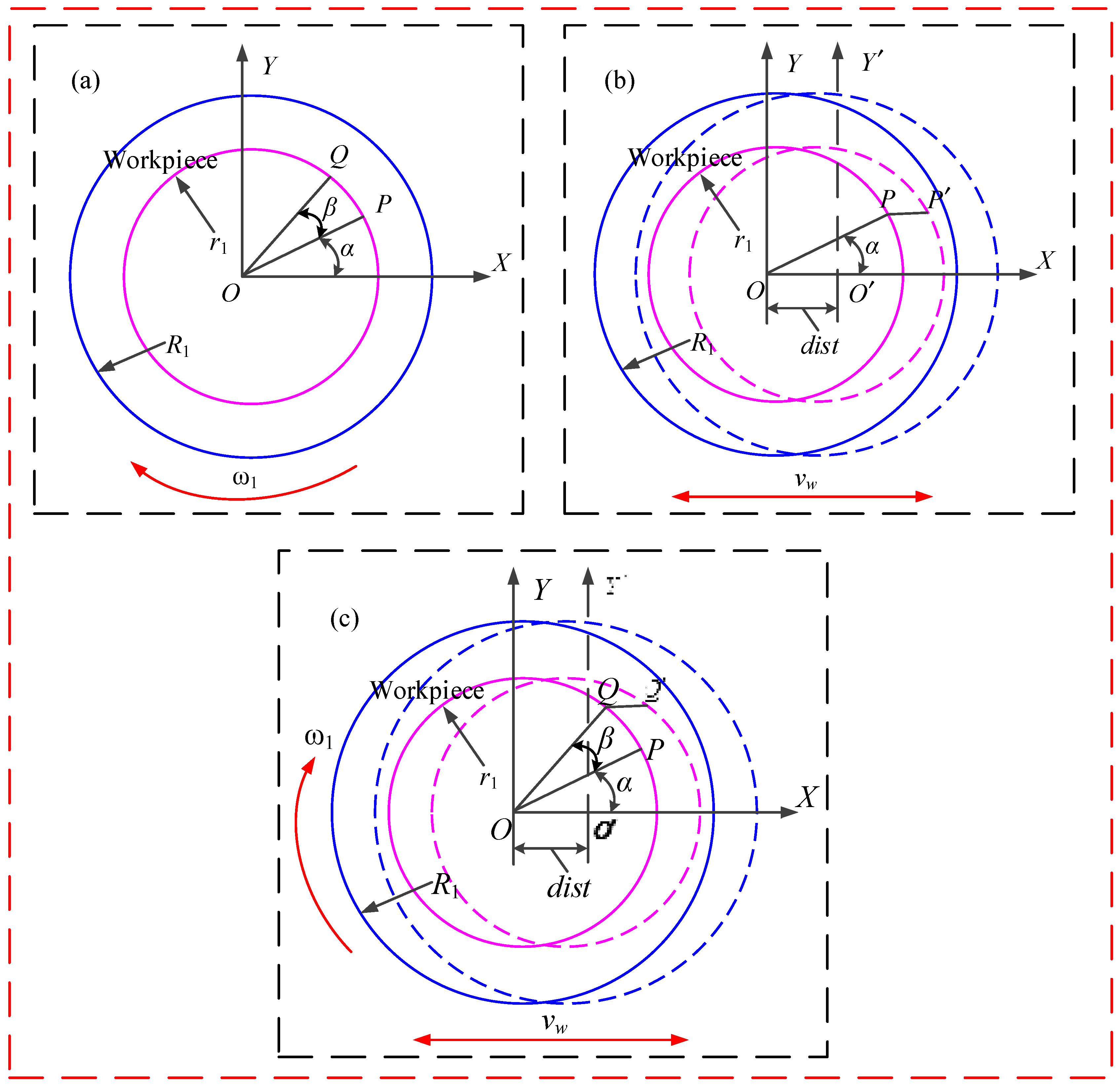
2.2. MRR Model of the RMRP
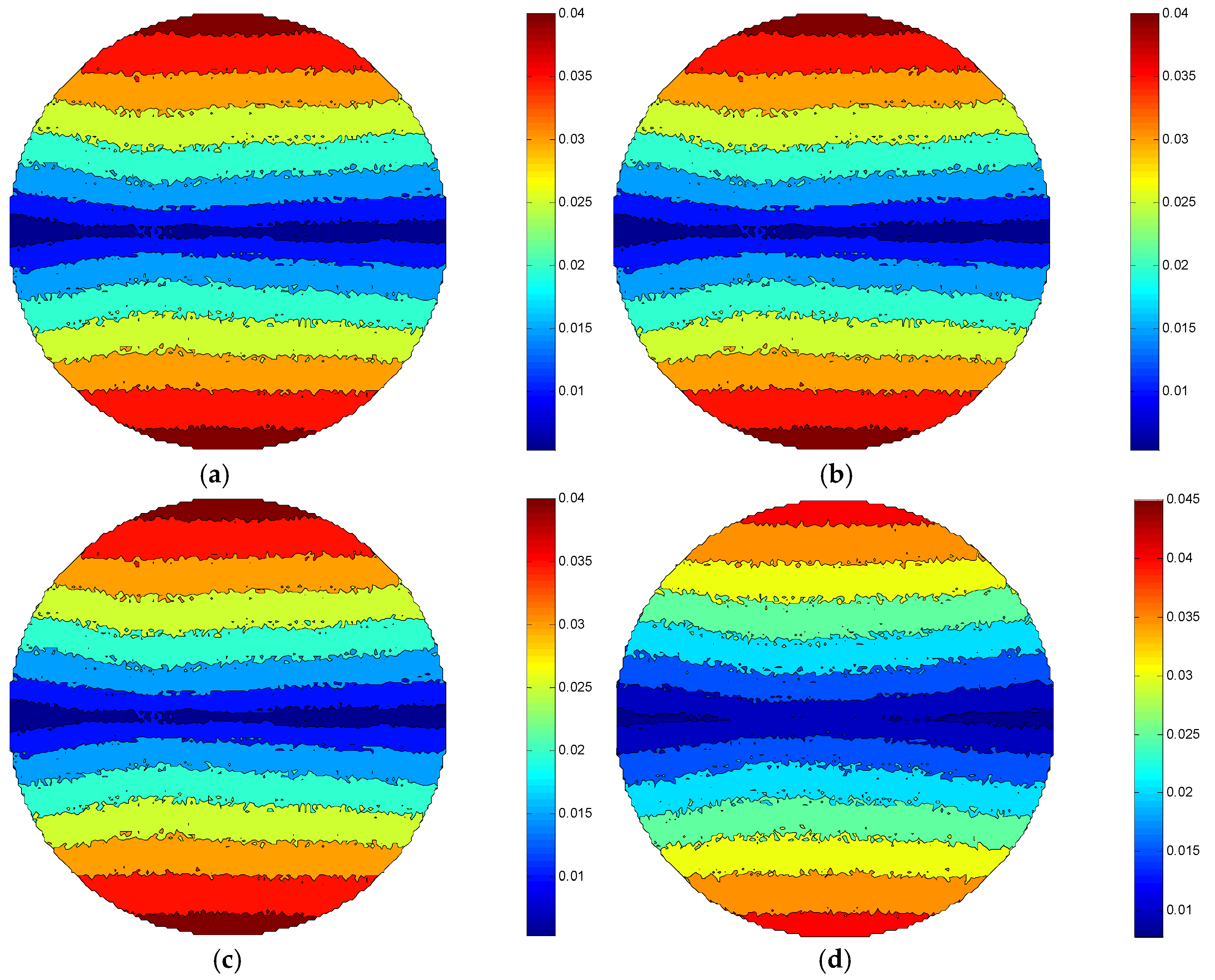
3. Simulation Analysis of the MRR Model
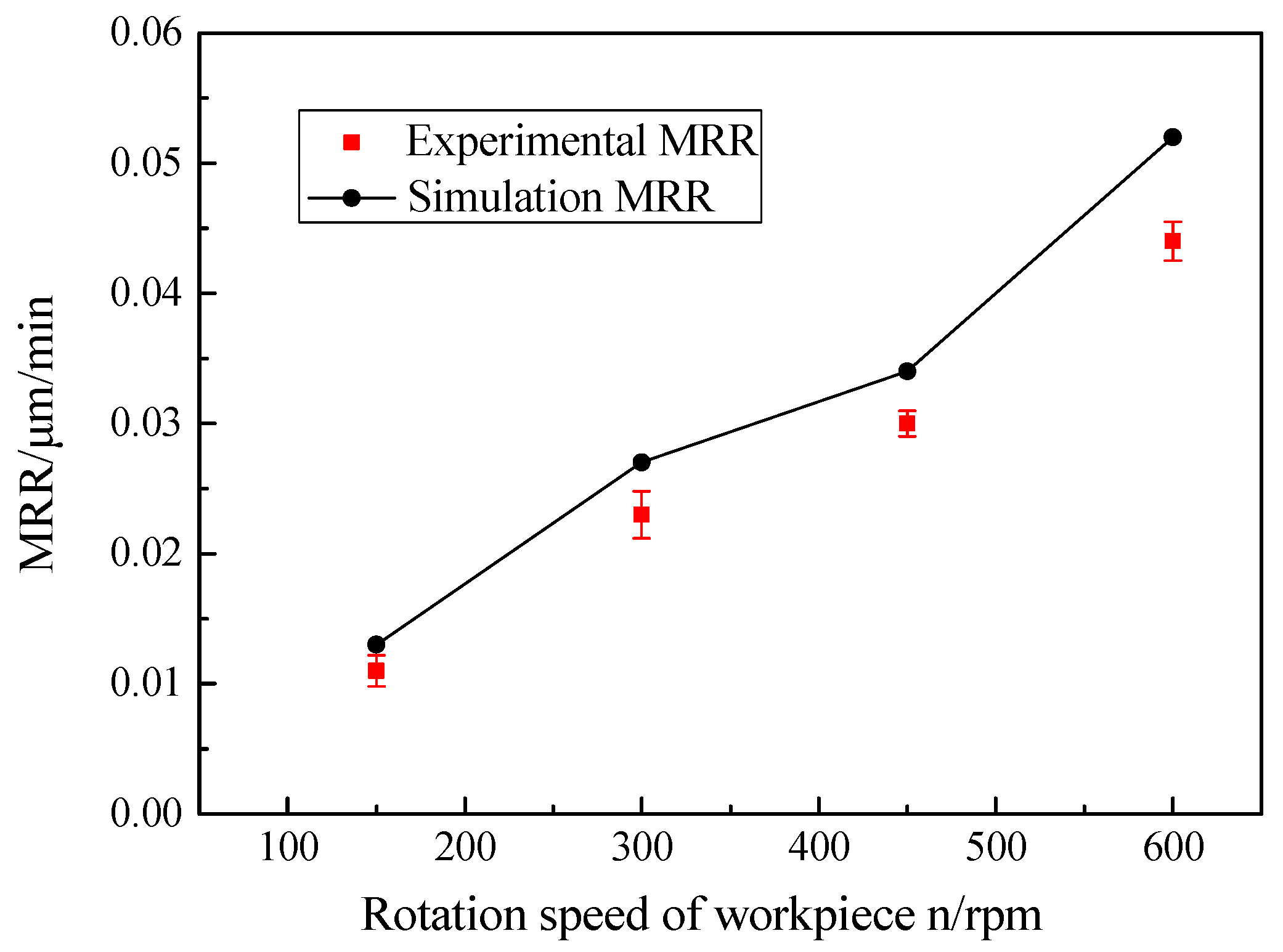
3.1. Effect of Workpiece Rotation Speed on MRR
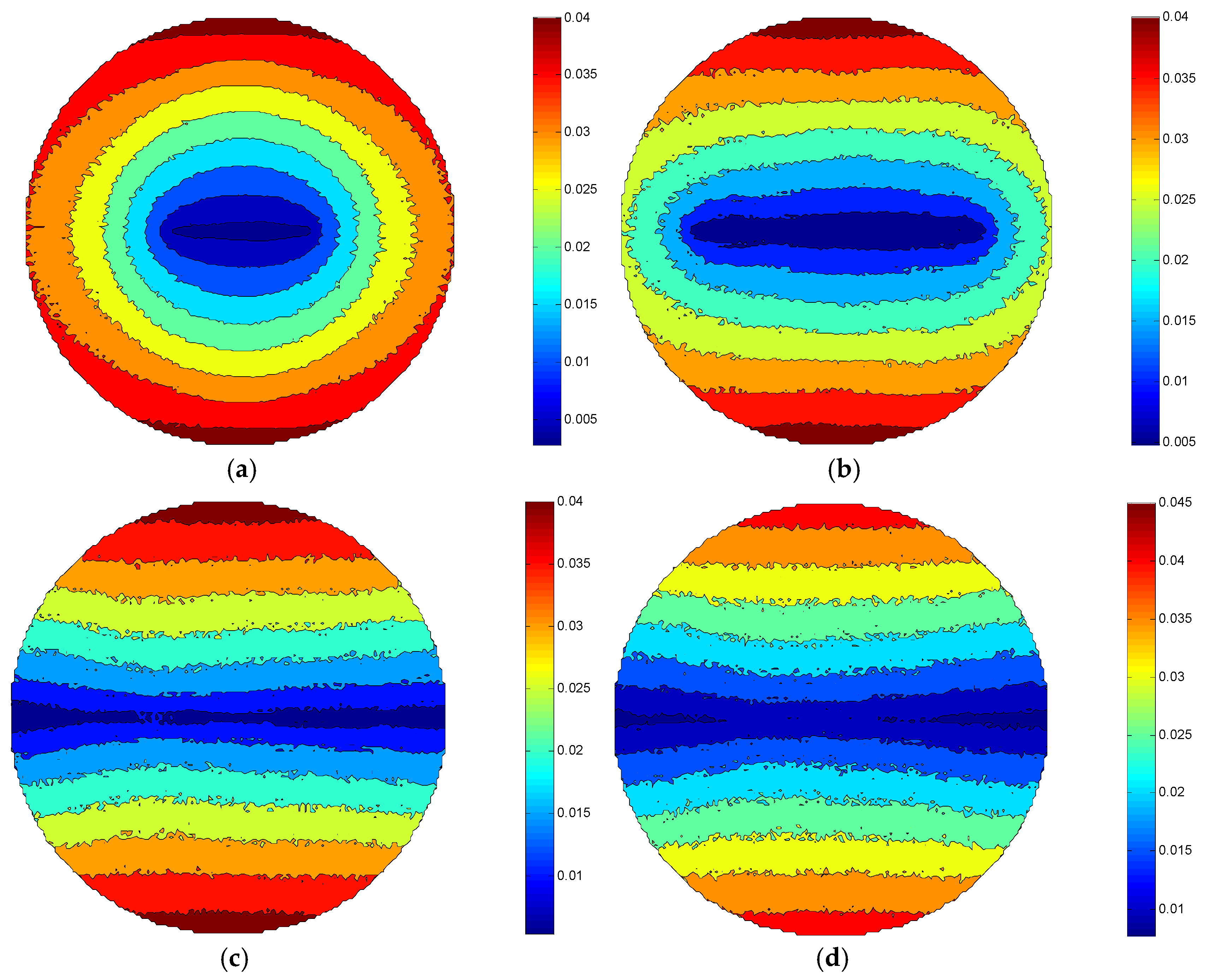
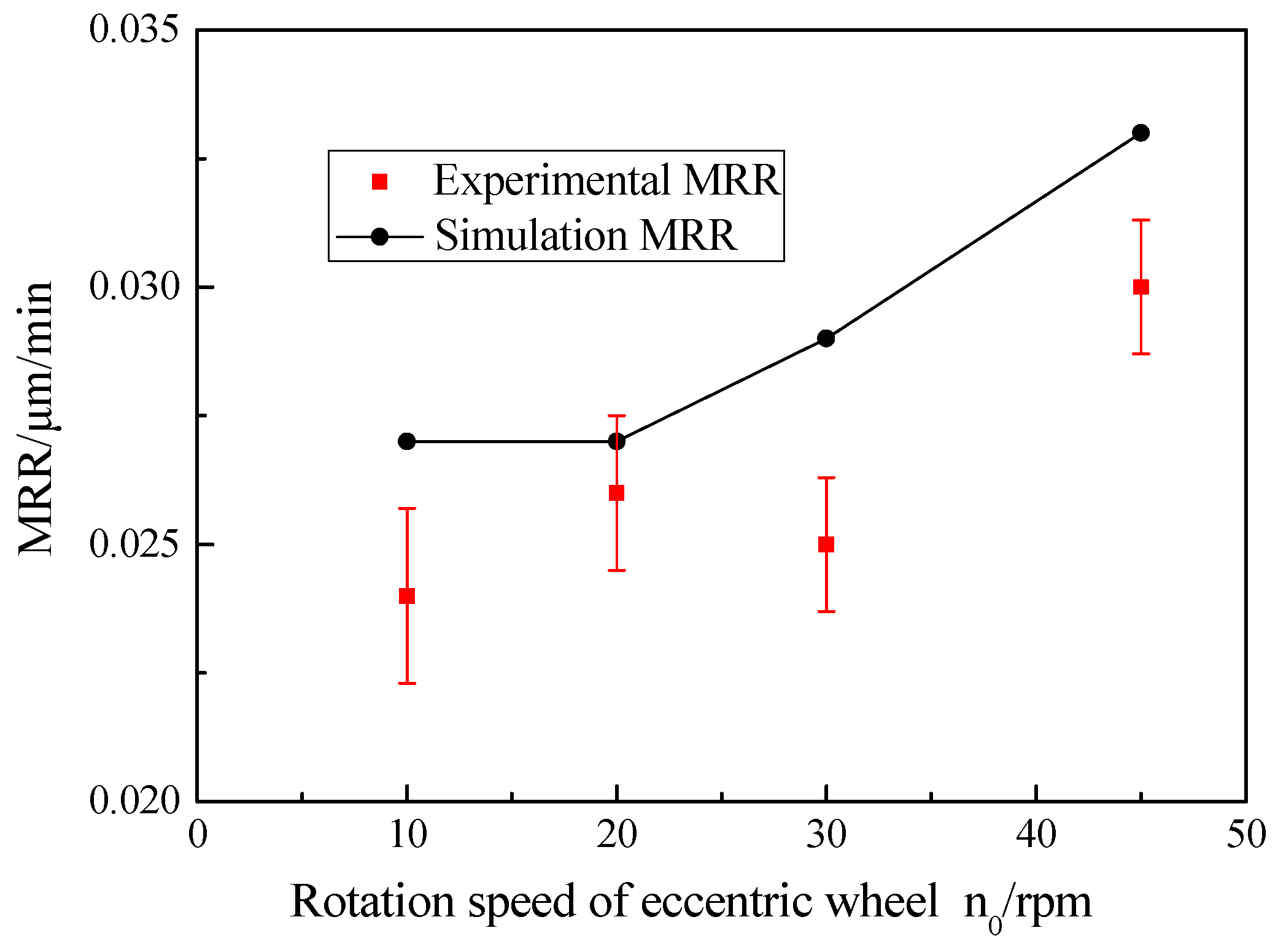
3.2. Effect of Eccentric Wheel Rotation Speed on MRR
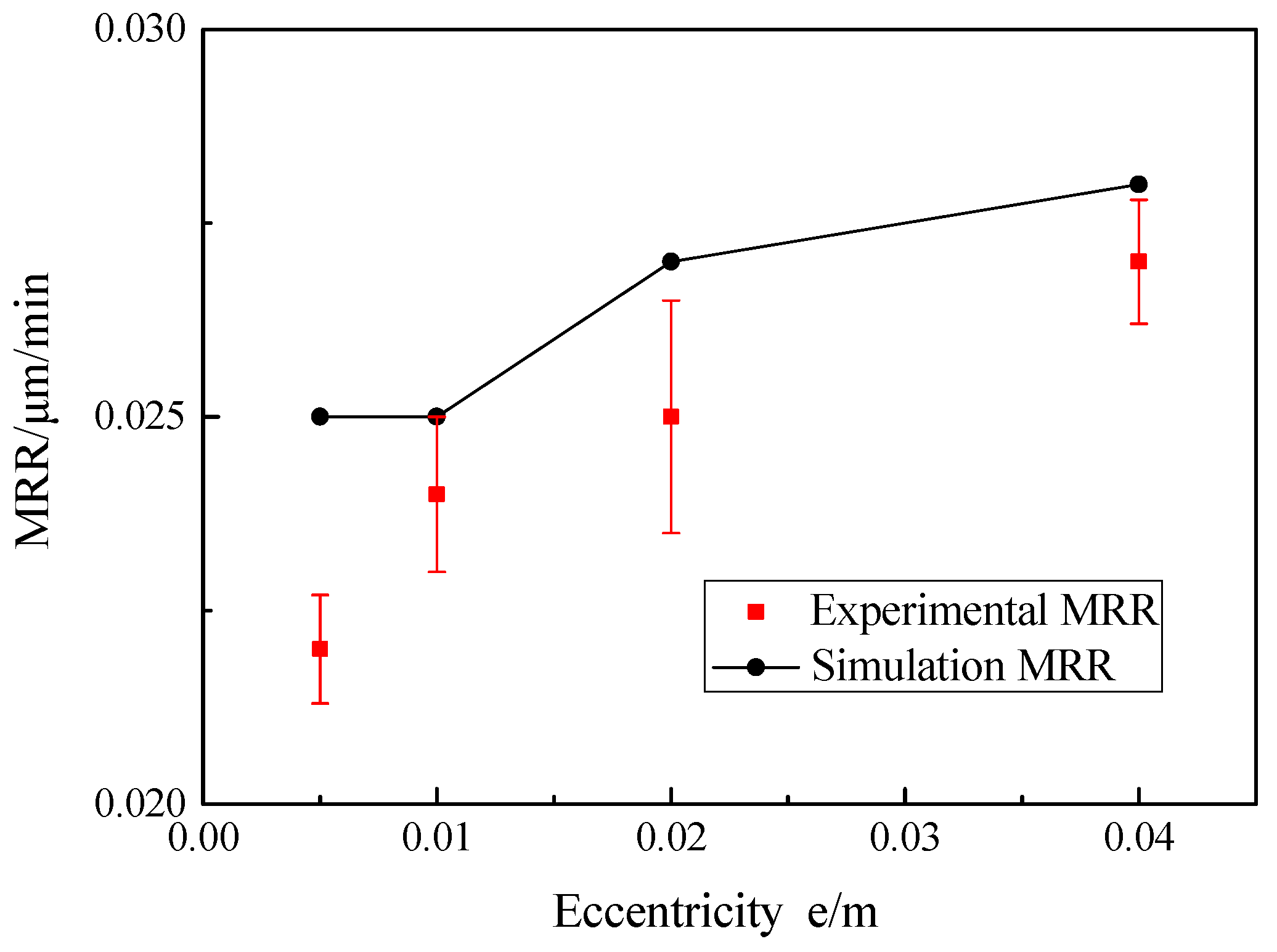
3.3. Effect of Eccentricity on MRR
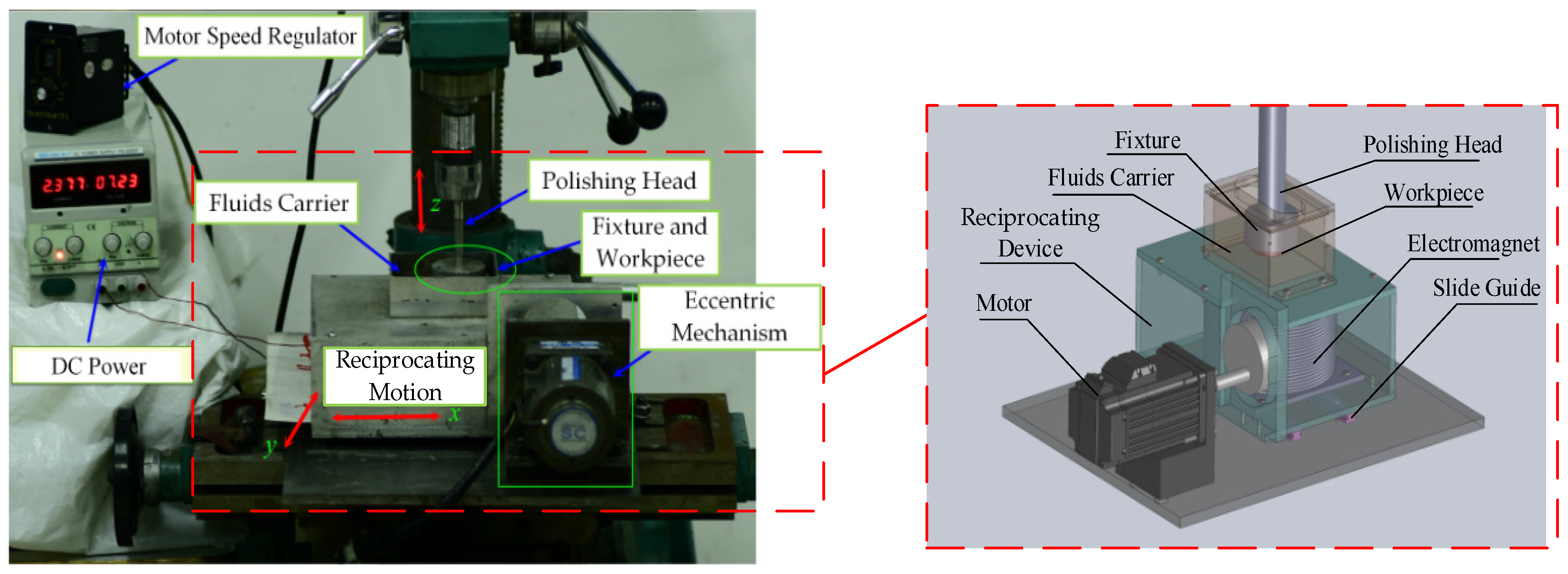
4. Experimental Details
4.1. Preparation of the MRP Fluids
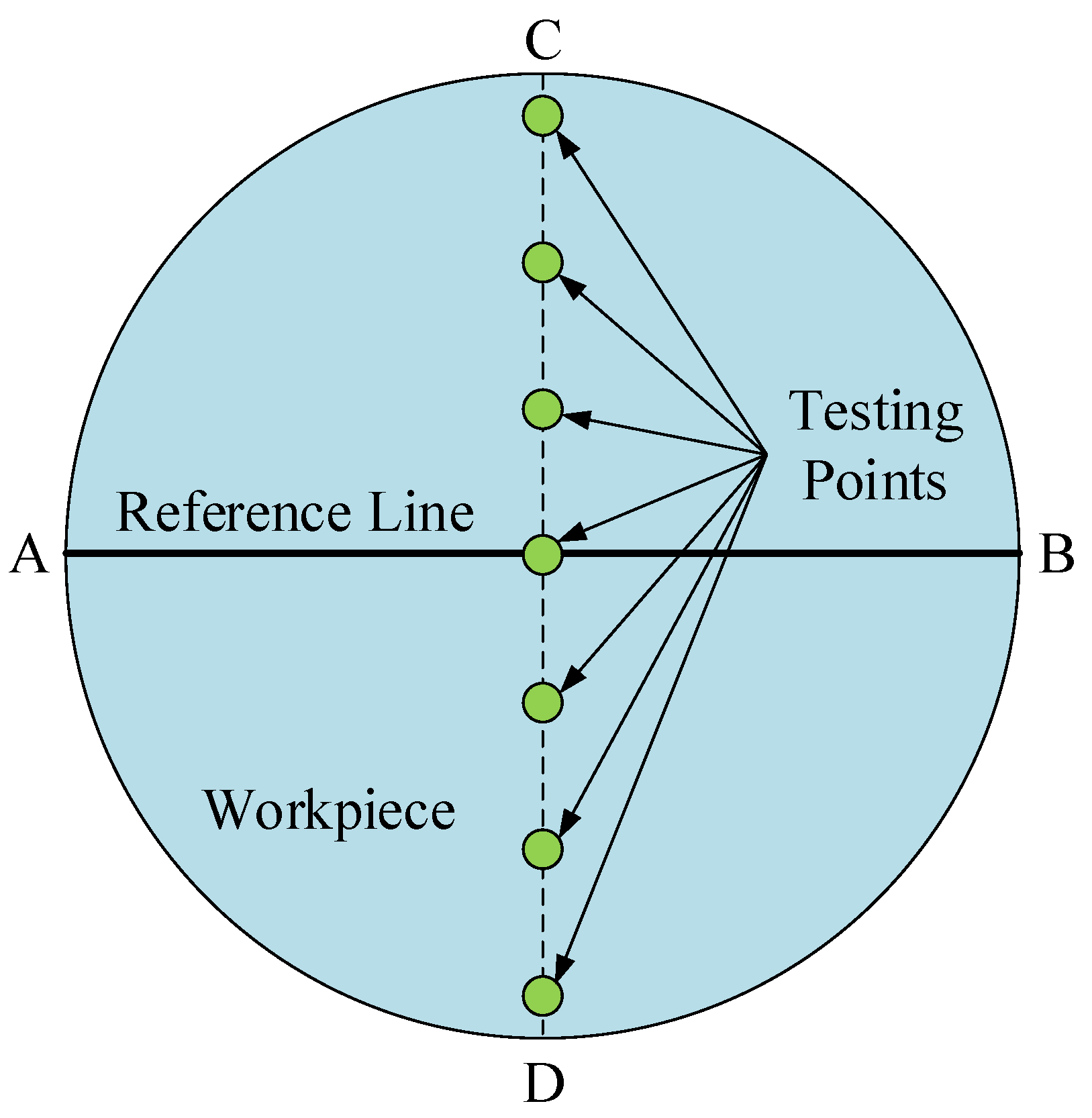
4.2. Experimental Conditions and Measurement Methods
5. Results and Discussion
5.1. Effect of Workpiece Rotation Speed on MRR
5.2. Effect of Eccentric Wheel Rotation Speed on MRR
5.3. Effect of Eccentricity on MRR
6. Conclusions
- The K9 optical flat glass was polished with the RMRP setup to study the effects of technological parameters on the MRR of a workpiece. The experimental results were in good agreement with the theoretical results under the same technical parameters and the average relative errors between the theoretical and experimental values were 16.77%, 10.59% and 7.38%, respectively, according to the effects of workpiece rotation speed, eccentric wheel rotation speed and eccentricity on MRR, then the efficacy of the MRR model of the RMRP was verified.
- It was found that the surface roughness reduced to Ra 50.8 ± 1.2 from initial Ra 330.3 ± 1.6 nm when the technical parameters of the workpiece rotation speed of 300 rpm, the eccentric wheel rotation speed of 20 rpm and the eccentricity of 0.02 m were applied; the surface roughness reduced to Ra 60.4 ± 1.6 from initial Ra 321.0 ± 1.2 nm when the technical parameters of the workpiece rotation speed of 300 rpm, the eccentric wheel rotation speed of 45 rpm and the eccentricity of 0.02 m were applied.
- As the rotational speed of the workpiece rose, the MRR of the workpiece increased significantly, and the experimental MRR values added from 0.0115 ± 0.0012 to 0.0443 ± 0.0015 μm/min. Compared with the effect of workpiece rotation speed on the MRR, the effect of eccentric wheel rotation speed and eccentricity on the MRR could be neglected.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, S.J.; To, S.; Wang, S.J.; Zhu, Z.W. A review of surface roughness generation in ultra-precision machining. Int. J. Mach. Tools Manuf. 2015, 91, 76–95. [Google Scholar] [CrossRef]
- Sidpara, A.M. Magnetorheological finishing: A perfect solution to nanofinishing requirements. Opt. Eng. 2014, 53, 092002. [Google Scholar] [CrossRef]
- Walker, D.D.; Brooks, D.; King, A.; Freeman, R.; Morton, R.; McCavana, G.; Kim, S.-W. The ‘Precessions’ tooling for polishing and figuring flat, spherical and aspheric surfaces. Opt. Express 2003, 11, 958–964. [Google Scholar] [CrossRef] [PubMed]
- Mori, Y.; Yamauchi, K.; Endo, K. Elastic emission machining. Precis. Eng. 1987, 9, 123–128. [Google Scholar] [CrossRef]
- Weiser, M. Ion beam figuring for lithography optics. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 1390–1393. [Google Scholar] [CrossRef]
- Kordonski, W.; Shorey, A. Magnetorheological (MR) Jet Finishing Technology. J. Intell. Mater. Syst. Struct. 2007, 18, 1127–1130. [Google Scholar] [CrossRef]
- Cho, C.-H.; Park, S.-S.; Ahn, Y. Three-dimensional wafer scale hydrodynamic modeling for chemical mechanical polishing. Thin Solid Films 2001, 389, 254–260. [Google Scholar] [CrossRef]
- Kordonski, W.; Gorodkin, S. Material removal in magnetorheological finishing of optics. Appl. Opt. 2011, 50, 1984–1994. [Google Scholar] [CrossRef]
- Singh, A.K.; Jha, S.; Pandey, P.M. Mechanism of material removal in ball end magnetorheological finishing process. Wear 2013, 302, 1180–1191. [Google Scholar] [CrossRef]
- Li, S.; Wang, Z.; Wu, Y. Relationship between subsurface damage and surface roughness of optical materials in grinding and lapping processes. J. Mater. Process. Technol. 2008, 205, 34–41. [Google Scholar] [CrossRef]
- Kordonski, W.; Golini, D. Multiple Application of Magnetorheological Effect in High Precision Finishing. J. Intell. Mater. Syst. Struct. 2002, 13, 401–404. [Google Scholar] [CrossRef]
- Song, W.; Choi, S.; Lee, D.; Lee, C. Micro-precision surface finishing using magneto-rheological fluid. Sci. China Technol. Sci. 2012, 55, 56–61. [Google Scholar] [CrossRef]
- Kordonski, W.; Golini, D. Fundamentals of magnetorheological fluid utilization in high precision finishing. J. Intell. Mater. Syst. Struct. 1999, 10, 683–689. [Google Scholar] [CrossRef]
- Barman, A.; Das, M. Toolpath generation and finishing of bio-titanium alloy using novel polishing tool in MFAF process. Int. J. Adv. Manuf. Technol. 2019, 100, 1123–1135. [Google Scholar] [CrossRef]
- Sidpara, A.; Jain, V. Effect of fluid composition on nanofinishing of single-crystal silicon by magnetic field-assisted finishing process. Int. J. Adv. Manuf. Technol. 2011, 55, 243–252. [Google Scholar] [CrossRef]
- Das, M.; Jain, V.K.; Ghoshdastidar, P.S. A 2D CFD simulation of MR polishing medium in magnetic field-assisted finishing process using electromagnet. Int. J. Adv. Manuf. Technol. 2015, 76, 173–187. [Google Scholar] [CrossRef]
- Jang, K.I.; Seok, J.; Min, B.K.; Lee, S. A 3D model for magnetorheological fluid that considers neighboring particle interactions in 2D skewed magnetic fields. Int. J. Precis. Eng. Manuf. 2009, 10, 115–118. [Google Scholar] [CrossRef]
- Kordonski, W.I.; Jacobs, S. Magnetorheological finishing. Int. J. Mod. Phys. B 1996, 10, 2837–2848. [Google Scholar] [CrossRef]
- Das, M.; Jain, V.; Ghoshdastidar, P. Nanofinishing of flat workpieces using rotational–magnetorheological abrasive flow finishing (R-MRAFF) process. Int. J. Adv. Manuf. Technol. 2012, 62, 405–420. [Google Scholar] [CrossRef]
- Harris, D.C. History of Magnetorheological Finishing. Proc. SPIE Int. Soc. Opt. Eng. 2011, 8016, 561–566. [Google Scholar]
- Kim, W.B.; Lee, S.H.; Min, B.K. Surface Finishing and Evaluation of Three-Dimensional Silicon Microchannel Using Magnetorheological Fluid. J. Manuf. Sci. Eng. 2005, 126, 772–778. [Google Scholar] [CrossRef]
- Seok, J.; Kim, Y.J.; Jang, K.I.; Min, B.K.; Lee, S.J. A study on the fabrication of curved surfaces using magnetorheological fluid finishing. Int. J. Mach. Tools Manuf. 2007, 47, 2077–2090. [Google Scholar] [CrossRef]
- Singh, A.K.; Jha, S.; Pandey, P.M. Design and development of nanofinishing process for 3D surfaces using ball end MR finishing tool. Int. J. Mach. Tools Manuf. 2011, 51, 142–151. [Google Scholar] [CrossRef]
- De Lacalle, L.L.; Lamikiz, A.; Salgado, M.; Herranz, S.; Rivero, A. Process planning for reliable high-speed machining of moulds. Int. J. Prod. Res. 2002, 40, 2789–2809. [Google Scholar] [CrossRef]
- Shorey, A.B. Mechanisms of Material Removal in Magnetorheological Finishing (MRF) of Glass. Ph.D. Thesis, University of Rochester, New York, NY, USA, 2000. [Google Scholar]
- DeGroote, J.E.; Marino, A.E.; Wilson, J.P.; Bishop, A.L.; Lambropoulos, J.C.; Jacobs, S.D. Removal rate model for magnetorheological finishing of glass. Appl. Opt. 2007, 46, 7927–7941. [Google Scholar] [CrossRef] [PubMed]
- Miao, C.; Shafrir, S.N.; Lambropoulos, J.C.; Mici, J.; Jacobs, S.D. Shear stress in magnetorheological finishing for glasses. Appl. Opt. 2009, 48, 2585–2594. [Google Scholar] [CrossRef]
- Li, M.; Lyu, B.; Yuan, J.; Dong, C.; Dai, W. Shear-thickening polishing method. Int. J. Mach. Tools Manuf. 2015, 94, 88–99. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, S.; Huang, H. Polishing characteristics and mechanism in magnetorheological planarization using a permanent magnetic yoke with translational movement. Precis. Eng. 2016, 43, 93–104. [Google Scholar] [CrossRef]
- Xiu, S.; Wang, R.; Sun, B.; Ma, L.; Song, W. Preparation and experiment of magnetorheological polishing fluid in reciprocating magnetorheological polishing process. J. Intell. Mater. Syst. Struct. 2018, 29, 125–136. [Google Scholar] [CrossRef]
- Pan, J.; Guo, M.; Yan, Q.; Zheng, K.; Xiao, X. Research on material removal model and processing parameters of cluster magnetorheological finishing with dynamic magnetic fields. Int. J. Adv. Manuf. Technol. 2019, 100, 2283–2297. [Google Scholar] [CrossRef]
- Jayswal, S.C.; Jain, V.K.; Dixit, P.M. Modeling and simulation of magnetic abrasive finishing process. Int. J. Adv. Manuf. Technol. 2005, 26, 477–490. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; Lacalle, L. Actively lubricated hybrid journal bearings based on magnetic fluids for high-precision spindles of machine tools. J. Intell. Mater. Syst. Struct. 2019, 30, 2257–2271. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; Norberto, L. Seals Based on Magnetic Fluids for High Precision Spindles of Machine Tools. Int. J. Precis. Eng. Manuf. 2018, 19, 495–503. [Google Scholar] [CrossRef]
- Carlson, J.D. What Makes a Good MR Fluid? J. Intell. Mater. Syst. Struct. 2002, 13, 431–435. [Google Scholar] [CrossRef]



| Computation Parameters | Values |
|---|---|
| Permeability of vacuum /H/m | |
| Relative permeability of MRP fluids | 3 |
| Material characteristics of MRP fluids KE | 2.9 |
| Density of MRP fluids | 1980 |
| Radius of the polishing brush R/m | 0.015 |
| Radius of the workpiece R1/m | 0.015 |
| Modified Preston coefficient /m2/N | |
| Modified constant | 37.8 |
| Working gap h/m | 0.001 |
| Simulation Parameters | Values | |||
|---|---|---|---|---|
| Rotation speed of workpiece n/rpm | 150 | 300 * | 450 | 600 |
| Rotation speed of eccentric wheel n0/rpm | 10 | 20 * | 30 | 45 |
| Eccentricity e/m | 0.005 | 0.01 | 0.02 * | 0.04 |
| Constituents of MRP Fluids | Volume Fraction (vol.%) | Size (μm) |
|---|---|---|
| CIPs | 40 | 2.2 |
| CeO2 | 5 | 2.5 |
| SDS | 3 | - |
| Deionized water | 52 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Xiu, S.; Sun, C.; Li, S.; Kong, X. Study on Material Removal Model by Reciprocating Magnetorheological Polishing. Micromachines 2021, 12, 413. https://doi.org/10.3390/mi12040413
Wang R, Xiu S, Sun C, Li S, Kong X. Study on Material Removal Model by Reciprocating Magnetorheological Polishing. Micromachines. 2021; 12(4):413. https://doi.org/10.3390/mi12040413
Chicago/Turabian StyleWang, Rensheng, Shichao Xiu, Cong Sun, Shanshan Li, and Xiangna Kong. 2021. "Study on Material Removal Model by Reciprocating Magnetorheological Polishing" Micromachines 12, no. 4: 413. https://doi.org/10.3390/mi12040413
APA StyleWang, R., Xiu, S., Sun, C., Li, S., & Kong, X. (2021). Study on Material Removal Model by Reciprocating Magnetorheological Polishing. Micromachines, 12(4), 413. https://doi.org/10.3390/mi12040413





