The Effect of Edge Mode on Mass Sensing for Strained Graphene Resonators
Abstract
1. Introduction
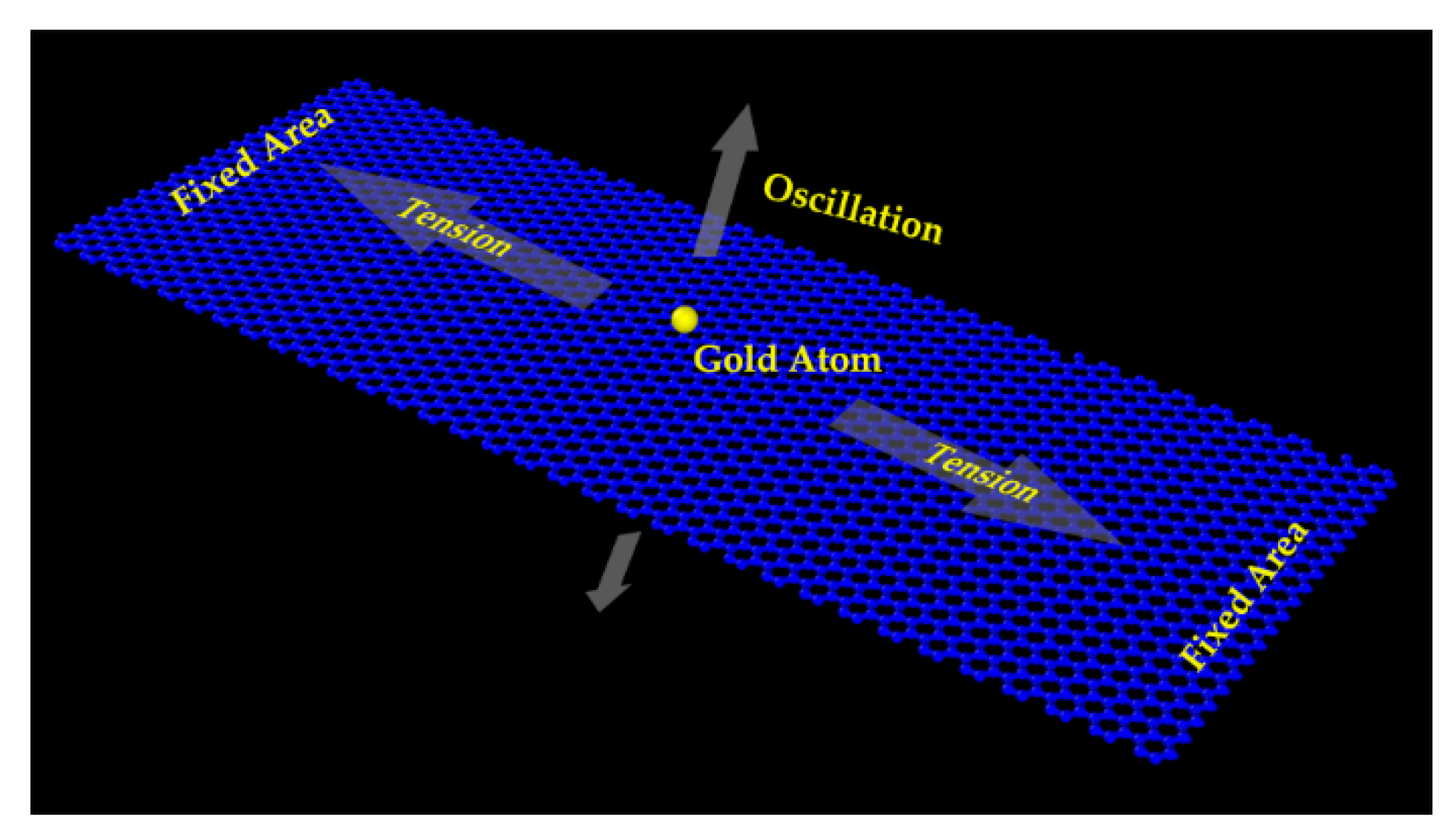
2. Simulation Structures and Methods
3. Results and Discussions
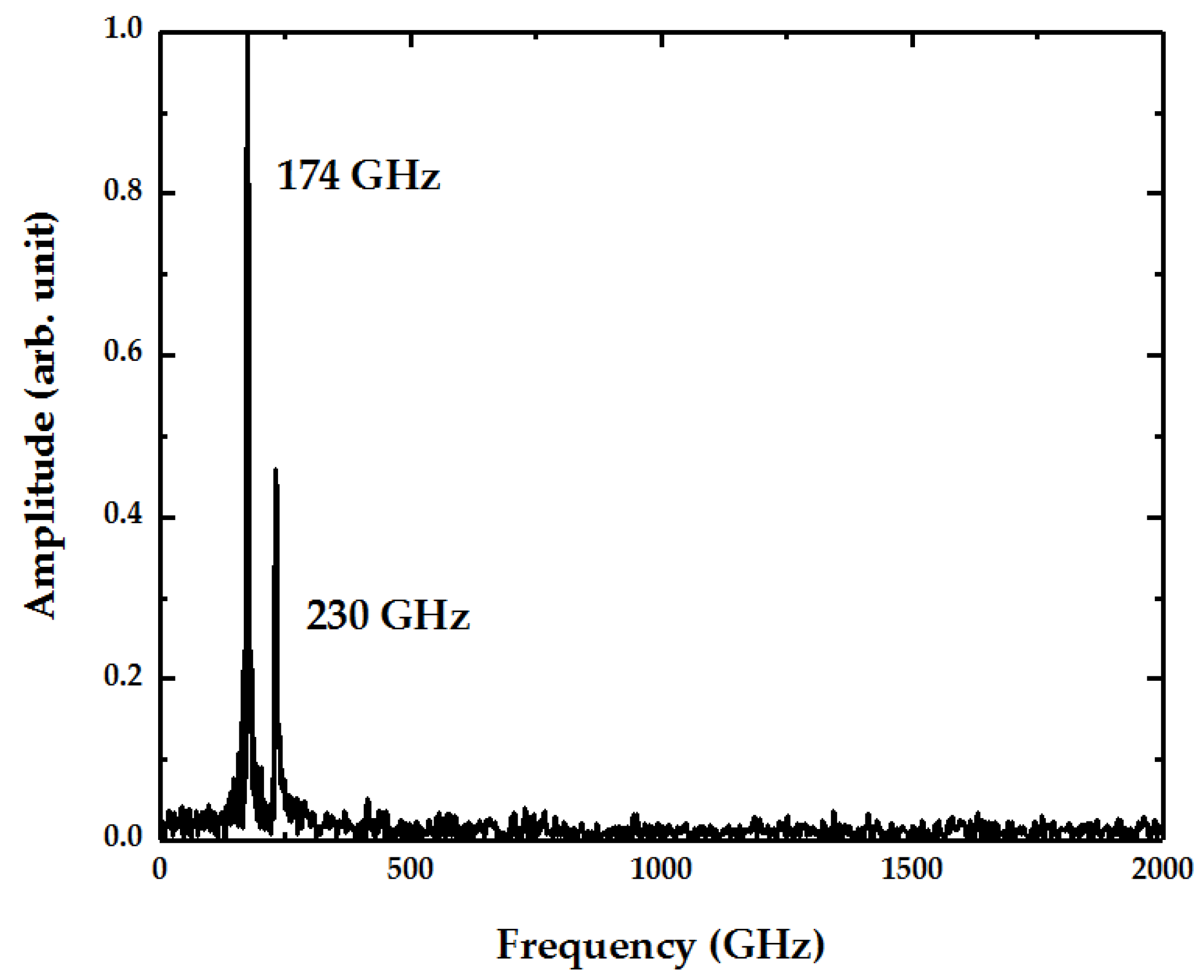
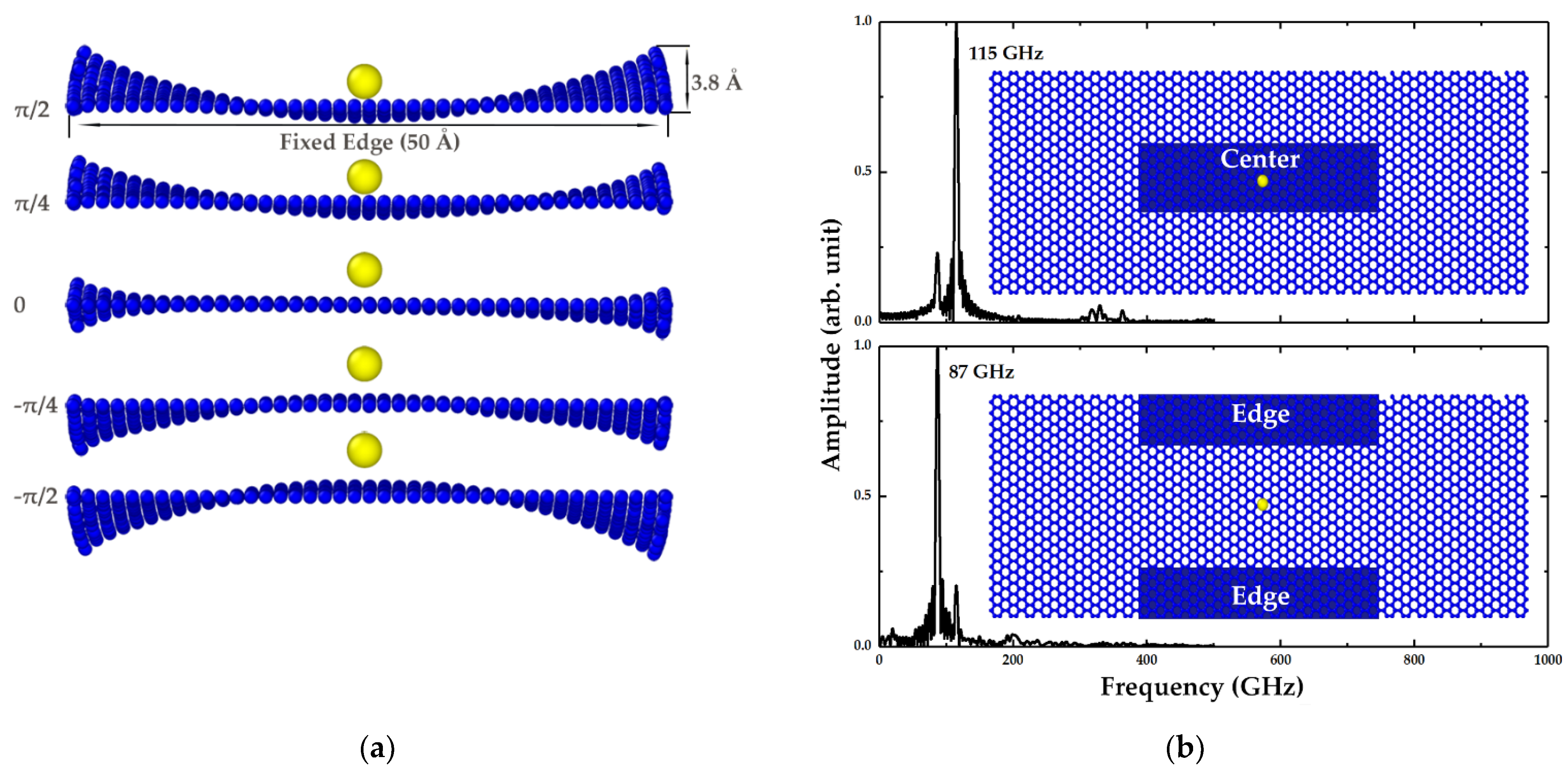
3.1. Two Distinct Vibration Eigenmodes
3.2. Effect of Edge Mode on Mass Sensing
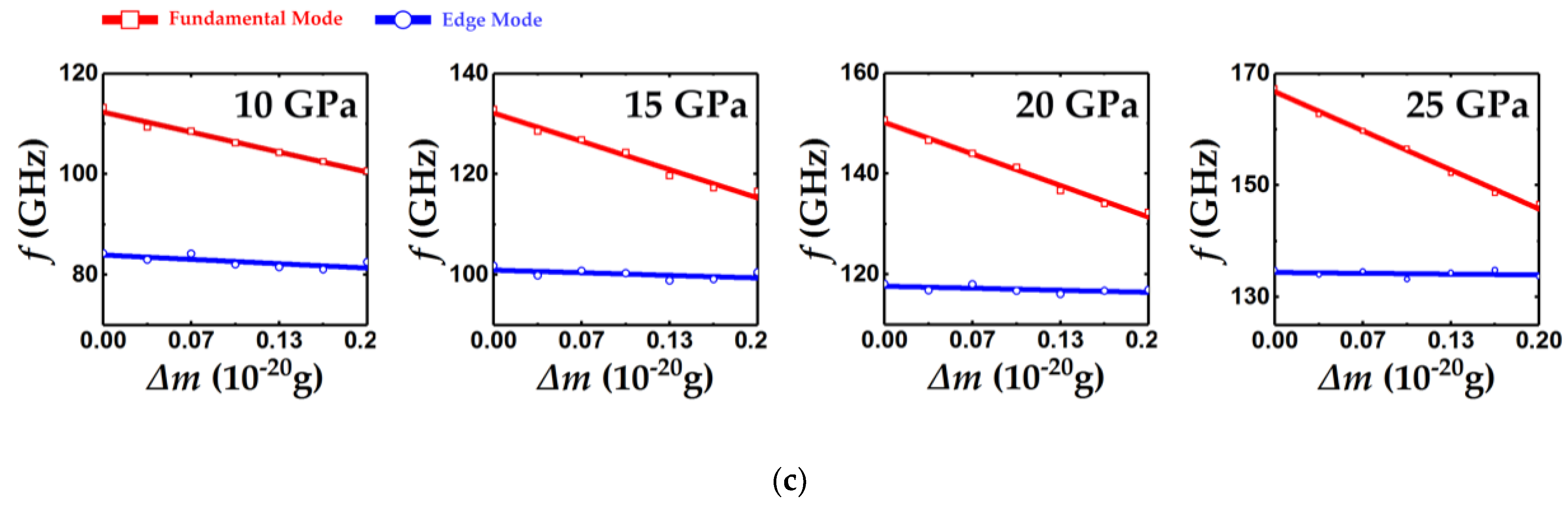
3.2.1. Distinct Response to Centrally Distributed Adsorbates
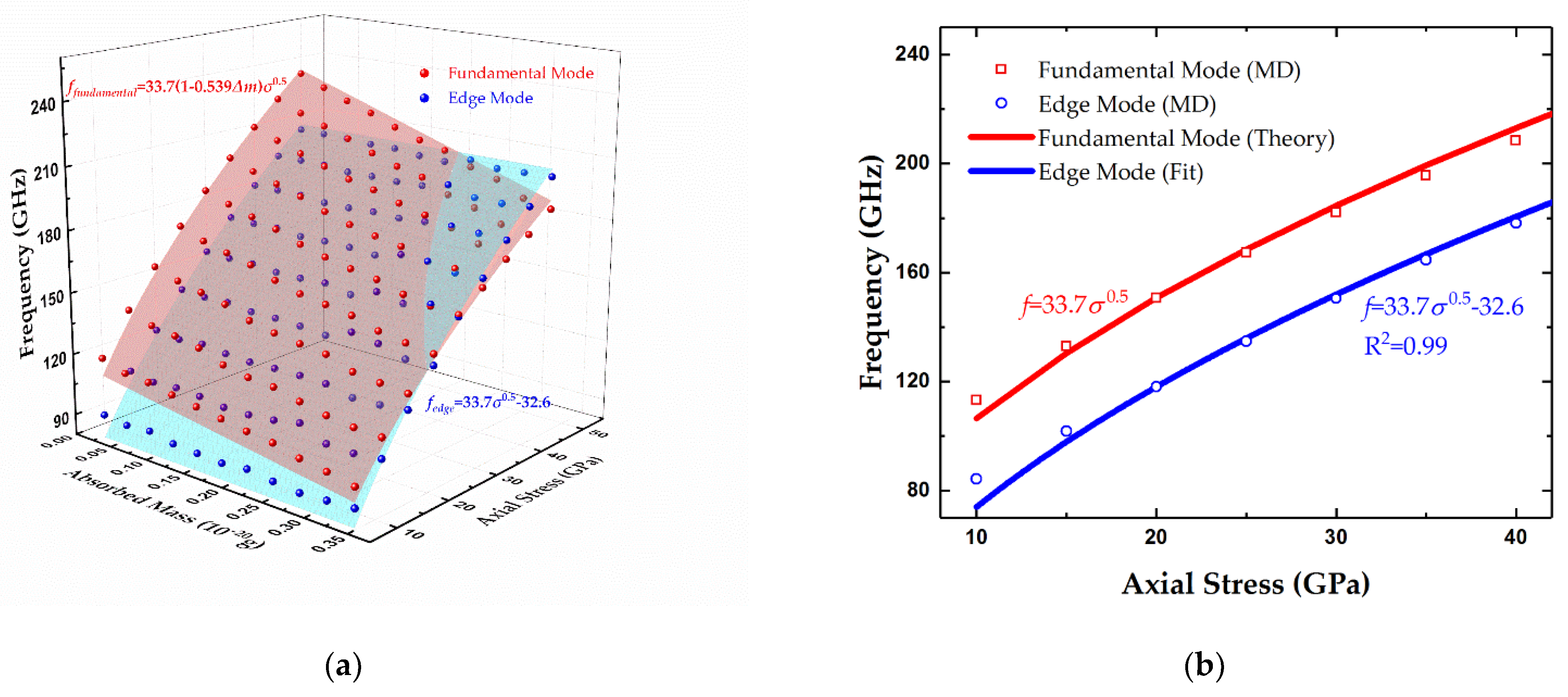
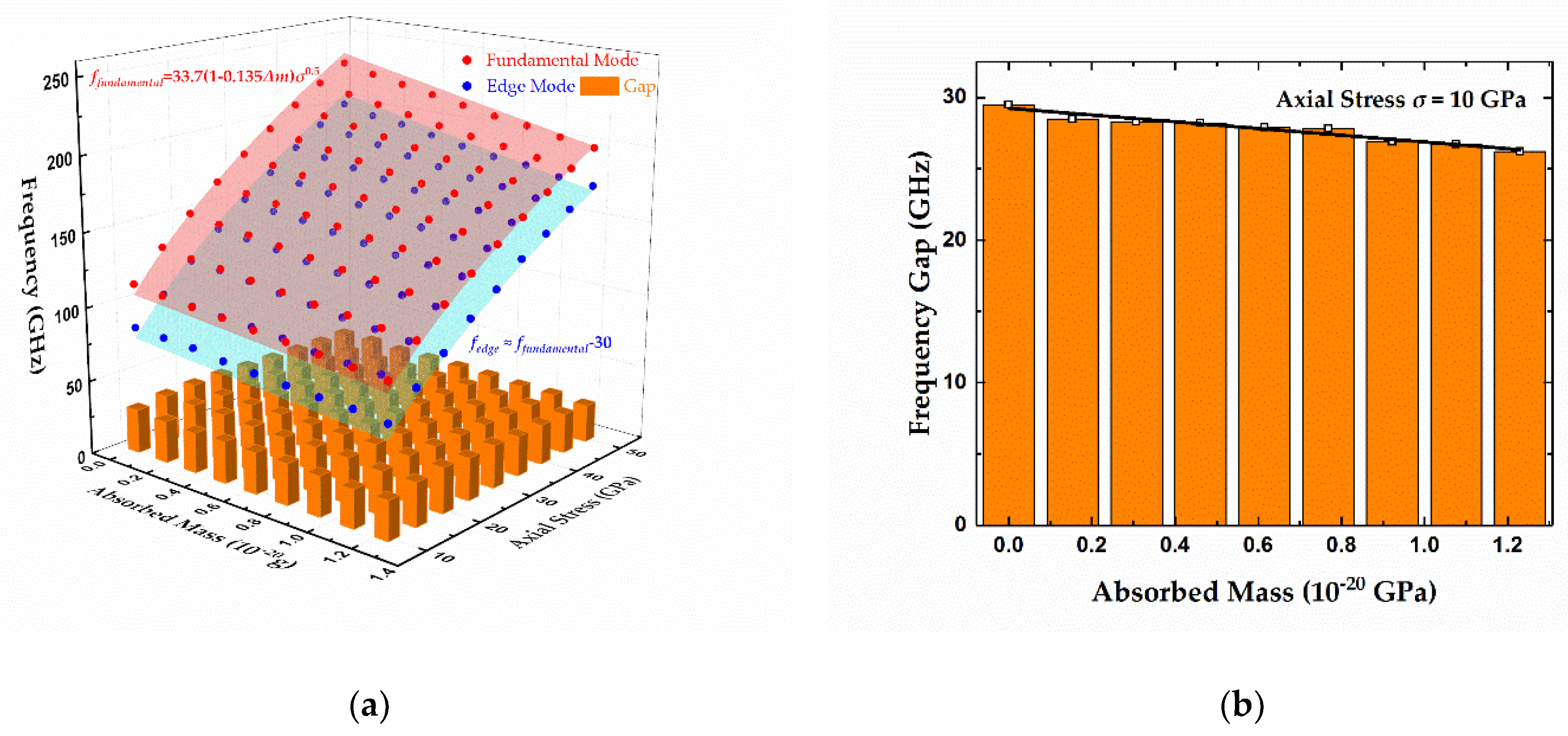
3.2.2. Determination of Centrally Distributed Mass in the Two Modes
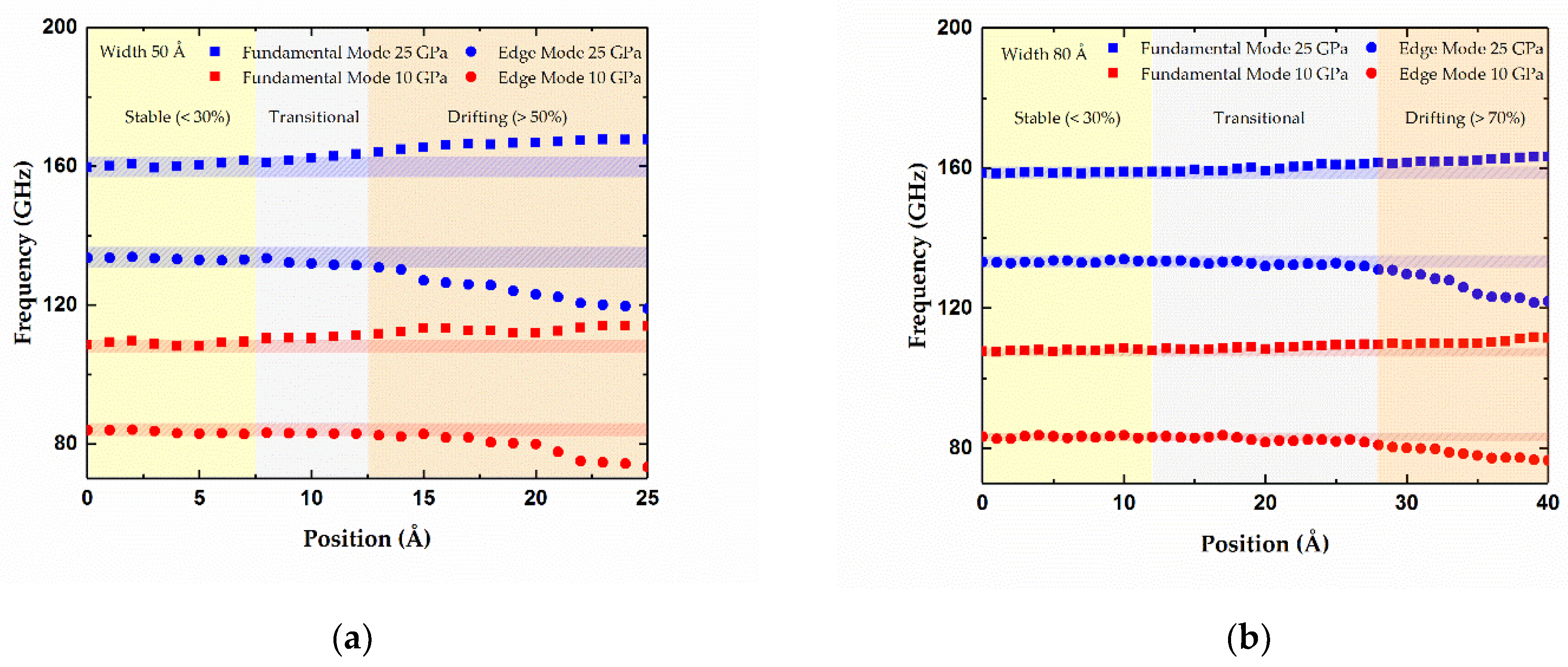
3.2.3. Constraints for Evenly Distributed Adsorbates
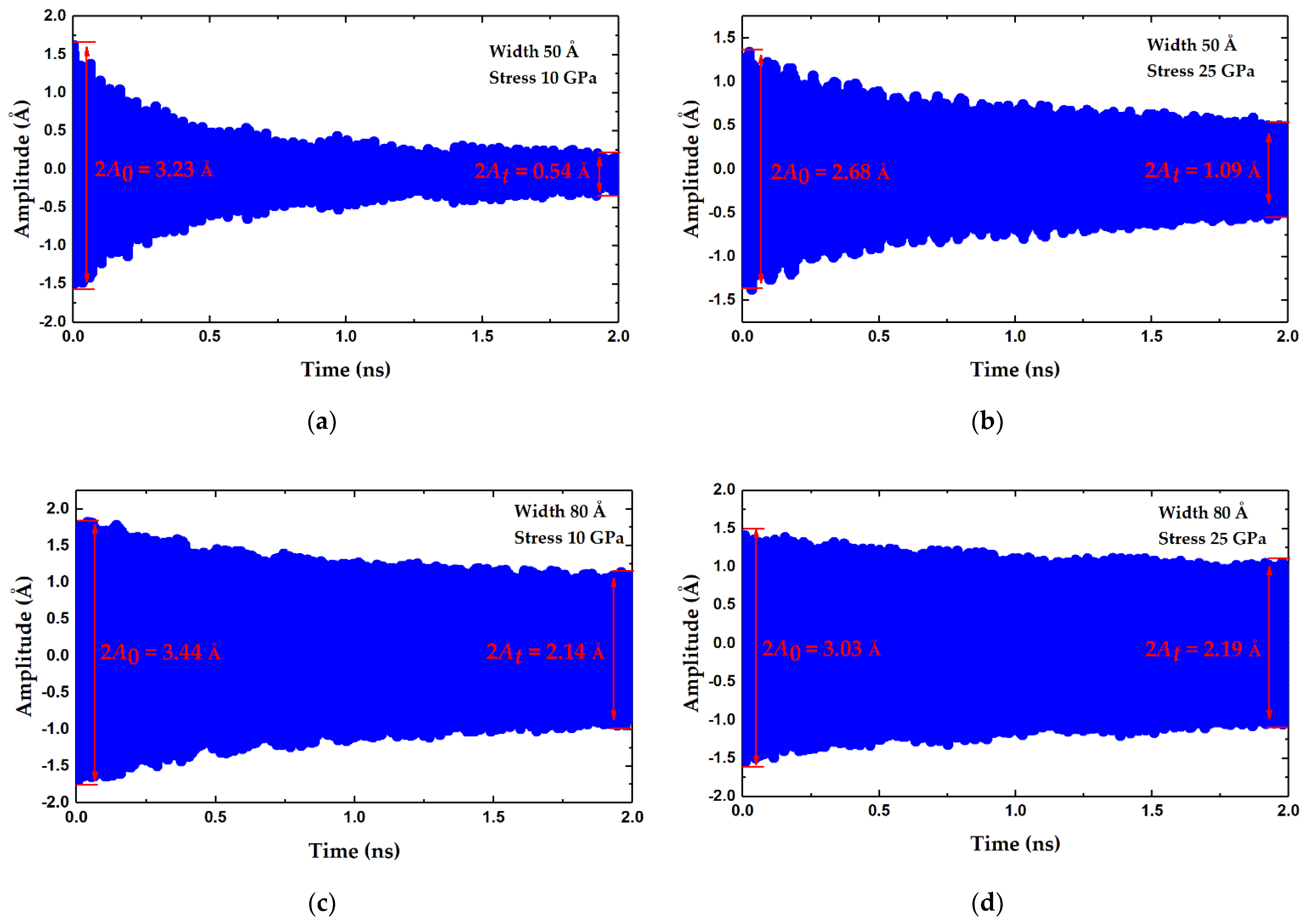
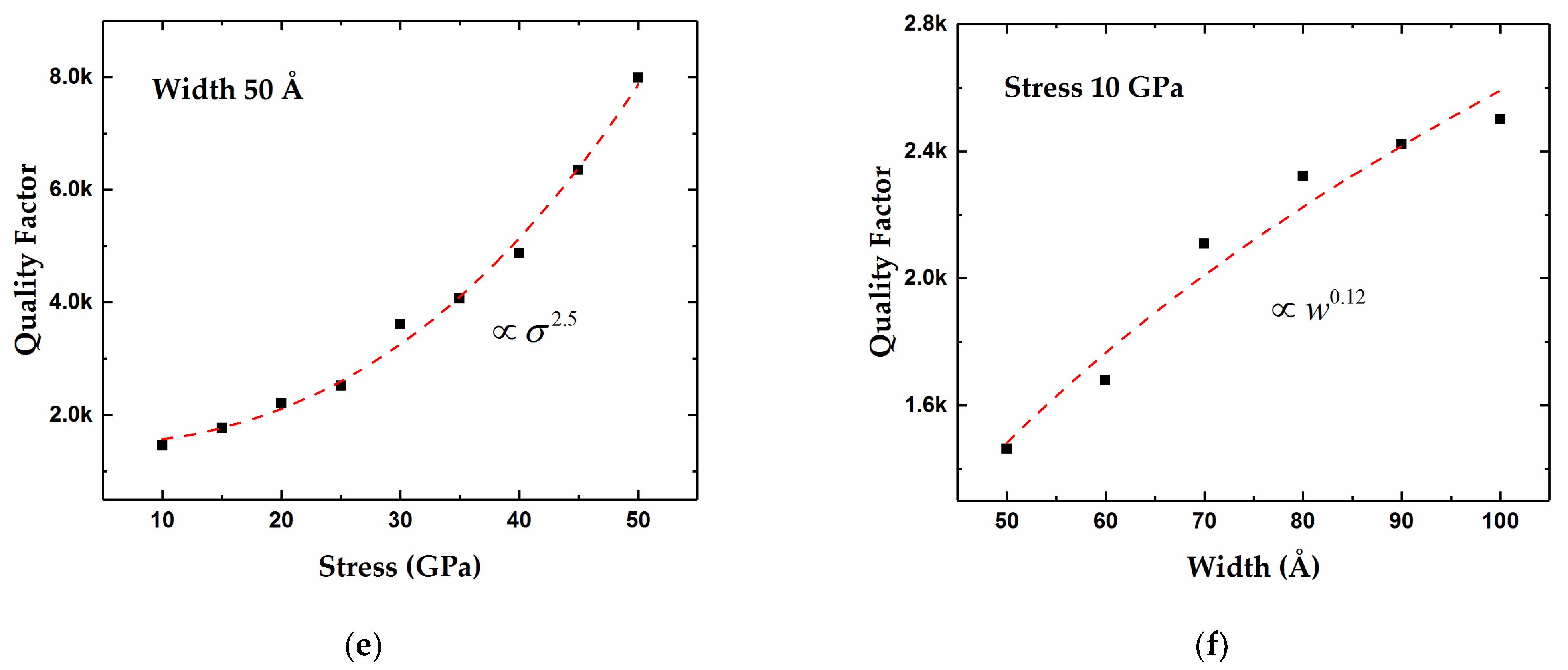
3.3. Effects of Edge Mode on the Q Factor
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef]
- Garciasanchez, D.; Van, A.D.Z.; Paulo, A.S.; Lassagne, B.; Mceuen, P.L.; Bachtold, A. Imaging mechanical vibrations in suspended graphene sheets. Nano Lett. 2008, 8, 1399–1403. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Rosenblatt, S.; Bolotin, K.I.; Kalb, W.; Kim, P.; Kymissis, I.; Stormer, H.L.; Heinz, T.F.; Hone, J. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 2009, 4, 861–867. [Google Scholar] [CrossRef]
- van der Zande, A.M.; Barton, R.A.; Alden, J.S.; Ruiz-Vargas, C.S.; Whitney, W.S.; Pham, P.H.; Park, J.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Large-scale arrays of single-layer graphene resonators. Nano Lett. 2010, 10, 4869–4873. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Navarro, C.; Burghard, M.; Kern, K. Elastic Properties of Chemically Derived Single Graphene Sheets. Nano Lett. 2008, 8, 2045–2049. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, B.; Wu, J.; Yang, R.; Dunn, M.L. Bending rigidity and Gaussian bending stiffness of single-layered graphene. Nano Lett. 2013, 13, 26–30. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Ren, P.; Wang, J.; Fan, C.; Er-Jun, L. Thermal Modulation of Plasmon Induced Transparency in Graphene Metamaterial. ES Energy Environ. 2020. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, Y.; Guo, J.; Lu, T.; Liu, J.; Zhou, J.; Xu, X. Superior Thermal Dissipation in Graphene Electronic Device Through Novel Heat Path by Electron-Phonon Coupling. ES Energy Environ. 2020. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Peres, N.M.R. The electronic properties of graphene and its bilayer. Vacuum 2009, 83, 1248–1252. [Google Scholar] [CrossRef]
- Sule, N.; Willis, K.J.; Hagness, S.C.; Knezevic, I. Simulation of carrier dynamics in graphene on a substrate at terahertz and mid-infrared frequencies. In Proceedings of the 2012 12th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Shanghai, China, 28–31 August 2012; pp. 79–80. [Google Scholar]
- Di Lecce, V.; Grassi, R.; Gnudi, A.; Gnani, E.; Reggiani, S.; Baccarani, G. Graphene Base Transistors: A Simulation Study of DC and Small-Signal Operation. IEEE Trans. Electron. Devices 2013, 60, 3584–3591. [Google Scholar] [CrossRef]
- Zhao, Y.; Niu, M.; Yang, F.; Jia, Y.; Cheng, Y. Ultrafast Electro-Thermal Responsive Heating Film Fabricated from Graphene Modified Conductive Materials. Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, S.; Long, Y.; Zhu, P.; Wu, F.; Liu, F.; Murugadoss, V.; Winchester, W.; Nautiyal, A.; Wang, Z.; et al. Recent Advances in Thermal Interface Materials. ES Mater. Manuf. 2020. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, H. An Integrated H-type Method to Measure Thermoelectric Properties of Two-dimensional Materials. ES Energy Environ. 2020. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Y.; Yin, R.; Zhao, W.; Li, X.; Qian, L. Magnetic negative permittivity with dielectric resonance in random Fe3O4@graphene-phenolic resin composites. Adv. Compos. Hybrid Mater. 2018, 1, 168–176. [Google Scholar] [CrossRef]
- Wu, N.; Bai, X.; Pan, D.; Dong, B.; Wei, R.; Naik, N.; Guo, Z. Recent Advances of Asymmetric Supercapacitors. Adv. Mater. Interfaces 2020, 8, 2001710. [Google Scholar] [CrossRef]
- Nidamanuri, N.; Li, Y.; Li, Q.; Dong, M. Graphene and Graphene Oxide-based Membranes for Gas Separation. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Nag, A.; Mitra, A.; Mukhopadhyay, S.C. Graphene and its sensor-based applications: A review. Sens. Actuators A Phys. 2018, 270, 177–194. [Google Scholar] [CrossRef]
- Kang, J.W.; Lee, J.H.; Hwang, H.J.; Kim, K.-S. Developing accelerometer based on graphene nanoribbon resonators. Phys. Lett. A 2012, 376, 3248–3255. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Hassanin, H.; Jumbu, N.; Deng, S.; Zuo, Q.; Jiang, K. Graphene–Alumina Nanocomposites with Improved Mechanical Properties for Biomedical Applications. ACS Appl. Mater. Interfaces 2016, 8, 2607–2616. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Shi, G. Graphene-based gas sensors. J. Mater. Chem. A 2013, 1, 10078. [Google Scholar] [CrossRef]
- Wehling, T.O.; Katsnelson, M.I.; Lichtenstein, A.I. Adsorbates on graphene: Impurity states and electron scattering. Chem. Phys. Lett. 2009, 476, 125–134. [Google Scholar] [CrossRef]
- Crowther, A.C.; Ghassaei, A.; Jung, N.; Brus, L.E. Strong Charge-Transfer Doping of 1 to 10 Layer Graphene by NO2. ACS Nano 2012, 6, 1865–1875. [Google Scholar] [CrossRef]
- Lu, G.; Park, S.; Yu, K.; Ruoff, R.S.; Ocola, L.E.; Rosenmann, D.; Chen, J. Toward Practical Gas Sensing with Highly Reduced Graphene Oxide: A New Signal Processing Method To Circumvent Run-to-Run and Device-to-Device Variations. ACS Nano 2011, 5, 1154–1164. [Google Scholar] [CrossRef]
- Duan, K.; Li, L.; Hu, Y.; Wang, X. Pillared graphene as an ultra-high sensitivity mass sensor. Sci. Rep. 2017, 7, 14012. [Google Scholar] [CrossRef]
- Jiang, J.W.; Park, H.S.; Rabczuk, T. Enhancing the mass sensitivity of graphene nanoresonators via nonlinear oscillations: The effective strain mechanism. Nanotechnology 2012, 23, 475501. [Google Scholar] [CrossRef] [PubMed]
- Arash, B.; Wang, Q.; Duan, W.H. Detection of gas atoms via vibration of graphenes. Phys. Lett. A 2011, 375, 2411–2415. [Google Scholar] [CrossRef]
- Kim, S.Y.; Park, H.S. On the utility of vacancies and tensile strain-induced quality factor enhancement for mass sensing using graphene monolayers. Nanotechnology 2010, 21, 105710. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kwon, O.K.; Kim, K.-S.; Park, J.; Kang, J.W. Molecular dynamics modeling and simulations of graphene-nanoribbon-resonator-based nanobalance as yoctogram resolution detector. Comput. Mater. Sci. 2013, 67, 329–333. [Google Scholar] [CrossRef]
- Youb Kim, S.; Park, S.H. The Importance of Edge Effects on the Intrinsic Loss Mechanisms of Graphene Nanoresonators. Nano Lett. 2009, 9, 969–974. [Google Scholar] [CrossRef]
- Kang, D.-K.; Yang, H.-I.; Kim, C.-W. Geometrically nonlinear dynamic behavior on detection sensitivity of carbon nanotube-based mass sensor using finite element method. Finite Elem. Anal. Des. 2017, 126, 39–49. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Tang, H.-L.; Li, D.-K.; Tang, G.-J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Eringen, A.C.; Wegner, J.L. Nonlocal Continuum Field Theories. Appl. Mech. Rev. 2003, 56, B20–B22. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A.; Ahmadian, M.T.; Vafai, A. Applications of single-layered graphene sheets as mass sensors and atomistic dust detectors. Solid State Commun. 2008, 145, 168–172. [Google Scholar] [CrossRef]
- Baimova, J.A.; Dmitriev, S.V.; Zhou, K. Strain-induced ripples in graphene nanoribbons with clamped edges. Phys. Status Solidi (b) 2012, 249, 1393–1398. [Google Scholar] [CrossRef]
- Le, M.-Q.; Batra, R.C. Mode-I stress intensity factor in single layer graphene sheets. Comput. Mater. Sci. 2016, 118, 251–258. [Google Scholar] [CrossRef]
- Fu, Y.; Zhao, P.; Yang, L.; Miao, R.; Zhang, C.; Guo, Z.; Liu, Y. Effect of Cocrystal Behavior on Sensitivity and Thermal Decomposition Mechanisms of CL-20/HMX via Molecular Dynamics Simulations. ES Mater. Manuf. 2018. [Google Scholar] [CrossRef]
- Tang, C.; Yu, X.; Li, G.; Yang, N.; Lü, J. Phonon Thermal Transport Properties of Graphene Periodically Embedded with Four- and Eight-membered Rings: A Molecular Dynamics Study. ES Mater. Manuf. 2018. [Google Scholar] [CrossRef]
- Zhang, B.; Mao, P.; Liang, Y.; He, Y.; Liu, W.; Liu, Z. Modulating Thermal Transport in Polymers and Interfaces: Theories, Simulations, and Experiments. ES Energy Environ. 2019. [Google Scholar] [CrossRef]
- Jiang, J.-W.; Wang, J.-S. Why edge effects are important on the intrinsic loss mechanisms of graphene nanoresonators. J. Appl. Phys. 2012, 111, 054314. [Google Scholar] [CrossRef]
- Rapaport, D.C.; Blumberg, R.L.; Mckay, S.R.; Christian, W. The Art of Molecular Dynamics Simulation. Comput. Sci. Eng. 2002, 1, 70–71. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical model for the structural properties of silicon. Phys. Rev. Lett. 1986, 56, 632–635. [Google Scholar] [CrossRef]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458–9471. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- O’Connor, T.C.; Andzelm, J.; Robbins, M.O. AIREBO-M: A reactive model for hydrocarbons at extreme pressures. J. Chem. Phys. 2015, 142, 024903. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Wongkoblap, A.; Junpirom, S.; Do, D.D. Adsorption of Lennard-Jones fluids in carbon slit pores of a finite length. A computer simulation study. Adsorpt. Sci. Technol. 2005, 23, 1–18. [Google Scholar] [CrossRef]
- Xiao, X.; Fan, S.-C.; Li, C.; Xing, W.-W. Stress-Insensitive Resonant Graphene Mass Sensing via Frequency Ratio. Sensors 2019, 19, 3027. [Google Scholar] [CrossRef] [PubMed]
- Atalaya, J.; Isacsson, A.; Kinaret, M.J. Continuum Elastic Modeling of Graphene Resonators. Nano Lett. 2008, 8, 4196–4200. [Google Scholar] [CrossRef]
- Alexander, S. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Yasumura, K.Y.; Stowe, T.D.; Chow, E.M.; Pfafman, T.; Kenny, T.W.; Stipe, B.C.; Rugar, D. Quality factors in micron- and submicron-thick cantilevers. J. Microelectromech. Syst. 2000, 9, 117–125. [Google Scholar] [CrossRef]
- Ekinci, K.L.; Roukes, M.L. Nanoelectromechanical systems. Rev. Sci. Instrum. 2005, 76, 061101. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Fan, S.-C.; Li, C. The Effect of Edge Mode on Mass Sensing for Strained Graphene Resonators. Micromachines 2021, 12, 189. https://doi.org/10.3390/mi12020189
Xiao X, Fan S-C, Li C. The Effect of Edge Mode on Mass Sensing for Strained Graphene Resonators. Micromachines. 2021; 12(2):189. https://doi.org/10.3390/mi12020189
Chicago/Turabian StyleXiao, Xing, Shang-Chun Fan, and Cheng Li. 2021. "The Effect of Edge Mode on Mass Sensing for Strained Graphene Resonators" Micromachines 12, no. 2: 189. https://doi.org/10.3390/mi12020189
APA StyleXiao, X., Fan, S.-C., & Li, C. (2021). The Effect of Edge Mode on Mass Sensing for Strained Graphene Resonators. Micromachines, 12(2), 189. https://doi.org/10.3390/mi12020189






