Numerical and Experimental Study of Cross-Sectional Effects on the Mixing Performance of the Spiral Microfluidics
Abstract
:1. Introduction
2. Materials and Methods
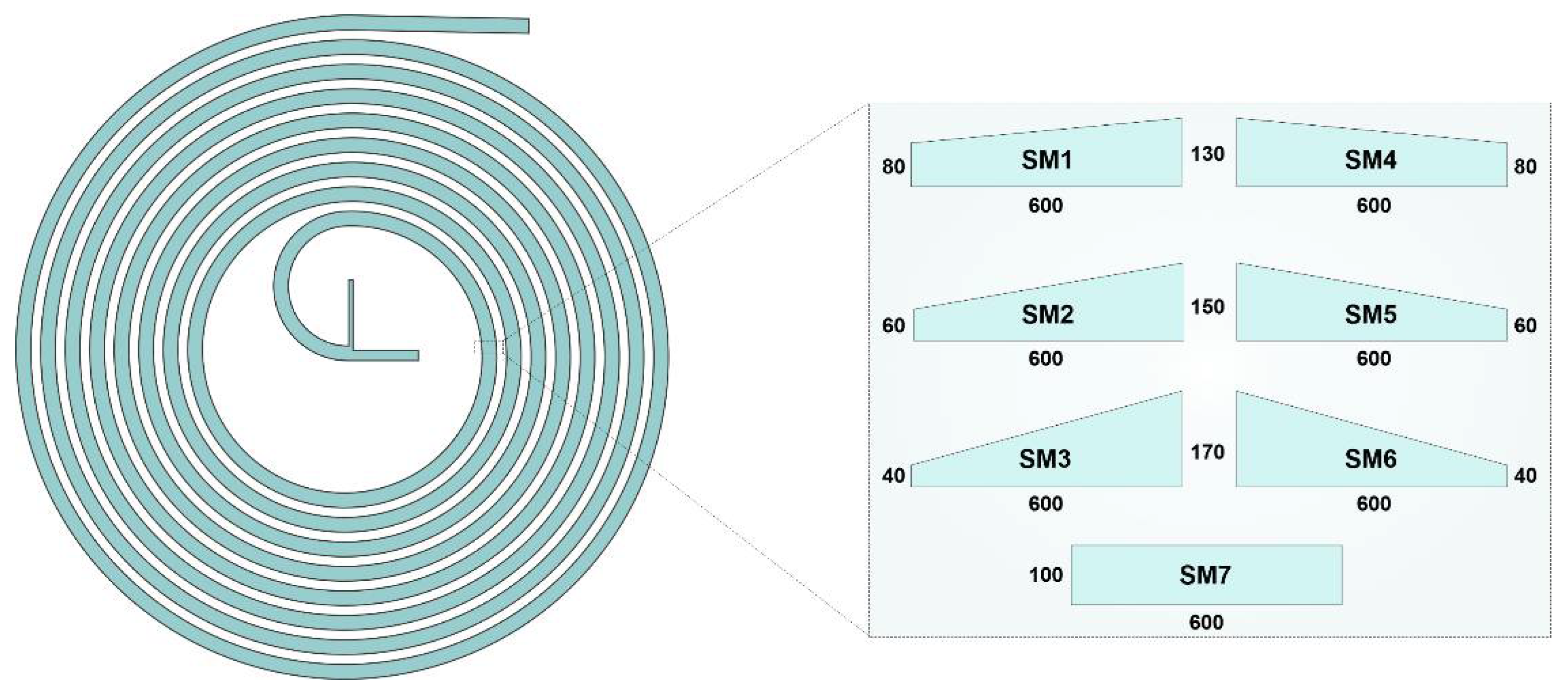
2.1. Spiral Designs and Fabrication Methods
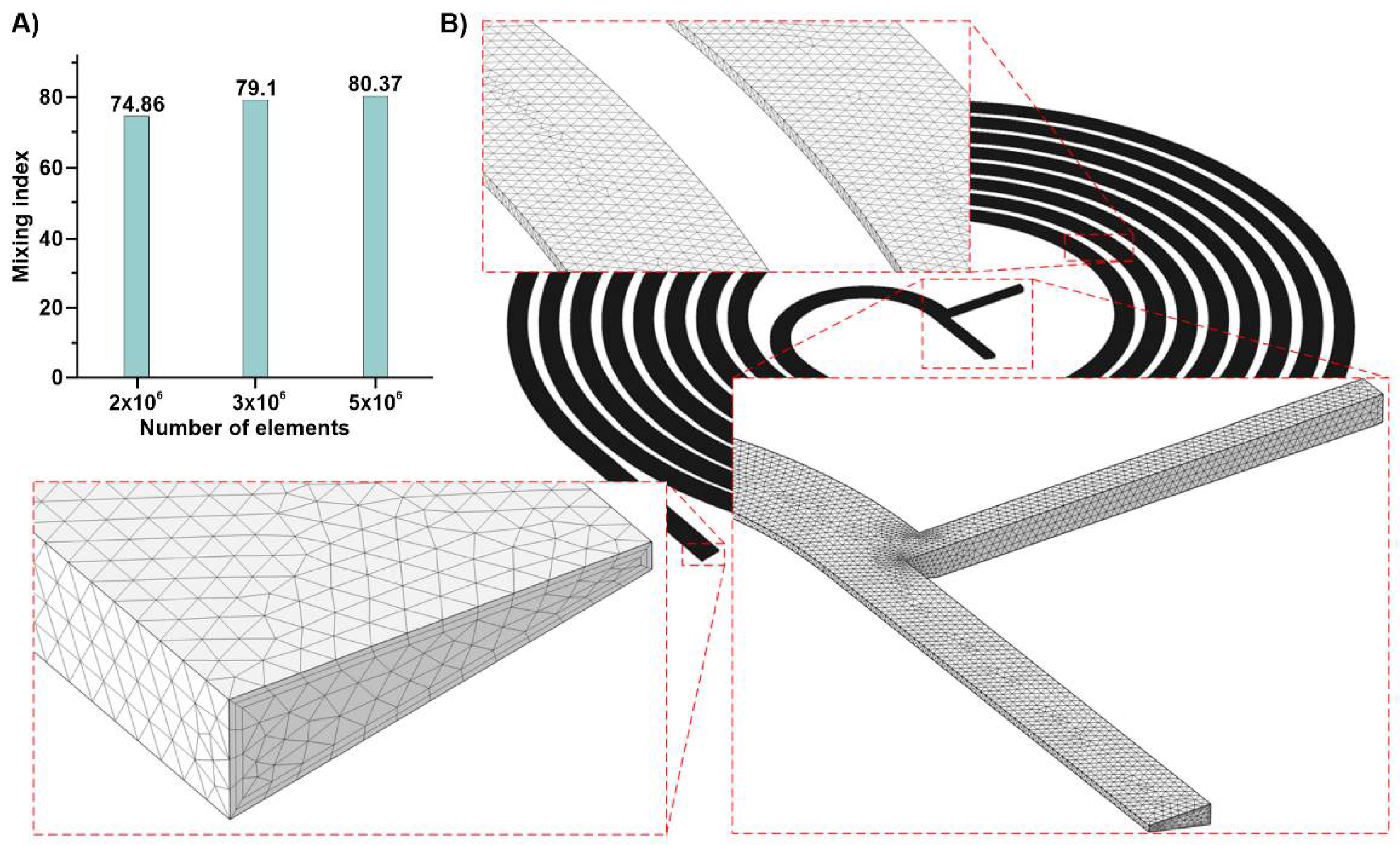
2.2. Numerical Model
2.3. Sample Preparation
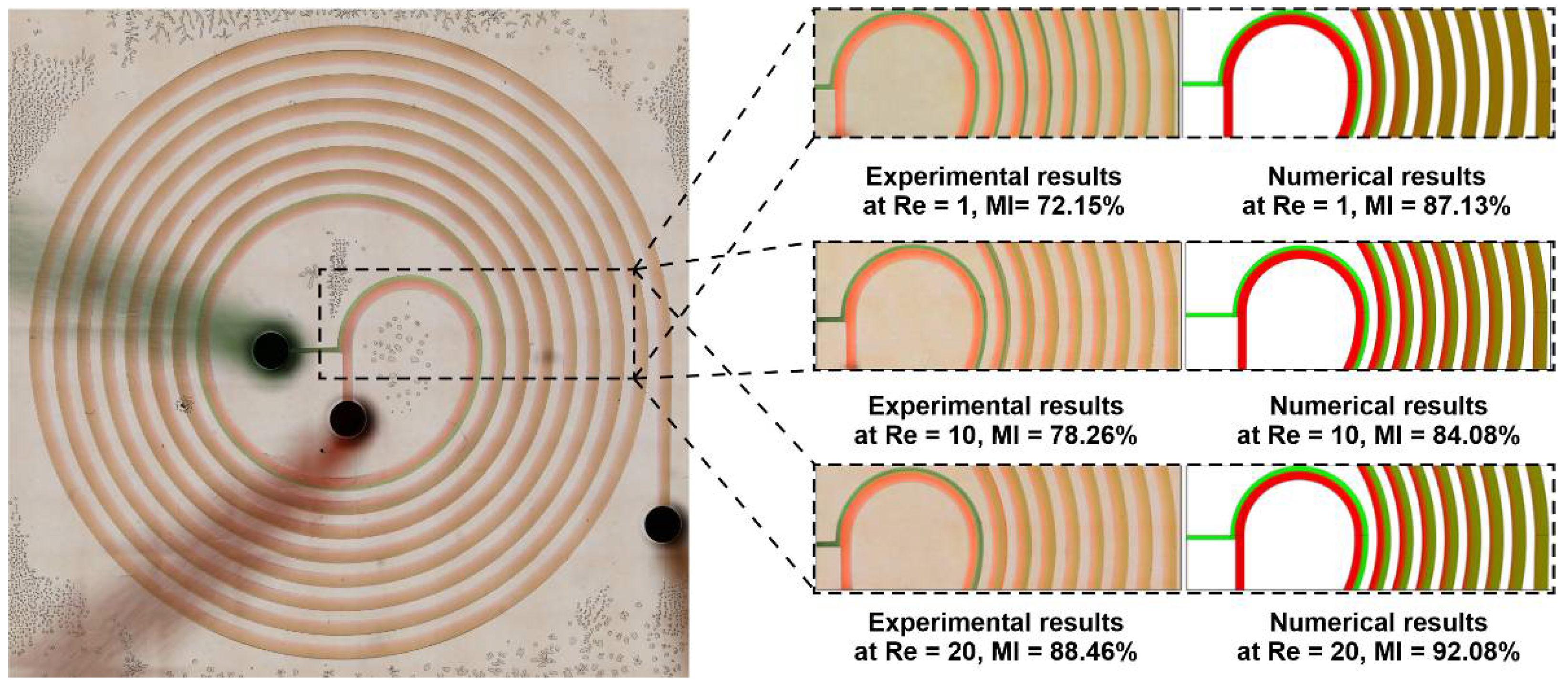
2.4. Experimental Results
3. Results and Discussions
3.1. Grid Study
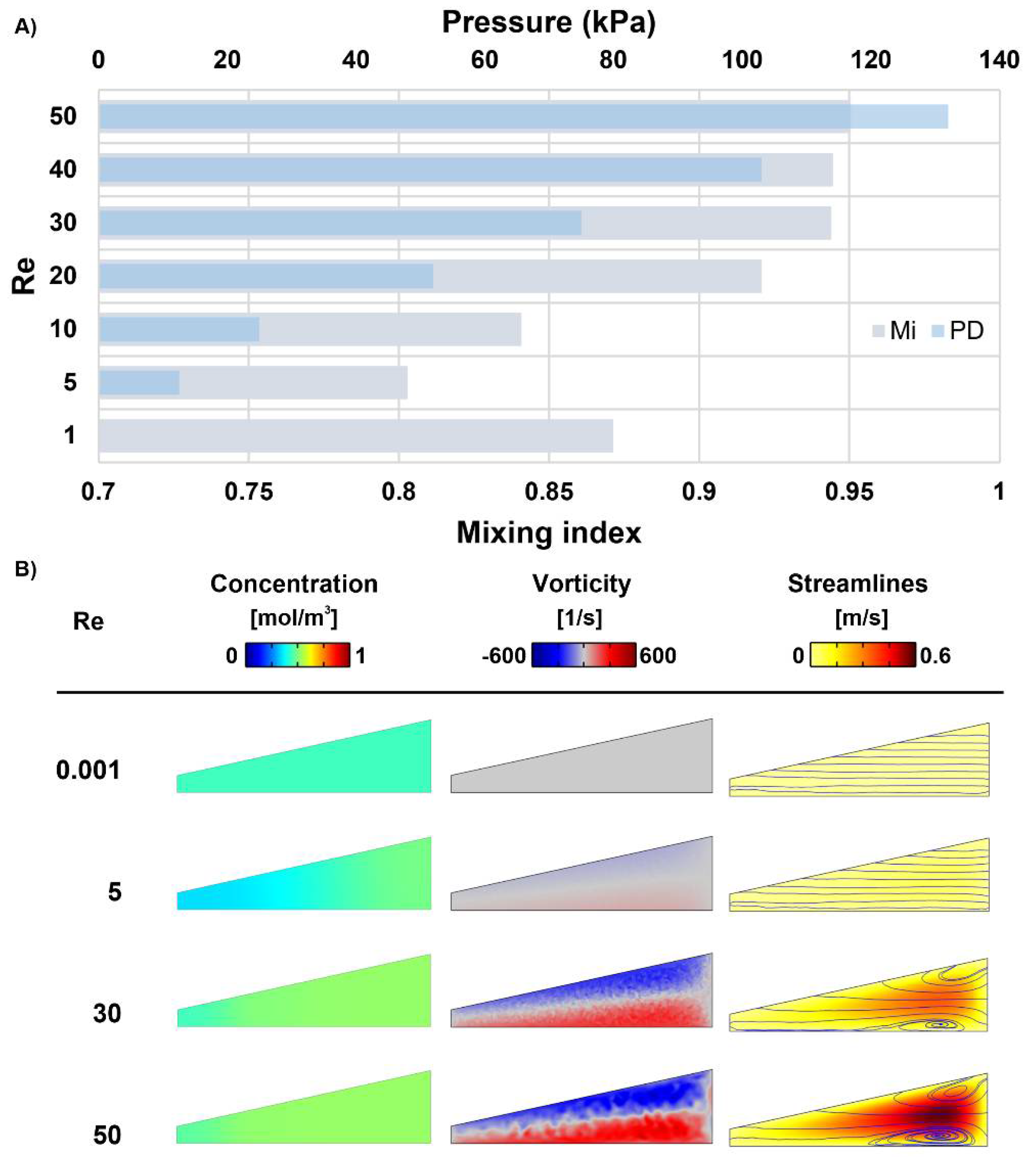
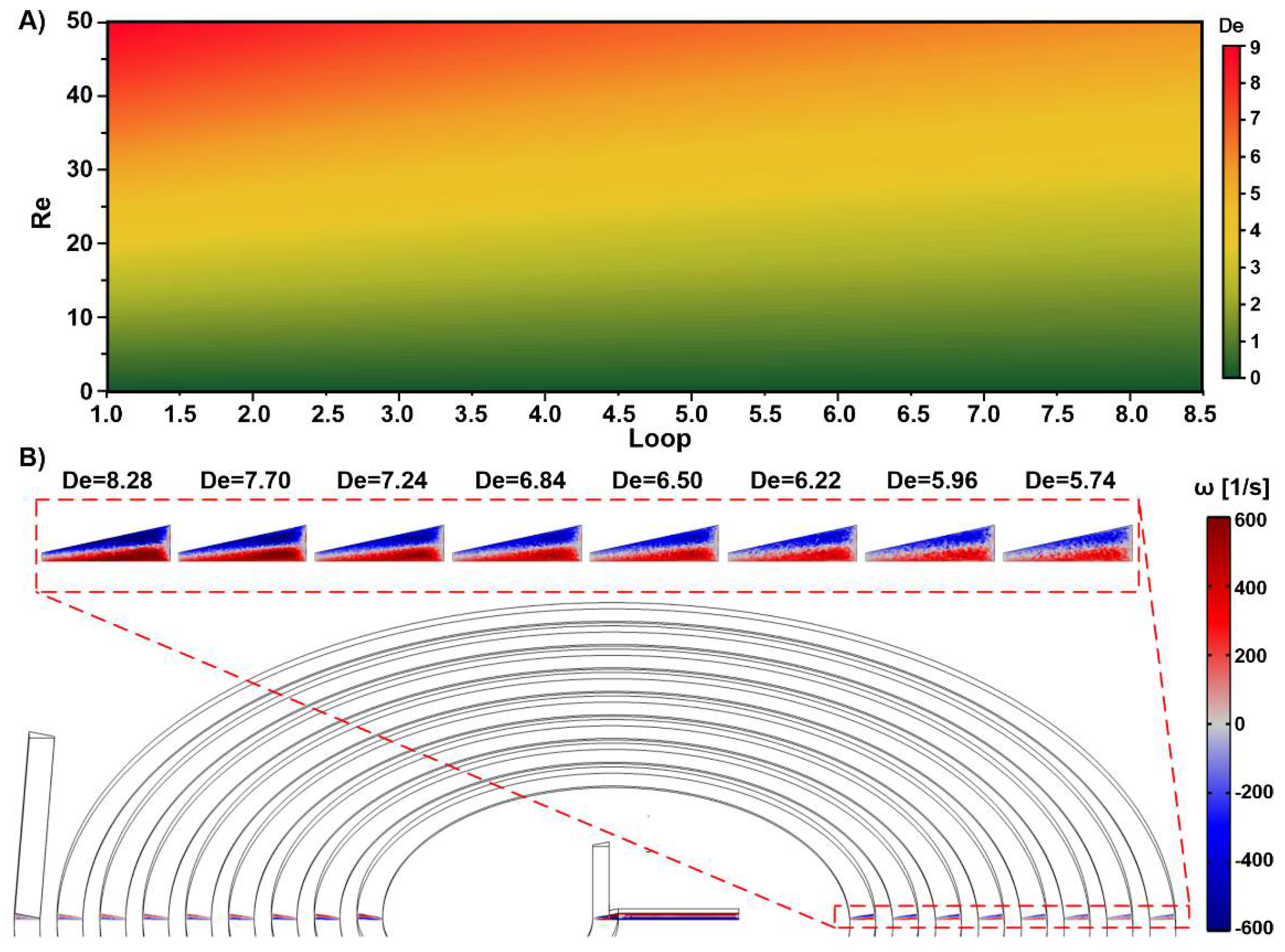
3.2. Spiral Micromixers with Various Cross-Sections
3.3. Numerical Validation
3.4. Nominated Designs: A Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franke, T.A.; Wixforth, A. Microfluidics for Miniaturized Laboratories on a Chip. ChemPhysChem 2008, 9, 2140–2156. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Damiati, S.; Kompella, U.B.; Damiati, S.A.; Kodzius, R. Microfluidic Devices for Drug Delivery Systems and Drug Screening. Genes 2018, 9, 103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, J.Y.; Wiederoder, M.; DeVoe, D.L. Isolation of intact bacteria from blood by selective cell lysis in a microfluidic porous silica monolith. Microsyst. Nanoeng. 2019, 5, 30. [Google Scholar] [CrossRef] [Green Version]
- Rzhevskiy, A.S.; Razavi Bazaz, S.; Ding, L.; Kapitannikova, A.; Sayyadi, N.; Campbell, D.; Walsh, B.; Gillatt, D.; Ebrahimi Warkiani, M.; Zvyagin, A.V. Rapid and Label-Free Isolation of Tumour Cells from the Urine of Patients with Localised Prostate Cancer Using Inertial Microfluidics. Cancers 2019, 12, 81. [Google Scholar] [CrossRef] [Green Version]
- Nowbahar, A.; Mansard, V.; Mecca, J.M.; Paul, M.; Arrowood, T.; Squires, T.M. Measuring Interfacial Polymerization Kinetics Using Microfluidic Interferometry. J. Am. Chem. Soc. 2018, 140, 3173–3176. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Xu, J.; Ma, W.; Zheng, W. PCR microfluidic devices for DNA amplification. Biotechnol. Adv. 2006, 24, 243–284. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.-h.; Xiao, Y.; Ferguson, S.; Huang, X.; Wang, N.; Hao, H.-X. Progress of crystallization in microfluidic devices. Lab A Chip 2017, 17, 2167–2185. [Google Scholar] [CrossRef] [PubMed]
- DeMello, A.J. Control and detection of chemical reactions in microfluidic systems. Nature 2006, 442, 394–402. [Google Scholar] [CrossRef] [PubMed]
- Lang, Q.; Ren, Y.; Hobson, D.; Tao, Y.; Hou, L.; Jia, Y.; Hu, Q.; Liu, J.; Zhao, X.; Jiang, H. In-plane microvortices micromixer-based AC electrothermal for testing drug induced death of tumor cells. Biomicrofluidics 2016, 10, 064102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minteer, S.D. Microfluidic Techniques: Reviews and Protocols; Humana Press: Totowa, NJ, USA, 2005. [Google Scholar]
- Channon, R.B.; Menger, R.F.; Wang, W.; Carrão, D.B.; Vallabhuneni, S.; Kota, A.K.; Henry, C.S. Design and application of a self-pumping microfluidic staggered herringbone mixer. Microfluid Nanofluid. 2021, 25, 31. [Google Scholar] [CrossRef]
- Rampalli, S.; Dundi, T.M.; Chandrasekhar, S.; Raju, V.R.K.; Chandramohan, V.P. Numerical Evaluation of Liquid Mixing in a Serpentine Square Convergent-divergent Passive Micromixer. Chem. Prod. Process. Model. 2020, 20190071. [Google Scholar] [CrossRef]
- Bazaz, S.R.; Hazeri, A.; Mchrizi, A.A. Increasing Efficiency of Micromixing Within a Biomicrofluidic Device Using Acceleration, Deceleration Technique. In Proceedings of the 2017 24th National and 2nd International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 30 November–1 December 2017; pp. 315–327. [Google Scholar]
- Tripathi, E.; Patowari, P.K.; Pati, S. Numerical investigation of mixing performance in spiral micromixers based on Dean flows and chaotic advection. Chem. Eng. Process.Process. Intensif. 2021, 169, 108609. [Google Scholar] [CrossRef]
- Bazaz, S.R.; Mehrizi, A.A.; Ghorbani, S.; Vasilescu, S.; Asadnia, M.; Warkiani, M.E. A hybrid micromixer with planar mixing units. RSC Adv. 2018, 8, 33103–33120. [Google Scholar] [CrossRef] [Green Version]
- Dean, W.R.; Hurst, J.M.J.M. Note on the motion of fluid in a curved pipe. Mathematika 1959, 6, 77–85. [Google Scholar] [CrossRef]
- Dean, W.R. The streamline motion of fluid in a curved pipe. Phil. Mag. 1928, 5, 673–693. [Google Scholar] [CrossRef]
- Nhien, N.T.T.; Huy, N.T.; Uyen, D.T.; Deharo, E.; Hoa, P.T.L.; Hirayama, K.; Harada, S.; Kamei, K. Effect of Inducers, Incubation Time and Heme Concentration on IC(50) Value Variation in Anti-heme Crystallization Assay. Trop. Med. Health 2011, 39, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Debayle, M.; Balloul, E.; Dembele, F.; Xu, X.; Hanafi, M.; Ribot, F.; Monzel, C.; Coppey, M.; Fragola, A.; Dahan, M.; et al. Zwitterionic polymer ligands: An ideal surface coating to totally suppress protein-nanoparticle corona formation? Biomaterials 2019, 219, 119357. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahmoodi, Z.; Mohammadnejad, J.; Razavi Bazaz, S.; Abouei Mehrizi, A.; Ghiass, M.A.; Saidijam, M.; Dinarvand, R.; Ebrahimi Warkiani, M.; Soleimani, M. A simple coating method of PDMS microchip with PTFE for synthesis of dexamethasone-encapsulated PLGA nanoparticles. Drug Deliv. Transl. Res. 2019, 9, 707–720. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-T.; Wereley, S.T.; Shaegh, S.A.M. Fundamentals and Applications of Microfluidics; Artech House: Norwood, MA, USA, 2019. [Google Scholar]
- Howell, J.P.B.; Mott, D.R.; Golden, J.P.; Ligler, F.S. Design and evaluation of a Dean vortex-based micromixer. Lab A Chip 2004, 4, 663–669. [Google Scholar] [CrossRef] [PubMed]
- Sudarsan, A.P.; Ugaz, V.M. Fluid mixing in planar spiral microchannels. Lab A Chip 2006, 6, 74–82. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X.; Feng, X.; Yang, C.; Mao, Z.-S. Investigation of Mixing Performance in Passive Micromixers. Ind. Eng. Chem. Res. 2016, 55, 10036–10043. [Google Scholar] [CrossRef]
- Kumar, V.; Aggarwal, M.; Nigam, K.D.P. Mixing in curved tubes. Chem. Eng. Sci. 2006, 61, 5742–5753. [Google Scholar] [CrossRef]
- Duryodhan, V.S.; Chatterjee, R.; Govind Singh, S.; Agrawal, A. Mixing in planar spiral microchannel. Exp. Therm. Fluid Sci. 2017, 89, 119–127. [Google Scholar] [CrossRef]
- Vatankhah, P.; Shamloo, A. Parametric study on mixing process in an in-plane spiral micromixer utilizing chaotic advection. Anal. Chim. Acta 2018, 1022, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, Z.; Wang, B.; Cai, Y.; Wan, Y. Vortices degradation and periodical variation in spiral micromixers with various spiral structures. Int. J. Heat Mass Transf. 2022, 183, 122168. [Google Scholar] [CrossRef]
- Niculescu, A.-G.; Chircov, C.; Bîrcă, A.C.; Grumezescu, A.M. Fabrication and Applications of Microfluidic Devices: A Review. Int. J. Mol. Sci. 2021, 22, 2011. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Whitesides, G.M. Soft Lithography. Annu. Rev. Mater. Sci. 1998, 37, 550–575. [Google Scholar] [CrossRef]
- Gale, B.K.; Jafek, A.R.; Lambert, C.J.; Goenner, B.L.; Moghimifam, H.; Nze, U.C.; Kamarapu, S.K. A Review of Current Methods in Microfluidic Device Fabrication and Future Commercialization Prospects. Inventions 2018, 3, 60. [Google Scholar] [CrossRef] [Green Version]
- Razavi Bazaz, S.; Hazeri, A.H.; Rouhi, O.; Mehrizi, A.A.; Jin, D.; Warkiani, M.E. Volume-preserving strategies to improve the mixing efficiency of serpentine micromixers. J. Micromech. Microeng. 2020, 30, 115022. [Google Scholar] [CrossRef]
- Chai, M.; Razavi Bazaz, S.; Daiyan, R.; Razmjou, A.; Ebrahimi Warkiani, M.; Amal, R.; Chen, V. Biocatalytic micromixer coated with enzyme-MOF thin film for CO2 conversion to formic acid. Chem. Eng. J. 2021, 426, 130856. [Google Scholar] [CrossRef]
- Warkiani, M.E.; Guan, G.; Luan, K.B.; Lee, W.C.; Bhagat, A.A.S.; Kant Chaudhuri, P.; Tan, D.S.-W.; Lim, W.T.; Lee, S.C.; Chen, P.C.Y.; et al. Slanted spiral microfluidics for the ultra-fast, label-free isolation of circulating tumor cells. Lab A Chip 2014, 14, 128–137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Razavi Bazaz, S.; Kashaninejad, N.; Azadi, S.; Patel, K.; Asadnia, M.; Jin, D.; Ebrahimi Warkiani, M. Rapid Softlithography Using 3D-Printed Molds. Adv. Mater. Technol. 2019, 4, 1900425. [Google Scholar] [CrossRef]
- Shrestha, J.; Ghadiri, M.; Shanmugavel, M.; Razavi Bazaz, S.; Vasilescu, S.; Ding, L.; Ebrahimi Warkiani, M. A rapidly prototyped lung-on-a-chip model using 3D-printed molds. Organs Chip 2019, 1, 100001. [Google Scholar] [CrossRef]
- Vasilescu, S.A.; Bazaz, S.R.; Jin, D.; Shimoni, O.; Warkiani, M.E. 3D printing enables the rapid prototyping of modular microfluidic devices for particle conjugation. Appl. Mater. Today 2020, 20, 100726. [Google Scholar] [CrossRef]
- Razavi Bazaz, S.; Rouhi, O.; Raoufi, M.A.; Ejeian, F.; Asadnia, M.; Jin, D.; Ebrahimi Warkiani, M. 3D Printing of Inertial Microfluidic Devices. Sci. Rep. 2020, 10, 5929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sidharthan, S.; Gandhi, A.D.; Balashanmugam, N.; Jeyaraj, P. Numerical Approach for Fabrication of Micromixers Using Microstereolithography. Procedia Mater. Sci. 2014, 5, 527–534. [Google Scholar] [CrossRef] [Green Version]
- White, F.M. Fluid Mechanics; McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]
- Balasubramaniam, L.; Arayanarakool, R.; Marshall, S.D.; Li, B.; Lee, P.S.; Chen, P.C.Y. Impact of cross-sectional geometry on mixing performance of spiral microfluidic channels characterized by swirling strength of Dean-vortices. J. Micromech. Microeng. 2017, 27, 095016. [Google Scholar] [CrossRef]
- Razavi Bazaz, S.; Amiri, H.A.; Vasilescu, S.; Abouei Mehrizi, A.; Jin, D.; Miansari, M.; Ebrahimi Warkiani, M. Obstacle-free planar hybrid micromixer with low pressure drop. Microfluid Nanofluid. 2020, 24, 61. [Google Scholar] [CrossRef]
- Mihandoust, A.; Bazaz, S.R.; Maleki-Jirsaraei, N.; Alizadeh, M.; Taylor, R.A.; Warkiani, M.E. High-Throughput Particle Concentration Using Complex Cross-Section Microchannels. Micromachines 2020, 11, 440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herrmann, N.; Neubauer, P.; Birkholz, M. Spiral microfluidic devices for cell separation and sorting in bioprocesses. Biomicrofluidics 2019, 13, 061501. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouhi, O.; Razavi Bazaz, S.; Niazmand, H.; Mirakhorli, F.; Mas-hafi, S.; A. Amiri, H.; Miansari, M.; Ebrahimi Warkiani, M. Numerical and Experimental Study of Cross-Sectional Effects on the Mixing Performance of the Spiral Microfluidics. Micromachines 2021, 12, 1470. https://doi.org/10.3390/mi12121470
Rouhi O, Razavi Bazaz S, Niazmand H, Mirakhorli F, Mas-hafi S, A. Amiri H, Miansari M, Ebrahimi Warkiani M. Numerical and Experimental Study of Cross-Sectional Effects on the Mixing Performance of the Spiral Microfluidics. Micromachines. 2021; 12(12):1470. https://doi.org/10.3390/mi12121470
Chicago/Turabian StyleRouhi, Omid, Sajad Razavi Bazaz, Hamid Niazmand, Fateme Mirakhorli, Sima Mas-hafi, Hoseyn A. Amiri, Morteza Miansari, and Majid Ebrahimi Warkiani. 2021. "Numerical and Experimental Study of Cross-Sectional Effects on the Mixing Performance of the Spiral Microfluidics" Micromachines 12, no. 12: 1470. https://doi.org/10.3390/mi12121470
APA StyleRouhi, O., Razavi Bazaz, S., Niazmand, H., Mirakhorli, F., Mas-hafi, S., A. Amiri, H., Miansari, M., & Ebrahimi Warkiani, M. (2021). Numerical and Experimental Study of Cross-Sectional Effects on the Mixing Performance of the Spiral Microfluidics. Micromachines, 12(12), 1470. https://doi.org/10.3390/mi12121470








