Characterization of Giant Magnetostrictive Materials Using Three Complex Material Parameters by Particle Swarm Optimization
Abstract
:1. Introduction
2. Characterization Methodology
2.1. Complex Parameters of GMM
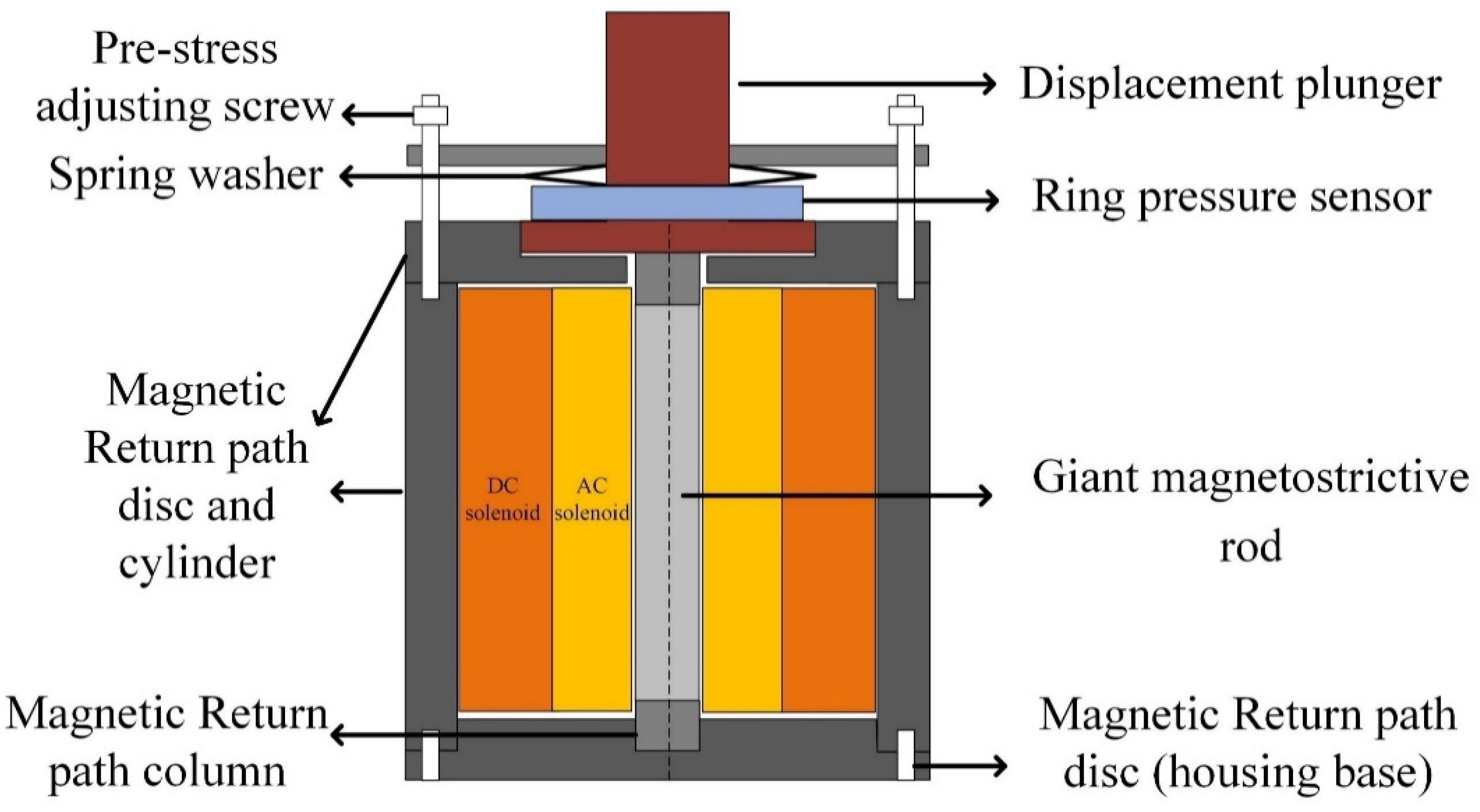
2.2. The Longitudinal Transducer
2.3. The Lumped Parameter Model for the Transducer
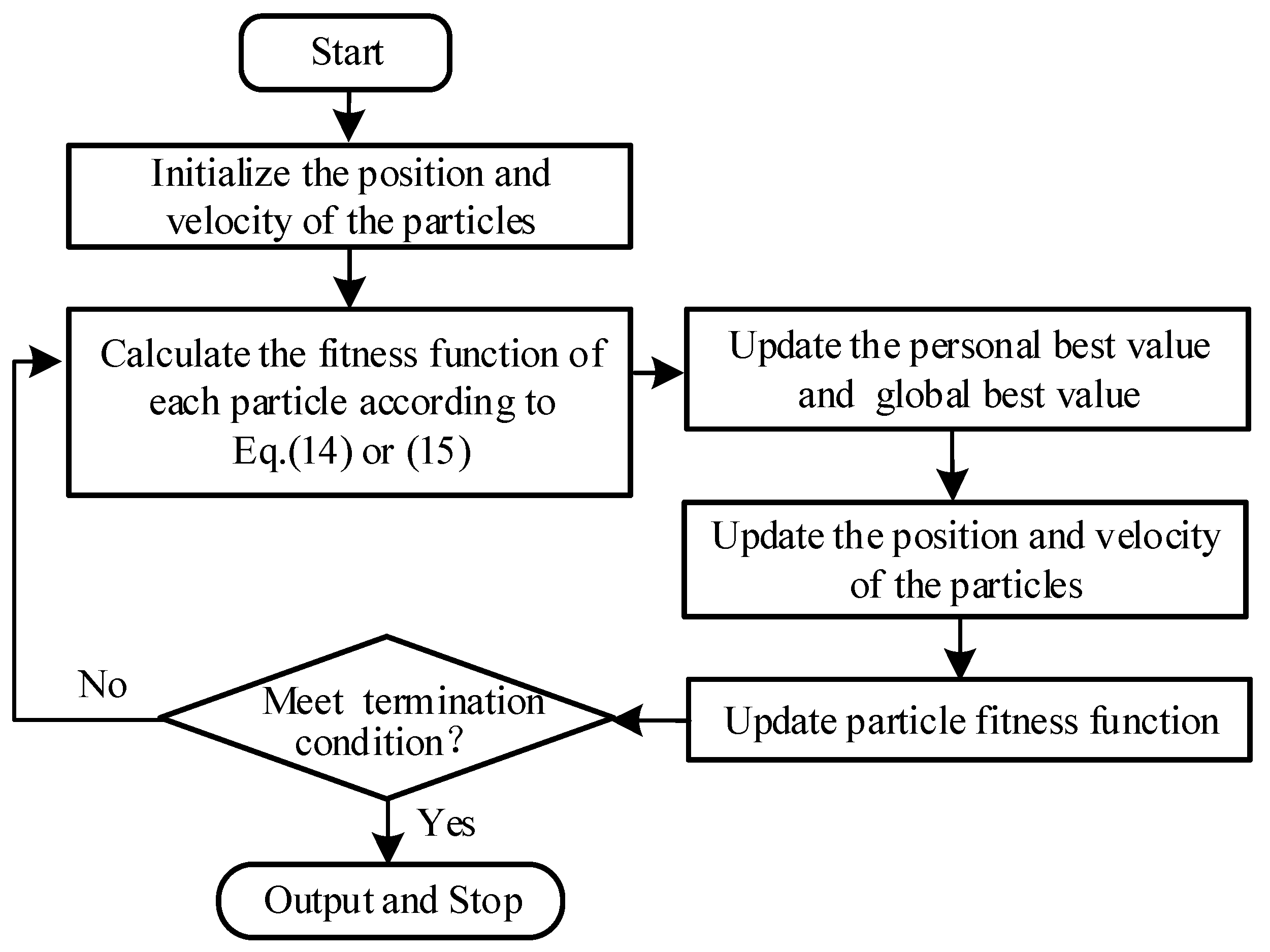
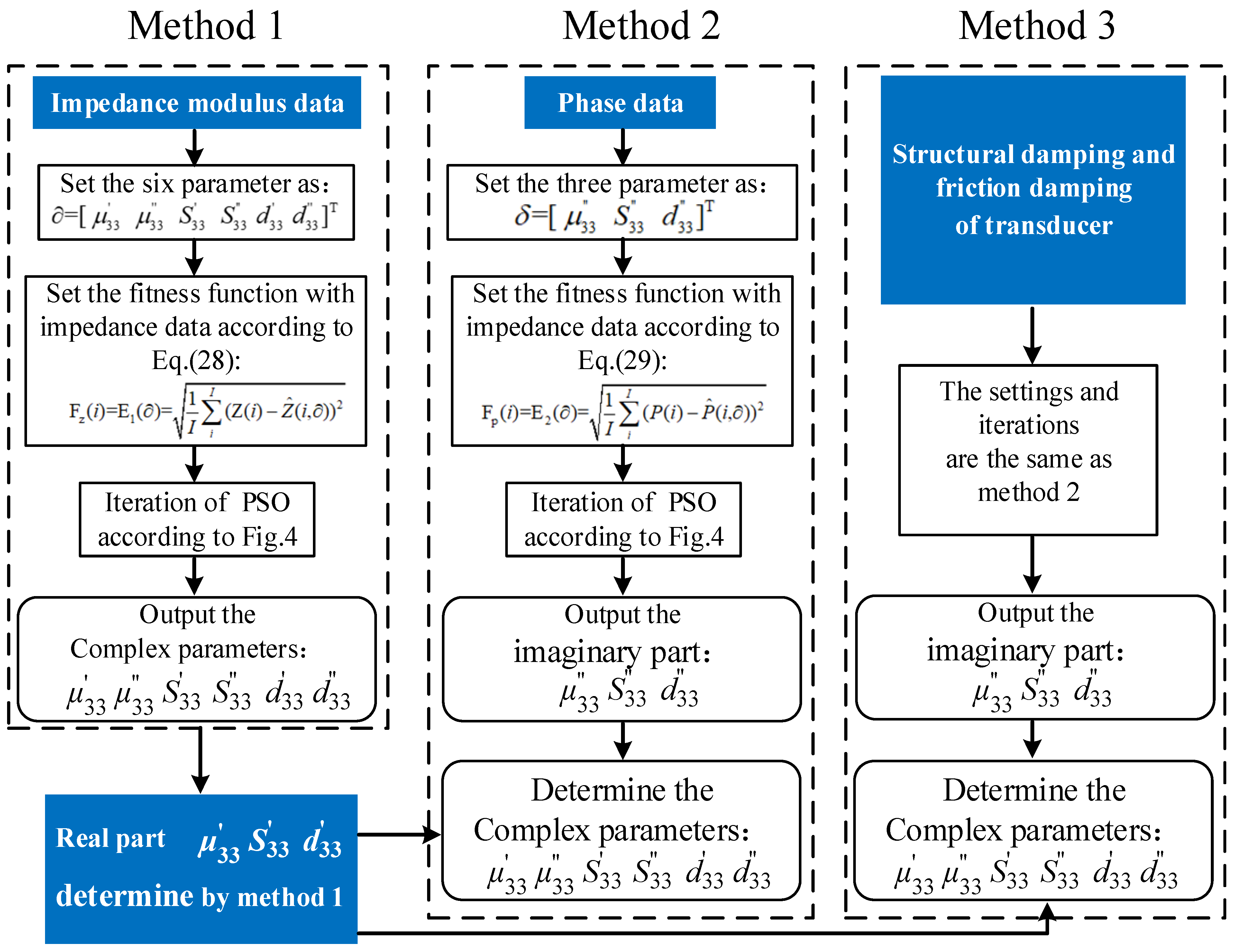
2.4. The Proposed Optimization Method
3. Experimental Measurement
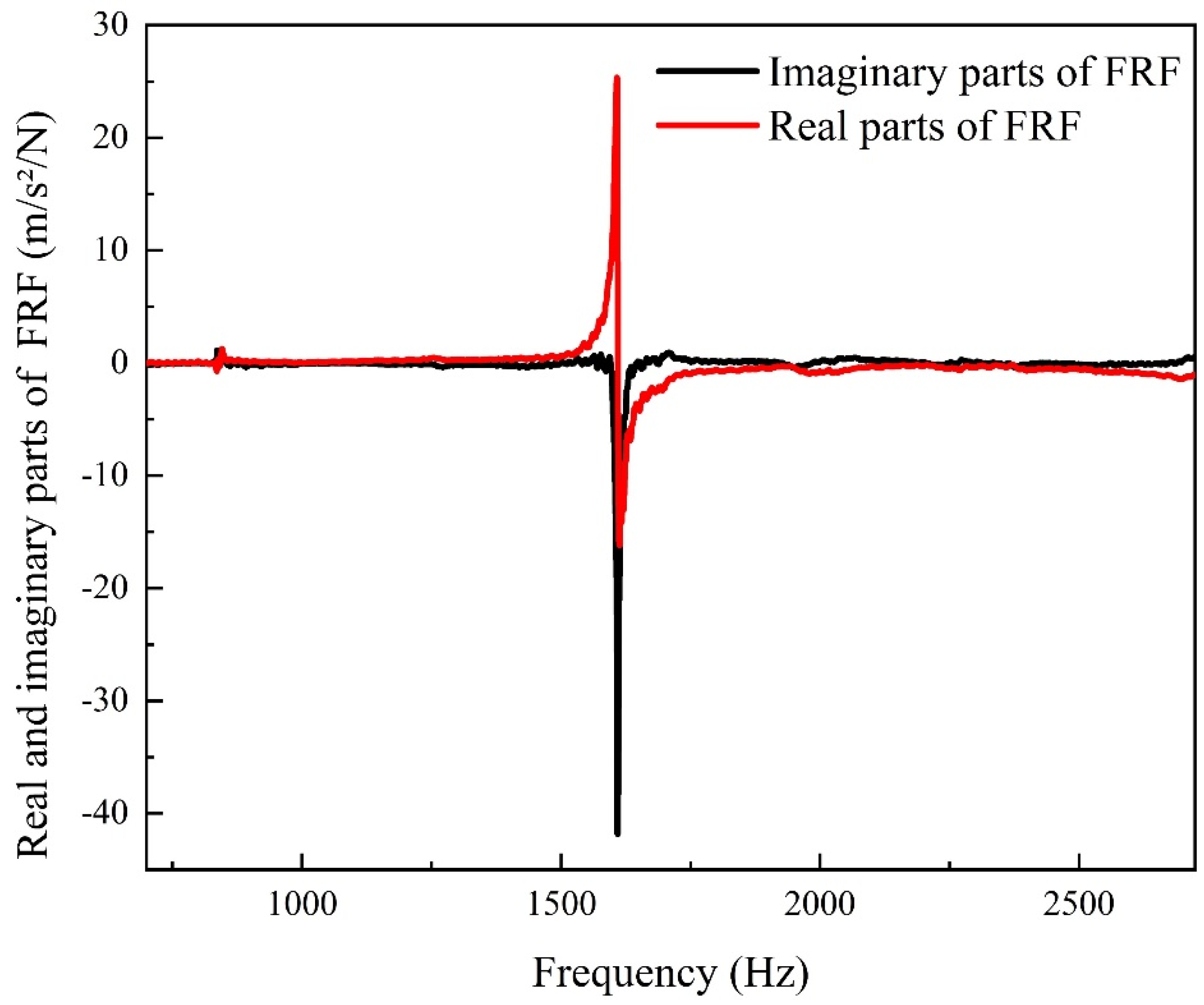
3.1. The Measurement of the Displacement Plunger’s Structural Damping
3.2. The Contact Damping Calculation
3.2.1. Morphology of the Rough Surfaces
3.2.2. Calculation of the Contact Damping
3.3. The Measurement of Impedance/Phase
3.4. Estimated Standard Uncertainty and Expanded Uncertainty of Measurement
4. Experimental Results
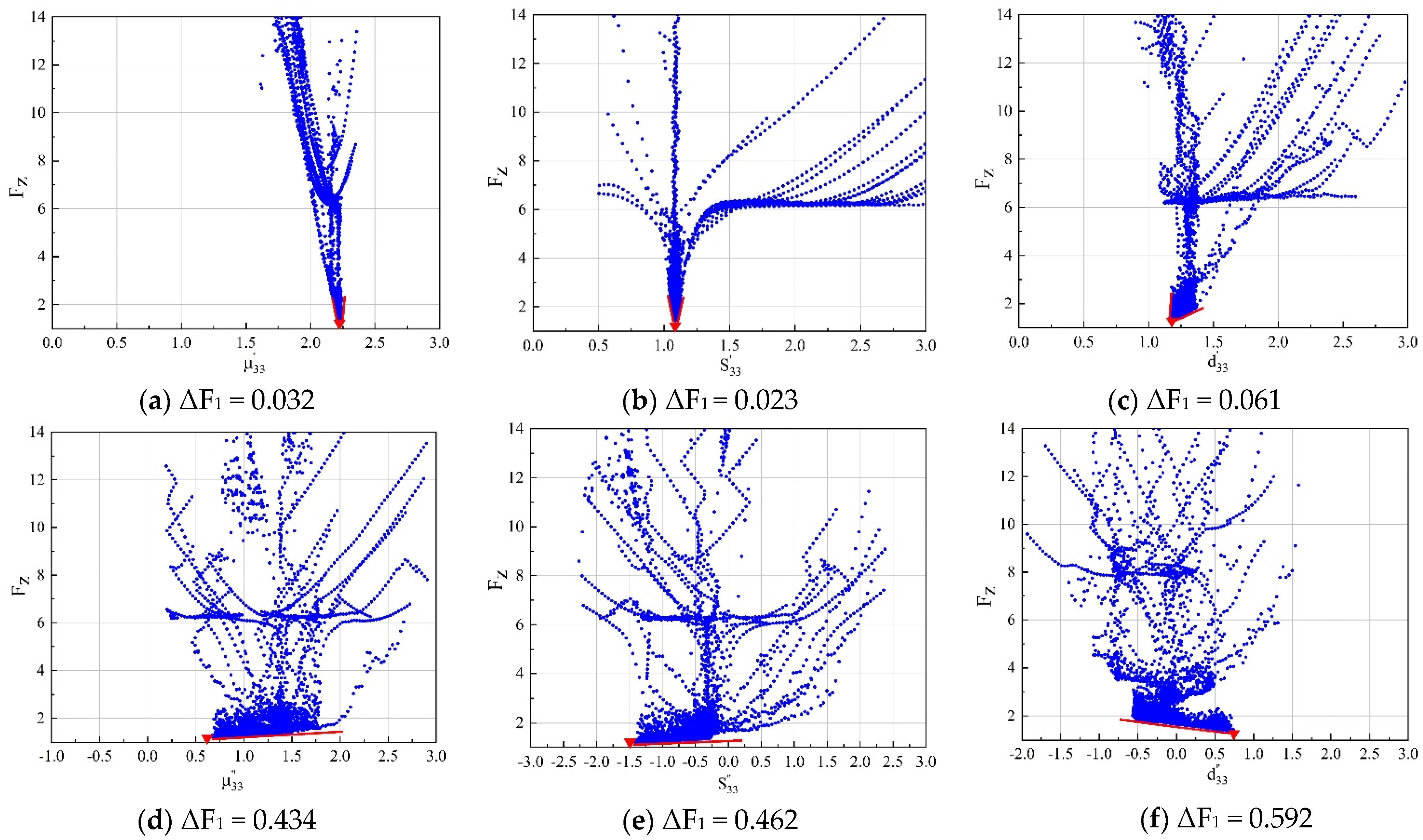
4.1. Sensitivities Analysis
4.1.1. Sensitivities of the Method 1
4.1.2. Sensitivities of the Method 2 and 3
4.1.3. Uncertainty of Damping and Sensitivity Analysis
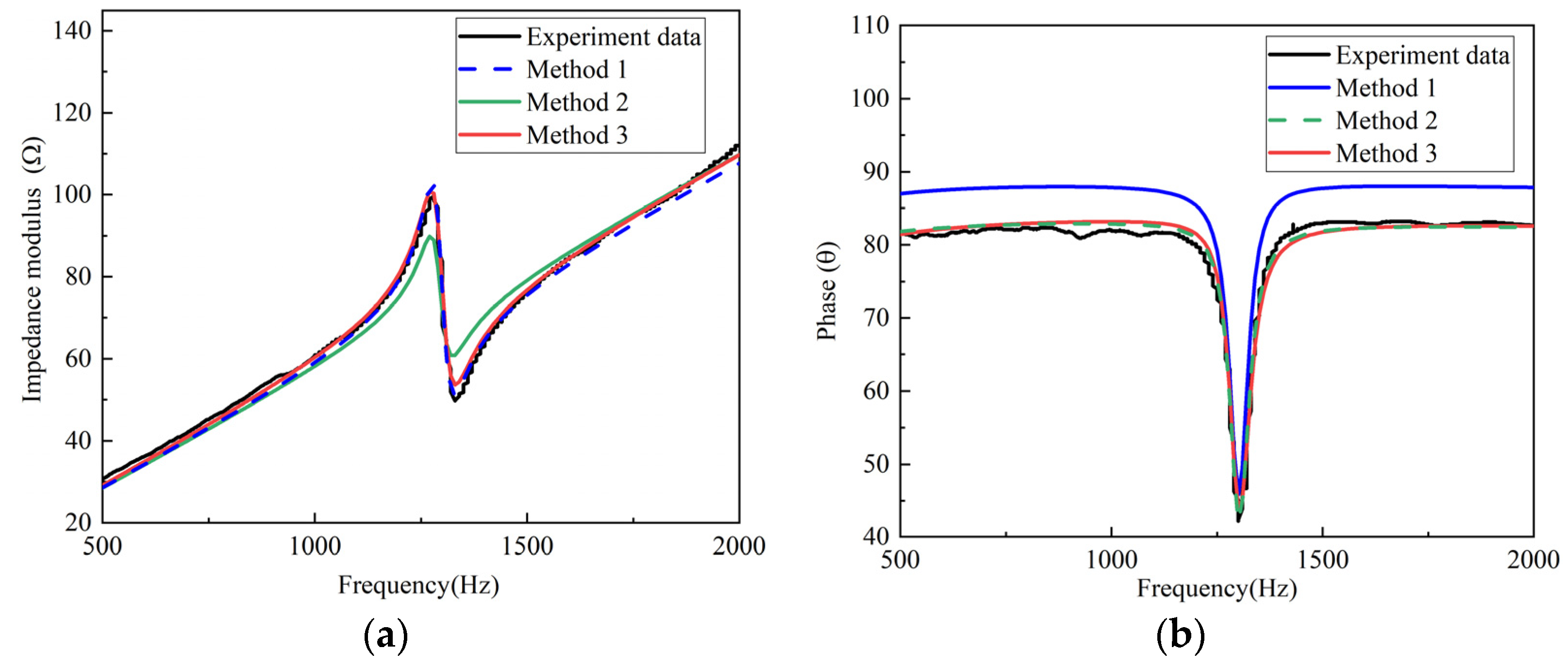
4.2. Comparison between Simulation and Experiments
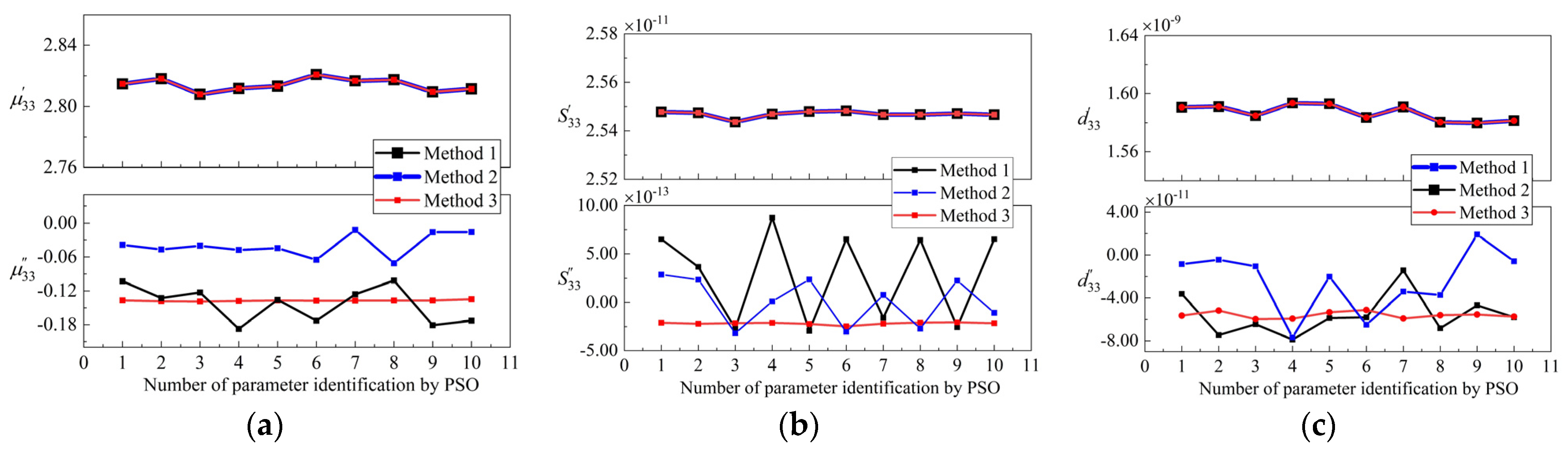
4.3. Stability and Uncertainty
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Damping Model of Contact Surface Based on a Three-Dimensional Fractal Topography

References
- Gandomzadeh, D.; Abbaspour-Fard, M.H. Numerical Study of the Effect of Core Geometry on the Performance of a Magnetostrictive Transducer. J. Magn. Magn. Mater. 2020, 513, 166823. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, J.; Feng, P.; Yu, D.; Wu, Z. An Amplitude Prediction Model for a Giant Magnetostrictive Ultrasonic Transducer. Ultrasonics 2020, 108, 106017. [Google Scholar] [CrossRef]
- Kim, J.; Jung, E. Finite Element Analysis for Acoustic Characteristics of a Magnetostrictive Transducer. Smart Mater. Struct. 2005, 14, 1273–1280. [Google Scholar] [CrossRef]
- Rupitsch, S.J.; Ilg, J. Complete Characterization of Piezoceramic Materials by Means of Two Block-Shaped Test Samples. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1403–1413. [Google Scholar] [CrossRef] [PubMed]
- Slaughter, J.C. Coupled Structural and Magnetic Models: Linear Magnetostriction in COMSOL. In Proceedings of the COMSOL Conference 2009, Boston, MA, USA, 8–10 October 2009. [Google Scholar]
- Mezheritsky, A.V. Elastic, Dielectric, and Piezoelectric Losses in Piezoceramics: How It Works All Together. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 695–707. [Google Scholar]
- Sherrit, S.; Masys, T.J.; Wiederick, H.D.; Mukherjee, B.K. Determination of the Reduced Matrix of the Piezoelectric, Dielectric, and Elastic Material Constants for a Piezoelectric Material with C∞ Symmetry. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1714–1720. [Google Scholar] [CrossRef] [PubMed]
- Wild, M.; Bring, M.; Halvorsen, E.; Hoff, L.; Hjelmervik, K. The Challenge of Distinguishing Mechanical, Electrical and Piezoelectric Losses. J. Acoust. Soc. Am. 2018, 144, 2128–2134. [Google Scholar] [CrossRef]
- Scheidler, J.J.; Asnani, V.M. Validated Linear Dynamic Model of Electrically-Shunted Magnetostrictive Transducers with Application to Structural Vibration Control. Smart Mater. Struct. 2017, 26, 035057. [Google Scholar] [CrossRef]
- Domenjoud, M.; Berthelot, E.; Galopin, N.; Corcolle, R.; Bernard, Y.; Daniel, L. Characterization of Giant Magnetostrictive Materials under Static Stress: Influence of Loading Boundary Conditions. Smart Mater. Struct. 2019, 28, 095012. [Google Scholar] [CrossRef]
- Sherrit, S.; Mukherjee, B.K. Characterization of Piezoelectric Materials for Transducers. arXiv 2007, arXiv:0711.2657. [Google Scholar]
- American, A.; Standard, N. An American National Standard: IEEE Standard on Piezoelectricity. IEEE Trans. Sonics Ultrason. 1987, 31, 8–10. [Google Scholar]
- Sherrit, S.; Wiederick, H.D.; Mukherjee, B.K.; Sayer, M. An Accurate Equivalent Circuit for the Unloaded Piezoelectric Vibrator in the Thickness Mode. J. Phys. D Appl. Phys. 1997, 30, 2354–2363. [Google Scholar] [CrossRef]
- Wild, M.; Bring, M.; Lars, H.; Hjelmervik, K. Characterization of Piezoelectric Material Parameters Through a Global Optimization Algorithm. IEEE J. Ocean. Eng. 2020, 45, 480–488. [Google Scholar] [CrossRef]
- Wild, M.; Hjelmervik, K.; Hoff, L.; Bring, M. Characterising Piezoelectric Material Parameters through a 3D FEM and Optimisation Algorithm. In Oceans 2017-Aberdeen; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Sun, X.; Li, S.; Dun, X.; Li, D.; Li, T.; Guo, R.; Yang, M. A Novel Characterization Method of Piezoelectric Composite Material Based on Particle Swarm Optimization Algorithm. Appl. Math. Model. 2019, 66, 322–331. [Google Scholar] [CrossRef]
- Jonsson, U.G.; Andersson, B.M.; Lindahl, O.A. A FEM-Based Method Using Harmonic Overtones to Determine the Effective Elastic, Dielectric, and Piezoelectric Parameters of Freely Vibrating Thick Piezoelectric Disks. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 243–255. [Google Scholar] [CrossRef] [Green Version]
- Daneshpajooh, H.; Choi, M.; Park, Y.; Scholehwar, T.; Hennig, E.; Uchino, K. Compressive Stress Effect on the Loss Mechanism in a Soft Piezoelectric Pb(Zr,Ti)O3. Rev. Sci. Instrum. 2019, 90, 075001. [Google Scholar] [CrossRef]
- Dapino, M.J.; Flatau, A.B.; Calkins, F.T. Statistical Analysis of Terfenol-D Material Properties. J. Intell. Mater. Syst. Struct. 2006, 17, 587–599. [Google Scholar] [CrossRef]
- Twarek, L.M.; Flatau, A.B. Dynamic Property Determination of Magnetostrictive Iron-Gallium Alloys. Smart Struct. Mater. Act. Mater. Behav. Mech. 2005, 5761, 209. [Google Scholar]
- Reed, I.M.; Greenough, R.D.; Jenner, A.G.I. Frequency Dependence of the Piezomagnetic Strain Coefficient. IEEE Trans. Magn. 1995, 31, 4038–4040. [Google Scholar] [CrossRef]
- Greenough, R.D.; Reed, I.M.; O’Connor, K.C.; Wharton, A.; Schulze, M.P. The Characterisation of Transducer Materials. Ferroelectrics 1996, 187, 129–140. [Google Scholar] [CrossRef]
- Greenough, R.D.; Wharton, A.D. Methods and Techniques to Characterise Terfenol-D. J. Alloys Compd. 1997, 258, 114–117. [Google Scholar] [CrossRef]
- Park, Y.; Zhang, Y.; Majzoubi, M.; Scholehwar, T.; Hennig, E.; Uchino, K. Improvement of the Standard Characterization Method on K33 Mode Piezoelectric Specimens. Sens. Actuators A Phys. 2020, 312, 112124. [Google Scholar] [CrossRef]
- Transducer, R. An Estimation Method of an Electrical Equivalent Circuit Considering Acoustic Radiation Efficiency for a Multiple Resonant Transducer. Electronics 2021, 10, 2416. [Google Scholar]
- Tao, M.; Zhuang, Y.; Chen, D.; Ural, S.O.; Lu, Q.; Uchino, K. Characterization of Magnetostrictive Losses Using Complex Parameters. Adv. Mater. Res. 2012, 490–495, 985–989. [Google Scholar] [CrossRef]
- Uchino, K. High-Power Piezoelectrics and Loss Mechanisms; CRC Press: Boca Raton, FL, USA, 2020; ISBN 9780081021354. [Google Scholar]
- He, X.; Zhang, P. A New Calculation Method for the Number of Radial Slots of a Terfenol Rod. Sci. China Ser. E Technol. Sci. 2009, 52, 336–338. [Google Scholar] [CrossRef]
- Meeks, S.W. A Mobility Analogy Equivalent Circuit of a Magnetostrictive Transducer in the Presence of Eddy Currents. J. Acoust. Soc. Am. 1980, 67, 683–692. [Google Scholar] [CrossRef]
- Hall, D.L. Dynamics and Vibration of Magnetostrictive Transducers; Iowa State University: Ames, IA, USA, 1994. [Google Scholar]
- Engdahl, G. Design Procedures For Optimal Use of Giant Design Procedures for Optimal Use of Giant Magnetostrictive Materials in Magnetostrictive Materials in Magnetostrictive Actuator Applications Magnetostrictive Actuator Applications. In Proceedings of the Actuator 2002, 8th International Conference New Actuators, Bremen, Germany, 10–12 June 2002; pp. 10–12. [Google Scholar]
- Karafi, M.R.; Khorasani, F. Evaluation of Mechanical and Electric Power Losses in a Typical Piezoelectric Ultrasonic Transducer. Sens. Actuators A Phys. 2019, 288, 156–164. [Google Scholar] [CrossRef]
- Abdullah, A.; Malaki, M. On the Damping of Ultrasonic Transducers’ Components. Aerosp. Sci. Technol. 2013, 28, 31–39. [Google Scholar] [CrossRef]
- GUM Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. Int. Organ. Stand. Geneva ISBN 2008, 50, 134.
- Joint Committee for Guides in Metrology (JCGM). Guide to the Expression of Uncertainty in Measurement—Part 6: Developing and Using Measurement Models; Joint Committee for Guides in Metrology (JCGM): Sèvres, France, 2020. [Google Scholar]
- Khater, M.E.; Akhtar, S.; Park, S.; Ozdemir, S.; Abdel-Rahman, E.; Vyasarayani, C.P.; Yavuz, M. Contact Damping in Microelectromechanical Actuators. Appl. Phys. Lett. 2014, 105, 1–5. [Google Scholar] [CrossRef]
- Xu, K.; Yuan, Y.; Chen, J. The Effects of Size Distribution Functions on Contact between Fractal Rough Surfaces. AIP Adv. 2018, 8, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Cheng, Y.; Liu, K.; Gan, L. A Revised Majumdar and Bushan Model of Elastoplastic Contact between Rough Surfaces. Appl. Surf. Sci. 2017, 425, 1138–1157. [Google Scholar] [CrossRef]
- Zhang, D.; Xia, Y.; Scarpa, F.; Hong, J.; Ma, Y. Interfacial Contact Stiffness of Fractal Rough Surfaces. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, S.; Zheng, Y.; Zhu, H. A Contact Stiffness Model of Machined Plane Joint Based on Fractal Theory. J. Tribol. 2010, 132, 1–7. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, J.; Cai, L.; Shi, W.; Liu, Z. Stiffness and Damping Model of Bolted Joint Based on the Modified Three-Dimensional Fractal Topography. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 279–293. [Google Scholar] [CrossRef]
- Liu, P.; Zhao, H.; Huang, K.; Chen, Q. Research on Normal Contact Stiffness of Rough Surface Considering Friction Based on Fractal Theory. Appl. Surf. Sci. 2015, 349, 43–48. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Ratto, M.; Campolongo, F.; Cariboni, J.; Gatelli, D. Global Sensitivity Analysis. The Primer Global Sensitivity Analysis. The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 9780470059975. [Google Scholar]
- Gopal, A.; Sultani, M.M.; Bansal, J.C. On Stability Analysis of Particle Swarm Optimization Algorithm. Arab. J. Sci. Eng. 2020, 45, 2385–2394. [Google Scholar] [CrossRef]




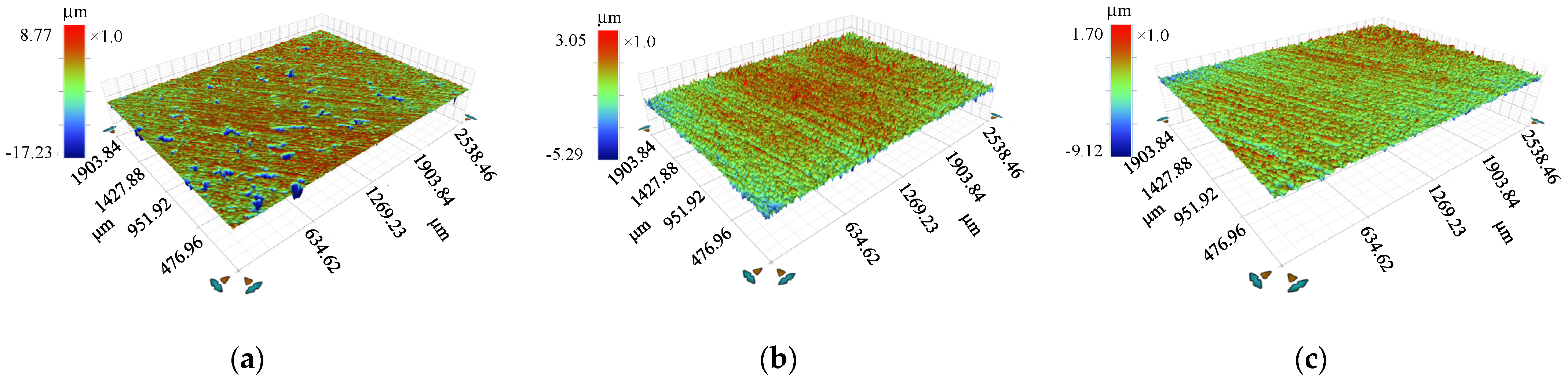


| 1 | 2 | 3 | 4 | 5 | 6 | Ave. | Standard Uncertainty | |
|---|---|---|---|---|---|---|---|---|
| Rq (μm) of the GMR | 0.577 | 0.490 | 0.539 | 0.706 | 0.910 | 0.744 | 0.661 | 0.012 |
| Rq (μm) of the magnetic column | 0.345 | 0.307 | 0.333 | 0.394 | 0.368 | 0.338 | 0.347 | 0.011 |
| Rq (μm) of the displacement plunger | 0.315 | 0.378 | 0.338 | 0.308 | 0.303 | 0.297 | 0.323 | 0.011 |
| Rough Surfaces of the GMR | Rough Surfaces of the Magnetic Column and Housing Base | Rough Surfaces of the Displacement Plunger | |
|---|---|---|---|
| D | 2.5747 | 2.6167 | 2.6214 |
| G (m) | 2.2525 × 10−10 | 2.8175 × 10−10 | 2.8890 × 10−10 |
| Contact Damping (N/(m/s)) | Deq | Geq (m) | |
|---|---|---|---|
| G-M surface | 36.5693 ± 0.1558 | 2.6167 ± 0.0011 | 4.3788 × 10−10 ± 9.6892 × 10−12 |
| M-D surface | 287.9776 ± 2.8382 | 2.6214 ± 0.0009 | 3.6296 × 10−10 ± 2.8896 × 10−13 |
| M-H surface | 24.6834 ± 0.0324 | 2.6167 ± 0.0011 | 3.4991 × 10−10 ± 2.4283 × 10−13 |
| Sum | 349.2303 ± 3.0274 | / | / |
| Measurement of Structural Damping | Measurement of Contacting Damping | Measurement of Impedance and Phase | |
|---|---|---|---|
| Standard Uncertainty (P = 68.27%, K = 1) | 0.4390 N/(m/s) | 3.0264 N/(m/s) | 0.00046 Ω/0.0058 deg |
| Expanded Uncertainty (P = 99%, K = 2.58) | 1.1326 N/(m/s) | 7.8081 N/(m/s) | 0.00118 Ω/0.0149 deg |
| Damping is the mean of the confidence interval | 0.049 | 0.085 | 0.029 |
| Damping is the upper limit of the confidence interval | 0.051 | 0.084 | 0.031 |
| Damping is the lower limit of the confidence interval | 0.048 | 0.082 | 0.027 |
| Method 1 | Method 2 | Method 3 | |
|---|---|---|---|
| RMSE of impedance modulus data | 1.8589 | 3.2979 | 1.3377 |
| RMSE of phase data | 6.2623 | 2.5243 | 1.6748 |
| R2 of impedance modulus data | 0.9963 | 0.9887 | 0.9981 |
| R2 of phase data | 0.4573 | 0.9170 | 0.9746 |
| Parameter | Search Range | Method 1 | Method 2 | Method 3 | |||
|---|---|---|---|---|---|---|---|
| [2, 3] | 2.814 | 1.460 × 10−3 | \ | \ | \ | \ | |
| [1 × 10−12, 1 × 10−10] | 2.547 × 10−11 | 5.013 × 10−4 | \ | \ | \ | \ | |
| [5 × 10−10, 5 × 10−9] | 1.587 × 10−9 | 3.420 × 10−3 | \ | \ | \ | \ | |
| [−0.3, 0.3] | −0.143 | 0.224 | −0.040 | 0.507 | −0.137 | 0.008 | |
| [−1 × 10−12, 1 × 10−12] | −2.861 × 10−13 | 1.653 | −7.170 × 10−15 | 33.818 | −2.178 × 10−13 | 0.052 | |
| [−9 × 10−11, 9 × 10−11] | −5.581 × 10−11 | 0.343 | −2.435 × 10−11 | 1.205 | −5.588 × 10−11 | 0.055 | |
| Relative standard uncertainty (P = 68.27%, K = 1) | 0.046% | 0.016% | 0.110% | 1.405% | 2.342% | 4.009% |
| Relative expanded uncertainty (P = 99%, K = 3) | 0.138% | 0.048% | 0.330% | 4.215% | 7.026% | 12.037% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yang, X.; Yang, M.; Wei, Y.; Zheng, H. Characterization of Giant Magnetostrictive Materials Using Three Complex Material Parameters by Particle Swarm Optimization. Micromachines 2021, 12, 1416. https://doi.org/10.3390/mi12111416
Chen Y, Yang X, Yang M, Wei Y, Zheng H. Characterization of Giant Magnetostrictive Materials Using Three Complex Material Parameters by Particle Swarm Optimization. Micromachines. 2021; 12(11):1416. https://doi.org/10.3390/mi12111416
Chicago/Turabian StyleChen, Yukai, Xin Yang, Mingzhi Yang, Yanfei Wei, and Haobin Zheng. 2021. "Characterization of Giant Magnetostrictive Materials Using Three Complex Material Parameters by Particle Swarm Optimization" Micromachines 12, no. 11: 1416. https://doi.org/10.3390/mi12111416
APA StyleChen, Y., Yang, X., Yang, M., Wei, Y., & Zheng, H. (2021). Characterization of Giant Magnetostrictive Materials Using Three Complex Material Parameters by Particle Swarm Optimization. Micromachines, 12(11), 1416. https://doi.org/10.3390/mi12111416





