A Novel High-Speed and High-Accuracy Mathematical Modeling Method of Complex MEMS Resonator Structures Based on the Multilayer Perceptron Neural Network
Abstract
:1. Introduction
2. Disk MEMS Resonator
2.1. Structure Description
2.2. Core Performance Indicators
2.2.1. Fundamental Frequency
2.2.2. Quality Factor
2.2.3. Mechanical Sensitivity
2.2.4. Mechanical Thermal Noise
2.3. Finite Element Analysis Method
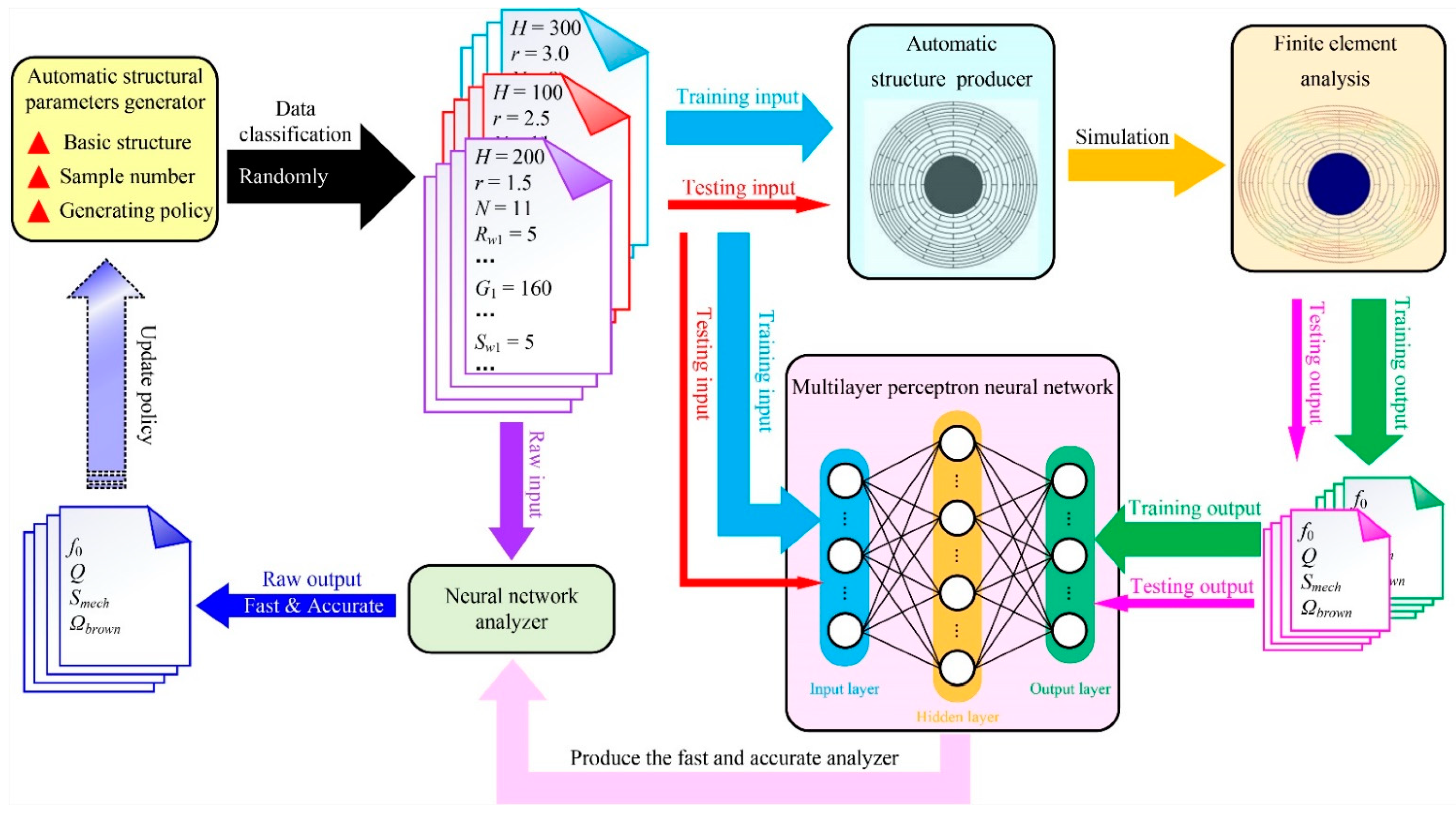
3. Multilayer Perceptron Neural Network Model
3.1. Dataset Definition
3.2. Multilayer Perceptron Neural Network
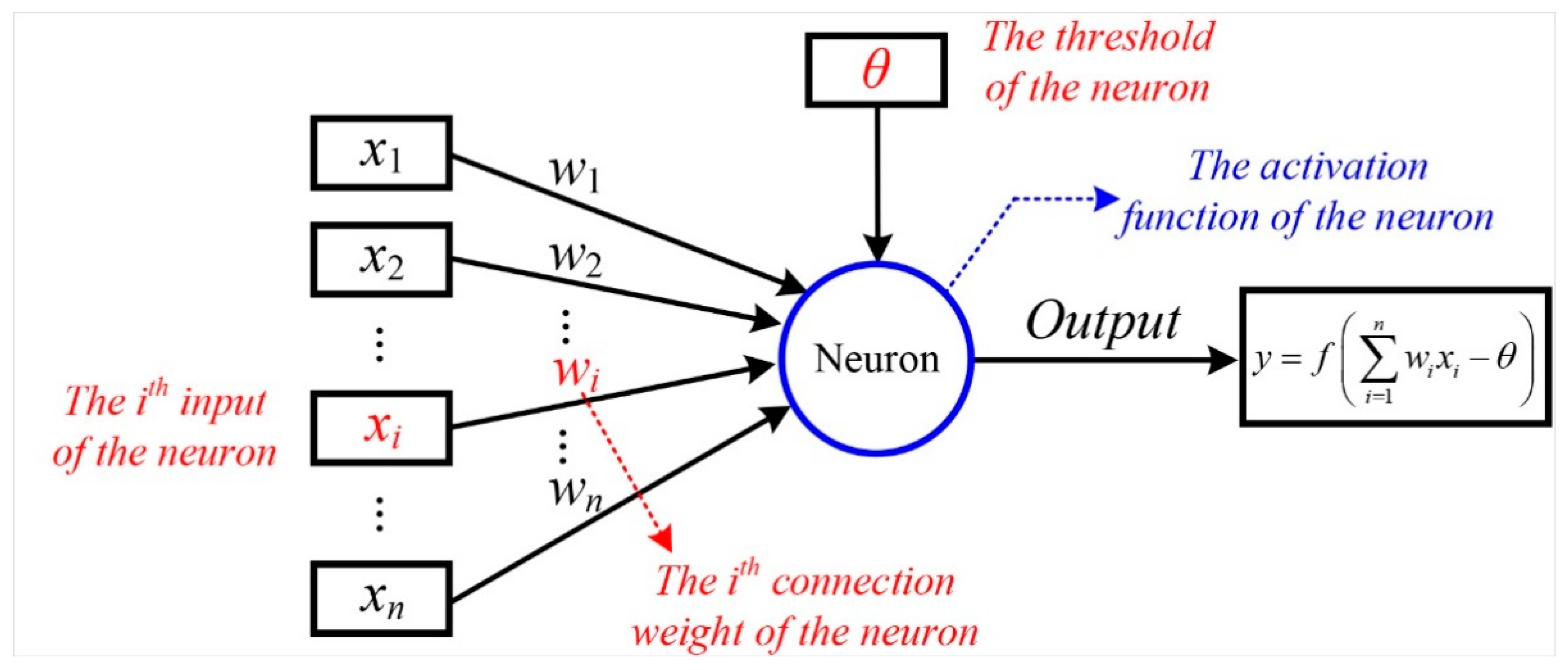
3.2.1. M-P Neuron Model
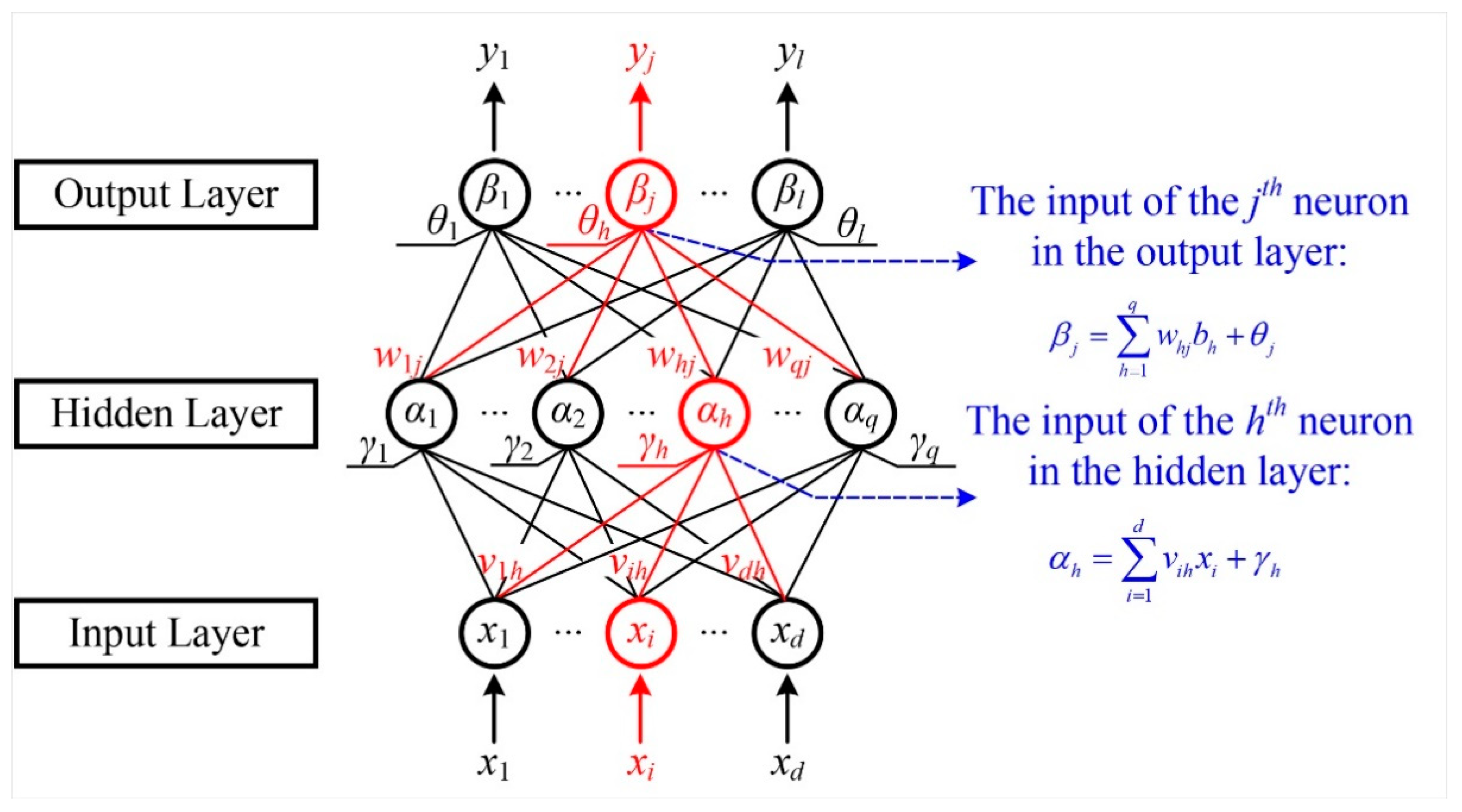
3.2.2. Multi-Layer Feedforward Neural Networks
3.2.3. Error Back Propagation Algorithm
4. Discussion
4.1. Neural Network Structure Parameters
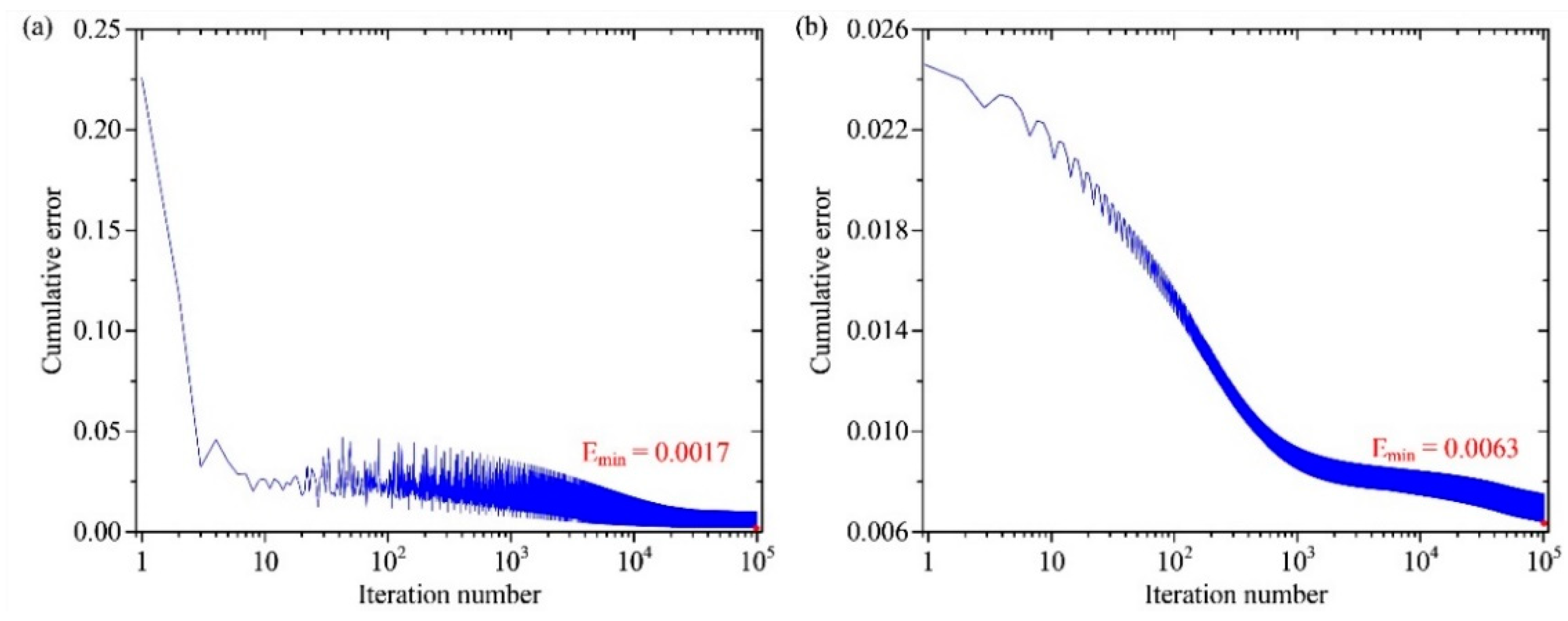
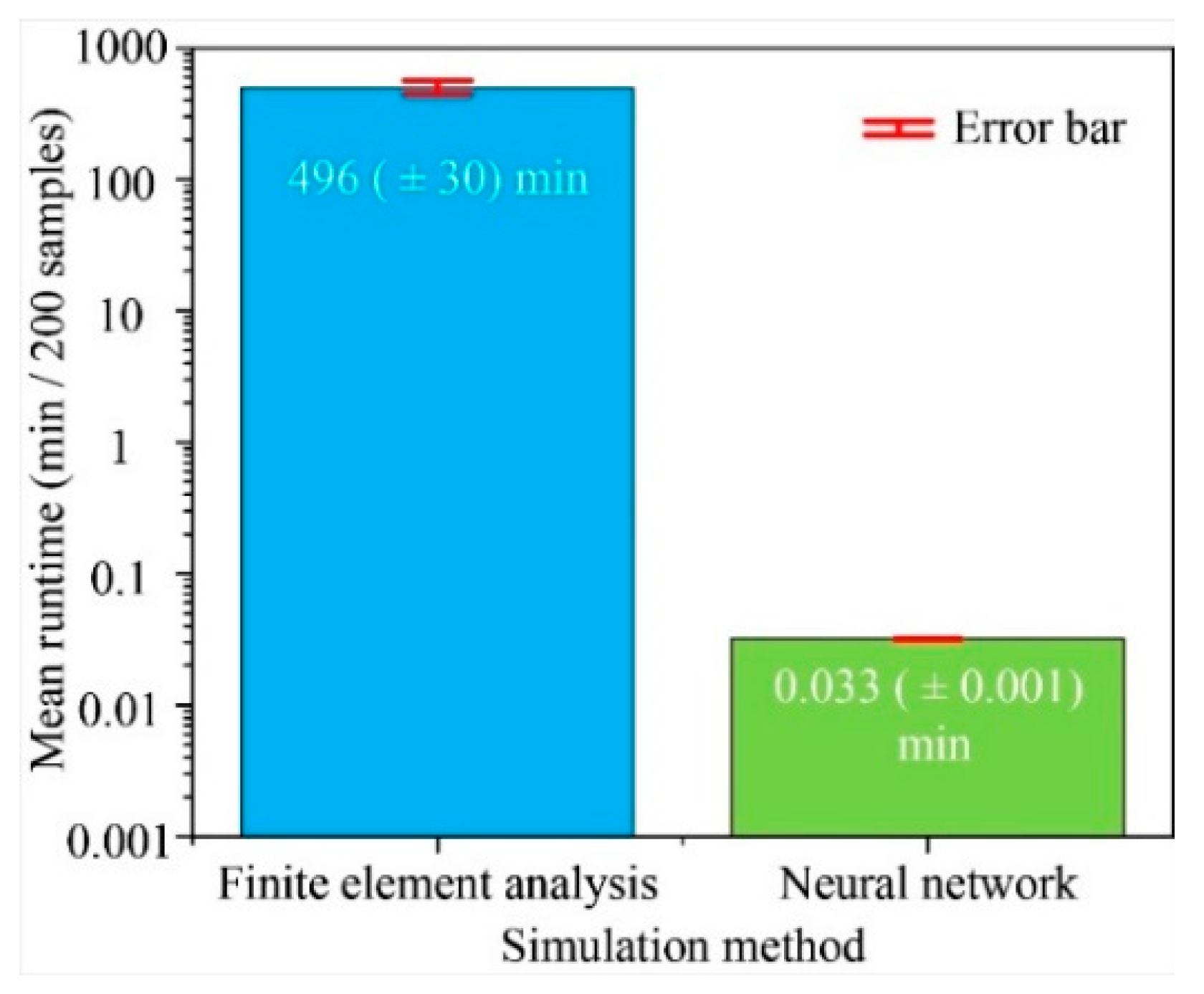
4.2. Neural Network Learning Performance
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Middlemiss, R.P.; Samarelli, A.; Paul, D.J.; Hough, J.; Rowan, S.; Hammond, G.D. Measurement of the earth tides with a MEMS gravimeter. Nature 2016, 531, 614–618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, X.; Zhang, T.; Jiang, Z.; Ren, J.; Huan, R. Frequency latching in nonlinear micromechanical resonators. Appl. Phys. Lett. 2017, 110, 143506. [Google Scholar] [CrossRef]
- Lu, K.; Li, Q.; Zhou, X.; Song, G.; Wu, K.; Zhuo, M.; Wu, X.; Xiao, D. Modal coupling effect in a novel nonlinear micromechanical resonator. Micromachines 2020, 11, 472. [Google Scholar] [CrossRef] [PubMed]
- Hanay, M.S.; Kelber, S.; Naik, A.K.; Chi, D.; Hentz, S.; Bullard, E.C.; Colinet, E.; Duraffourg, L.; Roukes, M.L. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 2012, 7, 602–608. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Jia, H.; Zheng, X.; Yang, R.; Ye, G.J.; Chen, X.H.; Feng, P.X. Resolving and tuning mechanical anisotropy in black phosphorus crystal via nanomechanical multimode resonance spectromicroscopy. Nano Lett. 2016, 16, 5394–5400. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Zhou, B.; Song, M.; Lin, Z.; Jin, S.; Zhang, R. Structural parameter identification of the center support quadruple mass gyro. IEEE Sens. J. 2017, 17, 3765–3775. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, C.; Xiao, D.; Sun, J.; Sobreviela, G.; Gerrard, D.D.; Chen, Y.; Flader, I.; Kenny, T.W.; Wu, X.; et al. Dynamic modulation of modal coupling in microelectromechanical gyroscopic ring resonators. Nat. Commun. 2019, 10, 4980. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Huang, J.; Yuan, W.; Chang, H. A high-sensitivity micromechanical electrometer based on mode localization of two degree-of-freedom weakly coupled resonators. J. Microelectromech. Syst. 2016, 25, 937–946. [Google Scholar] [CrossRef]
- Nagourney, T.; Cho, J.Y.; Shiari, B.; Darvishian, A.; Najafi, K. 259 Second ring-down time and 4.45 million quality factor in 5.5 kHz fused silica birdbath shell resonator. In Proceedings of the 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 790–793. [Google Scholar]
- Lu, K.; Zhou, X.; Li, Q.; Xiao, D. Coherent phonon manipulation in a disk resonator gyroscope with inertial resonance. In Proceedings of the 7th IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 23–26 March 2020; p. 9090063. [Google Scholar]
- Li, Q.; Xiao, D.; Zhou, X.; Xu, Y.; Zhuo, M.; Hou, Z.; He, K.; Zhang, Y.; Wu, X. 0.04 degree-per-hour MEMS disk resonator gyroscope with high-quality factor(510k) and long decaying time constant (74.9s). Microsyst. Nanoeng. 2018, 4, 32. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, D.; Zhou, X.; Hou, Z.; Zhuo, M.; Xu, Y.; Wu, X. Dynamic modeling of the multiring disk resonator gyroscope. Micromachines 2019, 10, 181. [Google Scholar] [CrossRef] [Green Version]
- Dennis, J.O.; Rabih, A.A.S.; Khir, M.H.M.; Ahmed, M.G.A.; Ahmed, A.Y. Modeling and finite element analysis simulation of MEMS based acetone vapor sensor for noninvasive screening of diabetes. J. Sens. 2016, 2016, 9563938. [Google Scholar] [CrossRef] [Green Version]
- Yoon, G.H.; Jensen, J.S.; Sigmund, O. Topology optimization of acoustic-structure interaction problems using a mixing finite element formulation. Int. J. Numer. Methods Eng. 2007, 70, 1049–1075. [Google Scholar] [CrossRef]
- Mao, Y.; He, Q.; Zhao, X. Designing complex architecture materials with generative adversarial networks. Sci. Adv. 2020, 6, eaaz4169. [Google Scholar] [CrossRef] [Green Version]
- Hanakata, P.Z.; Cubuk, E.D.; Campbell, D.K.; Park, H.S. Accelerated search and design of stretchable graphene kirigami using machine learning. Phys. Rev. Lett. 2018, 121, 255304. [Google Scholar] [CrossRef] [Green Version]
- Wilt, J.K.; Yang, C.; Gu, G.X. Accelerating auxetic metamaterial design with deep learning. Adv. Energy Mater. 2020, 22, 1901266. [Google Scholar]
- Challoner, A.D.; Ge, H.H.; Liu, J.Y. Boeing disc resonator gyroscope. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium-PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 504–514. [Google Scholar]
- Nitzan, S.; Ahn, C.H.; Su, T.H.; Li, M.; Ng, E.J.; Wang, S.; Yang, Z.M.; O’Brien, G.; Boser, B.E.; Kenny, T.W.; et al. Epitaxially-encapsulated polysilicon disk resonator gyroscope. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 625–628. [Google Scholar]
- Li, Q.; Xiao, D.; Zhou, X.; Hou, Z.; Xu, Y.; Wu, X. Quality factor improvement in the disk resonator gyroscope by optimizing the spoke length distribution. J. Microelectromech. Syst. 2018, 27, 414–423. [Google Scholar] [CrossRef]
- Ahn, C.H.; Shin, D.D.; Hong, V.A.; Yang, Y.; Ng, E.J.; Chen, Y.; Flader, I.B.; Kenny, T.W. Encapsulated disk resonator gyroscope with differential internal electrodes. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS 2016), Shanghai, China, 24–28 January 2016; pp. 962–965. [Google Scholar]
- Zhou, X.; Xiao, D.; Wu, X.; Wu, Y.; Hou, Z.; He, K.; Li, Q. Stiffness-mass decoupled silicon disk resonator for high resolution gyroscopic application with long decay time constant (8.695 s). Appl. Phys. Lett. 2016, 109, 263501. [Google Scholar] [CrossRef]
- Zhou, X.; Xiao, D.; Hou, Z.; Li, Q.; Wu, Y.; Yu, D.; Li, W.; Wu, X. Thermoelastic quality-factor enhanced disk resonator gyroscope. Proceedings of 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 1009–1012. [Google Scholar]
- Zhou, X.; Xiao, D.; Li, Q.; Hou, Z.; He, K.; Chen, Z.; Wu, Y.; Wu, X. Decaying time constant enhanced MEMS disk resonator for high precision gyroscopic application. IEEE/ASME Trans. Mechatron. 2018, 23, 452–458. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, Y.; Xiao, D.; Hou, Z.; Li, Q.; Yu, D.; Wu, X. An investigation on the ring thickness distribution of disk resonator gyroscope with high mechanical sensitivity. Int. J. Mech. Sci. 2016, 117, 174–181. [Google Scholar] [CrossRef]
- Wang, Z.; Lee, J.; Feng, P.X.L. Spatial mapping of multimode Brownian motions in high-frequency silicon carbide microdisk resonators. Nat. Commun. 2014, 5, 5158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Z. Machine Learning, 1st ed.; Tsinghua University Press: Beijing, China, 2016; pp. 97–106. [Google Scholar]
- Guo, R.; Xu, R.; Wang, Z.; Sui, F.; Lin, L. Accelerating MEMS design process through machine learning from pixelated binary images. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Gainesville, FL, USA, 25–29 January 2021; pp. 153–156. [Google Scholar]
- Liu, F.; Wang, X.; Wang, X.; Wang, L. Machine learning-based design and optimization of curved beams for multistable structures and metamaterials. Extreme Mech. Lett. 2020, 41, 101002. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Chen, C.T.; Gu, G.X. Generative deep neural networks for inverse materials design using backpropagation and active learning. Adv. Sci. 2020, 7, 1902607. [Google Scholar] [CrossRef] [Green Version]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
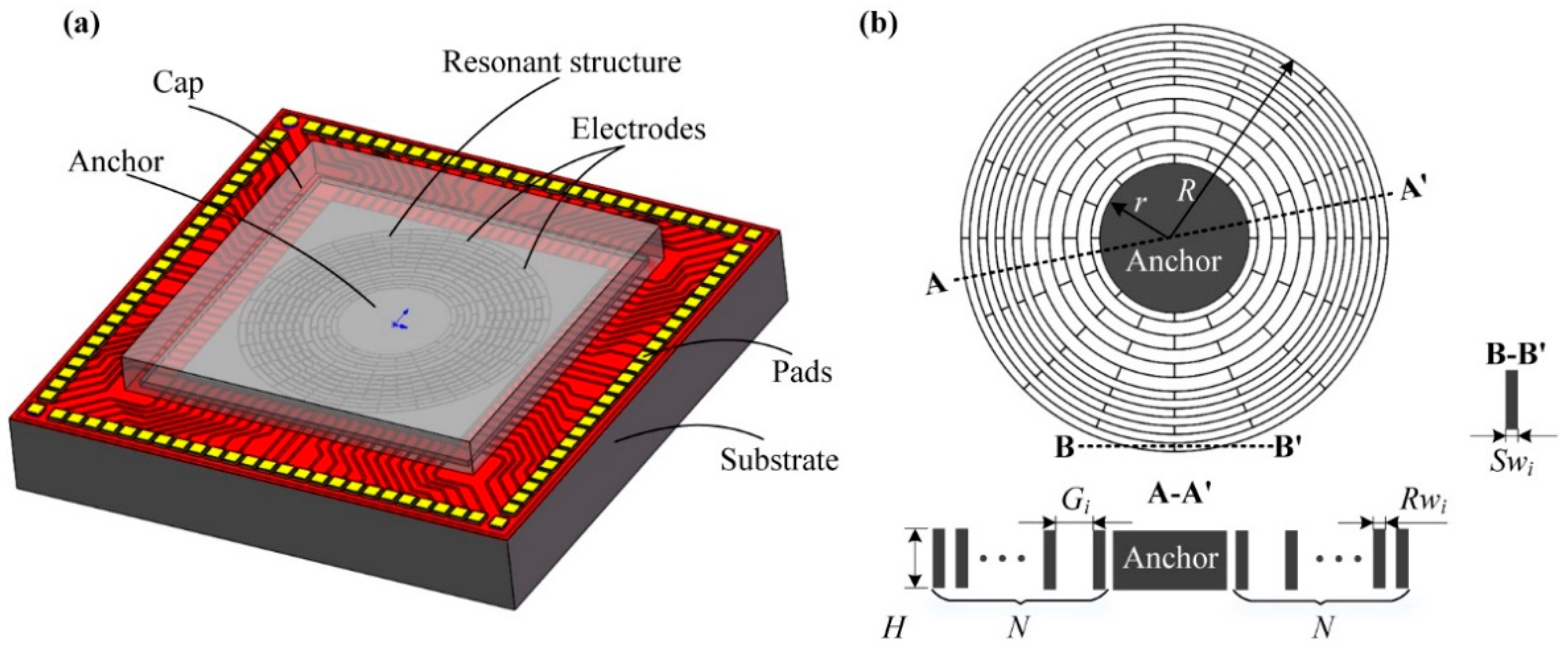


| Structural Parameter | Symbol | Value Range | Unit |
|---|---|---|---|
| Height | H | 100:100:500 | μm |
| Anchor radius | r | 1.5:0.5:5 | mm |
| Ring number | N | 5:1:20 | 1 |
| Ring width | Rw | 3:2:30 | μm |
| Ring gap | G | 100:20:600 | μm |
| Spoke width | Sw | 3:2:30 | μm |
| Core Performance Indicators | Symbol | Unit |
|---|---|---|
| Fundamental frequency | f0 | Hz |
| Quality factor | Q | 1 |
| Mechanical sensitivity | Smech | m/(°/s) |
| Mechanical thermal noise | Ωbrown | ° |
| Input: | ||
| Process: | 1 | Randomly initialize all connection weights and thresholds in the network within the range of (0, 1). |
| 2 | repeat | |
| 3 | for all do | |
| 4 | of the current sample according to the current parameters and Equation (13). | |
| 5 | Calculate the gradient index gj of the neurons in the output layer according to Equation (19). | |
| 6 | Calculate the gradient index eh of the hidden layer neuron according to Equation (24). | |
| 7 | Update the connection weights whj, vih and thresholds θj, γh in the neural network according to Equations (20)–(23). | |
| 8 | end for | |
| 9 | until satisfies the stop condition (the cumulative error is less than 10−3 or the number of iterations exceeds 105). | |
| Output: | Multi-layer perceptron neural network after optimizing connection weights and thresholds. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Lu, K.; Wu, K.; Zhang, H.; Sun, X.; Wu, X.; Xiao, D. A Novel High-Speed and High-Accuracy Mathematical Modeling Method of Complex MEMS Resonator Structures Based on the Multilayer Perceptron Neural Network. Micromachines 2021, 12, 1313. https://doi.org/10.3390/mi12111313
Li Q, Lu K, Wu K, Zhang H, Sun X, Wu X, Xiao D. A Novel High-Speed and High-Accuracy Mathematical Modeling Method of Complex MEMS Resonator Structures Based on the Multilayer Perceptron Neural Network. Micromachines. 2021; 12(11):1313. https://doi.org/10.3390/mi12111313
Chicago/Turabian StyleLi, Qingsong, Kuo Lu, Kai Wu, Hao Zhang, Xiaopeng Sun, Xuezhong Wu, and Dingbang Xiao. 2021. "A Novel High-Speed and High-Accuracy Mathematical Modeling Method of Complex MEMS Resonator Structures Based on the Multilayer Perceptron Neural Network" Micromachines 12, no. 11: 1313. https://doi.org/10.3390/mi12111313
APA StyleLi, Q., Lu, K., Wu, K., Zhang, H., Sun, X., Wu, X., & Xiao, D. (2021). A Novel High-Speed and High-Accuracy Mathematical Modeling Method of Complex MEMS Resonator Structures Based on the Multilayer Perceptron Neural Network. Micromachines, 12(11), 1313. https://doi.org/10.3390/mi12111313






