Peridynamic Simulation to Fracture Mechanism of CBN Grain in the Honing Wheel Dressing Process
Abstract
1. Introduction
2. PD Theory
2.1. Bond-Based PD Theory
2.2. Bond-Based PD Model with Rotation Effect
2.3. Damage Model
2.4. Numerical Discretization
3. Numerical Modeling
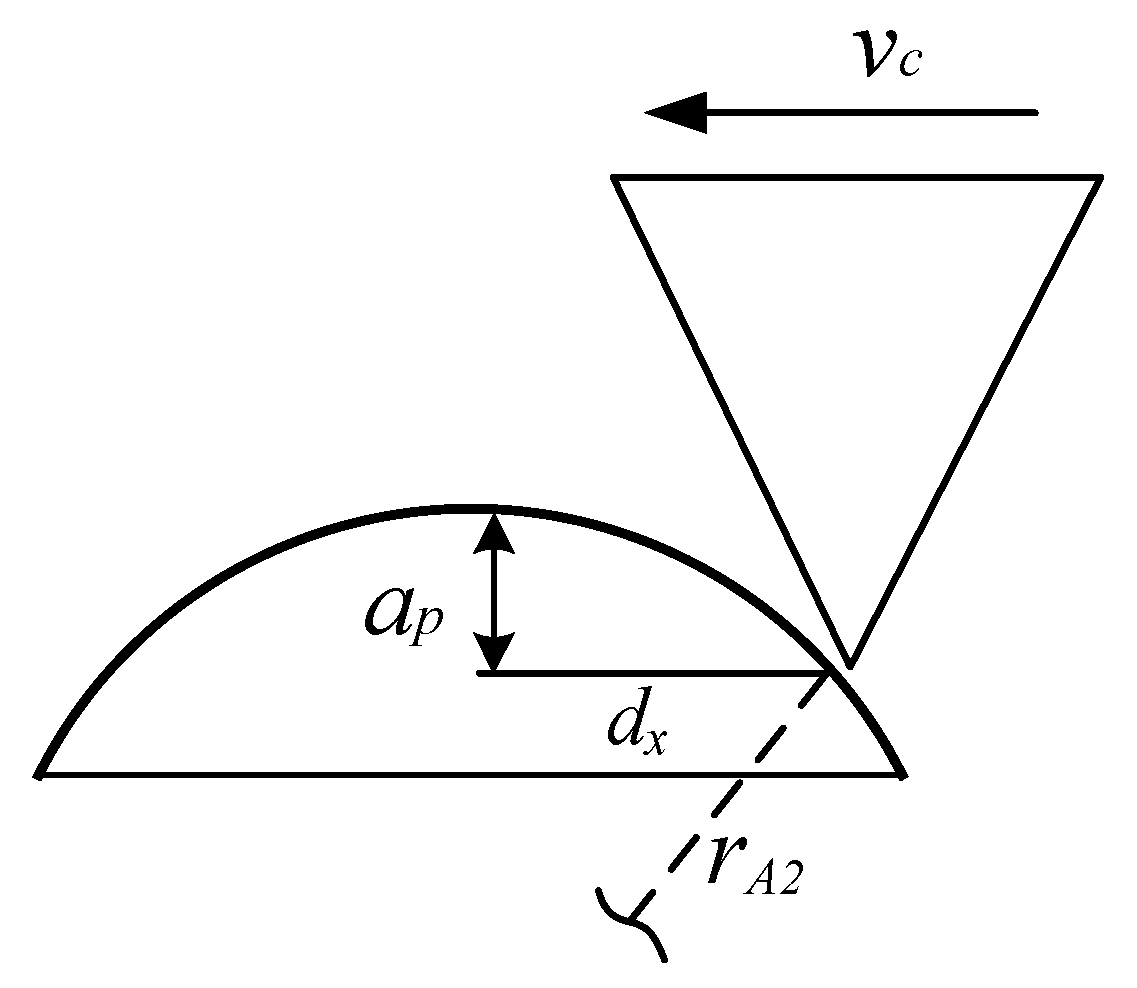
3.1. Simplification of Gear Honing Process
3.2. Simplification of Gear Honing Process
4. Results and Discussion
4.1. Model Validation
4.1.1. Experimental Setup
4.1.2. Comparison of Simulation and Experimental Results
4.2. Fracture Evolution of CBN Grain
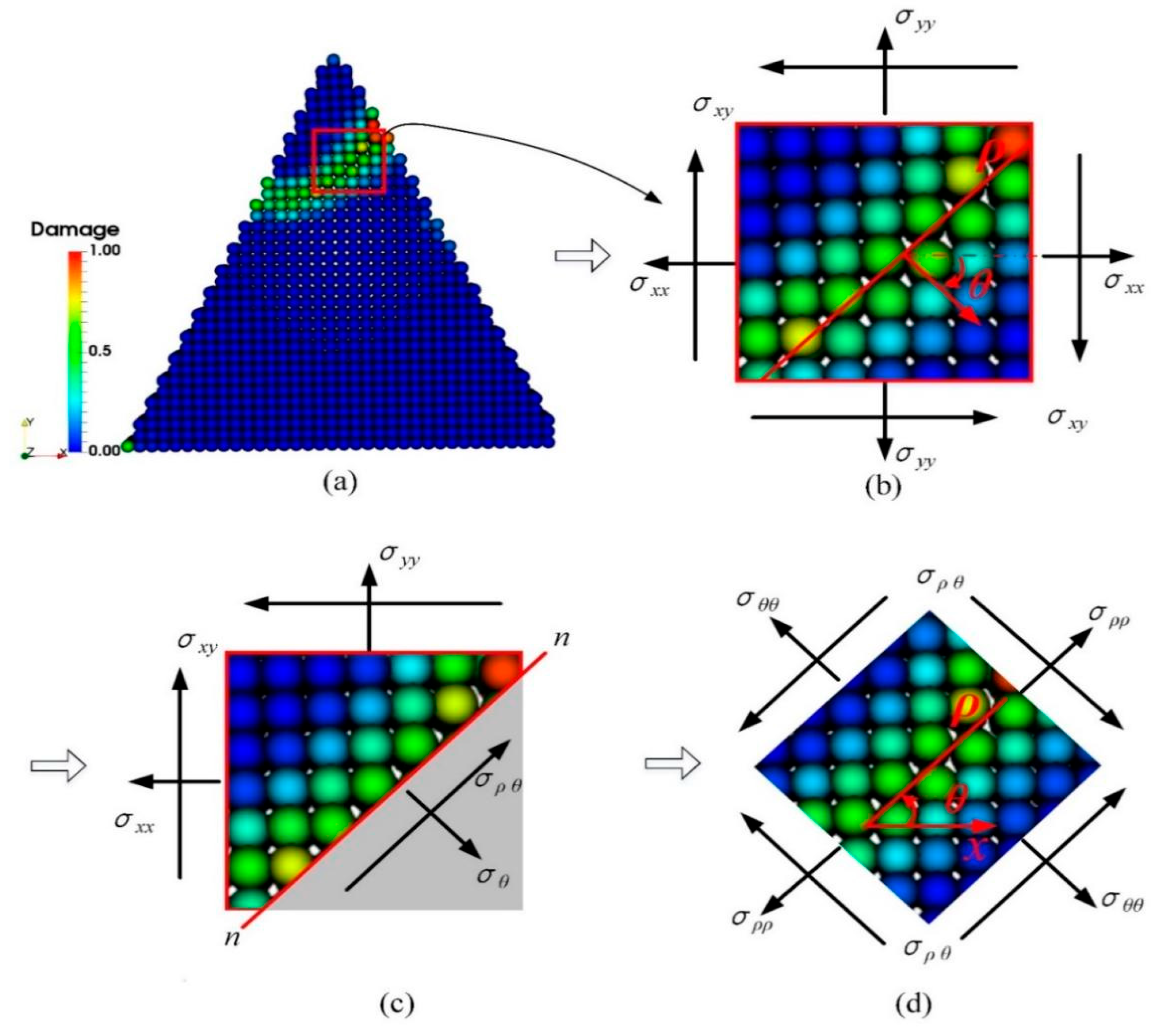
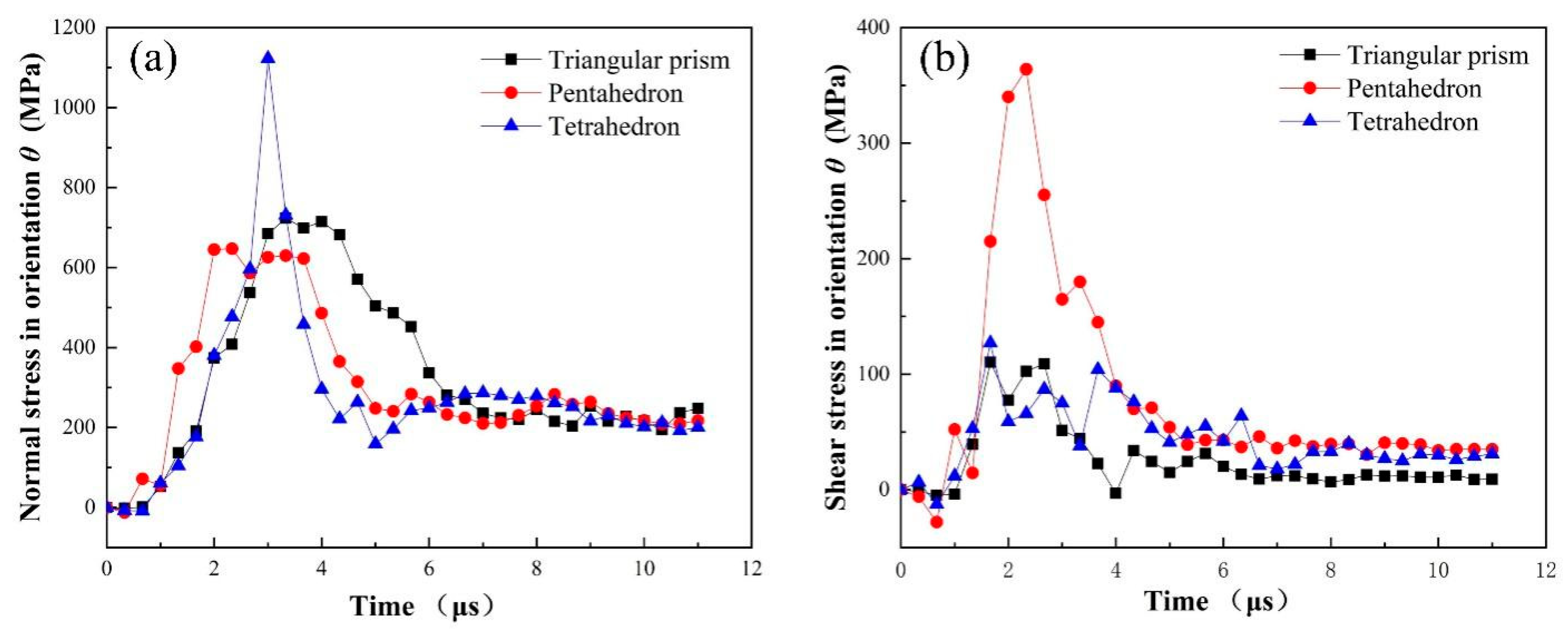
4.3. Stress Analysis of CBN Grain during Fracture Process
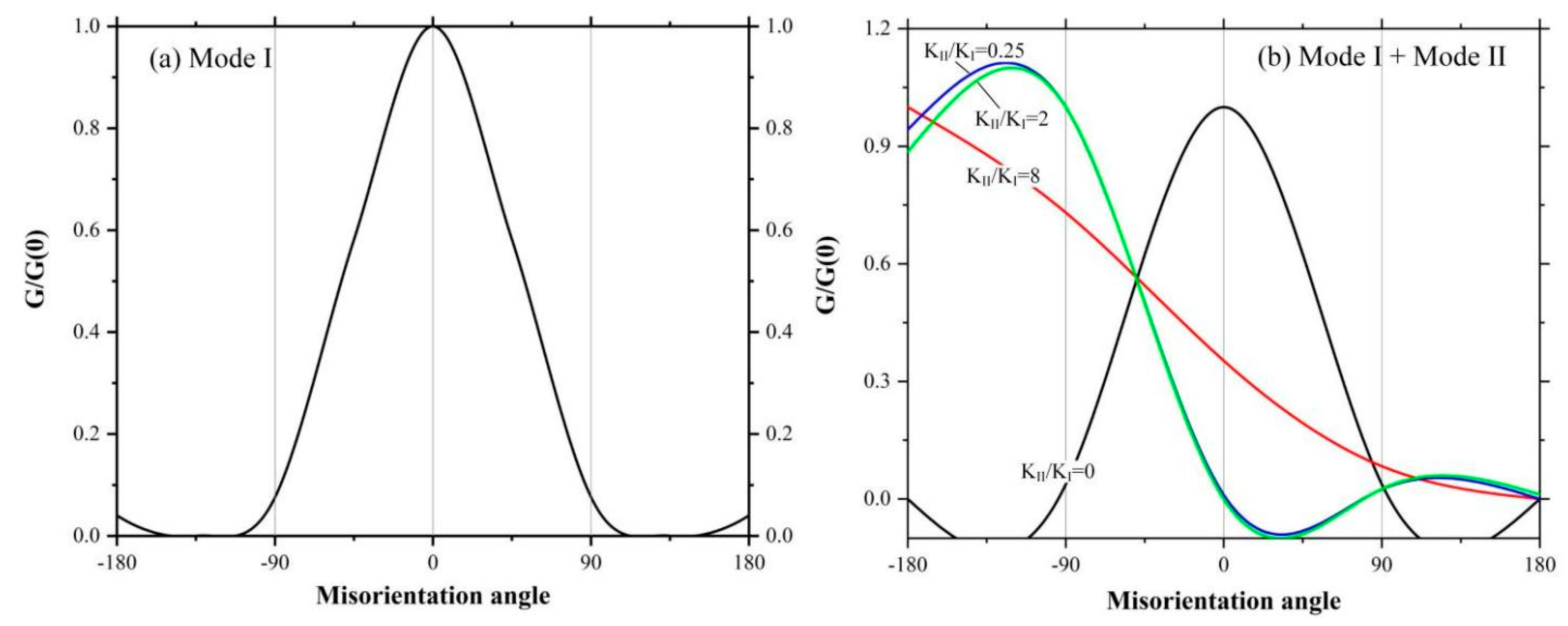
4.4. Fracture Mode Analysis
4.4.1. Modes of Crack Propagation
4.4.2. Instability of Crack Propagation Path
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CBN | cubic boron nitride |
| PD | Peridynamics |
| MD | mechanical dressing |
| EDD | electrical discharge dressing |
| ELID | electrolytic in-process dressing |
| PLD | pulsed laser dressing |
| FEM | the finite element method |
| SPH | smooth particle hydrodynamics |
| PMB | prototype micro elastic brittle |
| , , and | simplify the size of abrasive grain |
| the dressing depth | |
| external body force | |
| the material bond constant | |
| the horizontal distance that the grain moves | |
| the Young’s modulus | |
| the interaction force components between material points within the horizon | |
| PD bond force between material points x and x′ | |
| the critical energy of fracture | |
| the bulk modulus of the material | |
| the stress intensity factor | |
| the transformed stress intensity factor | |
| the stiffness in the tangential direction | |
| the mass | |
| the direction vector of material bond | |
| time step | |
| the analogous radius of dressing gear | |
| the distance between material points within the horizon | |
| the bond stretch ratio | |
| time | |
| the displacement field | |
| the acceleration at point in time step | |
| the volume of the material point at p | |
| the Poisson’s ratio | |
| the dressing speed | |
| , | the α component and β component the velocity of material point i |
| the critical micro-potential energy density | |
| the material micro-potential energy density | |
| mass density | |
| the relative displacement vector between material points | |
| the relative position vector between material points | |
| the grain orientation angle | |
| Ω | the volume of the domain within the PD horizon of material point i |
| , and | the normal stresses in the x, y and z directions |
| , and | the shear stresses |
References
- Klocke, F.; Gorgels, C.; Vasiliou, V. Analysis of the influence of gear dimensions on cutting speed and contact conditions during the gear honing process. Prod. Eng. Res. Dev. 2009, 3, 255–259. [Google Scholar] [CrossRef]
- Deng, H.; Xu, Z. Dressing methods of superabrasive grinding wheels: A review. J. Manuf. Process. 2019, 45, 46–69. [Google Scholar] [CrossRef]
- Klocke, F.; Thiermann, J.; Mattfeld, P. Influence of the dressing process on grinding wheel wear. Prod. Eng. Res. Dev. 2015, 9, 563–568. [Google Scholar] [CrossRef]
- Lv, M.; Zhang, M.D.; Xiong, C.X. The Error Analysis on Tooth Profiles with Electroplated CBN Hard Gear-Honing-Tools. Key Eng. Mat. 2009, 407–408, 73–76. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, X.; Han, J.; Wang, F.; Liang, Y.; Liu, L. Simulation to Microtopography Formation of CBN Active Abrasives on a Honing Wheel Surface. Coatings 2021, 11, 540. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, F.; Liang, Y.; Han, J.; Su, J.; Tong, Y.; Liu, L. Cutting Performance of Randomly Distributed Active Abrasive Grains in Gear Honing Process. Micromachines 2021, 12, 1119. [Google Scholar] [CrossRef] [PubMed]
- Bergs, T. Cutting force model for gear honing. CIRP Ann.-Manuf. Technol. 2018, 67, 53–56. [Google Scholar] [CrossRef]
- Mao, C.; Zhang, Y.; Peng, X.; Zhang, B.; Hu, Y.; Bi, Z. Wear mechanism of single cBN-WC-10Co fiber cutter in machining of Ti-6Al-4V alloy. J. Mater. Process. Technol. 2018, 259, 45–57. [Google Scholar] [CrossRef]
- Liu, W.; Deng, Z.; Shang, Y.; Wan, L. Parametric evaluation and three-dimensional modelling for surface topography of grinding wheel. Int. J. Mech. Sci. 2019, 155, 334–342. [Google Scholar] [CrossRef]
- Liu, W.; Deng, Z.; Shang, Y.; Wan, L. Effects of grinding parameters on surface quality in silicon nitride grinding. Ceram. Int. 2017, 43, 1571–1577. [Google Scholar] [CrossRef]
- Huang, H. Effects of truing/dressing intensity on truing/dressing efficiency and grinding performance of vitrified diamond wheels. J. Mater. Process. Tech. 2001, 117, 9–14. [Google Scholar] [CrossRef]
- Sanchez, J.A.; Pombo, I.; Cabanes, I.; Ortiz, R.; De Lacalle, L.L. Electrical discharge truing of metal-bonded CBN wheels using single-point electrode. Int. J. Mach. Tool Manuf. 2008, 48, 362–370. [Google Scholar] [CrossRef]
- Yu, J.; He, L.; Luo, H.; Yin, S. Experimental investigation on bronze-bonded CBN formed grinding wheel by means of electro-discharging dressing. Adv. Mat. Res. 2016, 1136, 97–103. [Google Scholar] [CrossRef]
- Watanabe, K.; Minami, H.; Masui, K. Electrical discharge truing for electroplated diamond tool-The effect of EDM condition and electrode material. Int. J. Electr. Mach. 2013, 18, 9–15. [Google Scholar] [CrossRef][Green Version]
- Mao, C.; Lu, J.; Zhao, Z.; Yin, L.; Hu, Y.; Bi, Z. Simulation and experiment of cutting characteristics for single cBN-WC-10Co fiber. Precis. Eng. 2018, 52, 170–182. [Google Scholar] [CrossRef]
- Warhanek, M.; Walter, C.; Huber, S.; Haenni, F.; Wegener, K. Cutting characteristics of electroplated diamond tools with laser-generated positive clearance. CIRP Ann. Manuf. Technol. 2015, 64, 317–320. [Google Scholar] [CrossRef]
- Doman, D.A.; Warkentin, A.; Bauer, R. A survey of recent grinding wheel topography models. Int. J. Mach. Tools Manuf. 2006, 46, 343–352. [Google Scholar] [CrossRef]
- Bergs, T.; Ohlert, M.; Prinz, S.; Barth, S. Modeling of the Fracture Behavior of CBN Grains during Single Grain Dressing using FEM. Procedia CIRP 2020, 93, 1514–1519. [Google Scholar] [CrossRef]
- Zhu, Y.; Ding, W.; Rao, Z.; Fu, Y. Effect of grinding wheel speed on self-sharpening ability of PCBN grain during grinding of nickel-based superalloys with a constant undeformed chip thickness. Wear 2019, 426–427, 1573–1583. [Google Scholar] [CrossRef]
- Narulkar, R.; Bukkapatnam, S.; Raff, L.M.; Komanduri, R. Graphitization as a precursor to wear of diamond in machining pure iron: A molecular dynamics investigation. Comp. Mater. Sci. 2009, 45, 358–366. [Google Scholar] [CrossRef]
- Eder, S.J.; Cihak-Bayr, U.; Pauschitz, A. Nanotribological simulations of multi-grit polishing and grinding. Wear 2015, 340–341, 25–30. [Google Scholar] [CrossRef]
- Ganzenmüller, C.; Hiermaier, S.; May, M. On the similarity of meshless discretizations of Peridynamics and Smooth-Particle Hydrodynamics. Comput. Struct. 2015, 150, 71–78. [Google Scholar] [CrossRef]
- Ren, J.; Hao, M.; Lv, M.; Wang, S.; Zhu, B. Molecular dynamics research on ultra-high-speed grinding mechanism of monocrystalline nickel. Appl. Surf. Sci. 2018, 455, 629–634. [Google Scholar] [CrossRef]
- Rashid, W.B.; Goel, S.; Luo, X. The development of a surface defect machining method for hard turning processes. Wear 2013, 302, 1124–1135. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Ha, Y.D.; Lee, J.; Hong, J. Fracturing patterns of rock-like materials in compression captured with peridynamics. Eng. Fract. Mech. 2015, 144, 176–193. [Google Scholar] [CrossRef]
- Bobaru, F.; Zhang, G. Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int. J. Fract. 2015, 196, 59–98. [Google Scholar] [CrossRef]
- Huang, D.; Lu, G.; Wang, C.; Qiao, P. An extended peridynamic approach for deformation and fracture analysis. Eng. Fract. Mech. 2015, 141, 196–211. [Google Scholar] [CrossRef]
- Zhu, Q.; Ni, T. Peridynamic formulations enriched with bond rotation effects. Int. J. Eng. Sci. 2017, 121, 118–129. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Shou, Y.; Kou, M. A novel conjugated bond linear elastic model in bond-based peridynamics for fracture problems under dynamic loads. Eng. Fract. Mech. 2018, 188, 151–183. [Google Scholar] [CrossRef]
- Ding, W.; Linke, B.; Zhu, Y.; Li, Z.; Fu, Y.; Su, H.; Xu, J. Review on monolayer CBN super abrasive wheels for grinding metallic materials. Chin. J. Aeronaut. 2017, 30, 109–134. [Google Scholar] [CrossRef]
- Parks, M.L.; Lehoucq, R.B.; Plimpton, S.J.; Silling, S.A. Implementing peridynamics within a molecular dynamics code. Comput. Phys. Commun. 2008, 179, 777–783. [Google Scholar] [CrossRef]
- Lawn, B. Fracture of Brittle Solids; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Hadavi, V.; Moreno, C.E.; Papini, M. Numerical and experimental analysis of particle fracture during solid particle erosion, part I: Modeling and experimental verifification. Wear 2016, 356–357, 135–145. [Google Scholar] [CrossRef]
- Rinaldi, A.; Mastilovic, S. The Krajcinovic approach to model size dependent fracture in quasi-brittle solids. Mech. Mater. 2014, 71, 21–33. [Google Scholar] [CrossRef]
- Dai, H.; Chen, G.; Zhou, C.; Fang, Q.; Fei, X. A numerical study of ultraprecision machining of monocrystalline silicon with laser nano-structured diamond tools by atomistic simulation. Appl. Surf. Sci. 2017, 393, 405–416. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Fang, F. Molecular dynamics study on nanometric cutting of ion implanted silicon. Comput. Mater. Sci. 2016, 117, 240–250. [Google Scholar] [CrossRef]
- Li, J.; Xie, Y.J.; Zheng, X.Y.; Cai, Y.M. Underlying fracture trends and triggering on Mode-II crack branching and kinking for quasi-brittle solids. Eng. Fract. Mech. 2019, 211, 382–400. [Google Scholar] [CrossRef]
- Ding, W.; Zhu, Y.; Zhang, L.; Xu, J.; Fu, Y.; Liu, W.; Yang, C. Stress charaterristics and fracture wear of brazed CBN grains in monolayer grinding wheels. Wear 2015, 332–333, 800–809. [Google Scholar] [CrossRef]
- Rao, Q.; Sun, Z.; Stephansson, O.; Li, C.; Stillborg, B. Shear fracture (Mode II) of brittle rock. Int. J. Rock Mech. Min. Sci. 2003, 40, 355–375. [Google Scholar] [CrossRef]

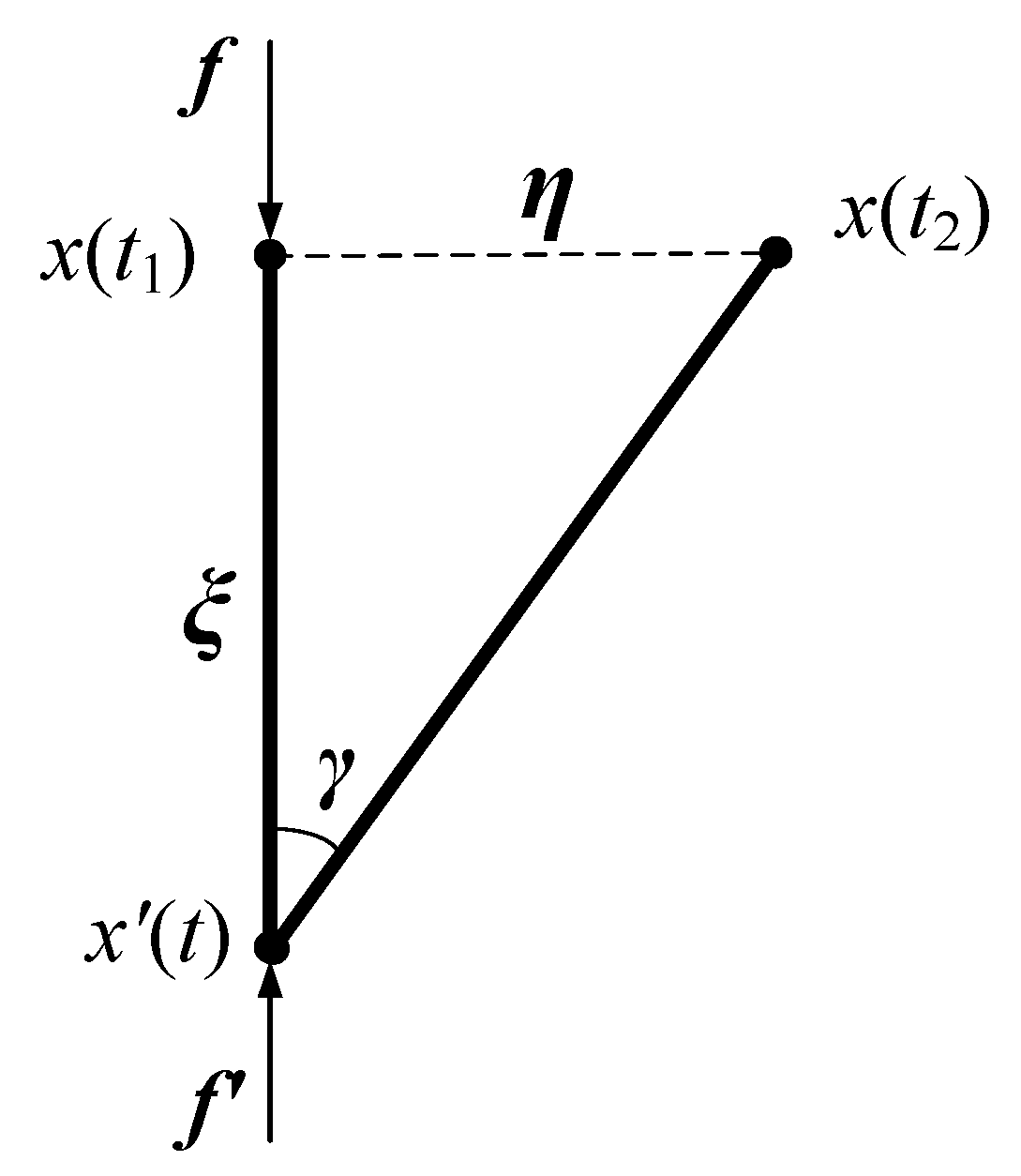







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Chen, Y.; Gao, Y.; Liang, Y.; Su, J.; Liu, L. Peridynamic Simulation to Fracture Mechanism of CBN Grain in the Honing Wheel Dressing Process. Micromachines 2021, 12, 1186. https://doi.org/10.3390/mi12101186
Wang F, Chen Y, Gao Y, Liang Y, Su J, Liu L. Peridynamic Simulation to Fracture Mechanism of CBN Grain in the Honing Wheel Dressing Process. Micromachines. 2021; 12(10):1186. https://doi.org/10.3390/mi12101186
Chicago/Turabian StyleWang, Fuwei, Yuanlong Chen, Yang Gao, Yuan Liang, Jie Su, and Lin Liu. 2021. "Peridynamic Simulation to Fracture Mechanism of CBN Grain in the Honing Wheel Dressing Process" Micromachines 12, no. 10: 1186. https://doi.org/10.3390/mi12101186
APA StyleWang, F., Chen, Y., Gao, Y., Liang, Y., Su, J., & Liu, L. (2021). Peridynamic Simulation to Fracture Mechanism of CBN Grain in the Honing Wheel Dressing Process. Micromachines, 12(10), 1186. https://doi.org/10.3390/mi12101186






